OFDM星座旋转调制自适应交织器设计

引用本文

周世东, 俞抒鹏, 肖立民, 钟晓峰. OFDM星座旋转调制自适应交织器设计. 清华大学学报: 自然科学版, 2014, 54(4): 458-463[Shidong ZHOU, Shupeng YU, Limin XIAO, et al. Adaptive interleaver design for rotated-modulation OFDM systems[J]. 2014, 54(4): 458-463] 复制到剪切板

Permissions

OFDM星座旋转调制自适应交织器设计

周世东, 俞抒鹏, 肖立民, 钟晓峰

清华大学电子工程系, 北京 100084

作者简介: 周世东(1969-), 男(汉), 江苏, 教授。E-mail:zhousd@tsinghua.edu.cn

基金:国家“九七三”重点基础研究发展计划(2012CB316000); 国家“八六三”高技术项目(2012AA01A502); 国家科技重大专项(20122X03001017-002);

摘要

为了改善正交频分复用(orthogonal frequency division multiplexing, OFDM)在稀疏多径信道环境中的抗衰落能力,提出一种基于星座旋转调制OFDM系统的自适应交织方法。利用OFDM系统的多载波特点将旋转调制中的分量交织引入到子载波间交织,根据统计信道状态信息或实时信道状态信息,采用该文设计的交织器搜索准则来选取最佳分量交织图案,接收端将最佳的分量交织图案的索引反馈给发送端,实现了自适应交织。仿真结果表明该方法在稀疏多径衰落信道下有优异的抗衰落性能和较高的频谱利用率。

关键词: 正交频分复用(OFDM); 旋转调制; 信号空间分集; 自适应交织; 衰落信道

中图分类号:TN929.5 文献标志码:A 文章编号:1000-0054(2014)04-0458-06

Adaptive interleaver design for rotated-modulation OFDM systems

Shidong ZHOU, Shupeng YU, Limin XIAO, Xiaofeng ZHONG

Department of Electronic Engineering, Tsinghua University, Beijing 100084, China

Fund:

Abstract

An adaptive interleaving method was designed for rotated-modulation (orthogonal frequency division multiplexing, OFDM) systems to improve the anti-fading in OFDM systems in sparse multipath channels. The multiple carriers in OFDM are used to add component interleaving into the sub-carrier interleaving using statistical or real channel state information. The interleaver search criterion was designed to select the best component interleaving map. The receiver uses the criterion to search for the best component interleaving and then feeds the map index back to the sending end for adaptive interleaving. Simulations show that this method has excellent anti-fading performance and is bandwidth-efficient in sparse multipath fading channels.

Keyword: orthogonal frequency division multiplexing (OFDM); rotated-modulation; signal space diversity; adaptive interleaving; fading channel

Show Figures

目前宽带传输在面临大时延扩展信道时需要正交频分复用(OFDM)技术,多径效应会造成频率选择性衰落使OFDM系统的个别子载波会处于信道深衰落中,因此需要分集技术来对抗信道的衰落^[1]。分集又可分为有编码和无编码的分集,有编码的分集需要增加冗余,因此会降低频谱利用率。文[2]最先提出了一种信号空间分集 (signal space diversity, SSD) 技术,是一种高频谱利用率的无编码分集技术。星座旋转调制属于信号空间分集的一种,通过对星座图旋转增加分集度。它不同于时间分集、频率分集和空间分集技术,其分集增益来至于系统的调制部分,不会增加时间、频率和功率资源的开销。在二维星座旋转中,旋转调制分集利用对发送符号的IQ分量随机交织的方式打破信道IQ的相关性来获得分集增益。OFDM系统与星座旋转调制相结合可以通过将旋转调制中的分量交织引入到子载波的交织中,将处于衰落中的子载波上的符号分量经过交织来获得频率分集增益。采用星座旋转调制配合分量交织是一种有效的分集手段,特别是在信号较强的多径数量很多的情况下采用高维星座旋转可以充分获得分集增益^[3]。但是,高维星座旋转的解调需要付出巨大的计算量^[2,4,5]。在实际信道环境(如广播、单频网等)中会遇到工作频率比较高、信号较强的多径数非常有限。此时,尽管多径数量不多,甚至各径本身也没有衰落,但由于多径信号强度相当,时延差异较大,造成不同子载波所经受的衰落起伏仍然很大。因此,可以通过频域分集来对抗个别子载波上的衰落对通信造成的影响。在这种情况下多径数量较少,采用高维星座旋转并不能获得更多的分集增益,并且带来较大的解调计算量。为此本文以二维星座旋转为例开展深入研究。文[6-7]介绍了将旋转调制应用于OFDM的方法,采用固定的分量交织方式即可在随机信道中获得较好的分集效果。然而,本文研究发现,当信号较强的多径数较少时,处于深衰落的子载波图案具有一定的规律性,固定交织图案有可能不足以把深衰落图案随机化。为此提出了一种根据信道先验信息的自适应交织图案选择策略和选择算法,包括基于实时信道信息和统计信道信息2类。实验发现, OFDM星座旋转调制系统采用自适应交织方式能在不增加旋转调制的旋转维度下增大分集增益。

1 旋转调制原理

标准的四相相移键控(QPSK)星座见图1, 星座点在I和Q上的投影有重合,无法仅从I或Q的分量值来区分星座符号,将标准的QPSK星座进行简单的旋转,各个星座点之间的Euclid距离没有改变但是每个星座点在I和Q上的投影不再互相重叠,可以仅从I路分量或者Q路分量就能够区分发送的星座符号。当信道的I和Q路分量衰落独立时,采用旋转调制就能获得二阶的分集增益。

	Figure Option View Download New Window Download As Powerpoint Slide
	图1 QPSK星座和旋转QPSK星座图

使用星座旋转调制技术时,需要对旋转后的符号进行IQ分量独立交织,使得符号的I和Q路分量经历独立的衰落。实际在对I和Q路分量分别进行独立交织始终都能转化为只将其中一个分量进行交织。星座旋转调制的架构见图2,信息经过星座映射后成为标准星座符号 u, x是经过星座旋转后的符号, α是信道衰落系数, N₀是噪声, y是接收端接收到的符号, r是经过IQ解交织后的符号, $\begin{matrix} \hat{u} \end{matrix}$ 是经过最大似然检测后对发送符号 u的估计。

	Figure Option View Download New Window Download As Powerpoint Slide
	图2 星座旋转调制架构

在相干检测条件下,接收端的离散时间复基带信号 r的向量表述可以写成^[4]:

$\begin{matrix} r = α☉x + n. (1) \end{matrix}$

其中 n=[ n₁, n₂,…, n_n]是噪声向量, n_i是均值为0、方差为 N₀的Gauss分布随机变量。 α=[ α₁, α₂,…, α_n], α_i满足Rayleigh分布,并且其二阶距 E[ $\begin{matrix} α_{i}^{2} \end{matrix}$ ] =1,☉代表分量形式的乘积,发送的星座符号 x=[ x₁, x₂,…, x_n], S是发送星座符号集合 x_i∈ S。在解分量交织后,接收端在有信道边信息(channel side information, CSI)时的最大似然检测可以表示为

$\begin{matrix} \min (x | r, α) = \overset{n}{\sum_{i = 1}} \underset{x_{i} \in S}{argmin} ({|r_{i} - α_{i} x_{i}|}^{2}) . (2) \end{matrix}$

根据文[4] 给出的二维旋转形式,采用QPSK调制二维星座旋转矩阵表达式为

$\begin{matrix} M = [\begin{matrix} cosθ & sinθ \\ - sinθ & cosθ \end{matrix}] . (3) \end{matrix}$

其中 θ是星座旋转的角度,在未编码情况下最佳旋转角度的选取原则是最大化最小分量距离的乘积 $\begin{matrix} {d_{p, \min}^{(L)}}^{} \end{matrix}$ ^[8],

$\begin{matrix} d_{p, \min}^{(L)} = \overset{(L)}{\prod_{x_{i} \neq y_{i}}} | x_{i} - y_{i} | . (4) \end{matrix}$

其中 |x_i-y_i|为任意两个星座点在 L维星座中第 i维分量上的距离。文[9-10]分析了二维星座旋转调制在Rayleigh和Rice信道下的性能。

2 OFDM星座旋转调制自适应交织

2.1 自适应交织器的优势

OFDM结合旋转调制利用频域上的IQ分量交织实现频率分集。分量交织使符号的I和Q分量经历独立的衰落,从而获得分集增益。实际情况中每个子载波的信道状态并不是充分独立的,并且信道状态是随着通信环境的改变而改变,固定的分量交织方式在一些信道条件下不能充分获得分集。以简单的两径信道为例,从图3可以看出,随着多径时延的增加,信道在频域上的起伏周期变小。采用文[7]固定的循环移位子载波的交织方式(见图4), 其中有 n个子载波 f₁, f₂,…, f_n,如果固定的循环移位的长度正好等于信道上的起伏周期会导致分量交织不能有效错开处于深衰落的子载波,导致旋转调制的分集性能大大降低。而采用多种交织图案的方式,发送时选择一种有效的错开深衰落的子载波的分量交织方式能够提高旋转调制的分集性能。

	Figure Option View Download New Window Download As Powerpoint Slide
	图3 两径信道频率响应

	Figure Option View Download New Window Download As Powerpoint Slide
	图4 循环位移子载波交织

2.2 OFDM星座旋转调制自适应交织系统模型

本文提出了自适应分量交织应用于OFDM旋转调制的方法,接收端根据当前每个子载波的信道状态通过交织器收索准则选择一种较优的分量交织方式,并将交织方式反馈给发送端,更新的交织方式能让较差的子载波上发送的符号分量交织到较好的子载波上发送,从而使得每个符号的其中某一个分量在信噪比较优的子载波上发送的概率增大。OFDM星座旋转调制自适应交织的通信系统模型如图5所示。

	Figure Option View Download New Window Download As Powerpoint Slide
	图5 OFDM星座旋转调制自适应交织系统架构

3 自适应交织器搜索准则

3.1 基于实时信道信息

从误符号率的角度来讨论选择交织方式的准则问题。 M-QAM在AWGN信道下的符号差错概率见式(5), 其中 M=4,16,64,256,…。在I和Q上是 $\begin{matrix} \sqrt[]{M} \end{matrix}$ 点的脉冲幅度调制(PAM), 取值为±1,±3,…,±( $\begin{matrix} \sqrt[]{M} \end{matrix}$ -1)。在AWGN信道下,噪声服从 N~ $\begin{matrix} (0, \frac{N_{0}}{2}) \end{matrix}$ ,其中 Q(·)是 Q函数, N₀是噪声功率^[11]。

$\begin{matrix} P_{e, M - QAM} \leq \frac{4 (\sqrt[]{M} - 1)}{\sqrt[]{M}} Q (\frac{d_{\min}}{\sqrt[]{2 N_{0}}}) . (5) \end{matrix}$

对于有频率选择性衰落的信道采用OFDM调制方式后,每个子载波上的符号等效经过一个平衰落信道, H=[ h₁, h₂,… h_n]中的 h_i是每个子载波上的信道状态信息,定义 α_i= $\begin{matrix} |h_{i}| \end{matrix}$ 。由于符号经过衰落等效星座点之间的距离减小,在衰落信道下 M-QAM的符号错误概率近似为

$\begin{matrix} P_{e, fading, M - QAM} = \frac{4 (\sqrt[]{M} - 1)}{\sqrt[]{M}} Q (\frac{α d_{\min}}{\sqrt[]{2 N_{0}}}) . (6) \end{matrix}$

设子载波数为 N_S,当调制阶数选定时,可以令常数 C= $\begin{matrix} \frac{4 (\sqrt[]{M} - 1)}{\sqrt[]{M}} \end{matrix}$ ,归一化符号平均功率时,星座点最小距离 d_min可以写成

$\begin{matrix} d_{\min} = \sqrt[]{\frac{6}{M - 1}} . (7) \end{matrix}$

对于OFDM系统,总的符号差错概率为

$\begin{matrix} \begin{matrix} P_{e, OFDM} = \frac{1}{N_{S}} \overset{N_{S}}{\sum_{m = 1}} P_{e, fading, M - QAM, m} = \\ \frac{C}{N_{S}} \overset{N_{S}}{\sum_{m = 1}} Q (\frac{α_{m} d_{\min}}{\sqrt[]{2 N_{0}}}) . (8) \end{matrix} \end{matrix}$

星座旋转的最佳角度是最大化最小分量乘积距离,也就是最大化每个分量上相邻星座点的距离,因此星座旋转角度为 θ=argtan $\begin{matrix} {(\frac{1}{2^{q}})}^{} \end{matrix}$ ^[7], q=lb $\begin{matrix} \sqrt[]{M} \end{matrix}$ 。这里设最小分量距离为 d_c,min,由于星座旋转并不改变相邻星座点的最小距离 d_min,分量最小距离和星座点最小距离关系为

$\begin{matrix} d_{\min} = \sqrt[]{1 + D^{2}} d_{c, \min} . (9) \end{matrix}$

其中 D与调制方式有关: 采用QPSK、 16QAM、 64QAM、 256QAM调制时 D分别为2、 4、 8和16。将式(7)代入式(9)求得最小分量距离的表达式为

$\begin{matrix} d_{c, \min} = \frac{d_{\min}}{\sqrt[]{1 + D^{2}}} = \sqrt[]{\frac{6}{(1 + D^{2}) (M - 1)}} . (10) \end{matrix}$

星座旋转调制在衰落信道下的最小距离为是被压缩后相邻星座点之间距离最小的2个星座点的距离。式(11)中 α_I和 α_Q分别是I和Q分量上的衰落系数。

$\begin{matrix} d_{\min} = \min (\sqrt[]{α_{I}^{2} + (D α_{Q})^{2}} d_{c, \min}, \sqrt[]{(D α_{I})^{2} + α_{Q}^{2}} d_{c, \min}) . (11) \end{matrix}$

OFDM旋转调制系统的符号差错概率可以通过将式(11)代入式(8)得到:

$\begin{matrix} P_{e, OFDM - Rotated} = \frac{C}{N_{S}} \overset{N_{S}}{\sum_{m = 1}} Q (\frac{\sqrt[]{α_{I, m}^{2} + α_{Q, m}^{2}} β d_{c, \min}}{\sqrt[]{2 N_{0}}}) . (12) \end{matrix}$

其中 β=min $\begin{matrix} (\sqrt[]{α_{I, m}^{2} + {(D α_{Q, m})}^{2}}, \sqrt[]{{(D α_{I, m})}^{2} + α_{Q, m}^{2}}) \end{matrix}$ , α_I, _m= $\begin{matrix} \frac{1}{\sqrt[]{2}} \end{matrix} \begin{matrix} |h_{m}| \end{matrix}$ , α_Q, _m= $\begin{matrix} \frac{1}{\sqrt[]{2}} \end{matrix} \begin{matrix} |h_{m}^{'}| \end{matrix}$ 。将式(10)以及 α_I和 α_Q代入式(12)得到

$\begin{matrix} P_{e, OFDM - Rotated} = \frac{C}{N_{S}} \overset{N_{S}}{\sum_{m = 1}} Q (\frac{\sqrt[]{| h_{m} |^{2} + | h_{m}^{'} |^{2}} η \sqrt[]{3}}{2 \sqrt[]{(M^{2} - 1) N_{0}}}) . (13) \end{matrix}$

其中 η=min( $\begin{matrix} \sqrt[]{| h_{m} |^{2} + M | h_{m}^{'} |^{2}} \end{matrix}$ , $\begin{matrix} \sqrt[]{M | h_{m} |^{2} + | h_{m}^{'} |^{2}} \end{matrix}$ ), M与调制方式有关: 采用QPSK、 16QAM、 64QAM、 256QAM调制时 M分别为4、 16、 64和256。

为了获得最小的符号差错概率,通过选取合适的| $\begin{matrix} h_{m}^{'} \end{matrix}$ |来最小化式(13), 由此得到自适应分量交织器最优搜索准则,就是遍历所有的交织图案使得式(13)的结果最小。其结果等价为

$\begin{matrix} \underset{g_{i} \in G}{argmin} (\overset{N_{S}}{\sum_{m = 1}} Q (\frac{\sqrt[]{{|h_{m}|}^{2} + {|h_{m}^{'}|}^{2}} η \sqrt[]{3}}{2 \sqrt[]{(M^{2} - 1) N_{0}}})) . (14) \end{matrix}$

其中 G是交织图案集,这里并不限定交织图案以及图案集合中的交织图案个数, g_i是交织图案集中的某一个交织图案, h_m和 $\begin{matrix} h_{m}^{'} \end{matrix}$ 分别是第 m个子载波上交织前和采用 g_i交织图案交织后的衰落系数。从交织图案搜索准则中可以看出,搜索准则主要是根据子载波上的信道状态的情况在交织图案集中选取出适应当信道条件的最佳交织图案。

3.2 基于统计信道信息

由于自适应分量交织需要反馈交织图案,会带来一定的时延,在快衰落信道下发送时的最优交织图案很可能就不再是最优的,需要对搜索准则进行改进。在通常的无线环境中,用户在一段时间内移动造成的多径时延的变化相对于每一径的功率变化是相对缓慢的,因此多径的时延变化较小,而多径的功率变化较快。针对这一特点采用统计一段时间内的信道信息来选取最佳的交织方式,能使发送端发送时选取的交织方式在一段时间内是平均最优的。

$\begin{matrix} \underset{g_{i} \in G}{argmin} (\overset{Z}{\sum_{z = 1}} (\overset{N_{S}}{\sum_{m = 1}} Q (\frac{\sqrt[]{{|h_{z, m}|}^{2} + {|h_{z, m}^{'}|}^{2}} η \sqrt[]{3}}{2 \sqrt[]{(M^{2} - 1) N_{0}}}))) . \end{matrix}$ (15)

其中 Z是统计的OFDM符号的个数。

3.3 自适应交织图案搜索实现方法

自适应分量交织的实施步骤为:

1) 接收端通过信道估计得到信道状态信息| h_m|。

2) 而后根据交织图案集中的交织方式将子载波上的信道状态信息进行交织得到| $\begin{matrix} h_{m}^{'} \end{matrix}$ |。

3) 根据最优分量交织器的搜索准则将| h_m|和 | $\begin{matrix} h_{m}^{'} \end{matrix}$ |代入准则式(14)中,遍历所有的交织图案并记录每个交织图案对应的差错概率。

4) 慢衰落信道时只需搜索一个OFDM符号的差错概率最小的交织图案,并将此交织图案作为下一次发送端采取的分量交织方式。快衰落信道时采用统计在一段时间内的多个OFDM符号,计算在一段时间内使总的差错概率最小的交织图案,并将此交织图案作为下一次发送端采取的分量交织方式。

5) 接收端将交织图案的索引发送给发送端。

3.4 自适应交织计算量分析与压缩

实际搜索准则可对每个子载波的信道状态信息进行计算,也可等间隔的选取子载波来计算以降低运算量。根据单个OFDM的交织图案搜索准则进行复杂度分析,设交织图案集合中的交织图案数为 T, 子载波数为 N_S, 评估间隔为 k(表示只使用序号为 k的整数倍的子载波上的信道状态信息)。将式(14)改写为

$\begin{matrix} \underset{g_{i} \in G}{argmin} (\overset{[N_{S} / k]}{\sum_{m = 1}} Q (\sqrt[]{| h_{mk} |^{2} + | h_{mk}^{'} |^{2}} ημ)) . \end{matrix}$ (16)

其中: ,实际上等价比较 |h_mk|²与的大小。 Q函数及常数 μ和开根号可以结合在一起用查表法实现。 |h_mk|²与多次用到,可以计算一次然后保存结果。最后的计算复杂度如表1所示

表1 基于实时信道信息的交织器搜索复杂度

Q函数(查表)	乘法	加 /减法	比较	反馈量
T $\begin{matrix} \frac{N_{S}}{k} \end{matrix}$	3 T $\begin{matrix} \frac{N_{S}}{k} \end{matrix}$	T $\begin{matrix} (3 \frac{N_{S}}{k} + 1) \end{matrix}$	T $\begin{matrix} \frac{N_{S}}{k} \end{matrix}$	[lb T]

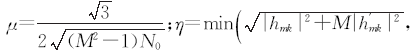
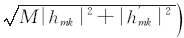
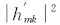
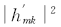
表1 基于实时信道信息的交织器搜索复杂度

采用统计信道信息的搜索准则,统计 Z个OFDM符号的最优搜索准则在搜索首个符号的最优交织图案时需要对 Z个符号的差错概率求和,而在对连续的最优交织搜索准则时,可以将先前已求和好的结果加上更新的符号的差错概率并减去最先前的符号差错概率,因此在连时间续搜索时的计算复杂度并没有比单个符号搜索的复杂度增大很多,其复杂度如表2所示。

表2 基于统计信道信息的交织器搜索复杂度

Q函数(查表)	乘法	加法	比较	反馈量
T $\begin{matrix} \frac{N_{S}}{k} \end{matrix}$	3 T $\begin{matrix} \frac{N_{S}}{k} \end{matrix}$	T $\begin{matrix} (3 \frac{N_{S}}{k} - 1) \end{matrix}$	T $\begin{matrix} \frac{N_{S}}{k} \end{matrix}$	[lb T]

表2 基于统计信道信息的交织器搜索复杂度

4 仿真结果与分析

对采用本文的自适应分量交织和文[7]的固定分量交织的OFDM旋转调制系统的性能进行比较。仿真参数如下: 天线数为1发1收; 子载波个数为2 048, 有效子载波数为1 200; 信号带宽为20 MHz; 调制方式为QPSK或16QAM; 编码方式为未编码; 衰落信道为COST 207典型城区(TU)信道模型^[12],最大Doppler频偏为20 Hz; 信道状态信息理想; 交织图案集为采用可变长度的循环移位子载波交织方式,其变长范围1<shift_len≤1 200,shift_len为整数。仿真以可变长度的循环移位子载波的交织方式为例,实际在自适应交织中并不限定交织图案,可以采用任意的交织图案。

慢变衰落信道的多径数目为6径,多径延时在0~5 μs上满足均匀分布随机生成,在给定一组随机时延后,每一径的功率都按照Rayleigh分布随机产生,在此信道条件上传输10个OFDM符号,自适应交织搜索准则的评估间隔分别为 k=1、 k=10和 k=20。误比特率(BER)的仿真结果如图6和7所示。

	Figure Option View Download New Window Download As Powerpoint Slide
	图6 慢变COST207信道QPSK-SSD的性能

	Figure Option View Download New Window Download As Powerpoint Slide
	图7 慢变COST207信道16QAM-SSD的性能

在慢变衰落信道中由于信道的状态变化缓慢,信道信息可以使用前一次接收到的信号估计出的信道状态信息来选取下一次发送时选取的交织方式。采用自适应交织大大提高了在衰落信道下的分集性能,随着 k的降低,分集性能提高,当 k=10时的性能与性能最佳的 k=1基本接近,实际情况下可以通过增大 k来降低自适应交织的复杂度。

在通常的无线环境中由于用户的移和天线位置的变化,多径功率的强度会急剧变化。在快衰落信道中自适应交织如果采用前一次接收估计的信道状态信息来搜索下一次发送的交织方式,就很可能因为信道状态的变化而不适用。因此在快衰落信道中采用统计一段时间内的信道信息来搜索最佳的交织方式。仿真环境: 其中快衰落信道多径延时随机生,成,在0~5 μs上满足均匀分布,在给定一组随机时延后,在传送每一个OFDM符号时每一径的功率都按照瑞利分布重新随机生成来实现信道的快变。在时延固定信道条件上传输10个OFDM符号,然后重新选取一组新的随机时延。自适应交织是在给定一组随机时延的基础上,接收端通过统计传输70个OFDM符号得出交织图案后再进行10个OFDM符号传输。实验仿真了在快衰落信道下多径数目分别为4和6时,系统分别采用自适应分量交织和固定的分量交织的误比特率,其中自适应交织搜索准则的 k=1。

图8比较了OFDM旋转调制系统在调制方式是QPSK时,采用自适应分量交织和固定分量交织在不同信道条件下的性能。BER=10^-3时,在4和6径的衰落信道中,自适应分量交织比固定分量交织方式分别有接近4和2 dB的分集增益。图9是调制方式为16QAM时采用自适应分量交织和固定分量交织在不同信道条件下的性能对比。

	Figure Option View Download New Window Download As Powerpoint Slide
	图8 快变COST207信道不同多径数时QPSK-SSD的性能

	Figure Option View Download New Window Download As Powerpoint Slide
	图9 快变COST207信道不同多径数时16QAM-SSD的性能

由图8和9可以看出,自适应分量交织的性能随着多径数目的增加而下降。这是因为当多径数目较少时,信道特性相对简单,信道的频域特性有明显的特征,随着多径数目的增加,信道的频域特征变得随机,子载波上的衰落变得更加独立,使得自适应交织的性能逐渐接近固定交织的性能。在实际无线通信环境,无线系统采用低的载波频率或周围环境较复杂的情况时多径数目增大,而采用较高的载波频率或周围环境较简单时多径数目会减小。在无线通信系统设计时可以根据实际的信道情况来选择是否采用自适应交织方案。对于多样性环境时如用户在室内时的多径时延较短,在户外时多径时延较长,在市区时多径数目较多,在郊区时多径数目较少,采用自适应分量交织能够对不同的信道环境有更强的鲁棒性,能让系统的性能维持在一个较好的水平上,因此OFDM旋转调制的自适应交织对于实际的通信系统有很好的应用价值。

5 结论

本文研究了分量交织器对旋转调制性能的影响,将分量交织引入到OFDM系统的子载波交织上,提出了一种稀疏多径信道环境中能通过信道状态信息来选取最佳分量交织器对抗多径衰落信道的方法。采用自适应分量交织和最优交织图案搜索准则能使得每个子载波上的符号分量尽可能的在信噪比高的子载波上发送,因此比采用固定的分量交织有着更大的分集增益。并且使用不同阶数的星座调制时,自适应分量交织都能有性能提高。鉴于以上优点, OFDM旋转调制自适应交织系统在未来的无线宽带传输中将有很大的应用前景。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Tse D, Viswanath P. Fundamentals of Wireless Communication [M]. Cambridge, UK: Cambridge University Press, 2005. [本文引用:1]
[2]	Boutros J, Viterbo E. Signal space diversity: A power and bandwidth-efficient diversity technique for Rayleigh fading channel [J]. IEEE Trans Inform Theory, 1998, 44(4): 1453-1467. [本文引用:1]
[3]	Tran N H, Nguyen H H, Le-Ngoc T. Application of signal space diversity over multiplicative fading channels[J]. IEEE Signal Processing Letters, 2009, 16(3): 204-207. [本文引用:1] [JCR: 1.639]
[4]	Oggier F, Viterbo E. Algebraic Number Theory and Code Design for Rayleigh Fading Channels [M]. Cambridge, UK: Cambridge University Press, 2004. [本文引用:2]
[5]	LI Yabo, XIA Xianggen, WANG Genyuan. Simple Iterative Methods to Exploit the Signal-Space Diversity[J]. IEEE Trans Commun, 2005, 53(1): 1112-1125. [本文引用:1]
[6]	WU Zhanji, FU Tingting, WANG Xu, et al. A novel Coding-Rotated-Modulation OFDM scheme [C]// Proc ICCTA. Beijing, China: IEEE, 2009: 517-520. [本文引用:1]
[7]	WU Zhanji, PENG Mugen, WANG Wenbo. Improved Coding-Rotated-Modulation Orthogonal Frequency Division Multiplexing System[J]. IET Commun, 2012, 6(3): 272-280. [本文引用:1] [JCR: 0.72]
[8]	Boutros J, Viterbo E, Rastello C, et al. Good lattice constellations for both Rayleigh fading and Gaussian channel[J]. IEEE Trans Inform Theory, 1996, 42(3): 502-518. [本文引用:1]
[9]	Kim J, Lee I. Analysis of symbol error rates for signal space diversity in Rayleigh fading channels [C]// Proc ICC. Beijing, China: IEEE, 2008: 4621-4625. [本文引用:1]
[10]	Kim J, Lee W, Kim JK, et al. On the symbol error rates for signal space diversity schemes over a Rician fading channel[J]. IEEE Trans on Commun. 2009, 57(8): 2204-2209. [本文引用:1]
[11]	Proakis J G, Salehi M. Digital Communications[M]. 5th ED. New York, NY: Mc-Graw-Hill, 2008. [本文引用:1]
[12]	Patzold M. Mobile Fading Channels[M]. Chichester, England: John Wiley &Sons Ltd, 2002. [本文引用:1]

2005

0.0

... 目前宽带传输在面临大时延扩展信道时需要正交频分复用(OFDM)技术,多径效应会造成频率选择性衰落使OFDM系统的个别子载波会处于信道深衰落中,因此需要分集技术来对抗信道的衰落^[1] ...

1998

0.0

... 但是,高维星座旋转的解调需要付出巨大的计算量^[2,4-5] ...

2009

1.639

0.0

... 采用星座旋转调制配合分量交织是一种有效的分集手段,特别是在信号较强的多径数量很多的情况下采用高维星座旋转可以充分获得分集增益^[3] ...

2004

0.0

... 但是,高维星座旋转的解调需要付出巨大的计算量^[2,4-5] ...

... 在相干检测条件下,接收端的离散时间复基带信号r的向量表述可以写成^[4]: ...

2005

0.0

... 但是,高维星座旋转的解调需要付出巨大的计算量^[2,4-5] ...

2009

0.0

2012

0.72

0.0

... 星座旋转的最佳角度是最大化最小分量乘积距离,也就是最大化每个分量上相邻星座点的距离,因此星座旋转角度为θ=argtan 12q^[7], q=lb M ...

1996

0.0

... 其中θ是星座旋转的角度,在未编码情况下最佳旋转角度的选取原则是最大化最小分量距离的乘积 dp,min(L)^[8], ...

2008

0.0

2009

0.0

2008

0.0

... 在AWGN信道下,噪声服从N~ 0,N02,其中Q(·)是Q函数,N₀是噪声功率^[11] ...

2002

0.0

... 衰落信道为COST 207典型城区(TU)信道模型 ^[12],最大Doppler频偏为20 Hz ...