2. 国网浙江省电力有限公司, 杭州 310007
2. State Grid Zhejiang Electric Power Company, Hangzhou 310007, China
随着化石能源储量的减少和环境保护压力的增长,能源消耗逐渐向清洁低碳转型。为了减少二氧化碳排放、实现区域资源优化配置、构建清洁低碳且安全高效的新一代电网,可再生能源装置及储能系统成为世界各国的研究焦点[1-2]。光伏、风电等可再生能源的广泛使用,深刻地改变了电力系统的结构和运行特点[3]。而微电网是聚合分布式电源、消纳可再生能源、平衡区域负荷的重要手段。通过构建微电网,可将供需平衡分散化,降低源荷不确定性给系统带来的不利影响[4-5]。
然而,与传统电力系统相比,微电网设备组成多样、调度控制策略繁多,呈现出复杂的动态特征。微电网的电源一般含有旋转发电机(如微型燃气轮机等)和逆变器型电源(如分布式电源储能等),这2种电源动态特性存在较大差异。微电网运行状态可以分为并网运行和孤岛运行2种;同时,逆变器型电源的控制策略包括PQ控制、PV控制、下垂控制等。微电网多样的运行方式和复杂的动态特性,给微电网稳定性分析带来了新的挑战。文[6-7]对多源微电网进行小信号建模,通过计算系统特征根,分析了微电网的小干扰稳定性。但是,微电网的元件之间存在交互作用,同时控制参数在系统运行过程中可以改变。传统的小干扰分析难以解决含不确定参数系统的稳定性问题,因此构建小干扰安全域对系统设计和控制具有重要意义。
判断系统鲁棒稳定性的方法众多。结构化奇异值(SSV)理论是处理鲁棒稳定性问题的重要手段, 因计算稳定半径μ也被称为μ方法。文[8]在M-Δ框架下建立了线性时不变系统的不确定模型,并利用SSV理论估计了不确定参数多机系统的鲁棒稳定半径;文[9]采用μ方法分析了DC/DC buck电路的参数不确定性问题,但是由于μ的准确值不易计算,故采用μ的下界估计鲁棒稳定半径;文[10]则利用μ方法研究了直流微电网的鲁棒稳定性问题。Kharitonov定理将区间多项式的稳定性问题转换为判定4个极点特征多项式的稳定性。文[11]通过Kharitonov定理设计了鲁棒电力系统稳定器;文[12]则利用广义Kharitonov定理设计了电力系统振荡阻尼器。值集法利用Mikhailov图判断系统鲁棒稳定性。文[13]通过计算系统特征多项式,并对系统进行降阶处理,分析了大规模电力系统的鲁棒稳定问题;文[14]采用了一种新型值集法,分析了风电注入空间下的鲁棒稳定问题;文[15]继续探索了值集法的相关性质,解决了组合爆炸和稳定裕度计算的问题;文[16]采用半正定规划(SDP)判断直流系统的鲁棒稳定性。以上方法均为充分条件,在判断鲁棒稳定性时仍有所不足。SSV方法的数学理论比较复杂,且准确的μ值不易计算;Kharitonov定理只适用于小系统的鲁棒稳定性分析,且特征多项式系数的耦合也会使结果更加保守;用值集法判断系统鲁棒稳定性简明直观,可以在复平面展示多维不确定性系统,但是其结果判断依赖人工识别Mikhailov图,难以系统地构建鲁棒小干扰稳定域。
上述文献着眼于评估确定参数范围的小干扰稳定性,没有构建全部参数空间下系统的小干扰安全域。本文将使系统保持小干扰稳定的所有参数集合称作小干扰安全域(SSSR)或参数安全域。文[17]利用Kharitonov定理建立了单机无穷大系统的小干扰安全域;文[18]采用多项式拟合确定了小干扰安全域边界;文[19]确定了含不确定风电注入系统的小干扰安全域;文[20]采用SSV理论建立了确定调度策略的电力系统的风电消纳域;文[21]利用了分岔计算研究了孤岛微电网的参数安全域。以上构建小干扰安全域的方法主要是计算安全域边界,本质上仍是逐点法的应用,不能全面准确构建系统的小干扰安全域。同时,小干扰安全域边界往往不规则且非凸,逐点创建超立方覆盖小干扰安全域重叠区域多,会耗费大量计算资源。
本文着眼于构建系统整体小干扰安全域,针对数学模型中含不确定参数的线性定常系统,给出了一种基于Kronecker矩阵与Kronecker相关矩阵的鲁棒稳定性判据,保证系统在不确定参数下的小干扰稳定。为构建系统小干扰安全域,对参数进行采样,对于稳定的采样参数,采用鲁棒稳定半径估算其周围小干扰稳定的邻域;对于不稳定的采样参数,采用参数灵敏度估算其周围小干扰失稳的邻域。设计了一种自适应覆盖算法,通过超立方覆盖能够形成系统小干扰稳定的参数集合,即小干扰安全域。该算法可以自动调整超立方体的大小,避免了冗余的搜索计算,提高了计算效率。
本文首先介绍多源微电网的数学模型,建立了多源微电网的状态空间方程;其次介绍鲁棒稳定判据,估算额定不确定参数下系统的鲁棒稳定半径;然后应用自适应覆盖算法计算小干扰安全域;最后通过2机微电网系统算例验证了本文算法。
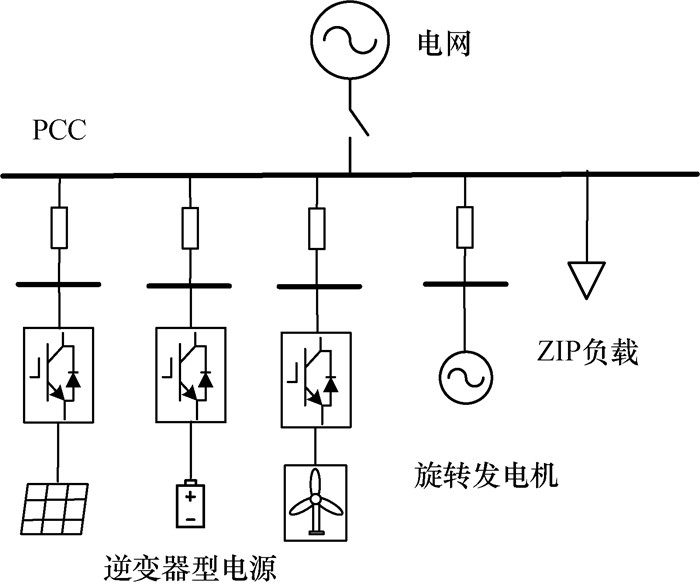
1 多源微电网的数学模型本文考虑的多源微电网结构如图 1所示。电源主要包括逆变器型电源和旋转发电机2类。小型直驱风机、光伏以及储能装置均可通过逆变器型电源统一表示。
|
| 图 1 多源微电网结构图 |
电源中含有旋转元件或模拟旋转元件的控制结构均可在各自的d-q坐标系下建模。为了统一全部电源状态空间方程,需将所有电源变换至公共的D-Q参考坐标系。假设系统同步旋转角速度为ω,第i个电源的d-q坐标和D-Q参考坐标角度差值为δi。坐标变换公式为
| $ \left[\begin{array}{c} f_{D i} \\ f_{Q i} \end{array}\right]=\left[\begin{array}{c} \cos \delta_{i} & -\sin \delta_{i} \\ \sin \delta_{i} & \cos \delta_{i} \end{array}\right]\left[\begin{array}{c} f_{d i} \\ f_{q i} \end{array}\right] . $ | (1) |
其中:fdi和fqi分别表示第i个电源的d和q轴电压或电流,fDi和fQi分别表示第i个电源的参考坐标系下D和Q轴的电压或电流。
1.1 旋转发电机模型该电源由同步机、调速器和励磁器构成,各个部分的状态空间方程如下。
1) 同步机模型:采用三阶同步机模型。
| $ \left\{\begin{array}{l} \dot{\delta}=\omega_{\mathrm{s}}(\omega-1), \\ T_{\mathrm{J}} \dot{\omega}=-D \omega+P_{\mathrm{m}}-P_{\mathrm{e}} ,\\ T_{d 0}^{\prime} \dot{E}_{q}^{\prime}=-E_{q}^{\prime}-\left(X_{d}-X_{d}^{\prime}\right) I_{d}+E_{\mathrm{fq}} ,\\ U_{d}=-R_{\mathrm{a}} I_{d}+X_{q} I_{q}, \\ U_{q}=E_{q}^{\prime}-X_{d}^{\prime} I_{d}-R_{\mathrm{a}} I_{q}, \\ P_{\mathrm{e}}=U_{d} I_{d}+U_{q} I_{q}+\left(I_{d}^{2}+I_{q}^{2}\right) R_{\mathrm{a}}. \end{array}\right. $ | (2) |
其中:δ是转子功角; ωs和ω分别为同步机额定角速度和实际角速度; D为系统的阻尼系数; TJ为系统的转子机械惯性时间常数; Td0′是d轴的暂态时间常数;Pm和Pe分别为同步机的机械功率和电磁功率;E′q为q轴次暂态电动势;Efq为同步机假想空载电动势;Ud、Uq和Id、Iq分别为同步发电机端口d、q轴的电压和电流;Xd、Xq和Xd′、Xq′分别为d、q轴同步电抗和次同步电抗。Ra为同步机电枢电阻值。
2) 调速器模型:采用PSAT软件中Type-Ⅱ型调速器模型。
| $ \left\{\begin{array}{l} T_{2} \dot{t}_{\mathrm{g}}=\frac{1}{R}\left(1-\frac{T_{1}}{T_{2}}\right)\left(\omega_{\mathrm{ref}}-\omega\right)-t_{\mathrm{g}}, \\ P_{\mathrm{m}}=t_{\mathrm{g}}+\frac{T_{1}}{R T_{2}}\left(\omega_{\mathrm{ref}}-\omega\right)+P_{\mathrm{m} 0}. \end{array}\right. $ | (3) |
其中:ωref为参考角速度;T1、T2为调速器的时间常数;R为下垂系数;tg为调速器内部状态变量。
3) 励磁器模型:采用简化ST1C型励磁模型,保留一个超前滞后环节。
| $ \left\{\begin{array}{l} T_{\mathrm{B}} \dot{v}_{\mathrm{R}}=-v_{\mathrm{R}}+V_{\mathrm{ref}}-v_{\mathrm{M}}-\frac{T_{\mathrm{C}}}{T_{\mathrm{R}}}\left(\left|V_{\mathrm{C}}\right|-v_{\mathrm{M}}\right), \\ T_{\mathrm{A}} \dot{E}_{\mathrm{fq}}=K_{\mathrm{A}} v_{\mathrm{R}}-E_{\mathrm{fq}}, \\ T_{\mathrm{R}} \dot{v}_{\mathrm{M}}=\left|V_{\mathrm{C}}\right|-v_{\mathrm{M}}, \\ V_{\mathrm{C}}=V_{\mathrm{t}}+\left(R_{\mathrm{c}}+j X_{\mathrm{c}}\right) I_{\mathrm{t}}. \end{array}\right. $ | (4) |
其中:vR为励磁电压;vM为同步机端子量测电压; VC为经过补偿后的电压值;KA为励磁增益;TA、TB、TC、TR为励磁器中的相关时间常数。
1.2 逆变器型电源模型逆变器型电源的控制环节由功率控制器和电压/电流控制器构成,在本文中逆变器采用下垂控制。同时,逆变器型电源模型有以下假设:1) 直流侧为理想电压源;2) 逆变器的开关过程可以被忽略;3) 电压/电流控制器的控制过程可以被忽略,逆变器输出电压始终跟随参考信号。同时为提高稳定性,在功率控制环节加入超前滞后矫正环节。
| $ \left\{ {\begin{array}{*{20}{l}} {\dot \theta = {\omega _{\rm{s}}}(\omega - 1),}\\ {\omega = {\omega _{{\rm{ref}}}} - {m_{\rm{p}}}\frac{{1 + s{T_{\rm{n}}}}}{{1 + s{T_{\rm{d}}}}}p,}\\ {p = {\omega _{\rm{c}}}{\rm{ }}\tilde p/\left( {s + {\omega _{\rm{c}}}} \right),}\\ {q = {\omega _{\rm{c}}}{\rm{ }}\tilde q/\left( {s + {\omega _{\rm{c}}}} \right),}\\ {\tilde p = {v_{{\rm{o}}d}}{i_{{\rm{o}}d}} + {v_{{\rm{o}}q}}{i_{{\rm{o}}q}},}\\ {\tilde q = {v_{{\rm{o}}d}}{i_{{\rm{o}}q}} - {v_{{\rm{o}}q}}{i_{{\rm{o}}d}},}\\ {v_{{\rm{od}}}^* = {V_{{\rm{ref}}}} - {n_q},}\\ {v_{{\rm{o}}q}^* = 0,}\\ {{v_{{\rm{o}}d}} - {v_d} = {R_{{\rm{eq}}}}{i_{{\rm{o}}d}} - {X_{{\rm{eq}}}}{i_{{\rm{o}}q}},}\\ {{v_{{\rm{o}}q}} - {v_q} = {X_{{\rm{eq}}}}{i_{{\rm{o}}d}} - {R_{{\rm{eq}}}}{i_{{\rm{o}}q}}.} \end{array}} \right. $ | (5) |
其中:p、q、
负载模型采用ZIP模型:
| $ \left\{\begin{array}{l} P_{\mathrm{ZIP}}=P_{0}\left(a_{1} \frac{U_{\mathrm{b}}^{2}}{U_{0}^{2}}+a_{2} \frac{U_{\mathrm{b}}}{U_{0}}+a_{3}\right), \\ Q_{\mathrm{ZIP}}=Q_{0}\left(b_{1} \frac{U_{\mathrm{b}}^{2}}{U_{0}^{2}}+b_{2} \frac{U_{\mathrm{b}}}{U_{0}}+b_{3}\right). \end{array}\right. $ | (6) |
其中:P0和Q0分别为额定负载的有功和无功功率;U0为母线额定电压;Ub为母线实际电压;a1、a2、a3和b1、b2、b3为ZIP的系数,满足a1+a2+a3=1和b1+b2+b3=1。
2 鲁棒稳定性判据判断线性系统稳定性需要计算系统状态矩阵A的特征值。A取决于系统元件参数和控制器参数,参数的改变会影响A的特征值从而影响系统小干扰稳定性。实际工程中,准确获取微电网全部参数具有一定难度。在参数未知的情况下也无法精确计算A的特征值。因此,研究含有不确定参数的线性系统鲁棒稳定性对构建系统小干扰安全域具有重要意义。
2.1 不确定参数系统的数学模型考虑以下含不确定参数的线性时不变系统[25]:
| $ \dot{\boldsymbol{x}}=\left(\boldsymbol{A}_{0}+\sum\limits_{i=1}^{p} \boldsymbol{A}_{\mathrm{p}, i} \alpha_{i}\right) \boldsymbol{x} . $ | (7) |
其中:
| $ \boldsymbol{A}(\alpha)=\sum\limits_{j=1}^{2^{p}} \mu_{j} \boldsymbol{A}_{j}, \quad \sum\limits_{j=1}^{2^{p}} \mu_{j}=1, \quad \mu_{j} \geqslant 0. $ | (8) |
其中:Aj(j=1, 2, …, 2p)表示超立方的所有极点,μj为参数。以含有1个不确定参数的三阶系统为例:
| $ \dot{\boldsymbol{x}}=\left[\begin{array}{ccc} \alpha_{1} & -2 & -1 \\ 2 & 2 \alpha_{1}-1 & 0 \\ 1 & 0.9 & -0.5 \end{array}\right] \boldsymbol{x}. $ | (9) |
如果以α1=0为额定参数,则有:
| $ \boldsymbol{A}_{0}=\left[\begin{array}{ccc} 0 & -2 & -1 \\ 2 & -1 & 0 \\ 1 & 0.9 & -0.5 \end{array}\right], \quad \boldsymbol{A}_{\mathrm{p}, 1}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 0 \end{array}\right] . $ |
假设
定义矩阵A的Kronecker矩阵为
| $ \mathscr{K}(\boldsymbol{A})=\boldsymbol{A} \oplus \boldsymbol{I}_{n}. $ | (10) |
其中“⊕”表示Kronecker和。对任意2个矩阵 A和B有:D=A⊕B=A×Im+ In+ B。
Bialternate和矩阵
| $ \mathscr{B}(\boldsymbol{A})_{p q, r s}=\left\{\begin{array}{cl} -a_{p s}, & r=q, s<q ; \\ a_{p r}, & r \neq p, s=q ; \\ a_{p p}+a_{q q}, & s=p, s=q ; \\ a_{q p}, & r=p, s \neq q ; \\ -a_{q r}, & s=p ; \\ 0, & \text { 其他. } \end{array}\right. $ | (11) |
其中
针对式(7)的不确定系统,A0为α=α0时的额定矩阵,应用Kronecker矩阵与Bialternate和矩阵可以估计系统鲁棒稳定半径rR[27]。
定理1 对于式(7)的不确定系统,如果不确定参数在以下范围内变化,那么系统始终保持稳定。
| $ \left\{\begin{array}{l} \max \limits_{i}\left(\alpha_{i}-\alpha_{0, i}\right)<r_{\mathrm{K}}, \\ r_{\mathrm{K}}=\frac{1}{\rho\left\{\sum\limits_{i=1}^{p}\left|\mathscr{K}\left(\boldsymbol{A}_{\mathrm{p}, i}\right) \mathscr{K}\left(\boldsymbol{A}_{0}\right)^{-1}\right|\right\}}. \end{array}\right. $ | (12) |
其中:ρ(·)表示计算矩阵的谱半径,|·|表示取矩阵所有元素的绝对值。
定理2 对于式(7)的不确定系统,如果不确定参数在以下范围内变化,那么系统始终保持稳定。
| $ \left\{\begin{array}{l} \max \limits_{i}\left(\alpha_{i}-\alpha_{0, i}\right)<r_{\mathrm{B}}, \\ r_{\mathrm{B}}=\min \left\{r_{1}, r_{2}\right\}, \\ r_{1}=\frac{1}{\rho\left\{\sum\limits_{i=1}^{p}\left|\boldsymbol{A}_{\mathrm{p}, i} \boldsymbol{A}_{0}^{-1}\right|\right\}}, \\ r_{2}=\frac{1}{\rho\left\{\sum\limits_{i=1}^{p}\left|\mathscr{B}\left(\boldsymbol{A}_{\mathrm{p}, i}\right) \mathscr{B}\left(\boldsymbol{A}_{0}\right)^{-1}\right|\right\}}. \end{array}\right. $ | (13) |
应用定理1和2及μ方法,分别计算式(9)的鲁棒稳定半径,结果分别为0.173、0.213和0.055。以上条件均为系统鲁棒稳定的充分条件,在鲁棒稳定半径内系统小干扰稳定。根据计算结果可知,不确定参数变化范围为-0.213≤α1≤0.213时,系统保持小干扰稳定。系统在建立不确定系统模型后,应用定理1和2可以快速计算系统的鲁棒稳定半径。与μ方法相比,本文提出的方法数学理论易于理解且计算过程比较简单。同时该方法的保守性较小,可以获得比较大的鲁棒稳定半径,有利于快速构建系统小干扰安全域。与Kharitonov定理相比,该方法计算鲁棒稳定半径仅需1次计算,无需重复迭代,有较高的计算效率。
同时,采用定理1和2计算出的结果有所不同,一般来讲定理1的结果比定理2的结果更为保守,这是由
小干扰安全域是使式(7)系统保持小干扰稳定的全部参数构成的集合,一般是非凸的。本节通过超立方的并集来覆盖小干扰稳定域,该算法的关键是确定超立方的中心和半径。
3.1 参数超立方的半径计算给定α,若该参数使系统小干扰稳定,可以在参数空间中确定一个以α为中心的超立方,应用定理1或2计算最大的半径rR,当参数在[α-1rR, α + 1rR]中变化时,系统均小干扰稳定。若该参数使系统不稳定,可以通过特征值灵敏度估算保证系统小干扰不稳定的超立方。特征值灵敏度计算公式为
| $ s_{i, k}=\frac{\partial \lambda_{i}}{\partial \alpha_{k}}=\boldsymbol{u}_{i}^{\mathrm{T}} \frac{\partial \boldsymbol{A}(\alpha)}{\partial \alpha_{k}} \boldsymbol{v}_{i}=\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{p}, k} \boldsymbol{v}_{i}. $ | (14) |
其中:λi为A(α)第i个特征值;αk为第k个不确定参数;ui和vi分别为左特征向量和右特征向量;si, k为特征值λi对参数αk的灵敏度。那么系统极点的特征向量可以按照以下公式估计:
| $ \lambda_{i, j}=\lambda_{i}+r \sum\limits_{k=1}^{p}(-1)^{z} s_{i, k} . $ | (15) |
根据极点的位置,z为0或1。选取A(α)中拥有最大正实部的特征值λmax,为保证参数超立方所有极点的最大特征值实部仍为正数,每个极点的临界半径为
| $ r_{j}=\frac{\lambda_{\max }}{\sum\limits_{k=1}^{p}(-1)^{z} s_{\max , k}}. $ | (16) |
选取最小的临界半径作为不稳定半径:
| $ r=\min \left\{r_{j}\right\}, \quad r_{j}>0, \quad j=1,2, \cdots, 2^{p}. $ | (17) |
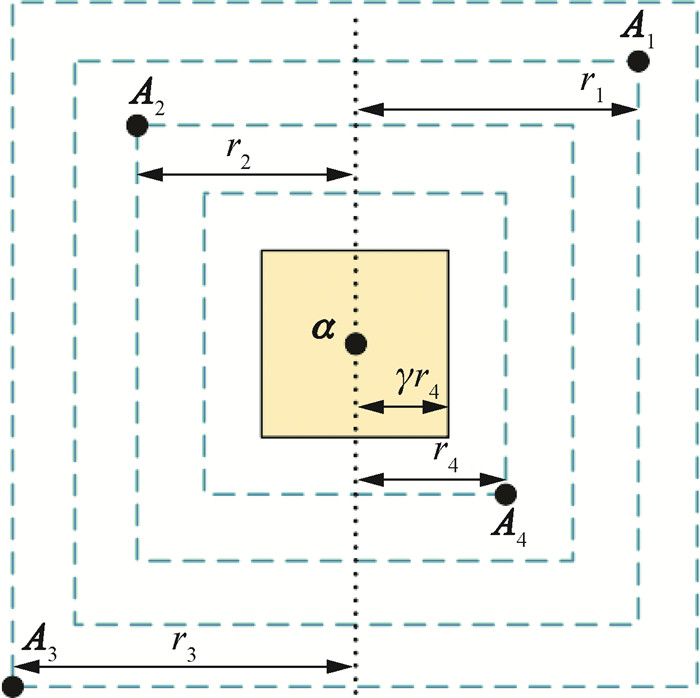
为避免不稳定半径估计偏大,引入系数γ∈(0, 1)控制不稳定超立方的大小。根据式(17)估计不确定超立方空间[α-1γr, α + 1γr]。图 2展示了含2个不确定参数时不稳定超立方的确定过程。其中,极点A4拥有最小超立方半径r4,因此以α为中心、γr4为半径的超立方为待求不稳定空间。
|
| 图 2 不稳定超立方空间计算示意图 |
3.2 自适应覆盖算法
为了快速有效计算系统全部小干扰安全域,本文提出了一种自适应覆盖算法。该算法主要分为分区和裁剪过程。首先在待判断的参数空间中选取均匀分布的参数点,如果所有的参数点均在不稳定超立方或稳定超立方中,该算法终止;否则,继续执行分区和裁剪过程。
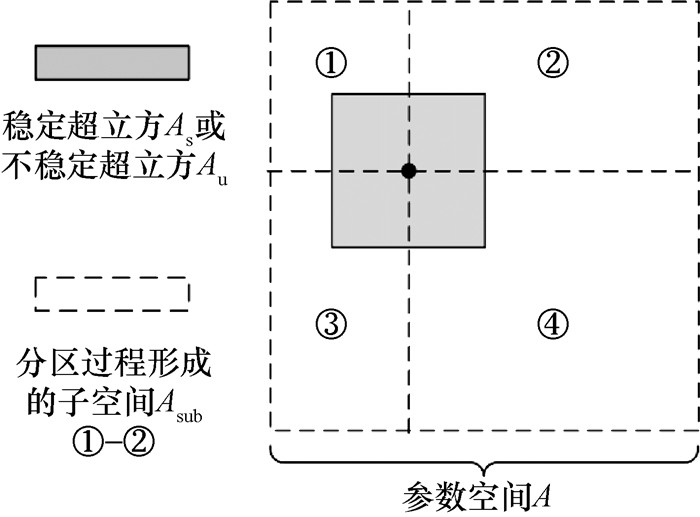
分区过程用于确定新的超立方中心点并构建新的参数超立方空间。对于确定参数α0,如果系统在α0上稳定,应用定理1或2确定参数稳定超立方Λs;反之,如果系统在α0上不稳定,应用式(16)和(17)确定参数不稳定超立方Λu。之后待预测的参数空间会被划分成2p个子区域。含2个参数的分区过程和超立方中心点选取分别如图 3和4所示。
|
| 图 3 分区过程示意图 |
|
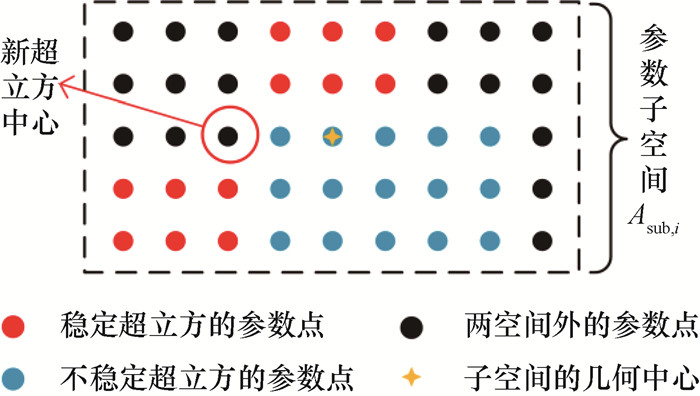
| 图 4 (网络版彩图)新超立方空间中心选取示意图 |
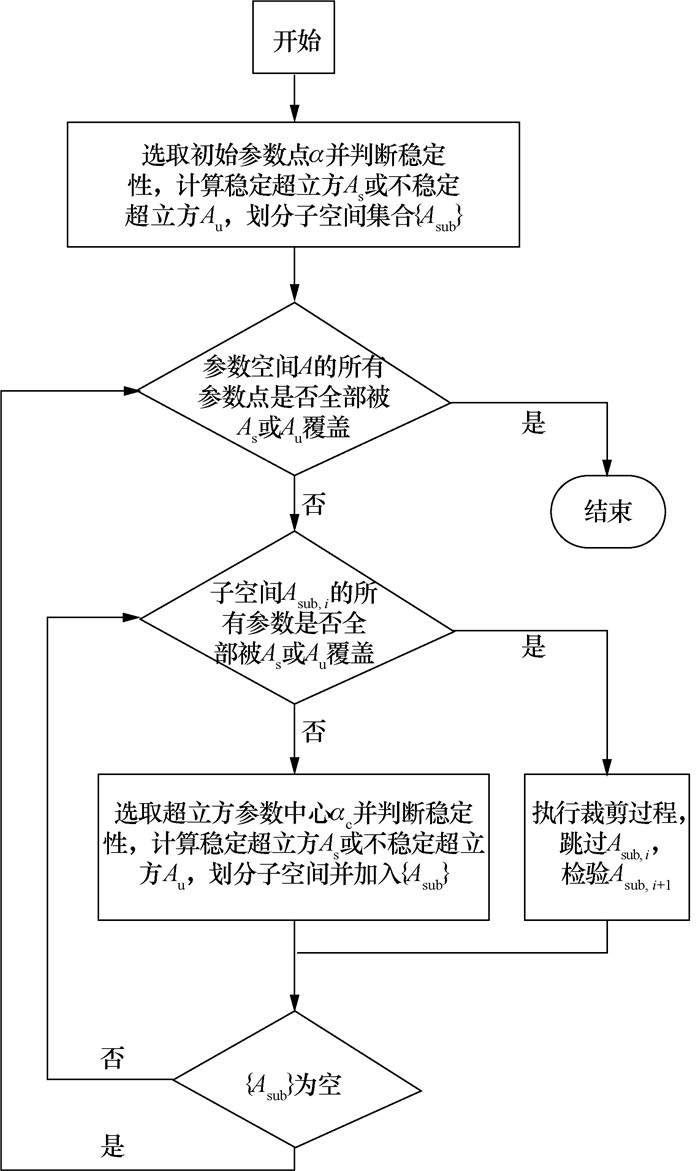
裁剪过程用于避免重复计算参数超立方,在计算超立方半径前,首先检验子区域内的参数点是否全部被稳定超立方和不稳定超立方覆盖,如果全部覆盖,则跳过此子区间;否则,选取距子区域几何中心最近的未预测参数点作为新的超立方中心,确定新的参数超立方。图 5为自适应覆盖算法流程图。
|
| 图 5 自适应覆盖算法流程图 |
3.3 简单示例
以文[24]中的单机无穷大系统验证自适应覆盖算法的有效性。该系统含有电力系统静态稳定器(PSS),励磁增益KA和PSS时间常数Tpss为不确定参数,共同影响系统小干扰稳定性。经线性化后,系统的小信号模型为
| $ \boldsymbol{A}=\left[\begin{array}{ccccc} 0 & 377 & 0 & 0 & 0 \\ -0.095\;82 & 0 & -0.098 & 0 & 0 \\ -0.317\;54 & 0 & -0.56 & 0.2 & 0 \\ 0.387\;35 K_{\mathrm{A}} & 50 K_{\mathrm{A}} & -2.029\;5 K_{\mathrm{A}} & -5 & 5 K_{\mathrm{A}} \\ 0 & -9 /\left(T_{\mathrm{pss}} / \mathrm{s}\right) & 0 & 0 & -1 /\left(T_{\mathrm{pss}} / \mathrm{s}\right) \end{array}\right] . $ |
以KA和1/Tpss为不确定参数,根据式(7)确定系统额定状态矩阵和摄动矩阵。参数变化范围为KA∈[0, 100]和1/Tpss∈[0, 100] s-1,参数间隔均为1。应用定理1和2计算系统小干扰安全域。
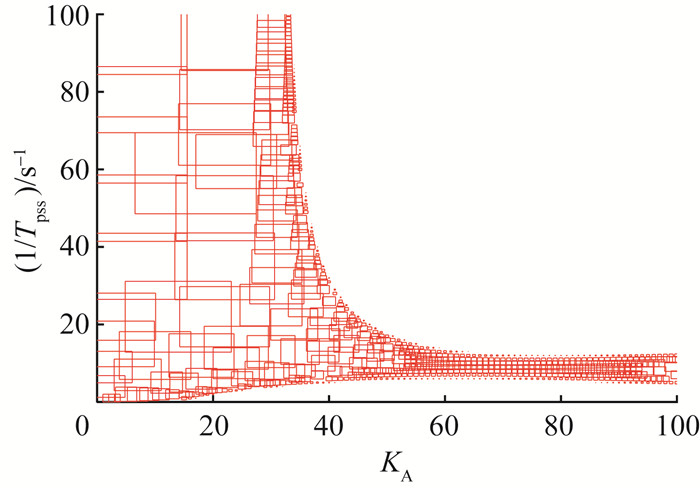
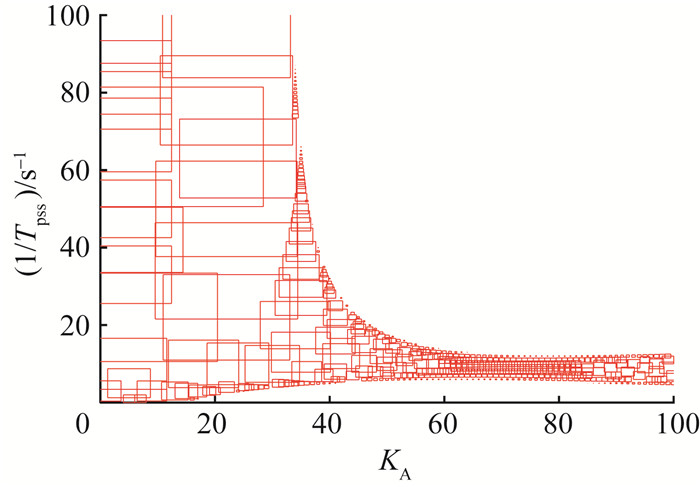
图 6和7都是应用自适应覆盖算法得到的小干扰安全域,但用于计算鲁棒稳定半径的依据不同,超立方覆盖形式有所差异,但小干扰安全域范围是一致的。在本算例中,采用定理2得到的鲁棒稳定半径更大,构建小干扰安全域所需的超立方个数更少,所需的计算量更小。以额定参数KA=20,Tpss=40 s为例,应用定理1和2计算得出的鲁棒稳定半径分别为9.44和13.91。文[24]方法得到与应用定理2方法同样大小的稳定空间需要27次迭代计算,而本文仅需要1步计算即可。由此可见,本文采用的鲁棒稳定判据具有较小的保守性,适合构建系统小干扰安全域。
|
| 图 6 根据定理1构建的小干扰安全域 |
|
| 图 7 根据定理2构建的小干扰安全域 |
4 算例分析 4.1 系统介绍
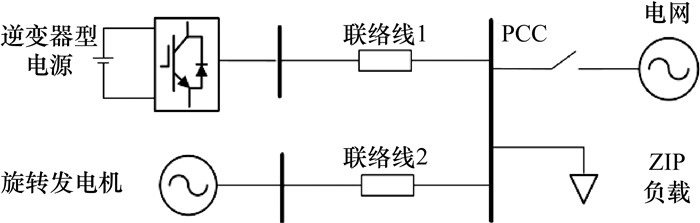
本文的微电网算例如图 8所示,微电网在孤岛模式下运行,系统含有1个旋转发电机、1个逆变器型电源和1个ZIP负载。负载总需求为20 MW,旋转发电机和逆变器型电源的功率输出均为10 MW。系统详细参数见表 1—3。
|
| 图 8 算例微电网结构图 |
| 参数 | 数值 |
| 转子电枢电阻Ra | 0.000 2 Ω |
| d轴同步电抗Xd | 2.85 Ω |
| d轴次暂态电抗Xd′ | 1.30 Ω |
| q轴同步电抗Xq | 0.17 Ω |
| d轴次暂态时间常数Td0′ | 5 s |
| 转子机械惯性时间常数TJ | 8 s |
| 阻尼系数D | 0.1 |
| 调速器下垂系数R | 0.04 |
| 调速器时间常数T1 | 0.1 s |
| 调速器时间常数T2 | 1 s |
| 励磁增益KA | 50 |
| 励磁时间常数TA | 0.01 s |
| 励磁时间常数TB | 0.01 s |
| 励磁时间常数TC | 1 s |
| 量测时间常数TR | 0.05 s |
| 参数 | 数值 |
| 滤波器截止频率ωc | 31.14 rad/s |
| 有功功率下垂系数mp | 1% |
| 无功功率下垂系数nq | 0.1% |
| 超前滞后环节时间常数Tld | 10 s |
| 超前滞后环节时间常数Tln | 4 s |
| 滤波器等效电阻Req | 0.1 Ω |
| 滤波器等效电抗Xeq | 0.3 Ω |
4.2 系统建模
本文考虑孤岛运行的微电网,微电网的各个动态元件通过系统网络连接,如果将系统的节点按照旋转发电机、逆变器型电源和负载的顺序排列,可以得到系统网络方程:
| $ \left[\begin{array}{c} \Delta \boldsymbol{i}_{\mathrm{g}} \\ \Delta \boldsymbol{i}_{\mathrm{i}} \\ \Delta \boldsymbol{i}_{\mathrm{L}} \end{array}\right]=\left[\begin{array}{ccc} \boldsymbol{Y}_{\mathrm{gg}} & \boldsymbol{Y}_{\mathrm{gi}} \boldsymbol{Y}_{\mathrm{gL}} & \\ \boldsymbol{Y}_{\mathrm{ig}} & \boldsymbol{Y}_{\mathrm{ii}} & \boldsymbol{Y}_{\mathrm{iL}} \\ \boldsymbol{Y}_{\mathrm{Lg}} & \boldsymbol{Y}_{\mathrm{L} \mathrm{i}} & \boldsymbol{Y}_{\mathrm{LL}} \end{array}\right]\left[\begin{array}{c} \Delta \boldsymbol{v}_{\mathrm{g}} \\ \Delta \boldsymbol{v}_{\mathrm{i}} \\ \Delta \boldsymbol{v}_{\mathrm{L}} \end{array}\right]. $ | (18) |
经Kron变换,保留含有动态过程的节点,得到系统收缩导纳矩阵YNET,各节点电压电流关系为
| $ \Delta \boldsymbol{i}_{D Q}=\boldsymbol{Y}_{\mathrm{NET}} \Delta \boldsymbol{v}_{D Q}. $ | (19) |
本文考虑孤岛运行的微电网,通过式(19)连接系统所有动态元件,构成系统的状态空间模型:
| $ \left\{\begin{array}{l} \Delta \boldsymbol{\dot{x}}=\boldsymbol{A} \Delta \boldsymbol{x}+\boldsymbol{B} \Delta \boldsymbol{i}_{D Q}, \\ \Delta \boldsymbol{v}_{D Q}=\boldsymbol{C} \Delta \boldsymbol{x}+\boldsymbol{D} \Delta \boldsymbol{i}_{D Q}. \end{array}\right. $ | (20) |
其中,x=[xg xi]T由微电网全部状态变量组成;利用式(19)消去式(20)中的代数变量,得到微电网整体状态空间模型:
| $ \left\{\begin{array}{l} \Delta \boldsymbol{\dot{x}}=\boldsymbol{A}_{\mathrm{sys}} \Delta \boldsymbol{x}, \\ \boldsymbol{A}_{\mathrm{sys}}=\boldsymbol{A}+\boldsymbol{B}\left(\boldsymbol{Y}_{\mathrm{NET}}-\boldsymbol{D}\right)^{-1} \boldsymbol{C} . \end{array}\right. $ | (21) |
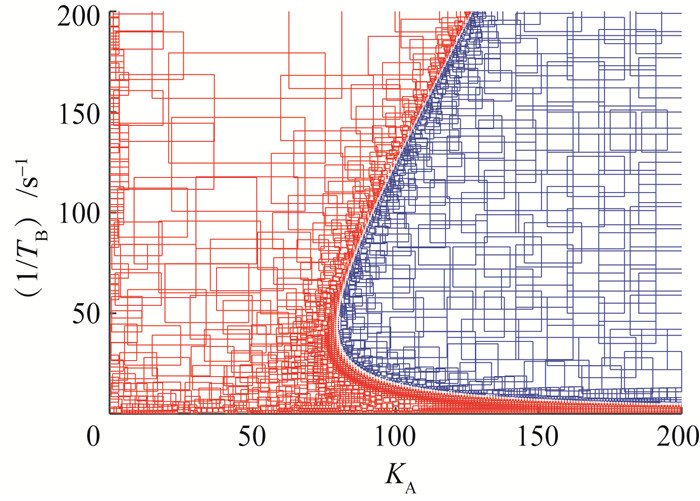
在本算例中ZIP负载系数为:a=1,b=0,c=0。不确定参数为励磁器增益KA、励磁器时间常数1/TB和TC、逆变器型微电源下垂系数mp。图 9和10为不同参数平面的小干扰安全域。红区区域为稳定参数域,蓝色为不稳定参数域。应用定理2构建系统小干扰安全域。
|
| 图 9 (网络版彩图)平面小干扰安全域 |
|
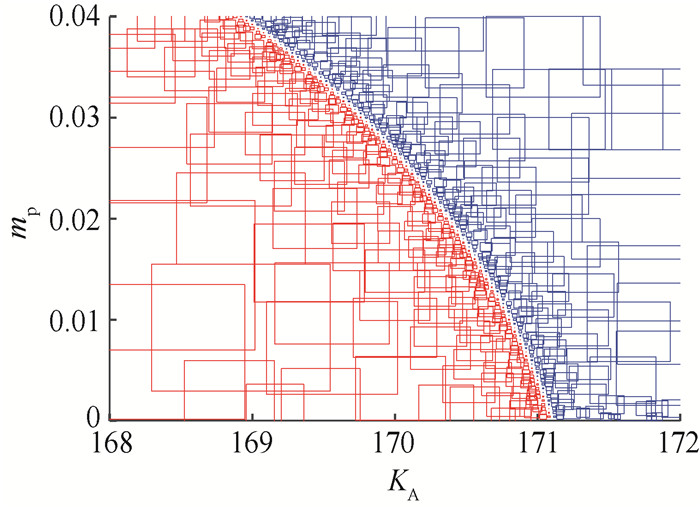
| 图 10 (网络版彩图)平面小干扰安全域 |
图 9为KA和1/TB平面上的小干扰安全域,其中KA∈[1, 200],1/TB∈[0, 200] s-1,并设置系统采样点间隔均为1。该小干扰安全域由一条不规则曲线组成,因此,常规的边界搜索方法不能确定完整的小干扰安全域。KA增大会提高系统的动态响应速度,但也会破坏微电网的整体稳定性,在本算例中KA小于73则系统都会保持稳定。图 10描述了KA和mp平面上的小干扰安全域,其中KA∈[168, 172]且采样点间隔为0.04,mp∈[0, 0.04]且采样点间隔为0.000 4。KA增大对系统小干扰稳定性有显著影响,表明逆变器型电源和旋转发电机的控制参数对微电网小干扰稳定性存在耦合作用,在微电网规划时需要综合考虑两者的影响。
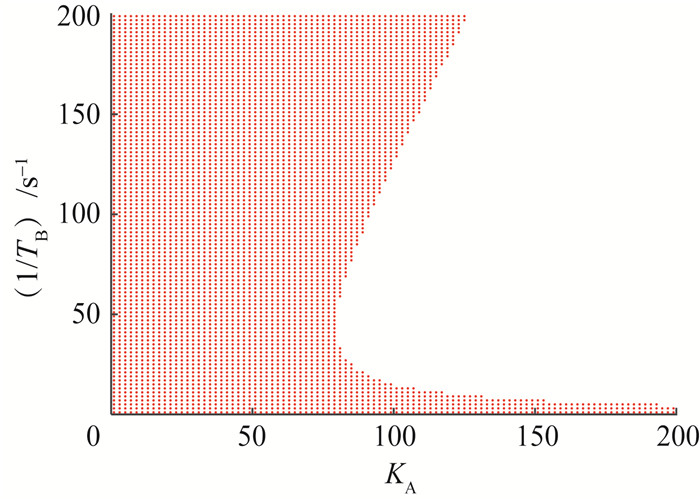
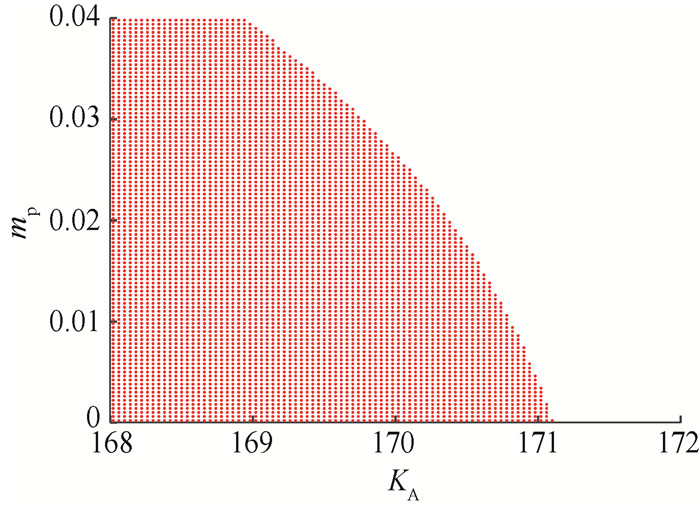
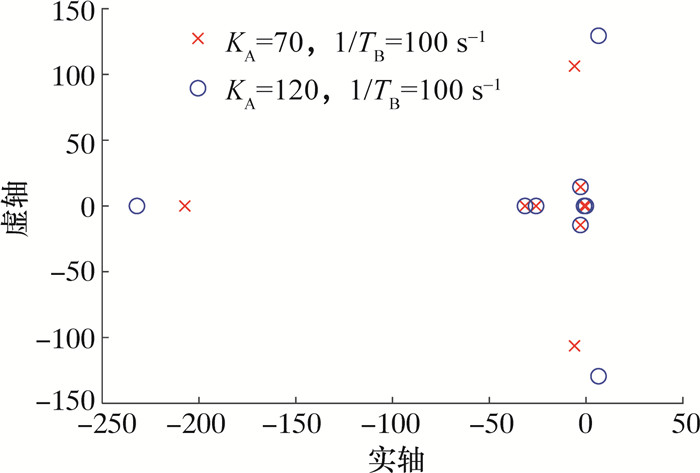
图 11和12为根据状态矩阵特征值,逐点计算系统的小干扰安全域结果。通过对比图 9和10的红色区域,验证了自适应覆盖算法的准确性。图 13为KA=70、1/TB=100 s-1和KA=120、1/TB=100 s-1时,系统的特征根分布图。可以发现,随着KA的增加,系统的1对特征根越过虚轴时系统变得不稳定。
|
| 图 11 逐点法确定的KA-(1/TB)平面小干扰安全域 |
|
| 图 12 逐点法确定的KA-mp平面小干扰安全域 |
|
| 图 13 不同参数系统特征根分布 |
自适应覆盖算法的准确度取决于采样点的间隔,采样点的间隔越小则小干扰安全域的准确度越高。小干扰安全域的最大误差不超过采样点的间隔大小。自适应覆盖算法搜索过程中,远离系统小干扰安全域边界时,稳定超立方边长较大;反之,则稳定超立方边长较小。该特性减少了安全域内部的冗余计算,也使安全域边界刻画更为精细。表 4为设置相同的采样点间隔下,逐点法和自适应覆盖算法的计算时间对比,验证了自适应覆盖算法的快速性。事实上,自适应覆盖算法无需选用较高的采样度就能得到令人满意的结果,如果按照图 9的采样间隔,则计算用时仅0.31 s。
5 结论
本文应用多源微电网的数学模型,通过基于Kronecker矩阵和Kronecker相关矩阵的鲁棒稳定性判据,估计了不确定系统的鲁棒稳定半径,为设计含有不确定参数的电力系统提供了重要方法。同时设计了一种搜索系统小干扰安全域的自适应覆盖算法,可以自动调节超立方空间的大小,高效识别系统的稳定区域和不稳定区域,避免重复计算。在算例分析中研究了含有旋转发电机和逆变器型电源的微电网的小干扰安全域。过大的励磁器增益会破坏系统的小干扰稳定性,同时旋转发电机和逆变器型电源的控制参数具有耦合关系,它们会共同影响系统小干扰稳定性。因此,小干扰安全域分析对多源微电网设计具有至关重要的作用。
| [1] |
周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904. ZHOU X X, CHEN S Y, LU Z X, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904. (in Chinese) |
| [2] |
周孝信, 鲁宗相, 刘应梅, 等. 中国未来电网的发展模式和关键技术[J]. 中国电机工程学报, 2014, 34(29): 4999-5008. ZHOU X X, LU Z X, LIU Y M, et al. Development models and key technologies of future grid in China[J]. Proceedings of the CSEE, 2014, 34(29): 4999-5008. (in Chinese) |
| [3] |
康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11. KANG C Q, YAO Z L. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11. (in Chinese) |
| [4] |
杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报, 2014, 34(1): 57-70. YANG X F, SU J, LÜ Z P, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70. (in Chinese) |
| [5] |
徐青山. 分布式发电与微电网技术[M]. 北京: 人民邮电出版社, 2011. XU Q S. Distributed generation and micro-grid[M]. Beijing: Posts & Telecom Press, 2011. (in Chinese) |
| [6] |
范元亮, 苗逸群. 基于下垂控制结构微网小扰动稳定性分析[J]. 电力系统保护与控制, 2012, 44(4): 1-7. FAN Y L, MIAO Y Q. Small signal stability analysis of microgrid droop controlled power allocation loop[J]. Power System Protection and Control, 2012, 44(4): 1-7. DOI:10.3969/j.issn.1674-3415.2012.04.001 (in Chinese) |
| [7] |
肖朝霞, 王成山, 王守相. 含多微型电源的微网小信号稳定性分析[J]. 电力系统自动化, 2009, 33(6): 81-85. XIAO Z X, WANG C S, WANG S X. Small signal stability analysis of microgrid containing multiple micro sources[J]. Automation of Electric Power Systems, 2009, 33(6): 81-85. DOI:10.3321/j.issn:1000-1026.2009.06.019 (in Chinese) |
| [8] |
DJUKANOVIC M, KHAMMASH M, VITTAL V. Application of the structured singular value theory for robust stability and control analysis in multi-machine power systems. I. Framework development[J]. IEEE Transactions on Power Systems, 1998, 13(4): 1311-1316. DOI:10.1109/59.736270 |
| [9] |
SUMSUROOAH S, ODAVIC M, BOZHKO S, et al. Robust stability analysis of a DC/DC buck converter under multiple parametric uncertainties[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5426-5441. DOI:10.1109/TPEL.2017.2736023 |
| [10] |
SUMSUROOAH S, ODAVIC M, BOZHKO S. μ approach to robust stability domains in the space of parametric uncertainties for a power system with ideal CPL[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 833-844. DOI:10.1109/TPEL.2017.2668900 |
| [11] |
RIGATOS G, SIANO P. Design of robust electric power system stabilizers using Kharitonov's theorem[J]. Mathematics and Computers in Simulation, 2011, 82(1): 181-191. DOI:10.1016/j.matcom.2010.07.008 |
| [12] |
KHUTORYANSKY E, PAI M A. Parametric robust stability of power systems using generalized Kharitonov's theorem[C]//Proceedings of the 36th IEEE Conference on Decision and Control. San Diego, CA, USA: IEEE, 1997, 4: 3097-3099.
|
| [13] |
ZHOU J H, SHI P, GAN D Q, et al. Large-scale power system robust stability analysis based on value set approach[J]. IEEE Transactions on Power Systems, 2017, 32(5): 4012-4023. DOI:10.1109/TPWRS.2017.2657642 |
| [14] |
SHI P, JIANG C, GAN D, et al. New value set approach for robust stability of power systems with wind power penetration[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 811-821. DOI:10.1109/TSTE.2018.2848703 |
| [15] |
ZHOU J H, ZHENG T Y, GAN D Q. Value-set-based power system robust stability analysis: Further results[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1383-1392. DOI:10.1109/TPWRS.2018.2878444 |
| [16] |
LIU J Z, ZHANG W, RIZZONI G. Robust stability analysis of DC microgrids with constant power loads[J]. IEEE Transactions on Power Systems, 2018, 33(1): 851-860. DOI:10.1109/TPWRS.2017.2697765 |
| [17] |
SIMFUKWE D D, PAL B C. Robust and low order power oscillation damper design through polynomial control[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1599-1608. DOI:10.1109/TPWRS.2012.2215348 |
| [18] |
YANG S, LIU F, ZHANG D, et al. Polynomial approximation of the small-signal stability region boundaries and its credible region in high-dimensional parameter space[J]. International Transactions on Electrical Energy Systems, 2013, 23(6): 784-801. DOI:10.1002/etep.1624 |
| [19] |
PAN Y F, MEI S W, LIU F, et al. Admissible region of large-scale uncertain wind generation considering small-signal stability of power systems[J]. IEEE Transactions on Sustainable Energy, 2016, 7(4): 1611-1623. DOI:10.1109/TSTE.2016.2570286 |
| [20] |
PAN Y F, LIU F, CHEN L J, et al. Towards the robust small-signal stability region of power systems under perturbations such as uncertain and volatile wind generation[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1790-1799. DOI:10.1109/TPWRS.2017.2714759 |
| [21] |
SHUAI Z K, PENG Y L, LIU X, et al. Parameter stability region analysis of islanded microgrid based on bifurcation theory[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6580-6591. DOI:10.1109/TSG.2019.2907600 |
| [22] |
KUNDU S, DU W, NANDANOORI S P, et al. Identifying parameter space for robust stability in nonlinear networks: A microgrid application[C]//American Control Conference. Philadelphia, PA, USA: IEEE, 2019: 3111-3116.
|
| [23] |
PULCHERIO M C, ILLINDALA M S, YEDAVALLI R K. Robust stability region of a microgrid under parametric uncertainty using bialternate sum matrix approach[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5553-5562. DOI:10.1109/TPWRS.2018.2815980 |
| [24] |
PAI M A, VOURNAS C D, MICHEL A N, et al. Applications of interval matrices in power system stabilizer design[J]. International Journal of Electrical Power and Energy Systems, 1997, 19(3): 179-184. DOI:10.1016/S0142-0615(96)00041-5 |
| [25] |
梅生伟. 现代鲁棒控制理论与应用[M]. 北京: 清华大学出版社, 2003. MEI S W. Modern robust control theory and application[M]. Beijing: Tsinghua University Press, 2003. (in Chinese) |
| [26] |
KUZNETSOV Y A. Elements of applied bifurcation theory[M]. Wilmersdorf: Springer Science & Business Media, 2013.
|
| [27] |
YEDAVALLI R K. Flight control application of new stability robustness bounds for linear uncertain systems[J]. Journal of Guidance, Control, and Dynamics, 1993, 16(6): 1032-1037. DOI:10.2514/3.21124 |
| [28] |
FULLER A T. Conditions for a matrix to have only characteristic roots with negative real parts[J]. Journal of Mathematical Analysis and Applications, 1968, 23(1): 71-98. DOI:10.1016/0022-247X(68)90116-9 |



