目前中国已建设了近10万座大坝,其中大量工程处于不同程度的病险状态[1-2]。通过引入数学统计领域的新方法、充分考虑大坝安全监测中的不确定因素,建立安全综合评价模型准确评价大坝的安全状态,是保障大坝安全的必要手段[3]。大坝综合安全评价已有诸多研究:何金平等[4]提出了基于改进云合并算法的大坝安全评价模型,适应大坝安全评价多指标、多层级等特点;李婷婷[5]以混凝土坝结构安全状况为评价目标,提出了基于粗糙集的模糊神经网络安全综合评价方法。施玉群等[6]建立了基于信息熵理论的大坝安全状态多效应量聚类融合评价模型, 实现大坝安全状态多效应量定量评价。此外,有限元计算[7-8]、多属性决策[9-11]、人工神经网络[12]、Bayes框架[13]等也被用于大坝安全综合评价研究中。这些评价方法已经应用于实际工程中,并取得了良好效果,但是存在不确定性处理欠佳、信息冲突问题难以处理、依赖样本数量等缺陷。
由于证据理论可在无先验知识的情况下表达不确定信息,相比于上述方法,可有效解决不确定性、冲突性的信息之间的组合问题,亦不存在依赖样本数量的缺陷,在大坝安全监控与安全评价领域得到广泛应用。Su等[14]结合证据理论和集对理论融合大坝安全多源时空信息,对大坝工程的安全状态进行评价和发展预测;何金平等[15]提出了一种适合于高拱坝Dempster-Shafer(D-S)证据融合评价的融合系数计算公式,建立了基于改进型证据理论的高拱坝多效应量融合模型;Wu等[16]提出一种融合云模型和证据理论的混合信息融合方法,对一座实际运行的尾矿坝进行安全评估;周心怡等[17]构建了考虑谷幅变形指标的大坝安全多源信息融合评价指标体系,采用云模型和证据理论相结合的方法来评价大坝的安全性。然而,目前基于证据理论的大坝安全综合评价的相关研究在证据的冲突处理和融合方面仍然存在不足。
在基于证据理论的大坝多源信息融合过程中,现有研究多采用Euclid距离等传统距离度量方法[18-19]对证据体进行客观赋权、处理证据冲突,但是存在综合评价结果准确性较差的问题;此外,大坝安全评价既具有一般综合评价问题的共同特性,也存在本身固有特点,即各监测类型对大坝安全评价结果的贡献和重要性是不同的。现有研究基于距离度量的计算方法可能得到不合理的客观融合权重,例如变形监测类型的权重小于环境量监测类型的权重。此外,受到测量仪器、人员操作以及环境等不确定因素影响,大坝安全监测数据采集和传输过程中易出现粗差,进而导致冲突信息的产生。常用的粗差识别方法有过程线方法、统计概率方法、机器学习方法等[20]。过程线方法费时费力且过于依赖专家经验。统计概率方法常假设残差序列服从正态分布,存在残差序列分布与实际分布不同的问题。相比于上述2种方法,机器学习方法由于基于数据驱动并且可以不考虑先验知识而得到广泛应用。在大坝安全监测粗差数据识别中,存在正负样本数量不平衡的问题,孤立森林(isolation forest,iForest)算法[21]作为无监督方法能够解决该问题,已经成为粗差识别的常用方法。然而,由于该方法仅对全局异常点敏感,难以有效考虑大坝安全监测数据的周期性与趋势性,导致粗差识别精度较低。
综上所述,本文提出考虑融合权重优化与冲突信息来源的大坝安全综合评价方法。在信息融合阶段,首先建立从监测点到监测项目再到监测类型的大坝安全评价信息融合层次结构,在监测点和监测项目(表观变形、量水堰、心墙土压力等)2个层级信息融合中使用卡方散度[22]度量证据体间距离从而获得证据组合权重。然后,通过Shannon熵量化证据体不确定性从而进而调整融合权重,克服了传统距离度量方法融合结果可靠性较差的缺陷,以此处理证据冲突问题。同时,针对现有研究基于距离度量的方式无法准确计算监测类型层级信息的融合权重,本文采用乘积标度法[23]确定各监测类型(变形、应力应变、环境量)层级的证据体主观融合权重。此外,提出基于鲁棒加权回归的季节趋势分解(seasonal-trend decomposition procedure based on loess,STL)-iForest算法的粗差剔除方法,解决冲突信息来源问题。该方法使用STL分解[24]消除数据周期性和趋势性对粗差剔除精度的影响,在此基础上利用iForest算法对余项进行处理,识别并剔除数据粗差,避免冲突证据产生。最后,将本文方法应用于中国西南地区某高心墙堆石坝的安全评价,结果表明本文方法既可全面可靠地处理大坝多源信息融合中的证据冲突问题,也可避免产生不合理的监测类型融合权重。
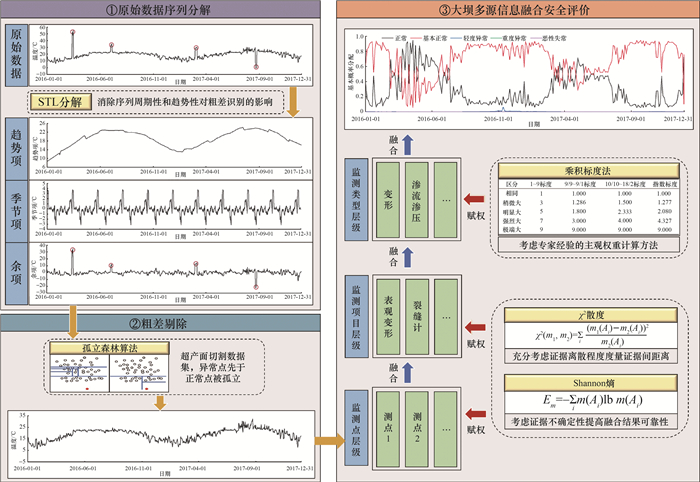
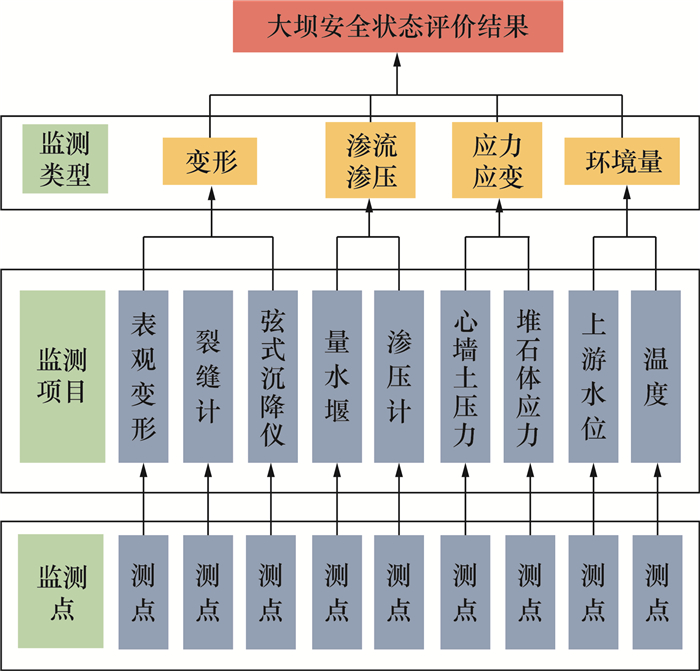
1 考虑融合权重优化与冲突信息来源的大坝安全综合评价方法本文提出的大坝安全综合评价方法的基本框架如图 1所示。本文将大坝安全评价的多源信息融合结构分为监测类型、监测项目、监测测点3个层次,从变形、渗流渗压、应力应变、环境量4个监测类型中选取了9个监测项目,见图 2。
|
| 图 1 本文方法框架 |
|
| 图 2 大坝安全评价信息融合层次结构 |
在证据融合阶段的监测点和监测项目层级中,在采用卡方散度对证据体进行距离度量得到客观融合权重的基础上,通过Shannon熵量化证据体不确定性调整权重获得可靠性更高的融合结果。对于监测类型层级信息,本文方法采用乘积标度法计算监测类型层级主观融合权重。此外,运用基于STL-iForest数据粗差剔除方法,预处理大坝原始安全监测数据,避免后续信息融合过程产生冲突证据,从来源上解决冲突信息的问题。
1.1 考虑融合权重优化的大坝多源信息融合安全评价本文提出的方法首先基于大坝安全综合评价指标范围(见表 1)和区间数法实现各监测点数据到基本概率分配(证据体)的转换。其次,在利用卡方散度获得证据体客观融合权重基础上,通过Shannon熵量化证据体不确定性,调整融合权重,实现监测点到监测项目层级信息的逐层融合。最后,基于大坝安全评价关于指标权重的已有研究,采用乘积标度法计算监测类型层级信息的主观融合权重,从而获得大坝安全状态评价的最终结果。
| 效应量 | 指标 | 正常 | 基本正常 | 轻度异常 | 重度异常 | 恶性失常 |
| 变形D1 | 表观变形D11/mm | (0, 250) | (-250, 450) | (-450, 650) | (-650, 850) | (-850, 1 000) |
| 裂缝计D12/mm | (0, 3) | (3, 6) | (6, 9) | (9, 12) | (12, 15) | |
| 弦式沉降仪D13/mm | (0, 420) | (-420, 600) | (-600, 750) | (-750, 900) | (-900, 1 000) | |
| 渗流渗压D2 | 量水堰D21/(L·s-1) | (0, 3.5) | (3.5, 6.5) | (6.5, 8.5) | (8.5, 10.5) | (10.5, 12.5) |
| 渗压计D22/m | (0, 100) | (-100, 200) | (-200, 300) | (-300, 400) | (-400, 500) | |
| 应力应变D3 | 心墙土压力D31/MPa | (0, 4.5) | (4.5, 6.5) | (6.5, 8.5) | (8.5, 10.5) | (10.5, 12.5) |
| 堆石体应力D32/MPa | (0, 4.0) | (4.0, 6.0) | (6.0, 8.0) | (8.0, 10.0) | (10.0, 12.0) | |
| 环境量D4 | 上游水位D41/m | (-765.0, 812.0) | (-812.0, 814.0) | (-814.0, 816.0) | (-816.0, 818.0) | (-818.0, 821.5) |
| 温度D42/℃ | (0, 8.00) | (8.00, 16.00) | (16.00, 24.00) | (24.00, 32.00) | (32.00, 40.00) |
1.1.1 基于区间数的基本概率分配计算方法
根据已有研究[23], 确定大坝安全等级可分为{正常,基本正常,轻度异常,重度异常,恶性失常}。选取的9个监测项目的等级取值范围见表 1。其中:变形、渗流渗压、应力应变的标准选取参考了已有的监测分析成果(资料来源于某工程竣工安全鉴定报告和工程安全监测资料综合分析报告);温度指标采用实际气温与历史年平均气温的差值。
采用区间法[25]结合表 1实现监测点数据到基本概率分配的转化。区间数法的2个重要定义如下:
1) 区间数距离。设X=[x1, x2]和Y=[y1, y2] 2个区间数,则区间数X和Y之间距离的二次方为
| $ \begin{gathered} D^{2}(X, Y)=\left[\left(x_{1}+x_{2}\right) / 2-\left(y_{1}+y_{2}\right) / 2\right]^{2}+ \\ {\left[\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)\right]^{2} / 12 .} \end{gathered} $ | (1) |
2) 区间相似度。X和Y的相似度S(X, Y)定义为
| $ S(X, Y)=1 /[1+\alpha D(X, Y)] . $ | (2) |
式中支持系数α>0,一般取5。
以温度在2017年5月25日的数据3.27 ℃为例说明具体计算过程:
1) 计算监测数据区间(3.27, 3.27) ℃与表 1中温度对应指标范围{(0, 8.00) ℃, (8.00, 16.00) ℃, (16.00, 24.00) ℃, (24.00, 32.00) ℃, (32.00, 40.00)} ℃之间的距离为{2.422 0, 9.030 3, 16.888 6, 24.837 6, 32.811 4};
2) 计算监测数据区间于对应指标范围之间相似度为{0.076 3, 0.021 7, 0.011 7, 0.008 0, 0.006 1};
3) 对相似度归一化得到基本概率分配{0.616 7, 0.175 2, 0.094 6, 0.064 6, 0.049 0}。
1.1.2 基于卡方散度的监测点和监测项目层级信息融合方法由于采用不精确的Mass函数赋值和识别框架不完整而产生的证据冲突,是制约证据理论应用的主要原因。本文基于通过证据预处理改善证据冲突的思路,在监测点和监测项目层级信息融合中引入卡方散度和Shannon熵,通过对证据间进行距离度量获得客观融合权重,而后基于证据不确定性度量结果调整权重,充分考虑证据体的离散程度和不确定性。
一个识别框架下的多个证据在融合中可以通过证据体间距离度量的方式获得客观融合权重。本文引入卡方散度[22]作为证据体间距离度量方法,该方法可以有效地判断证据之间的差异,并且敏锐感知证据变化,显著提高融合结果可靠性。卡方散度CD的具体定义为:
| $ \begin{gathered} \operatorname{CD}\left(m_{1}, m_{2}\right)=\frac{1}{2}\left[\chi^{2}\left(m_{1}, \frac{m_{1}+m_{2}}{2}\right)+\right. \\ \left.\chi^{2}\left(m_{2}, \frac{m_{1}+m_{2}}{2}\right)\right], \end{gathered} $ | (3) |
| $ \begin{gathered} \chi^{2}\left(m_{1}, m_{2}\right)= \\ \sum\limits_{i} \frac{\left(m_{1}\left(A_{i}\right)-m_{2}\left(A_{i}\right)\right)^{2}}{m_{2}\left(A_{i}\right)} . \end{gathered} $ | (4) |
式中:m1和m2为同一识别框架下的2个证据体,m1(Ai)和m2(Ai)分别为证据体m1和m2的焦元Ai对应的基本概率分配。
一个证据具有较大的信息熵,表明该证据被其他证据更好地支持[26]。本文使用Shannon熵度量证据的不确定性,以此调整证据的客观权重,进一步降低冲突信息的影响。证据m的Shannon熵Em具体定义为
| $ E_{m}=-\sum\limits_{i} m\left(A_{i}\right) \operatorname{lb} m\left(A_{i}\right) . $ | (5) |
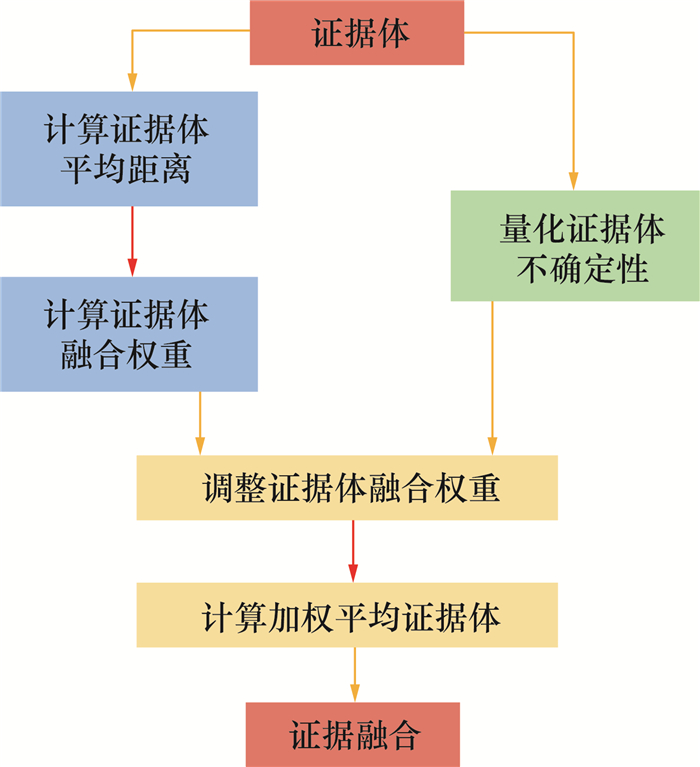
监测点和监测项目层级信息融合方法的流程见图 3,具体步骤如下:
|
| 图 3 监测点和监测项目层级信息融合方法 |
步骤1 通过式(3)计算证据体mi(i=1, 2, …, k)和mj(j=1, 2, …, k)两两之间距离dij。
步骤2 计算证据体mi与其他证据体的平均距离,
| $ d_{A i}=\frac{\sum\limits_{j=1, j \neq i}^{k} d_{i j}}{k-1} . $ | (6) |
步骤3 计算证据体mi融合权重,
| $ W_{i}=\frac{1 / d_{A i}}{\sum\limits_{j=1, j \neq i}^{k} d_{i j}} . $ | (7) |
步骤4 通过式(5)量化证据体mi的不确定性并归一化,
| $ U_{i}=\frac{\mathrm{e}^{-\sum\limits_{i} m\left(A_{i}\right) \mathrm{lb} \;m\left(A_{i}\right)}}{\sum\limits_{N=1}^{k} \mathrm{e}^{-\sum\limits_{N} m\left(A_{N}\right) \mathrm{lb}\; m\left(A_{N}\right)}} . $ | (8) |
步骤5 调整证据体的融合权重并且归一化得到最终的客观融合权重,
| $ U_{A i}=\frac{U_{i} \cdot W_{i}}{\sum\limits_{N=1}^{k}\left(U_{N} \cdot W_{N}\right)} . $ | (9) |
步骤6 计算加权平均证据体,
| $ A(m)=\sum\limits_{i=1}^{k}\left(U_{A i} \cdot m_{i}\right) . $ | (10) |
步骤7 通过Dempster组合规则对加权平均证据体进行融合,得到多证据的最终融合结果。
1.1.3 基于乘积标度法的监测类型层级信息融合方法在大坝安全评价中,变形、渗流渗压、应力应变和环境量各监测类型的重要性有明显差异,在多源信息融合过程中应考虑到这一点。上述客观融合权重计算方法在计算各监测类型融合权重时,可能会得到不合理的结果,例如变形监测类型的权重小于环境量监测类型的权重。为此,本文采用乘积标度法计算监测类型层级信息融合权重[23]。乘积标度法是在层次分析法4种标度的基础上,兼顾大坝安全综合评价的客观特点的一种赋权方法, 如表 2所示。本文充分考虑专家经验,运用乘积标度法确定监测类型层级信息融合中各证据体的主观权重,最后通过Dempster组合规则实现证据的主观加权融合。监测层级信息融合结果即为最终的大坝安全状态综合评价结果。
| 区分 | 1~9标度 | 9/9~9/1标度 | 10/10~18/2标度 | 指数标度 |
| 相同 | 1 | 1.000 | 1.000 | 1.000 |
| 稍微大 | 3 | 1.286 | 1.500 | 1.277 |
| 明显大 | 5 | 1.800 | 2.333 | 2.080 |
| 强烈大 | 7 | 3.000 | 4.000 | 4.327 |
| 极端大 | 9 | 9.000 | 9.000 | 9.000 |
1.2 基于STL-iForest的监测数据粗差剔除方法
大坝安全监测各效应量的时间序列蕴含不同的变化规律,例如上游水位和温度等环境量具有周期性变化规律;变形等具有一定的趋势性变化规律。由于iForest算法仅对全局异常值敏感,如果直接运用该算法对各效应量监测序列进行检测,极易忽略局部异常信息。因此,本文提出基于STL-iForest的监测数据粗差剔除方法。在STL分解消除原始数据周期性和趋势性的基础上,采用iForest算法识别并剔除数据粗差。
STL分解方法可将具有周期性的大坝安全监测时间序列数据分解为趋势分量、季节分量和余项,同时避免异常值和缺失值的影响。本文使用的加性模型表达式为
| $ Y_{t}=T_{t}+S_{t}+R_{t}, t \in[1, N] . $ | (11) |
式中: Yt、Tt、St和Rt分别为t时刻的时间序列数据、趋势分量、周期分量和余项分量。
iForest算法的基本原理是用一个随机超平面切割数据空间,将数据空间分为2个子空间,再对子空间进行切割,一直切割到每个子空间里只有一个数据节点,由此形成孤立树,其每个叶子节点中都只包含一个数据节点。离群点处的数据密度很低,因此数据分割过程很快就会停到一个子空间中,可根据叶子节点x到根节点的路径h(x)长度判断数据x是否是离群点[21]。
iForest由多个孤立树组成。给定一个含有n个监测数据点的数据集,树的平均高度为
| $ c(n)= \begin{cases}2 H(n-1)-2(n-1) / n, & n>2 ; \\ 1, & n=2 ; \\ 0, & n<2 .\end{cases} $ | (12) |
式中H(i)=ln i+0.577 215 664 9(Euler常数)。
样本点x的异常得分可定义为
| $ s(x, n)=2^{-\mathrm{E}(h(x)) c(n)} . $ | (13) |
式中E(h(x))为样本点x在iForest所有孤立树中路径长度的期望。异常分数的取值范围为[0, 1]。如果某样本点异常得分近似等于1,则该样本点为异常点,即该样本点为安全监测数据中应剔除的粗差。
2 工程应用 2.1 工程概况某高心墙堆石坝位于云南省澜沧江下游河段上,为Ⅰ等大(1)型工程,最大坝高261.5 m。在堆石坝施工期间布置了多种安全监测仪器,具有较为完备的监测系统,监测量包括变形、渗流、应力应变、温度和上游水位等。为验证本文方法的有效性,选取2016年1月1日至2017年12月31日的大坝安全监测数据序列作为试验数据进行大坝安全评价,具体见表 3。
| 效应量 | 指标 | 测点数 |
| 变形 | 表观变形 | 3 |
| 裂缝计 | 2 | |
| 弦式沉降仪 | 2 | |
| 渗流 | 量水堰 | 1 |
| 渗压计 | 2 | |
| 应力应变 | 心墙土压力 | 3 |
| 堆石体应力 | 2 | |
| 环境量 | 上游水位 | 1 |
| 温度 | 1 |
2.2 基于STL-iForest的大坝监测数据粗差剔除
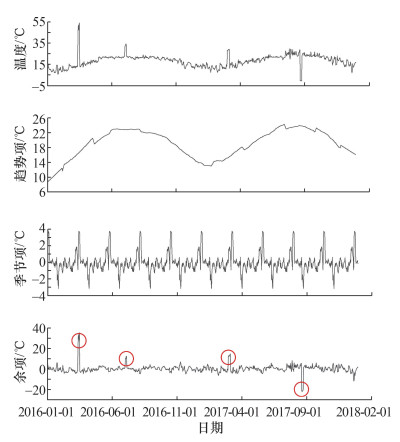
试验数据中存在粗差的数据序列信息见表 4。通过试验确定,当表观变形的2个序列、量水堰序列和温度序列STL分解的周期参数分别为60、60、48和72时,能够较好地分离出原始数据的周期项和趋势项。其中温度序列数据分解结果如图 4所示,序列被分解为趋势项、周期项和余项,圈红处为粗差点。可以看出,该分解方法可以将各序列的粗差保留在余项中,为后续的粗差识别奠定良好基础。
|
| 图 4 温度数据STL分解结果 |
利用iForest算法对4个序列的余项进行粗差识别,具体参数设置如下:iForest样本容量为256,最大层高为8,iForest数目为100,最大迭代次数为50次。异常得分的判断阈值v为
| $ v=r_{1}+\left(r_{2}-r_{1}\right)(f-1) / f \text {. } $ | (14) |
式中:r1表示阈值初始值,实际取值时可先取0.50,根据实际情况进行调整;r2为参数,文中取1.00; f为当前迭代次数。
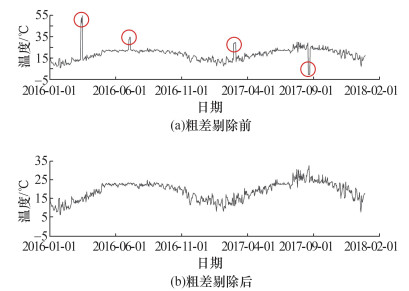
图 5以温度序列为例展示了粗差识别前后对比。可见,本文方法基本剔除了数据序列中明显的粗差点。
|
| 图 5 温度数据粗差剔除前后对比 |
2.3 大坝多源信息融合安全综合评价
2016年3月13日的各测点数据中,表观测点1存在粗差975.46 mm。经粗差剔除后,采用Hermite插值法补全数据。下面以此日数据为例说明融合计算过程:
1) 首先基于区间数法和表 1,将原始数据转化为基本概率分配,结果见表 5。下标中“-”之前的部分含义见表 1,表示效应量对应的指标;下标中“-”之后的部分结合表 3,代表对应指标的具体测点,例如D11-1代表第1个测点的表观变形。
| 监测点 | 正常 | 基本正常 | 轻度异常 | 重度异常 | 恶性失常 |
| D11-1 | 0.396 | 0.317 | 0.136 | 0.086 | 0.065 |
| D11-2 | 0.510 | 0.238 | 0.116 | 0.076 | 0.059 |
| D11-3 | 0.542 | 0.218 | 0.110 | 0.073 | 0.057 |
| D12-1 | 0.273 | 0.423 | 0.151 | 0.089 | 0.063 |
| D12-2 | 0.192 | 0.505 | 0.157 | 0.087 | 0.060 |
| D13-1 | 0.292 | 0.332 | 0.169 | 0.116 | 0.092 |
| D13-2 | 0.281 | 0.341 | 0.170 | 0.116 | 0.092 |
| D21 | 0.241 | 0.403 | 0.166 | 0.109 | 0.081 |
| D22-1 | 0.444 | 0.297 | 0.125 | 0.078 | 0.057 |
| D22-2 | 0.452 | 0.291 | 0.123 | 0.078 | 0.056 |
| D31-1 | 0.353 | 0.294 | 0.160 | 0.110 | 0.083 |
| D31-2 | 0.34 | 0.303 | 0.162 | 0.111 | 0.084 |
| D31-3 | 0.304 | 0.331 | 0.168 | 0.112 | 0.084 |
| D32-1 | 0.374 | 0.288 | 0.154 | 0.105 | 0.079 |
| D32-2 | 0.356 | 0.301 | 0.158 | 0.106 | 0.080 |
| D41 | 0.015 | 0.321 | 0.283 | 0.216 | 0.165 |
| D42 | 0.594 | 0.194 | 0.098 | 0.065 | 0.049 |
2) 运用1.1.2节提出的监测项目层级信息融合方法,按照图 2由监测点级信息逐层向上融合,结果见表 6。
| 指标 | 正常 | 基本正常 | 轻度异常 | 重度异常 | 恶性失常 |
| D1 | 0.158 | 0.838 | 0.004 | 0 | 0 |
| D2 | 0.460 | 0.449 | 0.057 | 0.022 | 0.012 |
| D3 | 0.661 | 0.321 | 0.015 | 0.003 | 0.001 |
| D4 | 0.303 | 0.331 | 0.195 | 0.108 | 0.063 |
3) 基于大坝安全评价中指标权重的已有研究[23],可知变形、渗流渗压、应力应变的重要性比值为D1∶D2∶D3=1.833∶1.354∶1。同时,考虑环境量并不能直接反映出大坝的安全状态,将应力应变相对于环境量的重要性定性于“明显大”,则D3∶D4= 2.071∶1。由此可得4个监测类型信息的融合权重为[0.393, 0.290, 0.214, 0.103]。如果使用1.1.2节提出的监测点和监测项目层级信息融合方法计算,各监测类型客观融合权重为[0.028, 0.357, 0.483, 0.132],显然是不合理的。最后,运用1.2节的监测类型层级信息融合方法计算得到最终融合结果,具体见表 7,可知大坝在2016年3月13日的安全状态可判定为基本正常,这与实际情况是相符的。
为了说明本文方法相对于传统证据理论方法的优势,将各方法对比结果展示于表 8。由于不能处理冲突信息,传统证据理论得到与实际情况完全相悖的评价结果,即大坝安全状态为恶性失常。本文方法充分考虑证据体的离散程度和不确定性,将大坝安全状态评价为基本正常,与实际情况相符。相比基于Euclid距离的证据理论和未剔除数据粗差的情况,本文方法将基本正常状态对应的概率提升至0.842,说明该方法具有更高的可靠性。
| 信息融合方法 | 正常 | 基本正常 | 轻度异常 | 重度异常 | 恶性失常 |
| 本文方法 | 0.158 | 0.842 | 0 | 0 | 0 |
| 本文方法(Euclid距离) | 0.282 | 0.718 | 0 | 0 | 0 |
| 本文方法(未剔除粗差) | 0.255 | 0.744 | 0 | 0 | 0 |
| 传统证据理论 | 0 | 0 | 0 | 0 | 1.000 |
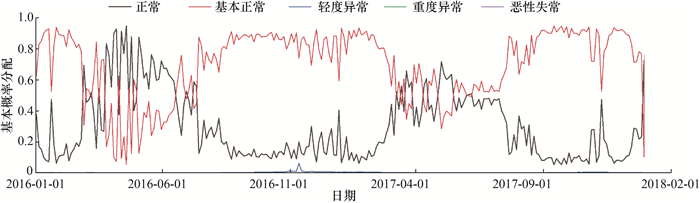
最后, 运用本文方法获得试验数据逐日的大坝安全评价结果,具体见图 6。可见,在试验数据的时间范围内,大坝安全状态处于正常或基本正常状态,安全评价结果符合实际情况。
|
| 图 6 大坝逐日安全状态评价结果 |
3 结论
建立大坝综合安全评价模型对工程的安全状态进行准确评价对保障大坝安全具有重要意义。本文针对基于证据理论的大坝安全综合评价已有研究中关于证据冲突和融合权重处理的不足,提出考虑融合权重优化和冲突信息来源的大坝多源信息融合安全评价方法,主要结论如下:
1) 针对已有研究多采用Euclid距离等方法确定证据体的融合权重,存在综合评价结果可靠性较差的问题,在使用卡方散度度量监测点和监测项目层级证据体间距离获得证据融合客观权重的基础上,通过Shannon熵度量证据体不确定性从而调整客观融合权重,最终实现准确的大坝安全状态评价。本文方法可以很大程度避免冲突证据的负面影响,提高融合结果的准确性,保证定性评价结果的可靠性。
此外,针对基于距离度量方式在监测类型层级得到与实际相悖的融合权重问题,本文基于大坝安全评价中指标权重的已有研究,采用乘积标度法计算各监测类型证据体主观融合权重,准确量化各监测类型对大坝安全综合评价结果的贡献差异。
2) 从冲突证据产生的原因出发,运用所提出的基于STL-iForest的数据粗差识别方法首先将安全监测数据序列分解为趋势项、周期项和余项,避免数据周期性和趋势性对粗差剔除准确性的影响。在此基础上准确剔除数据粗差,弥补了现有研究未能从来源上消除冲突证据的不足。
3) 以某高心墙堆石坝为例,基于变形、渗流渗压、应力应变和环境量监测数据,采用本文方法对大坝安全状态进行评价。以某一时刻为例,对比了不同方法的评价效果,本文所提方法将评价结果的对应概率由0.718提升至0.842,说明该方法具有更高的可靠性。同时,对于试验时间范围内的所有时间步,评价结果均处于正常或基本正常状态,与实际情况相符,说明该方法准确、实用。
| [1] |
中华人民共和国水利部. 2020年全国水利发展统计公报[M]. 北京: 中国水利水电出版社, 2021. Ministry of Water Resources, People's Republic of China. 2020 Statistic bulletin on China water activities[M]. Beijing: China Water & Power Press, 2021. (in Chinese) |
| [2] |
吴中如, 徐波, 顾冲时, 等. 大坝服役状态的综合评判方法[J]. 中国科学: 技术科学, 2012, 42(11): 1243-1254. WU Z R, XU B, GU C S, et al. Comprehensive evaluation methods for dam service status[J]. Science China: Technological Sciences, 2012, 42(11): 1243-1254. (in Chinese) |
| [3] |
何金平. 大坝健康状态综合诊断方法研究进展[J]. 水电与新能源, 2016(1): 1-6, 11. HE J P. Advances in comprehensive diagnostic methods for dam health status[J]. Hydropower and New Energy, 2016(1): 1-6, 11. (in Chinese) |
| [4] |
何金平, 高全. 一种适应大坝健康诊断的改进云合并算法[J]. 武汉大学学报(信息科学版), 2018, 43(7): 1022-1029. HE J P, GAO Q. An improved algorithm of cloud fusion for dam health diagnosis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1022-1029. (in Chinese) |
| [5] |
李婷婷. 混凝土坝健康诊断及其预警系统[D]. 南京: 河海大学, 2006. LI T T. Health diagnosis and early-warning system for concrete dam[D]. Nanjing: Hohai University, 2006. (in Chinese) |
| [6] |
施玉群, 何金平. 基于信息熵的大坝多效应量聚类融合诊断模型[J]. 水力发电学报, 2013, 32(5): 239-243. SHI Y Q, HE J P. Multiple effect quantity fusion diagnosis model of dam health based on information entropy and cluster analysis[J]. Journal of Hydroelectric Engineering, 2013, 32(5): 239-243. (in Chinese) |
| [7] |
徐小蓉, 何涛洪, 雷峥琦, 等. 超长坝段堆石混凝土重力坝蓄水运行安全评价[J]. 清华大学学报(自然科学版), 2022, 62(9): 1375-1387. XU X R, HE T H, LEI Z Q, et al. Safety evaluation of rock-filled concrete gravity dam with long section during the impoundment operation period[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(9): 1375-1387. (in Chinese) |
| [8] |
ORMANN L, ZARDARI M A, MATTSSON H, et al. Numerical analysis of strengthening by rockfill embankments on an upstream tailings dam[J]. Canadian Geotechnical Journal, 2013, 50(4): 391-399. DOI:10.1139/cgj-2012-0255 |
| [9] |
RIBAS J R, SEVERO J C R, FELIX L C G, et al. Prioritization of hydroelectric power plant earth dam safety procedures: A multi-criteria approach[J]. Environmental Earth Sciences, 2021, 80(24): 815. DOI:10.1007/s12665-021-10096-9 |
| [10] |
MASOUMI I, AHANGARI K, NOORZAD A. Integrated fuzzy decision approach for reliability improvement of dam instrumentation and monitoring[J]. Journal of Structural Integrity and Maintenance, 2018, 3(2): 114-125. DOI:10.1080/24705314.2018.1461546 |
| [11] |
YUCESAN M, KAHRAMAN G. Risk evaluation and prevention in hydropower plant operations: A model based on Pythagorean fuzzy AHP[J]. Energy Policy, 2019, 126: 343-351. DOI:10.1016/j.enpol.2018.11.039 |
| [12] |
闫滨, 高真伟, 李东艳. RBF神经网络在大坝安全综合评价中的应用[J]. 岩石力学与工程学报, 2008, 27(S2): 3991-3997. YAN B, GAO Z W, LI D Y. Application of radial basis function neural network to comprehensive evaluation of dam safety[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2): 3991-3997. (in Chinese) |
| [13] |
SEVIERI G, DE FALCO A. Dynamic structural health monitoring for concrete gravity dams based on the Bayesian inference[J]. Journal of Civil Structural Health Monitoring, 2020, 10(2): 235-250. |
| [14] |
SU H Z, WEN Z P, SUN X R, et al. Multisource information fusion-based approach diagnosing structural behavior of dam engineering[J]. Structural Control and Health Monitoring, 2018, 25(2): e2073. |
| [15] |
何金平, 马传彬, 施玉群. 高拱坝多效应量改进型D-S证据理论融合模型[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1397-1400. HE J P, MA C B, SHI Y Q. Multi-effect-quantity fusion model of high arch dam based on improved D-S evidence theory[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1397-1400. (in Chinese) |
| [16] |
WU X G, DUAN J C, ZHANG L M, et al. A hybrid information fusion approach to safety risk perception using sensor data under uncertainty[J]. Stochastic Environmental Research and Risk Assessment, 2018, 32(1): 105-122. |
| [17] |
周心怡, 胡蕾, 张启灵. 考虑谷幅收缩变形的高拱坝多源信息融合安全评判[J]. 长江科学院院报, 2023, 40(1): 87-93. ZHOU X Y, HU L, ZHANG Q L. Safety evaluation of high arch dam based on multi-source information fusion in consideration of valley shrinkage deformation[J]. Journal of Yangtze River Scientific Research Institute, 2023, 40(1): 87-93. (in Chinese) |
| [18] |
王燕, 叶伟, 马福恒. 基于D-S证据理论融合采空区多源信息的大坝安全评价[J]. 水利水电技术, 2020, 51(4): 175-183. WANG Y, YE W, MA F H. D-S evidence theory-based dam safety assessment fused with multi-source information of goaf area[J]. Water Resources and Hydropower Engineering, 2020, 51(4): 175-183. (in Chinese) |
| [19] |
叶伟, 马福恒, 周海啸. 加权优化的D-S证据理论在大坝安全评价中的应用[J]. 水电能源科学, 2016, 34(6): 96-99. YE W, MA F H, ZHOU H X. Application of weight optimized D-S evidence theory in dam safety evaluation[J]. Water Resources and Power, 2016, 34(6): 96-99. (in Chinese) |
| [20] |
LI B, YANG J, HU D X. Dam monitoring data analysis methods: A literature review[J]. Structural Control and Health Monitoring, 2020, 27(3): e2501. |
| [21] |
肖白, 周文凯, 姜卓. 基于孤立森林、模态分解和神经网络的空间负荷态势感知[J]. 电力系统自动化, 2022, 46(18): 190-198. XIAO B, ZHOU W K, JIANG Z. Spatial load situation awareness based on isolation forest, mode decomposition and neural networks[J]. Automation of Electric Power Systems, 2022, 46(18): 190-198. (in Chinese) |
| [22] |
GAO X Y, XIAO F Y. A generalized χ2 divergence for multisource information fusion and its application in fault diagnosis[J]. International Journal of Intelligent Systems, 2022, 37(1): 5-29. |
| [23] |
何金平. 大坝安全监测理论与应用[M]. 北京: 中国水利水电出版社, 2010. HE J P. Theory and application of dam safety monitoring[M]. Beijing: China Water & Power Press, 2010. (in Chinese) |
| [24] |
张力, 王红瑞, 郭琲楠, 等. 基于时序分解与机器学习的非平稳径流序列集成模型与应用[J]. 水科学进展, 2023, 34(1): 42-52. ZHANG L, WANG H R, GUO B N, et al. Integrated model and application of non-stationary runoff based on time series decomposition and machine learning[J]. Advances in Water Science, 2023, 34(1): 42-52. (in Chinese) |
| [25] |
康兵义, 李娅, 邓勇, 等. 基于区间数的基本概率指派生成方法及应用[J]. 电子学报, 2012, 40(6): 1092-1096. KANG B Y, LI Y, DENG Y, et al. Determination of basic probability assignment based on interval numbers and its application[J]. Acta Electronica Sinica, 2012, 40(6): 1092-1096. (in Chinese) |
| [26] |
XIAO F Y. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy[J]. Information Fusion, 2019, 46: 23-32. |



