犯罪侦查是公共安全、刑事科学等领域的重要研究方向，内容主要包括证据收集和证据推理。证据收集是侦查阶段的重点，也是推理作案行为和犯罪事实的基础。在放火、杀人、爆炸等刑事案件中，案件现场留下的证据对推理作案行为、确定犯罪嫌疑人十分关键。证据收集工作一般由公安机关承担。面对大量的刑事案件，公安机关存在人力和时间方面的压力。因此，高效准确地收集证据可减少公安机关人力资源损耗，提高办案效率，具有重要的现实意义。与此同时，不同证据在案件中的重要性不同：有的证据可以直接确定犯罪嫌疑人或确定犯罪行为，因而具有很高的价值；有的证据价值比较有限，比如某一犯罪事实已有十分充足的证据支撑，那么关于该犯罪事实的其他证据在案件推理中的作用就不大^[1]。具有高重要度的证据在侦查阶段被收集，甚至在侦查阶段早期被收集，对准确、高效侦破案件具有十分重要的意义。已有的关于证据收集方面的研究^[2-6]存在不充分、缺乏实际案例数据支撑的问题，因而需要进一步完善。

证据推理是侦查阶段的难点，是确定犯罪事实的方法和手段，其科学实质是不确定性推理^[7-9]。目前学界主要使用2类证据推理方法：基于逻辑的推理方法和概率推理方法。前者根据知识、规则进行案件推理，主要分为论证推理方法(argumentative approach)^[10]、故事推理方法(story approach)^[11-12]和混合推理方法(hybrid approach)^[13-14]；后者主要以概率论为基础，通过严格的数学推导，计算给定证据下相应犯罪主张的概率或概率之比，从而协助侦查审判。由于证据推理是严格的因果推理，而Bayes网络所包含的因果关系恰恰是一种适合进行不确定性因果推理的人工智能分析方法，其推理过程可以在Bayes网络上双向操作，具有正向推理和反向推理的能力^[15-16]。Bayes网络在刑事领域的应用最早可追溯到20世纪90年代，而后不断被学者更新发展^[17-18]。Taylor等^[19]针对生物物证提出了基于行为层级概率进行推理的Bayes网络模型；Fenton等^[20]则利用Bayes网络对杀人、放火^[21]、抢劫^[22]等案件进行了推理分析。然而，相关研究主要针对某类证据或某类案件具体场景，存在通用性不足的问题。

在“十四五”规划的重大战略背景下，国家大力推进智慧警务、数字公安等公安信息化建设，以实现更高水平的公安信息化、智能化和现代化。以上海为例，通过构建上海刑事案件智能辅助办案系统(“206”系统)，为办案人员收集和固定证据提供智能指引，促使公、检、法3个机关办案执行统一的证据标准，确保侦查、审查起诉的案件事实及证据经得起法律检验^[23]。因此，对案件侦查分析的自动化模型研究是实际警务工作的需求和重要发展方向。

在上述背景下，本文提出了基于Bayes网络的犯罪案件侦查决策支持模型。首先，提出了一种基于加权信息熵的证据重要度的计算方法；然后，在该方法基础上构建了基于Bayes网络的证据收集决策支持模型，对案件侦查阶段未收集证据的重要程度进行评价，并给出侦查建议和推理结果；最后，利用构建的决策支持模型对实际案例进行分析。

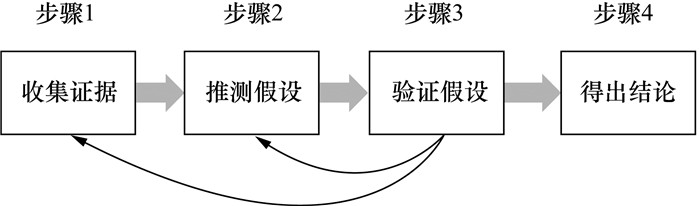
1 犯罪假设推理的Bayes网络模型

在犯罪侦查阶段，对案件的推理分析是一个重建犯罪^[24]的过程，如图 1所示，可分为4个步骤：收集证据、推测假设、验证假设、得出结论^[25-26]。

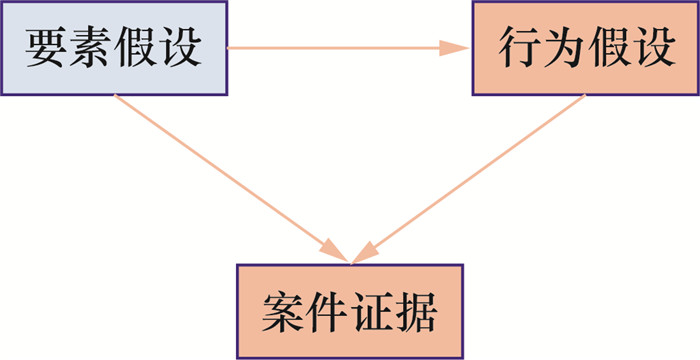
犯罪假设指基于收集的证据对案件的犯罪要素和作案行为进行假设和推测。因此，犯罪假设具体可以分为要素假设和行为假设。基于上述逻辑可以构建犯罪假设推理的Bayes网络模型，如图 2所示。

以“犯罪人O放置助燃物”这一作案行为对构建模型进行说明。“犯罪人O放置助燃物”行为中包含的犯罪要素和可能的案件证据，如表 1所示。

要素假设节点规则: 对于分析得到的每个犯罪要素, 建立相应的要素假设节点$H$。以表 1为例, 要素假设节点$H_{1}$为人员$O$是犯罪人, $H_{2}$为工具$A$是助燃物, $H_{3}$为工具$T$是盛装工具, $H_{4}$为地点$C$是中心现场。假设层中每一节点有2个状态, “是”和“否”, 其中“是”代表该假设成立, “否”代表该假设不成立。

行为假设节点规则: 行为节点$S$和行为地点节点$C$, 行为节点用于推理不同的作案行为, 地点节点用于进一步表达行为发生的位置, 这使推理结果能更加直观地展示作案行为和经过。每个行为节点有2个状态, “是”和“否”, 状态“是”表示该作案行为发生, 状态“否”表示该作案行为没有发生。以表 1为例, 可提取1个行为节点$S_{1}: O$放置助燃物。在完成行为节点构建后, 对每个行为节点构建地点节点, 用于表示行为是否在相应地点发生。每个地点节点也有2个状态, “是”和“否”, 状态“是”表示该行为在此地点发生, 状态“否”表示该行为没有在此地点发生。以表 1为例, 可以构建1个上述行为节点$S_{1}$的地点节点$C_{1}: O$放置助燃物的地点在$C$处。

案件证据节点规则: 案件证据节点包括物品痕迹类证据节点$F$和信息类证据节点$I$。物品痕迹类证据节点$F$由犯罪要素关联关系决定。每个物品痕迹类证据节点有2个状态, “是”和“否”, 其中“是”代表该证据存在，“否”代表该证据不存在。对于信息类证据节点, 考虑到作案行为与信息类证据间的因果关联, 如作案行为和视频监控/证人证言中行为的因果关联, 对每个行为层节点构建相应的信息类证据节点, 用于表达该行为/地点是否有信息类证据支持。以表 1为例, 已构建的行为节点$S_{1}$表示$O$放置助燃物; $C_{1}$表示$O$放置助燃物的地点在$C$处, 那么关于这2个节点的信息类证据节点就是$I_{S_{1}}$和$I_{C_{1}} ; I_{S_{1}}$表示关于$O$放置助燃物的信息类证据; $I_{C_{1}}$表示关于$O$在$C$处实施该行为的信息类证据。每个信息类证据节点也有2个状态, “是”和“否”, “是”代表该信息类证据被调查到，“否”代表该信息类证据没有被调查到。

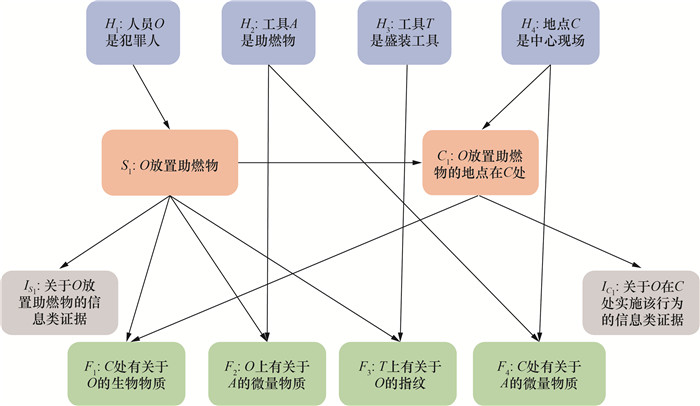
于是根据节点规则可以针对“犯罪人O放置助燃物”这一作案行为构建犯罪假设推理的Bayes网络模型，如图 3所示。

所构建的犯罪假设推理Bayes网络具体过程可参考文[27]，本文不再赘述。

2 基于加权信息熵的证据重要度计算方法

熵的概念来源于统计热力学，用于表达1个系统的有序程度。当系统越无序，即不确定性越大时，熵值越大；当系统越有序，即不确定性越小时，熵值越小。借助于熵的概念，Shannon^[28]提出了信息熵，可以用于表达随机变量的不确定性。

对于1个离散随机变量$X$, 其值域为$\operatorname{val}(X)=$ $\left\{x_{1}, x_{2}, \cdots, x_{m}\right\}$, 该随机变量的信息熵可表示为

$ \varepsilon(X)=-\sum\limits_{x \in \operatorname{val}(X)} P(x) \log P(x) . $

(1)

其中$P(x)$表示$X$取值为$x$的概率。

2.1 犯罪假设的信息熵

对于1个犯罪假设H，在收集到证据e时，其信息熵的计算公式为

$ \varepsilon(H \mid e)=-\sum\limits_{h \in \operatorname{val}(H)} P(h \mid e) \log P(h \mid e) . $

(2)

其中$P(h \mid e)$表示在给定证据$e$时犯罪假设$H$取值为$h$的后验概率。

对于1个证据变量E，其状态的确定可能会使H的后验概率发生改变，进而对信息熵的大小产生影响。利用条件熵来刻画查询E的状态后，犯罪假设H的信息熵可表示为

$ \begin{gathered} \varepsilon(H \mid E)=\sum\limits_{e \in \operatorname{val}(E)} P(e) \varepsilon(H \mid e)=- \\ \sum\limits_{e \in \operatorname{val}(E)} \sum\limits_{h \in \text { val }(H)} P(e) P(h \mid e) \log P(h \mid e)=- \\ \sum\limits_{e \in \operatorname{val}(E)} \sum\limits_{h \in \operatorname{val}(H)} P(h, e) \log P(h \mid e) . \end{gathered} $

(3)

其中，P(h, e)表示H取值为h、E取值为e的联合概率。

根据条件熵，当查询证据变量E的状态后，犯罪假设H的不确定性减少程度可表示为

$ \begin{gathered} \Delta \varepsilon(H, E)=\varepsilon(H)-\varepsilon(H \mid E)= \\ -\sum\limits_{h \in \operatorname{val}(H)} P(h) \log P(h)- \\ \left(-\sum\limits_{e \in \operatorname{val}(E)} \sum\limits_{h \in \operatorname{val}(H)} P(h, e) \log P(h \mid e)\right)= \\ -\sum\limits_{e \in \operatorname{val}(E)} \sum\limits_{h \in \operatorname{val}(H)} P(h, e) \log \frac{P(h, e)}{P(h) P(e)} . \end{gathered} $

(4)

其中Δε(H, E)表示H的信息熵减少程度。对于未收集的证据变量E₁和E₂，若Δε(H, E₁)＜Δε(H, E₂)，相比于E₁，则E₂对确定H的状态更重要。因为在查询E₂的状态后，H的不确定性会减少得更多。

2.2 犯罪假设的加权信息熵

加权信息熵可用于展现知识表达的精确程度^[27]。犯罪假设的不确定性同样可以用加权信息熵来表达。

侦查过程往往涉及多个假设变量，如针对犯罪人、作案工具、作案地点等的假设。为评估证据变量对所有犯罪假设的综合影响程度，可以利用信息熵平均减少比例的计算方法，即

$ \begin{gathered} \Delta \varepsilon_{\mathrm{AM}}\left(H_{\mathrm{set}}, E\right)=\frac{1}{K} \sum\limits_{H \in H_{\mathrm{set}}^{\varepsilon}} \frac{\varepsilon(H)-\varepsilon(H \mid E)}{\varepsilon(H)}= \\ \frac{1}{K} \sum\limits_{H \in H_{\mathrm{set}}^{\varepsilon}} \frac{\Delta \varepsilon(H, E)}{\varepsilon(H)} . \end{gathered} $

(5)

其中: $H_{\mathrm{set}}$表示假设变量所构成的变量集合, $\Delta \varepsilon_{\mathrm{AM}}\left(H_{\mathrm{set}}, E\right)$表示查询$E$使$H_{\mathrm{set}}$中假设变量信息熵减少的平均比例; $H_{\mathrm{set}}^{\varepsilon}$表示$H_{\mathrm{set}}$中信息熵不为0的假设变量组成的集合, $K$表示$H_{\mathrm{set}}^{\varepsilon}$中的假设变量数目。

式(5)中，每个假设变量同等重要。然而，在犯罪侦查过程中不同犯罪假设的地位一般不同，比如，犯罪人的假设往往比其他假设更关键。因此，考虑假设变量之间存在差异性，提出加权信息熵的证据重要度计算方法。

利用权重来表达犯罪假设间的差异性，记权重函数w是从假设集合到[0, 1]区间上的1个映射，

$ w: H_{\mathrm{set}} \rightarrow[0, 1] . $

(6)

当假设的权重越大, 它在侦查过程中就越关键。1个假设的权重大小由与其相关的特征所决定, 记离散变量$Q$是决定假设权重大小的特征变量, $Q$的值域为$\operatorname{val}(Q)$。令函数$f$是从假设集合到$\operatorname{val}(Q)$上的1个映射, 其用于确定假设所对应的特征; 记函数$z$将$\operatorname{val}(Q)$映射成权重值, 那么对于1个假设$H$, 其权重就等于$z(f(H))$, 即

$ w(H)=z(f(H)) . $

(7)

在进行证据重要度评估时，与低权重的假设变量相比，高权重假设变量的信息熵减少单位比例更具价值。因此，在式(5)中给每个假设变量的信息熵减少比例乘以权重系数，具体可表示为

$ \Delta \varepsilon_{\mathrm{WM}}\left(H_{\mathrm{set}}, E\right)=\frac{1}{K} \sum\limits_{H \in H_{\mathrm{set}}^{\varepsilon}} w(H) \times \frac{\Delta \varepsilon(H, E)}{\varepsilon(H)} . $

(8)

其中$\Delta \varepsilon_{\mathrm{WM}}\left(H_{\mathrm{set}}, E\right)$表示查询$E$使$H_{\mathrm{set}}$中假设变量信息熵减少的加权平均比例。利用$\Delta \varepsilon_{\mathrm{WM}}\left(H_{\mathrm{set}}\right.$, $E$) 可以评估未收集证据的重要程度。对于$E_{1}$和$E_{2}$, 若$\Delta \varepsilon_{\mathrm{WM}}\left(H_{\mathrm{set}}, E_{1}\right)<\Delta \varepsilon_{\mathrm{WM}}\left(H_{\mathrm{set}}, E_{2}\right)$, 从不确定性减少比例的角度看, 则$E_{2}$的重要程度更高。这是因为查询$E_{2}$会使所有假设变量信息摘减少的加权平均比例更多, 即更能确定所有关键假设的状态。

3 犯罪侦查决策支持模型构建与验证

基于犯罪假设的加权信息熵计算公式，结合犯罪假设推理的Bayes网络模型，进一步提出基于Bayes网络模型的犯罪侦查决策支持模型，以协助犯罪案件证据收集和推理。

3.1 模型构建

犯罪侦查决策支持模型由犯罪假设推理的Bayes网络模型和证据重要度计算2部分组成。Bayes网络模型用于计算假设变量和证据变量的概率分布，以供证据重要度评估时调用；式(8)所示的方法用于计算未收集证据的重要程度。模型在应用时，输入为已收集证据信息，输出为证据收集建议，主要针对物品痕迹类证据。证据收集建议由按照重要度大小排序的证据组成。

由于模型中的假设变量与证据变量均是二值分类变量，因此任意H的信息熵可以按式(9)进行计算；相应地，H关于E的条件熵可由式(10)进行计算：

$ \begin{gathered} \varepsilon(H)=-\left(P\left(h^{*}\right) \log P\left(h^{*}\right)+\right. \\ \left.\left(1-P\left(h^{*}\right)\right) \log \left(1-P\left(h^{*}\right)\right)\right), \end{gathered} $

(9)

$ \begin{gathered} \varepsilon(H \mid E)=P\left(e^{*}\right) \varepsilon\left(H \mid e^{*}\right)+ \\ \left(1-P\left(e^{*}\right)\right) \varepsilon\left(H \mid e^{0}\right) . \end{gathered} $

(10)

其中: $h^{*}$表示$H$取值“是”, $e^{*}$表示$E$取值“是”, $e^{0}$表示$E$取值“否”。

模型根据式(8)计算未收集证据的重要程度，在进行计算前需要确定假设的权重。一般而言，在案件情况未给定时，推理同类对象的假设应具有相同的权重。比如，犯罪人假设集合中的每个假设的权重应是相同的。因此，模型中具有相同模板参数的假设变量的权重是相同的，故将式(7)中的函数f设置为

$ f: H_{\text {set }} \rightarrow\left\{g_{1}, g_{2}, \cdots, g_{s}\right\} . $

(11)

其中$\left\{g_{1}, g_{2}, \cdots, g_{s}\right\}$为Bayes网络中的模型参数构成的集合。

至此，犯罪侦查决策支持模型构建完成。

3.2 模型验证

在完成犯罪侦查决策支持模型的构建后，针对不同类型的暴力犯罪案件，可以更新相应的Bayes网络结构，进而完成模型针对不同案件类型的细化。以下将主要阐述模型应用的算法流程，然后应用420例案件对构建的证据重要度模型进行验证。

1) 犯罪侦查决策支持模型应用算法流程。

证据收集决策支持模型进行证据重要度评估，并输出侦查建议的算法流程，如图 4所示。首先，基于要素假设、行为假设以及案件证据的输入，调用Bayes网络模型，推理网络中对变量赋值，为概率分布的计算奠定基础。然后，查询状态未确定的物品痕迹类证据变量，这些证据变量构成待收集的证据变量集合；依据加权信息熵减比例计算集合中的每个证据变量的重要度。最后，按照证据重要度的大小对所有状态未确定的物品痕迹类证据变量进行排序并输出。

2) 模型验证方法。

对于网络中的1个$H$和$E$, 当$E$取值为“是”, 即该证据存在时，假设变量取值为“是” (即该假设成立) 的后验概率的增加值可表示为

$ \Delta P(H, E)=P\left(h^{*} \mid e^{*}\right)-P\left(h^{*}\right) . $

(12)

其中：$P\left(h^{*} \mid e^{*}\right)$表示$E$取值为“是”时, 假设$H$成立的后验概率。$\Delta P(H, E)$可以用来比较未收集证据的重要度大小, 对于$E_{1}$和$E_{2}$, 若$\Delta P\left(H, E_{1}\right)>$ $\Delta P\left(H, E_{2}\right)$, 相比于$E_{2}$, 则$E_{1}$对于$H$的成立更重要。这是因为$E_{1}$对应的证据存在时, $H$成立的概率更高。

对于多个假设变量，同样可采用算术平均或加权平均的方法来综合评估证据的重要程度。

对于算术平均的方法，后验概率平均增加比例的计算式可表示为

$ \begin{gathered} \Delta P_{\mathrm{AM}}\left(H_{\mathrm{set}}, E\right)=\frac{1}{M} \sum\limits_{H \in H_{\mathrm{set}}^{p}} \frac{P\left(h^{*} \mid e^{*}\right)-P\left(h^{*}\right)}{P\left(h^{*}\right)}= \\ \frac{1}{M} \sum\limits_{H \in H_{\mathrm{set}}^{p}} \frac{\Delta P(H, E)}{P\left(h^{*}\right)} . \end{gathered} $

(13)

其中: $\Delta P_{\mathrm{AM}}\left(H_{\mathrm{set}}, E\right)$表示$E$的存在使假设集合$H_{\mathrm{set}}$中假设$H$成立概率增加的平均比例, $H_{\mathrm{set}}^{p}$是$H_{\text {set }}$中成立概率不为0的假设变量组成的集合, $M$表示$H_{\mathrm{set}}^{p}$中的假设变量数目。利用$\Delta P_{\mathrm{AM}}\left(H_{\mathrm{set}}, E\right)$可以比较证据间的重要性。对于$E_{1}$和$E_{2}$, 若$\Delta P_{\mathrm{AM}}\left(H_{\mathrm{set}}, E_{1}\right)>\Delta P_{\mathrm{AM}}\left(H_{\mathrm{set}}, E_{2}\right)$, 从假设成立的角度看, 则$E_{1}$更为重要。这是因为$E_{1}$的存在会使所有假设成立概率增加的平均比例更高。因此, 式(13) 所示方法可用于计算证据的重要度。

对于加权平均的方法，类似于加权信息熵，在式(13)中对每个假设的后验概率增加比例并乘以相应权重系数，可以计算后验概率的加权平均增加比例，即

$ \Delta P_{\mathrm{WM}}\left(H_{\mathrm{set}}, E\right)=\frac{1}{M} \sum\limits_{H \in H_{\mathrm{set}}^{p}} w(H) \times \frac{\Delta P(H, E)}{P\left(h^{*}\right)} . $

(14)

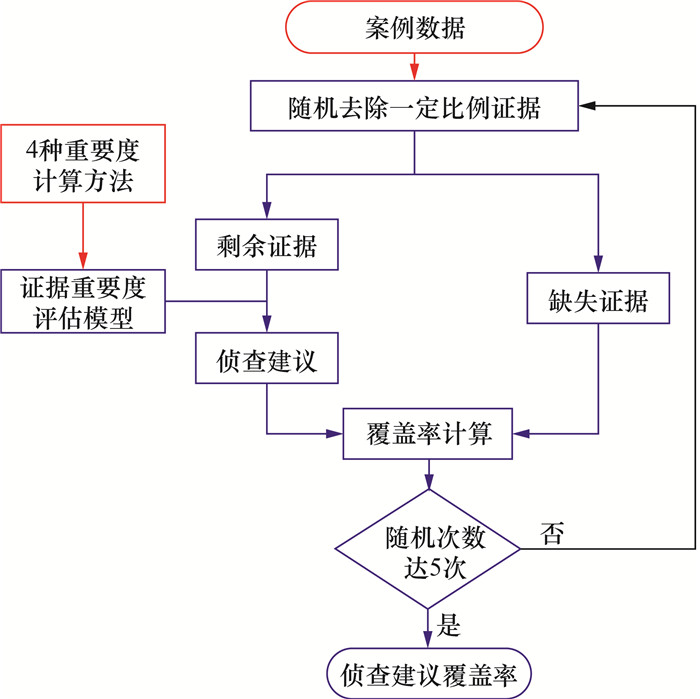
本研究收集到的放火、砍杀和爆炸类案件共计420个案例，应用案例数据对所构建的证据重要度评估模型进行验证。验证模型的方法流程如图 5所示。

其中，420例案例数据通过对公开法律文书中的信息进行编码得到。法律文书数据通过《北大法宝》等数据库收集。对于每个案例，先通过审理查明的事实和被告人供述，解析案件中的条件要素、作案行为和行为地点；再通过案例中的证据部分，解析物品痕迹类证据和信息类证据。

在完成案例信息录入后，对每个案例随机去掉一定比例的物品痕迹类证据，然后根据案件类型将未去除的所有证据输入至相应类型案件的证据重要度评估模型中，模型分别利用表 2中的4种方法^[28]计算状态未确定的证据的重要度，并输出前n个重要度最高的证据，此即模型输出的侦查建议；在全部案例均完成证据重要度评估后，分别计算每种方法中输出的证据对去掉的证据的覆盖率。覆盖率表示去掉的证据中有多少与模型输出的证据相同，可用于评价模型的性能，其计算公式为

$ C(n)=\frac{\sum\limits_{i \in D} \sum\limits_{j \in[1, n]} \ln \left(E_{j}^{i}, E_{M}^{i}\right)}{\sum\limits_{i \in D} N\left(E_{M}^{i}\right)} . $

(15)

其中: $C(n)$表示输出的前$n$个最重要的证据的覆盖率; $D$表示案例数据集; $E_{j}^{i}$表示模型对第$i$个案例输出的重要度排名为$j$的证据; $E_{M}^{i}$表示第$i$个案例中随机去掉的证据组成的集合, $N\left(E_{M}^{i}\right)$表示$E_{M}^{i}$中的证据个数; 当$E_{j}^{i} \in E_{M}^{i}$时, $\ln \left(E_{j}^{i}, E_{M}^{i}\right)=$ 1, 否则$\ln \left(E_{j}^{i}, E_{M}^{i}\right)=0$。

3) 计算结果与讨论。

按照上述步骤即可完成对4种证据重要度计算方法的一轮验证。为避免随机抽取的证据可能存在特异性并对验证结果产生影响，总共进行了5轮验证，即在给定的比例下随机抽取5次，最终每种方法的覆盖率取这5次结果的平均值。

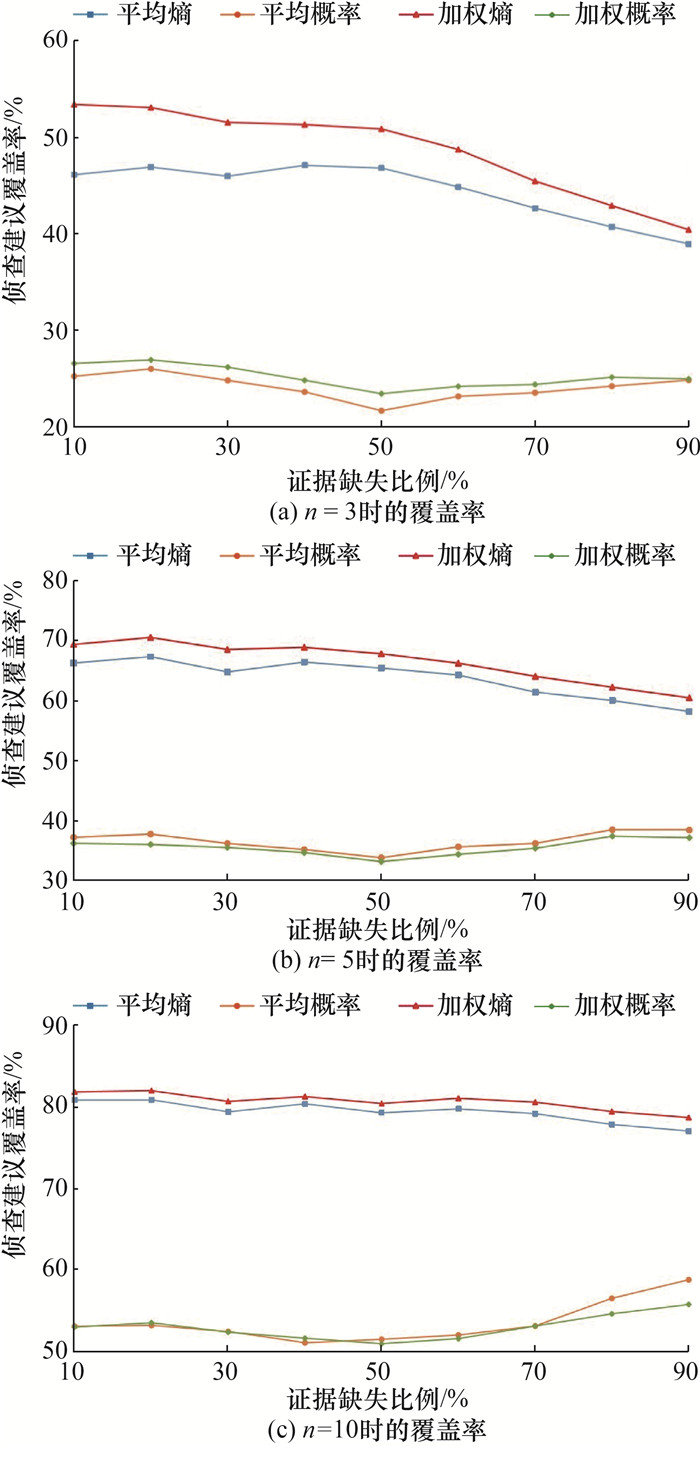
随机抽取的证据比例为10%, 20%, …, 90%，共9组；在每组比例中分别计算n为3、5和10时的侦查建议覆盖率，验证结果如图 6所示。

由图 6可知，基于加权信息熵的计算方法在所有方法中最优。在给定任意证据缺失比的情况下，加权信息熵方法给出的重要度排名前3、前5和前10的证据的覆盖率都是最高的。这是因为相比于基于后验概率的方法，信息熵方法同时考虑了潜在的物品痕迹类证据存在和不存在2种情况下对不确定性的影响，而后验概率的方法仅考虑证据存在时对不确定性的影响；相比于算术平均信息熵方法，加权信息熵着重考虑了犯罪人、作案工具和中心现场等假设，会更多地预测有助于降低这些假设不确定性的证据，而这部分证据在案件中往往会被收集以证明作案过程。

同时，验证结果表明，本文所提出的依据加权信息熵的证据重要度评估模型能够给出有效的侦查建议。当证据缺失50%时，模型给出的重要度排名前3的证据的覆盖率在50%以上，排名前5的证据的覆盖率在65%以上，排名前10的证据的覆盖率高于80%；当证据缺失90%时，模型给出的重要度排名前3的证据的覆盖率在40%以上，排名前5的证据的覆盖率高于60%，排名前10的证据的覆盖率高于75%。这表明模型给出的侦查建议是有效的，可以用来协助犯罪侦查。

3.3 犯罪侦查决策支持模型应用

利用实际案例“厦门公交车放火案”来说明模型的动态分析过程^[27]。案件基本情况为：2013年6月7日，厦门一辆公交车在行驶过程中突然着火，火灾共造成47人死亡，30多人受伤。经调查发现，该公交车内的油箱、蓄电池完好，但公交车上有流淌、燃烧痕迹，故分析认定引发该火灾的原因可能是人为放火。

利用放火案件证据收集决策支持模型对本案件进行推理分析。为了更好地验证模型的性能，将参照真实破案过程对模型进行测试。在案件实际分析过程中，证据随着时间的推移不断被丰富，因此模型的输入也应该逐渐得到丰富。为此，本研究将真实情况的分析过程分为3个阶段，并将模型的输出与实际调查结果进行比较。

1) 第一阶段，在现场主要收集到一些物品痕迹类证据，如表 3所示。

将上述证据输入至证据收集决策支持模型，设置公交车为案件的中心现场，并利用模型进行推理。模型输出的重要度排名前5的潜在证据，如表 4所示。需要说明的是，因为目前尚无与可能的犯罪人相关的信息输入，故模型未输出作案行为。

表 4输出的侦查建议符合逻辑。首先，目前尚无与助燃物、盛装工具、犯罪人、点火工具、转移工具相关的证据，而通过在现场收集与他们相关的证据，可以大大降低相应假设的不确定性，故模型输出了这5条最重要的建议。此外，可以看到重要度最高的侦查建议为“公交车上是否有关于助燃物的微量物质”，这是因为对该条证据进行查找能够将对应假设的不确定性降至很低。

2) 第二阶段，案件中收集到了现场勘查、检验鉴定以及调查得到的证据信息，具体如表 5所示。

通过对比表 4和5可知，模型在第一阶段输出的侦查建议有效。首先，模型提供的最重要的侦查建议为“公交车上是否有关于助燃物的微量物质”。而在本阶段，确实在公交车、公交车内的衣物、编织袋以及手拉车上检出了汽油(分别对应证据e₆、e₇、e₈、e₉)。其次，模型提供的另一条侦查建议为“公交车上是否有关于犯罪人的其他物品”，这与调查得到的信息类证据e₁₁存在相关性。最后，侦查建议还包括“公交车上是否有关于点火工具的微量物质”，这也与在公交车上发现打火机防风帽(证据e₅)一致。综上可知，模型能够提供有效的侦查建议以协助犯罪侦查。

在这一阶段，模型输出重要度排名前5的证据收集建议，如表 6所示。

3) 第三阶段在关联现场调查到了一些证据，具体如表 7所示。

通过对比表 6和表 7可以发现，模型可以输出有效的侦查建议以协助案件侦查。具体而言，模型提供的1个侦查建议为“关联现场上是否有关于白衣男子的其他物品”，而在本阶段，确实收集到了与其一致的证据e₁₃，即在关联现场陈某家中提取到了遗书；同时，该侦查建议也与陈某在关联现场购买汽油的信息类证据e₁₄相关。模型提供的另1个侦查建议为“白衣男子身上是否有关于汽油的燃烧痕迹”，这与在公交车上发现陈某被烧毁的尸体符合，即证据e₁₂。

通过对比案件的实际侦查结论与模型给出的推理结果，可以再次发现模型能够给出正确的侦查建议。

将上述证据输入继续推理，模型输出要素假设推理结果如表 8所示，对行为假设的推理结果如表 9所示。

本案件的真实侦查结论为：陈某因个人诉求无法得到满足，在私人售油点自行购买了汽油并放置家中，2013年6月7日用手拉车、编织袋等工具携带汽油乘坐公交车，待公交车行至金山站附近推倒装有编织袋的手拉车并点燃汽油，引起火灾。

通过对比案件的实际侦查结论与模型给出的推理结果，可以再次发现模型能够给出正确的侦查建议，并推理较为准确的犯罪人、作案工具以及作案行为。

4 结论

本文围绕犯罪侦查的决策支持模型进行了深入研究，主要成果如下：

1) 考虑不同证据在案件推理中的作用不同，引入信息熵来描述证据收集对犯罪假设不确定性的影响，提出了基于加权信息熵的证据重要度计算方法。

2) 构建了基于Bayes网络的犯罪侦查决策支持模型，对可能存在的但尚未被收集的物品痕迹类证据的重要度进行计算，并据此来输出侦查建议和推理结果。应用420例放火、砍杀和爆炸案件数据，并通过设置算术平均信息熵、算术平均后验概率，以及加权平均后验概率的重要度计算对照方法，对提出的模型进行了验证。

3) 利用模型对1例放火案件进行了实证分析，结果表明：提出的模型能够通过输出侦查建议和推理结果，实现案件的动态侦查决策支持和推理分析。

本文提出的犯罪侦查决策支持模型能够分析案件信息，输出有效的侦查建议和推理结论。然而，所构建的模型在实际应用过程中并不能完全替代刑侦领域专业人员的作用，而主要为在侦查初期提供分析结果，为侦查人员的下一步侦查决策提供科学依据。

此外，本文重点关注犯罪案件侦查阶段的证据收集和推理问题研究，但对证据收集过程中涉及的“证据标准”关注有限，应进一步深入研究，进而为侦查阶段证据收集工作的智能化和规范化提供支持。