2. 北京市市政工程设计研究总院有限公司, 北京 100082
2. Beijing General Municipal Engineering Design and Research Institute Co., Ltd., Beijing 100082, China
监视控制与数据采集(supervisory control and data acquisition, SCADA)系统能够提供管道流量和节点压力的测量数据,是水力模型参数校核的重要依据[1-4]。在待校核的模型参数中,节点用水量是动态时变的重要参数,直接影响供水管网延时(动态)水力模型的准确性。
供水管网水力模型参数的校核方法可分为试错法、显式法和隐式法等[5-7]。其中隐式校核方法是广泛采用的方法,隐式校核模型的求解方法主要可以分为2种:智能随机搜索算法[8]、迭代梯度算法[9-11]。其中迭代梯度算法计算时间短,且具有较高的校核精度,被广泛应用于供水管网水力模型的参数校核中。
经过代表性时刻工况测量数据校核后的供水管网静态水力模型,可以分析代表性工况下管网的运行状态,但当运行条件、模型参数发生变化时,静态水力模型难以满足使用需求[12]。根据SCADA系统测量数据进行管网水力模型参数的动态校核和更新,实现管网水力状态的动态模拟,是当前管网智慧化管理的应用情景。Davidson等[13]使用SCADA系统测量数据,采用最小二乘法校核得到模型各时刻的节点用水量。Cheng等[11]采用奇异值分解法,根据SCADA系统测量数据校核各时刻的节点用水量。上述方法校核了每个时间步的模型参数,但未考虑节点用水量在相邻时间步的相关性。对于某一用水类型的节点,其用水量的时间变化具有周期性规律[14],合理的动态水力模型应该体现出节点用水量在不同时刻的时变特征。
数据同化(data assimilation, DA)方法利用测量数据动态估计系统状态参数,在很多领域被广泛应用[15-16]。DA方法建立了相邻采样时间步之间的参数关系,近年来也被应用于管网水力模型参数动态校核和估计。DA方法根据t时刻模型参数值推断t+1时刻模型参数的预测值,再利用t+1时刻测量数据获得t+1时刻模型参数的后验值,进而根据预测值和后验值获取t+1时刻参数值。Kalman滤波(Kalman filter, KF)是常用的DA方法,经过不断改进已形成线性系统Kalman滤波(linear Kalman filter, LKF)[17-18]、扩展Kalman滤波(extend Kalman filter, EKF)[19]、集合Kalman滤波(ensemble Kalman filter, EnKF)[20]等方法。应用KF方法估计管网水力模型参数时,测量数据与模型参数之间为非线性关系。Todini[21]率先将KF引入供水管网水力模型参数校核和估计中,采用LKF方法近似表示非线性关系,计算模型参数后验值,但计算精度不高。EKF方法采用Taylor展开式的一阶项近似表示测量数据与模型参数之间的非线性关系[14, 16, 22]。Jung等[17]比较了EKF与LKF方法在水力模型参数估计中的效果,证明了EKF方法具有较高精度。Zhou等[12]提出了推断测量Kalman滤波(inferential-measurement Kalman filter, IMKF)方法,通过加权最小二乘法(weighted least square, WLS)迭代校核,计算与管网实际测量数据对应的模型参数后验值,避开了测量数据与参数后验值之间非线性关系的近似。
供水管网各类用户的用水量,在时变规律上遵循用水模式曲线,同类用户中不同节点的用水量系数值呈现相似性,用水量时变趋势呈现一致的规律。上述LKF、EKF和IMKF方法的研究应用中,在先验预测步骤中,近似采用单位矩阵预测用水量,即采用t时刻的估计用水量作为t+1时刻用水量预测值,未考虑节点用水量的时变模式对邻近时刻用水量的影响,在时间间隔较大时会导致较大误差[20]。
综上所述,为实现更合理准确的供水管网水力模型用水量动态估计,本文在EKF算法的先验预测步骤中根据用水模式曲线预测节点用水量,以期提高供水管网水力模型节点用水量动态估计的精度。将本文考虑用水模式曲线的EKF方法称为改进的扩展Kalman滤波(improved extend Kalman filter, IEKF)方法。最后,基于2个不同规模的案例管网,比较了LKF、EKF、IMKF、IEKF方法在不同的参数设置、测量噪声、采样间隔工况下的计算精度,验证了IEKF方法的有效性。
1 管网水力模型节点用水量动态估计 1.1 Kalman滤波方法KF方法主要包括2个步骤:先验预测、后验校核。在先验预测步骤中,根据上一个时刻的状态值预测当前时刻状态值;在后验校核步骤中,根据当前时刻的测量数据更新状态预测值,得到当前时刻的状态估计值。
由于在2个步骤中都存在着噪声的影响,因此该方法是一个滤波过程。先验预测步骤和后验校核步骤的参数关系可以表示为:
| $ \hat{\boldsymbol{x}}_{t+1 \mid t}=\boldsymbol{F}_{t+1} \hat{\boldsymbol{x}}_t+\boldsymbol{w}_{t+1}, \boldsymbol{w}_{t+1} \sim N\left(\mathbf{0}, \boldsymbol{U}_{t+1}\right) ; $ | (1) |
| $ \boldsymbol{z}_{t+1}=\hat{\boldsymbol{x}}_{t+1}+\boldsymbol{v}_{t+1}, \boldsymbol{v}_{t+1} \sim N\left(\mathbf{0}, \boldsymbol{R}_{t+1}\right) . $ | (2) |
式中:
步骤1 先验预测。根据t时刻的用水量估计结果,预测t+1时刻管网状态参数及其协方差矩阵,建立状态方程式:
| $ \hat{\boldsymbol{x}}_{t+1 \mid t}=\hat{\boldsymbol{x}}_t, $ | (3) |
| $ \boldsymbol{P}_{t+1 \mid t}=\boldsymbol{P}_t+\boldsymbol{U}_{t+1} . $ | (4) |
式中:
步骤2 后验校核。根据t+1时刻的测量数据,修正第t+1时刻状态参数预测值:
| $ \hat{\boldsymbol{x}}_{t+1}=\hat{\boldsymbol{x}}_{t+1 \mid t}+\boldsymbol{K}_{t+1}\left(\boldsymbol{z}_{t+1}-\hat{\boldsymbol{x}}_{t+1 \mid t}\right), $ | (5) |
| $ \boldsymbol{K}_{t+1}=\boldsymbol{P}_{t+1 \mid t}\left(\boldsymbol{P}_{t+1 \mid t}+\boldsymbol{R}_{t+1}\right), $ | (6) |
| $ \boldsymbol{P}_{t+1}=\left(\boldsymbol{I}-\boldsymbol{K}_{t+1}\right) \boldsymbol{P}_{t+1 \mid t} . $ | (7) |
式中:
1.1节所述的KF方法可以在线性系统中获得理想的结果,而供水管网水力模型参数动态估计校核问题是典型的非线性问题。针对非线性系统,式(5)中的测量数据zt+1与状态参数
| $ \boldsymbol{z}_{t+1}=h\left(\hat{\boldsymbol{x}}_{t+1}\right)+\boldsymbol{v}_{t+1}, \boldsymbol{v}_{t+1} \sim N\left(\mathbf{0}, \boldsymbol{R}_{t+1}\right) . $ | (8) |
式中:h(·)表示测量数据与状态参数之间的非线性函数,vt+1为测量噪声。
将h(
| $ h\left(\hat{\boldsymbol{x}}_{t+1}\right) \approx h\left(\hat{\boldsymbol{x}}_{t+1 \mid t}\right)+\boldsymbol{H}_{t+1}\left(\hat{\boldsymbol{x}}_{t+1}-\hat{\boldsymbol{x}}_{t+1 \mid t}\right), $ | (9) |
| $ \boldsymbol{H}_{t+1}=\left.\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}\right|_{\boldsymbol{x}=\hat{\boldsymbol{x}}_{t+1 \mid t}} . $ | (10) |
式中Ht+1为测量数据(节点压力、管道流量)对节点用水量的偏导数矩阵,即Jacobi矩阵[23]。
基于式(9)和(10)建立的非线性关系,IEKF的后验校核步骤可表示为:
| $ \hat{\boldsymbol{x}}_{t+1}=\hat{\boldsymbol{x}}_{t+1 \mid t}+\boldsymbol{K}_{t+1}\left(\boldsymbol{z}_{t+1}-h\left(\hat{\boldsymbol{x}}_{t+1 \mid t}\right)\right), $ | (11) |
| $ \boldsymbol{K}_{t+1}=\boldsymbol{P}_{t+1 \mid t} \boldsymbol{H}_{t+1}\left(\boldsymbol{H}_{t+1} \boldsymbol{P}_{t+1 \mid t} \boldsymbol{H}_{t+1}^{\mathrm{T}}+\boldsymbol{R}_{t+1}\right), $ | (12) |
| $ \boldsymbol{P}_{t+1}=\left(\boldsymbol{I}-\boldsymbol{K}_{t+1} \boldsymbol{H}_{t+1}\right) \boldsymbol{P}_{t+1 \mid t}. $ | (13) |
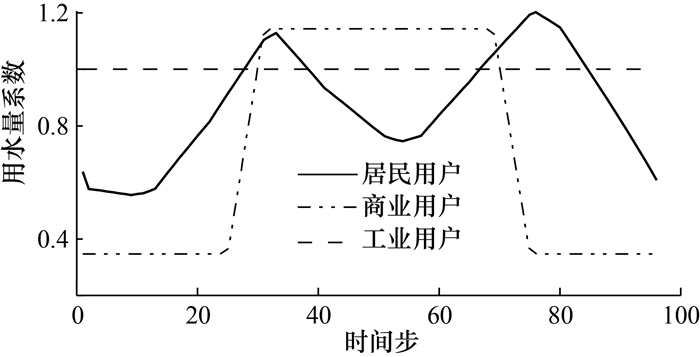
在先验预测步骤中,需要采用状态转移矩阵进行节点用水量的预测。为了获得更合理的预测结果,在IEKF方法中使用用水模式曲线来计算F矩阵。本研究中的用水模式曲线参考Kang等[22]的研究,3种主要用户的用水模式曲线类型如图 1所示。其中:工业类用户在一天内的用水较为平稳,居民类用户则出现显著的早晚用水高峰; 商业类用户在早晨和傍晚用水量起伏显著,而日间用水量保持稳定。将节点按用户类型分组,同一组节点遵循相同的用水规律。t+1时刻的Ft+1矩阵可表示为
| $ \boldsymbol{F}_{t+1}=\frac{\boldsymbol{\alpha}_{t+1}}{\boldsymbol{\alpha}_t} . $ | (14) |
|
| 图 1 不同类型用户的用水模式曲线(采样间隔15 min) |
式中:Ft+1为t+1时刻的状态转移矩阵,αt+1和αt分别为第t+1时刻和第t时刻的用水量系数矩阵。先验预测步骤的计算可表示为:
| $ \hat{\boldsymbol{x}}_{t+1 \mid t}=\boldsymbol{F}_{t+1} \hat{\boldsymbol{x}}_t, $ | (15) |
| $ \boldsymbol{P}_{t+1}=\boldsymbol{F}_{t+1} \boldsymbol{P}_t \boldsymbol{F}_{t+1}^{\mathrm{T}}+\boldsymbol{U}_{t+1} . $ | (16) |
此外,由式(15)可知,由于t时刻的状态参数值会影响t+1时刻的状态参数的先验预测值,初始时刻状态参数误差会向后传递,影响后续时刻状态参数预测精度。因此,为减小初始时刻状态参数误差,采用静态模型校核中被广泛采用的WLS[24]迭代求解初始时刻状态参数值。
为解决节点用水量估计问题中的欠定问题,根据用户类型对节点分组。IEKF方法中的状态参数为节点组用水量。引入分组矩阵GQ用于计算先验预测和后验校核中的状态参数
| $ G_Q(i, j)= \begin{cases}\frac{Q_{\mathrm{b} i}}{Q_{\mathrm{g} j}} & \left(i \in \operatorname{Group}_j\right), \\ 0 & \left(i \notin \operatorname{Group}_j\right) .\end{cases} $ | (17) |
| $ \hat{\boldsymbol{x}}_{t+1}=\boldsymbol{G}_Q^{-1} \cdot \boldsymbol{Q}_{t+1} . $ | (18) |
式中:GQ为分组矩阵,i表示节点,Groupj表示第j个节点组,Qbi为第i个节点的基础用水量,Qgj为第j个节点组的组用水量,
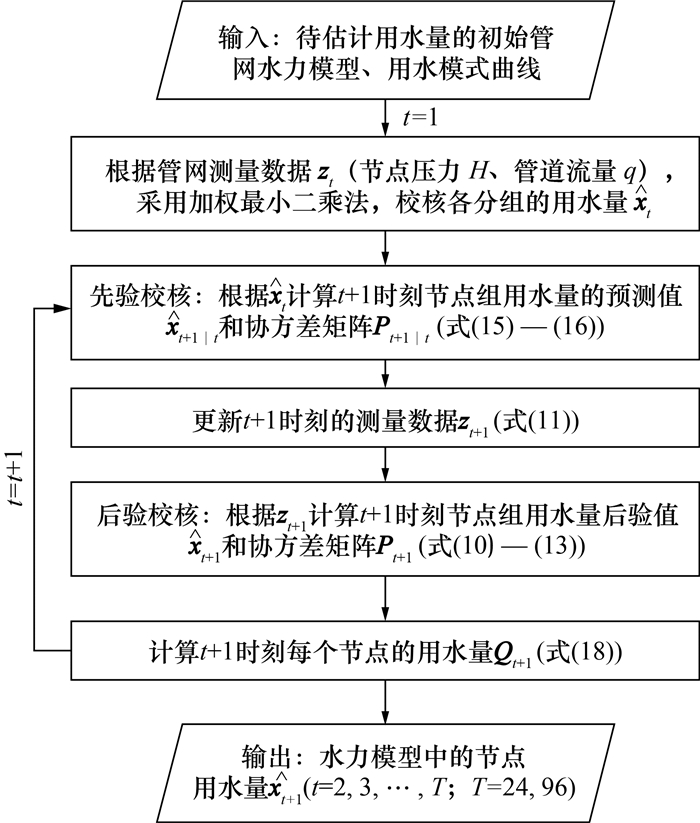
综合上述过程,IEKF的整体计算流程如图 2所示。
|
| 图 2 IEKF方法流程图 |
1.3 精度指标
采用计算结果与真实值之间的均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)描述第i个节点用水量估计结果的精度,计算公式如下:
| $ \operatorname{RMSE}_i =\sqrt{\frac{1}{N} \sum\limits_{t=1}^N\left(\hat{Q}_t-Q_t\right)^2}, $ | (19) |
| $ \operatorname{MAPE}_i =\frac{1}{N} \sum\limits_{t=1}^N \frac{\left|\hat{Q}_t-Q_t\right|}{Q_t} . $ | (20) |
式中:i表示节点编号,RMSEi为第i个节点的RMSE,MAPEi为第i个节点的MAPE,t表示时刻,N表示总时刻数,
为衡量节点用水量估计值对应的24 h时变曲线与真实时变曲线的相似程度,本文采用Nash-Sutcliffe效率(Nash-Sutcliffe efficiency, NSE)系数表示2条曲线的重合程度。NSE系数的取值范围为(-∞, 1)。NSE系数值越接近1,表明计算结果与真实曲线的重合程度越高。
| $ \mathrm{NSE}_i=1-\frac{\sum\limits_{t=1}^N\left|\hat{Q}_t-Q_t\right|}{\sum\limits_{t=1}^N\left|\hat{Q}_t-\bar{Q}_t\right|}. $ | (21) |
式中:NSEi为第i个节点的NSE系数,Qt为所有时刻节点用水量真实值的平均值。
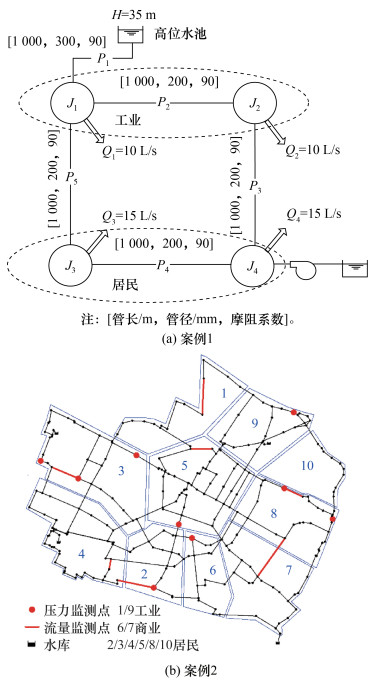
2 案例分析为了验证IEKF方法在不同规模管网下的适应性,选取了2个不同规模的案例管网[24-25]。案例1为简单管网,如图 3a所示,包括2个水源、5个管道和4个节点。节点被分为{J1, J2}和{J3, J4}共2组,其中节点组{J1, J2}为工业用户,节点组{J3, J4}为居民用户。节点组内各节点用水模式相同。在式(3)—(7)的状态估计中,每个节点组总用水量为1个待校核的状态参数。假定J2和J3为压力监测点,管道P1和水泵为流量监测点。此案例中监测点数量为4,待校核估计参数的数量为2,因此监测点冗余系数为2。
|
| 图 3 案例管网布局 |
案例2为一个高冗余环状管网,包括4个水源、336个管道、272个节点。用户分为3类,分别为工业类、居民类、商业类。所有用户节点被分为10组,每组节点对应1种用水模式曲线,各分组对应的用户类型详见图 3b;设置6个压力监测点、7个流量监测点。此案例中监测点数量为13,待校核估计参数的数量为10,监测点冗余系数为1.3。2个案例管网的用水模式曲线均参考Zhou等[24]的研究。
为了验证本文提出的IEKF方法的计算效率和精度,案例分析中将IEKF结果与另外3种基于KF的方法(LKF、EKF、IMKF)的结果进行比较。其中,IMKF方法在每个时刻的参数估计中采用拉丁超立方抽样获取协方差矩阵,在后验校核步骤采用WLS迭代求解。WLS迭代的具体步骤见Zhang等[23]和Liu等[26]的研究。LKF、EKF、IEKF方法在每个时刻的参数估计中仅需在后验校核步骤计算1次Jacobi矩阵。
2.1 噪声对计算结果的影响在基于KF的方法中,系统噪声和测量噪声对参数估计结果的影响较大,本节基于案例1比较了不同的系统噪声(先验预测步骤的预测误差)和测量噪声(后验校核步骤的监测误差)下的计算结果。采样间隔设置为15 min,分别测试了系统噪声Ut+1的对角元素ut+1取0.01、0.1、1、10时各方法的计算结果。表 1给出了在不同系统噪声设置下,LKF、EKF、IMKF、IEKF方法的计算时间和精度指标平均值。图 4给出了不同方法的模型精度指标随系统噪声的变化趋势。表 1中,IMKF的Jacobi矩阵计算次数与拉丁超立方抽样次数设置及WLS的迭代次数有关。本研究中拉丁超立方抽样次数A=100,平均每次WLS迭代次数B=6。因此,在全天24 h共96个时间步中,IMKF方法需计算大量Jacobi矩阵,导致计算时间较长,而LKF、EKF、IEKF方法计算时间较短。
| 方法 | 计算时间/s | Jacobi矩阵计算次数 | ut+1 | RMSE/(L·s-1) | MAPE/% | NSE系数 |
| LKF | 2.7 | 96 | 0.01 | 11.58 | 72.05 | -13.78 |
| 0.1 | 9.53 | 63.31 | -6.03 | |||
| 1 | 12.04 | 73.55 | -14.57 | |||
| 10 | 15.40 | 86.26 | -15.59 | |||
| EKF | 2.7 | 96 | 0.01 | 2.32 | 13.76 | 0.52 |
| 0.1 | 1.91 | 12.56 | 0.79 | |||
| 1 | 0.95 | 6.71 | 0.96 | |||
| 10 | 0.28 | 1.98 | 1.00 | |||
| IMKF | 1 115.0 | 96A·B | 0.01 | 2.56 | 12.84 | 0.05 |
| 0.1 | 1.77 | 7.82 | 0.72 | |||
| 1 | 0.84 | 5.10 | 0.88 | |||
| 10 | 0.41 | 3.19 | 0.97 | |||
| IEKF | 2.8 | B+95 | 0.01 | 0.000 2 | 0.00 | 1.00 |
| 0.1 | 0.000 4 | 0.00 | 1.00 | |||
| 1 | 0.000 9 | 0.00 | 1.00 | |||
| 10 | 0.001 5 | 0.00 | 1.00 | |||
| 注:A为拉丁超立方抽样次数,B为每次WLS的迭代次数。 | ||||||
根据表 1中的模型精度评价结果,在不同的系统噪声参数下,LKF方法的MAPE均大于60%,NSE系数小于0,即LKF方法不能得到合理的结果。EKF和IMKF方法的MAPE均小于15%,EKF方法的NSE系数在0.5~1之间,IMKF方法的NSE系数在0~1之间,EKF和IMKF方法得到了合理的计算结果。IEKF方法对应的结果误差很小,其中MAPE趋向于0,NSE系数趋向于1。与其他方法相比,IEKF方法的计算时间非常短,计算精度最高。
由图 4可知,对于EKF和IMKF方法,模型计算误差随着系统状态转移噪声ut+1的增大而减小,原因在于当测量噪声协方差固定时,较小的ut+1使得式(5)和(11)中的Kalman增益矩阵K的取值较小,即先验预测值获得较大的权重;这2种方法在先验预测步骤中采用前一个时刻的节点用水量(参数值),并采用单位矩阵作为状态转移矩阵F;根据式(11)—(13)可知,先验预测值权重较大,将使得基于实际测量数据的后验校核值较小,导致模型参数最终估计结果不准确。由表 1和图 4可知,EKF和IMKF对系统噪声的设置较敏感,需要设置较大的系统状态转移噪声值ut+1以增大Kalman增益矩阵K的取值,即增加后验校核步骤权重来得到更准确的结果。IEKF方法通过引入状态转移矩阵F,提高了先验预测步骤的准确性,进而提高了最终结果的精度。从图 4可知,在不同系统噪声设置下,IEKF结果的误差始终维持在较小值,说明IEKF对系统噪声的设置不敏感。
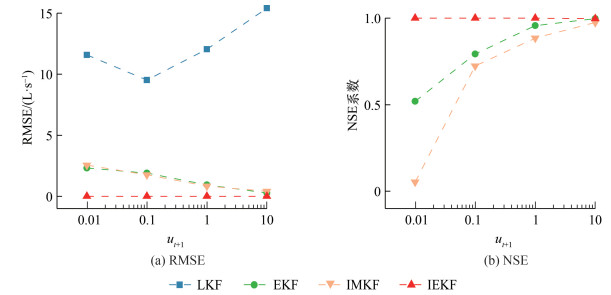
|
| 图 4 案例1不同系统噪声下的误差 |
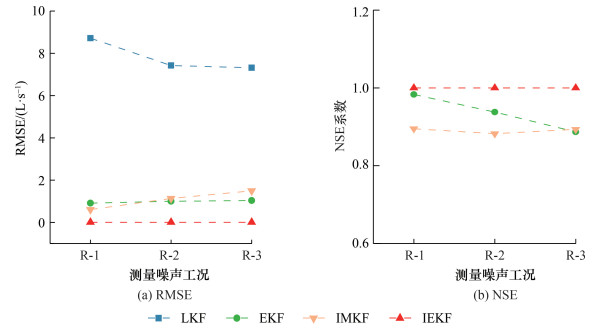
为进一步分析测量噪声Rt+1对计算结果的影响,分别设置3种测量噪声工况,其中节点水压测量值的标准差σH=0.3~0.9 m,管道流量测量值的标准差σq=5%~15%。R-1 (σH=0.3 m, σq=5%)、R-2(σH=0.6 m, σq=10%)、R-3(σH=0.9 m, σq=15%) 分别为3种噪声工况。表 2给出了在不同测量噪声设置下,各方法的计算结果精度指标平均值。图 5给出了不同方法的模型精度指标随测量噪声的变化趋势。
| 方法 | 测量噪声工况 | RMSE/(L·s-1) | MAPE/% | NSE系数 |
| LKF | R-1 | 8.71 | 61.60 | -1.51 |
| R-2 | 7.42 | 51.89 | -0.94 | |
| R-3 | 7.32 | 51.6 | -0.89 | |
| EKF | R-1 | 0.60 | 4.23 | 0.98 |
| R-2 | 1.13 | 7.79 | 0.94 | |
| R-3 | 1.49 | 10.10 | 0.89 | |
| IMKF | R-1 | 0.91 | 5.08 | 0.90 |
| R-2 | 1.00 | 5.38 | 0.88 | |
| R-3 | 1.03 | 6.21 | 0.89 | |
| IEKF | R-1 | 0.000 4 | 0.00 | 1.00 |
| R-2 | 0.000 6 | 0.00 | 1.00 | |
| R-3 | 0.001 6 | 0.00 | 1.00 |
|
| 图 5 案例1不同测量噪声工况下的误差 |
由表 2可知,在不同等级的测量噪声下,EKF方法对应的MAPE小于11%、NSE系数大于0.89;IMKF方法对应的MAPE小于7%、NSE系数大于0.9。EKF和IMKF均能得到合理结果, 但LKF方法不能得到合理的结果。IEKF方法对应的MAPE趋向于0、NSE系数趋向于1,对测量噪声不敏感,计算结果精度最高。
由图 5可知,随着测量噪声Rt+1的增加,EKF和IMKF方法结果误差呈增大趋势,尽管较大的Rt+1导致后验校核步骤的权重较小,但由于EKF和IMKF方法在先验预测步骤得到的参数值存在误差,若后验校核步骤仍存在较大测量噪声Rt+1,则直接降低最终参数估计结果的准确性。IEKF对测量噪声不敏感,在不同的测量噪声下的模型参数估计结果始终保持在较高的精度水平,原因在于使用式(14)中的状态转移矩阵,可以使先验预测步骤参数估计值的准确性提高,降低了由后验校核步骤中测量噪声引起的误差。因此,即使在较大的测量噪声下(σH=0.9 m, σq=15%),IEKF方法仍然给出准确的结果。
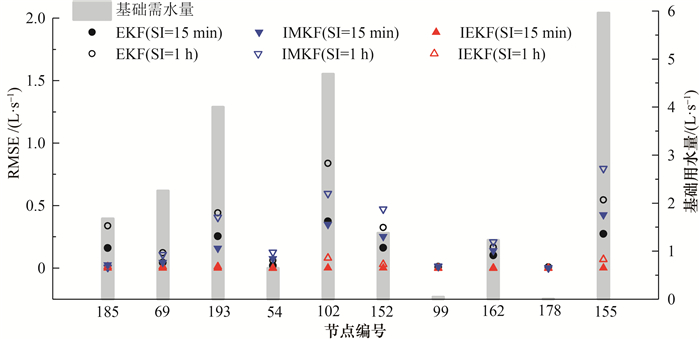
2.2 测量数据采样间隔对计算结果的影响根据2.1节的分析,LKF方法无法给出合理结果,因此后续研究中仅针对EKF、IMKF和IEKF 3种方法结果进行比较。在案例2中分别采用15 min和1 h的采样时间间隔(sampling interval, SI),比较各方法的计算精度。系统噪声Ut+1的对角元素设置为ut+1=1。对于测量噪声Rt+1,节点压力测量噪声方差设置为σH=0.3 m,管道流量测量噪声方差为σq=10%。图 6给出了不同采样间隔下,IMKF、EKF、IEKF的模型精度指标平均值。在每个分组中选取一个节点,图 7给出了各节点的RMSE值。
|
| 图 6 案例2不同采样间隔下的误差 |
|
| 图 7 案例2节点用水量估计误差(RMSE) |
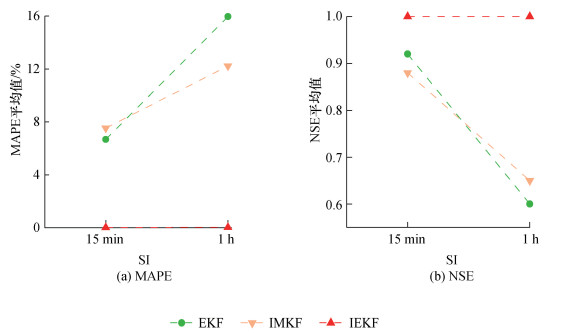
由图 6和7可知,SI由15 min增大到1 h时,EKF和IMKF的各项模型精度指标均表现出误差增大趋势。以图 6中的MAPE为例,EKF的MAPE增大了9.29%,IMKF的MAPE增大了4.27%。其原因在于当采样间隔1 h时,前后时刻间状态参数的变化较大,状态转移矩阵的设置会影响结果的误差。IEKF在2种采样间隔下的结果误差都很小,在SI=1 h时,MAPE=0.3%,NSE系数等于1,即使在较大的采样间隔下,IEKF得到的用水量估计结果也与真实值非常接近。
由图 6可知,当采样间隔为15 min时,EKF与IMKF方法模型精度指标平均值相似,IEKF方法的MAPE比EKF、IMKF方法的MAPE分别降低了6.65%、7.51%;IEKF方法的NSE系数比EKF、IMKF方法的NSE系数分别提高了0.08、0.12。当采样间隔为1 h时,IMKF的模型精度指标平均值小于EKF,IEKF方法的MAPE比EKF、IMKF方法的MAPE分别降低了15.93%、12.20%;IEKF方法的NSE系数比EKF、IMKF方法的NSE系数分别提高了0.40、0.35。
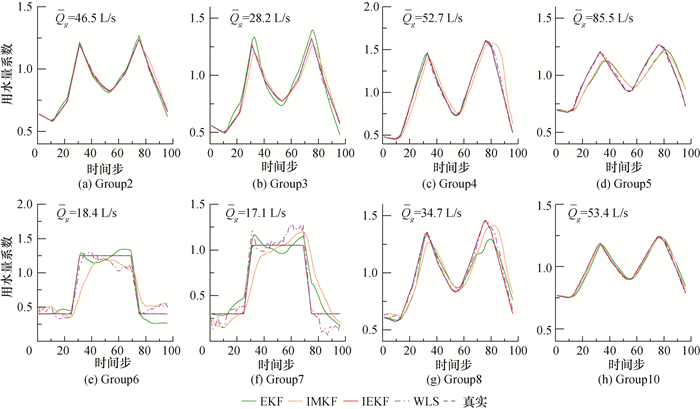
案例2中的10个分组包括工业类、居民类、商业类。Group1和Group9是用水量系数不随时间变化的工业类用户。为了分析不同方法计算结果的时变规律,图 8给出了各组在SI=15 min时(除Group1和Group9)的用水量系数估计结果。其中Group2—Group5、Group8、Group10为居民类用户,Group6和Group7为商业类用户。图中,Qg为各分组24 h的平均用水量。
|
| 图 8 案例2各节点组的用水量系数(SI=15 min) |
由图 8可知,IEKF在每个时刻的用水量系数结果都与真实系数接近,24 h的用水量时变曲线与真实曲线的趋势吻合,与图 6中的模型精度指标平均值结果规律一致,SI由15 min增大到1 h后,在先验预测步骤中预测误差增大,导致IMKF得到的用水量系数结果偏差较大。
由图 8e和8f可知,商业类节点组Group6和Group7用水量较小,节点压力和管道流量对节点组用水量的变化较敏感。在WLS迭代计算中,为了使得监测点处的模型模拟值与测量数据之间的误差达到预设精度,过度调整了节点用水量,导致迭代结果不准确。此外,迭代结果不准确导致拉丁超立方抽样计算得到的节点组用水量样本方差较大,使得IMKF计算中的Kalman增益矩阵K的取值较小,即先验预测值权重较大。
由图 8中所有节点组的用水量系数动态估计结果可知,IEKF能够更准确地捕捉居民类用户的用水高峰、低谷的时刻和用水量,以及用水量的突变。
2.3 用水模式曲线误差对计算结果的影响在IEKF方法中,用水模式曲线与真实用水曲线的偏差会对计算精度产生的一定影响。为进一步分析IEKF的计算精度和适应性,设置如下用水模式曲线误差工况:为反映节点实际用水量时变曲线与其所属类型的用水模式曲线之间的波动性,假定案例管网中的节点在每个时刻的真实用水量系数都是以该时刻的用水量曲线为均值、以5%为标准差的正态分布随机变量。在IEKF的先验预测步骤中采用与2.1和2.2节相同的各类用水模式曲线作为先验用水模式曲线,在后验校核步骤基于假定的真实用水模式曲线获得监测数据。对于EKF方法和IMKF方法,在后验校核步骤中采用与IEKF相同的假定真实用水模式曲线。
图 9给出了上述误差工况下,各分组(除工业类用户Group1和Group9)的用水量系数动态估计结果。图中,Qg为各分组24 h的平均用水量。
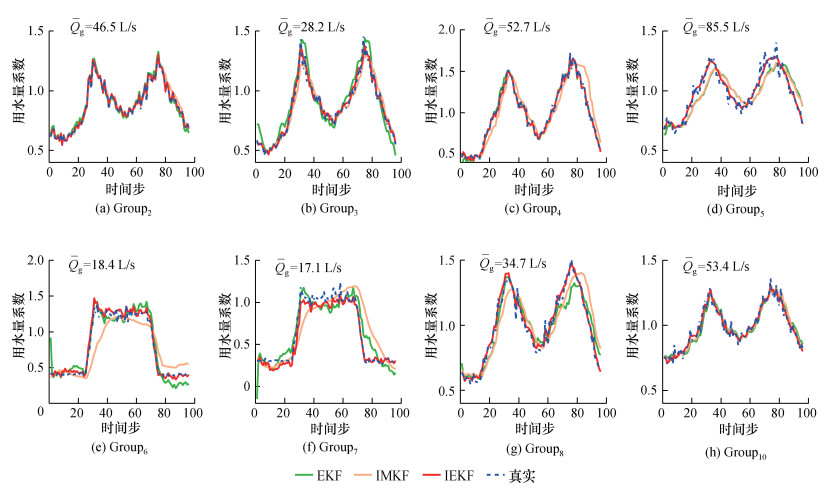
|
| 图 9 用水模式曲线误差工况下案例2各节点组的用水量系数(SI=15 min) |
由图 9可知,Qg最大的Group5在误差工况下EKF和IMKF的估计结果与真实用水模式曲线相比,都出现了明显的峰值偏差。在用水模式曲线存在误差的工况下,IEKF方法得到的所有分组的用水量系数曲线都与真实用水量系数曲线接近。与其他方法相比,IEKF方法能够更准确地捕捉用水高峰和用水量的突变,即IEKF方法对用水模式曲线误差的鲁棒性较高。
3 结论本研究将供水管网用户用水模式作为先验知识,应用于EKF的先验预测步骤,进行管网水力模型节点用水量的动态估计,为供水管网水力模型动态更新和校核提供了方法支撑。通过2个不同规模的案例管网,比较了4种基于KF的方法(LKF、EKF、IMKF、IEKF)的节点用水量估计结果,验证了IEKF方法的精度和适应性。本文得到的主要结论如下:
1) 在节点用水量估计问题中,LKF方法的线性化近似无法给出合理的结果;EKF、IEKF、IMKF方法均能适应非线性系统参数估计问题。IEKF方法将用水模式曲线引入先验预测步骤,考虑了不同类型用户用水量24 h的变化特征,计算精度较高,计算速度较快。IEKF方法的MAPE比EKF、IMKF方法的MAPE分别降低了15.93%、12.20%;IEKF方法的NSE系数比EKF、IMKF方法的NSE系数分别提高了0.40、0.35。
2) IMKF和EKF方法对系统噪声和测量噪声的设置较敏感,计算结果易受噪声设置的影响;IEKF对系统噪声和测量噪声均不敏感。EKF和IMKF在先验预测步骤忽略了前后时刻之间的用水量变化,在采样间隔增大时误差显著增大;IEKF能够适应更大的采样间隔,且在较大的采样间隔(1 h),IEKF相比于EKF和IMKF优势更显著。
3) 在24 h的估计周期内,IEKF在各个时刻的误差均较小,用水量系数曲线与监测曲线吻合,相比于EKF和IMKF方法,能够更准确地捕捉居民类用户的用水高峰、低谷的时刻和用水量,以及用水量的突变。此外,在用水模式曲线误差工况下,IEKF方法能够得到合理的估计结果,对用水模式曲线误差的鲁棒性较高。
| [1] |
KANG D, LANSEY K. Demand and roughness estimation in water distribution systems[J]. Journal of Water Resources Planning and Management, 2011, 137(1): 20-30. DOI:10.1061/(ASCE)WR.1943-5452.0000086 |
| [2] |
DINI M, TABESH M. A new method for simultaneous calibration of demand pattern and Hazen-Williams coefficients in water distribution systems[J]. Water Resources Management, 2014, 28(7): 2021-2034. DOI:10.1007/s11269-014-0592-4 |
| [3] |
DU K, LONG T Y, WANG J H, et al. Inversion model of water distribution systems for nodal demand calibration[J]. Journal of Water Resources Planning and Management, 2015, 141(9): 04015002. DOI:10.1061/(ASCE)WR.1943-5452.0000506 |
| [4] |
刘书明, 吴以朋, 车晗. 利用自识别的供水管网监测数据质量控制[J]. 清华大学学报(自然科学版), 2017, 57(9): 999-1003. LIU S M, WU Y P, CHE H. Monitoring data quality control for a water distribution system using data self-recognition[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(9): 999-1003. (in Chinese) |
| [5] |
WALSKI T M. Technique for calibrating network models[J]. Journal of Water Resources Planning and Management, 1983, 109(4): 360-372. DOI:10.1061/(ASCE)0733-9496(1983)109:4(360) |
| [6] |
ORMSBEE L E, WOOD D J. Hydraulic design algorithms for pipe networks[J]. Journal of Hydraulic Engineering, 1986, 112(12): 1195-1206. DOI:10.1061/(ASCE)0733-9429(1986)112:12(1195) |
| [7] |
DO N C, SIMPSON A R, DEUERLEIN J W, et al. Calibration of water demand multipliers in water distribution systems using genetic algorithms[J]. Journal of Water Resources Planning and Management, 2016, 142(11): 04016044. DOI:10.1061/(ASCE)WR.1943-5452.0000691 |
| [8] |
LETTING L K, HAMAM Y, ABU-MAHFOUZ A M. Estimation of water demand in water distribution systems using particle swarm optimization[J]. Water, 2017, 9(8): 593. DOI:10.3390/w9080593 |
| [9] |
任刚红, 杜坤, 和丽蓉, 等. 基于先验信息的供水管网阻力系数识别[J]. 土木建筑与环境工程, 2018, 40(2): 46-52. REN G H, DU K, HE L R, et al. Pipe resistance coefficient identification of water distribution system based on prior information[J]. Journal of Civil, Architectural & Environmental Engineering, 2018, 40(2): 46-52. (in Chinese) |
| [10] |
范江, 杜坤, 周明, 等. 基于加权最小二乘法的供水管网节点流量校核[J]. 土木建筑与环境工程, 2016, 38(3): 73-79. FAN J, DU K, ZHOU M, et al. Nodal demand calibration of water distribution system using the weighted least squares method[J]. Journal of Civil, Architectural & Environmental Engineering, 2016, 38(3): 73-79. (in Chinese) |
| [11] |
CHENG W P, YU T C, XU G. Real-time model of a large-scale water distribution system[J]. Procedia Engineering, 2014, 89: 457-466. DOI:10.1016/j.proeng.2014.11.212 |
| [12] |
ZHOU X, GUO S Y, XIN K L, et al. Maintaining the long-term accuracy of water distribution models with data assimilation methods: A comparative study[J]. Water Research, 2022, 226: 119268. DOI:10.1016/j.watres.2022.119268 |
| [13] |
DAVIDSON J W, BOUCHART F J C. Adjusting nodal demands in SCADA constrained real-time water distribution network models[J]. Journal of Hydraulic Engineering, 2006, 132(1): 102-110. DOI:10.1061/(ASCE)0733-9429(2006)132:1(102) |
| [14] |
HUTTON C J, KAPELAN Z, VAMVAKERIDOU-LYROUDIA L, et al. Dealing with uncertainty in water distribution system models: A framework for real-time modeling and data assimilation[J]. Journal of Water Resources Planning and Management, 2014, 140(2): 169-183. DOI:10.1061/(ASCE)WR.1943-5452.0000325 |
| [15] |
赵思浩, 陆明泉, 冯振明. 一种应用于GPS/低成本INS组合导航的自适应滤波算法[J]. 清华大学学报(自然科学版), 2011, 51(8): 1027-1030. ZHAO S H, LU M Q, FENG Z M. Adaptive filtering in GPS and low-cost INS integrated navigation systems[J]. Journal of Tsinghua University (Science and Technology), 2011, 51(8): 1027-1030. (in Chinese) |
| [16] |
金力, 吕鹏, 崔晓伟, 等. 新一代GNSS信号的自适应Kalman跟踪算法[J]. 清华大学学报(自然科学版), 2012, 52(9): 1249-1254, 1259. JIN L, LÜ P, CUI X W, et al. Adaptive Kalman tracking algorithm for new generation GNSS signals[J]. Journal of Tsinghua University (Science and Technology), 2012, 52(9): 1249-1254, 1259. (in Chinese) |
| [17] |
JUNG D, LANSEY K. Water distribution system burst detection using a nonlinear Kalman filter[J]. Journal of Water Resources Planning and Management, 2015, 141(5): 04014070. DOI:10.1061/(ASCE)WR.1943-5452.0000464 |
| [18] |
YE G L, FENNER R A. Kalman filtering of hydraulic measurements for burst detection in water distribution systems[J]. Journal of Pipeline Systems Engineering and Practice, 2011, 2(1): 14-22. DOI:10.1061/(ASCE)PS.1949-1204.0000070 |
| [19] |
LI Q, WU Z Y, RAHMAN A. Evolutionary deep learning with extended Kalman filter for effective prediction modeling and efficient data assimilation[J]. Journal of Computing in Civil Engineering, 2019, 33(3): 04019014. DOI:10.1061/(ASCE)CP.1943-5487.0000835 |
| [20] |
OKEYA I, KAPELAN Z, HUTTON C, et al. Online modelling of water distribution system using data assimilation[J]. Procedia Engineering, 2014, 70: 1261-1270. DOI:10.1016/j.proeng.2014.02.139 |
| [21] |
TODINI E. Using a Kalman filter approach for looped water distribution networks calibration [C]//International Conference on Computing and Control for the Water Industry; Water Industry Systems: Modelling and Optimization Applications. Baldock: Research Studies Press, 1999, 1: 327-336.
|
| [22] |
KANG D, LANSEY K. Real-time demand estimation and confidence limit analysis for water distribution systems[J]. Journal of Hydraulic Engineering, 2009, 135(10): 825-837. DOI:10.1061/(ASCE)HY.1943-7900.0000086 |
| [23] |
ZHANG Q Z, ZHENG F F, DUAN H F, et al. Efficient numerical approach for simultaneous calibration of pipe roughness coefficients and nodal demands for water distribution systems[J]. Journal of Water Resources Planning and Management, 2018, 144(10): 04018063. DOI:10.1061/(ASCE)WR.1943-5452.0000986 |
| [24] |
ZHOU X, XU W R, XIN K L, et al. Self-adaptive calibration of real-time demand and roughness of water distribution systems[J]. Water Resources Research, 2018, 54(8): 5536-5550. DOI:10.1029/2017WR022147 |
| [25] |
马锡涛. 城市供水管网功能抗震易损性与韧性概率特征分析[D]. 北京: 北京工业大学, 2022. MA X T. Seismic fragility and resilience probabilistic characteristic analysis of urban water supply networks [D]. Beijing: Beijing University of Technology, 2022. (in Chinese) |
| [26] |
LIU N D, DU K, TU J P, et al. Analytical solution of Jacobian matrices of WDS models[J]. Procedia Engineering, 2017, 186: 388-396. DOI:10.1016/j.proeng.2017.03.236 |



