引用本文
谢维强, 张晓平, 刘晓丽, 周小雄, 刘泉声. 基于多角度投影方法的砂土颗粒三维形态表征[J]. 清华大学学报(自然科学版), 2024, 64(2): 294-302.  
XIE Weiqiang, ZHANG Xiaoping, LIU Xiaoli, ZHOU Xiaoxiong, LIU Quansheng. Three-dimensional morphological characterization of sand particles based on a multiangle projection method[J]. Journal of Tsinghua University (Science and Technology), 2024, 64(2): 294-302.  
基于多角度投影方法的砂土颗粒三维形态表征
谢维强1,2, 张晓平3, 刘晓丽1, 周小雄1, 刘泉声3    
1. 清华大学 水沙科学与水利水电工程国家重点实验室, 北京 100084;
2. 深地科学与工程云龙湖实验室, 徐州 221116;
3. 武汉大学 岩土与结构工程安全湖北省重点实验室, 武汉 430072
收稿日期：2023-02-06
基金项目：国家自然科学基金面上项目(41941019, 51978541, 52079068)
作者简介：谢维强(1994-), 男, 助理研究员
通讯作者：张晓平, 教授, E-mail: jxhkzhang@163.com
摘要：砂土颗粒的形态学特征（尺寸和形状）对于评估砂土材料的力学特性至关重要，因此准确地量化其三维形态学特征是研究砂土材料力学特性的前提工作。相比三维测试（表征）方法，二维测试（表征）方法具有测试方式多、程序简单、成本低等优点。为研究二维图像对砂土颗粒三维形态的表征，利用三维激光扫描技术获取砂土颗粒的三维点云数据；然后利用计算机算法重构砂粒的三维模型，准确快速地自动提取砂粒的三维形态特征；借助算法获取了随机单一投影法、最大最小投影面积法（选自1 000张投影）和三正交方向投影法下的砂粒二维形态参数；分析了二维参数与三维参数之间的相关关系，提出了基于砂土颗粒二维形态特征表征三维形态特征的可靠方法。结果表明，砂土颗粒的三维尺寸（长、宽、厚）可使用相应的二维尺寸估算（线性拟合系数R2=0.735~0.994）；3种投影方法中，最大最小投影面积法和三正交方向投影法可准确地估算砂土颗粒的三维形态，为砂土材料的快速定量化表征提供了实用方法。
关键词：砂土颗粒    形态特征    三维激光扫描    二维投影    数字图像处理    
Three-dimensional morphological characterization of sand particles based on a multiangle projection method
XIE Weiqiang1,2, ZHANG Xiaoping3, LIU Xiaoli1, ZHOU Xiaoxiong1, LIU Quansheng3    
1. State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China;
2. Yunlong Lake Laboratory of Deep Underground Science and Engineering, Xuzhou 221116, China;
3. The Key Laboratory of Safety for Geotechnical and Structural Engineering of Hubei Province, Wuhan University, Wuhan 430072, China
Abstract: [Objective] The morphological characteristics (size and shape) of sand particles are critical for the evaluation of the mechanical properties of sand. Accurate quantification of these morphological characteristics is a prerequisite to investigating the mechanical properties of sand. Compared with the three-dimensional (3-D) test method, the two-dimensional (2-D) counterpart has the advantages of rich test types, simple procedures, and low cost. [Methods] To investigate the feasibility of 2-D images for 3-D morphological characterization of sand particles, 3-D laser scanning technology is employed in the present study to obtain the point cloud data of sand particles. Furthermore, a computer algorithm is developed to reconstruct the 3-D models of the sand particles. Thus, the 3-D morphological characteristics of the particles are accurately and quickly obtained. Three 2-D methods, namely the random single projection method, maximum and minimum projected area method (selected from 1 000 projections), and three orthogonal direction projection methods, are proposed for obtaining the 2-D morphological parameters of sand particles. [Results] Computer algorithms for reconstructing the 3-D model of sand particles based on a point cloud were proposed. The algorithms were used to automatically acquire the 3-D and 2-D morphological parameters. Thereafter, the correlations between the 3-D and 2-D parameters were analyzed. A practical method was proposed to obtain the 3-D morphological characteristics of the granular material based on the corresponding 2-D morphological characteristics. [Conclusions] The results reveal that there is a large gap between the 2-D parameters obtained from various angle projections, especially the area parameters in various projections. Notably, the error between the maximum and minimum area is as high as 40%. The random single angle projection method does not provide accurate 3-D information. A strong linear correlation exists between the 3-D and 2-D size parameters of the particles, and a moderate correlation exists between the shape parameters. An empirical relationship for estimating the 3-D morphology of sand particles using 2-D parameters is established. The 3-D parameters, namely the length, width, and thickness of the granular material, can be estimated using the corresponding 2-D parameters (R2=0.735-0.994). The fitting effects of the particle size parameters are better than those of the shape parameters. Additionally, the fitting effects of the maximum and minimum projected area and three orthogonal directional projection methods are better than those of the random single projection method. Among the three 2-D methods, the maximum and minimum projected area and three orthogonal direction projection methods can more accurately estimate the 3-D morphological characteristics of sand particles; thus, these are practical methods for the morphological quantification of granular materials.
Key words: sand particle    morphological characteristics    three-dimensional (3-D) laser scanning    two-dimensional (2-D) projection    digital image processing    

砂土材料作为一种散体材料，在岩土工程中广泛使用，如基坑换填、砂浆浇筑等。已有研究表明，砂土的形态特性对其工程特性包括物理特性、力学特性和水力特性具有显著影响[1-5]。为定量研究砂土颗粒形态对材料力学特性的影响规律，必须先准确重构砂粒的三维形态，并对其形态特征进行定量描述和表征。

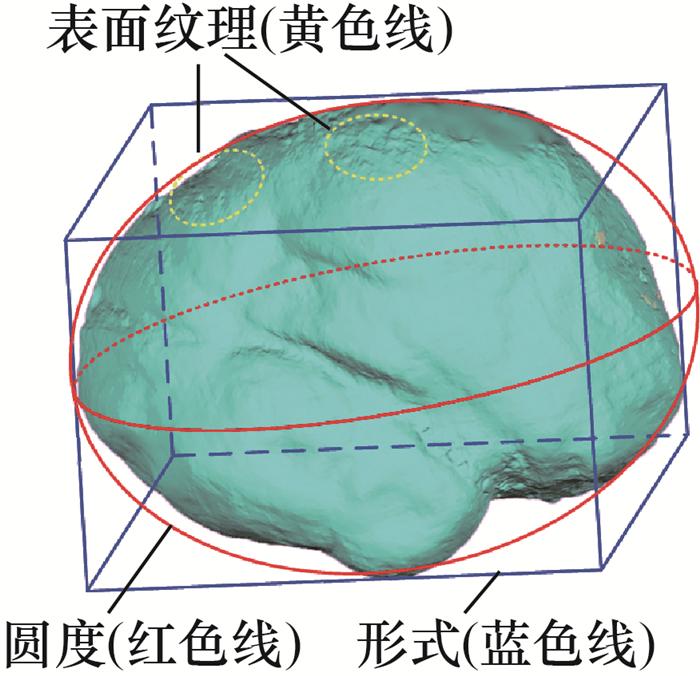
现有研究中，被广泛认可的形态学表征层面分为3个：形式、圆度和表面纹理[6]。这3种属性本质上是独立的，因为其中1种属性可在不影响其他2种属性的情况下发生很大变化。

大量研究表明，砂土颗粒的尺寸(属于形式)和形状(属于圆度)是影响其力学行为最重要的2个形态学特征[7-12]。工程实际中，操作员往往通过卡尺测量和使用不同孔径筛网筛分的方式获取砂粒3个正交方向维度的尺寸，并将砂粒尺寸用长度、宽度、级配和体积等参数表示[6]。然而这些获取方式非常繁琐，且人工测量误差大；最重要的是，使用卡尺测量和筛分的方式仅能获取砂土颗粒的尺寸特征，无法反映砂粒的形状特征。由此可见，现有研究缺乏一种标准、简单、高效、准确的方法量化砂土颗粒的尺寸和形状。

为准确获取砂土颗粒的三维形态特征，学者们采用了多种三维测量手段，如三维激光扫描[13-14]、X射线断层扫描[15-16]、扫描电子显微镜(scanning electron microscope，SEM)和微计算机断层扫描(computed tomography，CT)[17]。这些三维技术可通过获取砂粒的断层图像或表面空间坐标高精度地重构三维模型，进而得到准确的三维形态特征。然而这些技术存在明显不足：1) 若砂土颗粒表层呈白色(如石英含量高)，则激光难以捕捉断层或表面的点信息，从而造成重构信息缺失。2) 部分三维测量技术在实现全方位扫描时需要使用标志点对砂粒进行标记，这要求需重构的砂土颗粒尺寸应达到标志点进行标记的标准。3) 三维测量设备的成本通常较高，且测试耗时较长。

在工程实际中，通常通过二维图像快速获取物体的形态特征。数字图像处理(digital image processing，DIP) 技术基于相机捕获场景，将物体数字化为二维图像，经过一系列如图像增强、图像分割等处理提取物体的二维信息[18-20]。该技术成本低，且效率高，日常使用手机便可轻松获取砂粒的二维图像。但需注意的是，二维图像往往只是真实砂粒一个角度的投影，所得信息与三维形态特征有一定差距[21-22]。因此，二维图像对砂粒三维形态特征的表征效果与二维投影方法在岩土工程中的应用前景直接相关。

为探讨砂土颗粒二维投影表征三维形态的可行性及效果，本文采用三维激光扫描技术对20粒天然砂土颗粒进行了点云获取，并以计算机算法重构了砂土颗粒的三维模型，得到了砂土颗粒三维形态参数；多角度投影三维重构模型以模拟获取砂粒的二维图像；进而系统地研究了随机单一投影法、最大最小投影面积法[17](选自1 000张投影)和三正交方向投影法[6]，以验证这3种方法表征砂土颗粒尺寸和形状特征的潜力，建立了二维参数与三维参数的相关关系，提出了用二维图像快速有效获取砂粒三维形态特征的实用方法。

1 试验材料及方法 1.1 试验材料

为获取砂粒的形态学特征，本文采用了被广泛认可的尺寸特征及形状特征，这2个特征与砂粒材料3个层面的关系如图 1所示。

图 1 砂粒的3个形态学属性：形式、圆度和表面纹理[6]
图选项

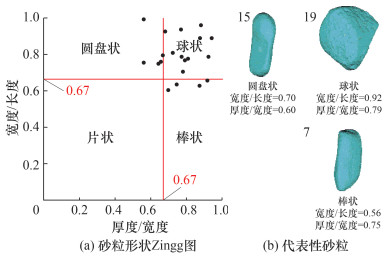
本试验使用的砂粒材料为天然砂粒，取自苏通特高压综合管廊工程经过的长江河床底部(北纬31°41′，东经120°46′)。在研究形态特征的砂粒数量方面，文[17, 23]曾采用超过20个的砂粒作为试验样本。在形态方面，能够进行三维重建的砂粒最小尺寸一般与三维测量装置和测试方法有关[24]。本文中，三维激光扫描装置需在对砂粒粘贴标记点后进行扫描，因此能够重建的最小砂粒尺寸约为5 mm。随机选取20个天然砂粒试验样本，其尺寸特征和形状特征分别如图 2和3所示，图 3中砂粒长、宽、厚为砂粒最小包容长方体的三维度尺寸。

图 2 20个天然砂粒试验样本
图选项

图 3 砂粒形状分布及3种形状的代表性砂粒
图选项

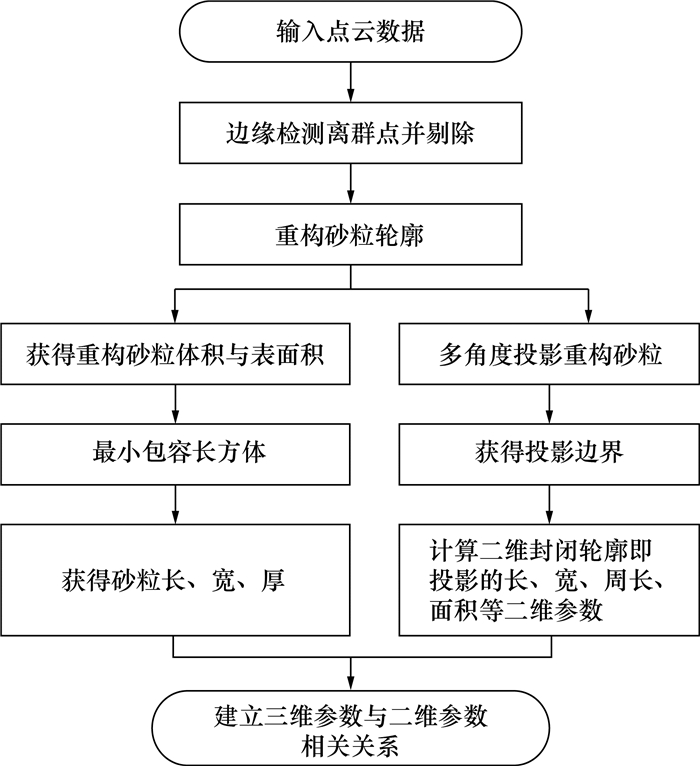
为定量获取砂粒形态参数，本文基于算法快速自动获取，如图 4所示。

图 4 砂粒三维、二维形态参数获取算法流程图
图选项

1.2 三维激光扫描

为精确获取砂粒的三维信息，采用手持式三维激光扫描仪(型号为：FreeScan X3)获取点云信息，试验时以0.02 mm的最大分辨率(即2个相邻点之间的最小距离为0.02 mm)捕捉砂粒外表面的空间点云，如图 5所示。实现砂粒的全方位扫描需要参照，而砂粒表面无法粘贴标志点，因此使用图 5b中的胶带及标志点作为参照。试验过程中，操作人员手持扫描仪进行全方位扫描以获取砂粒点云信息；之后将所获得的点云数据导入算法，将点云重构为三维模型，并自动计算砂粒的三维信息。该方法方便快捷，且无人工计算误差。

图 5 三维激光扫描及参数获取
图选项

尺寸和形状是表征砂粒形态特征的重要属性，文[17, 24-25, 27-28]出于不同的研究目的提出了多种表征参数，本文采用的三维尺寸参数和形状参数如表 1所示。长度、宽度和厚度是最基本的尺寸参数，体现了砂粒沿3个正交方向的延伸，可由砂粒的最小包容长方体确定[26]。球形度[27]是最为广泛使用的形状参数，越接近1代表砂粒越接近球体。所用参数均可通过算法自动计算。

表 1 砂土颗粒三维形态表征参数
类型 参数 定义
尺寸 长度L 最小包容长方体的长
宽度W 最小包容长方体的宽
厚度T 最小包容长方体的厚
体积V 砂粒整体外轮廓体积
表面积S 砂粒表面总面积
形状 伸长度e3D W/L[17, 24]
平整度F3D T/W[17, 24]
球形度ϕ3D $\sqrt[3]{36 {\rm{ \mathsf{ π} }} V^2}$/S[27-28]
注：参数值均为均值。
表选项

1.3 二维图像获取与处理

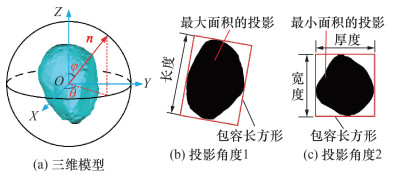
实际中，任意一张图像的拍摄均可看作是对物体某一角度的投影，为将这一思想应用到砂粒的形态表征中，本文采用对重构的三维模型进行任意角度投影的方式获取砂粒的二维图像，如图 6所示。O-XYZ坐标系为点云数据构成的最小包容长方体对应的参照系统，法向量n代表砂粒的投影方向，改变角度参数φ(n与Z轴的夹角)和θ(n与水平面的夹角)，便可实现对砂粒模型不同角度的投影。所得投影的二维尺寸和形状参数可由算法自动计算，主要表征参数如表 2所示。

图 6 二维图像获取及参数定义示意
图选项

表 2 砂土颗粒二维形态表征参数
类型 参数 定义
尺寸 长度li 最大面积投影上测得的最大Feret直径
宽度wi 最小面积投影上测得的最大Feret直径
厚度ti 最小面积投影上测得的最小Feret直径
投影面积Ai 砂粒外轮廓形成的总封闭面积
周长Pi 砂粒外轮廓的总长度
形状 伸长度ei2D wi/li[17, 24]
平整度fi2D ti/wi[17, 24]
圆度ϕi2D $\sqrt{4 {\rm{ \mathsf{ π} }} A_i}$/Pi[27-28]
注：参数均为均值；i为3种二维投影方法的编号，随机单一投影法为1，最大最小投影面积法为2，三正交方向投影法为3。
表选项

本文采用3种投影方法研究二维图像对砂粒三维形态特征的表征效果，包括随机单一投影法、最大最小投影面积法(选自1 000张投影)和三正交方向投影法。随机单一投影法采用对砂粒任意一角度的投影计算二维形态参数；最大最小投影面积法通过设置参数φ和θ从1 000个不同的角度投影砂粒，选出其中具有最大和最小面积的投影计算二维形态参数；三正交方向投影法采用砂粒3个正交方向的投影计算二维形态参数。

为准确获取砂粒的尺寸参数，且统一参数的定义，在最大最小投影面积法和三正交方向投影法中，砂粒的二维长度定义为在最大面积投影上测得的最大Feret直径，二维宽度为在最小面积投影上测得的最大Feret直径(不同于二维宽度为在最大面积投影上测得的最小Feret直径的常规定义，新定义更为准确，详见文[11])，二维厚度为在最小面积投影上测得的最小Feret直径，如图 6所示。

2 结果与讨论 2.1 多角度投影

砂粒的每一张二维图像均可视作三维实体某一角度的投影，因而角度的不同往往会影响该砂粒信息的表征效果。为检验从不同方向投影同一颗砂粒所得图像计算得到的二维参数的差异性，每颗砂粒均基于算法进行了1 000个不同角度的投影。图 7为砂粒1的1 000个投影的长度、宽度、周长和面积的频数分布图。可以看出，不同角度的二维参数存在较大差距，尤其是面积参数，最大和最小投影面积误差高达40%。二维参数在不同投影面表现出的差异性也说明任意单一角度的砂粒投影所得的参数具有随机性，并不能获得准确的三维形态参数，因此，多角度投影对砂粒的三维形态表征非常重要。

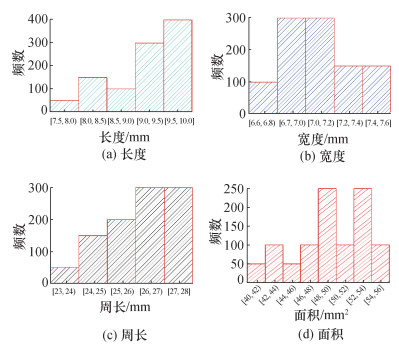
图 7 #1砂粒的1 000个投影所得二维参数的频率分布
图选项

为系统对比分析采用随机单一投影法、最大最小投影面积法和三正交方向投影法对二维图像的多角度投影的效果，将二维投影得到的二维尺寸与砂粒的三维尺寸进行比较，如图 8所示。随机单一投影法对砂粒尺寸的表征效果不理想，可发现该方法获得的砂粒二维长度和宽度明显高于相应砂粒的三维参数实际值；此外，随机单一投影法无法获得砂粒的厚度，因此在图 8c中，不存在t1对应的点。最大最小投影面积法和三正交方向投影法得到的二维尺寸参数与三维尺寸参数较为接近，说明多次投影所得的二维尺寸参数与砂土颗粒的真实三维尺寸参数非常接近，即使用最大最小投影面积法和三正交方向投影法多角度投影获取二维形态参数可提高对砂土颗粒三维形态的表征精度。

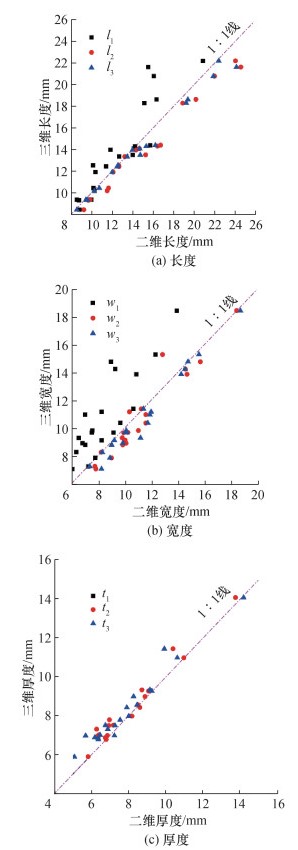
图 8 三维及二维尺寸参数比较
图选项

2.2 砂粒二维、三维形态参数相关性

为进一步分析砂粒二维形态参数与三维形态参数之间的相关性，采用Pearson相关系数作为参数的线性相关衡量指标，绝对值越接近1.000，表示参数之间的线性相关性越强。图 9显示了砂粒三维尺寸参数与二维尺寸参数之间的相关性，结果表明，这些尺寸参数之间具有非常强的线性相关性。原因是，一个尺寸参数的值通常会随着另一个参数的增加而增加。本文特别关注三维尺寸参数与相应的二维参数之间的相关性大小(即图 9中标红数据)。总体而言，砂粒三维尺寸与相应的二维尺寸具有极强的相关性；此外，最大最小投影面积法和三正交方向投影法得到的二维尺寸参数与三维尺寸参数相关性接近，且均高于随机单一投影法所得二维尺寸参数与三维尺寸参数的相关性，说明最大最小投影面积法和三正交方向投影法在表征砂粒尺寸方面具有更好的潜力。

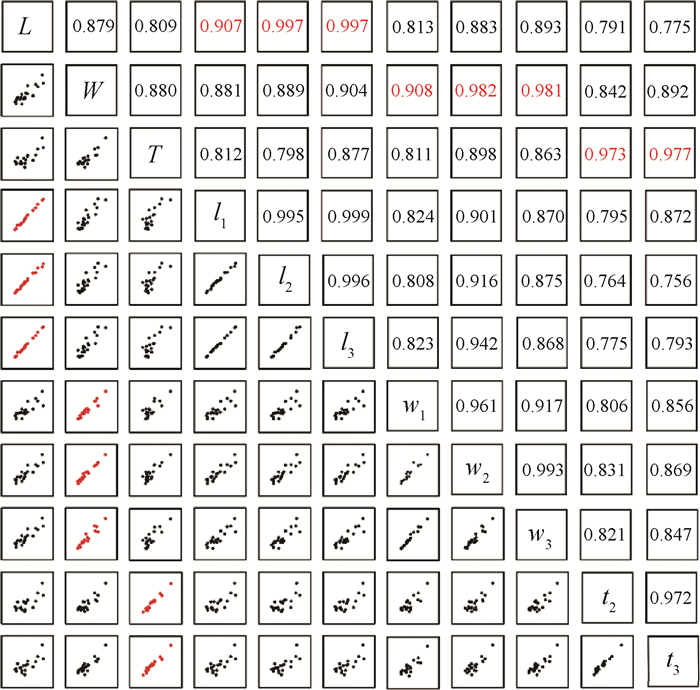
图 9 二维和三维尺寸参数相关性矩阵图
图选项

砂粒三维形状参数和相应的二维形状参数之间的Pearson相关系数如图 10所示。可以看出，形状参数之间的相关性普遍不如尺寸参数的相关性高；三维形状参数中的伸长度、平整度、球形度与二维形状参数中的圆度之间的相关性较低，即三维形状参数的伸长度、平整度和球形度所反映的形状信息是相对独立的。此外，最大最小投影面积法和三正交方向投影法得到的二维形状参数与相应三维形状参数相关性接近，且均远高于随机单一投影法所得二维形状参数与三维形状参数的相关性，随机单一投影法在表征砂粒三维形状参数上明显表现不足，这与单一方向的二维图像难以全面反映真实三维物体形貌信息的事实是一致的。

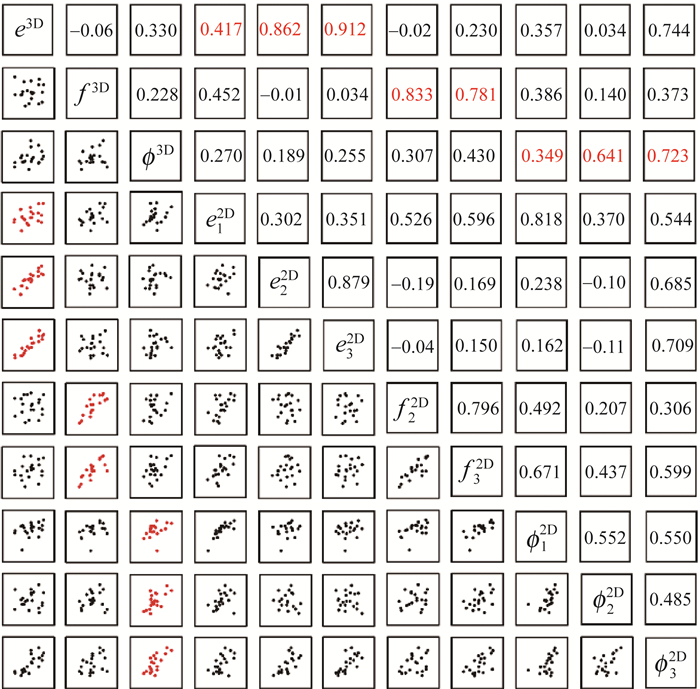
图 10 二维和三维形状参数相关性矩阵图
图选项

由以上的相关结果可知，砂粒的三维形态参数与二维形态参数均有一定程度的线性相关性，其中尺寸参数相关性极强，形状参数的相关性中等。原因可能与参数的定义有关，即尺寸参数为一维的线性指标，而形状参数涉及尺寸参数的乘除法甚至幂级数运算，所以形状参数对尺寸的数值更敏感。

2.3 基于二维参数的砂粒三维形态表征及验证

砂粒的三维形态参数与相应的二维形态参数之间具有较好的相关性，因此建立基于二维形态参数的砂粒三维形态表征是可能的。基于扫描及投影获取的砂粒二维、三维形态参数，建立了三维形态参数估算公式，如表 3所示，包括尺寸参数和形状参数。投影不具有厚度，因此t1和f12D无法通过随机单一投影法获取。从尺寸参数的线性拟合系数R2为0.735~0.994可知，砂土颗粒的三维尺寸(长、宽、厚)可使用相应的二维尺寸估算。对比R2可知砂粒尺寸参数的拟合效果普遍远优于形状参数的拟合效果；此外，最大最小投影面积法和三正交方向投影法的拟合效果远优于随机单一投影法的拟合效果。

表 3 砂粒三维形态参数估算公式
参数类型 参数 估算公式 R2
尺寸 L L=1.283l1-1.955 0.840
L=0.956l2+0.111 0.994
L=0.970l3+0.327 0.990
W W=1.240w1+0.228 0.735
W=1.045w2-0.897 0.921
W=1.019w3-0.738 0.971
T T=0.974t2+0.571 0.964
T=0.925t3+1.068 0.954
形状 e3D e3D=0.440e12D+0.465 0.174
e3D=0.792e22D+0.154 0.743
e3D=0.859e32D+0.077 0.832
f3D f3D=0.847f22D+0.177 0.694
f3D=0.858f32D+0.186 0.610
ϕ3D ϕ3D=0.377ϕ12D+0.474 0.122
ϕ3D=1.685ϕ22D-0.772 0.411
ϕ3D=1.149ϕ32D-0.244 0.523
表选项

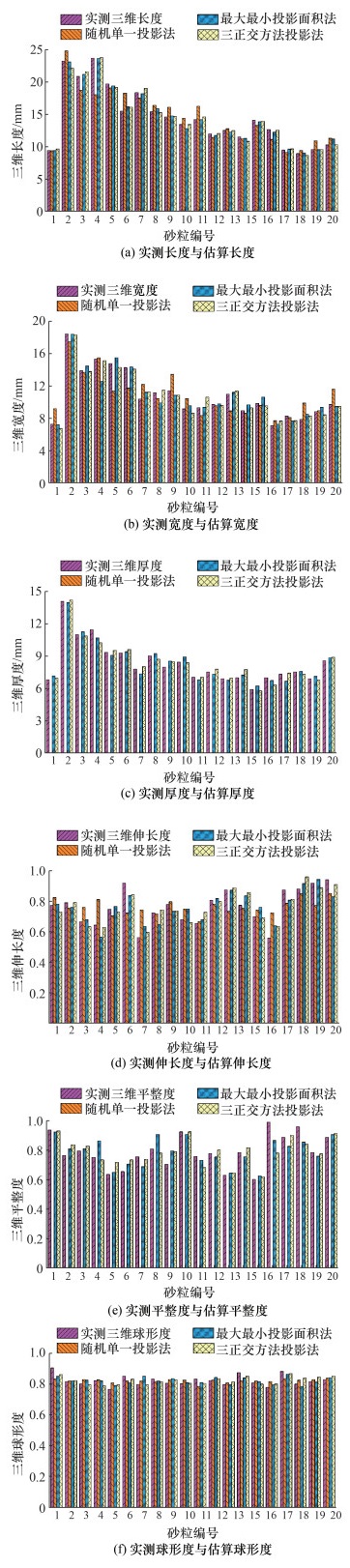
为进一步验证基于二维投影参数的砂粒三维形态参数估算公式对真实砂粒的信息表征效果，对比了砂粒的实测和估算三维形态参数，结果如图 11所示。可以看出，建立的估算公式对砂粒三维尺寸参数的表征效果较好，尺寸参数的估算值非常接近实测值；3种二维测试方法中，随机单一投影法离散性最大；对形状参数的估算偏差较大，原因是形状参数是砂粒的三维度属性，仅通过纯粹的二维图像难以获得其全面的形貌特征[17]。

图 11 砂粒形态参数实测值与估算值对比
图选项

总体上，通过二维图像参数表征砂土颗粒的三维形态特征是可行的，本文采用随机单一投影法、最大最小投影面积法和三正交方向投影法证实了这一结论。应注意的是，随机单一投影法在砂粒形态表征方面的效果不如其他2种方法好，且3种方法对砂粒的尺寸表征效果好于形状表征效果。这3种方法在工程实际中应用广泛，随机单一投影法使用最为普遍；三正交方向投影法在工程实际中使用可能具有一定困难；最大最小投影面积法的最大、最小投影面积易于从砂土颗粒的多角度投影中获得，因而最大最小投影面积法易于使用。这3种方法对颗粒材料的三维形态快速有效表征具有借鉴意义。

3 结论

准确地量化砂粒的三维形态学特征是研究砂土材料力学特性的前提工作，本文通过三维扫描获取砂粒点云信息，利用计算机算法重构砂粒三维模型进而快速自动获取其三维和二维形态参数，分析了三维参数与二维参数之间的相关性。结果表明：砂粒的三维与二维尺寸参数之间具有极强的线性相关性，形状参数之间表现出中等相关性。

本文提出了使用随机单一投影法、最大最小投影面积法和三正交方向投影法快速有效表征砂土颗粒三维形态参数的实现途径，建立了使用二维参数估算砂粒三维形态的经验关系。砂粒尺寸参数的拟合效果普遍远优于形状参数的拟合效果；此外，最大最小投影面积法和三正交方向投影法的拟合效果远优于随机单一投影法的拟合效果。

本文提出的方法对砂土颗粒的三维形态快速有效表征具有借鉴作用，为在不进行三维测量的情况下实现快速获取砂土颗粒的三维形态参数提供了可能，可应用于岩土工程材料表征及相关领域。

参考文献
[1]
高金翎. 砂土抗剪强度的主要影响因素及其研究现状分析[J]. 科教文汇, 2013(33): 110-115, 122.
GAO J L. Analysis of the main factors on the shear strength of sandy soil and the current research situation[J]. The Science Education Article Collects, 2013(33): 110-115, 122. (in Chinese)
[2]
周博. 基于能量耗散机制的砂土微观力学特性研究[D]. 武汉: 华中科技大学, 2013.
ZHOU B. Analysis of the microscopic mechanical property of sandy soils based on the energy dissipation mechanism [D]. Wuhan: Huazhong University of Science and Technology, 2013. (in Chinese)
[3]
彭仁. 颗粒形状对砂土力学性质影响的PFC模拟及定量分析研究[D]. 银川: 宁夏大学, 2011.
PENG R. PFC simulation and quantitative analysis of influence of particle shape on mechanical properties of sand [D]. Yinchuan: Ningxia University, 2011. (in Chinese)
[4]
刘清秉, 项伟, BUDHU M, 等. 砂土颗粒形状量化及其对力学指标的影响分析[J]. 岩土力学, 2011, 32(S1): 190-197.
LIU Q B, XIANG W, BUDHU M, et al. Study of particle shape quantification and effect on mechanical property of sand[J]. Rock and Soil Mechanics, 2011, 32(S1): 190-197. (in Chinese)
[5]
付茹, 胡新丽, 周博, 等. 砂土颗粒三维形态的定量表征方法[J]. 岩土力学, 2018, 39(2): 483-490.
FU R, HU X L, ZHOU B, et al. A quantitative characterization method of 3D morphology of sand particles[J]. Rock and Soil Mechanics, 2018, 39(2): 483-490. (in Chinese)
[6]
BARRETT P J. The shape of rock particles, a critical review[J]. Sedimentology, 1980, 27(3): 291-303. DOI:10.1111/j.1365-3091.1980.tb01179.x
[7]
汪轶群. 钙质砂宏细观力学特性试验及离散元模拟[D]. 杭州: 浙江大学, 2016.
WANG Y Q. Macro-and micro-mechanical behavior of calcareous sand and discrete element method analysis [D]. Hangzhou: Zhejiang University, 2016. (in Chinese)
[8]
孔亮, 彭仁. 颗粒形状对类砂土力学性质影响的颗粒流模拟[J]. 岩石力学与工程学报, 2011, 30(10): 2112-2119.
KONG L, PENG R. Particle flow simulation of influence of particle shape on mechanical properties of quasi-sands[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2112-2119. (in Chinese)
[9]
常在, 杨军, 程晓辉. 砂土强度和剪胀性的颗粒力学分析[J]. 工程力学, 2010, 27(4): 95-104.
CHANG Z, YANG J, CHENG X H. Granular mechanical analysis of the strength and dilatancy of sands[J]. Engineering Mechanics, 2010, 27(4): 95-104. (in Chinese)
[10]
ZHANG X P, XIE W Q, CAI K Y, et al. Evaluation of rock muck using image analysis and its application in the TBM tunneling[J]. Tunnelling and Underground Space Technology, 2021, 113: 103974. DOI:10.1016/j.tust.2021.103974
[11]
XIE W Q, ZHANG X P, YANG X M, et al. 3D size and shape characterization of natural sand particles using 2D image analysis[J]. Engineering Geology, 2020, 279: 105915. DOI:10.1016/j.enggeo.2020.105915
[12]
王步雪岩, 孟庆山, 韦昌富, 等. 多投影面下珊瑚砂砾颗粒形貌量化试验研究[J]. 岩土力学, 2019, 40(10): 3871-3878.
WANG B X Y, MENG Q S, WEI C F, et al. Quantitative experimental study of the morphology of coral sand and gravel particles under multiple projection surfaces[J]. Rock and Soil Mechanics, 2019, 40(10): 3871-3878. (in Chinese)
[13]
ASAHINA D, TAYLOR M A. Geometry of irregular particles: Direct surface measurements by 3-D laser scanner[J]. Powder Technology, 2011, 213(1-3): 70-78. DOI:10.1016/j.powtec.2011.07.008
[14]
LANARO F, TOLPPANEN P. 3D characterization of coarse aggregates[J]. Engineering Geology, 2002, 65(1): 17-30. DOI:10.1016/S0013-7952(01)00133-8
[15]
ERDOǦAN S T, GARBOCZI E J, FOWLER D W. Shape and size of microfine aggregates: X-ray microcomputed tomography vs. laser diffraction[J]. Powder Technology, 2007, 177(2): 53-63. DOI:10.1016/j.powtec.2007.02.016
[16]
LIN C L, MILLER J D. 3D characterization and analysis of particle shape using X-ray microtomography (XMT)[J]. Powder Technology, 2005, 154(1): 61-69. DOI:10.1016/j.powtec.2005.04.031
[17]
BAGHERI G H, BONADONNA C, MANZELLA I, et al. On the characterization of size and shape of irregular particles[J]. Powder Technology, 2015, 270: 141-153. DOI:10.1016/j.powtec.2014.10.015
[18]
YUE Z Q, BEKKING W, MORIN I. Application of digital image processing to quantitative study of asphalt concrete microstructure[M]. Transportation Research Board, 1995.
[19]
KWAN A K H, MORA C F, CHAN H C. Particle shape analysis of coarse aggregate using digital image processing[J]. Cement & Concrete Research, 1999, 29(9): 1403-1410.
[20]
陈海洋, 汪稔, 李建国, 等. 钙质砂颗粒的形状分析[J]. 岩土力学, 2005, 26(9): 1389-1392.
CHEN H Y, WANG R, LI J G, et al. Grain shape analysis of calcareous soil[J]. Rock and Soil Mechanics, 2005, 26(9): 1389-1392. (in Chinese)
[21]
HENTSCHEL M L, PAGE N W. Selection of descriptors for particle shape characterization[J]. Particle & Particle Systems Characterization, 2003, 20(1): 25-38.
[22]
FERNLUND J M R. Image analysis method for determining 3-D size distribution of coarse aggregates[J]. Bulletin of Engineering Geology & the Environment, 2005, 64(2): 159-166.
[23]
ALTUHAFI F, O'SULLIVAN C, CAVARRETTA I. Analysis of an image-based method to quantify the size and shape of sand particles[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2013, 139(8): 1290-1307.
[24]
BLOTT S J, PYE K. Particle shape: A review and new methods of characterization and classification[J]. Sedimentology, 2008, 55(1): 31-63. DOI:10.1111/j.1365-3091.2007.00892.x
[25]
王东伟, 陆武萍, 唐朝生, 等. 砂土微观结构样品制备技术及量化方法研究[J]. 岩土力学, 2019, 40(12): 4783-4792.
WANG D W, LU W P, TANG C S, et al. Sample preparation technique and microstructure quantification method for sandy soil[J]. Rock and Soil Mechanics, 2019, 40(12): 4783-4792. (in Chinese)
[26]
KOESAWE J. The minimal bounding box [Z/OL]. (2015-2-16)[2023-01-15]. http://www.mathworks.com/matlabcentral/fileexchange/18264-minimal-bounding-box. 2008.
[27]
WADELL H. Sphericity and roundness of rock particles[J]. The Journal of Geology, 1933, 41(3): 310-331.
[28]
WADELL H. Volume, shape, and roundness of rock particles[J]. The Journal of Geology, 1932, 40(5): 443-451.