现代商用飞机的高升力装置通常由单个或多个襟翼和缝翼组成,这些机械活动部件极大地增加了飞机的结构复杂性、成本和质量。环量控制技术作为新型的主动流动控制方式,能利用高速射流有效抑制流动分离,进一步简化了机翼的结构,同时有利于提高飞行稳定性,维持飞机高效率飞行。环量控制技术以从发动机或外界引气形成的高速射流代替活动机械部件,从而达到增升、降噪、增强机动性、提高隐身性[1-2]等效果。1962年,国外研究人员就已开展相关实验和数值研究[3],近年来逐渐开展样机验证工作,而国内的相关工作起步较晚。
前期国内外针对环量控制的大量工作聚焦于验证可行性,该技术被广泛用于飞机和风力机[4]叶片。在几何设计方面,宋彦萍等[5]探讨了圆、椭圆和对数螺线形Coanda表面射流附壁层与特征参数的关联性。郑无计等[6]基于超临界翼型改变后缘半径和射流口高度,研究了尾缘射流的气动增益效果。文[7-8]对内吹式襟翼进行了研究,文[9-14]探究了Coanda效应在飞翼布局上的应用。Jones等[15]利用脉冲气动襟翼设计了一款二维通用航空环量控制(circulation control,CC)翼型。Carmona等[16]探讨了不连续非圆表面机翼上环量控制的应用。Hoholis等[17]对DLR-F19通用无人机进行了环量控制的数值研究。Forster等[18]在超临界翼型和跨音速自由流Mach数(Ma)条件下,研究了不同Coanda半径/槽高比、喷口形状和喷口厚度对气动性能敏感性的影响。针对不同工况,文[19-20]提出了多喷口环量控制翼型,文[21-23]探讨了零质量射流、合成射流对动态失速和控制特性的影响。Li等[24]在亚音速到跨音速范围内测试了射流在不同动量系数下的收敛特性。Burnazzi等[25]比较了不同环境来流风量和飞行攻角下的响应机制,通过环量控制实现延迟器失速、能耗降低。
此外,研究人员期望提高对环量控制翼型升阻特性和失速攻角的预测能力。在分离预测方面,孙全兵[26]等研究表明,环量控制将使失速攻角的出现延迟,反向射流将产生偏航力矩。Wetzel等[27]观测了后缘流场的弯曲壁面射流,用于预测平均切向速度场和机翼后缘上方流动分离位置。Fu等[28]将环量控制翼型在不同动量系数下的升力、阻力曲线与4种常规机翼情况进行了比较,建立了襟翼偏转角与射流偏转的对应关系。通过分析精度提升的湍流模型的流场分离,Storm等[29]修改了湍流模式的变体模型,以捕捉非线性涡黏性效应和流线曲率效应的效果,发现v2-f湍流模型在环量控制流场生成方面能得到更精确的计算结果。Nishino等[30]采用大涡模拟,通过沿翼展方向设置周期性边界的方式,捕捉流动中湍流相关涡结构的发展过程。尽管现有实验和数值模拟结果可较好地反映环量控制的机理,但仍缺少Coanda效应影响下流动分离与失速现象的机理研究和规律性总结。
尖尾缘和环量控制翼型的增升机理不同,环量控制翼型无法用传统翼型的Kutta条件解释升力产生机制,前后驻点变化引起的环量变化仍是研究重点。研究人员不能有效识别环量控制中的分离控制和超环量控制阶段,需要足够多的计算数据绘制曲线才能大致判断[31]。首先,本文建立了Coanda偏转角与动量和升力系数之间的定量关系,直接观测流场中Coanda偏转角的变化即可大致预测分离的状态[32];其次,通过分析失速流场异常行为,提出了一种判断分离控制阶段和超环量控制阶段的新思路;最后,把表征射流强度的动量系数与体现气动特性的升力系数映射至实际流场中,利用单一变量Coanda偏转角,对翼型表面的流动分离进行有效监测,这对不同翼型的流动控制均有一定的借鉴意义。此外,本文研究成果一定程度上改善了环量控制翼型设计严重依赖经验调参的现状。
1 平台建立与算例验证本文采用美国国家航空航天局(National Aeronautics and Space Administration,NASA)设计的翼型NACA0012和环量控制翼型CC-E0020EJ作为验证基础。从Profili翼型数据库获取几何参数,使用ICEM-CFD完成网格划分,使用仿真模拟软件CFD++进行数值分析。
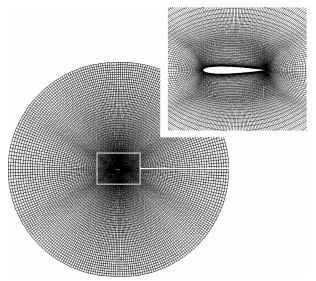
1.1 网格无关性验证选用NACA-0012结构网格完成网格无关性验证,O形拓扑翼型结构网格划分如图 1所示。在翼型周围及后缘对网格加密,翼型弦长1 m,壁面无滑移边界条件。给定远场边界条件:Ma为0.15,Reynolds数(Re)为6×106,环境温度T为288 K,湍流强度为0.02,湍流/层流黏度比为50。第1层网格高度为4.6×10-6 m,网格增长率为1.15,控制第1层网格高度,确保y+数小于1。在尾缘吹气的定常计算中,本文使用的压力远场距离为15倍弦长,与文[33-34]的相应数据相比,足以满足计算条件。使用Realizable k-ε湍流模型进行网格无关性分析,网格总数分别为粗网格15 680、中网格33 201、细网格59 302。对比3种网格的计算结果,并与NASA实验数据进行比较,不同网格密度的数据对比如表 1所示。粗网格下相对误差已收敛,中网格、细网格的计算结果趋于稳定,故选用中网格的计算方案[34]。
|
| 图 1 O形拓扑翼型结构网格划分 |
| 参数 | 粗网格 | 中网格 | 细网格 | NASA实验数据 |
| 网格数 | 15 680 | 33 201 | 59 302 | — |
| 升力系数 | 1.068 99 | 1.072 56 | 1.073 63 | 1.077 81 |
| 相对误差 | 0.82% | 0.39% | 0.39% | — |
1.2 NACA0012算例验证
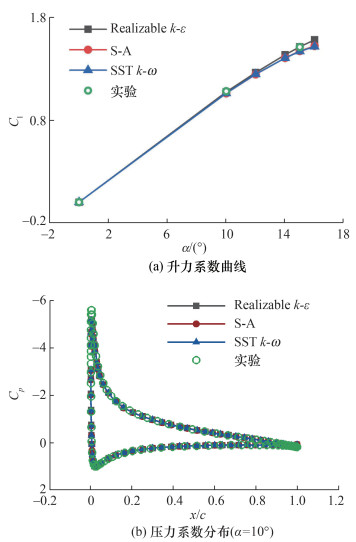
本文选用Spalart-Allmaras(S-A)、Realizable k-ε和剪切应力输运(shear stress transport, SST)k-ω共3种模型,计算条件为Ma=0.15,Re=6×106,与NASA实验数据对照。3种湍流模型在不同攻角α下的升阻力特性如图 2所示。图中Cl为翼型升力系数,Cp为压力系数,x、y为横、纵坐标,c为弦长,x/c表示横坐标在弦长上的相对位置,y/c表示纵坐标在弦长上的相对位置,本文c=1.0 m。
|
| 图 2 3种湍流模型在不同攻角下的升阻力特性 |
由图 2可知,当α为0°、10°、15°时3种模型的升力系数均与实验数据相符;α=10°时3种模型的翼型表面压力分布并无较大差异。Realizable k-ε、S-A、SST k-ε这3种模型的升力系数与实验数据的误差分别为0.94%、2.68%、4.07%。根据计算结果可以判断,Realizable k-ε模型误差较小;S-A和SST k-ε模型所需的迭代步数明显增加,且在复杂流场下收敛效率并不理想,故本文采用Realizable k-ε模型完成计算。
1.3 CC-E0020EJ算例验证CC-E0020EJ是标准的环量控制翼型,具有钝尾缘特征,这使其更易于观察Coanda效应。参考文[35-36]的几何与流场设置进行算例验证。
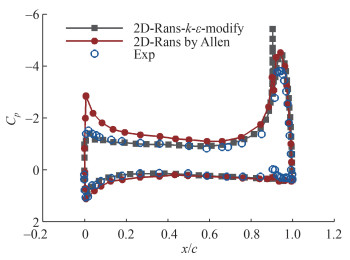
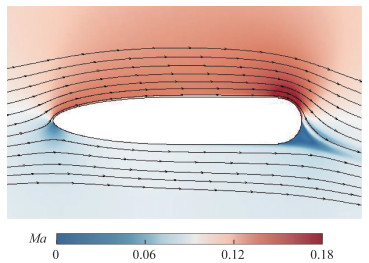
设置流场条件为Ma=0.10、Re=2.362 2×106、动量系数Cμ=0.047,对比升力系数与压力分布情况,CC-E0020EJ翼型的Ma云图如图 3所示,CC-E0020EJ翼型仿真及其与实验数据的对比如图 4所示。本文采用攻角修正的方法,修正后的攻角为-3°。攻角被修正后,翼型前缘的吸力峰及上下翼面均与实验数据高度吻合,钝尾缘的背风面也出现了与其他研究类似的压力分布,说明计算结果能反映流场分布情况。
|
| 图 3 CC-E0020EJ翼型的Ma云图 |
对计算中可能出现的误差进一步分析。由于实验模型的喷口高度不均,射流速度沿展向变化[37],环量控制的有效性降低。CC-E0020EJ的算例验证[38]表明:数值仿真结果与实验数据存在一定偏差,通常需要采用模拟风洞实验条件、边界条件修正及攻角修正等方法提高准确性。Shao等[34]的研究表明:展向流动和黏性壁效应会极大地影响环量控制翼型模拟的准确性,采用构建网格边界和曲率修正的方法可提高精度。Englar等[35]针对CFD与实验模型不同截面上的误差,采用了降低喷口落压比和负攻角修正的方法,发现α=-2°时的修正效果最佳。Allen等[36]提出,质量流量计算和等熵假设会导致升力系数存在5%的偏差,不同机翼截面与积分所得升力系数也存在偏差,需要对动量系数和喷口速度进行修正。即使采用曲率校正模型,也存在相比实验结果升力过高的情况[39]。综上所述,当采用本文修正方法时,数值仿真可达到所需计算精度。
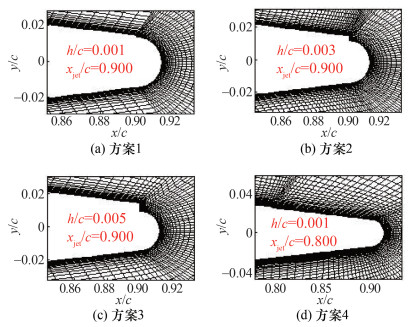
2 尾缘修型方案 2.1 翼型几何简化本文使用NACA-0012翼型作为环量控制的基础翼型,采用上翼面单边吹气的尾缘修型方案,探究环量控制翼型喷口高度与后缘半径比h/r及后缘半径与弦长比r/c对升力阻力增量的影响[40]。改变环量控制翼型尾缘的射流喷口位置和高度,探究Coanda效应的产生机制。4种修型方案的参数设置如表 2所示,其中射流喷口在翼型弦长上的相对位置表示为xjet/c,喷口高度在翼型弦长上的相对长度表示为h/c。图 5为设计后的4种修型方案中尾缘的翼型网络。图中,y/c表示纵坐标在弦长上(本文中c=1 m)的相对位置。
| 参数 | 方案1 | 方案2 | 方案3 | 方案4 |
| xjet/c | 0.900 | 0.900 | 0.900 | 0.800 |
| h/c | 0.001 | 0.003 | 0.005 | 0.001 |
| h/r | 7.16% | 23.13% | 41.77% | 7.16% |
| r/c | 1.53% | 1.42% | 1.31% | 1.53% |
|
| 图 5 4种修型方案中尾缘的翼型网格 |
根据文[35]的实验方案完成二维仿真计算,实验条件为:α=0°,Ma=0.083 6,Re=1.895×106,T=294.1 K,来流速度U∞=28.75 m/s。尾缘设计方案改变了射流喷口高度,而动量系数与喷口高度有关,为更加直观衡量射流在尾缘上的分离与附壁效果,采用无量纲的射流速度与来流速度的比值代表射流强度,并进行分析。
2.2 气动参数评估动量系数,即射流动量通量与自由来流动量通量的比值,是环量控制翼型的重要参数[41],用于衡量射流强度,表示如下:
| $ C_{\mu}=\frac{\dot{m} U_{\mathrm{jet}}}{q_{\infty} S}=\frac{\rho_{\mathrm{jet}} U_{\mathrm{jet}}^{2} A_{\mathrm{jet}}}{q_{\infty} S} $ | (1) |
其中:
射流喷口的边界条件为给定静温静压的速度入口。对于给定的Cμ,可计算获得射流的速度和质量流量,表示如下:
| $ U_{\mathrm{jet}}=\sqrt{\frac{U_{\infty}^{2} S C_{\mu}}{2 A_{\mathrm{jet}}}}, $ | (2) |
| $ \dot{m}=\rho_{\mathrm{jet}} U_{\mathrm{jet}} A_{\mathrm{jet}}=\rho_{\mathrm{jet}} U_{\infty} \sqrt{\frac{A_{\mathrm{jet}} S C_{\mu}}{2}}. $ | (3) |
本文考虑采用推阻分解方法[42],从翼型所受的合力中分解出射流产生的推力项和阻力项,单独考虑环量增加产生的气动增升效果。为此,引入有效升力系数Cl*、有效阻力系数Cd*及有效升阻比Cl*/Cd*,表示如下:
| $ C_{{\rm{l}}}^{*}=C_{{\rm{l}}}-C_{\mathrm{thr}} \sin \theta_{\mathrm{jet}}, $ | (4) |
| $ C_{\mathrm{d}}^{*}=C_{\mathrm{d}}-C_{\mathrm{thr}} \cos \theta_{\mathrm{jet}}+C_{\mathrm{E}}, $ | (5) |
| $ \frac{C_{{\rm{l}}}^{*}}{C_{\mathrm{d}}^{*}}=\frac{C_{{\rm{l}}}-C_{\mathrm{thr}} \sin \theta_{\mathrm{jet}}}{C_{\mathrm{d}}-C_{\mathrm{thr}} \cos \theta_{\mathrm{jet}}+C_{\mathrm{E}}}, $ | (6) |
| $ C_{\mathrm{E}}=\frac{\int\limits_{A_{\mathrm{jet}}} \frac{1}{2} \rho_{\mathrm{jet}} U_{\mathrm{jet}}^{3} \mathrm{~d} A}{q_{\infty} U_{\infty}}. $ | (7) |
其中:Cd为翼型阻力系数,Cthr为吹气射流产生反向力的总推力系数,CE为吹气所消耗的能量系数,θjet为射流和来流方向的夹角。
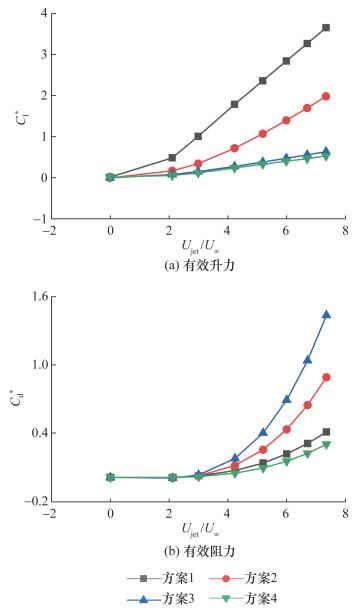
2.3 有效气动特性分析为验证尾缘修型方案的有效性,绘制不同修型方案下有效升力和阻力随Ujet/U∞的变化曲线,如图 6所示。可以看出,方案1的有效升力远大于其他方案,方案2居中,方案3和4均较小,说明方案1的增升效果最好;方案3的有效阻力增幅最大,方案2居中,方案1和4的有效阻力增幅最小,可推断方案1的能量消耗最少、阻力项最小。由上述结果初步判断:喷口高度越小,有效升阻比的适用范围越广、气动特性越好,方案1的增升减阻效果越好。
|
| 图 6 修型方案的有效升、阻力对比 |
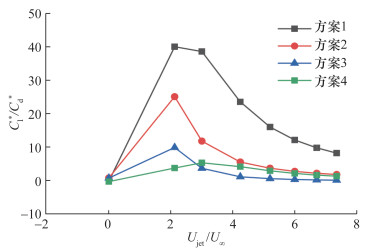
在此基础上进一步探究不同修型方案下有效升阻比的特性,4种修型方案的有效升阻比对比结果如图 7所示。对比方案1、2、3可知,改变喷口高度对有效升阻比产生的影响极大,射流喷口高度越小,有效升阻比越大;当Ujet/U∞=2.12时,方案1、2、3均达到最大值,方案1的有效升阻比最大,超过40。对比方案1和4可知,方案4的有效升阻比不超过7,气动特性较差;当Ujet/U∞接近3时,方案4的有效升阻比才达到最大值,这说明靠近圆弧形尾缘的射流喷口设计方案具有更好的气动特性,当射流远离时气动特性变差。综上所述,方案1的环量控制机翼吹气效率最高,Coanda效应最显著,与文[11]的结果吻合,后文研究按照此方案进行。
|
| 图 7 4种修型方案的有效升阻比对比结果 |
3 数值结果与分析 3.1 Coanda偏转角的物理意义
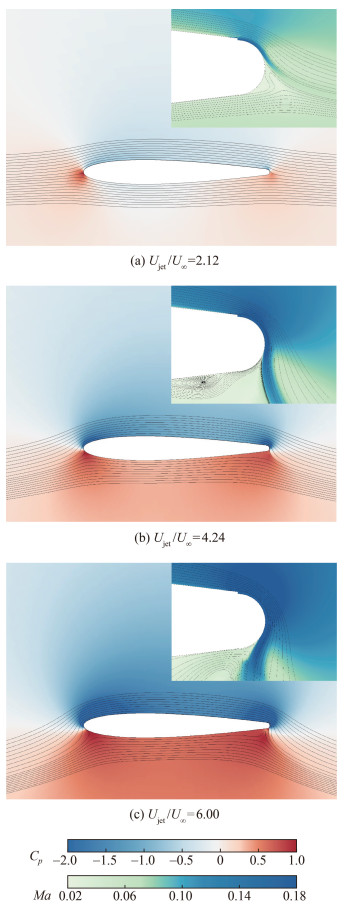
尾缘射流是Coanda效应产生的主要因素,通过对比翼型周围流场的压力分布变化和Ma分布云图,观察方案1中翼型尾缘的附壁效应,压力系数与Ma流场分布云图如图 8所示。
|
| 图 8 压力系数与Ma流场分布云图 |
由图 8可知,翼型上翼面压力减小、下翼面压力增大,射流与附壁表面分离后穿透流场。壁面边界层速度亏损与喷口后缘附近的不利压力梯度相互作用,导致α不变的情况下来流流场中近翼面的流线产生较大偏转,相当于传统机械装置的气动弯度增加。附壁分离与射流穿透结合将使后部移动下表面上的驻点向前移动,下表面上的后缘驻点向前移动。随着射流速度增加,停滞点相互靠近,环量增大。
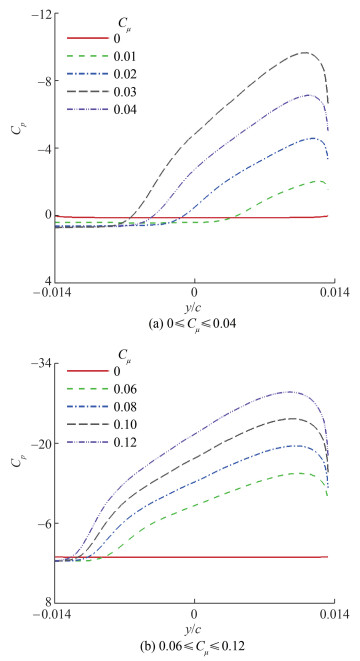
本文将射流出口到尾缘上出现分离的位置[31-32]定义为Coanda偏转角θ,即射流在翼型尾缘上的偏转程度。因为Coanda效应可以有效抑制尾缘分离,所以射流分离位置对环量控制的机理研究具有重要意义。以Cμ=0为基准线,观测小于基准线的位置,即射流影响区域,α=0°时翼型尾缘的压力系数分布如图 9所示。由图 9可知,压力系数先升后降,近喷口位置因卷吸大量外流场气体形成“吸力峰”,并且在尾缘半径的中轴线,即射流偏转角大于90°后,压力系数快速下降,下翼面底端形成压力大于0的逆压区,即Coanda效应的影响区域。
|
| 图 9 翼型尾缘的压力系数分布 |
对于动量相对较高的情况,高能量射流形成更大的湍流剪切层,压力系数随动量系数增大持续降低,对外界气流卷吸形成一个高速低压区。“吸力峰”随着射流增强逐渐后移,影响区域增大,提供的升力增量增加。与传统尖尾缘翼型的升力来源有所不同,需要引入Coanda偏转角补充说明其流场特征。
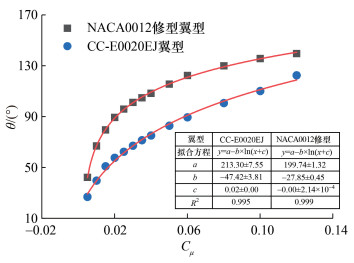
给定的远场边界条件:Ma=0.15,Re=6×106,T=288 K。本文在该条件下通过对NACA-0012修型翼型和CC-E0020EJ翼型进行数值仿真计算,研究了Coanda偏转角与动量系数的对应关系。动量系数与Coanda偏转角的对应关系如图 10所示。随着动量系数增大,Coanda偏转角增大。低动量系数的射流能形成较大的射流偏转角,Coanda偏转角的增长趋势较明显;当Cμ>0.04时,Coanda偏转角的增长趋势变缓,这与升力系数曲线的变化规律极其相似,同时符合超环量控制阶段的特点。在不同的翼型厚度、尾缘半径和喷口高度下,本研究发现,动量系数与Coanda偏转角均呈对数关系,得到拟合曲线的R2高达0.999、0.995,这说明Coanda偏转角与动量系数具有强相关性,Coanda偏转角可作为动量系数在流场空间的几何表征。在流场中, 由于Coanda偏转角易被观测,因此下一步工作将重点观测临界控制状况下的Coanda偏转角。
|
| 图 10 动量系数与Coanda偏转角的对应关系 |
3.2 0°攻角下控制阶段
与传统翼型的增升机理不同,环量控制翼型利用离心力和压力梯度达到平衡,使高速流体黏附在固体曲面上,通过改变前后驻点的相对位置改善升阻特性。但射流槽出口处的强剪切层、后滞点区域的多个逆流区导致流动情况变得更加复杂。因此,探究环量控制翼型在α=0°时的全局压力分布有助于分析不同工况下的复杂流动特性。
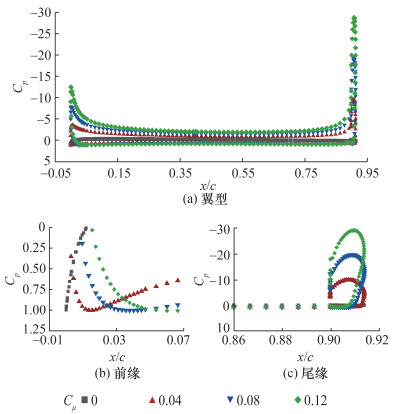
α=0°时不同动量系数的翼型、前缘、尾缘压力分布如图 11所示。由图 11可知,随着动量系数改变,前驻点沿流向逐渐后移,高速射流沿着翼型尾缘的圆形轮廓流动,前后驻点的变化改变了Kutta条件。下游流场中射流的影响区域传递至上游流场,使前驻点移至下翼面高压侧,这相当于增加翼型的攻角;而后驻点改变和高速射流从尾缘分离后产生的“气动襟翼”是升力增加的主要来源。“气动襟翼”的偏转角随动量系数增大而增大,相当于增大翼型的弯度,相比NACA0012的对称翼型,环量控制翼型的升力系数大幅度增加。由于与来流方向平行的射流口在环量控制翼型的钝尾缘形成背风区,来流对射流的偏转干扰较小。由图 11可知,Cμ=0.12的超环量控制阶段,压力系数依然保持稳定,表明气流仍然附着。
|
| 图 11 不同动量系数的翼型、前缘、尾缘压力分布 |
临界动量系数是环量控制中的重要概念,据此将环量控制分为分离控制和超环量控制阶段。动量系数小于临界动量系数为分离控制阶段,大于临界动量系数为超环量控制阶段。通过判断是否进入超环量控制阶段,即可确认临界动量系数,从而避免环量控制进入超环量控制阶段,以维持在分离控制阶段。根据文[34-35]对于超环量控制阶段的判断准则,超环量控制阶段的升力系数与Cμ的算数平方根呈正相关关系,但偏离线性趋势。此时,环量控制翼型虽然产生较高的升力,但阻力系数大幅线性增加、效率降低。为了通过调节射流强度达到较好的升阻特性,本文将通过预测超环量控制阶段,使环量控制维持在分离控制阶段。
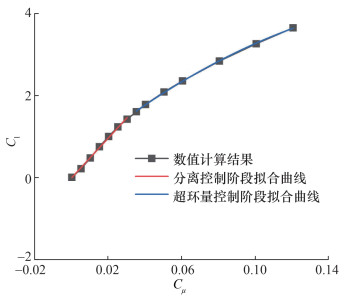
α=0°时NACA0012修型翼型的升力系数随动量系数的变化如图 12所示。当Cμ < 0.03时,环流控制起边界层控制作用,低动量射流抑制了钝尾缘的流动分离,起增升效果。当0.03≤Cμ≤0.04时,升力系数不再呈线性增加。当Cμ>0.04时,Coanda效应增强,升力系数高达3.70,远远大于常规翼型。
|
| 图 12 NACA0012修型翼型的Cl-Cμ曲线 |
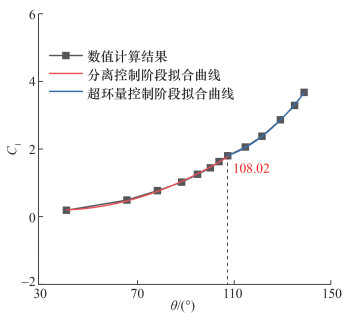
α=0°时NACA0012修型翼型升力系数随Coanda偏转角的变化如图 13所示。对比图 12和13可知,Cl-Cμ曲线在Cμ为0.03~0.04时从线性区域过渡至二次曲线区域,较难捕捉控制状态的转变位置。但由图 13中Cl-θ曲线可以发现,分离控制阶段和超环量控制阶段均为二次曲线,在θ=108.02°附近有一个较明显的转折点,此后控制状态进入超环量控制阶段。
|
| 图 13 NACA0012修型翼型的Cl-θ曲线 |
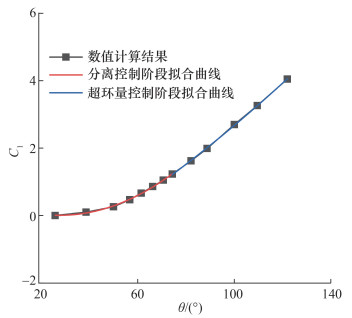
α=0°时CC-E0020EJ翼型升力系数随Coanda偏转角的变化如图 14所示。Cl-θ曲线的变化趋势与图 13类似,此处不再赘述。
|
| 图 14 CC-E0020EJ翼型的Cl-θ曲线 |
综上可知,翼型尾缘的射流偏转是环量控制翼型增升的主要原因,Coanda偏转角造成的外流场流线弯折相当于翼型弯度增加,并实现了环量可控。对比传统识别环量控制阶段的方式,Coanda偏转角可以作为准确判断控制状态是否进入超环量控制阶段的新途径,且具有较高的拟合精度。
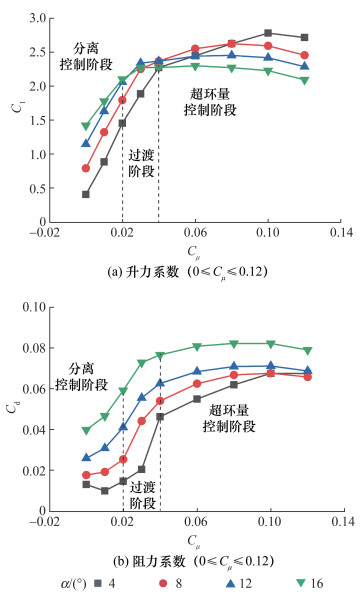
3.3 非0°攻角分离状态分析非0°攻角与0°攻角工况的流场特征及升阻特性不同。来流攻角的存在会使趋势变化更加复杂,较难捕捉,α=4°、8°、12°、16°时环量控制2个阶段的曲线形态将发生变化。α=4°、8°、12°、16°时不同动量系数的升力与阻力系数如图 15所示。由图 15可知,随着攻角增大,升力系数和阻力系数与动量系数的线性相关性更差;分离控制阶段,曲线随攻角增大逐渐上移,但曲线斜率降低;过渡阶段临界值发生偏移;超环量控制阶段,α=4°、8°、12°、16°时均出现升力系数减小的现象。
|
| 图 15 不同动量系数的升力与阻力系数 |
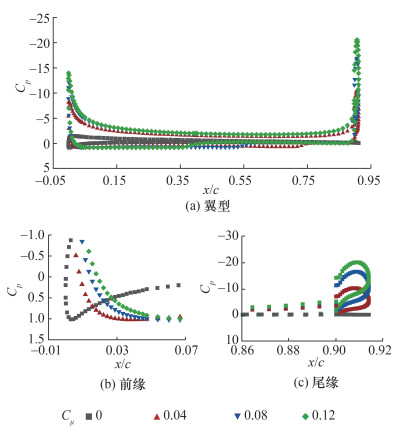
相比α=0°,本文以α=4°为例进行阐述。α=4°时不同动量系数的翼型、前缘、尾缘压力分布如图 16所示。由图 16可知,前驻点继续后移,前、后驻点在翼型下表面靠近,尾缘的压力系数相比α=0°较低,由于来流与射流出口的夹角使尾缘处压力分布的形态发生改变,因此升力增加量减少。在α=4°、Cμ≥0.04的工况下,气流附着在下翼面的同时完全附着在圆形尾缘上,此时下翼面的来流与反向射流相混合,并在下翼面形成了分离区,该速度“滞止区”的压力系数趋于0。这说明在对称翼型的非0°攻角及非对称翼型来流与射流形成夹角情况下,单纯观察升力和阻力系数的变化趋势无法准确判断环量控制的2个阶段,过渡阶段的模糊状态导致无法精准捕捉临界动量系数。因此,需要引入新的机制对流动分离及控制阶段变化进行判断。本文提出,通过观测流场中Coanda偏转角变化及下翼面是否出现“台阶区”,即可确认控制状态是否进入超环量控制阶段。
|
| 图 16 不同动量系数的翼型、前缘、尾缘压力分布 |
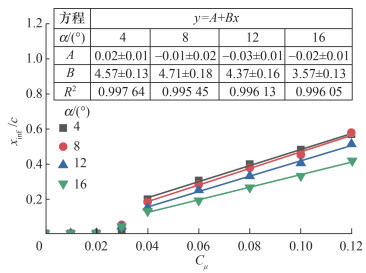
受射流影响的“台阶区”的定义为射流影响下出现压力系数损失的距离与翼型弦长的比值xinf/c,二维翼型下表现为“台阶区”长度。该现象为数值计算中的特殊现象,判断为数值解的结果。绘制不同攻角下“台阶区”长度随动量系数的变化,如图 17所示。由图可知,当α=4°,Cμ=0.04时,突然产生了受射流影响的“台阶区”;当α=8°、12°、16°,Cμ=0.03时,产生受射流影响的“台阶区”,说明随着飞行攻角增大,射流更容易影响下翼面区域。
|
| 图 17 受射流影响的“台阶区”长度随动量系数的变化 |
当Cμ≥0.04时,xinf/c随着动量系数增大呈线性增大趋势,“台阶区”逐渐从下翼面的尾缘向前缘推进。该现象的进一步解释如下:随着射流强度增大,喷口处产生的射流在翼型尾缘形成的Coanda偏转角增大,当Coanda偏转角超过180°时,则不能用Coanda偏转角衡量射流分离的位置,反向射流在来流速度掺混的作用下形成速度剪切层,此时下翼面的分离位置与射流动量系数呈线性关系,因为射流动量的衰减速率与距离成正比,研究人员可通过观测流场中的“台阶区”分析环量控制翼型所处的控制阶段。因此,设计射流强度应尽量避免Coanda偏转角超过180°。
4 结论本文在二维模型上进行了完整的气动特性分析,提出了一种高效利用Coanda效应的尾缘修型方法,有效升力系数比其他方案提高3倍左右。主要结论如下:
1) 翼型尾缘参数影响升阻比的最重要因素为射流喷口高度。在弦向相对位置为0.900且喷口相对高度为7.16%时,Coanda效应产生的升力系数的增幅较大,最佳有效升阻比提升至43。
2) 在0°攻角下Coanda偏转角随动量系数的变化趋势与对数关系曲线高度吻合,2种不同厚度、尾缘的翼型的拟合曲线具有相同的转折点及增长率变化特征,这表明Coanda偏转角是判断射流强度与气动增升效果的物理依据。
3) 在非0°攻角下引入受射流影响的“台阶区”,通过定量分析探究了4°、8°、12°、16°攻角下射流影响区位置与动量系数的强线性关系,尾缘大面积分离导致阻力激增,升力增长出现损失。
本文对比了0°攻角和非0°攻角下的环量控制阶段,研究了大动量系数射流下翼型气动特性的流动分离现象。在0°攻角下可由Coanda偏转角与升力系数曲线的二次曲线转折点判定分离控制、超环量控制阶段;在非0°攻角下需观测流场中的“台阶区”位置衡量气动效果。由此提出了判断分离控制与超环量控制阶段的新方法,为环量控制翼型的分离预测提供理论依据。
| [1] |
WOOD N, NIELSEN J. Circulation control airfoils-past, present, future [C]//23rd Aerospace Sciences Meeting. Reno, USA: AIAA, 1985: 204.
|
| [2] |
DJOJODIHARDJO H. Progress and development of Coanda jet and vortex cell for aerodynamic surface circulation control: An overview[J]. The SIJ Transactions on Advances in Space Research & Earth Exploration (ASREE), 2013, 1(1): 32-42. |
| [3] |
MACAULAY D I. Aerofoil boundary layer control systems: US3062483[P]. 1961-06-20.
|
| [4] |
乔晨亮, 许和勇, 叶正寅. 钝后缘风力机翼型的环量控制研究[J]. 力学学报, 2019, 51(1): 135-145. QIAO C L, XU H Y, YE Z Y. Circulation control on wind turbine airfoil with blunt trailing edge[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(1): 135-145. (in Chinese) |
| [5] |
宋彦萍, 杨晓光, 李亚超, 等. 环量控制翼型中柯恩达效应的数值模拟[J]. 工程热物理学报, 2010, 31(9): 1475-1479. SONG Y P, YANG X G, LI Y C, et al. Numerical simulation of Coanda effect in circulation control airfoil[J]. Journal of Engineering Thermophysics, 2010, 31(9): 1475-1479. (in Chinese) |
| [6] |
郑无计, 张登成, 张艳华, 等. 稳定射流环量控制的仿真研究[J]. 航空计算技术, 2014, 44(4): 67-70, 75. ZHENG W J, ZHANG D C, ZHANG Y H, et al. Simulation research of circulation control by steady jet[J]. Aeronautical Computing Technique, 2014, 44(4): 67-70, 75. (in Chinese) |
| [7] |
姜裕标, 张刘, 黄勇, 等. 内吹式襟翼环量控制翼型升力响应特性[J]. 航空学报, 2018, 39(7): 121807. JIANG Y B, ZHANG L, HUANG Y, et al. Lift response characteristics of a circulation control airfoil with internally blown flap[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121807. (in Chinese) |
| [8] |
张刘, 姜裕标, 何萌, 等. 内吹式襟翼控制机理和失速特性[J]. 空气动力学学报, 2021, 39(5): 53-62. ZHANG L, JIANG Y B, HE M, et al. Stall characteristics and circulation control of internally blown flap[J]. Acta Aerodynamica Sinica, 2021, 39(5): 53-62. (in Chinese) |
| [9] |
刘晓冬, 蔡为民, 张沛良, 等. 基于柯恩达效应的飞翼布局环量控制研究[J]. 西北工业大学学报, 2022, 40(4): 845-852. LIU X D, CAI W M, ZHANG P L, et al. Study on circulation control of flying wing based on Coanda effect[J]. Journal of Northwestern Polytechnical University, 2022, 40(4): 845-852. (in Chinese) |
| [10] |
邵帅, 郭正, 贾高伟, 等. 中等展弦比飞翼布局无人机后缘射流滚转控制研究[J/OL]. 航空学报. (2022-08-03) [2023-01-09]. http://kns.cnki.net/kcms/detail/11.1929.v.20220803.1027.012.html. SHAO S, GUO Z, JIA G W, et al. Roll control of a medium-aspect-ratio flying-wing UCAV based on trailing-edge jet [J/OL]. Acta Aeronautica et Astronautica Sinica. (2022-08-03) [2023-01-09]. http://kns.cnki.net/kcms/detail/11.1929.v.20220803.1027.012.html. (in Chinese) |
| [11] |
王磊, 杜海, 李秋实, 等. 环量控制机翼增升及滚转控制特性研究[J]. 空气动力学学报, 2021, 39(1): 43-51. WANG L, DU H, LI Q S, et al. Research on the lift-enhancement and roll control characteristics of a circulation control wing[J]. Acta Aerodynamica Sinica, 2021, 39(1): 43-51. (in Chinese) |
| [12] |
张琴林, 杜海, 孔文杰, 等. 机翼后缘吹气对偏航力矩的控制研究[J]. 航空科学技术, 2020, 31(5): 73-80. ZHANG Q L, DU H, KONG W J, et al. Study on control of yaw moment by trailing edge blowing[J]. Aeronautical Science & Technology, 2020, 31(5): 73-80. (in Chinese) |
| [13] |
何玉娟, 雷玉昌, 张登成, 等. 双射流环量控制翼型的控制力矩特性研究[J]. 北京航空航天大学学报, 2021, 47(12): 2641-2649. HE Y J, LEI Y C, ZHANG D C, et al. Control moment characteristics of double-jet circulation control airfoil[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(12): 2641-2649. (in Chinese) |
| [14] |
付志杰, 许和勇, 杜海, 等. 基于环量控制的虚拟舵面机翼气动特性计算研究[J]. 航空科学技术, 2020, 31(5): 11-22. FU Z J, XU H Y, DU H, et al. Investigation on flapless wing based on circulation control[J]. Aeronautical Science & Technology, 2020, 31(5): 11-22. (in Chinese) |
| [15] |
JONES G, VIKEN S, WASHBURN A, et al. An active flow circulation controlled flap concept for general aviation aircraft applications [C]//1st Flow Control Conference. St. Louis, USA: AIAA, 2002: 3157.
|
| [16] |
CARMONA H, CHÁZARO A, TRASLOSHEROS A, et al. CFD RANS simulation of 2D circulation control airfoil [M]//KLAPP J, SIGALOTTI L, MEDINA A, et al. Recent Advances in Fluid Dynamics with Environmental Applications. Cham: Springer, 2016: 81-101.
|
| [17] |
HOHOLIS G, STEIJL R, BADCOCK K. Circulation control as a roll effector for unmanned combat aerial vehicles[J]. Journal of Aircraft, 2016, 53(6): 1875-1889. DOI:10.2514/1.C033642 |
| [18] |
FORSTER M, STEIJL R. Design study of Coanda devices for transonic circulation control[J]. The Aeronautical Journal, 2017, 121(1243): 1368-1391. DOI:10.1017/aer.2017.65 |
| [19] |
王春雨, 孙茂. 多喷口环量控制翼型流动的研究[J]. 空气动力学学报, 1999, 17(4): 378-383. WANG C Y, SUN M. Aerodynamic properties of circulation control airfoil with multi-slot blowing[J]. Acta Aerodynamica Sinica, 1999, 17(4): 378-383. (in Chinese) |
| [20] |
杜海, 杨乐杰, 李铮, 等. 多级环量控制技术增升机理及能效分析[J]. 航空学报, 2022, 43(S2): 727709. DU H, YANG L J, LI Z, et al. Lifting mechanism and energy efficiency analysis of multistage circulation control technology[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(S2): 727709. (in Chinese) |
| [21] |
韩忠华, 宋文萍, 乔志德. OA212翼型主动流动控制的数值模拟研究[J]. 空气动力学学报, 2009, 27(6): 639-644. HAN Z H, SONG W P, QIAO Z D. Numerical simulation of active dynamic stall control on an OA212 rotor airfoil[J]. Acta Aerodynamica Sinica, 2009, 27(6): 639-644. (in Chinese) |
| [22] |
韩忠华, 乔志德, 宋文萍. 零质量射流推迟翼型失速的数值模拟[J]. 航空学报, 2007, 28(5): 1040-1046. HAN Z H, QIAO Z D, SONG W P. Numerical simulation of active flow control to airfoil stall using local synthetic jet[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1040-1046. (in Chinese) |
| [23] |
许晓平, 周洲. 飞翼布局无人机流动分离控制及机理分析[J]. 力学学报, 2014, 46(4): 497-504. XU X P, ZHOU Z. Active separaton control for the flying-wing UAV using synthetic jet[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 497-504. (in Chinese) |
| [24] |
LI Y H, QIN N. Airfoil gust load alleviation by circulation control[J]. Aerospace Science and Technology, 2020, 98: 105622. DOI:10.1016/j.ast.2019.105622 |
| [25] |
BURNAZZI M, RADESPIEL R. Assessment of leading-edge devices for stall delay on an airfoil with active circulation control[J]. CEAS Aeronautical Journal, 2014, 5(4): 359-385. DOI:10.1007/s13272-014-0112-5 |
| [26] |
孙全兵, 史志伟, 耿玺, 等. 基于主动流动控制技术的无舵面飞翼布局飞行器姿态控制[J]. 航空学报, 2020, 41(12): 124080. SUN Q B, SHI Z W, GENG X, et al. Attitude control of flying wing aircraft without control surfaces based on active flow control[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(12): 124080. (in Chinese) |
| [27] |
WETZEL D, GRIFFIN J, LIU F, et al. An experimental study of a circulation control airfoil trailing edge flow field [C]//5th Flow Control Conference. Chicago, USA: AIAA, 2010: 4576.
|
| [28] |
FU Z J, CHU Y W, CAI Y S, et al. Numerical investigation of circulation control applied to flapless aircraft[J]. Aircraft Engineering and Aerospace Technology, 2020, 92(6): 879-893. DOI:10.1108/AEAT-10-2019-0208 |
| [29] |
STORM T, MARSHALL D. Assessing the v2-f turbulence models for circulation control applications [C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, USA: AIAA, 2010: 1054.
|
| [30] |
NISHINO T, HAHN S, SHARIFF K. Calculation of the turbulence characteristics of flow around a circulation control airfoil using LES (invited paper) [C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, USA: AIAA, 2010: 347.
|
| [31] |
JONES G S, LIN J C, ALLAN B G, et al. Overview of CFD validation experiments for circulation control applications at NASA [C]//2008 International Powered Lift Conference. London, UK: NTRS, 2008: 20080031119.
|
| [32] |
JONES G, YAO C S, ALLAN B. Experimental investigation of a 2D supercritical circulation-control airfoil using particle image velocimetry [C]//3rd AIAA Flow Control Conference. San Francisco, USA: AIAA, 2006: 3009.
|
| [33] |
ITSARIYAPINYO P, SHARMA R N. Large eddy simulation of a NACA0015 circulation control airfoil using synthetic jets[J]. Aerospace Science and Technology, 2018, 82-83: 545-556. DOI:10.1016/j.ast.2018.09.039 |
| [34] |
SHAO S, GUO Z, HOU Z X, et al. Effects of Coanda jet direction on the aerodynamics and flow physics of the swept circulation control wing[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2022, 236(13): 2633-2654. DOI:10.1177/09544100211068728 |
| [35] |
ENGLAR R, JONES G, ALLAN B, et al. 2D circulation control airfoil benchmark experiments intended for CFD code validation [C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, USA: AIAA, 2009: 902.
|
| [36] |
ALLAN B, JONES G, LIN J. Reynolds-averaged Navier-Stokes simulation of a 2D circulation control wind tunnel experiment [C]//49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, USA: AIAA, 2011: 25.
|
| [37] |
TRAUB L W, BIEGNER M. Experimental evaluation of a self-contained circulation-control wing[J]. Journal of Aircraft, 2013, 50(3): 764-777. DOI:10.2514/1.C031937 |
| [38] |
XU H Y, QIAO C L, YANG H Q, et al. Active circulation control on the blunt trailing edge wind turbine airfoil[J]. AIAA Journal, 2018, 56(2): 554-570. DOI:10.2514/1.J056223 |
| [39] |
RUMSEY C L, NISHINO T. Numerical study comparing RANS and LES approaches on a circulation control airfoil[J]. International Journal of Heat and Fluid Flow, 2011, 32(5): 847-864. DOI:10.1016/j.ijheatfluidflow.2011.06.011 |
| [40] |
ENGLAR R J. Experimental investigation of the high velocity coanda wall jet applied to bluff trailing edge circulation control airfoils [R]. Bethesda: Research and Development Report, 1975.
|
| [41] |
JENSCH C, PFINGSTEN K C, RADESPIEL R. Numerical investigation of leading edge blowing and optimization of the slot geometry for a circulation control airfoil [M]//DILLMANN A, HELLER G, KLAAS M, et al. New Results in Numerical and Experimental Fluid Mechanics Ⅶ. Berlin, Heidelberg: Springer, 2010: 183-190.
|
| [42] |
张美红, 张冬云, 王美黎, 等. 基于CFD和推阻分解技术的全机溢流阻力预测与分析[J]. 空气动力学学报, 2016, 34(5): 625-630. ZHANG M H, ZHANG D Y, WANG M L, et al. CFD prediction and analysis of civil aircraft spillage drag based on thrust-drag bookkeeping method[J]. Acta Aerodynamica Sinica, 2016, 34(5): 625-630. (in Chinese) |