2. 西北工业大学 自动化学院, 西安 710072
2. School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
固定翼无人机凭借低成本、长航时、操作便捷、机动性强等优点,在智慧城市、工农业生产[1-2]和军事对抗[3]中得到快速发展与广泛运用。然而在大范围区域快速测绘、复杂环境协同作战、多点精确物资保障等任务中,随着未知环境下障碍的复杂化和任务难度的提升,单架无人机由于自身性能限制,很难快速完成大范围遍历的基础任务,更难以完成后续的复杂任务,因而通常需要组成无人机编队协同完成任务。不同于单架无人机在未知环境中的飞行,在研究多架无人机编队飞行时,不仅要考虑无人机编队与环境之间的避障,还要考虑无人机编队内部的避碰问题。因此,在复杂未知环境中实时进行无人机编队智能避障极具挑战性。在无先验知识的静态环境中,实现无人机编队自主规避障碍物仍是亟待解决的问题。
目前国内外无人机编队防撞策略大致可以分为5类,分别是基于纯数学优化[4]、基于启发式算法[5]、基于人工势场[6]、基于几何制导[7]和基于机器学习[8]的方法。基于纯数学优化、基于启发式算法和基于几何制导的3种方法通常需要构建离线三维地图,在全局地图或局部地图的基础上以路径搜索算法为基础,障碍物为约束,求取最优路径。这3种方法往往存在着大量的计算过程或复杂的建模过程[9],很难应用于未知环境下的无人机编队自主避障。基于人工势场的方法由于原理简单、实时性好等优点在无人机避障中得到广泛运用,为进一步解决其固有的死锁与目标不可达等问题[10-11],目前已有诸多学者开展相关研究[12-15],但在集群控制律设计过程中较难协调场函数参数,导致编队在多障碍物前出现拥堵甚至碰撞。
近年来,基于机器学习的相关方法受到广泛关注,其中,结合强化学习的方法由于不需要建立复杂的模型,只使用与环境交互学习的方法来获取策略,具有很好的实时性,相比其他类型的机器学习方法更具优势[16]。目前通过深度学习模型学习输入数据和输出动作的映射关系,智能体可具备处理高维空间下的端到端[17]决策问题的能力,能够避免复杂的离线地图构建工作。2015年,DeepMind团队提出基于深度Q网络(deep Q-network, DQN)的深度强化学习(deep reinforcement learning, DRL)方法[18],该方法采用端到端的训练方式,无需人工提取特征,但无法实现对连续控制量的输出。为解决上述问题,有学者提出了深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法,并于2021年基于DDPG完成了多无人机航路规划追击任务[19]。文[20]提出混合噪声优化DDPG算法实现无人机对机动目标的连续跟踪,提升了算法的收敛性能。文[21]针对雷达区域提出改进人工蜂群算法求解网络参数,避免了调整学习率导致的无效训练,但整个过程仍存在训练耗时长的弊端。此外,DDPG算法后期普遍存在价值高估的问题,导致训练效果波动较大。
本文基于集中式通信架构、强化学习和人工势场等理论方法提出了未知环境下无人机编队智能避障控制方法。该方法针对长机设计了基于贪婪选择的DDPG(Greedy-DDPG)训练方法,该方法通过将DDPG的随机探索策略改进为渐变的贪婪选择策略,缩短了训练时间,提升了训练效果。为保障飞行安全,基于人工势场和领从一致性设计了僚机群避障避碰控制方法,在跟随长机完成任务的同时实现无人机编队的避障与无人机编队内部的避碰。最后,通过不同场景下的Monte Carlo仿真实验,验证了所提方法的有效性和鲁棒性。
1 问题描述 1.1 预备知识在编队飞行过程中,假设每一架无人机都能接受长机位置速度信息,且与长机之间的信息交互不存在延时和数据丢失,同时僚机之间只可通过对自身探测范围进行探测从而感知其他僚机。僚机之间的信息交互可用G=(V, E)表示。V={1, 2, …, n}表示节点编号的非空集合,1个节点表示1架无人机。E={(i, j)|i, j∈V, i≠j}表示其边集,(i, j)表示无人机i和j可互相获取对方信息。显然本文考虑场景下G属于无向图,其Laplace矩阵定义为L=D(G)-B(G)。其中: D(G)=diag(d(i))表示节点i的入度矩阵,d(i)表示向节点i传输信息的节点数目,B(G)=(bij)表示节点i的临接矩阵,bij表示边(i, j)的权值。
| $ b_{i j}= \begin{cases}1, & R_{i j} \leqslant R_{\mathrm{s}}; \\ 0, & R_{i j}>R_{\mathrm{s}}.\end{cases} $ | (1) |
其中:Rij为无人机i与j之间的距离,Rs为无人机探测距离。
1.2 无人机模型本文为简化运算,选择在二维平面对仿真场景建立数学模型,考虑二维平面中包含n+1架无人机的模型(其中1架为领航长机),第k架无人机运动学方程设为二阶积分模型如下:
| $ \begin{gathered} \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{k}=\boldsymbol{v}_{k}, \\ \dot{\boldsymbol{v}}_{k}=\boldsymbol{u}_{k}, \end{array}\right. \\ k=1, 2, \cdots, n+1 . \end{gathered} $ | (2) |
其中:xk=(xkx, xky)表示无人机的位置状态,vk=(vkx, vky)表示其速度状态,uk=(ukx, uky)表示其加速度矢量。
相比多旋翼无人机,固定翼无人机通常无法实现在空中的悬停,因此需要考虑如下的飞行约束:
| $ \left\{\begin{array}{l} 0<v_{\min } \leqslant\left\|\boldsymbol{v}_{k}\right\|_{2} \leqslant v_{\max }, \\ \left|\dot{\theta}_{k}\right|<\dot{\theta}_{\max }. \end{array}\right. $ | (3) |
其中:vmin和vmax分别表示无人机k在一定高度飞行允许的最小和最大速度,
在无先验知识的情况下,本文假设静态环境中具有m个障碍物,每个障碍物可被描述为一定大小的圆形区域。
| $ c_{p}=\left(x_{p}, y_{p}, r_{p}\right), p=1, 2, \cdots, m . $ | (4) |
其中:(xp, yp)为第p个障碍物的圆心位置,rp为第p个障碍物的半径。
在编队飞行过程中,长机需要与障碍物保持距离以避免碰撞。
| $ \min \left(\left\|\left(x_{\rm{l}}, y_{\rm{l}}\right)-\left(x_{p}, y_{p}\right)\right\|_{2}\right)>r_{p} . $ | (5) |
其中(xl, yl)为长机位置坐标。
假设僚机可探测周围其他僚机信息,同时也可获取长机信息。在整个飞行过程中,无人机之间、无人机与障碍之间需要保持距离避免碰撞:
| $ \begin{gathered} \min \left(\left\|\left(x_{j}, y_{j}\right)-\left(x_{i}, y_{i}\right)\right\|_{2}\right)>r_{\text {safe }}, i \neq j ; \\ \min \left(\left\|\left(x_{i}, y_{i}\right)-\left(x_{p}, y_{p}\right)\right\|_{2}\right)>r_{p} ; \\ i, j=1, 2, \cdots, n+1 . \end{gathered} $ | (6) |
其中:(xi, yi)和(xj, yj)分别表示无人机i和j的位置坐标,rsafe表示无人机间最小安全距离。
定义 无人机编队控制的目标为编队按照指定构型无碰撞地稳定飞行到达指定目标,即在满足式(5)和(6)条件下稳定飞行到达指定目标。
| $ \begin{gathered} \lim _{t \rightarrow \infty}\left(\left(x_{\rm{l}}(t), y_{\rm{l}}(t)\right)-\left(x_{\mathrm{ta}}(t), y_{\mathrm{ta}}(t)\right)\right)=0 ; \\ \lim _{t \rightarrow \infty}\left(\boldsymbol{v}_{i}(t)-\boldsymbol{v}_{j}(t)\right)=0, \forall i \neq j ; \\ \lim _{t \rightarrow \infty}\left(\boldsymbol{r}_{i}(t)-\boldsymbol{r}_{i}^{\prime}(t)\right)=0, \forall i. \end{gathered} $ | (7) |
其中:(xta, yta)表示目标位置,vi(t)和vj(t)分别表示无人机i和j在t时刻的速度矢量,ri(t)和ri′(t)分别表示t时刻无人机i与长机间的真实位置矢量和期望位置矢量。
2 基于强化学习的长机避障方法DDPG在连续动作学习方面更为有效。为进一步利用该优点,本文引入贪婪选择改进DDPG来解决未知环境中的无人机避障问题。
2.1 优化目标长机在飞行过程中仅需满足式(5),由于只设计任务结束奖励不利于智能体进行学习,故将启发式奖励和任务结束奖励结合设计总奖励。启发式奖励分为动作输出奖励、障碍受力奖励、偏航奖励和距离奖励。
在定义任务结束奖励前需要对任务的终止条件进行定义:
| $ \text { isdone }= \begin{cases}1, & \left(\theta_{{\rm{l}}}-\theta_{\mathrm{ta}}\right)>\pi \text { 或 } \dot{r}_{\mathrm{ta}}>v_{\mathrm{stop}} \text { 或 } \\ & r_{\mathrm{ta}}<1 \text { 或碰撞; } \\ 0, & \text { 其他. }\end{cases} $ | (8) |
其中:isdone为1表示任务终止,为0表示任务未终止;θl表示长机航向角;θta表示长机当前位置与目标位置的夹角;rta表示长机当前位置与目标位置的距离;
任务结束奖励即isdone为1时的奖励值,根据结束时状态设计如下:
| $ R_{\mathrm{end}}= \begin{cases}-50, & r_{\mathrm{ta}} \geqslant 10 \mathrm{~m} \text { 或碰撞; } \\ 1, & 5 \mathrm{~m} \leqslant r_{\mathrm{ta}}<10 \mathrm{~m} ; \\ 2, & 1 \mathrm{~m} \leqslant r_{\mathrm{ta}}<5 \mathrm{~m} ; \\ 10, & 0.5 \mathrm{~m} \leqslant r_{\mathrm{ta}}<1 \mathrm{~m} ; \\ 30, & 0.1 \mathrm{~m} \leqslant r_{\mathrm{ta}}<0.5 \mathrm{~m} ; \\ 50, & r_{\mathrm{ta}}<0.1 \mathrm{~m} .\end{cases} $ | (9) |
动作输出奖励考虑到无人机实际应用中不能长时间保持较大角速率进行转向,故引入负奖励约束输出大小,具体设计如下:
| $ R_{a}=-\left|\frac{a}{a_{\max }}\right|+0.5, \frac{a}{a_{\max }}>0.3 . $ | (10) |
其中:a为长机当前输出,amax为长机最大输出。
由于本文强化学习主要考虑避障问题,故将无人机受到的斥力作为奖励的一部分引导无人机规避障碍物。由于人工势场法的斥力在靠近障碍时会急剧上升,考虑到训练的稳定性,将障碍受力奖励进行限幅,具体设计如下:
| $ R_{F}=\max \left(\min \left(4\left\|\boldsymbol{F}_{\text {repu }}\right\|_{2}, 4\right), -4\right) . $ | (11) |
其中Frepu表示长机所受斥力和。
在没有障碍的情况下,无人机需要快速向目标移动,故设计在受斥力较小的情况下的偏航奖励:
| $ \begin{gathered} R_{\theta}=-\left|2\left(\theta_{\rm{l}}-\theta_{\text {ta }}\right)\right|+0.4, \\ \left\|\boldsymbol{F}_{\text {repu }}\right\|_{2}<0.1 \text { 且 }\left|2\left(\theta_{\rm{l}}-\theta_{\text {ta }}\right)\right|>0.2 . \end{gathered} $ | (12) |
在整个飞行过程中无人机需要快速向目标抵进,故根据相对目标距离和速度进行距离奖励设计:
| $ R_{r}=\mathrm{e}^{-\frac{r_{\mathrm{ta}}}{200}}+\frac{\dot{r}_{\mathrm{ta}}}{5}. $ | (13) |
由式(9)—(13)可得到单个轮次的总奖励为
| $ \begin{aligned} & R_{\mathrm{epi}}=R_{\mathrm{end}}+\sum\limits_{t=0}^{\mathrm{end}}\left[R_{a}(t)+\right. \\ & \left.R_{F}(t)+R_{\theta}(t)+R_{r}(t)\right] . \end{aligned} $ | (14) |
其中:Ra(t)、RF(t)、Rθ(t)和Rr(t)分别为t时刻的动作输出奖励、障碍受力奖励、偏航奖励和距离奖励。强化学习需要优化参数使得Repi最大。
2.2 状态设计由于本文考虑的场景下,无人机对障碍仅能通过探测或集群信息共享得知,且环境中障碍物的位置未知,考虑到强化学习的状态量数目在学习过程中需要保持恒定,因此设计基于人工势场方法的状态输入。同时为避免由于该方法在接近障碍时受力快速增加导致的训练不稳定,将受力进行归一化处理。具体设计如下:
| $ s=\left(\frac{r_{\mathrm{ta}}}{k_{r}}, \tanh \left(\left\|\boldsymbol{F}_{\text {repu }}\right\|_{2}\right), \theta_{\mathrm{ta}}, \theta_{F}, \theta_{\rm{l}}\right) . $ | (15) |
其中:kr表示归一化系数,θF表示斥力与引力合力的方向角。
斥力设计如下:
| $ \begin{gathered} \boldsymbol{F}_{\text {repu }}=\boldsymbol{F}_{\text {rep1 }}+\boldsymbol{F}_{\text {rep2 }}, \\ \left\|\boldsymbol{F}_{\text {repl }}\right\|_{2}=k_{\text {rep }} \sum\limits_{p=1}^{m}\left(\frac{1}{\left\|\boldsymbol{\rho}_{k p}\right\|_{2}}-\frac{1}{\sigma_{o}}\right) \frac{\left\|\boldsymbol{\rho}_{k t}\right\|_{2}^{g}}{\left\|\boldsymbol{\rho}_{k p}\right\|_{2}^{2}}, \\ \left\|\boldsymbol{F}_{\text {rep2 }}\right\|_{2}=\frac{n}{2} k_{\text {rep }} \sum\limits_{p=1}^{m}\left(\frac{1}{\left\|\boldsymbol{\rho}_{k p}\right\|_{2}}-\frac{1}{\sigma_{o}}\right)^{2}\left\|\boldsymbol{\rho}_{k t}\right\|_{2}^{g-1} . \end{gathered} $$ $ | (16) |
其中:Frep1为障碍物与无人机连线方向的斥力;Frep2为无人机与目标点之间的斥力;krep为斥力系数;ρkp为障碍物圆心位置指向无人机位置的向量;ρkt为无人机k位置指向目标位置的向量;σo为斥力感知半径;g表示阶次,此处设定g≥1。引力设计如下:
| $ \boldsymbol{F}_{\text {att }}=\frac{1}{2} k_{\text {att }}\left\|\boldsymbol{\rho}_{k t}\right\|_{2}^{2}. $ | (17) |
其中katt为引力系数。同时为避免局部最优点,在无人机视线受到阻挡时将引力方向改变为垂直于受力方向且受视线遮挡较小的方向。
2.3 动作设计考虑到高维度强化学习训练难度的快速提升与固定翼无人机本身飞行特性,将速度控制基于人工势场的方法单独进行,而角度控制使用强化学习进行,即式(10)中的a可设计为
| $ a=\dot{\theta}. $ | (18) |
其中
DDPG训练时需要设计4个网络,分别是在线Actor网络、在线Critic网络、目标Actor网络和目标Critic网络。在线Actor网络用来拟合策略函数,网络权重参数为θnet,通过输入t时刻的状态st,得到可执行的动作at;在线Critic网络通过内部的值函数信息估计在线Actor网络中的对应梯度更新方向,网络权重参数为ωnet,输入为状态st和at,输出为评估的收益Q(st, at|ωnet)。目标Actor网络和目标Critic网络的网络权重参数分别为θnet′和ωnet′。
在选取动作时需要加入随机量,随机因子使用Ornstein-Uhlenbeck过程进行随机探索:
| $ v_{t}=v_{t-1}+\beta_{\text {attract }}\left(\mu_{v}-v_{t-1}\right) T_{\mathrm{s}}+U\left(0, {\mathit{\Sigma}}_{t}\right) \sqrt{T_{\mathrm{s}}} . $ | (19) |
其中:vt为当次的输出,vt-1为上次的输出,βattract为均值回归的速率,μv为vt的中心值,Ts为回归系数,U(0, Σt)为正态分布。
在线Actor网络采取策略梯度进行更新:
| $ \nabla_{\theta} J\left(\theta_{\text {net }}\right)=\frac{1}{N} \sum\limits_{t=1}^{N}\left[\nabla_{a_{t}} Q\left(s_{t}, a_{t} \mid \omega_{\text {net }}\right) \cdot \nabla_{\theta} \mu\left(s_{t} \mid \theta_{\text {net }}\right)\right]. $ | (20) |
其中N为经验数据(st, at, rt, st+1)采样的个数。
在线Critic网络通过最小化损失函数进行更新,其损失函数为
| $ \begin{gathered} \text { Loss }=\frac{1}{N} \sum\limits_{t=1}^{N}\left(r_{t}+\gamma Q^{\prime}\left(s_{t+1}, a_{t+1} \mid \omega_{\text {net }}^{\prime}\right)-\right. \\ \left.Q\left(s_{t}, a_{t} \mid \omega_{\text {net }}\right)\right)^{2} . \end{gathered} $ | (21) |
其中γ为奖励折扣因子。
DDPG算法采取软更新的方式更新目标参数以提高学习过程稳定性。目标Actor网络、目标Critic网络分别与在线Actor网络、在线Critic网络结构相同,更新方式分别为
| $ \begin{aligned} \theta_{\mathrm{net}}^{\prime} & =(1-\tau) \theta_{\mathrm{net}}^{\prime}+\tau \theta_{\mathrm{net}}, \\ \omega_{\mathrm{net}}^{\prime} & =(1-\tau) \omega_{\mathrm{net}}^{\prime}+\tau \omega_{\mathrm{net}} . \end{aligned} $ | (22) |
其中τ表示更新的速度,τ≪1。
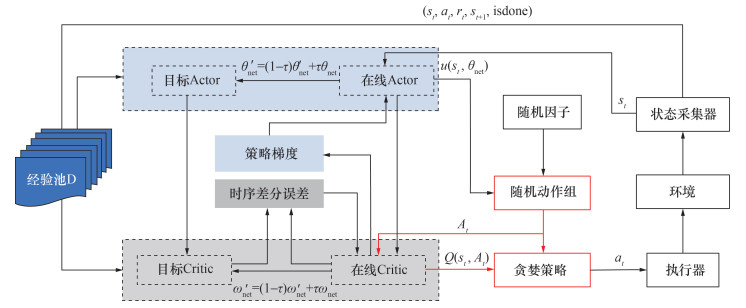
鉴于DDPG算法前期训练随机探索导致学习效果随机性较大,学习效率不高,本文引入贪婪选择,如图 1所示,在线Actor网络输出确定性动作后,对随机因子进行随机采样。得到随机动作组A后通过在线Critic网络进行价值评估,通过贪婪法选择动作at,之后与环境进行交互。由于前期在线Critic网络价值评估不够准确,相比随机获取的动作,在线Critic网络评估价值最高或最低的动作往往能提供更大的梯度以更新网络,以此来提高前期的训练速度。同时DDPG算法整个训练前期的每个轮次会以较少步数结束,导致对训练后期的每个轮次后期随机探索范围过小,探索不充分。为解决以上矛盾引入贪婪动作选择:
| $ a_{t}= \begin{cases}{\arg}\underset{a_{t} \in A_{t}}{\max }\left(Q\left(s_{t}, a_{t} \mid \omega_{\mathrm{net}}\right)\right), & P=\varepsilon_{1} ; \\ {\arg}\underset{a_{t} \in A_{t}}{\min }\left(Q\left(s_{t}, a_{t} \mid \omega_{\mathrm{net}}\right)\right), & P=\varepsilon_{2} ; \\ \text { 其他, } & P=1-\varepsilon_{1}-\varepsilon_{2} .\end{cases} $ | (23) |
|
| 图 1 Greedy-DDPG算法流程 |
其中:P表示选择概率;ε1和ε2分别表示选择最大和最小奖励对应动作的概率,ε2由ε2(Δ+1)=ε2(Δ)·rε2Δ确定;Δ表示当前训练轮次;rε2是ε2的衰减系数;At表示在状态st下通过随机因子采样得到的一组动作集合。图 2为Greedy-DDPG算法的伪代码,其中:episode和episodem分别表示轮次和最大轮次,rewarda和rewardE分别表示平均和期望的总奖励。

|
| 图 2 Greedy-DDPG算法伪代码 |
3 基于一致性法的僚机编队控制方法
使用第2章中训练完成的模型作为长机控制器,同时为避免无人机编队的队内碰撞,引入2.2节所设计的势场函数设计编队控制器。
3.1 编队控制律对于编队中处于任意状态的无人机,为保证在安全避碰避障到达目标的前提下实现无人机编队的一致性,对无人机编队中的僚机采用如下的协同避障控制协议:
| $ \boldsymbol{u}_{i}=-\sum\limits_{j=1}^{n} b_{i j}\left[\gamma_{0}\left(\hat{\boldsymbol{x}}_{i}-\hat{\boldsymbol{x}}_{j}\right)+\gamma_{1}\left(\hat{\boldsymbol{v}}_{i}-\hat{\boldsymbol{v}}_{j}\right)\right]-\\ \;\;\;\;\;\; h_{i}\left[\gamma_{0}\left(\hat{\boldsymbol{x}}_{i}\right)+\gamma_{1}\left(\hat{\boldsymbol{v}}_{i}\right)\right]+\boldsymbol{f}_{i} . $ | (24) |
其中:bij表示无人机i和j之间的通信连接关系;γ0>0;γ1>0;hi表示无人机i和长机之间通信链接关系,当在通信或感知范围内hi=1时定义无人机间的链接权重相等都为1;
为了便于后续分析,首先给出如下的引理。
引理1[22] 无向图G=(V, E)的Laplace矩阵L具有以下特性:
1) L是对称半正定矩阵,且0是矩阵的特征值,其特征向量是全为1的h维列向量1h;
2) 如果无向图是连通的,则0是矩阵的代数重度为1的特征值。
引理2[23] (LaSalle不变集原理)假定V是定义在Rn上的可微函数,且V(x)≥0,当且仅当x=0时V(x)=0成立。假定V(x)在紧集Ωc= {x∈Rn: V(x)≤C}上的导数满足
定理1 对于由n+1架无人机构成的拥有长机的无人机集群编队,在式(24)的作用下,无人机编队系统状态变量可实现如式(5)和(6)条件的渐近一致性,保证飞行编队无碰撞协同。
证明:将式(24)代入式(2)可得
| $ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{i}=\boldsymbol{v}_{i}, \\ \dot{\boldsymbol{v}}_{i}=-\sum\limits_{j=1}^{n} b_{i j}\left[\gamma_{0}\left(\hat{\boldsymbol{x}}_{i}-\hat{\boldsymbol{x}}_{j}\right)+\gamma_{1}\left(\hat{\boldsymbol{v}}_{i}-\hat{\boldsymbol{v}}_{j}\right)\right]- \\ h_{i}\left[\gamma_{0}\left(\hat{\boldsymbol{x}}_{i}\right)+\gamma_{1}\left(\hat{\boldsymbol{v}}_{i}\right)\right]+\boldsymbol{f}_{i}, \\ \quad i=1, 2, \cdots, n . \end{array}\right. $ | (25) |
假设
| $ \dot{\boldsymbol{v}}=-\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) \hat{\boldsymbol{x}}-\gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \hat{\boldsymbol{v}}+\boldsymbol{f}. $ | (26) |
将各架无人机状态值与期望值分离后可将式(26)改写为
| $ \begin{gathered} \dot{\boldsymbol{v}}=-\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{x}-\gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{v}+ \\ \gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{x}^{\prime}+\gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{v}^{\prime}+\boldsymbol{f}. \end{gathered} $ | (27) |
其中:L为僚机之间的Laplace矩阵,
| $ \boldsymbol{L}=\left(\begin{array}{cccc} \sum\limits_{j=1}^{n} b_{1 j} & -b_{12} & \cdots & -b_{1 n} \\ -b_{21} & \sum\limits_{j=1}^{n} b_{2 j} & \cdots & -b_{2 n} \\ \vdots & \vdots & & \vdots \\ -b_{n 1} & -b_{n 2} & \cdots & \sum\limits_{j=1}^{n} b_{n j} \end{array}\right); $ | (28) |
H为僚机与长机之间的链接矩阵,
| $ \boldsymbol{H}=\left(\begin{array}{cccc} h_{1} & 0 & \cdots & 0 \\ 0 & h_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & h_{n} \end{array}\right). $ | (29) |
因此无人机编队系统的运动学模型可表示为
| $ \begin{array}{r} \left(\begin{array}{l} \dot{\boldsymbol{x}} \\ \dot{\boldsymbol{v}} \end{array}\right)=\left(\begin{array}{cc} \mathbf{0} & \boldsymbol{I} \\ -\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) & -\gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \end{array}\right)\left(\begin{array}{l} \boldsymbol{x} \\ \boldsymbol{v} \end{array}\right)+ \\ \left(\begin{array}{l} \mathbf{0} \\ \boldsymbol{f} \end{array}\right)+\left(\begin{array}{cc} \mathbf{0} & \mathbf{0} \\ \boldsymbol{\gamma}_{0}(\boldsymbol{L}+\boldsymbol{H}) & \gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \end{array}\right)\left(\begin{array}{l} \boldsymbol{x}^{\prime} \\ \boldsymbol{v}^{\prime} \end{array}\right). \end{array} $ | (30) |
首先考虑以下齐次方程的稳定性。
| $ \left(\begin{array}{l} \dot{\boldsymbol{x}} \\ \dot{\boldsymbol{v}} \end{array}\right)=\left(\begin{array}{cc} \boldsymbol{0} & \boldsymbol{I} \\ -\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) & -\gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \end{array}\right)\left(\begin{array}{l} \boldsymbol{x} \\ \boldsymbol{v} \end{array}\right)+\left(\begin{array}{l} \mathbf{0} \\ \boldsymbol{f} \end{array}\right) . $ | (31) |
选取编队系统的总能量Hamilton函数,其中包括势能函数,具体定义如下:
| $ \psi(\boldsymbol{x}, \boldsymbol{v})=U(\boldsymbol{x})+\frac{1}{2} \boldsymbol{v}^{\mathrm{T}} \boldsymbol{v}+\frac{1}{2} \gamma_{0} \boldsymbol{x}^{\mathrm{T}}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{x} . $ | (32) |
对其求导并代入式(27)可得
| $ \begin{gathered} \dot{\psi}(\boldsymbol{v})=\boldsymbol{v}^{\mathrm{T}}\left(\dot{U}(x)+\dot{\boldsymbol{v}}+\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{x}\right)= \\ \boldsymbol{v}^{\mathrm{T}}\left[-\boldsymbol{f}-\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{x}-\gamma_{1}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{v}+\right. \\ \left.\boldsymbol{f}+\gamma_{0}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{x}\right]=-\gamma_{1} \boldsymbol{v}^{\mathrm{T}}(\boldsymbol{L}+\boldsymbol{H}) \boldsymbol{v}= \\ -\gamma_{1} \boldsymbol{v}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{v}-\gamma_{1} \boldsymbol{v}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{v}= \\ -\gamma_{1} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} b_{i j}\left(\boldsymbol{v}_{i}^{\mathrm{T}}\left(\boldsymbol{v}_{i}-\boldsymbol{v}_{j}\right)\right)-\gamma_{1} \boldsymbol{v}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{v} \leqslant \\ -\gamma_{1} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} b_{i j}\left[\left(\frac{1}{2} \boldsymbol{v}_{i}^{\mathrm{T}}\right)^{2}+\left(\boldsymbol{v}_{i}-\boldsymbol{v}_{j}\right)^{2}\right]- \\ \gamma_{1} \sum\limits_{i=1}^{n} h_{i} \boldsymbol{v}_{i}^{\mathrm{T}} \boldsymbol{v}_{i} \leqslant 0 . \end{gathered} $ | (33) |
即在γ1和γ0均大于0的前提下,当t→∞时,ψ(x, v)单调递减,此时定义集合LH(c)={(x, v)|ψ(x, v)≤c}为有界集,若无人机初始状态(x(0), v(0))∈LH(c),那么ψ(x(t), v(t))≤c对所有t均成立,且LH(c)为不变集,对应∀(x, v)∈LH(c)ψ(x, v)≥0,
接下来求解非齐次方程式(30)的特解,无人机编队飞行的约束条件为
综上,当参数设置满足γ1>0和γ0>0时,编队内所有无人机的状态值都将趋于最大不变集Ω={v|
首先在相同给定参数下使用DDPG与Greedy-DDPG算法训练强化学习中的决策网络。然后针对单架无人机选取一定范围内的初始条件对基于人工势场的方法、DDPG和Greedy-DDPG算法的单架无人机避障进行Monte Carlo模拟,以验证本文方法的泛化能力。对于无人机集群编队飞行,将选取部分初始条件验证编队飞行效果。
4.1 基于强化学习的长机避障 4.1.1 参数设定本文设计的Actor网络和Critic网络均由2个全连接层构成,全连接网络结构简单且运算方便,时间复杂度低。故结合Actor网络输入状态和输出动作、Critic网络输入状态和输入动作及输出Q值的特点,根据2.2和2.3节选定的五维状态和一维动作,设计DDPG网络结构如表 1所示。
| 层数 | Actor网络 | Critic网络 |
| 输入层 | 5 | 1(动作)+5(状态) |
| 隐藏层1 | 60 | 80(动作)+80(状态) |
| 隐藏层2 | 80 | 60(动作)+60(状态) |
| 输出层 | 1 | 1 |
表 1中输出层通过tanh函数进行最终的值函数输出。强化学习过程中的算法参数设置如表 2所示。
| 训练参数 | 数值 |
| Actor网络学习率 | 0.001 |
| Critic网络学习率 | 0.001 |
| N | 128 |
| 经验池大小 | 50 000 |
| 网络噪声 | 0.8 |
| 网络噪声衰减速率 | 1×10-6 |
| 网络噪声回归常数 | 0.3 |
| ε1 | 0.3 |
| ε2 | 0.1 |
| rε2 | 0.95 |
| kr | 200 |
| vstop/(m·s-1) | 8 |
| 停止平均奖励 | 8 000 |
| 网络更新率 | 0.001 |
| 单次实验最大步长/s | 60 |
| 仿真步长/s | 0.01 |
由于实际飞行中,无人机和障碍都会受到一定物理约束,设定为vmax=20 m/s,vmin=4 m/s,θ·max=0.5 π rad/s2,Rs=40 m,无人机最大加速率为1 m/s2,障碍物圆心x和y坐标范围分别为[100, 230] m和[0, 150] m,障碍最大和最小半径分别为25和20 m,障碍物之间最小距离为30 m,障碍物数量m=5。
无人机初始和目标位置见表 3,为提高泛化能力需对训练中每轮次的初始位置与运行方向进行随机选取,选取流程如下:1) 在表 3中4组初始位置随机选取一组作为基础初始值;2) 基础初始值的x和y各添加在[-30, 0] m分布的随机值形成新的初始位置;目标位置的x和y各添加在[0, 20] m分布的随机值形成新的目标位置;3) 初始航向角由初始无人机与目标相对角度关系决定,加入小范围随机值,初始航向角大小确定方式如下:
| $ \theta_{i 0}=\theta_{\mathrm{ta}}+0.1-0.2 \operatorname{rand}(1) . $ | (34) |
| 序号 | 初始位置 | 目标位置 |
| 1 | (5 m, 100 m) | (300 m, 200 m) |
| 2 | (150 m, 240 m) | (150 m, -80 m) |
| 3 | (0 m, 0 m) | (300 m, 200 m) |
| 4 | (0 m, 200 m) | (300 m, -50 m) |
其中rand(1)为0~1随机数。
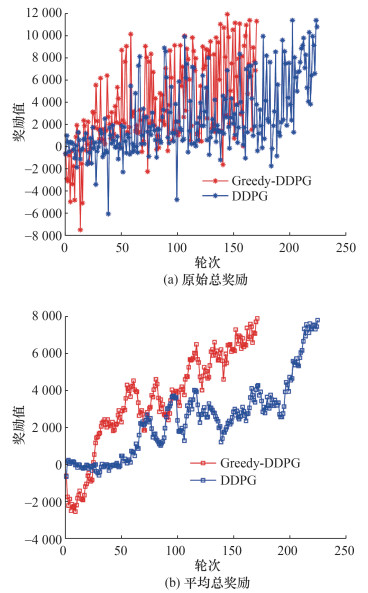
本文实验硬件CPU为i7-11800H,GPU为RTX 3060,Greedy-DDPG训练时长为2 h 7 min,DDPG训练时长为2 h 15 min。基于表 2参数的训练得到原始实验结果(见图 3a);为了方便观察是否满足停止条件,在原始结果基础上进行了平均处理(见图 3b)。
|
| 图 3 训练图像 |
由图 3可知,Greedy-DDPG算法在进行170个轮次后,平均奖励达到了期望奖励值,即长机可通过学习实现未知环境下的障碍规避。相比DDPG算法,Greedy-DDPG算法的奖励曲线上升明显更快,训练过程初始奖励更低,这是由于前期在线Critic网络无法正确对动作与状态进行价值评估。当Greedy-DDPG中的在线Critic网络在前期快速完成对价值函数的逼近后,平均奖励开始快速上升,符合探索函数设定预期效果。同时由于加速了在线Critic网络的逼近,促使整体训练时长缩短了5.9%。
使用相同场景对3种算法进行结果验证,设定初始位置为(5 m, 100 m),设定目标位置为(300 m, 150 m),初始角度为0,初始速度为10 m/s,期望速度为10 m/s。随机障碍物验证场景参数如表 4所示。
| 障碍物位置 | 障碍物半径/m |
| (156.883 m, 77.547 m) | 21.505 |
| (121.702 m, 3.942 m) | 21.066 |
| (117.535 m, 156.039 m) | 21.732 |
| (237.000 m, 103.852 m) | 21.984 |
| (239.791 m, 24.075 m) | 21.190 |
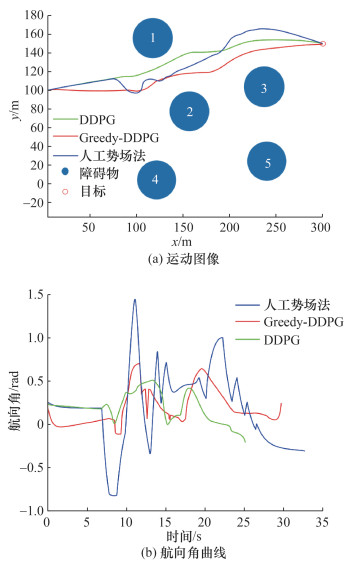
由此得到验证场景下的运动图像和航向角曲线如图 4所示。基于人工势场的方法在10~15 s面对障碍物1和2时航向角剧烈波动。这是由于受到探测距离的限制,无人机感知障碍物时间存在差异,在感知障碍物数目变化后,合力方向发生突变导致。相比基于人工势场的方法,Greedy-DDPG方法全程航迹更为平缓,在遇到障碍物1和2时,航向角波动更小。
|
| 图 4 验证场景下运动图像及航向角曲线 |
DDPG方法全程航迹也相对平滑,在飞行过程中DDPG方法仅感知到单障碍物,虽然输入未出现突变,航向角平滑,但由表 5可以看出,DDPG方法在避障过程中距离障碍物更近,离障碍物1最近距离仅为9.1 m,虽有利于自身避障,但在编队中作为长机时,贴近障碍的避障方式会压缩僚机的机动空间,增大编队飞行安全风险。相比之下,Greedy-DDPG方法距离障碍物1、2和3的最小距离分别为23.2、19.0和17.8 m,扩大了僚机的机动空间,有利于编队避障。
为进一步验证本文提出方法的有效性,选取随机训练环境参数(障碍物半径为20~25 m,个数为5),大型障碍参数(障碍物半径为50~60 m,个数为2)、小型密集障碍(障碍物半径为10~15 m,个数为10)。障碍物圆心位置同表 3。通过Monte Carlo模拟可以得到无人机到达目标0.5 m内的概率,如表 6所示。
| % | |||||||||||||||||||||||||||||
| 场景 | Greedy-DDPG | DDPG | |||||||||||||||||||||||||||
| 随机训练环境 | 97.50 | 85.20 | |||||||||||||||||||||||||||
| 大型障碍 | 95.50 | 72.70 | |||||||||||||||||||||||||||
| 小型密集障碍 | 96.40 | 86.80 | |||||||||||||||||||||||||||
由表 6可知,Greedy-DDPG在随机训练环境下的效果优于其他2种场景,符合预期效果。同时Greedy-DDPG的避障任务完成率在所有场景下都优于DDPG算法。相比DDPG算法,Greedy-DDPG在未训练环境的性能下降更小,因而本文针对未知环境下无人机避障提出的强化学习训练方法比DDPG算法具有更好的泛化性。
4.1.2 基于一致性的无人机编队避障避碰验证为验证所设计的无人机编队避障避碰算法性能,设定长机初始位置为(0 m, 0 m),目标位置为(350 m, 250 m),初始角度为0,初始速度为10 m/s,期望速度为10 m/s。障碍物验证场景参数如表 7所示,编队中各僚机的初始参数如表 8所示。
| 障碍物位置 | 障碍物半径/m |
| (156.883 m, 77.547 m) | 21.189 |
| (121.702 m, 3.943 m) | 22.566 |
| (117.535 m, 156.039 m) | 20.869 |
| (237.000 m, 103.852 m) | 24.295 |
| (239.791 m, 24.075 m) | 22.525 |
| 僚机位置 | 速度/(m·s-1) |
| (-19.628 m, 0 m) | 10 |
| (21.241 m, 0 m) | 10 |
| (0 m, 21.153 m) | 10 |
| (0 m, -18.399 m) | 10 |
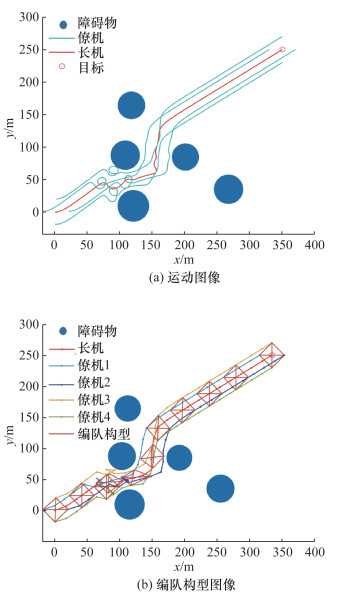
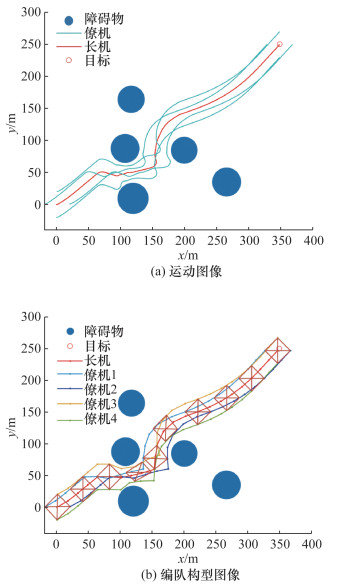
使用式(24)的编队控制律对编队进行仿真,得到实验结果如图 5和6所示。
|
| 图 5 基于人工势场方法的编队避障图像 |
|
| 图 6 基于Greedy-DDPG的集中式双层编队避障图像 |
在无人机编队初期未探索到障碍物时,无人机编队可以保持构型稳定飞行;在遇到障碍时,无人机编队根据自身情况动态调整构型,完成避障与避碰任务;当无人机编队离开障碍区时,无人机编队快速恢复构型,并稳定飞行到目的地。同时,使用强化学习作为长机的编队飞行路径比基于人工势场的方法更加平滑,特别是在遇到狭缝时,基于人工势场方法的长机路径有更大波动,导致僚机为完成编队构型的路径整体波动加剧。
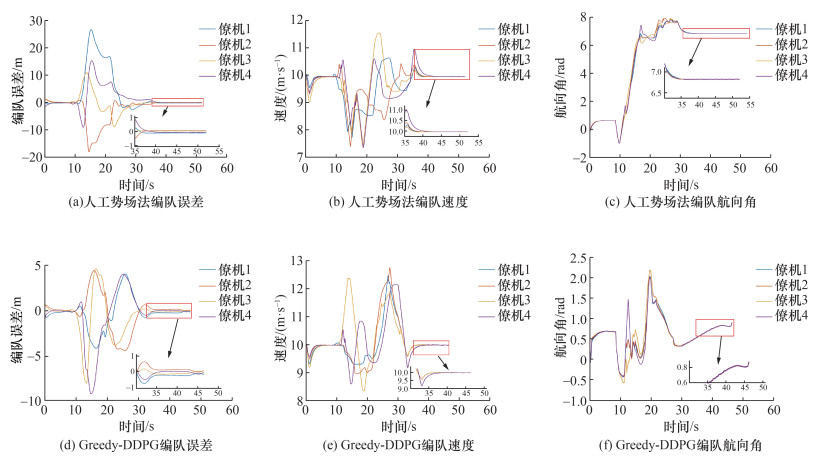
由图 7可以看出,基于人工势场方法的无人机集群避障编队误差明显大于基于Greedy-DDPG的无人机编队,两者最终稳定时,编队误差基本趋于一致。在编队速度上,基于人工势场方法的无人机编队集群为了避障倾向于低速通过;而基于Greedy-DDPG算法的无人机编队中长机路径更加平滑,更有利于固定翼无人机编队快速通过,可避免编队内部堵塞导致的碰撞。在航向角上,两者基本都能保障无人机编队的一致性,但由于人工势场下的无人机编队倾向于低速通过,导致僚机为避免碰撞原地盘旋,对无人机的性能要求提高,不利于编队飞行。
|
| 图 7 编队集群避障编队误差、速度和航向角 |
5 结论
本文根据无人机探测能力、机动能力与未知障碍物的几何特性等因素,结合强化学习与人工势场法,设计了一种未知环境下无人机编队智能避障控制方法。针对DDPG学习过程中存在的训练速度较慢与价值高估问题,提出了改进的贪婪选择策略,保障前期快速训练的同时,一定程度上抑制了价值高估导致的训练效果下降问题。在此基础上,将训练完成的模型代入多场景Monte Carlo仿真,结果表明,本方法泛化性良好。设计了集中式双层无人机编队的控制算法,以充分利用长机智能性提升飞行安全。仿真实验数据表明无人机编队避障效果良好,比基于人工势场的算法飞行路径更为平滑、飞行耗时少。该方法可实现编队跟随长机实现协同任务,僚机避障避碰且一致性收敛效果良好。
下一步将考虑固定翼无人机的复杂动力学特性,针对分布式网络通信架构,研究基于强化学习的无人机编队避碰避障方法。
| [1] |
ISMAIL A, BAGULA B A, TUYISHIMIRE E. Internet-of-things in motion: A UAV coalition model for remote sensing in smart cities[J]. Sensors, 2018, 18(7): 2184. DOI:10.3390/s18072184 |
| [2] |
YANG J H, QIAN J C, GAO H W. Forest wildfire monitoring and communication UAV system based on particle swarm optimization[J]. Journal of Physics: Conference Series, 2021, 1982(1): 012068. DOI:10.1088/1742-6596/1982/1/012068 |
| [3] |
TORTONESI M, STEFANELLI C, BENVEGNU E, et al. Multiple-UAV coordination and communications in tactical edge networks[J]. IEEE Communications Magazine, 2012, 50(10): 48-55. DOI:10.1109/MCOM.2012.6316775 |
| [4] |
LINDQVIST B, SOPASAKIS P, NIKOLAKOPOULOS G. A scalable distributed collision avoidance scheme for multi-agent UAV systems [C]//2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Prague, Czech Republic: IEEE, 2021: 9212-9218.
|
| [5] |
SHIVGAN R, DONG Z Q. Energy-efficient drone coverage path planning using genetic algorithm [C]//2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR). Newark, NJ, USA: IEEE, 2020: 1-6.
|
| [6] |
陈博琛, 唐文兵, 黄鸿云, 等. 基于改进人工势场的未知障碍物无人机编队避障[J]. 计算机科学, 2022, 49(S1): 686-693. CHEN B C, TANG W B, HUANG H Y, et al. Pop-up obstacles avoidance for UAV formation based on improved artificial potential field[J]. Computer Science, 2022, 49(S1): 686-693. (in Chinese) |
| [7] |
李樾, 韩维, 陈清阳, 等. 基于改进的速度障碍法的有人/无人机协同系统三维实时避障方法[J]. 西北工业大学学报, 2020, 38(02): 309-318. LI Y, HAN W, CHEN Q Y, et al. Real-time obstacle avoidance for manned/unmanned aircraft cooperative system based on improved velocity obstacle method[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 309-318. (in Chinese) |
| [8] |
PEDRO D, MATOS-CARVALHO J P, FONSECA J M, et al. Collision avoidance on unmanned aerial vehicles using neural network pipelines and flow clustering techniques[J]. Remote Sensing, 2021, 13(13): 2643. DOI:10.3390/rs13132643 |
| [9] |
刘钢, 汤俊, 刘陈, 等. 无人飞行器集群协同行为建模技术综述[J]. 系统工程与电子技术, 2021, 43(8): 2221-2231. LIU G, TANG J, LIU C, et al. Survey of cooperative behavior modeling technology for unmanned aerial vehicles clusters[J]. Systems Engineering and Electronics, 2021, 43(8): 2221-2231. (in Chinese) |
| [10] |
张殿富, 刘福. 基于人工势场法的路径规划方法研究及展望[J]. 计算机工程与科学, 2013, 35(6): 88-95. Zhang D F, Liu F. Research and development trend of path planning based on artificial potential field method[J]. Computer Engineering & Science, 2013, 35(6): 88-95. (in Chinese) |
| [11] |
陈廷斌, 张奇松, 杨晓光. 基于改进人工势场-鱼群算法的LBS最短路径修正研究[J]. 计算机应用与软件, 2015, 32(6): 259-262. CHEN T B, ZHANG Q S, YANG X G. On LBS shortest path correction based on improved artificial fish swarm algorithm with potential field[J]. Computer Applications and Software, 2015, 32(6): 259-262. (in Chinese) |
| [12] |
代冀阳, 王村松, 殷林飞, 等. 飞行器分层势场路径规划算法[J]. 控制理论与应用, 2015, 32(11): 1505-1510. DAI J Y, WANG C S, YIN L F, et al. Hierarchical potential field algorithm of path planning for aircraft[J]. Control Theory & Applications, 2015, 32(11): 1505-1510. (in Chinese) |
| [13] |
仇恒坦, 平雪良, 高文研, 等. 改进人工势场法的移动机器人路径规划分析[J]. 机械设计与研究, 2017, 33(4): 36-40. QIU H T, PING X L, GAO W Y, et al. Mobile robot path planning based on improved artificial potential field method[J]. Machine Design & Research, 2017, 33(4): 36-40. (in Chinese) |
| [14] |
MCINTYRE D, NAEEM W, XU X D. Cooperative obstacle avoidance using bidirectional artificial potential fields [C]//2016 UKACC 11th International Conference on Control (CONTROL). Belfast, UK: IEEE, 2016: 1-6.
|
| [15] |
LI J C, FANG Y W, CHENG H Y, et al. Large-scale fixed-wing UAV swarm system control with collision avoidance and formation maneuver[J]. IEEE Systems Journal, 2023, 17(1): 744-755. DOI:10.1109/JSYST.2022.3212068 |
| [16] |
张云燕, 魏瑶, 刘昊, 等. 基于深度强化学习的端到端无人机避障决策[J]. 西北工业大学学报, 2022, 40(5): 1055-1064. ZHANG Y Y, WEI Y, LIU H, et al. End-to-end UAV obstacle avoidance decision based on deep reinforcement learning[J]. Journal of Northwestern Polytechnical University, 2022, 40(5): 1055-1064. (in Chinese) |
| [17] |
王庭晗, 罗禹贡, 刘金鑫, 等. 基于考虑状态分布的深度确定性策略梯度算法的端到端自动驾驶策略[J]. 清华大学学报(自然科学版), 2021, 61(9): 881-888. WANG T H, LUO Y G, LIU J X, et al. End-to-end self-driving policy based on the deep deterministic policy gradient algorithm considering the state distribution[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(9): 881-888. (in Chinese) |
| [18] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7450): 529-533. |
| [19] |
张耀中, 许佳林, 姚康佳, 等. 基于DDPG算法的无人机集群追击任务[J]. 航空学报, 2020, 41(10): 324000. ZHANG Y Z, XU J L, YAO K J, et al. Pursuit missions for UAV swarms based on DDPG algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(10): 324000. (in Chinese) |
| [20] |
LI B, YANG Z P, CHEN D Q, et al. Maneuvering target tracking of UAV based on MN-DDPG and transfer learning[J]. Defence Technology, 2021, 17(2): 457-466. DOI:10.1016/j.dt.2020.11.014 |
| [21] |
高敬鹏, 胡欣瑜, 江志烨. 改进DDPG无人机航迹规划算法[J]. 计算机工程与应用, 2022, 58(8): 264-272. GAO J P, HU X Y, JIANG Z Y. Unmanned aerial vehicle track planning algorithm based on improved DDPG[J]. Computer Engineering and Applications, 2022, 58(8): 264-272. (in Chinese) |
| [22] |
陈浩. 复杂条件下固定翼无人机集群编队控制研究[D]. 长沙: 国防科技大学, 2020. CHEN H. Research on formation control of fixed-wing UAV swarms in complex environments [D]. Changsha: National University of Defense Technology, 2020. (in Chinese) |
| [23] |
SHEVITZ D, PADEN B. Lyapunov stability theory of nonsmooth systems[J]. IEEE Transactions on Automatic Control, 1994, 39(9): 1910-1914. DOI:10.1109/9.317122 |



