淡水资源和能源短缺是当今世界面临的双重危机,严重制约乃至阻碍经济发展[1-3]。随着可再生能源开发利用程度不断提高和海水淡化技术的日益成熟,可再生能源与海水淡化的集成必将成为“双碳”目标下解决淡水危机和能源危机的重要途径之一[4]。太阳能是当前可再生能源重要的发展方向,主要分为光伏发电与光热发电2种方式[5]。2022年底,全球光热发电装机容量达到11.2 GW[6]。光热电站(concentrating solar power, CSP)可产生多级闪蒸大量消耗的热能与反渗透单元所需要的电能,因此光热电站与以多级闪蒸、反渗透为主要技术方法的海水淡化系统集成具有天然优势[7-8]。
Wang等[9]构建了基于光热电站、风力发电与海水淡化集成的可再生能源供应系统,该系统可用于海岛供水供电。Alhaj等[10]建立了光热电站驱动的热脱盐系统模型,其二氧化碳(CO2)排放较传统热脱盐法降低了47%。Pati等[11-12]构建了用于研究光热电站与多级闪蒸集成可能性的算法,该算法可评估光热电站与多级闪蒸集成后的系统最优配置、经济效益与环境影响。Liu等[13]构建了混合光热供能海水淡化系统的调度模型,使混合系统的功率波动和费用得到降低。Zhang等[14]提出了反渗透混合光热供能集成系统的实时动态能量管理策略,该策略可根据各时刻天气状况变化实时调整系统工作方案。Rezk等[15]提出了以燃料电池解决光热供能间歇性问题的策略,并与反渗透系统耦合,通过燃料电池的集成及合理的策略调控,降低了系统产能波动性。以上研究表明,合理的调度策略在一定程度上可以解决可再生能源间歇性导致的各项问题。但是,面对更加极端且连续的天气状况时,这些调度策略可能失效。设计柔性能力较强的可再生能源与海水淡化集成的联产系统以满足复杂天气状况下用户能量需求是该领域亟待解决的重要课题。
为此,本文构建了光热电站与多级闪蒸和反渗透海水淡化集成的水热电联产系统。同时,提出了集成系统的柔性设计方法,以降低系统的波动性,使系统在复杂天气状况下能够连续运行。
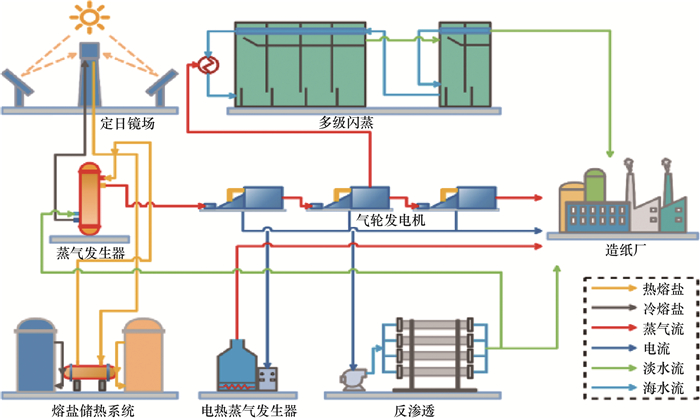
1 系统数学模型如图 1所示,本文提出的光热电站与海水淡化集成系统由光热电站、多级闪蒸(multistage flashing, MSF)、反渗透(reverse osmosis, RO)、电热蒸气发生器、双罐熔盐储热单元、储水单元构成,进行水、热、电联产。
|
| 图 1 海水淡化-光热电站集成联产系统结构 |
● 热力循环系统、气轮发电机工作流体采用水蒸气;
● MSF单元生产的淡水盐度为0;
● RO单元最终排放盐度小于6%;
● 忽略各单元的热损失,各热交换环节以换热效率形式体现;
● CSP、MSF、RO及储能单元在稳定状态下工作;
● 忽略MSF单元的耗电量和RO单元的耗热量。
1.1 光热电站光热电站集热功率为
| $ W_{\mathrm{sf}, t}=\eta_{\mathrm{so}} N_{\mathrm{sc}, t} S_{\mathrm{sc}} D_t . $ | (1) |
其中:Wsf, t为各时刻光热电站集热功率,W;ηso为光热转换效率;Nsc, t为各时刻处于工作状态的镜场单元数;Ssc为镜场单元面积,m2;Dt为各时刻光照强度,W/m2。
| $ C_{\mathrm{CSP}}=a_1 C_{\mathrm{inst}}+\sum\limits_{t=1}^T C_{\mathrm{cop}, t}. $ | (2) |
其中:CCSP、Cinst、Ccop, t分别为年总费用、投资费用、各时刻操作费用,$;a1为资金回收因子。
1.2 储热单元本文采用双罐熔盐储热单元在热量过剩时储存热量,在热量不足时释放热量。
| $ W_{\mathrm{st}, t}=M_{\mathrm{st}, t} \frac{C_{p, \mathrm{~m} 1}\left(T_{\mathrm{m}, \mathrm{h}}-T_{\mathrm{m}, \mathrm{c}}\right)}{3\;600} . $ | (3) |
| $ W_{\mathrm{re}, t}=\eta_{\mathrm{re}} M_{\mathrm{re}, t} \frac{H_{\mathrm{h} 1}-H_{\mathrm{s1}}}{3\;600}. $ | (4) |
| $ \begin{gathered} Q_{\mathrm{stt}, t}=Q_{\mathrm{stt}, t-1}+\varepsilon_1 W_{\mathrm{st}, t} \times 3\;600- \\ \varepsilon_2 W_{\mathrm{re}, t} \times 3\;600 . \end{gathered} $ | (5) |
其中:Wst, t为储热功率,Wre, t为放热功率, W;Cp, m1为储热时熔盐比热容,J·kg-1·K-1;Mst, t为各时刻储热时蒸气流量,Mre, t为各时刻放热时蒸气流量,kg/h;Tm, h、Tm, c分别为高、低温熔盐温度,K;ηre为放热效率;Hh1为进口蒸气焓值,Hs1为出口蒸气焓值,J/kg;Qstt, t和Qstt, t-1分别为t时刻和t-1时刻储热系统内储热总量,J;ε1、ε2为二进制变量,取值为0或1且不可同时取0或1。
| $ C_{\mathrm{sh}}=a_1\left(C_{\mathrm{ta}}+C_{\mathrm{salt}}\right)+\sum\limits_{t=1}^1 C_{\mathrm{as}, t} . $ | (6) |
其中:Csh为年总费用,$;Cta为储热单元建造费用,$;Csalt为熔盐费用,$;Cas, t为各时刻储热系统辅助设备及操作费用,$。
1.3 电热蒸气发生器| $ W_{\mathrm{es}, t}=\eta_{\mathrm{eh}} M_{\mathrm{S} 3, t} \frac{H_{\mathrm{m} 2}-H_{\mathrm{w}}}{3\;600}. $ | (7) |
其中:Wes, t为各时刻电热蒸气功率,W;ηeh为电热转换效率;MS3, t为各时刻设备蒸气质量流量,kg/h;Hw为水焓值,Hm2为水蒸气焓值,J/kg。
| $ C_{\mathrm{es}}=k_{\mathrm{es}} M_{\mathrm{S} 3, \text { design }} \text {. } $ | (8) |
其中:Ces为电热蒸气发生器年总费用,$;kes为电热蒸气发生器投资系数;MS3, design为设备额定生产蒸气质量流量,kg/h。
1.4 海水淡化| $ M_{\mathrm{MSF}, t}=M_{r, t}\left(1+y-(1-y)^{N_{\mathrm{MSF}, \text { design }}-1}\right) . $ | (9) |
其中:MMSF, t为多级闪蒸每小时总淡水产量,kg/h;NMSF, design为多级闪蒸设计级数;Mr, t为各时刻第r级淡水产量,kg/h;y为产水率。
| $ C_{\mathrm{MSF}}=C_{\mathrm{dm}}+\sum\limits_{t=1}^T C_{\mathrm{om}, t}. $ | (10) |
其中:CMSF为年总费用,$;Cdm为年投资费用,$;Com, t为各时刻操作费用,$。
| $ M_{\mathrm{RO}, t}=N_{\mathrm{RO}, t} A_{\mathrm{RO}}\left(J_{\mathrm{w}} \rho_{\mathrm{d}}+J_{\mathrm{s}}\right) . $ | (11) |
其中:MRO, t为各时刻反渗透每小时淡水产水量,kg/h;NRO, t为各时刻运行设备数;ARO为单台反渗透设备膜面积,m2;Jw为反渗透膜纯水通量,Js为反渗透膜盐通量,m/s;ρd为淡水密度,kg/m3。
| $ C_{\mathrm{RO}}=C_{\mathrm{RI}}+C_{\mathrm{RV}}+C_{\mathrm{RW}}+C_{\mathrm{RF}}+C_{\mathrm{RT}} . $ | (12) |
其中:CRO为反渗透单元的年总费用,$;CRI为年投资费,$;CRV、CRW、CRF、CRT分别为各反渗透单元的操作费用,$。
1.5 约束条件| $ 0 \leqslant W_{\mathrm{sf}, t} \leqslant W_{\mathrm{sf}, \max }. $ | (13) |
| $ M_{\mathrm{st}, t}<0.8 M_{\mathrm{s}, \mathrm{T}}, $ | (14) |
| $ W_{\mathrm{re}, t} \times 3\;600 \leqslant 0.8 Q_{\mathrm{stt}, t}, $ | (15) |
| $ 0.5 M_{\mathrm{MSF}\text{max}} \leqslant M_{\mathrm{MSF}, t} \leqslant M_{\mathrm{MSF}\text{max}} \text {, } $ | (16) |
| $ 0 \leqslant M_{\mathrm{RO}, t} \leqslant M_{\mathrm{ROmax}} . $ | (17) |
Wsf, max为最大集热功率,W;Ms, T为储热的导热熔盐总质量,kg;MMSFmax为多级闪蒸的额定产量,MROmax为反渗透的的额定产量,kg。
1.6 目标函数系统的设计目标为:在满足用户需求的条件下系统年总费(Csystem)用最小。
| $ \min \left\{C_{\text {system }}\right\}=\min \left\{C_{\mathrm{CSP}}+C_{\mathrm{MSF}}+C_{\mathrm{RO}}+C_{\mathrm{ce}}+C_{\mathrm{sh}}\right\} . $ | (18) |
系统模型所包含的全部约束条件可分为等式约束和不等式约束,分别描述为以下形式:
| $ U_n(d, z, \theta) \leqslant 0, \quad n \in N . $ | (19) |
| $ E_m(d, z, \theta)=0, \quad m \in M. $ | (20) |
系统设计成功的必要条件为满足所有等式约束等于0的情况下,所有不等式约束小于或等于0,即:
| $ \begin{gathered} U_n(d, z, \theta) \leqslant 0, \\ \text { s.t. } \quad E_m(d, z, \theta)=0, \\ \forall m \in M, \quad n \in N . \end{gathered} $ | (21) |
式中: d为设计变量,例如气轮机各出入口蒸气焓值、多级闪蒸顶温或末温、反渗透膜两侧压差等;z为系统模型中的决策变量,例如光热电站镜场单元数、多级闪蒸换热面积、反渗透单元数等;θ为模型中的不确定变量,例如各时刻进入气轮机的蒸气流量、多级闪蒸产水量等。Un和Em分别代表不等式约束和等式约束;M、N分别为等式约束、不等式约束的数量。
设计变量d在设计阶段可变,在系统运行阶段不变。当工况发生变化时,不确定变量θ受到影响随之发生变化,而柔性设计的目标是确定合适的z使θ一直在保持在合理范围内。因此, 通过代换可得到系统设计的可行性操作方程:
| $ \begin{gathered} \psi(z, \theta)=\min \max U_n(d, z, \theta) \\ \text { s.t. } E_m(d, z, \theta) \leqslant 0 \quad \forall m \in M, n \in N . \end{gathered} $ | (22) |
式(22)表示通过不断调整z得到相应的θ,使最大的不等式约束Un达到最小值,ψ(z, θ)代表最大的不等式约束取到的最小值。当ψ(z, θ)≤0时,即最大的不等式约束满足小于或等于0,则模型内任意不等式约束皆满足小于或等于0,即系统设计是可行的。特别地,当ψ(z, θ)=0时,此时不等式约束取到边界值,对计算结果的影响是最大的,称之为边界约束。
系统设计时,以对用户供能的满足率和过剩率作为系统供能指标,并设定联产系统各种能量供给的满足率不得低于用户需求的95%,过剩率不超过5%,故本文提出的柔性指数计算方法为
| $ \mathrm{Flu}=\sum\limits_{t=1}^T\left(\left|\theta_{\mathrm{e}, N+}-1.05\right|+\left|\theta_{\mathrm{e}, N-}-0.95\right|\right) . $ | (23) |
式中:Flu代表模型的柔性指数;θe, N+和θe, N-分别代表不确定变量中处于供能过剩时和处于供能不足时的供需比, 当系统供需比低于0.95或高于1.05时,系统在该时刻处于供需异常状态。
柔性指数数值越大意味着系统处于供需异常状态的时刻越多,系统偏差值越大,系统柔性能力越弱;当Flu为0时意味着系统能量供给各时刻均在用户需求的最低标准与最高标准之间。因此,本文柔性设计的目标是使系统柔性指数最大程度接近0。
2.2 边界约束检验考虑柔性设计后,系统模型构成了一个非线性且不可微分的模型,直接求解难度较大,本文根据Grossmann和Floudas提出的边界约束法[20],采用Karush-Kuhn-Tucker (KKT)条件优化ψ(z, θ)。KKT条件是确定某点为极值点的必要条件,在非线性规划领域里发挥了重要作用。
| $ U_n(d, z, \theta)+S_n=0 \quad \forall n \in N . $ | (24) |
| $ \sum\limits_{n=1}^N \lambda_n=1 . $ | (25) |
| $ \sum\limits_{m=1}^M \mu_m \frac{\partial E_m}{\partial z}+\sum\limits_{n=1}^N \lambda_n \frac{\partial U_n}{\partial z}=0. $ | (26) |
| $ \sum\limits_{m=1}^M \mu_m \frac{\partial E_m}{\partial d}+\sum\limits_{n=1}^N \lambda_n \frac{\partial U_n}{\partial d}=0. $ | (27) |
| $ S_n-G\left(1-\nu_n\right) \leqslant 0 \quad \forall n \in N . $ | (28) |
| $ \lambda_n-\nu_n \leqslant 0 \quad \forall n \in N . $ | (29) |
| $ S_n \geqslant 0, \quad \lambda_n \geqslant 0, \quad \nu_n \in\{0, 1\} . $ | (30) |
式中:Sn为不等式约束Un的松弛变量,μm和λn分别为Em和Un的Lagrange乘子,G为Sn的上限。νn为一个仅等于0或1的二进制变量,当Un=0时,νn=1,此时的约束为边界约束。利用该计算过程,最终可得到在该系统规模下的系统柔性指数、各不确定变量的计算结果及限制系统柔性能力的边界约束。
2.3 柔性能力优化柔性指数计算模型及KKT条件实现了系统柔性能力的表征及分析,在此基础上解除边界约束对柔性指数的限制,以优化系统的柔性能力。柔性能力优化过程如下:
1) 根据供需比数据判断系统各产能单元或储能单元规模是否过大或不足,确定系统优化方向;
2) 检索边界约束关联的决策变量,根据优化方向按照设定步长改变决策变量取值从而实现对边界约束极限值的改变,得到新一代的决策变量及约束条件;
3) 将决策变量新值代回模型并进行新一次的供需比及柔性指数计算;
4) 随着迭代次数的增加,边界约束数量逐渐减少,各决策变量取值趋于合理,最终系统柔性能力得以增强,柔性设计完成。
2.4 柔性设计双层算法基于上文所述模型,通过对模型中决策变量类型的分析发现部分决策变量呈非线性相关,判定所要求解的问题类型为混合整数非线性问题。该问题可转化为一个双层算法的求解问题:外层算法通过GAMS求解系统模型获得系统的初始规模,内层算法通过MATLAB求解柔性设计模型实现系统柔性能力优化。对于柔性设计算法求解工具,本文利用GAMS及MATLAB两款软件的强大计算求解能力,并通过GDX、EXECL等软件实现两款软件的交互,以达到求解算法最佳。该双层算法具有较强的普适性,因其外层算法的系统数学模型可根据不同类型的系统进行变换,其内层算法可替换相应的决策变量,即可实现对新系统的柔性设计。系统柔性设计流程如图 2所示。

|
| 图 2 柔性设计流程 |
3 案例分析
案例中光照强度数据来源为位于青海省德令哈市的气象观测站,光热电站相关数据来源为位于该市的一座50 MW光热电站,用户能量需求数据则为位于该市的一座大型造纸厂在全年内各时刻的电、热、水需求。海水淡化水源为青海湖,其面积近年来在不断增大,利用海水淡化技术处理青海湖的苦咸水来补给青海省缺乏的淡水资源具有良好发展前景。
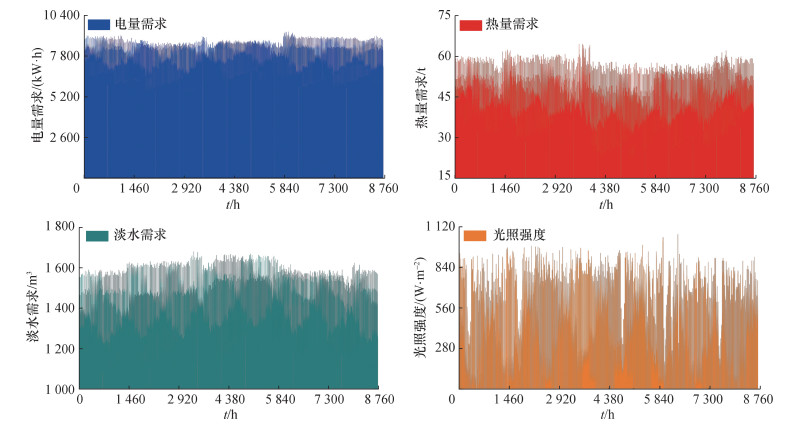
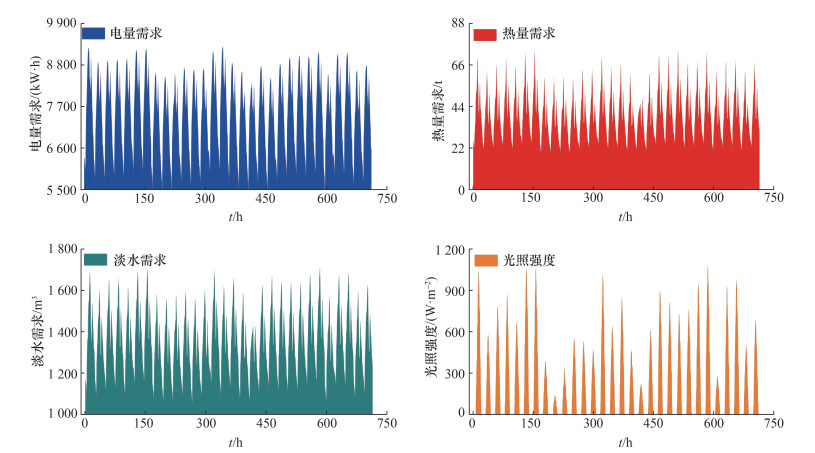
如图 3所示,用户需求在全年各季和各小时之间都存在波动。由于柔性设计模型复杂,为节约计算时间和提高准确性,本文在图 3所示的全年中选取一个典型月作为柔性设计阶段所用案例。如图 4所示,该典型月案例在150~250 h、380~420 h和590~620 h时段光照条件较差,其他时段光照强度能够在正常强度范围内规律波动或强于正常强度,这说明典型月案例能够涵盖光照正常时段、光照连续充足时段及光照连续不足时段3种情况,即典型月案例能够依据复杂天气状况条件来检验设计所得系统的柔性能力强弱。
|
| 图 3 典型年中各种能量需求和光照强度 |
|
| 图 4 典型月中各种能量需求和光照强度 |
4 结果与讨论 4.1 固定工况优化设计
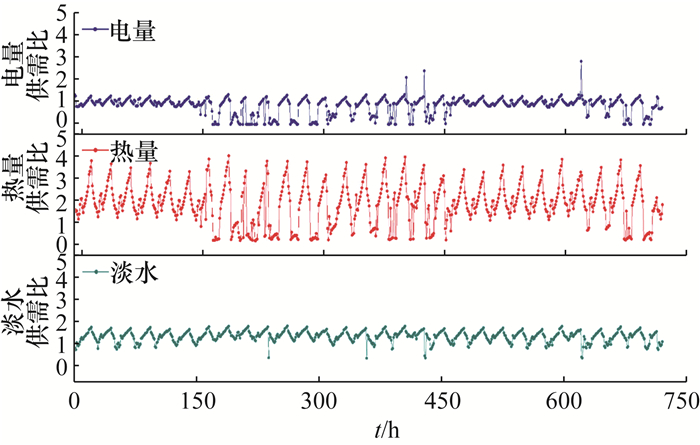
本研究选用各典型月案例各时刻平均值作为设计工况,即光照强度为279 W/m2、电量需求为190 556 kW·h、热量需求为1 081.5 t、淡水需求为34 285 m3。表 1所示为固定工况下优化结果。光热电站装机容量为36 MW,多级闪蒸和反渗透日产量分别为19 200 m3/d和35 100 m3/d,电热蒸气发生器日产量为360 t/d,储热单元设计容量为8.91×108 J。系统年总费用为1.68×107 $,产电、产热、产水成本分别为2.3×10-2 $/(kW·h)、23.19 $/t、0.96 $/m3。从图 5中可以看出,系统电能、热能、淡水的供需比波动范围分别为0.000~2.872、0.159~4.059、0.307~1.773;在720个运行时刻中,分别有656、707、437个运行时刻处于供需异常状态,电能、热能、淡水供需异常比例分别为91.11%、98.19%、60.69%。
| 单元 | 系统指标 | 固定工况 | 柔性设计 |
| 光热电站 | 装机容量/MW | 36 | 32 |
| 镜场面积/m2 | 410 000 | 230 000 | |
| 费用/$ | 4.89×106 | 3.29×106 | |
| 多级闪蒸 | 日产量/(m3·d-1) | 39 000 | 16 800 |
| 热交换面积/m2 | 5 600 | 7 850 | |
| 费用/$ | 3.05×106 | 2.49×106 | |
| 反渗透 | 日产量/(m3·d-1) | 35 100 | 35 100 |
| 膜数量 | 450 | 450 | |
| 费用/$ | 8.34×106 | 8.43×106 | |
| 储热 | 设计容量/J | 8.91×108 | 1.32×109 |
| 热罐体积/m3 | 7 020 | 12 140 | |
| 费用/$ | 4.14×105 | 6.61×105 | |
| 电热蒸气发生器 | 日产量/(t·d-1) | 360 | 300 |
| 费用/$ | 1.43×105 | 1.31×105 | |
| 总费用/$ | 1.68×107 | 1.50×107 | |
|
| 图 5 典型月中各运行时刻的供需比波动 |
4.2 柔性指数变化
为提高联产系统柔性能力,将固定工况设计结果作为初始系统规模,并采用本文提出的柔性设计方法,得到柔性设计联产系统。
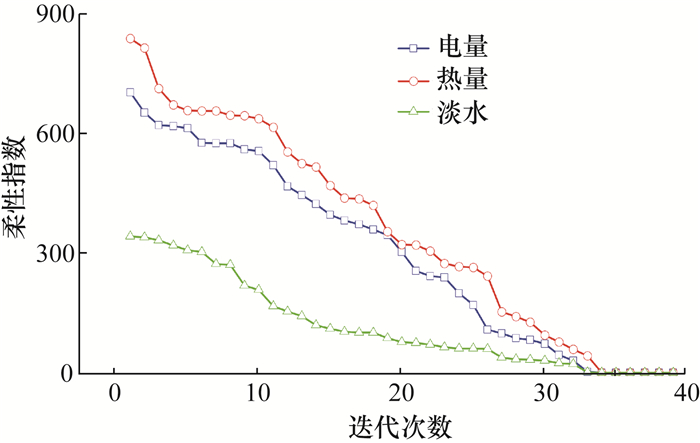
如图 6所示,以固定工况设计的系统规模作为柔性设计过程的初始系统规模,电能、热能和淡水的初始柔性指数分别为704.36、839.61和341.55。模型在计算时设置约束极限值(1±0.05)及各变量初始改变步长为2.5%,最大迭代次数为50次。共进行39次迭代计算,通过对边界约束及其对应变量的不断优化,各柔性指数的值逐渐变小,在第34次时各柔性指数收敛为0且后续迭代不再发生变化,此时系统模型中的边界约束得以检测并被解除,系统规模更加合理,在典型月中各时刻均能符合供能约束,说明此时系统的柔性能力得到较大提升。
|
| 图 6 系统的柔性指数变化 |
4.3 柔性设计结果
如表 1所示,柔性设计的光热电站装机容量及多级闪蒸日产量较固定工况设计分别降低11.11%、12.56%。光热电站及多级闪蒸规模偏大属于限制系统柔性的边界约束,柔性设计根据系统运行情况进行了多次柔性增强,因此光热电站及多级闪蒸规模下降。反渗透规模前后无变化,原因是反渗透单元灵活性较强,工况变化的影响不大。
柔性设计的储热单元容量相较固定工况设计提高46.15%,原因是固定工况下各负荷的波动程度远小于实际负荷波动程度,系统需扩大储能单元容量以应对天气状况及需求波动,因此固定工况设计的储能单元容量远小于柔性设计的储能单元容量。综上可见,能量生产单元变化幅度远小于能量调控单元,由此可推断柔性设计更倾向于增强系统的能量储放能力,而非能量生产能力。
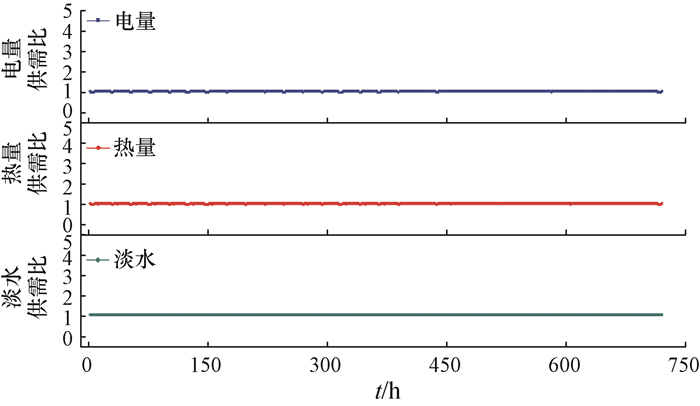
如图 7所示,柔性设计所得系统在典型月未出现供需异常时刻。淡水供需比在典型月各时刻稳定保持在1.05,电能供需比和热能供需比虽仍存在一定程度的波动,但均处在0.95~1.05的供能要求之内。在天气状况较差的150~450 h时段,由于系统的能量调控能力提高,系统仍能稳定满足能量需求,说明根据柔性设计方法得到的联产系统在复杂天气状况下稳定供能能力明显增强,同时系统产能波动也被显著抑制。
|
| 图 7 柔性设计工况能量供需比的对比 |
4.4 系统柔性能力验证
为了进一步验证柔性设计所得系统在包括季节变化等更复杂天气条件下的柔性能力,本文运用图 3所示典型年案例对柔性设计所得系统进行性能验证。
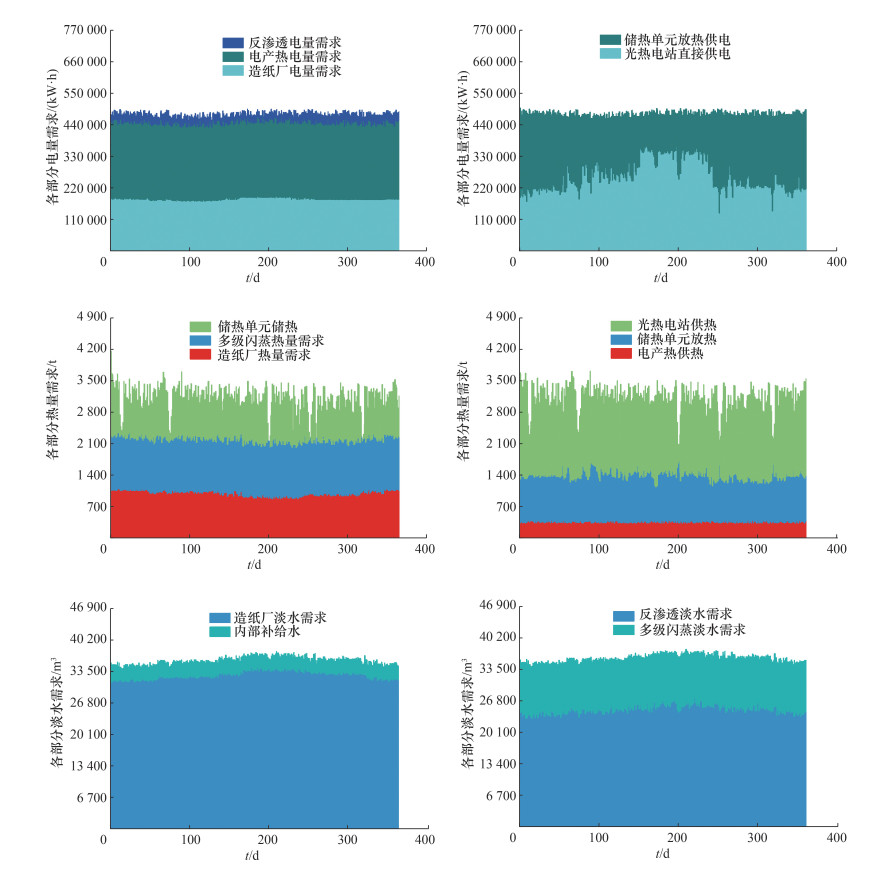
如图 8所示,经调度优化后,系统内电热蒸气发生器、多级闪蒸、反渗透单元负荷均在较小范围内波动,但光热电站及储热单元负荷波动水平仍然较大,原因为光热电站负荷受天气状况影响较大,产能波动存在一定不可控性,而储热单元需不断调整运行状态以降低系统整体波动水平,因此负荷波动较严重。
|
| 图 8 全年以天为单位柔性设计系统能量分配 |
在全年8 760个运行时刻,光热电站共稳定运行2 825个时刻,反渗透单元共稳定运行3 237个时刻,储热单元稳定储放热1 012个时刻,电热蒸气发生器共稳定运行7 828个时刻,光热电站、反渗透单元、储热单元、电热蒸气发生器稳定运行时刻较调度优化前分别增加25.62%、53.94%、15.81%、8.82%;多级闪蒸共稳定运行5 129个时刻,较调度优化前减少9.24%,与反渗透单元稳定运行时刻增加比例相比较小。系统整体波动水平减弱,在全年各运行时刻系统均可满足各类能量供需要求,表明本文建立的调度优化模型可行有效。
4.5 系统节能减排效益根据集成系统有效供给用户与各耗能单元的电能和热能总量,通过消耗单位质量煤炭产生各能量及各类气体之间的数量换算关系,得到集成系统有效运行一年等效节约的煤炭质量和减少排放的各类气体质量,具体结果如表 2所示。
系统全年产生的有效能量可等效减少消耗166 617 t煤炭,等效减少排放CO2 436 538 t、SO2 1 416 t和NOx 1 233 t。由此可见,本文所设计的联产系统对于海水淡化由高耗能产业转换为零排放产业以及可再生能源向高耗能产业渗透具有指导意义。
5 结论本文提出了光热电站-海水淡化集成联产系统,该系统相较于传统串联式系统实现了水、热、电联产;提出了光热电站-海水淡化集成联产系统的柔性指数和柔性设计方法。结果表明,与固定工况设计相比,柔性设计方法得到的系统年总费用降低了10.70%,在典型月案例中电能、热能、淡水供需异常比例分别由固定工况设计时的91.11%、98.19%、60.69%下降到0%。同时,在典型年案例中各单元供能负荷虽存在波动,但在任意时刻均实现了供能目标。该系统在案例条件下稳定运行一年,可节约用煤166 617 t,分别减少排放CO2 436 538 t、SO2 1 416 t和NOx 1 233 t,比传统供能模式的海水淡化系统具备优秀的节能减排效益。
综上所述,本文提出的系统优化方法在技术上与经济上均存在可行性,同时联产系统具有出色的节碳减排效益,有助于推动可再生能源联产系统应用于更多领域。
| [1] |
IHSANULLAH I, ATIEH M A, SAJID M, et al. Desalination and environment: A critical analysis of impacts, mitigation strategies, and greener desalination technologies[J]. Science of the Total Environment, 2021, 780: 146585. DOI:10.1016/j.scitotenv.2021.146585 |
| [2] |
LIM Y J, GOH K, KURIHARA M, et al. Seawater desalination by reverse osmosis: Current development and future challenges in membrane fabrication: A review[J]. Journal of Membrane Science, 2021, 629: 119292. DOI:10.1016/j.memsci.2021.119292 |
| [3] |
YADAV A, LABHASETWAR P K, SHAHI V K. Membrane distillation using low-grade energy for desalination: A review[J]. Journal of Environmental Chemical Engineering, 2021, 9(5): 105818. DOI:10.1016/j.jece.2021.105818 |
| [4] |
BUNDSCHUH J, KACZMARCZYK M, GHAFFOUR N, et al. State-of-the-art of renewable energy sources used in water desalination: Present and future prospects[J]. Desalination, 2021, 508: 115035. DOI:10.1016/j.desal.2021.115035 |
| [5] |
金勇, 马吉明, 朱守真, 等. 可再生能源开发及多能互补分析: 以青海为例[J]. 清华大学学报(自然科学版), 2022, 62(8): 1357-1365. JIN Y, MA J M, ZHU S Z, et al. Renewable energy development and multi-energy complementation, taking Qinghai as an example[J]. Journal of Tsinghua University (Science & Technology), 2022, 62(8): 1357-1365. (in Chinese) |
| [6] |
FELDMAN D, HOSKINS J, MARGOLIS R. Q4 2017/Q1 2018 Solar industry update [R/OL]. Golden, USA: National Renewable Energy Laboratory, 2018. https://www.nrel.gov/docs/fy18osti/71493.pdf.
|
| [7] |
高降宇, 陈蓓, 黄帅博. 计及碳交易机制的含光热电站海岛微网能量管理策略[J/OL]. 电子科技, 2023: 1-8. [2023-08-13]. https://doi.org/10.16180/j.cnki.issn1007-7820.2024.08.016. GAO X Y, CHEN B, HUANG S B. Energy management strategy of island microgrid with photothermal power station including carbon trading mechanism [J/OL]. Electronic Science and Technology, 2023: 1-8. [2023-08-13]. https://doi.org/10.16180/j.cnki.issn1007-7820.2024.08.016. (in Chinese) |
| [8] |
汪致洵, 林湘宁, 刘畅, 等. 基于光热电站水电联产的独立海岛综合供给系统容量优化配置[J]. 中国电机工程学报, 2020, 40(16): 5192-5203. WANG Z X, LIN X N, LIU C, et al. Optimal planning of integrated supply system in independent islands based on cogeneration of concentrating solar power plants[J]. Proceedings of the CSEE, 2020, 40(16): 5192-5203. (in Chinese) |
| [9] |
WANG Z X, LIN X N, TONG N, et al. Optimal planning of a 100% renewable energy island supply system based on the integration of a concentrating solar power plant and desalination units[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105707. |
| [10] |
ALHAJ M, AL-GHAMDI G S. Integrating concentrated solar power with seawater desalination technologies: A multi-regional environmental assessment[J]. Environmental Research Letters, 2019, 14(7): 074014. DOI:10.1088/1748-9326/ab1d74 |
| [11] |
PATI S, VERMA O P. Energy integration of solar assisted multiple stage evaporator and optimum parameter selection[J]. Energy, 2022, 239: 122162. DOI:10.1016/j.energy.2021.122162 |
| [12] |
PATI S, VERMA O P. Integration of solar field with multiple stage evaporator to sustain eco-energy in pulp and paper plant[J]. Journal of Cleaner Production, 2022, 333: 130148. DOI:10.1016/j.jclepro.2021.130148 |
| [13] |
LIU B Y, ZHOU B W, YANG D S, et al. Optimal planning of hybrid renewable energy system considering virtual energy storage of desalination plant based on mixed-integer NSGA-Ⅲ[J]. Desalination, 2022, 521: 115382. DOI:10.1016/j.desal.2021.115382 |
| [14] |
ZHANG G Z, HU W H, CAO D, et al. Data-driven optimal energy management for a wind-solar-diesel-battery-reverse osmosis hybrid energy system using a deep reinforcement learning approach[J]. Energy Conversion and Management, 2021, 227: 113608. DOI:10.1016/j.enconman.2020.113608 |
| [15] |
REZK H, SAYED E T, AL-DHAIFALLAH M, et al. Fuel cell as an effective energy storage in reverse osmosis desalination plant powered by photovoltaic system[J]. Energy, 2019, 175: 423-433. DOI:10.1016/j.energy.2019.02.167 |
| [16] |
PRIETO C, CABEZA L F. Thermal energy storage (TES) with phase change materials (PCM) in solar power plants (CSP). Concept and plant performance[J]. Applied Energy, 2019, 254: 113646. DOI:10.1016/j.apenergy.2019.113646 |
| [17] |
AZHAR M S, RIZVI G, DINCER I. Integration of renewable energy based multigeneration system with desalination[J]. Desalination, 2017, 404: 72-78. DOI:10.1016/j.desal.2016.09.034 |
| [18] |
ALSEHLI M, CHOI J K, ALJUHAN M. A novel design for a solar powered multistage flash desalination[J]. Solar Energy, 2017, 153: 348-359. DOI:10.1016/j.solener.2017.05.082 |
| [19] |
MITO M T, MA X H, ALBUFLASA H, et al. Variable operation of a renewable energy-driven reverse osmosis system using model predictive control and variable recovery: Towards large-scale implementation[J]. Desalination, 2022, 532: 115715. DOI:10.1016/j.desal.2022.115715 |
| [20] |
GROSSMANN I E, FLOUDAS C A. Active constraint strategy for flexibility analysis in chemical processes[J]. Computers & Chemical Engineering, 1987, 11(6): 675-693. |



