2. 清华大学 机械工程系, 北京 100084
2. Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China
水运仪象台是北宋年间建成的一座大型天文仪器,代表中国古代天文仪器制造的最高水平。南宋以来,对水运仪象台的研究与复原吸引了诸多学者的注意。
清华大学历代学人对水运仪象台研究作出了卓越贡献。20世纪50年代,清华大学刘仙洲教授率先对水运仪象台的结构原理进行了探索[1]。2000年以来,清华大学科技史暨古文献研究所在国家自然科学基金委的资助下,启动“水运仪象台工作原理的研究和复原试验”项目[2],在文献考证[3]、机械分析[4]等方面取得了一系列重大成就。2012年,清华大学机械工程系、中国科学院国家天文台和中国科学院自然科学史研究所联合进行了1∶3水运仪象台的复原,模型在第28届国际天文学联合会大会上展出。2019年,清华大学科学博物馆获得唐仲英基金会资助,开始1∶1模型的复原工作。建成后的水运仪象台模型将陈列于即将落成的清华大学科学博物馆大厅之中,成为清华大学向社会大众展示中国古代科技文化的重要窗口。
可以说,自从水运仪象台进入现代学界视野以来,就与清华大学产生了密不可分的联系。而在当前清华大学科学博物馆进行水运仪象台复原的工作中,选择何种复原方案成为首先需要考虑的问题。
据《新仪象法要》(以下简称《法要》)记载,枢轮是水运仪象台的核心装置,承担向其他机构输出动力的重要任务。目前,学界就枢轮结构形成了“翻斗”[5-10]和“定斗”[11-12]2种复原方案,前者主张受水壶可以独立于枢轮转动,后者认为受水壶必须固定在枢轮上,不能自由活动。
最新研究显示,作为翻斗方案核心部件的受水壶转轴不仅没有直接记载在《法要》中,而且其建立在Joseph Needam对《法要》关键术语的错误翻译的基础上;“定斗”的关键部件亦缺乏文献依据[13]。因此,与原文的符合程度,不宜再被视作判定复原方案优劣的唯一标准。新的复原模型也就不能只是简单地遵从其中某一种方案进行,而应当从不同方案中去芜存菁。
从博物馆展陈的角度来说,复原模型能否长期可靠地运行,是选取方案时的重要考量因素。目前学界尚无此类研究。鉴于此,本文尝试通过计算对比各部件在2种方案中的受力大小,以判断何种设计有助于保持更长时间的稳定运行,从而为复原工作提供更多参考。
1 结构原理与计算方法 1.1 定斗方案枢轮的结构原理定斗方案枢轮结构的简化示意如图 1所示。

|
| 1—右天锁;2—天衡;3—天关;4—左天锁;5—天条;6—水管;7—格叉;8—固定式受水壶,9—关舌;10—枢轴 图 1 定斗方案示意图 |
在定斗方案中,枢轮静止时枢轮右下部分各受水壶内的水产生了促使枢轮转动的力矩。但是,由于格叉阻挡,枢轮无法转动。左天锁保持打开状态,不与枢轮接触。
随着水流注入,最右侧受水壶内的水量逐渐增加,所有受水壶内的水对枢轴产生的总转矩逐渐增大,枢轮作用在格叉上的力也逐渐增大,最终超过设定的格叉受力阈值,平衡被打破,枢轮压下格叉而发生转动。
在枢轮转动过程中,枢轮受到关舌、天关产生的缓冲作用;而当枢轮拨动关舌时,关舌经由天条、天衡等部件拉动左天锁,使左天锁下落进入关闭状态。于是,当枢轮与天关脱离接触之后,经过一小段距离,就会撞击到已处于关闭状态的左天锁,并在左天锁的阻挡下发生反转,最终在右天锁的阻挡下回到静止状态。左天锁在和枢轮脱离接触之后,迅速回到打开状态。
1.2 翻斗方案枢轮的结构原理翻斗方案枢轮结构的简化示意如图 2所示。

|
| 1—右天锁;2—天衡;3—天关;4—左天锁;5—天条;6—水管;7—格叉;8—翻斗式受水壶;9—关舌;10—枢轴 图 2 翻斗方案示意图 |
在翻斗方案中,枢轮静止时,枢轮右下部分各受水壶内的水产生了促使枢轮转动的力矩。但是,由于左天锁抵住了轮辐,枢轮无法转动。最右侧的可绕轴转动的受水壶被格叉阻挡,也无法转动。此时天关在枢轮之上,没有与枢轮接触。
随着水流注入,最右侧受水壶内的水量逐渐增加,该受水壶内的水对转轴产生的转矩逐渐增大,作用在格叉上的力也逐渐增大,最终超过设定的格叉受力阈值,平衡被打破,该受水壶独自压下格叉而发生转动。
在该受水壶转动过程中,受水壶拨动关舌;关舌经由天条、天衡等部件拉动左天锁,使左天锁抬起进入打开状态,枢轮不再受到左天锁的阻挡。于是,枢轮在所有受水壶内的水对枢轴产生的转矩作用下发生转动。与此同时,天关因天衡的作用,其右半部分下落。
在枢轮转动过程中,最上方的一条轮辐会先拨动天关的右半部分,经由天关、天衡帮助左天锁及时下落进入关闭状态。于是,当枢轮与天关脱离接触之后,最上方的轮辐就会撞击已处于关闭状态的左天锁,并在左天锁的阻挡下发生反转,最终在右天锁的阻挡下回到静止状态。
1.3 计算方法在2种方案中,与枢轮直接接触的部件均为格叉、关舌、天关和左天锁。格叉、关舌和天关是有受力阈值的机构,一旦受力超过设定的阈值,它们就会自动让开,这样机构不易受损,并且这3个部件在2种方案中的功能也不尽相同。因此,本文不将这3个部件的受力状况纳入比较。
左天锁在2种方案中的功能完全相同,即承受枢轮转动产生的冲击,促使枢轮停转。左天锁没有自动让开的机制,容易在碰撞时受损。左天锁一旦受损,枢轮就无法正常运转。因此,左天锁的受力情况能够较好地反映2种方案在运行稳定性上的差异。
此外,由于力的作用是相互的,左天锁所受来自枢轮的冲力,其大小等于左天锁对枢轮产生的冲力。因此分析左天锁的受力状况,最终又可以帮助分析枢轮的受力状况。
基于以上分析,本文将计算目标确定为左天锁的受力数据。要获得该数据,必须先得到枢轮在不同时刻的转矩。由于枢轮为中心对称结构,自身重力对枢轴产生的合转矩为零。因此,促使枢轮转动的转矩,仅由两侧不平衡分布的水提供。为此,本文先计算枢轮处于不同状态时水所产生的转矩,随后结合刚体定轴转动的相关定理计算左天锁的受力数值。
1.4 参数设定本文按照1∶1的比例在软件中建立2种方案的模型,并按照古尺标准,即1尺=314 mm对《法要》中的尺寸数进行换算[14]。与格叉、关舌、天关和左天锁相关的参数下标字母分别为b、c、d和e。
1) 在2种方案中均适用的参数。
格叉与枢轮受水壶接触点到轴心的水平方向距离Xb=1 727 mm。关舌与受水壶接触点到枢轴的水平方向距离Xc=1 701 mm。天关与枢轮接触点到枢轴的垂直方向距离Yd=1 727 mm。左天锁与枢轮接触点到枢轴的垂直方向距离Ye=1 701 mm。
受水壶长度l=314 mm,满水时水的质量m=4.738 kg,重力加速度g=9.8 N/kg。
本文计算比较的对象是左天锁,为公平计,将定斗方案左天锁作用时间te1和翻斗方案左天锁作用时间te2均设为0.5 s。
2) 适用于定斗方案的参数。
本文不比较格叉、关舌和天关的受力情况,但这3个部件会对定斗方案中处于转动状态的枢轮施加反向力矩,影响左天锁所受冲力的计算结果。并且,关舌和天关的阻力在定斗方案中可以调整。因此,需要且可以对三者做设定。本文设定在定斗方案中,格叉作用时间tb1=1 s;关舌阻力Fc1=20 N,作用时间为tc1=2 s;天关阻力Fd1=150 N,作用时间td1=2 s。关舌和天关同时作用于枢轮上。
3) 适用于翻斗方案的参数。
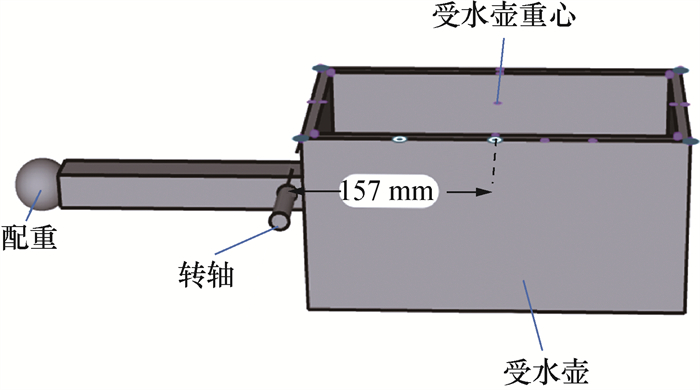
翻斗式受水壶(见图 3)在靠近枢轮一端带有配重。未注水时,受水壶及配重整体的重心恰好在转轴位置,因此受水壶能保持平衡姿态。也就是说,受水壶和配重对于转轴的合力矩恒为0,因此,促使受水壶发生绕轴转动的力矩全部来自于水。
|
| 图 3 翻斗式受水壶示意图 |
受水壶重心在自身中心位置。转轴在受水壶一端,与受水壶重心的距离d=157 mm(忽略转轴到受水壶侧面之间的微小距离)。受水壶每次转动时所经过的角度θ=10°。
翻斗方案中,在受水壶压下格叉、击打关舌之后,枢轮才开始转动。因此,无须考虑格叉、关舌阻力对枢轮转动产生的影响。但是,二者的作用时间会影响枢轮转动时间。出于公平考虑,将翻斗方案的格叉作用时间tb2和关舌作用时间tc2设为与定斗方案一致,即tb2=1 s, tc2=2 s。翻斗方案的天关没有缓冲作用,对枢轮的阻力可忽略不计,Fd2=0 N。
2 2种方案的受力分析 2.1 定斗方案受力分析1) 枢轮运动过程水产生的转矩计算。
在定斗方案中,为了确定水对枢轮产生的转矩变化情况,把枢轮运动过程分为2种状态:1) 1号受水壶未被注入水时,总转矩为最小值;2) 1号受水壶刚注满水、枢轮即将发生运动时,总转矩为最大值。计算结果如表 1所示。
| 受水壶序号 | 状态1 | 状态2 | |||
| 质量/kg | 距离/mm | 质量/kg | 距离/mm | ||
| 1 | 0 | 0 | 4.738 | 1 570 | |
| 2 | 3.664 | 1 546 | 3.664 | 1 546 | |
| 3 | 2.521 | 1 475 | 2.521 | 1 475 | |
| 4 | 1.596 | 1 360 | 1.596 | 1 360 | |
| 5 | 1.098 | 1 203 | 1.098 | 1 203 | |
| 6 | 0.773 | 1 009 | 0.773 | 1 009 | |
| 7 | 0.532 | 785 | 0.532 | 785 | |
| 8 | 0.335 | 537 | 0.335 | 537 | |
| 9 | 0.162 | 273 | 0.162 | 273 | |
| 总质量/kg | 10.681 | 15.419 | |||
| 总转矩/(N·mm) | 140 102 | 213 001 | |||
| 注:表 1—2中“质量”表示相应受水壶中水的质量;“距离”表示相应受水壶到枢轴的水平方向距离。 | |||||
| 受水壶序号 | 状态1 | 状态2 | 状态3 | |||||
| 质量/kg | 距离/mm | 质量/kg | 距离/mm | 质量/kg | 距离/mm | |||
| 1 | 0 | 0 | 4.738 | 1 570 | 3.664 | 1 570 | ||
| 2 | 2.521 | 1 546 | 2.521 | 1 546 | 2.521 | 1 546 | ||
| 3 | 1.596 | 1 475 | 1.596 | 1 475 | 1.596 | 1 475 | ||
| 4 | 1.098 | 1 360 | 1.098 | 1 360 | 1.098 | 1 360 | ||
| 5 | 0.773 | 1 203 | 0.773 | 1 203 | 0.773 | 1 203 | ||
| 6 | 0.532 | 1 009 | 0.532 | 1 009 | 0.532 | 1 009 | ||
| 7 | 0.335 | 785 | 0.335 | 785 | 0.335 | 785 | ||
| 8 | 0.162 | 537 | 0.162 | 537 | 0.162 | 537 | ||
| 9 | 0 | 273 | 0 | 273 | 0 | 273 | ||
| 总质量/kg | 7.017 | 11.755 | 10.681 | |||||
| 总转矩/(N·mm) | 93 703 | 166 602 | 150 077 | |||||

|
| 图 4 定斗方案受水壶序号示意图 |
计算结果显示,在定斗方案中,枢轮处于状态1时,总转矩为最小值(M1min)为140 102 N·mm,枢轮处于状态2时,总转矩为最大值(M1max)为213 001 N·mm。
2) 各机构受力计算。
在定斗方案中,每个运动周期时长T1=48 s。在第43 s时,枢轮突破平衡开始转动,在转动过程中受到格叉、关舌、天关的阻力。枢轮与关舌、天关脱离接触后,又经过1.5 s才撞击左天锁。设左天锁所受冲力为Fe1。
格叉要抵消枢轮静止时水的总转矩,需满足
| $ \boldsymbol{F}_{\mathrm{b}_1} \cdot X_{\mathrm{b}}=\boldsymbol{M}_{1_{\max }} $ | (1) |
其中:格叉阻力为123.34 N。要使枢轮最终回到
静止状态,需要枢轮所受合冲量矩为0,即
| $ \overline{\boldsymbol{M}}_1 \Delta t_1-\boldsymbol{M}_{\mathrm{b}_1} t_{\mathrm{b}_1}-\boldsymbol{M}_{\mathrm{c}_1} t_{\mathrm{c}_1}-\boldsymbol{M}_{\mathrm{d}_1} t_{\mathrm{d}_1}-\boldsymbol{M}_{\mathrm{c}_1} t_{\mathrm{c}_1}=\mathbf{0}, $ | (2) |
| $ \overline{\boldsymbol{M}}_1=\left(\boldsymbol{M}_{1_{\min }}+\boldsymbol{M}_{1_{\max }}\right) /2, $ | (3) |
| $ \boldsymbol{M}_{\mathrm{b}_1}=\boldsymbol{F}_{\mathrm{b}_1} \cdot X_{\mathrm{b}}, $ | (4) |
| $ \boldsymbol{M}_{\mathrm{c}_1}=\boldsymbol{F}_{\mathrm{c}_1} \cdot X_{\mathrm{c}}, $ | (5) |
| $ \boldsymbol{M}_{\mathrm{d}_1}=\boldsymbol{F}_{\mathrm{d}} \cdot Y_{\mathrm{d}}, $ | (6) |
| $ \boldsymbol{M}_{\mathrm{e}_1}=\boldsymbol{F}_{\mathrm{e}_1} \cdot Y_{\mathrm{e}} . $ | (7) |
其中:Δt1=5 s为枢轮转动时间;M1为该时间内水产生的平均转矩,用M1min和M1max的算术平均值近似代替计算。Mb1、Mc1、Md1和Me1分别为格叉、关舌、天关和左天锁对枢轴产生的转矩。根据式(3)—(7)解得左天锁所受冲力为98.31 N。
2.2 翻斗方案受力分析1) 枢轮运动过程水产生转矩的计算。
在翻斗方案中,为了确定水产生的转矩变化情况,把枢轮运动过程分为3种状态:1) 1号受水壶内还未注入水时;2) 1号受水壶刚注满水即将转动时;3) 1号受水壶刚结束转动、枢轮即将开始转动时。
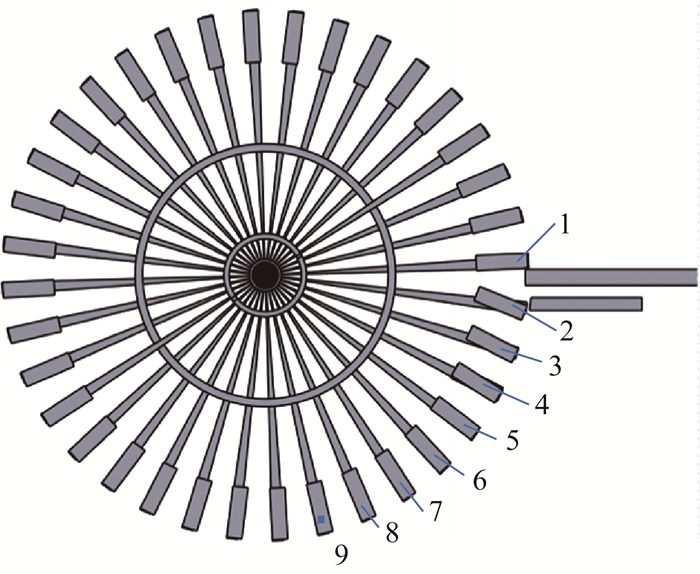
受水壶转矩计算结果如表 2所示,翻斗方案示意图如图 5所示。
|
| 图 5 翻斗方案受水壶序号示意图 |
计算结果显示,在翻斗方案中,枢轮即将开始转动时,所受总转矩为150 077 N·mm。枢轮每次转动结束时,所受总转矩为93 703 N·mm。二者的算术平均值为121 890 N·mm。
2) 各机构受力计算。
在翻斗方案中,每个运动周期时长T2=48 s。在第43 s,受水壶突破平衡,并依次受到格叉、关舌的作用力。格叉作用时长tb2=1 s,关舌作用时长tc2=2 s。受水壶冲击关舌后停止转动,同时天关和左天锁升起,枢轮开始转动。枢轮转动时间Δt2=2 s。
格叉阻力Fb2由单个满水受水壶内的水产生的转矩Mf决定,表示如下:
| $ \boldsymbol{F}_{\mathrm{b}_2} \cdot l=\boldsymbol{M}_{\mathrm{f}}, $ | (8) |
| $ \boldsymbol{M}_{\mathrm{f}}=m \cdot \boldsymbol{g} \cdot d $ | (9) |
解得Fb2大小为23.22 N。
左天锁所受冲击力Fe2可由冲量定理计算得到,表示如下:
| $ \overline{\boldsymbol{M}}_2 \Delta t_2-\boldsymbol{M}_{\mathrm{e}_2} t_{\mathrm{e}_2}=\mathbf{0}, $ | (10) |
| $ \boldsymbol{M}_{\mathrm{e}_2}=\boldsymbol{F}_{\mathrm{e}_2} \cdot \boldsymbol{Y}_{\mathrm{e}} . $ | (11) |
其中:M2为枢轮转动过程中水产生的平均转矩,用枢轮在状态3和状态1下所受总转矩的算术平均值近似代替计算,大小为121 890 N·mm。
解得Fe2大小为286.63 N。
3 结论对2种方案结构原理的考察表明,在各部件中,左天锁最能够准确反映2种方案的运行稳定性差异,因此本文最终选取左天锁作为分析对象。
计算结果显示,翻斗方案的左天锁每次撞击枢轮时所受的力为286.63 N,定斗方案为98.31 N,前者数值约为后者的3倍。造成这一结果的原因是:对于定斗方案,在枢轮转动过程中,经过格叉、关舌、天关的缓冲作用,枢轮的冲量矩已被大量消耗。因此,枢轮撞击左天锁前瞬间的冲量矩已经很小,左天锁所承受的冲力也就很小。翻斗方案中没有这些部件的缓冲作用,因而使左天锁受到的冲力较大。
由于力的作用是相互的,所以左天锁受到的冲力越大,对枢轮的反作用力就越大,进而影响枢轮的运行稳定性,而且在定斗方案中,左天锁撞击的是受水壶的底部;而在翻斗方案中,左天锁撞击的是枢轮一侧的轮辐边缘,否则每次左天锁的撞击导致的就是受水壶翻转而不是枢轮止动。这就使翻斗方案的轮辐撞击接触面积远小于定斗方案,进而导致枢轮在每次撞击左天锁时受到的压强要大得多,加剧了轮辐的变形损坏。左天锁还可以通过维修或更换来延长使用寿命,但枢轮一旦损坏,对水运仪象台运行稳定性的影响将难以挽回。
总之,由于缓冲部件、枢轮和左天锁接触面积等方面存在差异,使定斗方案中的枢轮和左天锁所受冲击更小,运行稳定性更好。新复原模型可以在吸纳定斗方案这一优点的基础上进行制作。
| [1] |
刘仙洲. 中国在计时器方面的发明[J]. 清华大学学报(自然科学版), 1957, 3(2): 57-70. LIU X Z. On Chinese invention of time-keeping apparatus[J]. Journal of Tsinghua University (Science and Technology), 1957, 3(2): 57-70. (in Chinese) |
| [2] |
高宣. 水运仪象台工作原理的研究与复原试验工作[C]//机械技术史(3): 第三届中日机械技术史国际学术会议论文集. 昆明, 中国: 中国机械工程学会机械史分会, 2002: 274-279. GAO X. Work of principle research and reconstruction experiment on the astronomical clock tower[C]//History Mechanical Technology (3): Proceedings of the Third China-Japan International Conference on History of Mechanical Technology. Kunming, China: Chinese Mechanical Engineering Society Mechanical History Branch, 2002: 274-279. (in Chinese) |
| [3] |
刘蔷. 关于宋代水运仪象台的古文献综考[C]//机械技术史(3): 第三届中日机械技术史国际学术会议论文集. 昆明, 中国: 中国机械工程学会机械史分会, 2002: 265-273. LIU Q. Research on the ancient documents of the astronomical clock tower of Song Dynasty[C]//History of Mechanical Technology (3): Proceedings of the Third China-Japan International Conference on History of Mechanical Technology. Kunming, China: Chinese Mechanical Engineering Society Mechanical History Branch, 2002: 265-273. (in Chinese) |
| [4] |
高瑄, 陆震, 王春洁, 等. 利用仿真技术对古代水力机械的复原实验[J]. 清华大学学报(自然科学版), 2006, 46(11): 1801-1804. GAO X, LU Z, WANG C J, et al. Simulations of the mechanics of ancient hydraulic machines[J]. Journal of Tsinghua University (Science and Technology), 2006, 46(11): 1801-1804. DOI:10.3321/j.issn:1000-0054.2006.11.001 (in Chinese) |
| [5] |
COMBRIDGE J H. The celestial balance: A practical reconstruction[J]. Horological Journal, 1962(104): 82-86. |
| [6] |
COMBRIDGE J H. The Chinese water-balance escapement[J]. Nature, 1964, 204(4964): 1175-1177. DOI:10.1038/2041175a0 |
| [7] |
NEEDHAM J. Science and civilization in China[M]. Cambridge: Cambridge University Press, 1965.
|
| [8] |
胡维佳. 《新仪象法要》中的"擒纵机构"和星图制法辨正[J]. 自然科学史研究, 1994, 13(3): 244-253. HU W J. On the "escapement" and star-mapping in the Xin Yi Xiang Fa Yao[J]. Studies in the History of Natural Sciences, 1994, 13(3): 244-253. (in Chinese) |
| [9] |
胡维佳. 宋代水运仪象台研究与复原中的两个问题[J]. 自然科学史研究, 2007, 26(3): 449-454. HU W J. New problems in the study and reconstruction of the Song Dynasty water-powered armillary sphere and celestial globe tower[J]. Studies in the History of Natural Sciences, 2007, 26(3): 449-454. (in Chinese) |
| [10] |
张柏春, 张久春. 水运仪象台复原之路: 一项技术发明的辨识[J]. 自然辩证法通讯, 2019, 41(4): 43-51. ZHANG B C, ZHANG J C. A review of the reconstruction of the Astronomical Clock-tower[J]. Journal of Dialectics of Nature, 2019, 41(4): 43-51. (in Chinese) |
| [11] |
李志超. 水运仪象志[M]. 合肥: 中国科学技术大学出版社, 1997. LI Z C. The astronomical clock tower summarization[M]. Hefei: University of Science and Technology of China Press, 1997. (in Chinese) |
| [12] |
唐乐为, 唐晓强, 李铁民, 等. 宋代水运仪象台天柱系统传动特性[J]. 清华大学学报(自然科学版), 2014, 54(11): 1497-1501. TANG L W, TANG X Q, LI T M, et al. Driving characteristics of the transmission-shaft system in the Song Dynasty astronomical clock tower[J]. Journal of Tsinghua University (Science and Technology), 2014, 54(11): 1497-1501. (in Chinese) |
| [13] |
徐思源, 王哲然. 水运仪象台两种复原方案探源[J]. 中国科技史杂志, 2023, 44(2): 264-273. XU S Y, WANG Z R. Revisiting the two approaches for the reconstruction of the driving-wheel in Su Song's astronomical clock-tower[J]. The Chinese Journal for the History of Science and Technology, 2023, 44(2): 264-273. (in Chinese) |
| [14] |
丘光明, 邱隆, 杨平. 中国科学技术史: 度量衡卷[M]. 北京: 科学出版社, 2001. QIU G M, QIU L, YANG P. The history of science and technology in China (metrology, weights and measures volume)[M]. Beijing: Science Press, 2001. (in Chinese) |



