随着混合动力车辆在国内的销量提升,用户对低噪声、低振动和高舒适性的需求越来越高,因此发动机抖动问题受到越来越多的关注。发动机的抖动问题多出现在发动机启动时刻,传统燃油车的发动机在原地启动后始终保持运行,产生的抖动影响较小;而混合动力车内的发动机启动时刻由整车控制策略决定,发动机启动时刻不仅会在原地启动工况出现,也会在加速工况出现,尤其是在电池电量较低、城市路况拥堵的情况下行驶时,为保持电池电量,发动机会频繁地由电动车(electric vehicles, EV)模式切换为混动车(hybrid electric vehicles, HEV)模式,让发动机介入发电。与燃油车相比,混动车因发动机介入而引起抖动问题出现的概率大,更易导致驾乘体验感下降。因此,研究混动车发动机介入抖动机理和解决方案,成为近年来国内外学者的热门研究课题。
Ohn等[1]研究了复合功率分流混动发动机原地介入抖动的产生原因,发现抖动激励源为气缸压力波动和点火后快速上升的发动机转矩,提出了减小空燃比、延迟点火等解决发动机介入抖动的方法。Kuang[2]发现,混动发动机启动过程中的抖动由气缸压力波动、点火后发动机转矩突变及电机补偿转矩不足或不合理引起。王博等[3]对混动车辆原地发动机点火瞬间车身抖动问题开展了实验研究,发现进气压力和点火角是影响发动机点火瞬间输出转矩的主要因素。胡云峰等[4]设计了发动机启停控制器,通过优化发动机启动控制策略解决发动机原地启动冲击问题。在车型开发前期阶段,石岩等[5]利用实验设计(design of experiment, DOE)软件优化悬置橡胶衬套设计,研究了该优化设计对发动机介入抖动的控制方法。王道勇等[6]从悬置设计角度出发,研究了发动机启停时动力总成悬置系统的设计方法。
上述研究中的发动机介入抖动出现在发动机点火后[1-6],而混动发动机介入抖动现象常出现于集成启动发电一体化发电机(integrated starter generator, ISG)倒拖发动机阶段。此外,已有研究多聚焦于混动发动机原地启动引起的整车抖动问题,而对混动车辆加速过程中发动机介入引起抖动的问题关注较少。而混动车辆在加速过程发动机介入瞬间,车辆受驱动电机扭矩作用,使总成的刚体模态和悬置隔振特性完全不同于原地发动机介入工况,其抖动产生源头和传递路径的作用机理都更复杂。
本文针对某混动运动型多用途汽车(sport utility vehicle,SUV)加速工况发动机介入引起的整车抖动问题开展了实验研究和仿真分析,研究了该工况下发动机介入抖动的源头机理和传递路径作用机制,提出了相应的解决方案,并结合主观评价和整车实验验证了解决方案有效。
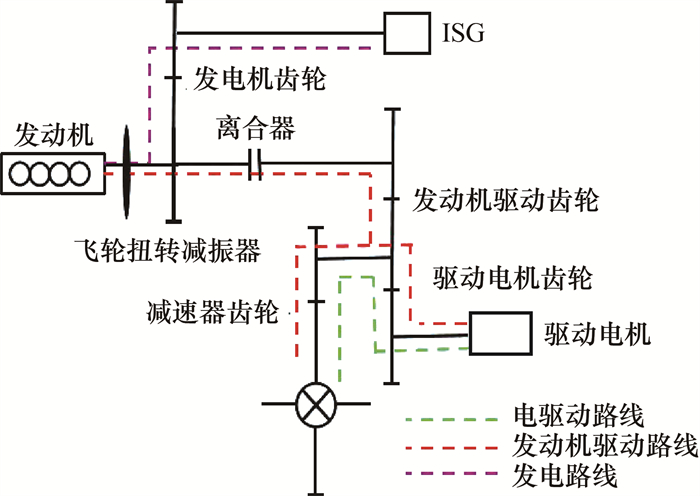
1 混动总成发动机介入抖动的理论分析混动总成结构原理如图 1所示。ISG通过发电机齿轮与混动变速箱输入轴连接,混动变速箱输入轴左侧通过飞轮扭转减振器与发动机曲轴连接。在发动机介入过程中,发动机由ISG通过发电机齿轮反向拖动介入,在此过程中发动机离合器处于断开状态,发动机不参与驱动整车。该混动发动机为一台直列4缸1.5 L排量的自然吸气汽油机,为获得低油耗,采用具有高压缩比(ε=15.5)的Atkinson循环技术。
|
| 图 1 混动总成结构原理 |
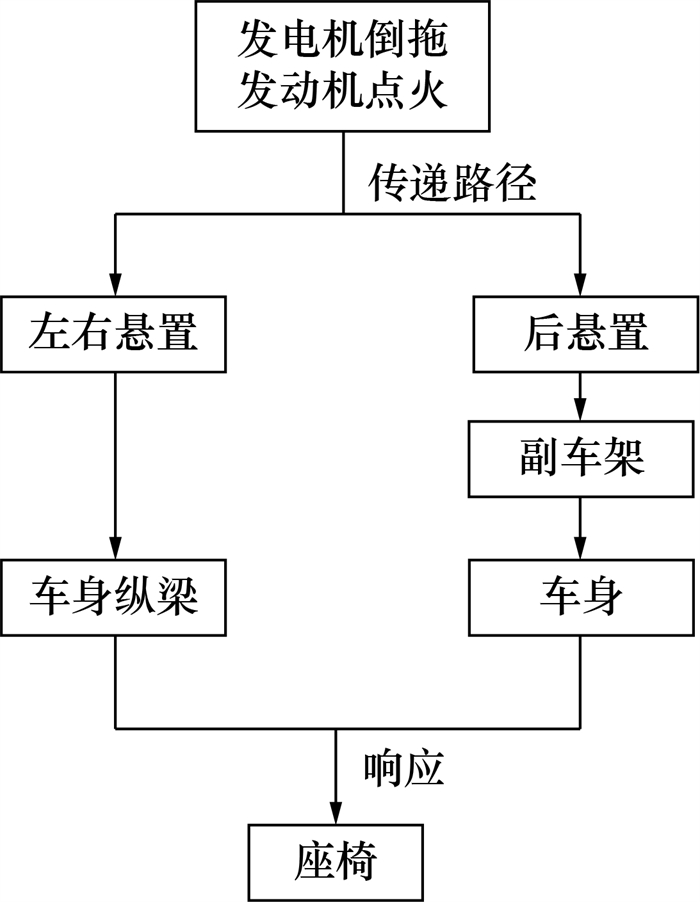
发动机介入抖动的源头-传递路径-响应模型如图 2所示,激励源为混动总成的启动激励扭矩,激励扭矩使总成产生扭转振动后,通过3个动力总成悬置传递至车身和座椅导轨。
|
| 图 2 发动机介入抖动的源头-路径-响应模型 |
1.1 混动总成扭转动力学模型
混动总成启动激励扭矩主要为气缸压力扭矩,往复惯性激励扭矩影响很小,可忽略不计。发动机单缸气缸压力扭矩Tg表示如下:
| $ T_{\mathrm{g}}=\frac{{\rm{\mathsf{π}}} D^2}{4} p_{\mathrm{g}} r \frac{\sin (\alpha+\beta)}{\cos \beta} . $ | (1) |
其中:D为发动机气缸直径;r为曲柄半径;pg为气缸压力;α为相对于上止点的曲柄转角;β为连杆摆角。
对于点火顺序为1-3-4-2的直列四缸发动机,第3、4、2缸的气缸压力相对于第1缸的气缸压力分别存在π、2π、3π的相位差。
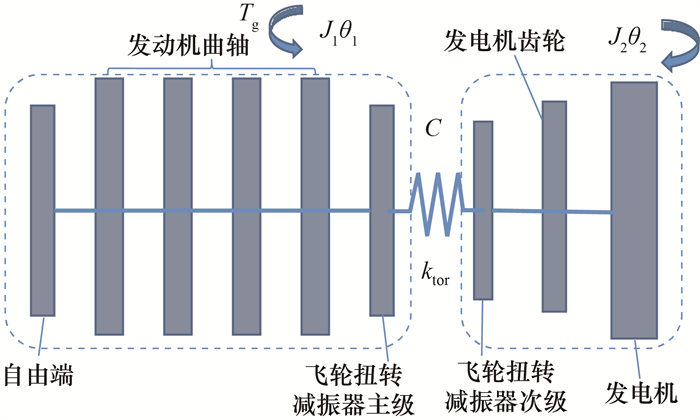
在发动机介入工况下,离合器始终处于断开状态,因此仅对发动机-飞轮扭转减振器-发电机系统建立动力学模型。图 3为发动机介入工况下混动总成等效动力学模型。其中:C和ktor分别为飞轮扭转减振器的阻尼系数和扭转刚度;θ1和θ2分别为飞轮扭转减振器主级侧和次级侧的扭转角;将发动机曲轴系统、飞轮扭转减振器主级的惯量等效为转动惯量J1,即飞轮扭转减振器主级侧的转动惯量;将飞轮扭转减振器次级、发电机齿轮和发电机的惯量等效为转动惯量J2,即飞轮扭转减振器次级侧的转动惯量。
|
| 图 3 发动机介入工况下混动总成等效动力学模型 |
基于该模型,建立的双质量扭振系统动力学方程表示如下:
| $ \left\{\begin{array}{l} J_1 \ddot{\theta}_1-C\left(\dot{\theta}_1-\dot{\theta}_2\right)-k_{\text {tor }}\left(\theta_1-\theta_2\right)=T_{\mathrm{g}}, \\ J_2 \ddot{\theta}_2+C\left(\dot{\theta}_1-\dot{\theta}_2\right)+k_{\text {tor }}\left(\theta_1-\theta_2\right)=0 . \end{array}\right. $ | (2) |
其中:
不考虑阻尼的影响,则由式(2)可近似求得该系统的扭转模态频率ftor,表示如下:
| $ f_{\text {tor }}=\frac{1}{2 {\rm{\mathsf{π}}}} \sqrt{k_{\text {tor }}\left(\frac{1}{J_1}+\frac{1}{J_2}\right)} . $ | (3) |
由式(3)可知,上述双质量扭振系统的模态频率由J1、J2和ktor决定。通过调整ktor,可以改变传动系扭转模态频率,通常一阶扭转模态频率均在0~20.0 Hz[7]。
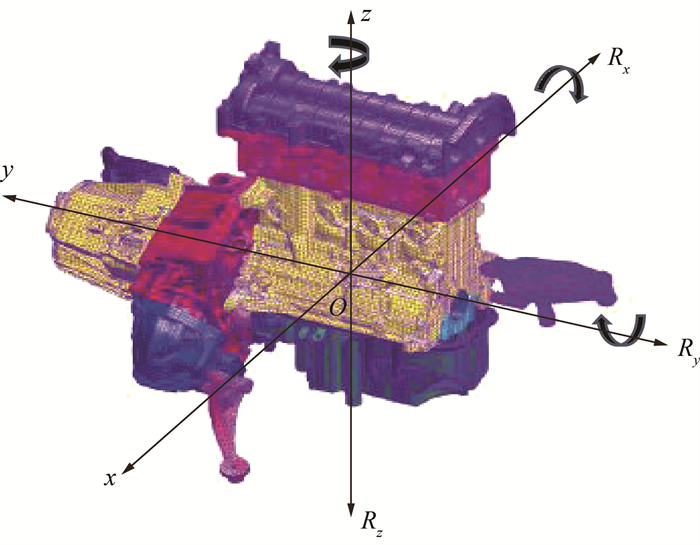
1.2 动力总成刚体动力学模型动力总成和悬置构成的装配体具有六自由度低频刚体模态,分别为沿x、y、z轴方向的平动和绕x、y、z轴方向的转动(即Rx向、Ry向和Rz向),动力刚体模态示意图如图 4所示。
|
| 图 4 动力刚体模态示意图 |
动力总成和悬置组成的六自由度无阻尼自由振动线性微分方程表示如下:
| $ \boldsymbol{M} \ddot{\boldsymbol{q}}+\boldsymbol{K} \boldsymbol{q}=\mathbf{0} $ | (4) |
其中:M为动力总成的质量矩阵,q为整车坐标系的位移列向量,
由式(4)可知,动力总成刚体模态与动力总成质量、惯量张量、悬置橡胶衬套刚度和悬置安装位置相关。其中,悬置的位置和刚度是决定动力总成刚体模态的主要因素,当悬置刚度增大时,动力总成刚体模态频率会增大。动力总成刚体模态频率通常为5.0~25.0 Hz[8],因此传动系扭转模态易与动力总成刚体模态发生耦合作用。
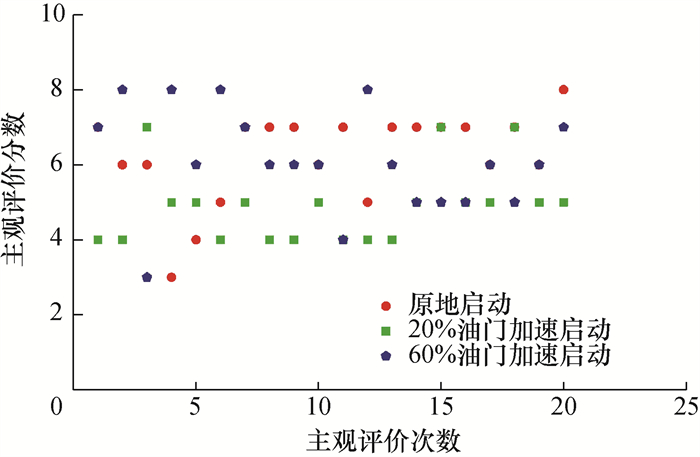
2 问题现象描述和实验方案设计电池荷电状态(state of charge, SOC) 指电池当前电量与最大容量的比值。该混动车型处于低电量状态(SOC约为18%),以小油门(约20%油门深度)从原地开始加速,首先靠驱动电机起步,当加速至车速约20 km/h时,ISG反向拖动发动机介入工作,在发动机介入瞬间,整车存在明显抖动冲击感,驾驶员侧抖动强烈,主观体验极差。图 5为各种工况下的主观评价分数记录,其中6分以下为不能接受,7分以上为较好水平。通过多次主观评价发现,该抖动现象的量级存在随机性,有时抖动较大、有时抖动较小。此外,在主观评价中还发现,原地启动或者以60%油门加速启动时,发动机介入时整车抖动都较轻微。
|
| 图 5 主观评价分数记录 |
为分析上述问题的机理,本文设计了如下实验。实验对象为搭载上述混动总成的一台SUV。在实验开始前通过原地发电模式,对发动机进行充分热机,使发动机水温达90 ℃以上,同时控制电池SOC约为18%。实验过程分别设置3种工况,具体设置如表 1所示,每个工况各采集20组数据。
| 工况 | 工况设置 |
| 原地启动 | 原地启动发动机 |
| 20%油门加速启动 | 从原地开始,快速踩下油门踏板至20%深度,保证整车加速至40 km/h后停止 |
| 60%油门加速启动 | 从原地开始,快速踩下油门踏板至60%深度,保证整车加速至40 km/h后停止 |
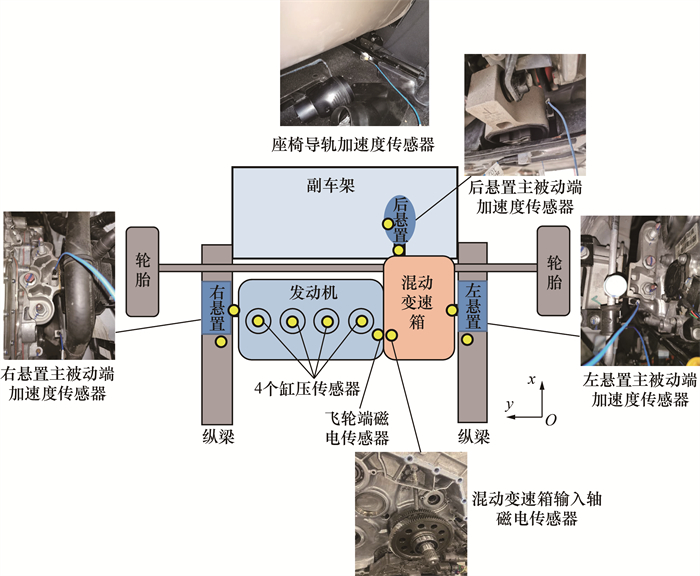
实验测点布置和实际测点照片如图 6所示。在混动总成的曲轴侧和发电机附近布置磁电传感器,用于测试曲轴和发电机的扭振特性;在发动机的4个缸安装缸压传感器,用于测试发动机的燃烧激励特性。该混动系统的悬置布置形式为三点钟摆式,左悬置和右悬置布置在纵梁上方,后悬置布置在副车架上方。在混动总成的3个悬置的主动端和被动端布置了加速度传感器,用于测试总成振动的传递特性。在座椅导轨上布置加速度传感器,用于测试座椅的响应特性。此外,实验过程中通过控制器局域网络(controller area network,CAN)信息采集了发动机扭矩、发电机扭矩和驱动电机扭矩。
|
| 图 6 实验测点布置和实际测点照片 |
3 结果与分析
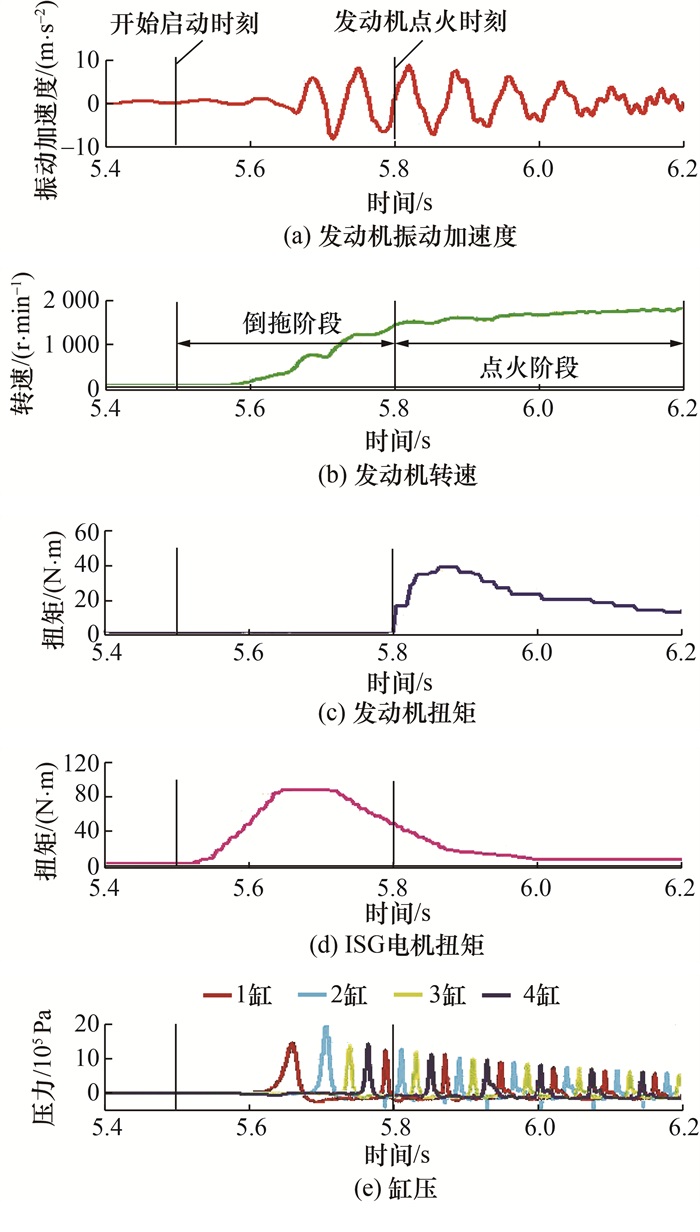
由于发动机介入瞬间各点的振动时域数据包含非发动机主阶频率成分,因此对信号进行5~30 Hz滤波处理。图 7为20%油门加速启动工况下发动机介入抖动的一组测试结果。可以看出,ISG开始倒拖发动机时发动机并未点火,在倒拖阶段中,该发动机采用了超高压缩比(ε=15.5),缸内残余气体被压缩后产生较高的缸压,导致发动机产生剧烈的振动;当发动机被ISG拖至一定转速后,ISG开始卸载扭矩,发动机开始点火、正向带动ISG工作。由图 7可以看出,最高缸压出现在倒拖阶段,而非点火阶段。
|
| 图 7 20%油门加速启动工况下发动机介入抖动测试结果 |
3.1 发动机介入抖动量级的随机性机理
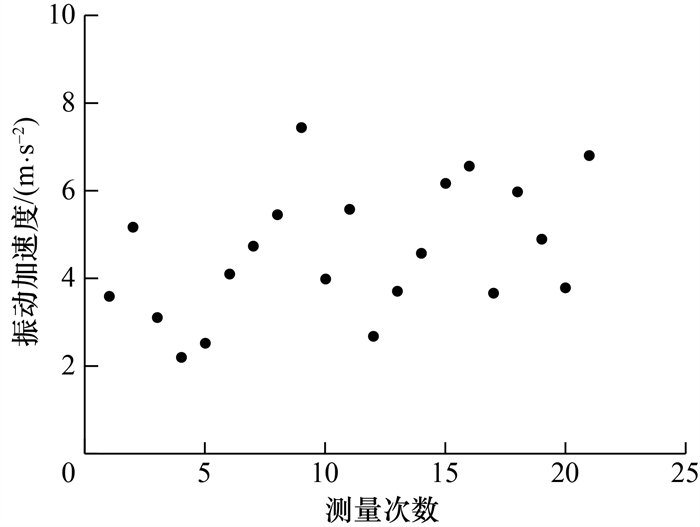
对20%油门加速启动工况下发动机介入抖动的20组数据进行了统计,20次测试下发动机振动与测量次数关系如图 8所示。可以看出,随着采集次数变化,发动机介入抖动的量级存在波动,抖动量级呈随机性。
|
| 图 8 20次测试下发动机振动与测量次数关系 |
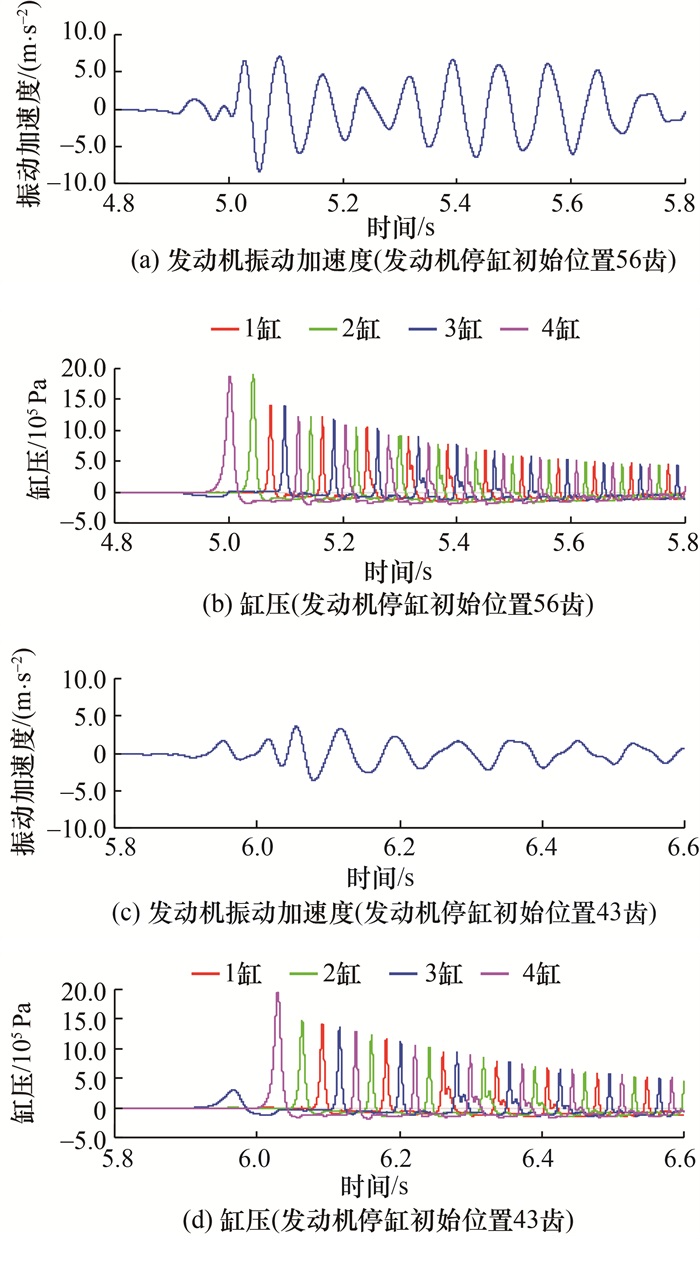
为了分析发动机介入抖动量级具有随机性的原因,选取抖动量级差异较大的2组数据(第4组和第9组)进行深入分析。图 9为20%油门加速启动工况下发动机介入抖动的发动机振动与缸压的关系,其中图 9a和9b的发动机停缸初始位置为56齿,图 9c和9d的发动机停缸初始位置为43齿。可以看出,发电机反拖发动机介入瞬间,二者的第一循环缸压存在明显差异;第一循环缸压的峰值越大,则发动机振动的幅值越大,表明发动机介入瞬间第一循环缸压的大小决定抖动量级。在发动机介入瞬间,发动机并未点火,因此第一循环缸压激励不是由燃烧产生的,而是由活塞压缩缸内气体产生的。据此推测,第一循环缸压的差异造成两者的初始停缸位置差异。
|
| 图 9 20%油门加速启动工况下发动机介入抖动的发动机振动与缸压的关系 |
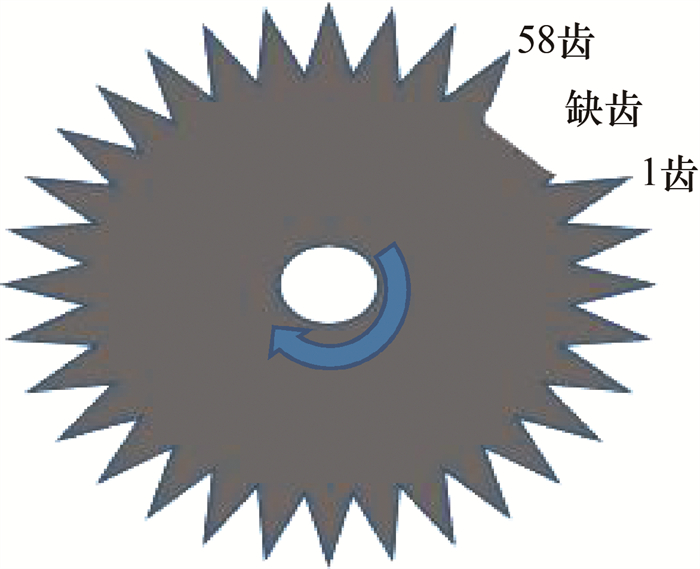
通过曲轴位置传感器信号判断发动机的初始停缸位置。图 10为曲轴位置信号盘示意图,信号盘原有58个齿,每2个齿之间代表曲轴转角为6°。
|
| 图 10 曲轴位置信号盘示意图 |
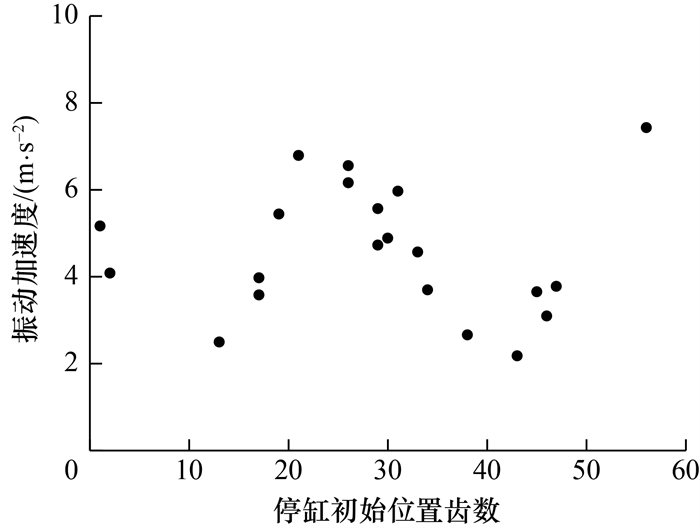
将图 8中20组数据的横坐标转化为停缸初始位置齿数,获得的20次测试下发动机振动与停缸初始位置关系如图 11所示。可以看出,发动机介入抖动的量级随曲轴齿位呈正弦规律变化:在58和30齿附近抖动量级较大,在15和45齿附近抖动量级较小。
|
| 图 11 20次测试下发动机振动与停缸初始位置关系 |
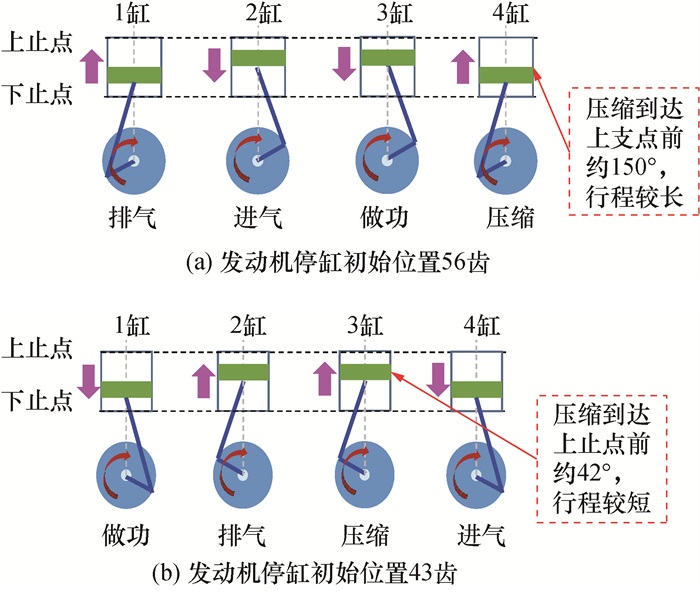
图 12为发动机停缸初始位置分别为56和43齿的活塞运行原理图。可以看出,当发动机停缸初始位置在56齿时,第4缸处于压缩行程初期,离压缩上止点150°,此时压缩行程较长,因此造成第一循环缸压的峰值较大,如图 12a所示;当发动机停缸初始位置在43齿时,第3缸处于压缩行程末期,离压缩上止点42°,此时压缩行程较短,造成第一循环缸压的峰值较低,如图 12b所示。
|
| 图 12 不同发动机停缸初始位置下的活塞运行原理图 |
综上可知,发动机停缸初始位置决定了第一循环缸压的峰值大小,当第一个处于压缩行程气缸的活塞位置离上止点越远时,压缩行程越长,第一循环缸压峰值越大,反之亦然。第一循环缸压峰值越大,则发动机介入抖动量级越大。但发动机每次启动时,发动机停缸初始位置是随机的,因此难以通过控制发动机第一循环缸压峰值来减小发动机介入抖动量级。
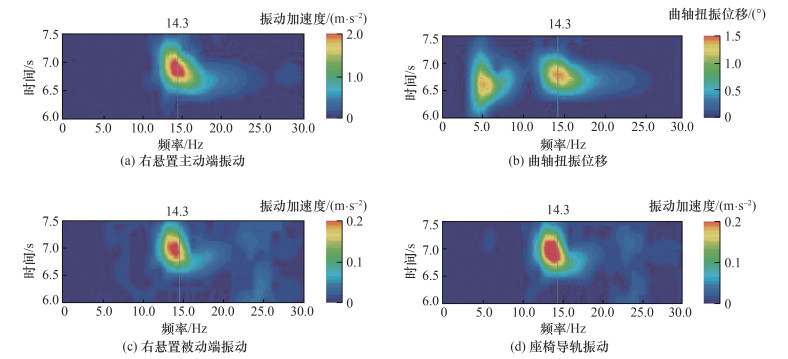
3.2 发动机介入抖动的模态耦合机理 3.2.1 发动机介入抖动的频域分析为了分析振动的激励频率,需要对以上采集的时域数据进行Fourier变换处理,转化为频域数据。将第9组测试数据的右悬置主被动端振动、曲轴扭振位移和座椅导轨振动转化为频域,如图 13所示。
|
| 图 13 20%油门加速启动工况下的右悬置主被动端振动、曲轴扭振位移和座椅导轨振动 |
从图 13中可以看出,右悬置主被动端振动、座椅导轨振动和曲轴扭振位移的峰值频率均出现在14.3 Hz附近。因此,本文推测,机理为动力总成刚体模态和传动系扭转模态耦合,导致座椅导轨振动大。
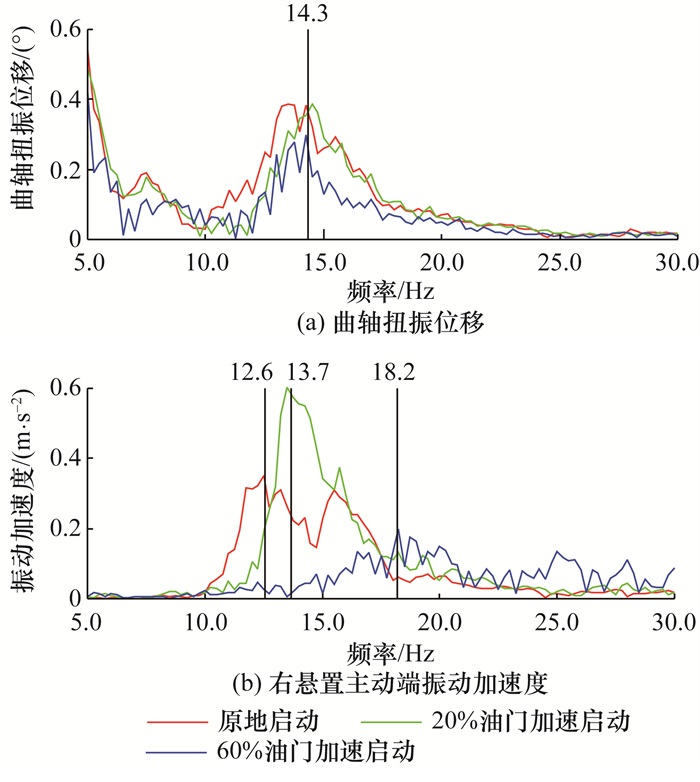
3.2.2 传动系扭转模态及动力总成刚体模态的耦合分析由图 5主观评价结果可知,原地启动或者60%油门加速启动工况下,发动机介入时整车抖动都较20%油门加速启动工况下轻微。因此,选取了原地启动、20%油门加速启动和60%油门加速启动这3种工况下的相同停缸初始位置的数据进行对比分析。图 14为3种工况下发动机介入抖动的频域分析。可以看出,3种工况下曲轴扭振位移的峰值频率都处于14.3 Hz附近,且峰值频率变化较小,推测该频率为传动系扭转模态频率。采用式(3)进行计算,传动系扭转模态频率为14.4 Hz,与实测结果吻合较好。
|
| 图 14 3种工况下发动机介入抖动的频域分析 |
由图 14还可以发现,20%油门加速启动工况下发动机振动峰值频率(13.7 Hz)和传动系扭转模态频率(14.3 Hz)最接近,因此20%油门加速启动工况下发动机振动峰值最大,主观感受最差。而原地启动和60%油门加速启动这2种工况下发动机介入瞬间的发动机振动峰值频率分别为12.6和18.2 Hz,与传动系扭转模态频率分别避频1.7和3.9 Hz,因此这2种工况下的发动机振动峰值下降显著。本文推测,3种工况下发动机振动峰值频率为动力总成的刚体模态频率,会随着工况变化而变化。
由于瞬态过程的刚体模态无法通过测试获得,因此对3种工况下动力总成刚体模态进行了理论计算分析。表 3和4分别为3种工况下动力总成悬置受力F和橡胶衬套刚度kbu。由表 3和4可以发现,从原地启动工况到20%油门加速启动工况,再到60%油门加速启动工况,动力总成所受扭矩载荷不断增大,其反作用于3个动力总成悬置x向的力显著增大,使动力总成悬置橡胶衬套在x向上被压缩,从而导致橡胶衬套x向的刚度也显著增大;由于施加在动力总成悬置y和z向的载荷变化较小,因此橡胶衬套y和z向刚度几乎不变。
| 工况 | 部件 | ||||
| 原地启动 | 0 | 右悬置 | 9 | —16 | —992 |
| 左悬置 | 2 | —1 | —1 458 | ||
| 后悬置 | —11 | 17 | —49 | ||
| 20%油门加速启动 | 666 | 右悬置 | 1 308 | —12 | —968 |
| 左悬置 | 1 955 | 2 | —1 420 | ||
| 后悬置 | —3 263 | 10 | —115 | ||
| 60%油门加速启动 | 2 933 | 右悬置 | 3 998 | —7 | —929 |
| 左悬置 | 5 926 | 5 | —1 360 | ||
| 后悬置 | —9 924 | 3 | —158 |
| 工况 | 部件 | ||||
| 原地启动 | 0 | 右悬置 | 325 | 60 | 326 |
| 左悬置 | 383 | 98 | 362 | ||
| 后悬置 | 382 | 510 | 180 | ||
| 20%油门加速启动 | 666 | 右悬置 | 603 | 60 | 326 |
| 左悬置 | 743 | 98 | 362 | ||
| 后悬置 | 450 | 510 | 180 | ||
| 60%油门加速启动 | 2 933 | 右悬置 | 863 | 60 | 326 |
| 左悬置 | 1 513 | 98 | 362 | ||
| 后悬置 | 1 450 | 510 | 180 |
将3种工况下的悬置橡胶衬套刚度作为仿真输入条件,代入式(4),可以计算获得3种工况下的动力总成刚体模态频率,具体结果见表 5。可以看出,从原地启动工况到20%油门加速启动工况,再到60%油门加速启动工况,动力总成Ry和Rz向刚体模态频率均显著提高。3种工况下动力总成Ry向刚体模态频率计算值和实测值的对比如表 6所示,可知二者吻合较好。
| Hz | |||||||||||||||||||||||||||||
| 工况 | 方向 | ||||||||||||||||||||||||||||
| x | y | z | Rx | Ry | Rz | ||||||||||||||||||||||||
| 原地启动 | 10.1 | 4.2 | 8.5 | 15.6 | 12.5 | 15.9 | |||||||||||||||||||||||
| 20%油门加速启动 | 11.7 | 4.2 | 8.5 | 15.7 | 14.6 | 19.8 | |||||||||||||||||||||||
| 60%油门加速启动 | 19.6 | 4.2 | 8.5 | 15.7 | 19.0 | 29.7 | |||||||||||||||||||||||
| 工况 | 计算值/Hz | 实测值/Hz | 误差/% |
| 原地启动 | 12.5 | 12.6 | 0.8 |
| 20%油门加速启动 | 14.6 | 13.7 | 6.2 |
| 60%油门加速启动 | 19.0 | 18.2 | 4.2 |
综上可知,传动系扭转模态和动力总成Ry向刚体模态的耦合作用是发动机介入抖动量级大的直接原因。
3.2.3 动力总成刚体模态和传动系扭转模态避频解耦的效果验证根据3.2.2节可知,动力总成刚体模态频率和传动系扭转模态频率接近,2种模态的耦合作用放大了总成振动,因此可通过改变其中一种模态验证模态避频解耦后的改善效果。由图 14的测试结果可知,不同工况下的动力总成瞬态刚体模态频率差异较大,而不同工况下的传动系扭转模态频率几乎不变,因此通过改变传动系扭转模态频率实现避频的方法更可靠。由式(3)可知,可以通过降低飞轮扭转减振器的扭转刚度降低传动系扭转模态频率。将飞轮扭转减振器的扭转刚度从7.08(N·m)/(°)降低为5.40(N·m)/(°)后,传动系扭转模态频率的理论计算值可由14.4 Hz降低为12.6 Hz,如表 7所示。
| 方案 | ||||
| 原状态 | 7.08 | 0.09 | 0.11 | 14.4 |
| 降低扭转刚度 | 5.40 | 0.09 | 0.11 | 12.6 |
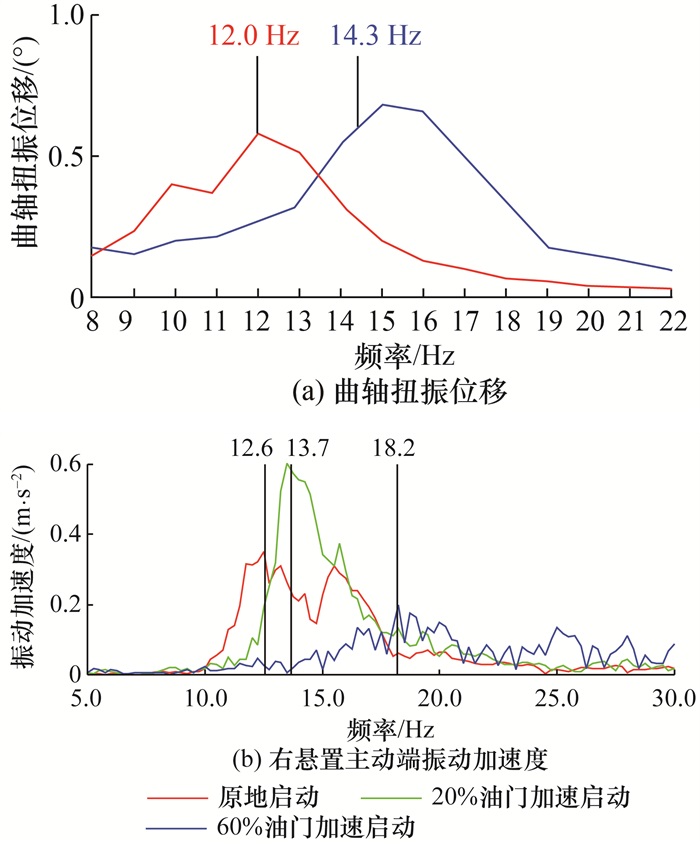
图 15为降低飞轮扭转减振器的扭转刚度前后20%油门加速启动工况下发动机介入抖动测试结果对比。可以看出,当飞轮扭转减振器的扭转刚度降低后,传动系扭转模态频率的实测值从14.3 Hz降低至约12.0 Hz,而动力总成刚体模态(Ry向)频率仍在14.0 Hz附近,两者模态避频超过2.0 Hz,达到模态解耦效果,使发动机振动幅值降低为原来的1/2,主观改善效果明显。
|
| 图 15 降低飞轮扭转减振器的扭转刚度前后20%油门加速启动工况下发动机介入抖动测试结果对比 |
由上可知,动力总成刚体Ry模态和传动系扭转模态耦合,是发动机介入抖动的根本原因。为控制发动机介入过程车内座椅振动,需要保证传动系扭转模态和动力总成Ry向刚体模态避频,以实现二者模态解耦。根据动力总成的Ry向刚体模态频率会随着加速油门深度增加而增大的特性,应保证传动系扭转模态频率低于原地启动时动力总成Ry向刚体模态频率2.0 Hz以上,只有这样才可确保在所有工况下(包括原地发动机介入工况和不同油门加速发动机介入工况)传动系扭转模态和动力总成Ry向刚体模态完全避频,实现完美的模态解耦。
3.3 悬置橡胶衬套刚度优化及效果验证动力总成3个悬置的隔振性能的强弱都会影响发动机介入瞬间引起的整车抖动量级的大小。本文以右悬置为例,尝试通过优化悬置结构改善发动机介入瞬间引起的整车抖动量级。
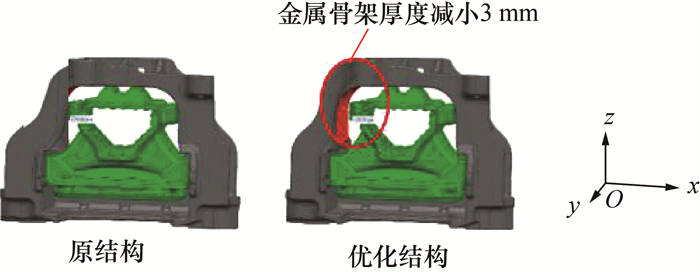
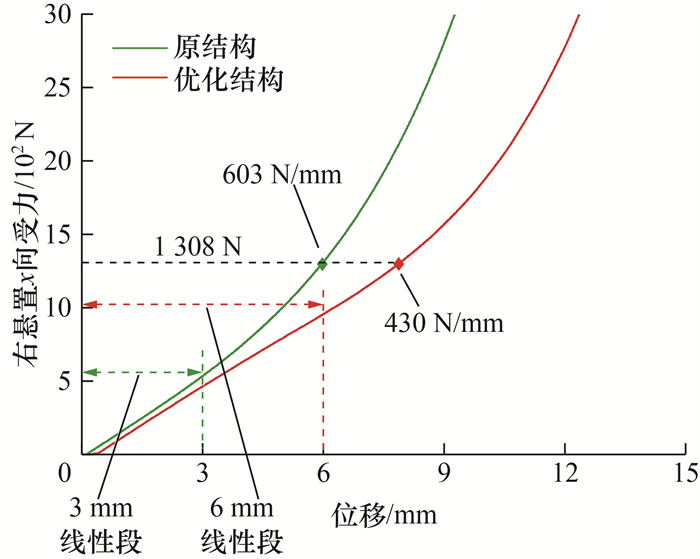
图 16和17分别为右悬置优化前后的结构对比及右悬置x向受力与位移的关系曲线对比。与原结构相比,优化结构并没有改变悬置橡胶衬套部分,而仅对悬置金属骨架内侧在x方向的厚度减小了3 mm。由于悬置橡胶衬套结构未变,因此怠速等受力较小的工况下悬置橡胶衬套3个方向的刚度都维持不变,这样可避免影响怠速工况下的动力总成悬置解耦率。金属骨架内侧在x方向的厚度减小了3 mm,因此使较大受力情况下悬置橡胶衬套在x向的压缩量减小,从而降低悬置橡胶衬套刚度。由表 3可知,在20%油门加速启动工况下右悬置x向的受力大小为1 308 N,对应至图 17可得,优化结构的悬置橡胶衬套刚度由603 N/mm降低为430 N/mm,理论上可提高右悬置的隔振率。
|
| 图 16 右悬置优化前后的结构对比 |
|
| 图 17 右悬置优化前后的右悬置x向受力与位移的关系曲线对比 |
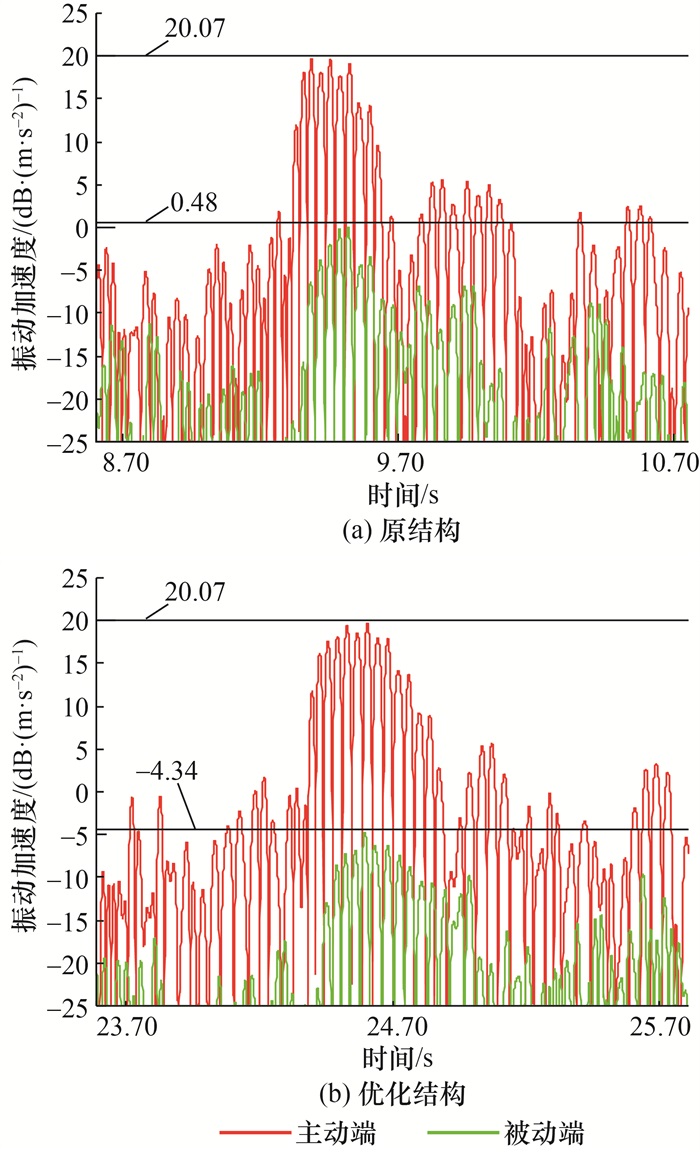
将优化结构右悬置装车进行实车测试验证。在20%油门加速启动工况下,原结构和优化结构的测试结果对比如图 18所示。可以看出,优化前后的主动端振动差异较小,而被动端振动加速度由0.48 dB/(m·s-2)下降为—4.34 dB/(m·s-2),表明结构优化后右悬置的隔振率明显提升。
|
| 图 18 原结构和优化结构状态下发动机介入间的右悬置主被动端振动时域对比 |
综上可知,通过降低悬置橡胶衬套刚度,提高悬置的隔振性能,保证悬置对动力总成振动能量极强的衰减能力,可改善发动机介入引起的整车抖动量级。
4 结论针对某混动SUV发动机介入时引起整车抖动的问题,本文采用实验和仿真相结合的方法,对该问题的源头产生机理及路径传递机理进行了深入研究,结论如下:
1) 混动发动机介入瞬间的抖动出现在发动机点火之前ISG倒拖发动机阶段,其抖动水平由第一循环缸压峰值大小决定,而发动机第一循环缸压峰值由停缸初始位置决定。当第一个处于压缩行程气缸的活塞位置离上止点越远时,压缩行程越长,第一循环缸压峰值越大,从而导致发动机介入瞬间的抖动程度越严重。
2) 传动系扭转模态频率应低于原地启动时动力总成Ry向刚体模态频率2.0 Hz以上,以保证传动系扭转模态和动力总成Ry向刚体模态能在所有工况下都完全解耦。
3) 动力总成悬置是发动机介入抖动问题的重要传递路径。通过优化悬置橡胶衬套的限位结构,可降低悬置橡胶衬套刚度,提高悬置隔振率,使从混动总成传递至车内的振动发生衰减。
| [1] |
OHN H, MIN K. Combustion stability analysis during engine stop and restart in a hybrid powertrain[J]. International Journal of Automotive Technology, 2009, 10(2): 241-249. DOI:10.1007/s12239-009-0029-x |
| [2] |
KUANG M. An investigation of engine start-stop NVH in a power split powertrain hybrid electric vehicle[R]. Detroit: Warrendale SAE International, 2006.
|
| [3] |
王博, 张振东, 于海生, 等. 发动机启动引起的混合动力汽车振动分析与控制[J]. 汽车工程, 2019, 41(2): 184-190, 205. WANG B, ZHANG Z D, YU H S, et al. Analysis and control on vibration resulted from engine start of hybrid electric vehicle[J]. Automotive Engineering, 2019, 41(2): 184-190, 205. (in Chinese) |
| [4] |
胡云峰, 顾万里, 梁瑜, 等. 混合动力汽车启停非线性控制器设计[J]. 吉林大学学报(工学版), 2017, 47(4): 1207-1216. HU Y F, GU W L, LIANG Y, et al. Start-stop control of hybrid vehicle based on nonlinear method[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(4): 1207-1216. (in Chinese) |
| [5] |
石岩, 白炜, 王志卫. 动力总成悬置布置形式对启动振动的影响研究[J]. 北京汽车, 2019(1): 38-43. SHI Y, BAI W, WANG Z W. Study on the influence of powertrain mounting arrangement on starting vibration[J]. Beijing Automotive Engineering, 2019(1): 38-43. (in Chinese) |
| [6] |
王道勇, 赵学智, 上官文斌, 等. 发动机启停时动力总成悬置系统的设计方法研究[J]. 振动与冲击, 2018, 37(8): 141-145. WANG D Y, ZHAO X Z, SHANGGUAN W B, et al. A design method of a power train mounting system to improve key on /off vibration of a car[J]. Journal of Vibration and Shock, 2018, 37(8): 141-145. (in Chinese) |
| [7] |
WU H W, WU G Q. Driveline torsional analysis and clutch damper optimization for reducing gear rattle[J]. Shock and Vibration, 2016, 2016: 8434625. |
| [8] |
HU J F, CHEN W W, HUANG H. Decoupling analysis for a powertrain mounting system with a combination of hydraulic mounts[J]. Chinese Journal of Mechanical Engineering, 2013, 26(4): 737-745. DOI:10.3901/CJME.2013.04.737 |



