2. 清华大学 水利部水圈科学重点实验室, 北京 100084;
3. 清华大学 水利水电工程系, 北京 100084
2. Key Laboratory of Hydrosphere Sciences of the Ministry of Water Resources, Tsinghua University, Beijing 100084, China;
3. Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China
马尼拉俯冲带位于南海东部,是南海区域最有可能发生大型地震的区域[1-2]。现有研究认为马尼拉俯冲带有可能发生8.8~9.2级地震[3-4]。海底大地震可能诱发大型海啸,对南海沿岸和南海内岛礁地区造成破坏性的灾害。有关古海啸沉积物的调查研究表明,巨大的海啸曾影响了华南沿海和南海诸岛[5]。历史上南海马尼拉海沟地震诱发的海啸对南海周边各地区均产生了不同程度的影响[6]。其中,Lau等[7]基于数据来源的清晰性和可信度分析,发现南海东北部有不同可信度的海啸记录58次,菲律宾火山地震研究所记录了1589—2012年41个可信度较高的海啸事件[8]。评估马尼拉俯冲带最大可能地震引发的海啸危险性,能更科学地制定海岸及海上工程设施抵御地震海啸淹没灾害的设计标准,为海域内岛礁的防灾减灾策略制定提供支撑。
马尼拉俯冲带的地震潜力可通过大地测量数据反演。随着全球导航卫星系统发展,使用地表GPS水平速度场数据反演断层闭锁程度和滑动亏损速率的方法得到广泛应用[9-14]。马尼拉海沟位于深海,有关其闭锁情况的研究较少,且现有研究中对其闭锁程度的估计差异较大。Galgana等[15]根据1996—2002年吕宋岛52个GPS站的观测结果,反演得到马尼拉海沟的闭锁程度很低,闭锁系数为0.01。Hsu等[16]使用GPS数据反演得到马尼拉海沟14.5 °N~17.0 °N区域部分锁定,平均闭锁系数为0.4。Hsu等[3]推算马尼拉海沟15 °N~19 °N区域闭锁系数为0.34~0.48。根据断层的闭锁程度可以估算断层静态地震矩累积速率,进而判断地震潜力。TDEFNODE是Mccaffrey[17]开发的负位错反演程序,可用来反演断层的闭锁情况,并估计地震潜力。
海啸的强度不仅取决于地震震级,还受其他地震参数的影响。研究表明,断层滑移的非均匀性对海啸的影响也十分显著[18-20]。现有的非均匀滑移模型多基于Herrero等[21]的地震的运动学自相似破裂过程模型,如Gallovicf等[22]的具有随机源模型的地震合成模型和Mai等[23]的地震破裂与地面运动模拟(codes for earthquake repture and ground-mation simulation,CERS)等。非均匀滑动具有随机性,同时也受到一些约束,如在断层的高闭锁区域地震滑动可能更大。因此,可以将TDEFNODE反演的闭锁分布用作滑动分布的约束条件。
本研究旨在探明马尼拉俯冲带发生极端地震情景时对南海诸岛造成的海啸危险性。研究将通过负位错模型反演获得马尼拉俯冲带的地震潜力和断层闭锁分布,并考虑大地震时断层滑动的非均匀性和随机性,基于大规模海量情景模拟,分析最大可能震级地震产生的海啸,给出主要岛礁附近的最大可能海啸灾害分布。
1 研究区域和分析方法以南海海域东侧马尼拉俯冲带发生极端地震情景为背景,分析地震诱发的海啸灾害。马尼拉俯冲带位于菲律宾海板块和巽他板块的交界处,是南海最有可能引发大型地震海啸的构造带。考虑海域内岛礁海拔一般较低,部分岛礁上有常住人口,易受海啸灾害影响,岛礁的承灾能力较弱,因此选取南海海域的主要岛礁作为关注点位。
基于地震潜力评估反演模型、大地震断层滑动分布模型和海啸生成传播演进模型展开分析,分析方法框架如图 1所示。首先,地震潜力评估模型采用Mccaffrey[17]开发的断层负位错反演TDEFNODE模型,以GPS水平速度场数据和历史地震目录作为基础数据,通过板块之间相对运动反演断层闭锁和滑动亏损估算最大可能震级。其次,选取500年一遇的地震震级作为极端地震情景,采用Blaser等[24]的地震标度关系确定断层破裂尺度和平均滑移,并考虑早期常用的简化均匀滑移假定和Mai等[23]的断层非均匀滑移模型,结合断层闭锁空间分布,构造特定震级下各种可能的断层滑移分布情景。最后,通过高效的地震生成演进模拟方法[25],实现大量地震海啸情景的模拟仿真,最终统计分析关注点位上的海啸波高统计特征值。
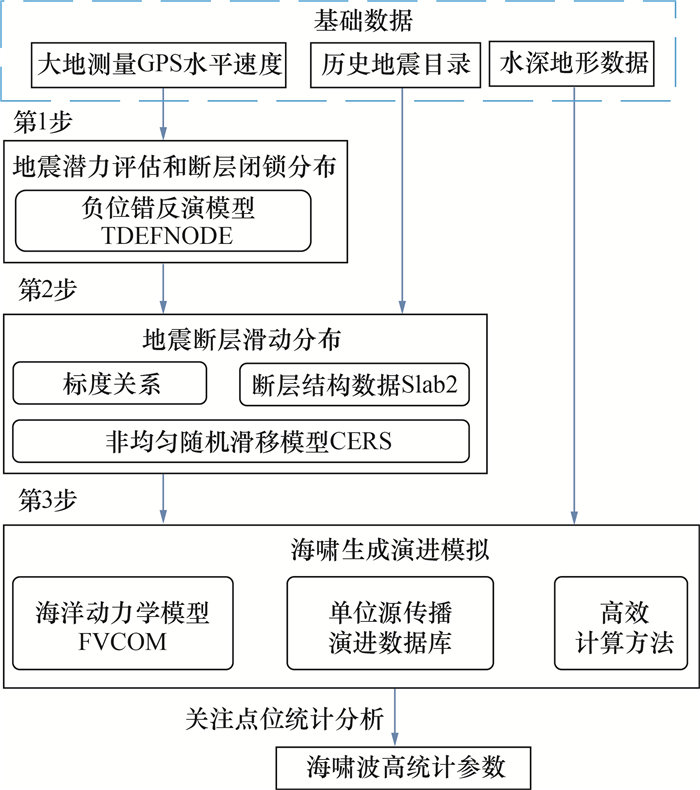
|
| 图 1 分析方法框架 |
基础数据源包括GPS大地水平速度数据、马尼拉俯冲带附近地震数据和海域水深地形数据等。其中,GPS大地水平速度数据选用Kreemer等[26]收集整理的GPS速度场数据,在全球范围内共22 511条记录,统一到ITRF08参考框架下。在研究关注的马尼拉海沟附近,Kreemer等[26]的数据库中有约80个GPS观测站的数据,此外还选取了约50个位于周边地区的GPS观测站用来限制巽他板块和菲律宾海板块的运动。在模型中,剔除不确定性较大的数据,最终选取144个GPS观测站参与反演,如图 2所示,图上箭头表示GPS水平速度的方向。根据美国地质调查局(United States Geological Survey,USGS)的历史地震数据库,1900—2022年马尼拉俯冲带范围(119 °E~123 °E,13 °N~22 °N)共有地震记录5 992条,其中历史最大震级为7.7级。海域水深地形数据参考美国国家海洋和大气管理局的ETOPO1[27]。
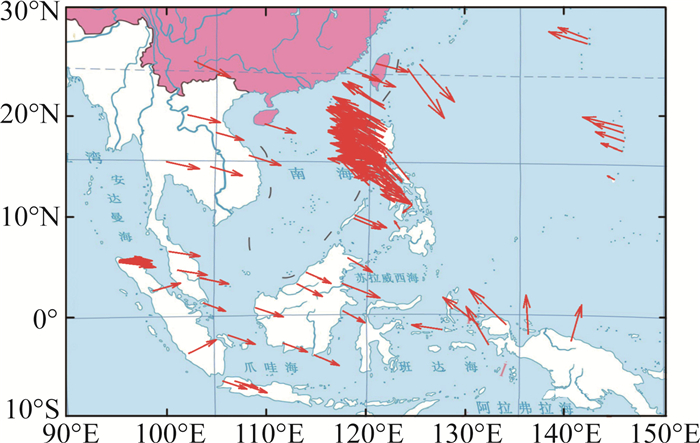
|
| 基于中国标准地图制作,审图号为GS(2021)5449号。 图 2 GPS大地水平速度分布 |
岛礁观测点选取如图 3所示。1—7为西沙的宣德群岛,其中1为永兴岛、2为南沙洲、3为南岛、4为北岛、5为赵述岛、6为西沙洲、7为东岛;8为东沙的东沙岛;9—15为西沙的永乐群岛,其中9为金银岛、10为甘泉岛、11为珊瑚岛、12为鸭公岛、13为晋卿岛、14为琛航岛、15为中建岛;16—19为南沙群岛,其中16为太平岛、17为永暑岛、18为渚碧岛、19为美济岛。
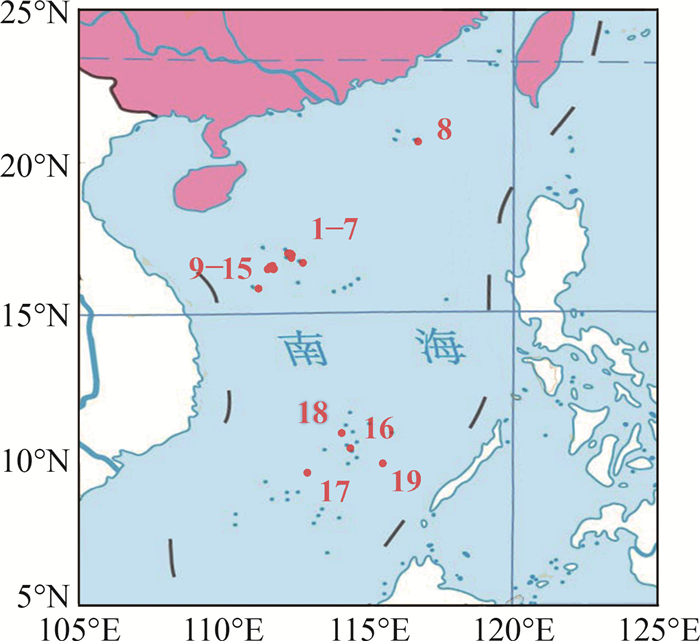
|
| 基于中国标准地图制作,审图号为GS(2021)5449号。 图 3 研究区域和观测点位置 |
2 结果与讨论 2.1 地震潜力评估
断层闭锁可与地震潜力联系,用来预测未来的地震危险性。通常而言,在高锁定区域断层以更快的速度累积滑动亏损,进而累积更多的应力,在下一次地震事件中更有可能成为破裂的起点或产生更大的滑动。使用TDEFNODE反演地震间块体的旋转和断层闭锁。参考Hsu等[3]的研究,将马尼拉海沟周边地区划分为9个块体,并给定块体旋转Eular极的初值。马尼拉俯冲带的几何形状参考Slab2模型进行插值[28]。研究采用Gauss型和Gamma型2种参数化方案进行断层闭锁程度的反演。Gauss型是指在断层沿倾向剖面上闭锁系数分布呈Gauss函数;Gamma型是指在断层沿倾向剖面上闭锁系数分布呈指数型。反演结果的卡方值分别为3.422和4.492,表明反演结果较可靠。根据滑动亏损的计算结果,当取剪切模量μ为4×1010 N/m2时,马尼拉海沟全断层面的地震矩累积率在Gauss和Gamma型分布模型中分别为2.20×1020和1.63×1020 N·m/a,但同时地震会释放地震矩。根据USGS的历史地震数据库,1900—2022年马尼拉俯冲带范围共有地震记录5 992条,其中历史最大震级为7.7级。根据震级与地震矩之间的关系,可以统计得到1900—2022年历史地震累积释放地震矩为3.65×1021 N·m,平均每年地震矩释放率为2.97×1019 N·m/a。假设未来地震矩累积率和释放的速率保持不变,那么2种模型实际的地震矩累积率分别为1.90×1020和1.33×1020 N·m/a。以该速率累积地震矩,那么200年累积的地震矩可引发的最大地震震级分别为9.0和8.9级,500年最大震级分别为9.3和9.2级。
然而,目前很多研究表明马尼拉全断层在一场大地震中断裂的可能性很小。例如,Bautista等[28]认为马尼拉海沟17 °N以南俯冲的南海残留洋中脊可能导致板块撕裂,进而阻止破裂的传播。Yu等[4]认为马尼拉海沟16 °N~17 °N附近断层倾角和走向角的剧烈变化可能抑制断裂的传播。Zhu等[30]认为板块撕裂的位置更偏南一些,在14.0 °N~14.5 °N之间。从这一位置向南,马尼拉海沟的走向向东南偏东急剧弯曲。南段的地震活动也明显比15 °N以北的地震活动深。此外,15 °N附近的黄岩海山也被认为是阻止断裂的屏障[16, 30]。因此,参考最新研究成果,以14.5 °N为界将马尼拉俯冲带分为2段。此外,一些地震破裂动力学的研究结果表明,闭锁模型估算得到的静态累积地震矩只能释放40%~50%,这是断层的非均匀性所致[31-32]。因此,在进行地震潜力评估时,考虑静态累积地震矩40%的释放率,估算得到每段上500年的最大震级如表 1所示。
| 分段范围 | 评估参量 | Gauss模型 | Gamma模型 |
| 南段13.0 °N~14.5 °N | 地震矩累积率/(N·m·a-1) | 3.08×1019 | 0.34×1019 |
| 500年最大矩震级 | 8.5 | 7.9 | |
| 北段14.5 °N~22.0 °N | 地震矩累积率/(N·m·a-1) | 14.75×1019 | 12.00×1019 |
| 500年最大矩震级 | 8.9 | 8.9 |
本研究以马尼拉俯冲带最大地震海啸为例进行分析,认为500年地震矩累积的最大震级即为可能最大震级。因此选取北段发生8.9级地震作为海啸情景。
2.2 滑动非均匀性对海啸波高的影响特定震级下,地震情景仍具有强随机性。震中位置及破裂面上滑移分布情形多种多样。早期在海啸评估中破裂面的滑移常假定为均匀分布,这是由于强不确定性背后的大量情景分析需要耗费大量的计算资源。然而,是否考虑断层滑动不均匀性,也将对评估结果产生一定影响。对比相对简单的均匀滑移分布模型,非均匀滑移分布是实际大地震断层运动的更合理假定。
本研究中非均匀滑移场的构造考虑了断层闭锁分布与地震时断层滑移的相关性,在Mai等[23]的地震破裂与地面运动模拟模型CERS的基础上,添加了闭锁分布的贡献权重。随机部分满足波数k平方的统计规律。确定性部分在原CERS模型中考虑为破裂面上的均匀分布,大小为根据地震标度关系计算的平均滑移。本文考虑闭锁分布的影响,假定平均意义上滑动分布与闭锁分布一致,按照闭锁分布重新分配了确定性部分,使多情景统计意义上高闭锁的位置滑动更大。
采用Slab2的三维断层面数据构建马尼拉断层三维几何结构。将马尼拉断层面北段划分为长宽均为0.1 °的网格,共有75×20=1 500个子断层。每个子断层中心的经纬度、深度、走向角、倾角和滑移角由Slab2的数据插值获得。每次地震破裂滑动的空间分布被投影到相应的子断层上,在每个子断层上滑动均匀,由随机滑移模型生成的高分辨滑动平均得到。地震破裂的大小采用Blaser等[24]的经验标度关系来确定。以一场8.9级地震为例,震源中心位于120.9 °E、19.5 °N,非均匀滑移和均匀滑移分布分别如图 4a和4b所示,可见非均匀滑移分布和均匀滑移分布差异很大。
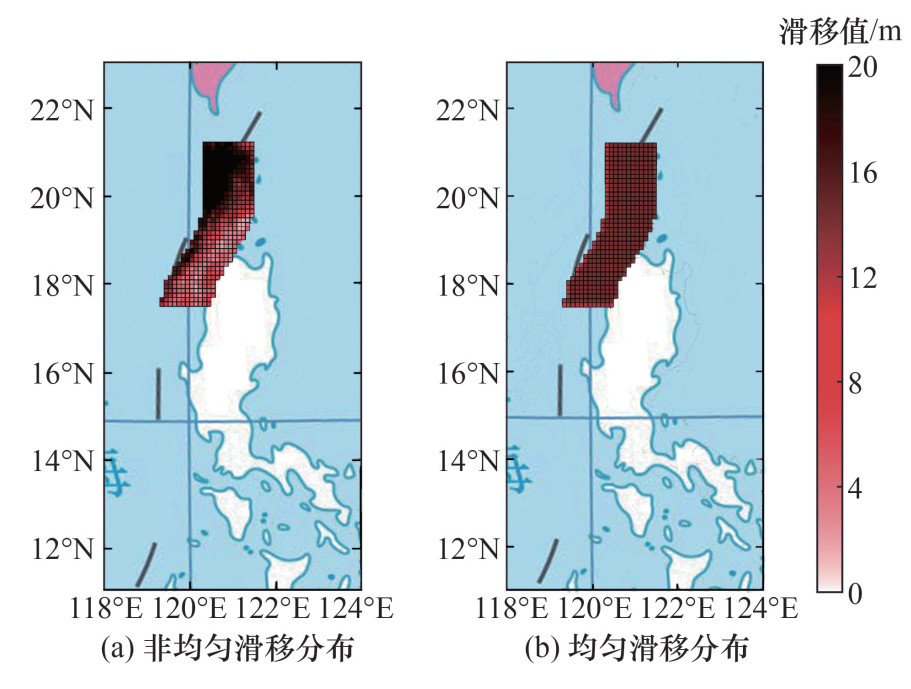
|
| 基于中国标准地图制作,审图号为GS(2021)5449号。 图 4 8.9级地震滑移分布 |
研究采用文[33]模型给出的地震发生时的水面初始扰动。2种滑移在永兴岛(观测点1)产生的海啸过程如图 5所示,其中T为时间,ζ为水位。考虑非均匀滑移分布可能使海啸波高增加,也可能使海啸波高降低。由于非均匀滑移具有随机性,不同的随机滑移可能对海啸波高产生不同的影响,因此研究考虑大量随机海啸情景。
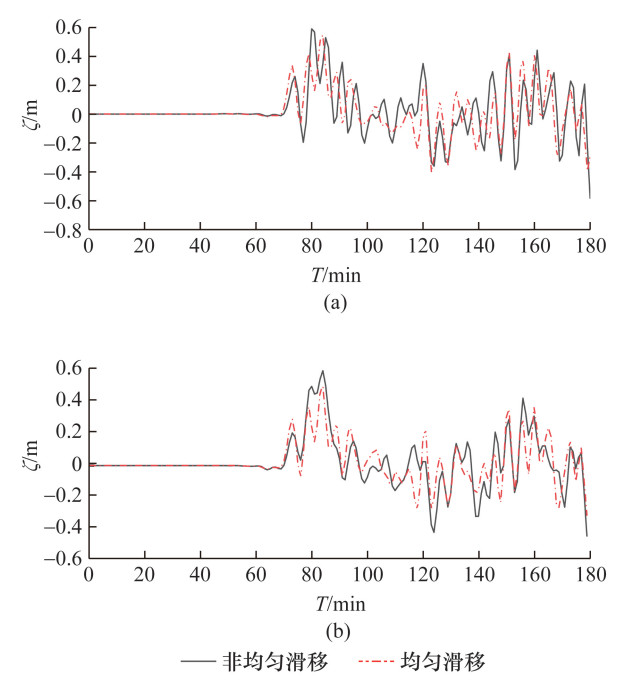
|
| 图 5 2场8.9级地震在观测点1的海啸过程 |
2.3 海啸危险性空间分布和随机特性
若以0.1 °为间隔划分可能的震源位置,则马尼拉俯冲带北段上发生8.9级地震的可能震源位置有186个,对于每个地震海啸事件,考虑1个均匀分布滑移情景和3 600个非均匀滑移情景,其中包括只考虑随机滑移、只考虑闭锁分布,以及闭锁分布和随机滑移按不同比例组合形成的非均匀滑移分布,共约70万个海啸情景。应用Zhang等[25]的高效海啸传播演进分析方法实现大规模海啸情景模拟。针对每个海啸情景,计算位于100 m等深线上19个岛礁观测点的水位波动序列,得到各个海啸情景的最大波高。
图 6给出了所有非均匀滑移情景的海啸波高平均值,与均匀滑移情景的平均波高对比。可以看出,平均意义上,均匀滑移情景显著低估海啸波高,在西沙的宣德群岛尤为明显。与非均匀滑移相比,仅考虑均匀滑移会低估海啸波高19.01%~49.45%。其中,西沙的宣德群岛会低估海啸波高40.55%,永乐群岛海啸波高低估了33.25%,东沙群岛低估了19.01%,南沙群岛低估了42.87%。西沙位于马尼拉俯冲带海啸的主要辐射方向上,受滑动变化的影响较大,而南沙的海啸波高较小,因此变化相对较大。滑动非均匀性对海啸波高的影响包括2部分,一部分是随机滑移对滑动分布的集中,另一部分是闭锁分布对滑移在断层浅处的集中。两者结合使断层浅处在平均意义上产生了更大的滑移,进而产生更大的海啸灾害。平均意义上,基于均匀滑移假设,会对极端地震诱发的海啸危险性评估造成系统性低估。
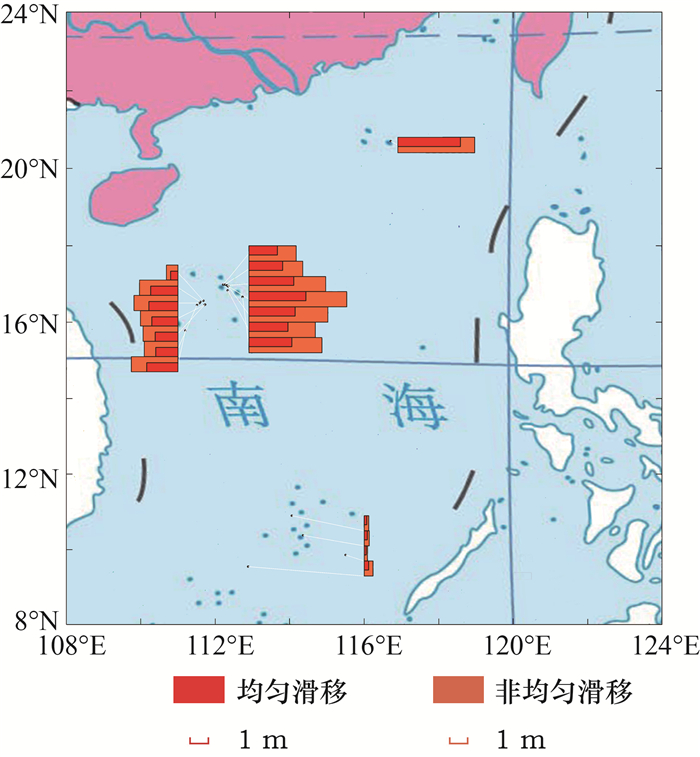
|
| 基于中国标准地图制作,审图号为GS(2021)5449号。 图 6 非均匀滑移和均匀滑移产生的南海诸岛海啸空间分布 |
非均匀滑移的海啸情景统计结果表明,8.9级地震产生的海啸波高平均值为0.17~5.05 m,各观测点位存在较大差异。其中,西沙宣德群岛的南岛可能面临的海啸灾害最大,各情景平均波高最大可达5.05 m,宣德群岛均值为3.65 m;东沙群岛和西沙永乐群岛次之,分别为4.07 m和1.83 m;南沙群岛的海啸灾害最小,为0.28 m。宣德群岛和东沙群岛离震源位置更近,且海啸传播路径上无其他岛礁阻隔,海啸波高更大。南沙群岛和永乐群岛距离震源较远,且海啸传播路径上有较多岛礁,因此即使在最大可能地震海啸情景中,这些岛礁面临的海啸灾害也较小。
由于非均匀滑移具有随机性,不同海啸情景中海啸波高可能更大,也可能更小。对所有非均匀滑移情景的海啸波高进行统计分析,得到海啸波高的误差线如图 7所示。可以看出,即使在同一震级下,海啸波高也有较大随机性。在所有非均匀情境中,东沙岛海啸波高最大值为6.2 m,宣德群岛的南岛处海啸波高最大可达9.0 m。若将所有情景的海啸波高按照Gauss分布统计,东沙岛海啸波高的均值为4.1 m,一个标准差范围为1.8~6.2 m。
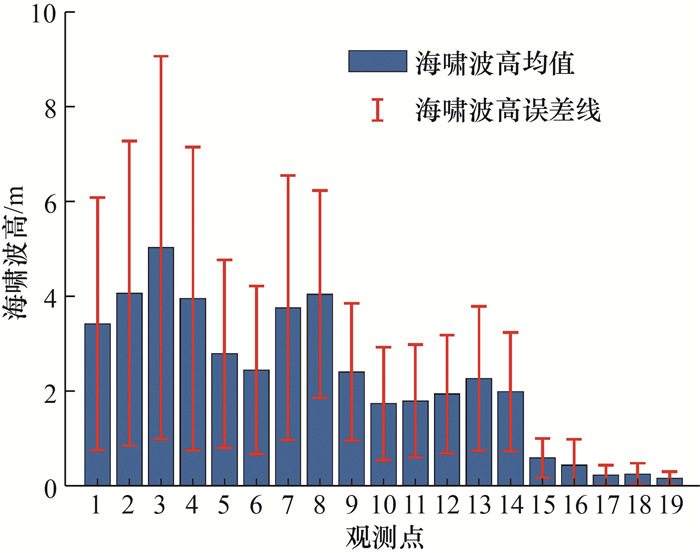
|
| 图 7 非均匀情景中南海诸岛海啸波高均值和误差线 |
3 结论
马尼拉最大可能地震海啸灾害评估的难点在于震源具有不确定性,包括可能最大震级的大小和破裂的形态。本文通过将闭锁分布引入非均匀滑移模型,对这2方面问题提出了解决方案。首先,采用负位错模型反演水平速度场数据得到马尼拉俯冲带的2种闭锁分布;根据闭锁分布和滑动亏损分布的结果,估算马尼拉俯冲带北段的可能最大震级为8.9级。其次,将闭锁模型引入随机滑移模型,用闭锁分布重新分配确定性滑移部分,实现闭锁分布对随机滑移的约束。最后,利用改进的非均匀滑移模型模拟了最大可能地震海啸。主要结论如下:
1) 与非均匀滑移模型相比,均匀滑移模型会使极端地震情景的海啸波高被低估19.01%~49.45%,在西沙的宣德群岛和南沙群岛,海啸波高的低估尤为明显。非均匀滑移模型是实际断层滑移的更真实模化,为了充分评估海啸灾害风险,在海啸灾害评估中应采用非均匀滑移模型。
2) 西沙群岛的宣德群岛和东沙群岛的海啸灾害整体水平较高,南沙群岛的海啸灾害整体水平较低。
在未来海啸灾害评估工作中,需要对断层滑移分布的模型进行更深入的研究,以提高海啸灾害评估的准确性。在海啸预报工作中,亦可考虑将滑移的非均匀性纳入海啸预报预警系统中,通过集合预报等手段为海啸预警和风险管理提供更科学可靠的支撑。
| [1] |
MEGAWATI K, SHAW F, SIEH K, et al. Tsunami hazard from the subduction megathrust of the South China Sea: Part Ⅰ. Source characterization and the resulting tsunami[J]. Journal of Asian Earth Sciences, 2009, 36(1): 13-20. DOI:10.1016/j.jseaes.2008.11.012 |
| [2] |
HONG NGUYEN P, BUI Q C, DINH NGUYEN X. Investigation of earthquake tsunami sources, capable of affecting Vietnamese coast[J]. Natural Hazards, 2012, 64(1): 311-327. DOI:10.1007/s11069-012-0240-3 |
| [3] |
HSU Y J, YU S B, LOVELESS J P, et al. Interseismic deformation and moment deficit along the Manila subduction zone and the Philippine Fault system[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(10): 7639-7665. DOI:10.1002/2016JB013082 |
| [4] |
YU H Y, LIU Y J, YANG H F, et al. Modeling earthquake sequences along the Manila subduction zone: Effects of three-dimensional fault geometry[J]. Tectonophysics, 2018, 733: 73-84. DOI:10.1016/j.tecto.2018.01.025 |
| [5] |
SUN L G, ZHOU X, HUANG W, et al. Preliminary evidence for a 1 000-year-old tsunami in the South China Sea[J]. Scientific Reports, 2013, 3(1): 1655. DOI:10.1038/srep01655 |
| [6] |
ZHAO X, JIANG Y P, REN Z Y, et al. Historical tsunami records and potential tsunami scenarios near Haikou coastal region[J]. Natural Hazards, 2017, 89(2): 625-645. DOI:10.1007/s11069-017-2983-3 |
| [7] |
LAU A Y A, SWITZER A D, DOMINEY-HOWES D, et al. Written records of historical tsunamis in the northeastern South China Sea: Challenges associated with developing a new integrated database[J]. Natural Hazards and Earth System Sciences, 2010, 10(9): 1793-1806. DOI:10.5194/nhess-10-1793-2010 |
| [8] |
BAUTISTA M L P, BAUTISTA B C, SALCEDO J C, et al. Philippine tsunamis and Seiches (1589—2012)[M]. Quezon: Philippine Institute of Volcanology and Seismology, 2012.
|
| [9] |
LI S S, FREYMUELLER J T. Spatial variation of slip behavior beneath the Alaska Peninsula along Alaska-Aleutian subduction zone[J]. Geophysical Research Letters, 2018, 45(8): 3453-3460. DOI:10.1002/2017GL076761 |
| [10] |
OZAWA S, NISHIMURA T, SUITO H, et al. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake[J]. Nature, 2011, 475(7356): 373-376. DOI:10.1038/nature10227 |
| [11] |
ADER T, AVOUAC J P, JING L Z, et al. Convergence rate across the Nepal Himalaya and interseismic coupling on the Main Himalayan Thrust: Implications for seismic hazard[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4): B04403. |
| [12] |
MORENO M, ROSENAU M, ONCKEN O. 2010 Maule earthquake slip correlates with pre-seismic locking of Andean subduction zone[J]. Nature, 2010, 467(7312): 198-202. DOI:10.1038/nature09349 |
| [13] |
BANERJEE P, BVRGMANN R. Convergence across the northwest Himalaya from GPS measurements[J]. Geophysical Research Letters, 2002, 29(13): 1652. |
| [14] |
FLETCHER H J, BEAVAN J, FREYMUELLER J, et al. High interseismic coupling of the Alaska subduction zone SW of Kodiak Island inferred from GPS data[J]. Geophysical Research Letters, 2001, 28(3): 443-446. DOI:10.1029/2000GL012258 |
| [15] |
GALGANA G, HAMBURGER M, MCCAFFREY R, et al. Analysis of crustal deformation in Luzon, Philippines using geodetic observations and earthquake focal mechanisms[J]. Tectonophysics, 2007, 432(1-4): 63-87. DOI:10.1016/j.tecto.2006.12.001 |
| [16] |
HSU Y J, YU S B, SONG T R A, et al. Plate coupling along the Manila subduction zone between Taiwan and northern Luzon[J]. Journal of Asian Earth Sciences, 2012, 51: 98-108. DOI:10.1016/j.jseaes.2012.01.005 |
| [17] |
MCCAFFREY R. Time-dependent inversion of three- component continuous GPS for steady and transient sources in northern Cascadia[J]. Geophysical Research Letters, 2009, 36(7): L07304. |
| [18] |
MELGAR D, WILLIAMSON A L, SALAZAR-MONROY E F. Differences between heterogenous and homogenous slip in regional tsunami hazards modelling[J]. Geophysical Journal International, 2019, 219(1): 553-562. DOI:10.1093/gji/ggz299 |
| [19] |
LI L L, SWITZER A D, CHAN C H, et al. How heterogeneous coseismic slip affects regional probabilistic tsunami hazard assessment: A case study in the South China Sea[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(8): 6250-6272. DOI:10.1002/2016JB013111 |
| [20] |
YUAN Y, LI H W, WEI Y, et al. Probabilistic tsunami hazard assessment (PTHA) for southeast coast of Chinese Mainland and Taiwan Island[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(2): e2020JB020344. DOI:10.1029/2020JB020344 |
| [21] |
HERRERO A, BERNARD P. A kinematic self-similar rupture process for earthquakes[J]. Bulletin of the Seismological Society of America, 1994, 84(4): 1216-1228. DOI:10.1785/BSSA0840041216 |
| [22] |
GALLOVIĆ F, BROKEŠOVÁ J. On strong ground motion synthesis with k-2 slip distributions[J]. Journal of Seismology, 2004, 8(2): 211-224. DOI:10.1023/B:JOSE.0000021438.79877.58 |
| [23] |
MAI P M, BEROZA G C. A spatial random field model to characterize complexity in earthquake slip[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B11): 2308. |
| [24] |
BLASER L, KRUGER F, OHRNBERGER M, et al. Scaling relations of earthquake source parameter estimates with special focus on subduction environment[J]. Bulletin of the Seismological Society of America, 2010, 100(6): 2914-2926. DOI:10.1785/0120100111 |
| [25] |
ZHANG X X, NIU X J. Probabilistic tsunami hazard assessment and its application to southeast coast of Hainan Island from Manila Trench[J]. Coastal Engineering, 2020, 155: 103596. DOI:10.1016/j.coastaleng.2019.103596 |
| [26] |
KREEMER C, BLEWITT G, KLEIN E C. A geodetic plate motion and global strain rate model[J]. Geochemistry, Geophysics, Geosystems, 2014, 15(10): 3849-3889. DOI:10.1002/2014GC005407 |
| [27] |
AMANTE C, EAKINS B W. ETOPO1 arc-minute global relief model: Procedures, data sources and analysis[M]. Boulder: NOAA National Geophysical Data Center, 2009.
|
| [28] |
HAYES G P, MOORE G L, PORTNER D E, et al. Slab2, a comprehensive subduction zone geometry model[J]. Science, 2018, 362(6410): 58-61. DOI:10.1126/science.aat4723 |
| [29] |
BAUTISTA B C, BAUTISTA M L P, OIKE K, et al. A new insight on the geometry of subducting slabs in northern Luzon, Philippines[J]. Tectonophysics, 2001, 339(3-4): 279-310. DOI:10.1016/S0040-1951(01)00120-2 |
| [30] |
ZHU G H, YANG H F, YANG T, et al. Along-strike variation of seismicity near the extinct mid-ocean ridge subducted beneath the Manila trench[J]. Seismological Research Letters, 2023, 94(2A): 792-804. DOI:10.1785/0220220304 |
| [31] |
YANG H F, YAO S L, HE B, et al. Earthquake rupture dependence on hypocentral location along the Nicoya Peninsula subduction megathrust[J]. Earth and Planetary Science Letters, 2019, 520: 10-17. DOI:10.1016/j.epsl.2019.05.030 |
| [32] |
YAO S L, YANG H F. Hypocentral dependent shallow slip distribution and rupture extents along a strike-slip fault[J]. Earth and Planetary Science Letters, 2022, 578: 117296. DOI:10.1016/j.epsl.2021.117296 |
| [33] |
OKADA Y. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1135-1154. DOI:10.1785/BSSA0750041135 |



