2. 天津水运工程科学研究院, 天津 300456;
3. 中国农业大学 北京市供水管网系统安全与节能工程技术研究中心, 北京 100083;
4. 佛山恒益热电有限公司, 佛山 528100;
5. 河海大学 海岸灾害及防护教育部重点实验室, 南京 210024
2. Tianjin Research Inst. for Water Transport Engineering, Tianjin 300456, China;
3. Beijing Eng. Research Center of Safety and Energy Saving Technol. for Water Supply Network System, China Agricultural University, Beijing 100083, China;
4. Foshan Ever Profit Power Plant Co., Ltd., Foshan 528100, China;
5. Key Lab. of Ministry of Education for Coastal Disaster and Protection, Hohai University, Nanjing 210024, China
海上风电单桩基础的存在影响着周边流场,形成强紊动水流以及漩涡,进而引起单桩周围的局部冲刷[1-2]。当冲刷深度达到一定程度时,单桩基础的稳定性就会受到威胁[3-6]。近几十年来,波浪条件下单桩基础受局部冲刷的深度的变化规律[7]、预测方法[8]及相关机理[9]等研究取得了一定的成果。
单桩冲刷深度的预测是海上风电设计中的重要内容,冲刷深度的估值过高会增加工程成本,估值过低则可能导致结构的失效[10]。一些学者已经根据小比尺物理模型单桩冲刷的试验获得了影响冲刷深度的主要参数,并建立了相关公式。根据衍射参数D/L(D为单桩的直径,L为波浪的波长),冲刷可分为大直径(D/L≥0.04)和小直径(D/L<0.04)[11]单桩冲刷。对于波浪条件下小直径单桩冲刷,Kobayashi等[12]和Sumer等[13]认为KC(Keulegan-Carpenter)是影响平衡冲刷深度的主要参数。KC=UT/D,U表示近底水质点特征速度,T表示谱峰周期。Sumer等[13]利用小比尺的水槽试验得到了关于KC>6的经验公式。Zanke等[14]考虑了泥沙特征对冲刷的影响,得到了波浪、单向流和往复流条件下统一的平衡冲刷深度公式。Dogan[11]的小比尺水槽试验考虑了相对粗糙床面材料的影响,从而改进了Sumer等[13]的公式。
为了方便计算,一些学者也得到了既适用于大直径又适用于小直径单桩的平衡冲刷深度公式。如Webb等[15]利用前人的大直径和小直径单桩冲刷深度数据,对Sumer等[13]的公式重新进行拟合,得到了含有新的相关系数的公式。Qi等[16]根据组合波流条件下马蹄形漩涡尺度与平衡冲刷深度的关系,拓展得到了基于Froude数的组合波流条件下的平衡冲刷深度公式,该公式不仅包括了KC<4的大直径单桩冲刷情况,也包括了Sumer等[17-18]研究的KC较大的小直径单桩冲刷情况,并且该公式的简化形式也可适用于纯波条件下的冲刷情况。Raaijmakers等[19]通过改进Breusers等[20]的纯流条件下的公式,得到了组合波流条件下的平衡冲刷深度公式,经验证可适用于一些小KC的冲刷情况,也可以被简化用于波流极限情况即纯波条件下。Dogan[11]基于KC和D/L、改进的Ursell数,得到了适用于大直径和小直径单桩的平衡冲刷深度公式。以上公式主要是在小比尺条件下即小比尺水槽试验的基础上建立的。而在大比尺条件下,Chen等[21]发现受比尺效应的影响,Sumer等[13]提出的公式对大比尺条件下的冲刷深度预测结果偏低;Prepernau等[22]也给出了相似的结论;其他公式的适用性是否也会受到比尺效应的影响,如何提高现有公式的预测准确度等问题,有待进一步的研究。
海上风电实际施工过程中,当风电单桩完成矗立但不能及时采取冲刷防护措施时,会形成冲刷坑。冲刷坑体积的估算,对于计算填充所需的抛石或混凝土的体积具有重要意义。目前很少有研究涉及单桩周围冲刷坑体积的变化及相应的影响因素。Link等[23]分析了恒定流条件下冲刷坑体积的变化并提出了相应预测公式。Hartvig等[24]基于恒定流和不规则波条件下冲刷坑体积的变化,分析了单桩周围的冲刷和回填过程。Chen等[21]对试验后的冲刷坑体积进行了简单拟合得到了相应的预测公式。Welzel等[25]基于冲刷坑体积研究了组合波流条件下导管架型结构物周围空间被侵蚀的过程。
目前波浪条件下的单桩冲刷试验主要是在小比尺条件即小比尺水槽试验中进行的,在大比尺条件下的试验研究较少。由于大比尺物理模型试验有助于最大限度地减少比尺效应的负面影响,能更准确地验证模型方法,因此本文在大比尺水槽中进行了一系列动床冲刷试验,研究不规则波条件下单桩周围的平衡冲刷深度和冲刷坑体积。
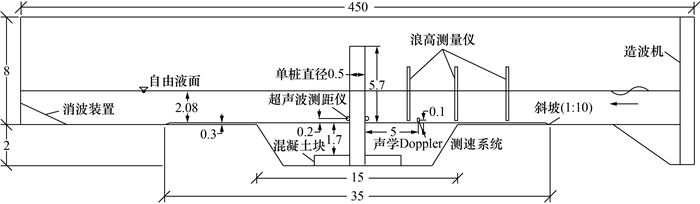
1 试验设置与过程本试验在天津水运工程研究所大型波流水槽中进行。该水槽为目前全球最大的波浪水槽。水槽长度、宽度和深度分别为450、5和8 m,一端配有活塞式造波机,另一端安装了消波装置以处理波反射。在水槽中间区域底部设置长度为35 m、宽度为5 m的沙层,其中单桩周围区域沙层厚度为2.3 m,沿水槽纵向长度为15 m,以此模拟1种可充分侵蚀的沙床。泥沙的中值粒径d50=0.1 mm,不均匀系数
|
| 图 1 波浪水槽物理模型(单位:m) |
在距离单桩上游5 m且沙床表面上方0.1 m的位置安装了声学Doppler测速系统,以监测底部的流速。在水槽上游的侧壁上安装了3个电容式浪高测量仪记录波浪参数。以上2种仪器的采样频率均为20 Hz。使用12台水下单点超声波测距仪对单桩周围12个点的冲刷过程进行实时监测,仪器采样频率为1 Hz,测距范围为3.5~110.0 cm,紧贴桩壁等角度沿12个径向方向、距离沙床表面上方0.2 m均匀分布。每次测试结束后,利用三维激光扫描仪测量冲刷坑的体积。扫描范围为距单桩中心下游为7 m、上游为2 m,左右宽度均为5 m的矩形区域,该区域内的深度测量精度约为1 mm。
本文进行了4次测试,只考虑不规则波条件,采用联合北海波浪计划(Joint North Sea Wave Project,JONSWAP)频谱进行模拟。所有工况的有效波高H1/3(波高按大小顺序排序后,取前1/3的平均值)为0.73~0.88 m;谱峰周期Tp(波能密度最大时对应的周期)为3.51~7.78 s;KC均为4~9;D/L为0.017~0.037,且均在动床冲刷条件下完成。本文利用相对平衡冲刷深度S/D和相对冲刷坑体积V/D3分别作为评价平衡冲刷深度S和冲刷坑体积V的指标,测试条件和结果如表 1所示。
| 工况 | H1/3/m | Tp/s | U/(m·s-1) | KC | D/L | S/D | V/D3 |
| 1 | 0.73 | 3.51 | 0.57 | 4.0 | 0.037 | 0.16 | 0.15 |
| 2 | 0.88 | 4.09 | 0.55 | 4.5 | 0.033 | 0.34 | 1.12 |
| 3 | 0.56 | 7.78 | 0.45 | 7.0 | 0.017 | 0.48 | 2.13 |
| 4 | 0.76 | 7.50 | 0.60 | 9.0 | 0.019 | 0.70 | 4.58 |
2 平衡冲刷深度
在纯波条件下,小直径单桩周围的平衡冲刷深度主要取决于KC。Sumer等[13]提出了预测平衡冲刷深度的经验公式:
| $ S / D=1.3[1-\exp (-0.03(\mathrm{KC}-6))], \mathrm{KC} \geqslant 6. $ | (1) |
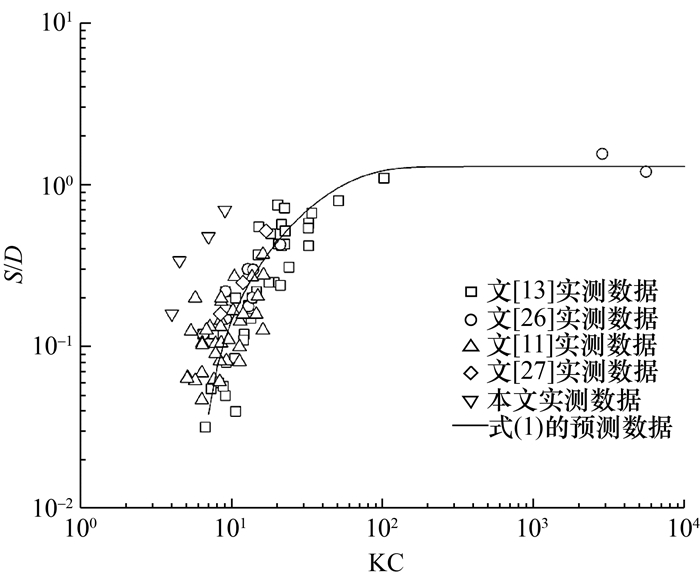
本文利用不同波和比尺条件下的S/D实测值验证式(1)的准确性,实测数据来自开展小比尺水槽规则波试验的文[11, 13, 26],开展大比尺水槽规则波试验的文[27],以及本文开展的大比尺水槽不规则波试验。结果表明,在前人研究中,无论是在规则波还是不规则波条件下,无论是大比尺水槽还是小比尺水槽试验,实测值的分布趋势基本与式(1)预测的一致;但本文试验的实测值明显大于预测值,如图 2所示。
|
| 图 2 不同波和比尺条件下的S/D实测值与预测曲线的对比 |
为了进一步验证相关公式的准确性,本文对小直径单桩的平衡冲刷深度公式进行了总结。Zanke等[14]根据文[13]的冲刷理论,引入泥沙特征因素参数Uc,得到了如下公式:
| $ S / D=2.5\left(1-0.5 \frac{U_{\mathrm{c}}}{U}\right) X_{\text {rel }} . $ | (2) |
其中:Xrel为大KC与小KC之间的过渡函数,Uc为水流条件下泥沙起动的水深平均流速。Xrel与Uc的表征形式如下:
| $ X_{\text {rel }} =\frac{X_{\text {eff }}}{1+X_{\text {eff }}}, $ | (3) |
| $ \begin{align*} X_{\text {eff }} & =0.03\left(1-0.35 U_{\mathrm{c}} / U\right)(\mathrm{KC}-6) ; \\ U_{c} & =1.4\left(2 \sqrt{s g d_{50}}+10.5 \nu / d_{50}\right) . \end{align*} $ | (4) |
其中:Xeff为半个波周期内的泥沙相对位移,s为相对密度,g为重力加速度,ν为运动黏滞系数。
Dogan[11]利用大直径和小直径单桩的冲刷深度数据,分析了平衡冲刷深度和KC、D/L与改进后的Ursell数间的关系,分别得到了式(5)、(6)和(7)。
| $ S / D=1.3[1-\exp (-0.022(\mathrm{KC}-4))], \mathrm{KC} \geqslant 4; $ | (5) |
| $ S / D=0.0037 \frac{\mathrm{KC}^{2 / 3}}{\sqrt{D / L}}; $ | (6) |
| $ S / D=0.75\left[1-\exp \left(-0.015 U_{\mathrm{rp}}^{0.6}\right)\right], U_{\mathrm{rp}} \leqslant 10^{5}. $ | (7) |
其中Urp为改进后的Ursell数,
式(5)根据小比尺条件下不同泥沙粒径的大量动床冲刷试验数据对式(1)进行了改进。式(6)和(7)代表 2种对大直径和小直径单桩均适用的相对平衡冲刷深度公式。
除此之外,Webb等[15]在式(1)的基础上对大直径、小直径单桩的冲刷深度数据进行了重新拟合,更新了相关的系数值,得到
| $ S / D=1.3[1-0.99 \exp (-0.022(\mathrm{KC}-0.1))] . $ | (8) |
Raaijmakers等[19]和Qi等[16]提出的波流条件下的平衡冲刷深度公式可以简化为纯波条件的公式:
| $ S / D=1.5 \tanh \left(\frac{h}{D}\right) K_{\mathrm{w}} K_{\mathrm{h}} , $ | (9) |
| $ \lg (S / D)=-0.8 \exp \left(0.14 / F r_{\mathrm{a}}\right)+1.11 . $ | (10) |
其中:Kw为波浪作用的修正因子,在纯波条件下Kw=1-exp(-0.012KC);Kh为桩高修正系数,Kh=(hp/h)0.67,hp为桩高;Froude数Fra=Ua/
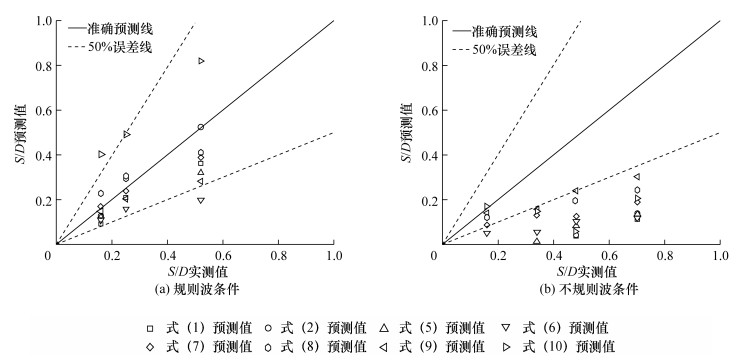
利用文[27]以及本文试验数据,对比验证式(1)、(2)、(5)—(10)在大比尺试验中规则波与不规则波条件下的适用性,结果如图 3所示。在规则波条件下,各公式预测出的最大冲刷深度分布在50%的误差范围内;在不规则波条件下,式(7)和(10)的预测值并不随实测值增大而增大。结合表 1和图 2可知,增大的实测值对应着增大的KC值,而式(7)和(10)的预测值并不符合该趋势,说明这2个公式在不规则波条件下不适用。这是因为这2个公式分别未考虑U(与泥沙起动有关)和波浪非线性的影响。此外,在不规则波条件下,各公式的预测值基本不分布在50%的误差线内,说明相比规则波条件,不规则波条件下各公式的预测准确度有待提高。
|
| 图 3 大比尺试验中不同波条件下S/D预测值与实测值的对比 |
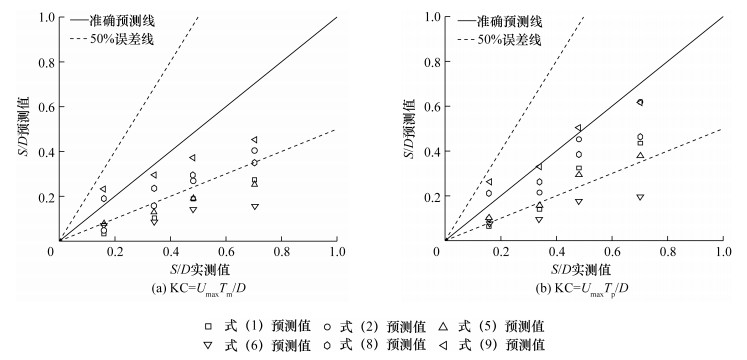
Prepernau等[22]曾通过大比尺水槽试验表明式(1)低估了在不规则波下的冲刷深度,并建议采用波的最大轨迹速度Umax和平均波周期Tm代替文[17]采用的U和Tp来表征KC,再通过式(1)计算平衡冲刷深度,则结果将与大比尺水槽的试验值吻合。因此,本文使用KC=UmaxTm/D对S/D分别基于式(1)、(2)、(5)、(6)、(8)和(9)进行了预测,并与实测值进行了比较。结果表明,除式(8)和(9)以外,其余公式的预测值大部分不分布在50%的误差范围内(见图 4a)。事实上,Prepernau等[22]模拟的是整个风暴潮的连续过程,其中包括了不同波能情况下的冲刷回填,实质上是研究考虑比尺效应影响下冲刷回填后的平衡冲刷深度计算问题。Sumer等[18]认为无论最初有或无冲刷坑的波浪冲刷试验,都可以用相同KC通过式(1)计算平衡冲刷深度。但本文试验结果显示,针对最初床面有冲刷坑情况下,计算冲刷回填后的平衡冲刷深度的方法,并不适合最初床面平整的情况。
|
| 图 4 不同KC值计算方法下S/D预测值与实测值的对比 |
为了提高各公式的整体准确度,本文使用KC=UmaxTp/D对S/D分别基于式(1)、(2)、(5)、(6)、(8)和(9)进行了预测,由于预测值都是随着KC的增大而增大,而Umax、Tp计算出的KC已经是不同组合条件下的最大KC,因此该预测值也是可预测值的最大值,结果如图 4b所示。对比图 4a和4b可以看出,利用Umax、Tp表征KC而计算出的预测值更接近实测值,表明在不规则波条件下的小直径单桩冲刷试验中,使用KC=UmaxTp/D可以提高各公式的准确性。但是式(1)和(6)的预测值整体上仍未进入50%的误差范围内。
3 冲刷坑体积目前为止,很少有研究系统地分析实验室和工程现场的冲刷坑体积。冲刷坑体积通常随着平衡冲刷深度的增加而增加。基于文[11, 14, 15, 19]中描述平衡冲刷深度、冲刷坑体积与KC的函数,对式(5)、(2)、(8)和(9)进行非线性回归,分别得到以下4种冲刷坑体积计算公式:
| $ \begin{gathered} V / D^3=39.738\{1.3-1.3 \exp [-0.02(\mathrm{KC}-4)]\}^{2.241}= \\ 39.738 f^{2.241}(\mathrm{KC}) ; \end{gathered} $ | (11) |
| $ \begin{gathered} V / D^{3}=10.506\left[2.5\left(1-0.5 \frac{U_{\mathrm{c}}}{U_{\max }}\right) X_{\mathrm{rel}}\right]^{1.785}= \\ 10.506 f^{1.785}(\mathrm{KC}) ; \end{gathered} $ | (12) |
| $ \begin{gathered} V / D^{3}=62.057\{1.3-1.287 \exp [-0.022 \\ (\mathrm{KC}-0.1)]\}^{3.387}=62.057 f^{3.387}(\mathrm{KC}) . \end{gathered} $ | (13) |
| $ \begin{gathered} V / D^{3}=19.695\left[\tanh \left(\frac{h}{D}\right) K_{\mathrm{w}} K_{\mathrm{h}}\right]^{3.042}= \\ 19.695 f^{3.042}(\mathrm{KC}) . \end{gathered} $ | (14) |
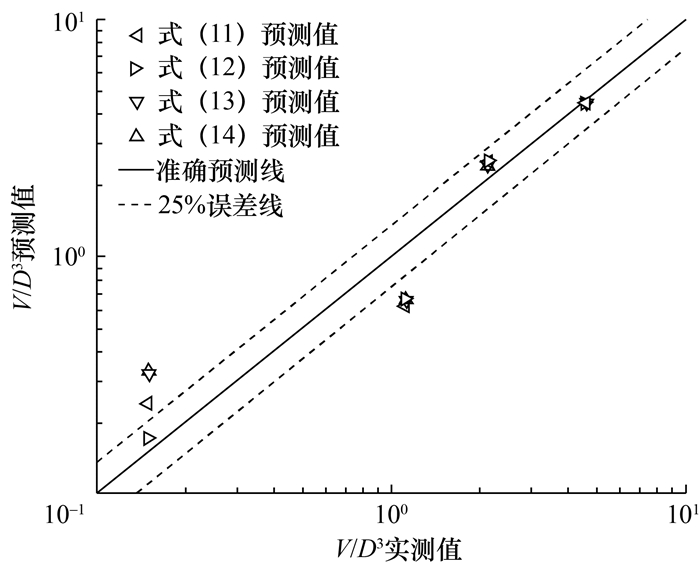
图 5为式(11)—(14)计算的冲刷坑体积预测值和实测值。4个公式的预测值分布在25%误差范围内的概率分别为50%、75%、50%和50%,因此式(12)可以作为合理估计冲刷坑体积的预测公式。在海上风电建设工程现场,往往在完成矗立单桩之后,铺设防护措施之前,冲刷坑就已经形成,但在现有行业规范中并没有对冲刷坑体积进行系统的统计或预测。因此,式(12)的建立具有较强的现实意义和实用价值。
|
| 图 5 冲刷坑体积预测值与实测值 |
4 结论
本文通过大比尺物理模型试验,对不规则波条件下的单桩局部冲刷进行研究,结果表明:前人研究的平衡冲刷深度公式在规则波条件下具有较好的适用性,而在不规则波条件下的预测值普遍小于实测值。本文通过改进KC的计算方法, 有效提高了各公式在不规则波条件下的预测准确度;以现有平衡冲刷深度公式为基础提出了局部冲刷坑体积预测公式,为单桩防护施工时抛石冗余量的估算提供了简便快捷的预测方法。
| [1] |
CHEN G, LI X B, SUN B, et al. Effect of incoming boundary layer thickness on the flow dynamics of a square finite wall-mounted cylinder[J]. Physics of Fluids, 2022, 34(1): 015105. DOI:10.1063/5.0076541 |
| [2] |
QI W G, LIU J, GAO F P, et al. Quantifying the spatiotemporal evolution of the turbulent horseshoe vortex in front of a vertical cylinder[J]. Physics of Fluids, 2022, 34(1): 015110. DOI:10.1063/5.0076648 |
| [3] |
WARDHANA K, HADIPRIONO F C. Analysis of recent bridge failures in the United States[J]. Journal of Performance of Constructed Facilities, 2003, 17(3): 144-150. DOI:10.1061/(ASCE)0887-3828(2003)17:3(144) |
| [4] |
IMAM B M, CHRYSSANTHOPOULOS M K. Causes and consequences of metallic bridge failures[J]. Structural Engineering International, 2012, 22(1): 93-98. DOI:10.2749/101686612X13216060213437 |
| [5] |
DU S, WANG Z, WANG R, et al. Effects of flow intensity on local scour around a submerged square pile in a steady current[J]. Physics of Fluids, 2022, 34(8): 085126. DOI:10.1063/5.0103556 |
| [6] |
REHMAN K, WANG Y C, WASEEM M, et al. Tree-based machine learning models for prediction of bed elevation around bridge piers[J]. Physics of Fluids, 2022, 34(8): 085105. DOI:10.1063/5.0098394 |
| [7] |
SUMER B M, FREDSØE J. The mechanics of scour in the marine environment[M]. London: World Scientific, 2002.
|
| [8] |
WHITEHOUSE R. Scour at marine structures: A manual for practical applications[M]. London: Thomas Telford, 1998.
|
| [9] |
GUAN D W, XIE Y X, YAO Z S, et al. Local scour at offshore windfarm monopile foundations: A review[J]. Water Science and Engineering, 2022, 15(1): 29-39. DOI:10.1016/j.wse.2021.12.006 |
| [10] |
梁森栋. 海洋环境中结构基础冲刷防护措施及预警模型研究[D]. 北京: 清华大学, 2014. LIANG S D. Study on Scour Countermeasures and Forecasting for Structure Foundations in Marine Environment[D]. Beijing: Tsinghua University, 2014. (in Chinese) |
| [11] |
DOGAN M. The equilibrium depth of wave scour around both slender and large piles[J]. Ocean Engineering, 2021, 236: 109474. DOI:10.1016/j.oceaneng.2021.109474 |
| [12] |
KOBAYASHI T, ODA K. Experimental study on developing process of local scour around a vertical cylinder[M]. Tobe: Coastal Engineering, 1995.
|
| [13] |
SUMER B M, FREDSØE J, CHRISTIANSEN N. Scour around vertical pile in waves[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1992, 118(1): 15-31. DOI:10.1061/(ASCE)0733-950X(1992)118:1(15) |
| [14] |
ZANKE U C E, HSU T W, ROLAND A, et al. Equilibrium scour depths around piles in noncohesive sediments under currents and waves[J]. Coastal Engineering, 2011, 58(10): 986-991. DOI:10.1016/j.coastaleng.2011.05.011 |
| [15] |
WEBB B M, MATTHEWS M T. Wave-induced scour at cylindrical piles: Estimating equilibrium scour depth in a transition zone[J]. Transportation Research Record, 2014, 2436(1): 148-155. DOI:10.3141/2436-15 |
| [16] |
QI W G, GAO F P. Equilibrium scour depth at offshore monopile foundation in combined waves and current[J]. Science China Technological Sciences, 2014, 57(5): 1030-1039. DOI:10.1007/s11431-014-5538-9 |
| [17] |
SUMER B M, FREDSØE J. Scour around pile in combined waves and current[J]. Journal of Hydraulic Engineering, 2001, 127(5): 403-411. DOI:10.1061/(ASCE)0733-9429(2001)127:5(403) |
| [18] |
SUMER B M, PETERSEN T U, LOCATELLI L, et al. Backfilling of a scour hole around a pile in waves and current[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2013, 139(1): 9-23. DOI:10.1061/(ASCE)WW.1943-5460.0000161 |
| [19] |
RAAIJMAKERS T, RUDOLPH D. Time-dependent scour development under combined current and waves conditions- laboratory experiments with online monitoring technique[C]// Proceedings 4th International Conference on Scour and Erosion. Tokyo: Japanese Geotechnical Society, 2008: 152-161.
|
| [20] |
BREUSERS H N C, NICOLLET G, SHEN H W. Local scour around cylindrical piers[J]. Journal of Hydraulic Research, 1977, 15(3): 211-252. DOI:10.1080/00221687709499645 |
| [21] |
CHEN S G, GONG E Y, ZHAO X, et al. Large-scale experimental study on scour around offshore wind monopiles under irregular waves[J]. Water Science and Engineering, 2022, 15(1): 40-46. DOI:10.1016/j.wse.2021.12.003 |
| [22] |
PREPERNAU U, GRVNE J, Schmidt-Koppenhagen R, et al. Large-scale model tests on scour around slender monopile under live-bed conditions[C]// Proceedings of the 2nd International conference on the Application of Physical Modeling to Port and Coastal Protection. Bari: The American Society of Civil Engineers, 2008: 2-5.
|
| [23] |
LINK O, ZANKE U. On the time-dependent scour-hole volume evolution at a circular pier in uniform coarse sand[C]// Proceedings 2nd International Conference on Scour and Erosion. Singapore: The American Society of Civil Engineers, 2004.
|
| [24] |
HARTVIG P A, THOMSEN J M C, FRIGAARD P, et al. Experimental study of the development of scour and backfilling[J]. Coastal Engineering Journal, 2010, 52(02): 157-194. DOI:10.1142/S0578563410002154 |
| [25] |
WELZEL M, SCHENDEL A, SCHLURMANN T, et al. Volume-based assessment of erosion patterns around a hydrodynamic transparent offshore structure[J]. Energies, 2019, 12(16): 3089. DOI:10.3390/en12163089 |
| [26] |
KAWATA Y, TSUCHIYA Y. Local scour around cylindrical piles due to waves and currents combined[J]. Coastal Engineering Proceedings, 1988, 1(21): 97. |
| [27] |
CHEN B, LI S W. Experimental study of local scour around a vertical cylinder under wave-only and combined wave-current conditions in a large-scale flume[J]. Journal of Hydraulic Engineering, 2018, 144(9): 04018058. DOI:10.1061/(ASCE)HY.1943-7900.0001502 |



