引用本文
王振宇, 王磊. 多策略帝王蝶优化算法及其工程应用[J]. 清华大学学报(自然科学版), 2024, 64(4): 668-678.  
WANG Zhenyu, WANG Lei. Improved monarch butterfly optimization algorithm and its engineering application[J]. Journal of Tsinghua University (Science and Technology), 2024, 64(4): 668-678.  
多策略帝王蝶优化算法及其工程应用
王振宇, 王磊    
西安理工大学 计算机科学与工程学院, 西安 710048
收稿日期：2023-07-18
基金项目：国家自然科学基金资助项目(62176146)
作者简介：王振宇(1993—), 男, 博士研究生
通讯作者：王磊, 教授, E-mail: leiwang@xaut.edu.cn
摘要：针对帝王蝶优化算法存在的收敛速度慢、寻优精度低和易陷入局部极值等缺陷, 提出了一种多策略改进的帝王蝶优化算法。首先, 采用正向正态云发生器对父代帝王蝶个体执行非线性云化操作, 增加候选解数量, 提高算法的局部开发能力; 之后, 引入基于凸透镜成像的反向学习策略, 应用到当前最优个体上产生新的个体, 提高算法收敛速度和寻优精度; 最后, 在调整算子中融入自适应策略, 增加种群的多样性, 避免算法陷入局部最优。通过对8个基准测试函数的寻优对比, 以及Wilcoxon秩和检验结果的对比, 发现改进算法具有更好的收敛性能、寻优性能和鲁棒性。与此同时, 通过工程应用中压力容器设计和焊接梁设计的优化对比, 进一步验证了改进算法处理实际工程问题时的优越性。
关键词：帝王蝶优化算法    正态云模型    凸透镜成像    自适应调整率    压力容器设计    焊接梁设计    
Improved monarch butterfly optimization algorithm and its engineering application
WANG Zhenyu, WANG Lei    
School of Computer Science and Engineering, Xi'an University of Technology, Xi'an, 710048, China
Abstract: [Objective] In recent years, a large number of nonconvex, highly nonlinear, multimodal, and multivariable complex optimization problems have emerged in scientific and engineering technology design due to the continuous development of science and technology. Owing to their advantages such as simple programming, flexible operation, and efficient optimization, intelligent optimization algorithms have become research hotspots to address diverse complex optimization problems in engineering applications. They have been successfully used to solve practical problems such as neural networks, resource allocation, and target tracking. In this research, multiple strategies were developed to improve the existing monarch optimization algorithm to address its shortcomings, such as slow convergence speed, low optimization accuracy, and ease of falling into local extremum. [Methods] First, the forward normal cloud generator is used to perform nonlinear cloud operation on the parent monarch butterfly, increasing the number of candidate solutions and improving the local development ability of the algorithm. Subsequently, an opposition-based learning strategy based on convex lens imaging is used to the current optimal individual which is generated by normal cloud generator to generate new individuals and improve the convergence accuracy and speed of the algorithm. Finally, adaptive strategies are incorporated into the adjustment operator to diversify the population. [Results] Several experiments were performed on benchmark functions to verify the performance of the algorithm: (1) Different strategies proposed were analyzed using ablation experiments to verify their effectiveness. The results revealed that the proposed strategies can effectively improve the algorithm's performance. (2) The improved algorithm was compared with other swarm intelligent optimization algorithms, and the results revealed that the improved algorithm can achieve the best results on most test functions. (3) The improved algorithm was also compared with other improved versions of monarch optimization algorithm, and the results revealed that the improved algorithm exhibited more advantages such as fast convergence speed and high convergence precision. (4) The Wilcoxon rank sum test and Friedman test were used to verify the performance of the proposed algorithm. The results revealed that the improved algorithm is superior to other algorithms. [Conclusions] The optimization and comparison results of the pressure vessel design and welded beam design in engineering applications further verified the superiority of the improved algorithm in addressing real-world engineering problems.
Key words: monarch butterfly optimization algorithm    normal cloud model    convex lens imaging    adaptive adjustment rate    pressure vessel design    welded beam design    

科学和工程技术设计中存在着大量非凸、高度非线性、多峰多变量的复杂优化问题，智能优化算法具有编程简单、操作灵活以及寻优高效等优点，在处理工程应用中各种复杂优化问题的研究中成为热点[1]，且已成功用于解决神经网络[2]、资源分配[3]以及目标跟踪[4]等实际问题。

智能优化算法中的帝王蝶优化(monarch butterfly optimization，MBO)算法是由Wang等[5]于2019年提出的一种模拟帝王蝶的迁徙和适应环境行为的新型智能优化算法，MBO算法与其他智能优化算法相比，具有需调节参数少、寻优稳定性强、更易于编程实现等优点。然而，MBO算法迭代过程中也存在收敛速度慢、寻优精度低、易陷入局部极值等不足。针对以上不足，众多研究者提出各种改进策略，例如，文[6]为解决云环境下负载不均衡问题，在响应时间差的基础上为MBO算法定义了响应阈值的概念，从而简化和调整迁移算子，结果表明，所提改进算法在解决实际问题方面有较好的适用性，但参数较多，且仍然会在运算后期陷入局部最优；文[7]为解决算法易陷入局部最优的问题，引入了传递函数和步长参数更新方法，并将改进后的算法用于特征选择优化问题，但算法改进步骤较多，时间复杂度较高；文[8]为充分利用种群共享信息，在迁移和调整算子中将个体进化方式修正为基于维度方向的均值而非单个个体，促进了算法快速收敛，但算法在对高维函数寻优时仍会陷入局部最优。

在智能优化算法中，提高种群多样性、协调算法全局勘探与局部开发间的转换，以及优化个体的位置更新过程，都是提高算法寻优性能的有效措施。为了提高MBO算法的寻优性能和收敛精度，本文提出一种多策略帝王蝶优化(multi-strategy monarch butterfly optimization，MMBO)算法。首先，对目标父代个体进行云化操作，扩大搜索范围，保证算法的收敛精度；其次，利用凸透镜成像反向学习策略对帝王蝶最佳位置进行更新扰动，避免算法陷入局部最优；最后，将MBO算法的调整算子更新为自适应调整算子，使调整率随着迭代次数的变化进行线性调整，增强算法的寻优能力。通过8个基准测试函数对算法进行寻优性能测试，并将算法应用于压力容器设计和焊接梁设计，结果表明MMBO算法相比其他算法更具优势。

1 改进帝王蝶优化算法 1.1 基于正态云模型的迁移算子

在所有不确定因素中，随机性与模糊性属于最为普遍的特征，为了克服MBO算法处理不确定因素时的不足，选择正向正态云模型呈现定量描述与定性概念之间的不确定性转换，该模型常用一个3元组(期望Ex, 熵En, 超熵He)描述云模型的3个数字特征，再利用正向发生器产生模型的若干2维点——云滴。

图 1展现了正态云发生器的云滴分布，可用于说明云滴分布与云模型的数字特征间的相关性。确定度表示每个云滴对应的概率密度值。当En增加时，云滴的分布范围扩大，而离散度随着He的增加而增加，这反映了正态云模型的随机性和模糊性。

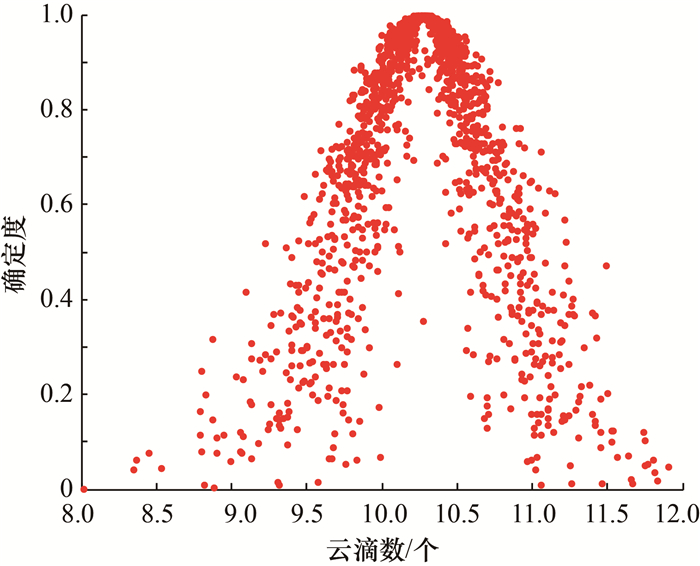
图 1 正态云发生器的云滴分布
图选项

MBO算法利用Levy飞行策略增加网格分布密度，然而新网格是随机的，不一定分布在最优解附近，因此需要更多的迭代次数和更高的调整率才能实现高精度搜索，难以保证自身认知的局部开发能力。为此，本文利用正向正态云发生器对随机选择的2个父代个体(xr1和xr2)分别执行云化操作，以生成新的取值空间信息。Ex作为云的重要组成部分，其设置不改变初始策略，仍以随机个体的位置为基准，以体现保守能力；En体现探索范围，不同的En衡量了后代个体与xr1或xr2之间的径向距离；调整He可获得不同的个体离散度，n则决定了生成后代的数量。据此给出新的迁移算子公式：

$\boldsymbol{X}_{i, k}^{t+1}= \begin{cases}G\left(x_{r 1, k}^t, \mathrm{En}, \mathrm{He}, n\right), & r \leqslant p ; \\ G\left(x_{r 2, k}^t, \mathrm{En}, \mathrm{He}, n\right), & r>p ;\end{cases}$ (1)
$\operatorname{En}=\frac{\delta\left(\boldsymbol{X}_{\max }(k)-\boldsymbol{X}_{\min }(k)\right)}{\tan \left(\frac{\pi t}{4 T_{\max }}+\frac{\pi}{4}\right)} ;$ (2)
$\mathrm{He}=\frac{1}{10} \mathrm{En}.$ (3)

其中：Xi, kt+1为个体Xi迭代至第(t+1)代时的第k维分量，t为迭代次数；G为正态云发生函数；r为[0, 1]的随机数，服从均匀分布；p为种群选择概率；δ为控制系数，用于调节云滴的不确定性分布；Xmax(k)和Xmin(k)分别为第k维边界的最大值和最小值；Tmax为最大迭代次数。En和He采取了非线性递减的形式，随着t的增加，种群逐步向最优解靠近，从而逐步缩小更新范围，提高搜索精度。

1.2 凸透镜成像的反向学习策略

MBO在执行后期的种群多样性降低，帝王蝶群体集中在最佳个体附近，如果最佳个体陷入局部最优，则帝王蝶群体难以跳出局部极值的空间区域，这会导致算法的寻优精度降低。为解决这一问题，本文采用凸透镜成像的反向学习方法对帝王蝶群体进行扰动，以此增强种群多样性，增强算法跳出局部最优的能力。

本文利用物理学中的凸透镜成像原理来模拟帝王蝶寻找反向点的过程。设在决策向量[lb, ub]上有1个高度为h的个体Q，其在x轴的投影为Y(Y为全局最优个体)。选取[lb, ub]的中点作为基点位置O，并在基点位置放置一个焦距为F的凸透镜。个体Q通过凸透镜成像可以得到一个高度为h*的倒像Q*，此时便产生了反向个体Y*。根据凸透镜成像原理可得

$\frac{\frac{\mathbf{u b}+\mathbf{l b}}{2}-\boldsymbol{Y}}{\boldsymbol{Y}^*-\frac{\mathbf{u b}+\mathbf{l} \mathbf{b}}{2}}=\eta.$ (4)

其中$\eta=\frac{h}{h^*}$，称为伸缩因子。

反向个体为

$\boldsymbol{Y}^*=\frac{\mathbf{u b}+\mathbf{l} \mathbf{b}}{2}+\frac{\mathbf{u b}+\mathbf{l b}}{2 \eta}-\frac{\boldsymbol{Y}}{\eta}.$ (5)

将式(5)推广至全局搜索空间可得

$\boldsymbol{Y}_j^*=\frac{\mathbf{u} \mathbf{b}_j+\mathbf{l} \mathbf{b}_j}{2}+\frac{\mathbf{u } \mathbf{b}_j+\mathbf{l} \mathbf{b}_j}{2 \eta}-\frac{\boldsymbol{Y}_j}{\eta}.$ (6)

其中：Yj和Yj*分别为Y和Y*的第j维向量，ubj和lbj分别为ub和lb的第j维向量。同时，本文引入贪婪机制对反向学习后的个体进行选择，以获得最优个体。贪婪机制的数学模型为

$\boldsymbol{Y}_{\text {new }}(t)= \begin{cases}\boldsymbol{Y}^*, & f(\boldsymbol{Y}) \geqslant f\left(\boldsymbol{Y}^*\right) ; \\ \boldsymbol{Y}, & f(\boldsymbol{Y})<f\left(\boldsymbol{Y}^*\right) .\end{cases}$ (7)

其中Ynew(t)为第t代的个体适应度。

1.3 自适应调整算子

调整率(adjusting rate, AR)体现的是帝王蝶个体突变的能力。在进化前期，若个体搜索步长较大，则可在更广范围内探索，较快地定位至全局最优解附近，也能避免较早陷入局部极值，此时AR应取较小值，为突变预留更大的概率区间；在进化后期，为缩小搜索范围，深入地在局部区域挖掘，应降低突变概率，保持较大的AR。本文提出的AR公式为：

$\mathrm{AR}=|m t-n|, $ (8)
$n=\mathrm{AR}_{\max } \exp \left(-0.5\left(\frac{t}{T_{\max }}\right)^2\right)-\mathrm{AR}_{\text {min }} , $ (9)
$m=\frac{\exp \left(2\left(1-\frac{t}{T_{\max }+1}\right)\right)-\exp \left(-2\left(1-\frac{t}{T_{\max }+1}\right)\right)}{T_{\max }}.$ (10)

其中: ARmax和ARmin分别是AR的上界和下界，取值范围均为[0, 1]。为扩大参数选取的范围，设定ARmax= 0.8，ARmin=0.2。

1.4 MMBO实现步骤

步骤1  对算法参数进行初始化，包括δ、n、Tmax、空间维度D和种群规模N；

步骤2  将原始种群初始化为2个子种群，各种群利用式(1)—(3)对个体进行云化操作；

步骤3  利用式(6)对帝王蝶个体进行凸透镜成像的反向学习策略，并利用式(7)选择出最优个体；

步骤4  根据式(8)更新AR；

步骤5  达到Tmax则退出循环，未达到则返回步骤2。

2 算法性能测试与分析

选取文[9]中的8个基准函数进行寻优测试，其中f1~f4为单峰函数，能够表征算法在搜索和收敛方面的能力；f5~f8为多峰函数，能够表征函数跳出局部极值的能力；所有函数的最优值也即最小值均为0。详细信息如表 1所示。

表 1 测试函数信息
编号 名称 取值范围 特征
f1 Sphere [-100, 100] 单峰
f2 Step [-100, 100] 单峰
f3 Schwefel 2.22 [-10, 10] 单峰
f4 Schwefel 1.2 [-100, 100] 单峰
f5 Rastrigin [-5.12, 5.12] 多峰
f6 Ackley [-32, 32] 多峰
f7 Griewank [-600, 600] 多峰
f8 Penalized1 [-50, 50] 多峰
表选项

性能测试仿真实验采用的计算机配置为：Intel Core i5-4210U处理器(主频为1.70 GHz)，64位操作系统。使用软件为MATLAB2016。

为确保实验公平性和结果准确性，设置δ=0.2，n=5，N=50，D=30，Tmax=500。按照智能优化算法的随机实验原则，采用完全随机生成初始解的方式以初始化搜索空间。为降低随机初始解对实验结果的影响，每组实验均独立运行50次并以平均值、标准差、最优值作为算法性能的评价指标。其中，平均值反映算法的收敛精度和寻优性能，最优值反映算法的最大寻优程度，标准差反映算法的稳定性。

2.1 不同改进策略的寻优性能对比

为了分析提出的改进策略对MBO算法的有效性以及性能的影响，分别利用MBO算法、仅引入正态云模型的CMBO(cloud monarch butterfly optimization)算法、仅引入凸透镜成像反向学习策略的LMBO(lens monarch butterfly optimization)算法、仅引入自适应调整算子的AMBO(adaptive monarch butterfly optimization)算法和引入全部3种改进策略的MMBO算法，对基准函数进行优化测试，结果如表 2所示。可以看出，CMBO算法对性能的改进能力有限，仅采用正态云化策略不能完全避免算法陷入局部最优，而LMBO算法可以寻找到函数f1和f2的理论最优值，这是由于凸透镜成像的反向学习策略产生反向解，引导种群向全局最优值靠拢；在固定维度的多峰函数f8上，所有算法寻找的最优值的数量级较为接近，MMBO算法的标准差最小，LMBO、AMBO和CMBO算法的标准差为第2—4小，均优于MBO，进一步验证了MMBO算法的稳定性；MMBO算法比MBO算法在求解精度上有很大提升，寻优性能更加稳定。

表 2 不同改进策略对比结果
函数 算法 最优值 平均值 标准差
f1 MBO 2.58×10-13 1.68×10-10 6.83×10-11
CMBO 2.16×10-18 6.25×10-15 8.58×10-12
LMBO 0 0 0
AMBO 3.51×10-23 1.23×10-20 1.78×10-18
MMBO 0 0 0
f2 MBO 6.35×10-28 9.85×10-26 8.12×10-24
CMBO 9.35×10-39 6.35×10-35 5.52×10-33
LMBO 0 0 0
AMBO 1.16×10-37 8.18×10-36 5.24×10-34
MMBO 0 0 0
f3 MBO 6.39×10-13 2.58×10-9 5.81×10-7
CMBO 5.17×10-19 1.59×10-17 9.85×10-15
LMBO 3.53×10-20 6.57×10-18 5.36×10-16
AMBO 2.18×10-16 5.69×10-13 4.15×10-16
MMBO 5.13×10-22 6.52×10-21 8.52×10-20
f4 MBO 1.34×10-5 7.17×10-3 8.82×10-4
CMBO 2.58×10-12 6.35×10-8 9.94×10-7
LMBO 2.57×10-15 2.81×10-12 5.86×10-15
AMBO 5.14×10-16 2.25×10-12 1.25×10-11
MMBO 7.65×10-16 5.68×10-15 9.64×10-12
f5 MBO 6.23×10-4 6.54×10-2 1.24×10-5
CMBO 1.27×10-16 6.51×10-12 5.57×10-10
LMBO 5.87×10-14 3.58×10-12 2.54×10-12
AMBO 4.14×10-10 8.25×10-9 5.12×10-7
MMBO 6.35×10-21 1.68×10-19 2.64×10-18
f6 MBO 7.85×10-1 1.01×101 3.65×10-1
CMBO 2.28×10-7 3.84×10-5 3.87×10-5
LMBO 1.23×10-8 5.38×10-5 5.35×10-5
AMBO 8.32×10-8 6.82×10-7 4.32×10-6
MMBO 8.88×10-16 8.88×10-16 8.88×10-16
f7 MBO 5.98×10-4 2.32×10-1 1.52×10-2
CMBO 7.35×10-10 5.24×10-8 1.23×10-6
LMBO 5.37×10-9 9.68×10-7 5.24×10-8
AMBO 5.22×10-13 8.56×10-11 5.12×10-10
MMBO 1.86×10-16 4.45×10-13 8.53×10-13
f8 MBO 9.38×10-2 9.36 5.24×10
CMBO 4.32×10-7 7.14×10-5 7.25×10-3
LMBO 3.56×10-8 5.69×10-6 5.12×10-7
AMBO 5.21×10-8 6.19×10-8 1.29×10-5
MMBO 2.39×10-8 6.83×10-6 7.21×10-8
表选项

2.2 MMBO算法与其他算法的对比分析

为了充分验证本文所提改进算法的性能，将MMBO算法与MBO及以下算法进行比较：1)增强型黑猩猩优化算法(improved chimp optimization algorithm，IChOA)[10]；2)多策略融合的改进灰狼优化(tent grey wolf optimization，TGWO)算法[11]；3)蚁群优化(ant colony optimization，ACO)算法[12]；4)海鸥优化算法(seagull optimization algorithm，SOA)[13]。

IChOA是一种基于翻筋斗觅食策略的改进黑猩猩优化算法；TGWO算法是一种基于Tent混沌映射初始化种群的改进灰狼算法，ACO算法和SOA作为经典的群智能优化算法，已被运用在不同的学科和工程领域。各算法的设置参考了文[10-13]，如表 3所示。以最优值、平均值、标准差作为算法性能的评价指标，实验结果如表 4所示。可以看出，MMBO在所有测试函数的结果均优于其他算法。对于函数f1和f2，MMBO能够寻找到理论最优值，寻优性能明显优于其他算法，说明改进算法具有较高的开发寻优能力，能够提高收敛精度。而对于其他测试函数，MMBO也能够寻找到更接近理论最优值的值，表明算法在自适应的调整率下跳出了函数的局部极值，提高了全局搜索能力。

表 3 算法参数设置
算法 参数设置
IChOA 随机向量r1∈[0, 1], 随机向量r2∈[0, 1], 收敛因子f∈(0, 2.5), 控制系数u∈[0, 1]
TGWO 非线性调节系数λ1=0.2, 非线性调节系数λ2=0.2, 权重因子初值bs=0.3, 权重因子终值bf=1
ACO 信息因子α=1, 期望因子β=2, 信息素Q=1
SOA 变化次数控制参数fc=2，螺旋控制参数u=1, 螺旋控制参数v=1
表选项

表 4 不同算法求解函数的结果对比
函数 算法 最优值 平均值 标准差
f1 MBO 8.84×10-12 1.52×10-10 6.58×10-11
ACO 4.23×10-4 5.35×10-3 6.25×10-5
TGWO 9.32×10-9 8.54×10-7 4.32×10-9
IChOA 9.68×10-12 5.32×10-9 5.38×10-10
SOA 6.23×10-2 3.56 5.35×10-1
MMBO 0 0 0
f2 MBO 5.82×10-27 9.85×10-26 9.13×10-22
ACO 8.52×10-7 5.05×10-5 6.84×10-4
TGWO 1.13×10-12 4.15×10-12 6.11×10-10
IChOA 9.79×10-11 5.14×10-10 5.38×10-9
SOA 1.32×10-6 2.32×10-5 5.28×10-5
MMBO 0 0 0
f3 MBO 5.26×10-12 2.15×10-9 3.62×10-7
ACO 8.23 5.12×10 6.25
TGWO 6.32×10-8 2.25×10-7 5.21×10-5
IChOA 6.35×10-6 2.14×104 2.57×10-4
SOA 3.56×102 6.23×106 5.28×104
MMBO 6.83×10-22 7.33×10-21 8.52×10-20
f4 MBO 6.85×10-5 6.16×10-3 5.23×10-4
ACO 6.12×10-1 6.83×102 5.21×10-1
TGWO 2.14×10-4 5.23×10-3 2.91×10-6
IChOA 5.26×10-12 5.34×10-12 4.35×10-10
SOA 2.36×10-1 5.32×10 8.58
MMBO 1.13×10-16 3.68×10-15 9.61×10-12
f5 MBO 5.85×10-3 6.54×10-2 1.24×10-5
ACO 1.23×10-2 7.11×10-1 6.32×10
TGWO 4.83×10-12 2.21×10-9 6.87×10-11
IChOA 6.58×10-19 3.25×10-15 1.35×10-17
SOA 2.56×10-3 5.17 1.27×10-1
MMBO 6.38×10-21 1.65×10-20 2.51×10-18
f6 MBO 7.85×10-1 1.67×10 4.93×10-1
ACO 5.69×10-3 6.75×10-2 2.57×10-3
TGWO 3.67×10-8 2.69×10-6 6.87×10-4
IChOA 2.35×10-6 1.17×10-5 1.23×10-5
SOA 1.58×10 9.21×103 2.35
MMBO 8.88×10-16 8.88×10-16 8.88×10-16
f7 MBO 5.98×10-4 2.95×10-1 1.36×10-2
ACO 6.25×10-6 1.25×10-4 5.85×10-4
TGWO 9.63×10-5 2.58×10-4 6.32×10-5
IChOA 5.24×10-9 2.35×10-7 5.24×10-10
SOA 5.28×10-3 2.57×10-1 2.39×10-2
MMBO 4.52×10-16 4.49×10-11 8.61×10-13
f8 MBO 5.35×10-1 9.11 6.68×10
ACO 5.31×106 7.65×108 2.24×106
TGWO 5.33×10-13 8.25×10-9 6.35×10-1
IChOA 4.58×10-12 1.23×10-9 2.57×10-8
SOA 3.27×10-2 2.57 5.38×10-1
MMBO 5.32×10-14 6.77×10-10 7.15×10-8
表选项

2.3 MMBO算法与其他改进MBO算法的对比分析

将MMBO算法与其他性能优异的改进MBO算法进行对比，包括基于知识驱动的增强型MBO算法(improved MBO algorithm with a knowledge-driven learning mechanism，KDLMBO)[14]、基于协方差的聚类MBO算法(covariance-based clustered MBO，CCMBO)[15]。对比算法的参数分别按照文[14]和[15]设置，实验结果如表 5所示。可以看出，MMBO算法在8组测试函数的寻优能力明显优于其他算法。对于函数f1和f2，MMBO算法相比其他算法始终保持着寻优性能的第1位，并且拥有优异的稳定性，其收敛速度比MBO也有一定的提升；对于函数f3，MMBO算法的寻优结果仅次于KDLMBO，寻优能力位居第2；对于函数f6，MMBO算法能够在多个极值点的测试函数中寻得理论最优值。总体来说，无论单峰函数还是多峰函数，MMBO算法均表现出优异的寻优能力和稳定性。

表 5 不同改进MBO求解函数的结果对比
函数 算法 最优值 平均值 标准差
f1 MBO 8.84×10-12 6.58×10-11 1.52×10-10
KDLMBO 6.37×10-26 5.35×10-22 5.17×10-25
CCMBO 1.96×10-25 1.57×10-24 1.78×10-27
MMBO 0 0 0
f2 MBO 5.82×10-28 9.85×10-26 8.12×10-24
KDLMBO 6.18×10-45 2.47×10-44 2.17×10-42
CCMBO 6.87×10-50 5.27×10-49 6.67×10-3
MMBO 0 0 0
f3 MBO 5.26×10-05 2.15×10-03 3.62×10-05
KDLMBO 8.84×10-24 4.56×10-21 6.32×10-20
CCMBO 6.87×10-19 3.56×10-16 6.22×10-15
MMBO 5.69×10-21 7.32×10-20 5.56×10-19
f4 MBO 6.85×10-05 6.16×10-03 5.23×10-04
KDLMBO 8.26×10-07 1.27×10-04 2.27×10-04
CCMBO 5.31×10-07 4.18×10-06 5.24×10-09
MMBO 6.38×10-16 1.65×10-12 5.58×10-14
f5 MBO 2.85×10-15 6.87×10-13 3.24×10-12
KDLMBO 5.58×10-20 5.74×10-18 6.27×10-15
CCMBO 4.31×10-21 1.34×10-20 6.17×10-17
MMBO 2.36×10-23 7.18×10-21 4.25×10-19
f6 MBO 7.85×10-01 1.67×10+01 4.93×10-01
KDLMBO 1.17×10-12 1.19×10-10 5.87×10-09
CCMBO 5.36×10-15 8.56×10-15 6.32×10-14
MMBO 8.88×10-16 8.88×10-16 8.88×10-16
f7 MBO 5.98×10-08 2.95×10-03 1.36×10-06
KDLMBO 2.87×10-17 2.14×10-16 5.31×10-19
CCMBO 9.32×10-18 4.25×10-16 1.27×10-19
MMBO 1.32×10-18 9.83×10-16 8.55×10-15
f8 MBO 5.35×10-12 6.37×10-09 1.38×10-06
KDLMBO 6.32×10-13 7.57×10-10 1.48×10-09
CCMBO 6.56×10-13 5.39×10-11 8.59×10-08
MMBO 2.58×10-14 3.26×10-12 7.15×10-09
表选项

2.4 收敛曲线分析

收敛速度、收敛精度和避免局部最优能力是检验优化算法的重要指标。为反映MMBO算法的动态收敛特性，图 2展示了MMBO算法在3个基准测试函数f1、f2、f8上的平均收敛曲线。可以看出，MMBO算法在3个测试函数上的曲线收敛速度均明显快于其他算法，在函数f1上更是在第400代左右就能达到理论最优值；同时，MMBO算法的收敛结果更准确, 从迭代的开始至结束都能寻找到更优值。以上结果表明，MMBO算法融入了3种改进策略，可以极大地优化原生算法的收敛精度和跳出局部最优解的能力，这些优化策略的应用还可以进一步提高算法综合优化的性能。

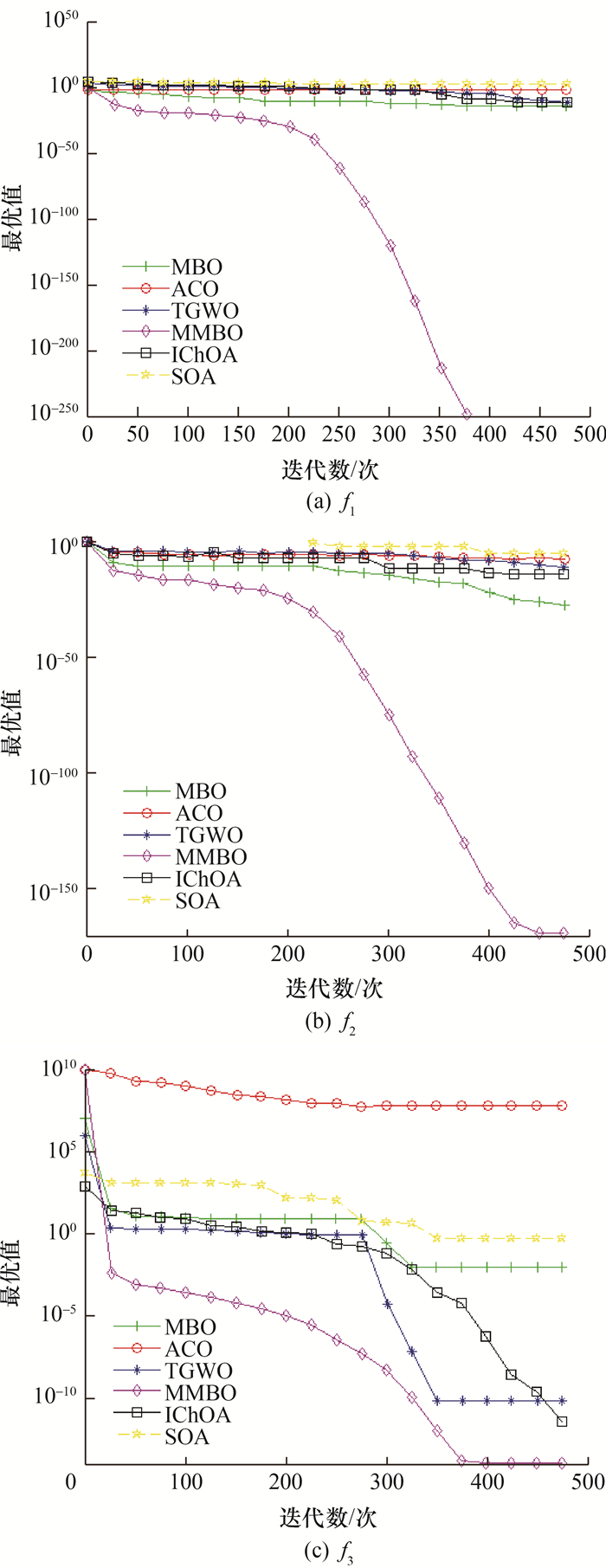
图 2 平均收敛曲线
图选项

2.5 Wilcoxon秩和检验

基于算法50次独立运行后的平均值和标准差来评价算法性能是较为片面的。为了全面检测算法的性能，本文引入Wilcoxon秩和检验的方法，利用MATLAB2016将MMBO算法与TGWO、IChOA、ACO、SOA算法在函数f1~f8上进行30次独立运算，并在选定的显著水平条件下进行均值对比。一般而言，当2种算法的均值相差小于3个数量级左右，认为性能相当；原始算法(MMBO算法)的均值高于对比算法5个数量级左右，认为原始算法更优；对比算法的均值高于原始算法3个数量级以上，认为原始算法更劣。依据前人经验，选择在显著性水平为5%的条件下计算秩和检验结果[16, 17]，实验结果如表 6所示，符号“+”“-”和“=”分别表示MMBO算法的性能优于、劣于和相当于对比算法，可以看出，仅在f8函数上MMBO算法和IChOA的性能相当，其余函数上MMBO算法均优于其他几种算法。

表 6 Wilcoxon秩和检验的结果
函数 TGWO IChOA ACO SOA
f1 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+)
f2 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+)
f3 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+)
f4 7.36×10-10(+) 3.25×10-12(+) 3.25×10-12(+) 3.25×10-12(+)
f5 7.36×10-10(+) 7.36×10-10(+) 3.25×10-12(+) 3.25×10-12(+)
f6 3.25×10-12(+) 7.36×10-10(+) 3.25×10-12(+) 3.25×10-12(+)
f7 3.25×10-12(+) 7.36×10-10(+) 3.25×10-12(+) 3.25×10-12(+)
f8 3.25×10-12(+) 7.36×10-10(=) 3.25×10-12(+) 3.25×10-12(+)
显著性差异统计(+/=/-) 8/0/0 7/1/0 8/0/0 8/0/0
表选项

2.6 Friedman检验

为了进一步检验MMBO算法和其他算法所存在的显著性差别，本文使用Friedman检验方法[18]对MMBO和3.2节中的5种对比算法进行非参数检验，该检验是一种多样本齐一性的统计检验，公式为

$F_{\mathrm{f}}=\frac{12 m}{c(c+1)}\left[\sum\limits_j R_j^2-\frac{c(c-1)^2}{4}\right].$ (11)

其中：Ff是最终秩；c是算法数量；Rj是第j个算法的平均排名；m是实验次数，本节取值为50；该检验假设实验数据服从自由度为(c-1)的卡方分布。通过对50次的实验数据进行排序并计算最终秩, 即可得到每个算法在不同测试函数上的最终秩。

本次检验使用的数据来自表 4，经检验，MBO、ACO、TGWO、IChOA、SOA与MMBO算法的最终秩分别为6.25、5.78、3.50、3.83、4.52与1.17，其中MMBO算法得出的最终秩最小，且与其他算法的最终秩差异十分突出，在统计学意义上具有显著性，说明MMBO算法改进策略具有较强的有效性。

2.7 工程优化问题

解决实际工程问题是算法研究的目的之一，在测试函数中的结果并不能完全体现算法在实际问题中的应用效果。本文选择了压力容器设计和焊接梁设计这2个典型的实际问题，以验证MMBO在工程应用中的性能。

2.7.1 压力容器设计问题

压力容器设计问题的目标是实现压力容器的型号配对，且成形和焊接的成本最小。压力容器的头尾两端均有封盖，头部一端的封盖呈半球状，该问题需要优化4个变量，分别是容器壁厚度Ts、顶盖壁厚度Th、内径S和容器管身长度L，压力容器设计模型如图 3所示。

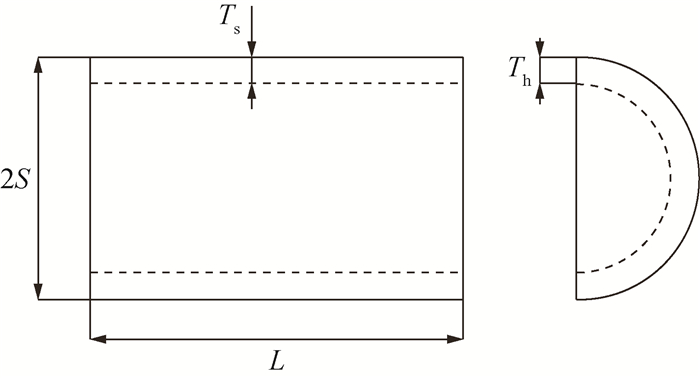
图 3 压力容器设计模型
图选项

目标函数为

$\begin{aligned} f_{\min }= & 0.6224 T_{\mathrm{s}} S L+1.7781 T_{\mathrm{h}} S^2+ \\ & 3.1661 T_{\mathrm{s}}^2 L+19.84 T_{\mathrm{s}}^2 S\end{aligned}$ (12)

约束条件为

$\begin{gathered}-T_{\mathrm{s}}+0.0193 S \leqslant 0, \\ -S+0.00954 S \leqslant 0, \\ -\pi \frac{S^2}{\mathrm{~cm}^2}-\frac{4}{3} \pi \frac{S^3}{\mathrm{~cm}^3}+1296000 \leqslant 0, \\ \frac{L}{\mathrm{~cm}}-240 \leqslant 0, \\ 0 \leqslant T_{\mathrm{s}}, \quad T_{\mathrm{h}} \leqslant 99, \\ 10 \leqslant S, \quad L \leqslant 200 .\end{gathered}$

将MMBO算法与3.2节所提算法进行对比。各算法分别独立运行50次，取运行结果的平均值作为最优解，结果如表 7所示。可以看出，MMBO算法的整体优化结果明显优于其他算法，得到的最低成本最小，这表明MMBO算法能以最优制造成本得到最佳压力容器设计方案，验证了MMBO算法在压力容器设计问题上具有优越的适用性和稳定性。

表 7 压力容器设计问题中各算法的最优解
算法 Ts/cm Th/cm S/cm L/cm fmin/元
MBO 1.870 7 1.675 9 103.793 8 472.982 8 6 293.894 6
ACO 1.996 2 1.709 9 103.539 8 396.884 4 6 367.011 2
TGWO 1.916 7 1.584 5 115.637 1 475.890 3 7 170.033 6
IChOA 2.114 3 1.568 5 106.968 3 338.416 9 5 720.889 4
SOA 2.139 4 1.433 1 117.313 7 501.038 6 8 002.509 8
MMBO 1.908 3 1.590 4 102.155 2 347.283 5 5 062.979 2
表选项

2.7.2 焊接梁设计问题

焊接梁设计问题的目标是保证安全性能的同时降低焊接梁制造成本，该问题需要优化的4个变量分别是焊缝宽度h、连接梁长度Ls、连接梁高度ts以及连接梁厚度b，焊接梁设计模型如图 4所示。

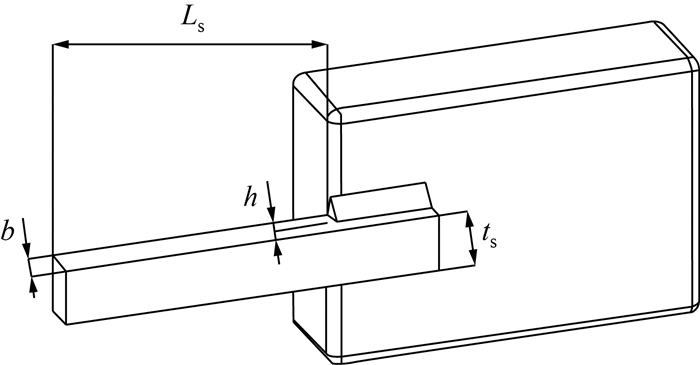
图 4 焊接梁设计模型
图选项

目标函数为

$f_{\min }=1.104\;71 h^2 L_{\mathrm{s}}+0.048\;11 t_{\mathrm{s}} b\left(14+L_{\mathrm{s}}\right).$ (13)

内部约束参数包括剪切应力τ、横梁弯曲应力σ、横梁挠度β、屈曲载荷W、焊接梁内部压力E，焊接梁外部压力G，横梁外侧长度L，局部载荷量M，轴面受力U。其中：τmax为13 600 N，σmax为30 000 N，βmax为0.25 m，W为6 000 N，G为1.2×107 N，L为14 cm，E为3×107 N。部分参数与变量的关系为

$\tau^{\prime}=\frac{P}{2 h L_{\mathrm{s}}}, \quad \tau^{\prime \prime}=M U J, \quad M=W\left(L+\frac{L_{\mathrm{s}}}{2}\right) ;$
$\begin{gathered}J=2 \sqrt{2} h L_{\mathrm{s}}\left[\frac{L_{\mathrm{s}}^2}{12}+\left(\frac{h+t_{\mathrm{s}}}{2}\right)^2\right] ; \\ U=\sqrt{\frac{L_{\mathrm{s}}^2}{4}+\left(\frac{h+L_{\mathrm{s}}}{2}\right)^2} .\end{gathered}$

约束条件为

$\begin{gathered}\sqrt{\left(\tau^{\prime}\right)^2+\frac{\tau^{\prime} \tau^{\prime \prime} L_{\mathrm{s}}}{R}+\left(\tau^{\prime \prime}\right)^2} 2 \leqslant 0, \\ \frac{6 W L}{t_{\mathrm{s}}^2 b}-\sigma_{\max } \leqslant 0, \\ h-b \leqslant 0, \end{gathered}$
$\begin{gathered}0.104\;71 h^2+0.048\;11 t_{\mathrm{s}} b\left(14+L_{\mathrm{s}}\right)-5 \leqslant 0, \\ 0.125-\frac{h}{\mathrm{~cm}} \leqslant 0, \\ \frac{4 W L^3}{E t_{\mathrm{s}}^2 b}-\delta_{\max } \leqslant 0, \\ W-\frac{4.013 E t_{\mathrm{s}} b^3}{6 L^2}\left(1-\frac{t_{\mathrm{s}}}{2 L} \sqrt{\frac{E}{4 G}}\right) \leqslant 0, \\ 0.1 \leqslant h, \quad L_{\mathrm{s}} \leqslant 2, \\ 0.1 \leqslant t_{\mathrm{s}}, \quad b \leqslant 10 .\end{gathered}$

将MMBO与3.2节所提算法进行对比。各算法分别独立运行50次，取运行结果平均值作为最优解，结果如表 8所示。可以看出，MMBO算法得到的焊缝宽度最大，横梁长度最小，横梁宽度和横梁厚度适中，最低成本最小，这表明MMBO在求解焊接梁设计问题时更具优势。

表 8 焊接梁设计问题中各算法的最优解
算法 h/cm Ls/cm ts/cm b/cm fmin/元
MBO 0.520 2 8.933 9 22.928 1 0.523 0 1.729 337 7
ACO 0.519 7 8.147 3 23.568 4 0.519 4 1.719 222 6
TGWO 0.485 9 8.962 6 22.962 1 0.522 5 1.710 829 3
IChOA 0.517 1 8.962 1 22.982 7 0.513 8 1.705 198 2
SOA 0.480 3 9.080 8 22.952 5 0.522 5 1.712 903 1
MMBO 0.522 5 8.262 9 22.953 0 0.522 5 1.695 258 4
表选项

通过以上2个工程问题的求解，进一步验证了MMBO算法在实际的工程问题中能够找到更优的解，具有较高的工程应用价值。

3 结论

本文针对标准帝王蝶优化算法的不足，提出多策略帝王蝶优化(MMBO)算法，引入正态云模型扩大算法的搜索范围，加入凸透镜成像反向学习策略加快算法收敛速度，提出自适应的调整算子帮助算法摆脱局部最优解。通过对基准测试函数进行寻优仿真实验，验证了MMBO算法中各项改进策略具有一定的协作互补性，针对原始MBO算法各阶段的缺陷均有较好的改进作用，能达到比其他对比算法更好的寻优效果。MMBO算法在优化压力容器设计问题和焊接梁设计问题中表现出一定的求解优势，验证了MMBO算法优越的寻优能力及工程实用性。

参考文献
[1]
HAN M, GAO L, LI A, et al. An overview of high utility item sets mining methods based on intelligent optimization algorithms[J/OL]. Knowledge and Information Systems. https://doi.org/10.1007/s10115-022-01741-1.
[2]
ESSA F A, MOHAMED A E, AMMAR H E. An enhanced productivity prediction model of active solar still using artificial neural network and harris hawks optimizer[J]. Applied Thermal Engineering, 2020(170): 115020.
[3]
向子权, 杨家其, 李慧琳, 等. 基于离散灰狼算法的资源分配问题求解[J]. 华中科技大学学报(自然科学版), 2021, 49(08): 81-85.
XIANG Z Q, YANG J Q, LI H L, et al. Resource allocation problem solving based on discrete gray wolf algorithm[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(08): 81-85. (in Chinese)
[4]
NENAVATH H, KUMAR JATOTH D R, et al. A synergy of the sine-cosine algorithm and particle swarm optimizer for improved global optimization and object tracking[J]. Swarm and Evolutionary Computation, 2018, 43: 1-30. DOI:10.1016/j.swevo.2018.02.011
[5]
WANG G G, SUASH D, CUI Z H. Monarch butterfly optimization[J]. Neural Computing and Applications, 2019, 31(7): 1995-2014. DOI:10.1007/s00521-015-1923-y
[6]
KAVIARASAN R, HARIKRISHNA P, ARULMURUGAN A. Load balancing in cloud environment using enhanced migration and adjustment operator based monarch butterfly optimization[J]. Advances in Engineering Software, 2022, 169: 1-11.
[7]
SUN L, SI S S, XU J C, et al. Feature selection using binary monarch butterfly optimization[J]. Applied Intelligence, 2023, 53: 706-727. DOI:10.1007/s10489-022-03554-9
[8]
ABDELMONEM M, MOHAMED A T. A hybridization of differential evolution and monarch butterfly optimization for solving systems of nonlinear equations[J]. Journal of Computational Design and Engineering, 2019, 6: 354-367. DOI:10.1016/j.jcde.2018.10.006
[9]
YAO X, LIU Y. Evolutionary programming made faster[J]. IEEE transactions on evolutionary computation, 1999, 3(2): 82-102. DOI:10.1109/4235.771163
[10]
DU N T, ZHOU Y Q, DENG W. Improved chimp optimization algorithm for three-dimensional path planning problem[J]. Multimedia Tools and Applications, 2022(81): 27397-27422.
[11]
刘志强, 何丽, 袁亮, 等. 采用改进灰狼算法的移动机器人路径规划[J]. 西安交通大学学报, 2022, 56(10): 49-60.
LIU Z Q, HE L, YUAN L, et al. path planning of mobile robot based on TGWO Algorithm[J]. Journal of Xi'an Jiaotong University, 2022, 56(10): 49-60. (in Chinese)
[12]
DORIGO M, MANIEZZO V, COLORNI A. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 1996, 26(1): 29-41. DOI:10.1109/3477.484436
[13]
Gaurav D, Vijay K. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems[J]. Knowledge-Based Systems, 2019, 165(1): 169-196.
[14]
XU T P, ZHAO F Q, TANG J X, et al. A knowledge-driven monarch butterfly optimization algorithm with self-learning mechanism[J]. Applied Intelligence, 2023(53): 12077-12097.
[15]
SAMANEH Y, ESMAEIL H, MOHAMMAD M. CCMBO: a covariance-based clustered monarch butterfly algorithm for optimization problems[J]. Memetic Computing, 2022, 14(3): 377-394. DOI:10.1007/s12293-022-00359-8
[16]
Wilcoxon F. Individual comparisons by ranking methods[J]. Biometrics Bull, 1945, 1(6): 80-83. DOI:10.2307/3001968
[17]
王宗山, 丁洪伟, 王杰, 等. 基于正交设计的折射反向学习樽海鞘群算法[J]. 哈尔滨工业大学学报, 2022, 54(11): 122-136.
WANG Z S, DING H W, WANG J, et al. Salp swarm algorithm based on orthogonal refracted opposition-based learning[J]. Journal of Harbin Institute of Technology, 2022, 54(11): 122-136. (in Chinese)
[18]
Friedman M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance[J]. Journal of the American Statistical Association, 1937, 32(200): 675-701. DOI:10.1080/01621459.1937.10503522