2. 上海市计算机软件评测重点实验室, 上海 201112
2. Shanghai Key Laboratory of Computer Software Evaluating and Testing, Shanghai 201112, China
全球大约有50%的人口使用在线社交网络[1]。在在线社交网络环境中,用户能够轻松地接收并转发信息,这极大地促进了信息的快速传播,但同样也加剧了谣言等不良信息、计算机病毒等恶意软件的广泛快速扩散,以及信息泄露问题的频繁发生[2]。准确预测信息传播的路径在阻止有害信息传播和用户信息泄露以及确保网络用户的安全性上显得尤为关键[3]。
微观扩散预测技术旨在发现信息传播过程中下一个即将被感染的节点,是一种揭示信息传播路径的关键策略[4]。传统的微观扩散预测方法主要分为基于时间序列的方法和数据驱动的方法。前者主要采用如差分/微分方程[5]、随机过程[6]和博弈论[7]等数学分析技术来构建信息传播模型;后者则是从原始数据中提取结构和时间等多方面的特征,进而采用机器学习算法来完成预测任务。受限于选用数学模型的合理性、手工特征提取的完整性,这两种传统方法的预测准确性通常较低。
近年来,深度学习在社交网络分析和预测中得到了越来越多的应用。Zhao等[8]提出了一种依赖于信息扩散序列以及用户间社交关系的方法。该方法借助长短时记忆网络从信息扩散序列中挖掘时间特性,并结合图神经网络从网络拓扑图中提取节点特征进行微观信息扩散预测。Feng等[9]提出了一种利用双曲嵌入进行信息扩散预测的方法。该方法将社交网络结构与信息扩散的级联模式映射到两个带有可调曲率的潜在超球面空间中,并引入了一个融合位置嵌入的共同注意力机制,通过整合信息扩散的级联特性与社交链接来有效地预测下一个感染节点。Yang等[10]提出一种基于强化学习的多尺度扩散预测模型。该模型使用强化学习方法将宏观扩散尺度信息融入基于循环神经网络的微观扩散模型中,并通过将社交网络节点的二阶结构特征以及信息扩散序列中的时序特征相连接进行微观扩散预测。Wang等[11]提出了一种序列神经网络结构注意力模型。该模型使用循环神经网络对信息扩散过程中的序列特性进行建模,采用注意力机制捕获社交网络图中节点之间的结构依赖关系,并通过门控机制将序列特性和结构关系进行建模,提高了微观扩散预测的精度。Huang等[12]设计了一种多通道图卷积异构扩散网络,通过构建多种元路径,从异构图的全局拓扑结构、节点的成对关系强度以及局部结构的角度来描述特定的社会关系,采用图卷积神经网络实现信息扩散预测。Fatemi等[13]提出了一种无监督学习模型。该模型使用图卷积神经网络进行节点分类,并设计了一种基于局部频谱滤波器的特征选择器识别图中具有影响力的节点,通过在真实数据集上应用SIR(易感者susceptible,感染者infectious,痊愈者recovered)模型验证了关键节点对信息扩散的影响。与传统方法相比,这些基于深度学习的模型具有更高的预测准确性。
然而,上述文献所提方法在建模中只考虑了社交网络信息扩散过程中的静态特征。针对社交网络中用户的交互及兴趣的动态变化,Yuan等[14]设计了一种动态异构图卷积神经网络模型。该模型结合社交网络图和信息扩散图来学习复杂的信息扩散过程,并将时间信息编码到异构表示中来表示用户的动态偏好,使用多头注意力机制对扩散序列建模,实现了微观扩散预测。Wang等[15]设计了一种基于自动编码器的动态模型。该模型使用动态编码器从历史扩散序列中推断用户兴趣的变化,并采用了注意力解码器,集成上一时间步的节点特征和用户序列的信息进行微观扩散预测。Cao等[16]为捕获用户之间复杂的交互关系,将信息扩散图按时间划分为子图,设计了一种动态结构时间图卷积神经网络提取信息扩散图的时序特征来表示用户兴趣的动态演变,并通过将时序特征与社交网络的结构特征相融合,进行微观信息扩散预测。Sun等[17]通过结合用户之间的社交关系和信息扩散层面的交互来描述用户的全局特性,使用超图注意力网络学习用户的动态偏好,并使用记忆增强的嵌入查找方法强化级联内部的特征交互描述,实现微观扩散预测。Zhao等[18]提出采用动态映射机制来捕获信息传播的整体结构特征及动态演化过程,并使用深度时序卷积网络提取信息扩散的高层次表示,从而进行扩散预测。Miyazawa等[19]提出的图卷积网络模型针对动态图数据,采用基于时间的小批量处理策略,在提高训练速度的同时模拟用户的动态偏好变化,从而实现了微观扩散预测。
可见,采用深度学习方法可以在社交网络中有效实现微观扩散预测,但目前方法存在对信息传播过程中的特征提取不充分的问题,例如未考虑传播链上最近感染的节点对信息后续传播的影响更大,以及邻居节点变化对消息传播路径的影响等,因此预测准确性仍不够高。为了解决这些问题,需要从多个角度描述信息扩散过程,并发现更多的隐藏特征。本文提出了一种基于多特征融合和深度学习的微观扩散预测框架(multi-feature fusion and deep learning for prediction, MFFDLP)。该框架基于信息扩散序列和社交网络图,采用门控循环单元(gate recurrent unit, GRU)提取局部时序特征和全局时序特征,以形成信息扩散序列表示;根据历史信息构建信息扩散图,使用级联图注意力网络(graph attention network, GAT)提取信息扩散子图中节点特征和边特征,通过嵌入查找形成当前信息扩散序列中相应节点的动态扩散特征;使用双多头注意力机制捕获静态和动态扩散特征的上下文信息,实现了高精度微观扩散预测。
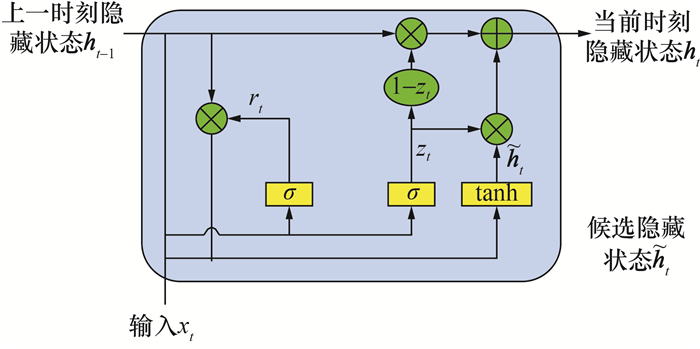
1 门控循环单元神经网络与图注意力网络 1.1 门控循环单元神经网络循环神经网络目前在许多领域的序列数据建模中展现出了有效性[20]。GRU神经网络[21]能够有效处理远距离依赖关系,避免训练过程中出现梯度消失等问题。因此,本文采用GRU对信息扩散序列进行建模,捕捉信息扩散过程中的时序特征。一个典型的GRU结构如图 1所示。
|
| 图 1 GRU结构示意图 |
图 1中:ht为当前时刻的隐藏状态,ht-1为上一时刻的隐藏状态,
| $r_t=\sigma\left(\boldsymbol{W}_r \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]\right) . $ | (1) |
| $z_t=\sigma\left(\boldsymbol{W}_z \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]\right) .$ | (2) |
| $\tilde{\boldsymbol{h}}_t=\tanh \left(\boldsymbol{W} \cdot\left[r_t \circ \boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]\right) .$ | (3) |
| $\boldsymbol{h}_t=\left(1-z_t\right) \circ \boldsymbol{h}_{t-1}+z_t \circ \tilde{\boldsymbol{h}}_t .$ | (4) |
其中:xt为t时刻的输入向量,[ ]表示共享链,Wr、Wz和W均为权值矩阵,“∘”表示矩阵的Hadamard乘积。隐藏状态ht编码了t时刻所有已经被感染的节点的信息。
1.2 图注意力网络图卷积神经网络目前广泛应用于非Euclid图结构中。图注意力网络GAT[22]采用注意力机制代替了图卷积网络中的卷积核运算,能够为同一邻域的重要节点分配更大的权重。因此,本文采用GAT学习信息扩散子图中节点特征和边特征,捕获节点的动态扩散表征。
设GAT的输入向量为v={v1, v2, …, vN},
| $k_i^n=a\left(\left[\boldsymbol{W} \boldsymbol{h}_{v_i}, \boldsymbol{W} \boldsymbol{h}_{v_i^n}\right]\right), v_i^n \in\left\{N^i\right\}.$ | (5) |
其中:{Ni}是节点vi的所有邻居节点集合;a为一个计算权重的共享注意力机制,在图注意力网络中,采用非线性激活函数LeakyReLU进行归一化,
| $a_i^n=\frac{\exp \left(\operatorname{LeakyReLU}\left(k_i^n\right)\right)}{\sum\limits_{n=1}^{\left|N_i\right|} \exp \left(\operatorname{LeakyReLU}\left(k_i^n\right)\right)}.$ | (6) |
其中|Ni|是节点vi的所有邻居节点的数量。
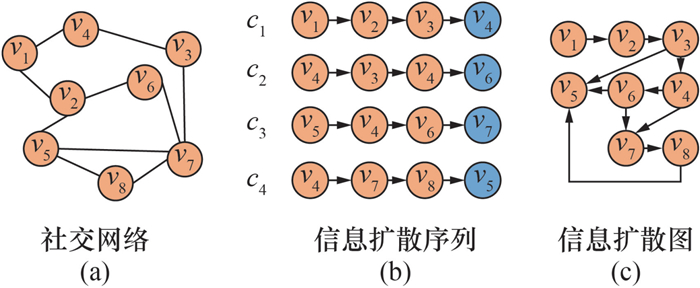
2 社交网络及信息扩散社交网络及其信息扩散和传播如图 2所示。
|
| 图 2 社交网络及其信息扩散和传播 |
一个典型的社交网络如图 2a所示,其中v表示用户或节点。设V表示图中的节点集合,E表示图中的边集合,E⊆V×V,则社交网络可表示为GS(V, E)。
在社交网络中,一条信息的扩散可以用信息扩散序列表示,如图 2b所示。其中:cm(m=1, 2, 3,4) 为消息m在节点之间的传播过程,节点vk将消息cm转发给用户vk+1可表示为cm={(vkm, vk+1m)}。假设图 2b中每个序列中最后一个节点为预测节点,则之前的节点组成的扩散序列称为历史信息扩散序列。多条消息的历史信息扩散序列构成信息扩散图GⅠ,如图 2c所示。
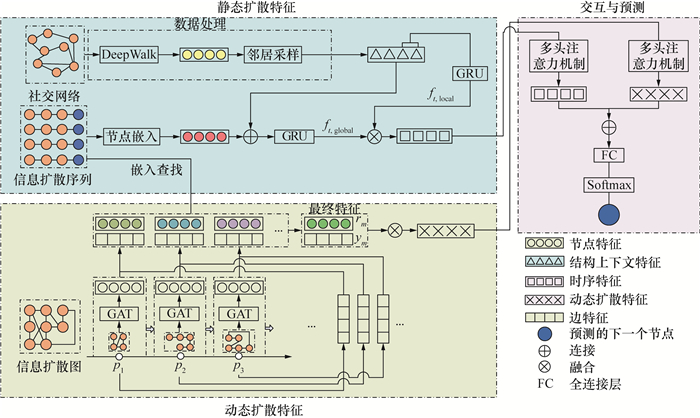
3 基于多特征融合的微观扩散预测模型为了有效提高微观信息扩散预测的精度,本文提出了一种基于多特征融合和深度学习的微观扩散预测框架MFFDLP,所提框架如图 3所示。
|
| 图 3 基于多特征融合和深度学习的微观扩散预测框架MFFDLP |
1) 提取静态扩散特征。首先,从社交网络图和信息扩散序列中分别提取节点嵌入和节点结构上下文信息。其次,使用GRU来提取信息扩散过程中的局部和全局时序特征。将这两种特征融合在一起,形成信息静态扩散序列特征。
2) 提取动态扩散特征。动态扩散特征代表了用户兴趣的变化。首先,根据历史信息扩散序列建立信息扩散图,按照时间顺序划分成若干扩散子图,基于GAT依次对每个子图提取节点特征和边特征;基于嵌入查找方法,从信息扩散子图中提取当前扩散序列中感染节点的节点特征和边特征,并将两种特征相融合作为节点动态扩散特征。
3) 预测下一个感染节点。为了进一步挖掘信息扩散中潜在的特征演化过程,并融合静态和动态两种扩散特征,使用双多头注意力机制分别捕捉时序特征和动态扩散特征的上下文信息,采用全连接层FC对两种特征进行融合,最后基于Softmax预测下一个感染节点。
MFFDLP是一个基于GAT、GRU和多头注意力机制的端到端通用框架,除社交网络外,也适用于其他具有节点、边以及时序信息的复杂网络,如生物网络、交通系统等。
3.1 数据处理为了获得网络节点的向量表示,对社交网络图GS(V, E) 采用DeepWalk[23]算法进行网络节点嵌入。DeepWalk是一种结合了随机游走和词向量的网络节点表示方法。该方法采用随机游走的方式从图中提取节点序列,借助词向量算法Word2vec[24]将潜在的社会关系编码到一个低维的连续向量空间中,从而获得一个节点的向量表示,
| $\boldsymbol{v}=\left(v^1, v^2, \cdots, v^l\right).$ | (7) |
其中l为嵌入维度。
然后,使用邻域采样算法[25]来降低算法复杂性,这在某种程度上也使模型的泛化性能得到了提升。
设社交网络图中有K个节点,对于节点vk(k= 1, 2, …, K),从其一阶邻居随机采样M个节点,节点vk的结构上下文信息为
| $\boldsymbol{s}_{v_k}=\operatorname{ReLU}\left(\boldsymbol{W} \cdot \frac{1}{M} \sum\limits_{k=1}^M \boldsymbol{v}_k+\boldsymbol{b}\right)$ | (8) |
其中:W和b分别是权重矩阵和偏置向量,激活函数ReLU( )=max( )。
3.2 特征提取 3.2.1 静态扩散特征信息扩散是一个基于结构和时间的过程,当前的信息扩散受到当前节点的邻居和传播链上之前节点的影响。提取全局时序特征和局部时序特征是实现准确预测的关键。考虑到节点感染的时间性,本文使用GRU来提取静态扩散特征。
1) 全局时序特征。
全局时序特征描述了预测时刻之前所有感染节点在信息传播过程中的影响。给定一条信息扩散序列,将每一个节点表示为l维的向量xv=(xv1, xv2, …, xvl)。将该向量与按式(8)提取的社交网络全部节点结构上下文信息sv相连接,形成增强节点表示x′ v。
| $\boldsymbol{x}_v^{\prime}=\operatorname{Concat}\left(\boldsymbol{x}_v, \boldsymbol{s}_v\right).$ | (9) |
其中Concat( )表示连接。基于GRU得到全局时序特征,
| $\boldsymbol{f}_{t, \text { global }}=\operatorname{GRU}\left(\boldsymbol{f}_{t-1, \text { global }}, \boldsymbol{x}_v^{\prime}\right).$ | (10) |
2) 局部时序特征。
对于一条传播信息,距离当前受感染节点越近的节点,受到的影响越大。因此,为了描述这一特征,本文使用GRU进一步提取局部时序特征。
对于一条传播信息,设t时刻感染了k个节点,其中{vk-n+1, vk-n+2, …, vk}为最近感染的n个节点,基于GRU得到局部时序特征ft, local,
| $\boldsymbol{f}_{t, \text { local }}=\operatorname{GRU}\left(\boldsymbol{f}_{t-1}\right., \text { local }, \left.\boldsymbol{s}_{v_k}\right).$ | (11) |
3) 时序特征融合。
参考文[17]中的特征融合方法,按式(12)将局部时序特征与全局时序特征进行融合:
| $\begin{gathered}\boldsymbol{f}_{\text {Fusion }}=\operatorname{Fusion}\left(\boldsymbol{f}_{t, \text { local }}, \boldsymbol{f}_{t, \text { global }}\right)= \\ \alpha \boldsymbol{f}_{t, \text { local }}+(1-\alpha) \boldsymbol{f}_{t, \text { global }} .\end{gathered}$ | (12) |
| $\alpha=\frac{\exp \left(\boldsymbol{w}^{\mathrm{T}} \sigma\left(\boldsymbol{w}_{\mathrm{R}} \boldsymbol{f}_{t, \text { local }}\right)\right)}{\exp \left(\boldsymbol{w}^{\mathrm{T}} \sigma\left(\boldsymbol{w}_{\mathrm{R}} \boldsymbol{f}_{t, \text { local }}\right)\right)+\exp \left(\boldsymbol{w}^{\mathrm{T}} \sigma\left(\boldsymbol{w}_{\mathrm{R}} \boldsymbol{f}_{t, \text { global }}\right)\right)}.$ | (13) |
其中:α为权重,w和wR为可学习的转换矩阵。
3.2.2 动态扩散特征在社交网络中,用户的个人喜好和兴趣在很大程度上决定了他是否会转发和传播信息,但用户的偏好和兴趣通常会随着时间的推移而变化,而且一个用户的变化还会影响到其周围的用户。本文在预测中考虑这一因素,首先根据历史扩散序列构建信息扩散图,再基于信息扩散时间,将信息扩散图划分为若干子图,然后使用级联GAT获取每个子图中的节点特征,并聚合出边特征。此外,通过嵌入查找方法,得到扩散序列中的节点特征和边特征,然后融合为节点交互特征,即动态扩散特征。
1) 信息扩散图及其子图划分。
如图 2所示,根据历史信息扩散序列建立信息扩散图GⅠ,并基于信息扩散时间将信息扩散图划分为若干子图GⅠ={GⅠ1, GⅠ2, …, GⅠQ},Q为划分的子图个数,每个子图反映一段时间内用户的互动和兴趣。随着时间的推移,会产生新的子图来反映新用户在下一时间段内的互动和兴趣。
2) 节点特征和边特征。
使用图注意力网络GAT依次对每个子图提取节点特征,由节点特征聚合出边特征,从而得到增强节点表示。具体可以分为以下2步:
(1) 提取初始节点和边的特征。
对于第1时间区间子图GⅠ1,使用从社交网络图中学习到的节点表示v作为GAT的初始节点输入,则信息扩散图GⅠ1中节点的初始边可表示为
| $\boldsymbol{e}_{i, j}^1=\sigma\left(\sum\limits_{v_i^1 \in e_{i, j}^1} \boldsymbol{W}_1^1 \boldsymbol{v}^1\right).$ | (14) |
其中:上标1表示第1个扩散子图,j=1, 2, …, J,J为与节点vi1相连的边的条数,σ表示激活函数ReLU,
(2) 更新节点特征和边特征。
在不同的子图中,即使是同一节点也会受到不同邻居的影响。因此,在第q个子图中,节点特征viq更新为
| $\boldsymbol{v}_i^q=\sigma\left(\sum\limits_{e_{i, j}^q \in\left\{\varepsilon_i^q\right\}} \boldsymbol{W}_2^q \boldsymbol{e}_{i, j}^q\right).$ | (15) |
其中:上标q表示第q个扩散子图,
此外,为了更好地利用和保存边特征,利用节点更新后的向量来再一次更新边的表示,
| $\boldsymbol{e}_{i, j}^q=\sigma\left(\sum\limits_{v_i^q \in e_{i, j}^q} \boldsymbol{W}_3^q \boldsymbol{v}_i^q\right)$ | (16) |
其中
(3) 嵌入查找。
嵌入查找是指查找信息扩散子图,根据信息扩散子图中的节点表示,更新扩散序列中相应的节点表示。
对于信息扩散序列cm,节点vim参与信息扩散,若该节点划分在第q个信息扩散子图,则取该子图中节点vi的表示viq作为cm中节点vi的表示,当前扩散序列中所有节点的表示为
| $\boldsymbol{r}_m=\left[\left(\boldsymbol{v}_i^q\right)\right] \in \mathbb{R}^{\left|c_m, v\right| \times l}.$ | (17) |
该扩散序列中所有边的表示为
| $\boldsymbol{y}_m=\left[\left(\boldsymbol{e}_{i, j}^q\right)\right] \in \mathbb{R}^{\mid c_m, e^{\mid \times l}}.$ | (18) |
其中:i=1, …, |cm, v|,|cm, v|是该条信息扩散序列的节点数量;j=1, …, |cm, e|, |cm, e|是该条信息扩散序列的边的数量。
(4) 特征融合。
使用融合策略将节点特征和边特征相融合得到信息动态扩散特征,即
| $\boldsymbol{I}=\operatorname{Fusion}\left(\boldsymbol{r}_m, \boldsymbol{y}_m\right).$ | (19) |
其中I即为动态扩散特征。
3.2.3 上下文交互特征在得到信息扩散表示和动态扩散特征后,为了进一步发现信息扩散的上下文交互情况,使用双多头注意力机制分别对信息扩散表示和动态扩散特征进行再次挖掘,将两种特征相融合后采用Softmax实现对下一个感染节点的预测。
注意力机制可以使神经网络具备专注于其输入(或特征)子集的能力, 其计算方法为[26]
| $\operatorname{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{Softmax}\left(\frac{\boldsymbol{Q \boldsymbol { K } ^ { \mathrm { T } }}}{\sqrt{d_k}}+\boldsymbol{M}\right) \boldsymbol{V} .$ | (20) |
其中:Q、K、V分别表示查询、键和值。M为掩码矩阵,
使用多头注意力机制后的信息扩散表示F和动态扩散特征I′如下:
| $\boldsymbol{F}_i=\operatorname{Attention}\left(\boldsymbol{f}_{\text {Fusion }} \boldsymbol{W}_i^Q, \boldsymbol{f}_{\text {Fusion }} \boldsymbol{W}_i^{\boldsymbol{K}}, \boldsymbol{f}_{\text {Fusion }} \boldsymbol{W}_i^{\boldsymbol{V}}\right).$ | (21) |
| $\boldsymbol{F}=\left[\boldsymbol{F}_1, \boldsymbol{F}_2, \cdots, \boldsymbol{F}_z\right] \boldsymbol{W}^{\boldsymbol{F}}.$ | (22) |
| $\boldsymbol{I}_i^{\prime}= {\rm Attention} \left(\boldsymbol{I} \boldsymbol{W}_i^Q, \boldsymbol{I} \boldsymbol{W}_i^{\boldsymbol{K}}, \boldsymbol{I} \boldsymbol{W}_i^{\boldsymbol{V}}\right).$ | (23) |
| $\boldsymbol{I}^{\prime}=\left[\boldsymbol{I}_1^{\prime}, \boldsymbol{I}_2^{\prime}, \cdots, \boldsymbol{I}_z^{\prime}\right] \boldsymbol{W}^{\boldsymbol{I}}.$ | (24) |
其中:WiQ、WiK、WiV、WF、WI均为可学习的转换矩阵,1≤i≤z。
在获得时序特征和节点交互特征的最终表示之后,将这两个特征进行融合,以进行下一步预测。
3.3 预测在预测阶段,信息扩散序列被送入全连接层,最后使用Softmax输出下一个感染用户的概率,
| $p=\operatorname{Softmax}\left(\left[\boldsymbol{W}_{\mathrm{p}} \cdot \operatorname{Concat}\left(\boldsymbol{F}, \boldsymbol{I}^{\prime}\right)+\boldsymbol{b}_{\mathrm{p}}\right]+\mathbf{Mask}_m\right).$ | (25) |
其中:Wp是一个可训练的权重矩阵,用于将Concat(F, I′)映射到用户向量空间; bp表示偏置向量;Maskm是屏蔽操作,用于屏蔽已被感染的节点。
4 算法流程图基于多特征融合的微观扩散预测算法如图 4所示。

|
| 图 4 基于多特征融合的微观扩散预测算法 |
5 实验 5.1 数据集
本文实验选用了Twitter、Douban和Memetracker 3个公共数据集。Twitter数据集[27]记录了2010年10月期间推文在用户之间的传播路径,在该数据集中,以Twitter上用户之间的关注关系作为用户的社交关系。Douban数据集[28]中的数据来源于一个社交网站(https://www.douban.com/)。在该网站上,用户可以分享他们看过的书和电影,并关注其他人的阅读和观看状态。如果两个用户共同做一件事情(如阅读同一本书),则认为他们之间存在交互关系。Memetracker数据集[29]收集了在线新闻和博客帖子,并记录了其中引用最频繁的句子。该数据集将每个句子视为一条信息,网站的每个URL视为一个用户。该数据集没有社交网络图。
3个数据集的详细信息见表 1。表 1中:#Users表示社交网络中节点数,#Links表示社交网络中用户的交互关系的数量,#cascade表示数据集中消息的条数,Ave.Length表示信息扩散序列的平均长度。
| 数据集 | Douban | Memetracker | |
| #Users | 12 627 | 23 123 | 4 709 |
| #Links | 309 631 | 348 280 | |
| #cascade | 3 435 | 3 475 | 12 661 |
| Ave.Length | 33.64 | 21.76 | 16.24 |
在实验中按80%、10%、10% 的比例将数据集划分为训练集、验证集和测试集。
5.2 评价指标采用以下两个指标评价模型的预测性能:
1) Hit@k:模型预测得分最高的前k个节点中包含实际感染节点的比率;
2) Map@k:模型预测得分最高的前k个节点的平均精度均值。
5.3 实验环境及条件本文实验所使用的计算机操作系统为64位Windows 10,CPU为E5-2620 v4,内存为32 GB。本文的仿真实验在Python 3.7中进行,模型是利用Pytorch[30]来实现的,参数更新使用的是Adam算法。学习率设置为10-3,训练集的batch size设置为16。信息扩散图划分为8个区间[12, 23],初始用户嵌入维度为l=64,初始局部邻域采样节点数量M=3,初始多头注意力机制的头的数量设置为8。本文将在实验中选择最佳的参数,并在数据集上评估该参数配置。使用交叉熵损失函数作为目标函数用于训练。
5.4 实验结果 5.4.1 参数实验本节的参数实验均在Twitter数据集上进行。
1) 实验1:节点嵌入维度l。
本实验的目的是为了选取最佳的节点嵌入维度l,嵌入维度的选取范围为l={16, 32, 64, 128},实验结果如表 2所示。
| % | |||||||||||||||||||||||||||||
| 嵌入维度l | Hit@10 | Hit@50 | Hit@100 | Map@10 | Map@50 | Map@100 | |||||||||||||||||||||||
| 16 | 28.39 | 44.61 | 55.59 | 14.88 | 15.61 | 15.77 | |||||||||||||||||||||||
| 32 | 32.46 | 48.40 | 58.43 | 20.90 | 21.62 | 21.76 | |||||||||||||||||||||||
| 64 | 35.03 | 50.51 | 59.48 | 23.75 | 24.15 | 24.58 | |||||||||||||||||||||||
| 128 | 34.59 | 49.77 | 58.30 | 23.69 | 24.38 | 24.50 | |||||||||||||||||||||||
从表 2中可以看出,节点嵌入维度l=64时,指标Hit@k均为最高。指标Map@k虽然在k=50时要略低于嵌入维度为128时的情况,但是在k=10以及k=100时都达到最优。因此,本文选择的节点嵌入维度l=64。
2) 实验2:邻域采样节点数量M。
本实验的目的是为了选取局部邻域采样节点的最佳窗口大小M,选取的范围为M={1, 2, 3, 4, 5},实验结果如表 3所示。
| % | |||||||||||||||||||||||||||||
| 节点数量M | Hit@10 | Hit@50 | Hit@100 | Map@10 | Map@50 | Map@100 | |||||||||||||||||||||||
| 1 | 35.22 | 50.52 | 59.14 | 23.68 | 24.37 | 24.50 | |||||||||||||||||||||||
| 2 | 34.55 | 50.54 | 59.24 | 23.50 | 24.23 | 24.35 | |||||||||||||||||||||||
| 3 | 35.03 | 50.51 | 59.48 | 23.75 | 24.15 | 24.58 | |||||||||||||||||||||||
| 4 | 35.09 | 50.19 | 59.33 | 23.67 | 24.37 | 24.50 | |||||||||||||||||||||||
| 5 | 35.29 | 50.01 | 58.98 | 23.46 | 24.12 | 24.25 | |||||||||||||||||||||||
从表 3中可以看出,虽然在M=3时两个指标没有在k为任意值的情况下均达到最优,但是在k=100时,M=3均为最优。因此,本文选择的邻域采样节点数量M=3。
3) 实验3:多头注意力机制头的数量z。
本实验的目的是为了选取多头注意力机制头的最佳数量z,选取的范围为z={2, 4, 6, 8, 10, 12, 14},实验结果如表 4所示。
| % | |||||||||||||||||||||||||||||
| 头的数量z | Hit@10 | Hit@50 | Hit@100 | Map@10 | Map@50 | Map@100 | |||||||||||||||||||||||
| 2 | 35.30 | 51.42 | 59.63 | 24.18 | 24.91 | 25.03 | |||||||||||||||||||||||
| 4 | 35.02 | 50.29 | 59.21 | 23.67 | 24.40 | 24.52 | |||||||||||||||||||||||
| 6 | 35.52 | 50.99 | 59.45 | 23.91 | 24.59 | 24.71 | |||||||||||||||||||||||
| 8 | 35.03 | 50.51 | 59.48 | 23.75 | 24.15 | 24.58 | |||||||||||||||||||||||
| 10 | 34.77 | 50.25 | 59.11 | 23.33 | 24.05 | 24.18 | |||||||||||||||||||||||
| 12 | 34.47 | 49.94 | 58.89 | 23.32 | 24.04 | 24.17 | |||||||||||||||||||||||
| 14 | 34.37 | 50.43 | 59.44 | 22.90 | 23.62 | 23.74 | |||||||||||||||||||||||
从表 4中可以看出,多头注意力机制头的数量z=2时,在大多数情况下Hit@k和Map@k两个指标都达到了最优。因此,本文选择的头的数量z=2。
5.4.2 消融实验为验证模型各部分的性能,在Twitter数据集上进行消融实验。MFFDLP模型的几个变体如下:
w/o SG:在MFFDLP模型的基础上,移除社交图。
w/o DS:在MFFDLP模型的基础上,移除扩散序列。
w/o ATT:在MFFDLP模型的基础上,移除多头注意力机制。
w/o LTF:在MFFDLP模型的基础上,移除局部时间特征。
w/o DDC:在MFFDLP模型的基础上,移除动态扩散特征。
消融实验结果如表 5所示。可以看出,当仅采用社交网络图或者信息扩散图时,预测性能总体都不理想,指标得分相近。当同时采用社交网络图和信息扩散图后,再引入多头注意力机制,预测精度得到较大幅度提升,如在k=100时,Hit@100和Map@100分别提升了3.90%和1.86%。进一步,引入局部时序特征,除了在Hit@10上性能略有下降,在其他指标上预测精度都有提升,在各指标上平均提升了0.31%。信息动态扩散特征的引入,继续全面提升了模型总体预测性能,在各指标上平均提升了0.36%。总体而言,与各模型变体相比,本文所提模型的预测性能最好。
| % | |||||||||||||||||||||||||||||
| 模型 | Hit@10 | Hit@50 | Hit@100 | Map@10 | Map@50 | Map@100 | |||||||||||||||||||||||
| w/o SG | 32.53 | 47.37 | 55.92 | 21.50 | 22.17 | 22.30 | |||||||||||||||||||||||
| w/o DS | 32.40 | 47.40 | 56.77 | 21.67 | 22.35 | 22.48 | |||||||||||||||||||||||
| w/o ATT | 32.93 | 47.03 | 55.73 | 22.40 | 23.05 | 23.17 | |||||||||||||||||||||||
| w/o LTF | 35.83 | 51.20 | 59.03 | 23.21 | 24.59 | 24.70 | |||||||||||||||||||||||
| w/o DDC | 35.20 | 50.76 | 59.53 | 23.85 | 24.26 | 24.69 | |||||||||||||||||||||||
| 本文模型 | 35.30 | 51.42 | 59.63 | 24.18 | 24.91 | 25.03 | |||||||||||||||||||||||
5.4.3 对比实验
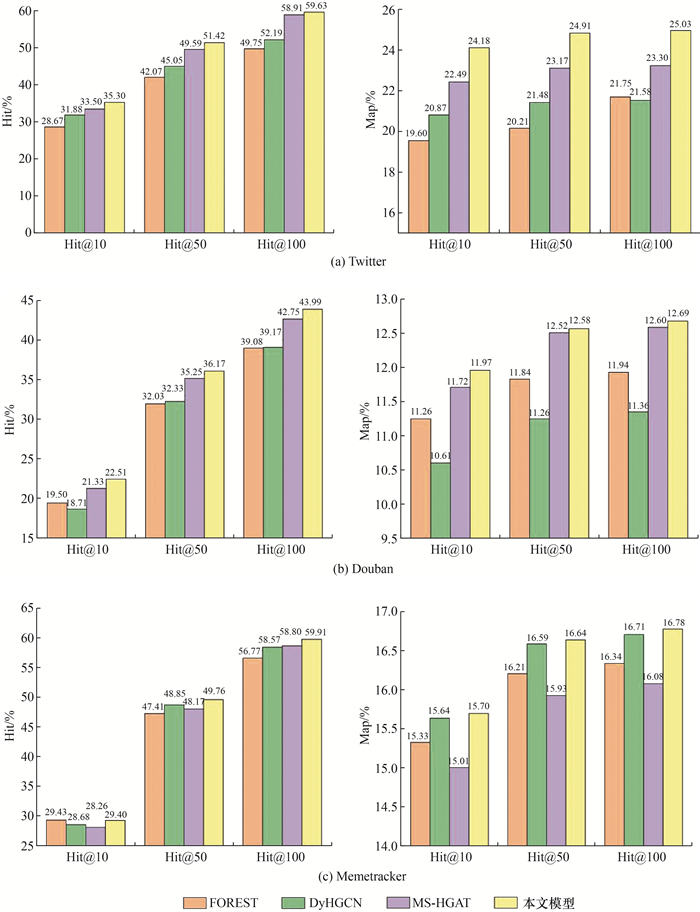
为了证明本文所提出的框架的有效性,使用FOREST[10]、DyHGCN[14]和MS-HGAT[17]3个目前先进的微观扩散预测模型作为对比模型进行实验。其中,MS-HGAT模型在Twitter和Douban数据集上的实验结果来自文[17],其他实验数据均是本文复现的结果。复现中,使用的参数均为原文献中的参数。从图 5可以看出,MFFDLP在所有数据集上的总体表现都优于其他模型。从图 5a中可以看出,在Twitter数据集上,与其他3个模型相比,指标Hit@100、Map@10、Map@50和Map@100提高显著,最高分别达9.88%、4.58%、4.70%和3.45%。从图 5b中可以看出,与Twitter数据集相比,MFFDLP在Douban数据集上的性能提高并不显著,但与其他模型相比,指标Hit@100、Map@10、Map@50和Map@100的提升最高,分别达到了4.91%、1.36%、1.32%和1.33%。由于数据集Memetracker没有潜在的社交关系图,因此从图 5c可以看出,与FOREST相比,MFFDLP的指标Hit@10略有下降,但其他指标仍有小幅提升。
|
| 图 5 本文模型与FOREST、DyHGCN和MS-HGAT模型在3个数据集中的对比实验 |
上述对比实验证明了本文所提MFFDLP框架的有效性。FOREST与MFFDLP相比,由于它未考虑动态特征,因此精度较低;DyHGCN、MS-HGAT与MFFDLP相比,虽然它们也构建了信息扩散子图,但由于未采用深度学习模型挖掘深层时序特征,因此性能也低于MFFDLP。
5.4.4 扩展实验为了证明模型的可扩展性,本实验在原模型中进一步引入社交网络用户的性别、年龄和兴趣爱好3类用户个性信息。其中:性别为{男,女};年龄区间为[15, 80];兴趣爱好预设10种,分别为{音乐,阅读,旅行,运动,绘画,编程,烹饪,摄影,园艺,游戏}。为了能够对比实验结果,实验仍采用Twitter数据集。但由于原始Twitter数据集中并不包含这3类信息,因此本文作者为每个节点随机分配这3类个性信息,其中兴趣爱好随机分配3种。进一步,采用Word2vec分别提取性别特征向量gen、年龄特征向量age和兴趣爱好特征向量inter。然后,参考式(12),将这3个特征与式(7)得到的节点特征v进行融合。模型框架其他部分保持不变。实验结果如表 6所示。表 6中:MFFDLP-gen、MFFDLP-age和MFFDLP-inter分别表示MFFDLP模型中添加了性别、年龄和兴趣,MFFDLP-all则表示同时添加3类个人信息。
| % | |||||||||||||||||||||||||||||
| 特征 | Hit@10 | Hit@50 | Hit@100 | Map@10 | Map@50 | Map@100 | |||||||||||||||||||||||
| MFFDLP-gen | 34.48 | 50.33 | 58.93 | 23.42 | 24.16 | 24.29 | |||||||||||||||||||||||
| MFFDLP-age | 34.37 | 50.16 | 59.11 | 23.39 | 24.11 | 24.23 | |||||||||||||||||||||||
| MFFDLP-inter | 34.62 | 50.31 | 59.29 | 23.51 | 24.22 | 24.35 | |||||||||||||||||||||||
| MFFDLP-all | 34.70 | 49.74 | 59.25 | 23.49 | 24.18 | 24.31 | |||||||||||||||||||||||
从表 6可以看出,给节点赋予个性化信息后,MFFDLP-gen、MFFDLP-age、MFFDLP-inter和MFFDLP-all在Hit@k和Map@k两个指标上的得分比MFFDLP略有下降,但是总体仍然维持了较高的预测水平,说明MFFDLP模型具有良好的扩展性和通用性。同时,可以看到,MFFDLP-inter除Hit@10和Hit@50分别略低于MFFDLP-all和MFFDLP-gen外,在其他指标上都是最优的;MFFDLP-all除Hit@50略低于MFFDLP-gen外,在Hit@10上表现最优,在其他指标上都表现为次优,仅低于MFFDLP-inter。可见,用户兴趣在信息扩散预测中更加重要。
6 结论预测信息的传播路径有助于防止有害信息的传播和发现信息泄露的路径。为了更好地刻画传播过程、提高预测精度,本文提出了一种基于多特征融合和深度学习的微观扩散预测框架MFFDLP。该框架综合利用社交图、信息扩散序列和扩散图,从社交图和信息扩散序列中提取节点嵌入及其结构上下文,应用GRU获得局部和全局时序特征,得到信息扩散序列表征。为了描述影响信息扩散的节点动态变化,构建了扩散图及其子图,通过级联GAT模型挖掘每个时间段的网络节点特征和边特征,形成节点动态扩散表征。最后,利用双多头注意力机制进一步从静态和动态特征中提取上下文信息。
在多个数据集上多个模型的对比实验结果表明,MFFDLP能够提高信息扩散的预测精度。未来,考虑到用户倾向于转发自己感兴趣的内容,将进一步探索如何融合扩散信息本身的特征来提高扩散预测模型的性能。
| [1] |
Statista. Social media: Statistic & facts[R/OL]. (2023-08-31)[2023-08-31]. https://www.statista.com/topics/1164/social-networks/.
|
| [2] |
MEEL P, VISHWAKARMA D K. Fake news, rumor, information pollution in social media and web: A contemporary survey of state-of-the-arts, challenges and opportunities[J]. Expert Systems with Applications, 2020, 153: 112986. DOI:10.1016/j.eswa.2019.112986 |
| [3] |
GRINBERG N, JOSEPH K, FRIEDLAND L, et al. Fake news on Twitter during the 2016 U.S. presidential election[J]. Science, 2019, 363(6425): 374-378. DOI:10.1126/science.aau2706 |
| [4] |
张志扬, 张凤荔, 谭琪, 等. 基于深度学习的信息级联预测方法综述[J]. 计算机科学, 2020, 47(7): 141-153. ZHANG Z Y, ZHANG F L, TAN Q, et al. Review of information cascade prediction methods based on deep learning[J]. Computer Science, 2020, 47(7): 141-153. (in Chinese) |
| [5] |
MATSUBARA Y, SAKURAI Y, PRAKASH B A, et al. Rise and fall patterns of information diffusion: Model and implications[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China: Association for Computing Machinery, 2012: 6-14.
|
| [6] |
YU L Y, CUI P, WANG F, et al. From micro to macro: Uncovering and predicting information cascading process with behavioral dynamics[C]//Proceedings of 2015 IEEE International Conference on Data Mining. Atlantic, USA: IEEE, 2015: 559-568.
|
| [7] |
CAO X Y, CHEN Y, JIANG C X, et al. Evolutionary information diffusion over heterogeneous social networks[J]. IEEE Transactions on Signal and Information Processing over Networks, 2016, 2(4): 595-610. |
| [8] |
ZHAO J H, ZHAO J L, FENG J. Information diffusion prediction based on cascade sequences and social topology[J]. Computers and Electrical Engineering, 2023, 109: 108782. DOI:10.1016/j.compeleceng.2023.108782 |
| [9] |
FENG S S, ZHAO K Q, FANG L T, et al. H-Diffu: Hyperbolic representations for information diffusion prediction[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(9): 8784-8798. DOI:10.1109/TKDE.2022.3209067 |
| [10] |
YANG C, WANG H, TANG J, et al. Full-scale information diffusion prediction with reinforced recurrent networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(5): 2271-2283. DOI:10.1109/TNNLS.2021.3106156 |
| [11] |
WANG Z T, CHEN C Y, LI W J. A sequential neural information diffusion model with structure attention[C]//Proceedings of the 27th ACM International Conference on Information and Knowledge Management. Torino, Italy: Association for Computing Machinery, 2018: 1795-1798.
|
| [12] |
HUANG N B, ZHOU G, ZHANG M L, et al. MC-RGCN: A multi-channel recurrent graph convolutional network to learn high-order social relations for diffusion prediction[C]//Proceedings of 2021 IEEE International Conference on Data Mining. Auckland, New Zealand: IEEE, 2021: 1108-1113.
|
| [13] |
FATEMI B, MOLAEI S, PAN S R, et al. GCNFusion: An efficient graph convolutional network based model for information diffusion[J]. Expert Systems with Applications, 2022, 202: 117053. DOI:10.1016/j.eswa.2022.117053 |
| [14] |
YUAN C Y, LI J C, ZHOU W, et al. DyHGCN: A dynamic heterogeneous graph convolutional network to learn users' dynamic preferences for information diffusion prediction[C]//Proceedings of European Conference Machine Learning and Knowledge Discovery in Databases. Ghent, Belgium: Springer-Verlag, 2020: 347-363.
|
| [15] |
WANG R J, HUANG Z J, LIU S Z, et al. DyDiff-VAE: A dynamic variational framework for information diffusion prediction[C/OL]//Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. Virtual Event. New York, USA: Association for Computing Machinery, 2021: 163-172.
|
| [16] |
CAO Z M, HAN K, ZHU J H. Information diffusion prediction via dynamic graph neural networks[C]//Proceedings of the IEEE 24th International Conference on Computer Supported Cooperative Work in Design. Dalian, China: IEEE, 2021: 1099-1104.
|
| [17] |
SUN L, BAO Y, ZHANG X B, et al. MS-HGAT: Memory-enhanced sequential hypergraph attention network for information diffusion prediction[C/OL]//Proceedings of the 36th AAAI Conference on Artificial Intelligence. 34th Conference on Innovative Applications of Artificial Intelligence. The 12th Symposium on Educational Advances in Artificial Intelligence. Virtual Event. Washington DC, USA: AAAI Press, 2022: 4156-4164.
|
| [18] |
ZHAO Q H, ZHANG Y Z, FENG X D. Predicting information diffusion via deep temporal convolutional networks[J]. Information Systems, 2022, 108: 102045. DOI:10.1016/j.is.2022.102045 |
| [19] |
MIYAZAWA H, MURATA T. Graph convolutional network with time-based mini-batch for information diffusion prediction[C]//Proceedings of the 9th International Conference on Complex Networks and Their Applications. Cham, Germany: Springer, 2021: 53-65.
|
| [20] |
MIKOLOV T, KARAFIáT M, BURGET L, et al. Recurrent neural network based language model[C]//Proceedings of the 11th Annual Conference of the International Speech Communication Association. Makuhari, Japan: DBLP, 2010: 1045-1048.
|
| [21] |
CHUNG J, GULCEHRE C, CHO K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[C]//NIPS 2014 Workshop on Deep Learning. Montreal, Canada: NIPS, 2014.
|
| [22] |
VELI AČU KOVI AC'U P, CASANOVA A, LIÒ P, et al. Graph attention networks[C]//Proceedings of the 6th International Conference on Learning Representations. Vancouver, Canada: ICLR, 2018.
|
| [23] |
PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: Association for Computing Machinery, 2014: 701-710.
|
| [24] |
MIKOLOV T, CHEN K, CORRADO G, et al. Efficient estimation of word representations in vector space[C]//Proceedings of the 1st International Conference on Learning Representations. Scottsdale, USA: ICLR, 2013.
|
| [25] |
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[C]//Proceedings of the 5th International Conference on Learning Representations. Toulon, France: ICLR, 2017: 1-14.
|
| [26] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA: Curran Associates, 2017: 6000-6010.
|
| [27] |
HODAS N O, LERMAN K. The simple rules of social contagion[J]. Scientific Reports, 2014, 4(1): 4343. DOI:10.1038/srep04343 |
| [28] |
ZHONG E H, FAN W, WANG J W, et al. ComSoc: Adaptive transfer of user behaviors over composite social network[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China: IEEE, 2012: 696-704.
|
| [29] |
LESKOVEC J, BACKSTROM L, KLEINBERG J. Meme-tracking and the dynamics of the news cycle[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France: Association for Computing Machinery, 2009: 497-506.
|
| [30] |
PASZKE A, GROSS S, MASSA F, et al. PyTorch: An imperative style, high-performance deep learning library[C]//Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates, 2019: 721.
|


