随着宽带雷达/通信技术的兴起，高精度高采样率模数转换器成为制约宽带系统硬件成本和功耗的重要因素。同时，高精度高采样率模数转换器产生的海量数据也给数据传输、存取和处理带来了挑战。在接收机中采用低精度量化技术是该问题的一种有效的解决方法。此时，目标感知/信道估计问题可以抽象为广义线性模型(generalized linear model，GLM)中的参数估计问题^[1-2]。

GLM得到观测值的过程可以描述为：待估计参数$\mathit{\boldsymbol{x}} \in \mathbb{R}^N$经过线性变换得到隐变量，$\boldsymbol{A} \in \mathbb{R}^{M \times N}$是线性变换对应的矩阵，即测量矩阵；隐变量再经过逐位非线性变换(componentwise nonlinear transform)即可得到观测值。

求解广义线性模型的方法可以分为两大类：确定性方法和Bayes方法。确定性方法首先获取模型的似然函数，然后使用信号的l₁范数||x||₁来施加稀疏性约束，最后利用凸优化或贪婪方法进行求解。这类方法能够保证收敛性，但通常需要手动调整正则化参数以获得适当的稀疏度。Bayes方法则引入信号的稀疏先验分布，利用似然函数和先验分布得到后验均值和后验方差。在迭代过程中，Bayes方法可以通过近似计算进行求解，从而降低计算复杂度。此外，Bayes方法还能通过期望最大化算法自动学习先验分布中的参数和噪声方差参数，并提供估计的不确定度。常见的Bayes方法包括稀疏Bayes学习(sparse Bayesian learning，SBL)^[3-4]和广义近似消息传递(generalized approximate message passing，GAMP)^[2]算法等。SBL算法性能稳定，但每次迭代过程均涉及矩阵求逆运算，计算复杂度相对较高。GAMP算法计算复杂度较低，但对测量矩阵A相对敏感。当测量矩阵A的元素不满足独立次Gauss分布时，该算法可能会发散。有关GAMP算法收敛性的证明可以参考文[5]。为了提高GAMP的稳健性，阻尼衰减机制被引入GAMP算法中以保证其收敛性^[5-6]。然而，阻尼衰减过强也会在一定程度上减缓算法的收敛速度、降低算法的运行效率。为此，学者们提出了自适应GAMP (adaptive GAMP，AD-GAMP)^[7]，该算法可以通过自适应步长机制调整算法步长。当测量矩阵的元素稍微偏离次Gauss分布时，AD-GAMP仍能正常工作。然而，由于AD-GAMP没有从根本上消除或减小测量矩阵的相关性，当测量矩阵的相关性较强时，AD-GAMP算法的性能仍然较差。广义向量近似消息传递(generalized vector approximate message passing，GVAMP)算法^[8]以及正交近似消息传递(orthogonal approximate message passing，OAMP)算法(等价于向量近似消息传递(vector approximate message passing，VAMP)算法^[9-10])^[11]均通过将因子节点图中的变量节点转换为向量节点，基于期望传播(expectation propagation)方法进行问题求解，可以保证算法在更广泛的一类测量矩阵(右旋转不变矩阵)中收敛。其中：OAMP或VAMP用于求解标准线性模型，而GVAMP用于求解GLM。

酉变换近似消息传递(unitary approximate message passing，UAMP)算法^[12-14]则通过对测量矩阵进行奇异值分解(singular value decomposition，SVD)来改善测量矩阵特性，减小其相关性，以达到更加稳健的重构性能。UAMP算法只能用于求解标准线性模型，无法应用于广义线性模型的求解。为此，文[15]将UAMP算法进行推广得到广义酉变换近似消息传递(generalized unitary approximate message passing，GUAMP)算法。然而，GUAMP算法在一些场景下会在平衡点附近来回振荡，即使经过多次迭代也无法收敛到最优值。为此，本文拟提出一种改进算法以提高GUAMP算法的稳健性。

1 AD-GUAMP算法

本章给出AD-GUAMP算法的设计原理及设计方法。首先简要介绍GUAMP算法，细节可参考文[15]。

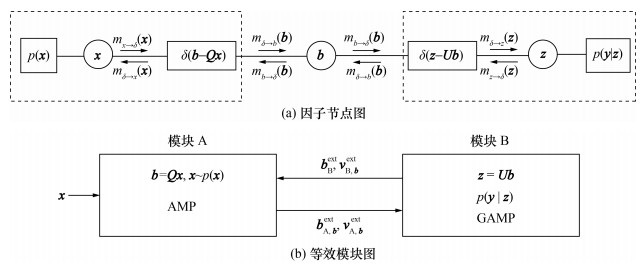
GUAMP算法的核心思想是通过对矩阵A进行奇异值分解，得到A=UΣV^T的分解形式。其中：U是由左奇异向量按列排放形成的左奇异矩阵；V是由右奇异向量按列排放形成的右奇异矩阵；Σ是奇异值矩阵，它是一个对角矩阵，对角线上的元素由奇异值构成。在此基础上，引入额外的隐变量$\boldsymbol{b} \in \mathbb{R}^M$，可以得到等价的模型表示：

$ \boldsymbol{x} \sim p(\boldsymbol{x})=\prod\limits_{i=1}^{N} p\left(x_{i}\right), $

(1a)

$ \boldsymbol{b}=\boldsymbol{Q} \boldsymbol{x}, \quad \boldsymbol{Q}=\mathit{\boldsymbol{ \boldsymbol{\varSigma}}} \boldsymbol{V}^{\mathrm{T}}, $

(1b)

$ \mathit{\boldsymbol{z}}= \boldsymbol{Ub}, $

(1c)

$ \boldsymbol{y}=\mathcal{Q}(\boldsymbol{z}+\boldsymbol{w}). $

(1d)

其中：x是待估计的信号向量，符合概率分布p(x)；b是x通过乘以矩阵Q获得的隐变量。Q的计算公式为Q=ΣV^T。进一步，通过矩阵U与隐变量b的乘积得到表示为z的中间变量。最终，通过添加噪声w，将中间变量z进行量化操作$\mathcal{Q}$，得到观测向量y。这样的等价表示使得GUAMP算法可以对隐变量b进行迭代推断，从而间接地对信号向量x进行估计。

如图 1^[15]所示，GUAMP算法可以通过构建因子节点图来说明其推断过程。图 1a中：圆圈表示变量节点，可以推断对应变量边缘分布；方框表示因子节点，包含模型中先验与观测信息；m_x→δ(x)表示从节点x传递到节点δ的消息，实际上表征的是变量x的伪线性观测分布，由于该分布为Gauss分布，可以使用分布的均值$\hat{r}$和方差τ^r表示。图 1b可以分解为一个近似消息传递(approximate message passing, AMP)模块与一个GAMP模块。借鉴文[16-17]中的Bayes推断框架，可以将GUAMP算法分解成模块A和模块B两个模块，模块A运行AMP算法，模块B运行GAMP算法，且两个模块来回迭代并交互信息，不断改善对信号的估计性能。算法具体流程如下：

首先，初始化模块A传入模块B的外信息(extrinsic information)，包括外均值b_A^ext与外方差v_{A, b}^ext，可以看作变量b的先验信息。此时模块B等价的观测模型为：

$ \boldsymbol{b} \sim p(\boldsymbol{b})=\mathcal{N}\left(\boldsymbol{b}_{\mathrm{A}}^{\mathrm{ext}}, \operatorname{diag}\left(\boldsymbol{v}_{\mathrm{A}, \boldsymbol{b}}^{\mathrm{ext}}\right)\right), $

(2a)

$ \boldsymbol{z}=\boldsymbol{U} \boldsymbol{b}, $

(2b)

$ p(\boldsymbol{y} \mid \boldsymbol{z})=\prod\limits_{i=1}^{M} p\left(y_{i} \mid z_{i}\right). $

(2c)

该模型正好可以通过GAMP算法进行求解。此时等价测量矩阵相关性已去除，因此算法鲁棒性较好。模块B运行GAMP算法会得到变量b的伪观测值b_B^ext和伪方差v_{B, b}^ext。由于变量b的先验分布(模块A传给模块B的关于变量b的消息)是Gauss分布，根据期望传播方法^[18-19]，模块B传给模块A的外信息与变量b的伪观测值、伪方差等价，即模块B传给模块A的外均值为b_B^ext、外方差为v_{B, b}^ext。此时对应模块A的等价观测模型为：

$ \boldsymbol{x} \sim p(\boldsymbol{x})=\prod\limits_{i=1}^{N} p\left(x_{i}\right), $

(3a)

$ \boldsymbol{b}=\boldsymbol{Q} \boldsymbol{x}, \quad \boldsymbol{Q}=\mathit{\boldsymbol{ \boldsymbol{\varSigma}}} \boldsymbol{V}^{\mathrm{T}}, $

(3b)

$ \boldsymbol{b}_{\mathrm{B}}^{\mathrm{ext}}=\boldsymbol{b}+\widetilde{\boldsymbol{w}}, \quad \widetilde{\boldsymbol{w}} \sim \mathcal{N}\left(\mathbf{0}, \operatorname{diag}\left(\boldsymbol{v}_{\mathrm{B}, \boldsymbol{b}}^{\mathrm{ext}}\right)\right). $

(3c)

可以看出，模块B传递给模块A的外部信息可以被用作模块A的伪观测值和伪方差。在模块A中运行AMP算法，并输出变量b的等效先验信息，将其作为模块B的输入，通过这个迭代过程来实现闭环。相较于GAMP和GVAMP算法，GUAMP算法在处理相关矩阵时表现出更好的鲁棒性^[11]。然而，本文作者通过数值仿真实验发现，GUAMP算法在平衡点附近会出现振荡现象，并且在低稀疏度情况下性能稍逊于GAMP和GVAMP算法。此外，随着测量矩阵相关性的增加，与AD-GAMP相比，GUAMP算法的性能会迅速恶化。这些仿真实验结果表明，有必要对GUAMP算法进行改进，以提高其稳健性。

由于GUAMP算法可以分解成AMP和GAMP两个模块，因此本文针对这两个模块分别构造相应的目标函数，以寻求特定结构的后验分布，并设计相应的步长。针对模块A的模型参考式(3)，可以得到变量x和变量b的联合后验分布为

$ \begin{gather*} p\left(\boldsymbol{x}, \boldsymbol{b} \mid \boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)= \\ p(\boldsymbol{x}) \delta(\boldsymbol{b}-\boldsymbol{Q} \boldsymbol{x}) p\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }} \mid \boldsymbol{b}\right) \cdot K^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right). \end{gather*} $

(4)

其中K(b_B^ext)是归一化常数，用于保证后验概率密度函数p(x, b|b_B^ext)积分为1。同时，期望得到x和b的近似后验分布为

$ \widetilde{p}(\boldsymbol{x}, \boldsymbol{b})=\widetilde{p}(\boldsymbol{x}) \delta(\boldsymbol{b}-\boldsymbol{Q x}). $

(5)

因此，为了求得$\widetilde{p}(\boldsymbol{x}, \boldsymbol{b})$，需要求解如下的优化问题：

$ \min\limits_{\widetilde{p}(\boldsymbol{x}, \boldsymbol{b}), \widetilde{p}(\boldsymbol{x})} D\left(\widetilde{p}(\boldsymbol{x}, \boldsymbol{b}) \| p\left(\boldsymbol{x}, \boldsymbol{b} \mid \boldsymbol{b}_{\mathrm{B}}^{\mathrm{ext}}\right)\right), $

(6a)

$ \text { s.t. } \;\;\;\; \widetilde{p}(\boldsymbol{x}, \boldsymbol{b})=\widetilde{p}(\boldsymbol{x}) \delta(\boldsymbol{b}-\boldsymbol{Q} \boldsymbol{x}) . $

(6b)

其中D(p₁||p₂)表示两个分布p₁与p₂的Kullback-Leibler(KL)散度。待求解的变量是概率密度函数$\widetilde{p}(\mathit{\boldsymbol{x}})$，这是一个无穷维的优化问题，难以进行正常求解。为此，本文首先对问题(6a)中的目标函数D($\widetilde{p}$(x, b)||p(x, b|b_B^ext))进行化简。将约束(6b)代入化简模块A的目标函数得到

$ \begin{gather*} D\left(\widetilde{p}(\boldsymbol{x}, \boldsymbol{b}) \| p\left(\boldsymbol{x}, \boldsymbol{b} \mid \boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)\right) \triangleq \int_{\boldsymbol{x}, \boldsymbol{b}} \widetilde{p}(\boldsymbol{x}, \boldsymbol{b}) \ln \frac{\widetilde{p}(\boldsymbol{x}, \boldsymbol{b})}{p\left(\boldsymbol{x}, \boldsymbol{b} \mid \boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)} \mathrm{d} \boldsymbol{x} \mathrm{d} \boldsymbol{b}= \\ \int_{\boldsymbol{x}, \boldsymbol{b}} \widetilde{p}(\boldsymbol{x}, \boldsymbol{b}) \ln \frac{\widetilde{p}(\boldsymbol{x})}{p(\boldsymbol{x}) p\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }} \mid \boldsymbol{b}\right) K^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)} \mathrm{d} \boldsymbol{x} \mathrm{d}\boldsymbol{b}= \\ \int_{\boldsymbol{x}} \widetilde{p}(\boldsymbol{x}) \ln \frac{\widetilde{p}(\boldsymbol{x})}{p(\boldsymbol{x})} \mathrm{d} \boldsymbol{x}+\int_{\boldsymbol{b}} \widetilde{p}(\boldsymbol{b}) \ln \frac{\widetilde{p}(\boldsymbol{b})}{p\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }} \mid \boldsymbol{b}\right) C^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)} \mathrm{d} \boldsymbol{b}+\int_{\boldsymbol{b}} \widetilde{p}(\boldsymbol{b}) \ln \frac{1}{\widetilde{p}(\boldsymbol{b})} \mathrm{d} \boldsymbol{b}+\ln \frac{C^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)}{K^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)}= \\ D\left(\widetilde{p}_{\mathit{\boldsymbol{x}}} \| p_{\mathit{\boldsymbol{x}}}\right)+D\left(\widetilde{p}_{\boldsymbol{b}} \| p_{\boldsymbol{b}_{\mathrm{B}}^{\text {ext }} \mid \boldsymbol{b}} C^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)\right)+H_{\mathrm{A}}\left(\widetilde{p}_{\boldsymbol{b}}\right)+\ln \frac{C^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)}{K^{-1}\left(\boldsymbol{b}_{\mathrm{B}}^{\text {ext }}\right)}. \end{gather*} $

(7)

其中：H_A($\widetilde{p}_{\mathit{\boldsymbol{b}}}$)表示随机变量b分布为$\widetilde{p}_{\mathit{\boldsymbol{b}}}$的熵，C^－1(b_B^ext)为归一化常数，满足∫p(b_B^ext|b)db=C(b_B^ext)。尽管b_B^ext会随着迭代而发生变化，但这里预期ln[C^－1(b_B^ext)/K^－1(b_B^ext)]对KL散度的影响较式(7)的前3项小，且经过少许次迭代后该值趋于稳定，因此在式(7)中，本文将该项视为常数。至此，式(6a)和(6b)表述的优化问题可以近似为:

$ \min\limits_{\widetilde{p}(\boldsymbol{b}), \widetilde{p}(\boldsymbol{x})} J_{\mathrm{A}}\left(\widetilde{p}_{\mathit{\boldsymbol{x}}}, \widetilde{p}_{\boldsymbol{b}}\right), $

(8a)

$ \text { s.t. }\;\;\widetilde{p}_{\boldsymbol{b}}=T_{Q} \widetilde{p}_{\mathit{\boldsymbol{x}}} . $

(8b)

其中

$ \begin{gather*} J_{\mathrm{A}}\left(\widetilde{p}_{\boldsymbol{x}}, \widetilde{p}_{\boldsymbol{b}}\right) \triangleq D\left(\widetilde{p}_{\boldsymbol{x}} \| \prod\limits_{j=1}^{N} p_{x}\left(\boldsymbol{x}_{j}\right)\right)+ \\ D\left(\widetilde{p}_{\boldsymbol{b}} \| \prod\limits_{i=1}^{M} p_{b_{\mathrm{B}}^{\mathrm{ext}} \mid b}\left(b_{\mathrm{B}, i}^{\mathrm{ext}} \mid b_{i}\right) C^{-1}\left(b_{\mathrm{B}, i}^{\mathrm{ext}}\right)\right)+H_{\mathrm{A}}\left(\widetilde{p}_{\boldsymbol{b}}\right). \end{gather*} $

(9)

T_Q为变换函数，即随机向量b的每个元素是通过随机向量x的各元素线性加权得到的，即可以通过一个线性变换矩阵Q和随机向量b的分布p(x)来表征分布p(b)。约束项$\widetilde{p}_{\mathit{\boldsymbol{b}}}$=T_Q$\widetilde{p}_{\mathit{\boldsymbol{x}}}$表示变量b的分布$\widetilde{p}_{\mathit{\boldsymbol{b}}}$ 可通过变量x的分布$\widetilde{p}_{\mathit{\boldsymbol{x}}}$ 求得。上述优化问题中待求解的分布仍非常复杂，很难进行有效求解，因此下面作进一步假设。假设变量x与b各分量独立可分，即x与b的概率密度函数分别满足：

$ \widetilde{p}_{\boldsymbol{x}}(\boldsymbol{x}) =\prod\limits_{j=1}^{N} \widetilde{p}_{x}\left(x_{j}\right), $

(10)

$ \widetilde{p}_{\boldsymbol{b}}(\boldsymbol{b}) =\prod\limits_{i=1}^{M} \widetilde{p}_{b}\left(b_{i}\right). $

(11)

此外，当给定分布的一阶矩和二阶矩时，熵函数H_A($\widetilde{p}$(b))存在上界，且服从Gauss分布。对于给定一阶矩和二阶矩，Gauss分布的熵值是所有分布中最大的。因此，将熵函数H_A($\widetilde{p}_{\mathit{\boldsymbol{b}}}$)用对应Gauss分布的上界H_{A, G}($\widetilde{p}_{\mathit{\boldsymbol{b}}}$, τ_A^p)替代以简化代价函数，其中τ_A^p为经矩匹配后Gauss分布的方差。最后，将问题中关于分布的约束$\widetilde{p}_{\mathit{\boldsymbol{b}}}$=T_Q$\widetilde{p}_{\mathit{\boldsymbol{x}}}$弱化为矩匹配约束，则式(8a)和(8b)的优化问题可以化简为:

$ \min\limits_{\widetilde{p}(\boldsymbol{b}), \widetilde{p}(\boldsymbol{x})} \widetilde{J}_{\mathrm{A}}\left(\widetilde{p}_{\boldsymbol{x}}, \widetilde{p}_{\boldsymbol{b}}\right), $

(12a)

$ \begin{array}{ll} \text { s. t. } & \mathscr{E}\left[\boldsymbol{b} \mid \widetilde{p}_{\boldsymbol{b}}\right]=\boldsymbol{Q} \mathscr{E}\left[\boldsymbol{x} \mid \widetilde{p}_{\boldsymbol{x}}\right], \\ & \boldsymbol{\tau}_{A}^{p}=\boldsymbol{Q}^{2} \operatorname{var}\left[\boldsymbol{x} \mid \widetilde{p}_{\boldsymbol{x}}\right] . \end{array} $

(12b)

其中

$ \begin{array}{*{20}{c}} \widetilde{J}_{\mathrm{A}}\left(\widetilde{p}_{x}, \widetilde{p}_{b}\right) \triangleq \sum\limits_{j=1}^{N} \underbrace{D\left(\tilde{p}_{x}\left(x_{j}\right) \| p_{x}\left(x_{j}\right)\right)}_{\text {第1项 }}+ \\ \sum\limits_{i=1}^{M} \underbrace{D\left(\widetilde{p}_{b}\left(b_{i}\right) \| p_{b_{\mathrm{B}}^{\mathrm{ext}} \mid b}\left(b_{\mathrm{B}, i}^{\mathrm{ext}} \mid b_{i}\right) C_{i}^{-1}\left(b_{\mathrm{B}, i}^{\mathrm{ext}}\right)\right)}_{\text {第 } 2 \text { 项 }}+ \\ \sum\limits_{i=1}^{M} \underbrace{H_{\mathrm{A}, \mathrm{G}}\left(\widetilde{p}_{b}\left(b_{i}\right), \tau_{\mathrm{A}, i}^{p}\right)}_{\text {第3项 }} . \end{array} $

(13)

其中：$\mathscr{E}$[b|$\widetilde{p}_{\mathit{\boldsymbol{b}}}$]表示变量b在分布$\widetilde{p}_{\mathit{\boldsymbol{b}}}$(b)下对应的均值，Q²表示对矩阵Q各分量逐位取平方运算，var表示取随机变量的方差。目标函数$\widetilde{J}_{\mathrm{A}}$($\widetilde{p}_{\mathit{\boldsymbol{x}}}$, $\widetilde{p}_{\mathit{\boldsymbol{b}}}$)(见式(13))可分为3项，现分别进行分析。对于$\widetilde{J}_{\mathrm{A}}$($\widetilde{p}_{\mathit{\boldsymbol{x}}}$, $\widetilde{p}_{\mathit{\boldsymbol{b}}}$)中的第1项，根据GAMP算法，可以将变量x_j的近似后验分布写为$\widetilde{p}_{x}$(x_j)=p_x(x_j)$\mathcal{N}$(x_j; $\hat{r}_{\mathrm{A}, j}$, τ_{A, j}^r)·X_j($\hat{r}_{\mathrm{A}, j}$, τ_{A, j}^r)^－1。其中：$\hat{r}_{\mathrm{A}, j}$和τ_{A, j}^r为变量x_j的伪观测值与伪方差，X_j($\hat{r}_{\mathrm{A}, j}$, τ_{A, j}^r)是保证$\widetilde{p}_{x_{j}}$(x_j)为概率密度函数的归一化常数。将x近似后验分布的表达式代入式(13)，此时第1项可以表示为

$ \begin{gather*} D\left(\tilde{p}_{x}\left(x_{j}\right) \| p_{x}\left(x_{j}\right)\right)= \\ \int \widetilde{p}_{x}\left(x_{j} ; \hat{r}_{\mathrm{A}, j}, \tau_{\mathrm{A}, j}^{r}\right) \cdot \\ \ln \frac{p_{x}\left(x_{j}\right) \mathcal{N}\left(x_{j} ; \hat{r}_{\mathrm{A}, j}, \tau_{\mathrm{A}, j}^{r}\right)}{p_{x}\left(x_{j}\right) X_{j}\left(\hat{r}_{\mathrm{A}, j}, \tau_{\mathrm{A}, j}^{r}\right)} \mathrm{d} x_{j}= \\ -\ln X_{j}\left(\hat{r}_{\mathrm{A}, j}, \tau_{\mathrm{A}, j}^{r}\right)- \\ \frac{\ln 2 {\mathsf{π}} \tau_{\mathrm{A}, j}^{r}}{2}-\frac{\left|\hat{x}_{j}-\hat{r}_{\mathrm{A}, j}\right|^{2}+\tau_{j}^{x}}{2 \tau_{j}^{x}} . \end{gather*} $

(14)

其中：$\hat{x}_j$与τ_j^x分别表示变量x_j的后验均值和后验方差。若先验参数服从Bernoulli-Gauss分布，即p_x(x_j)=(1－λ)δ(x_j)+λ $\mathcal{N}$(x_j; x_{p, j}, τ_{p, j}^x)。其中：x_{p, j}与τ_{p, j}^x为变量x_j非零元素服从的Gauss分布对应的均值与方差，λ为稀疏度，此时$\hat{x}_j$与τ_j^x可由式(15)和(16)计算得到：

$ \hat{x}_{j}=\frac{\lambda}{\lambda+(1-\lambda) \exp \left(-M_{j}\right)} \frac{\tau_{p, j}^{x} \hat{r}_{\mathrm{A}, j}+\tau_{\mathrm{A}, j}^{r} x_{p, j}}{\tau_{\mathrm{A}, j}^{r}+\tau_{p, j}^{x}} . $

(15)

$ \begin{gather*} \tau_{j}^{x}=\frac{\lambda}{\lambda+(1-\lambda) \exp \left(-M_{j}\right)} \cdot \\ \left(\left(\frac{\tau_{p, j}^{x} \hat{r}_{\mathrm{A}, j}+\tau_{\mathrm{A}, j}^{r} x_{p, j}}{\tau_{\mathrm{A}, j}^{r}+\tau_{p, j}^{x}}\right)^{2}+\frac{\tau_{p, j}^{x} \tau_{\mathrm{A}, j}^{r}}{\tau_{p, j}^{x}+\tau_{\mathrm{A}, j}^{r}}\right)- \\ \left(\frac{\lambda}{\lambda+(1-\lambda) \exp \left(-M_{j}\right)} \frac{\tau_{p, j}^{x} \hat{r}_{\mathrm{A}, j}+\tau_{\mathrm{A}, j}^{r} x_{p, j}}{\tau_{\mathrm{A}, j}^{r}+\tau_{p, j}^{x}}\right)^{2} . \end{gather*} $

(16)

其中

$ M_{j}=\frac{1}{2} \ln \frac{\tau_{\mathrm{A}, j}^{r}}{\tau_{\mathrm{A}, j}^{r}+\tau_{p, j}^{x}}+\frac{\left(\hat{r}_{\mathrm{A}, j}\right)^{2}}{2 \tau_{\mathrm{A}, j}^{r}}-\frac{\left(\hat{r}_{\mathrm{A}, j}-x_{p, j}\right)^{2}}{2\left(\tau_{\mathrm{A}, j}^{r}+\tau_{p, j}^{x}\right)} $

(17)

对于$\widetilde{J}_{\mathrm{A}}$($\widetilde{p}_{\mathit{\boldsymbol{x}}}$, $\widetilde{p}_{\mathit{\boldsymbol{b}}}$)(见式(13))中的第2项，经化简可得

$ \begin{gather*} D\left(\widetilde{p}_{b}\left(b_{i}\right) \| p_{b_{\mathrm{B}}^{\text {ext } \mid b}}\left(\widetilde{b}_{i} \mid b_{i}\right)\right)= \\ -\ln C_{i}\left(\hat{p}_{\mathrm{A}, i}, \tau_{\mathrm{A}, i}^{p}\right)-\frac{1}{2} \ln \left(2 {\mathsf{π}} \tau_{\mathrm{A}, i}^{p}\right)- \\ \frac{\left|\hat{b}_{i}-\hat{p}_{\mathrm{A}, i}\right|^{2}+\tau_{i}^{b}}{2 \tau_{\mathrm{A}, i}^{p}} \end{gather*} $

(18)

其中：$\hat{b}_i$与τ_i^b为变量b_i的后验均值与后验方差，$\hat{p}_{\mathrm{A}, i}$和τ_{A, i}^p分别为变量b_i的先验均值与先验方差，即模块A传给模块B的外信息。C_i($\hat{p}_{\mathrm{A}, i}$, τ_{A, i}^p)为归一化项。模块B传给模块A的消息服从Gauss分布，此时b_i的先验与似然分布均为Gauss分布。因此，$\hat{b}_i$与τ_i^b可根据式(19)和(20)计算得到：

$ \frac{1}{\tau_{i}^{b}}=\frac{1}{\tau_{\mathrm{B}, i}^{r}}+\frac{1}{\tau_{\mathrm{A}, i}^{p}}, $

(19)

$ \frac{\hat{b}_{i}}{\tau_{i}^{b}}=\frac{\hat{r}_{\mathrm{B}, i}}{\tau_{\mathrm{B}, i}^{r}}+\frac{\hat{p}_{\mathrm{A}, i}}{\tau_{\mathrm{A}, i}^{p}} . $

(20)

$\widetilde{J}_{\mathrm{A}}$($\widetilde{p}_{\mathit{\boldsymbol{x}}}$, $\widetilde{p}_{\mathit{\boldsymbol{b}}}$)(见式(13))中的第3项是Gauss分布的熵函数，经计算可得

$ \begin{gather*} H_{\mathrm{A}, \mathrm{G}}\left(\widetilde{p}_{b}\left(b_{i}\right), \tau_{\mathrm{A}, i}^{p}\right) \triangleq \\ \frac{1}{2} \frac{\operatorname{var}\left[b_{i} \mid \widetilde{p}_{b}\left(b_{i}\right)\right]}{\tau_{\mathrm{A}, i}^{p}}+\ln \left(2 {\mathsf{π}} \tau_{\mathrm{A}, i}^{p}\right). \end{gather*} $

(21)

其中var[b_i|$\widetilde{p}_{b}$(b_i)]表示变量b_i服从分布$\widetilde{p}_{b}$(b_i)下所对应的方差。

模块B构造的目标函数与上面的推导过程类似。对于模块B，变量b和变量z的联合后验分布为

$ \begin{gather*} p\left(\boldsymbol{b}, \boldsymbol{z} \mid \boldsymbol{b}_{\mathrm{A}}^{\text {ext }}, \boldsymbol{y}\right)= \\ p\left(\boldsymbol{b} \mid \boldsymbol{b}_{\mathrm{A}}^{\text {ext }}\right) \delta(\boldsymbol{z}-\boldsymbol{U} \boldsymbol{b}) p(\boldsymbol{y} \mid \boldsymbol{z}) \cdot S^{-1}(\boldsymbol{y}) . \end{gather*} $

(22)

其中：S(y)为归一化常数使得式(22)关于变量b、z积分为1。期望得到b和z的后验分布为

$ \widetilde{p}(\boldsymbol{b}, \boldsymbol{z})=\tilde{p}(\boldsymbol{b}) \delta(\boldsymbol{z}-\boldsymbol{U} \boldsymbol{b}) . $

(23)

因此，模块B也可以构造如下的优化问题：

$ \min\limits_{\widetilde{p}(\boldsymbol{b}, \boldsymbol{z}), \widetilde{p}(\boldsymbol{b})} D\left(\widetilde{p}(\boldsymbol{b}, \boldsymbol{z}) \| p\left(\boldsymbol{b}, \boldsymbol{z} \mid \boldsymbol{y}, \boldsymbol{b}_{\mathrm{A}}^{\mathrm{ext}}\right)\right), $

(24a)

$ \text { s. t. } \quad \widetilde{p}(\boldsymbol{b}, \boldsymbol{z})=\widetilde{p}(\boldsymbol{b}) \delta(\boldsymbol{z}-\boldsymbol{U} \boldsymbol{b}). $

(24b)

其中b_A^ext为模块A传给模块B的外信息，包含变量b的先验信息。经过简化后，可以得到与模块B目标函数为：

$ \min\limits_{\widetilde{p}(\boldsymbol{b}), \widetilde{p}(z)} J_{\mathrm{B}}\left(\widetilde{p}_{\boldsymbol{b}}, \widetilde{p}_{z}\right), $

(25a)

$ \begin{array}{ll} \text { s.t. } & \mathscr{E}\left[\boldsymbol{z} \mid \widetilde{p}_{z}\right]=\boldsymbol{U} \mathscr{E}\left[\boldsymbol{b} \mid \widetilde{p}_{\boldsymbol{b}}\right], \\ & \boldsymbol{\tau}_{\mathrm{B}}^{p}=\boldsymbol{U}^{2} \operatorname{var}\left[\boldsymbol{b} \mid \widetilde{p}_{\boldsymbol{b}}\right] . \end{array} $

(25b)

其中

$ \begin{array}{*{20}{c}} & J_{\mathrm{B}}\left(\widetilde{p}_{b}, \widetilde{p}_{z}\right) \triangleq \sum\limits_{i=1}^{M} \underbrace{D\left(\widetilde{p}_{b}\left(b_{i}\right) \| p_{b \mid b_{\mathrm{A}}^{\mathrm{ext}}}\left(b_{i}\right)\right)}_{\text {第1 项 }}+ \\ & \sum\limits_{i=1}^{M} \underbrace{D\left(\widetilde{p}_{z}\left(z_{i}\right) \| p_{y \mid z}\left(y_{i} \mid z_{i}\right) Z_{i}^{-1}\left(y_{i}\right)\right)}_{\text {第 } 2 \text { 项 }}+ \\ & \sum\limits_{i=1}^{M} \underbrace{H_{\mathrm{B}, \mathrm{G}}\left(\widetilde{p}_{z}\left(z_{i}\right), \tau_{\mathrm{B}, i}^{p}\right)}_{\text {第3项 }} . \end{array} $

(26)

Z_i(y_i)为归一化常数。与模块A的计算方法类似，J_B($\widetilde{p}_{\mathit{\boldsymbol{b}}}$, $\widetilde{p}_{\mathit{\boldsymbol{z}}}$)中的第1项可以化简为

$ \begin{gather*} D\left(\widetilde{p}_{b}\left(b_{i}\right) \| p_{b \mid b_{\mathrm{A}}^{\mathrm{ext}}}\left(b_{i}\right)\right)=-\ln B_{i}\left(\hat{r}_{\mathrm{B}, i}, \tau_{\mathrm{B}, i}^{r}\right)- \\ \frac{\ln \left(2 {\mathsf{π}} \tau_{\mathrm{B}, i}^{r}\right)}{2}-\frac{\left|\hat{b}_{i}-\hat{r}_{\mathrm{B}, i}\right|^{2}+\tau_{i}^{b}}{2 \tau_{\mathrm{B}, i}^{r}} . \end{gather*} $

(27)

其中：$\hat{r}_{B, i}$与τ_{B, i}^r为变量b_i的伪线性观测值与对应方差，$\hat{b}_i$与τ_i^b为变量b_i的后验均值与方差，B_i($\hat{r}_{{\rm{B}}, i}$, τ_{B, i}^r)为归一化常数。D($\widetilde{p}_{b}$(b_i)||p_bA^ext|b(b_i)) 是变量b_i的近似后验分布与它从A模块接收到的先验分布的K-L散度，而D($\widetilde{p}_{b}$(b_i)||p_bB^ext|b(b_i)) 是变量b_i的近似后验分布与它从B模块接收到的似然分布的K-L散度。J_B($\widetilde{p}_{\mathit{\boldsymbol{b}}}$, $\widetilde{p}_{\mathit{\boldsymbol{z}}}$)中的第2项可以表示为

$ \begin{gather*} D\left(\widetilde{p}_{z}\left(z_{i}\right) \| p_{y \mid z}\left(y_{i} \mid z_{i}\right) \cdot Z_{i}^{-1}\right)= \\ -\ln E_{i}\left(\hat{p}_{\mathrm{B}, i}, \tau_{\mathrm{B}, i}^{p}\right)-\frac{1}{2} \ln \left(2 {\mathsf{π}} \tau_{\mathrm{B}, i}^{p}\right)- \\ \frac{\left|\hat{z}_{i}-\hat{p}_{\mathrm{B}, i}\right|^{2}+\tau_{i}^{z}}{2 \tau_{\mathrm{B}, i}^{p}} . \end{gather*} $

(28)

其中：$\hat{p}_{\mathrm{B}, i}$与τ_{B, i}^p为变量z_i的先验均值与方差，$\hat{z}_i$与τ_i^z为变量z_i的后验均值与方差，当已知似然分布时可以求解；E_i($\hat{p}_{\mathrm{B}, i}$, τ_{B, i}^p)为归一化常数。J_B($\widetilde{p}_{\mathit{\boldsymbol{b}}}$, $\widetilde{p}_{\mathit{\boldsymbol{z}}}$)中的第3项可以表示为

$ \begin{gather*} H_{\mathrm{B}, \mathrm{G}}\left(\widetilde{p}_{z}\left(z_{i}\right), \tau_{\mathrm{B}, i}^{p}\right) \triangleq \\ \frac{1}{2} \frac{\operatorname{var}\left[z_{i} \mid \widetilde{p}_{z}\right]}{\tau_{\mathrm{B}, i}^{p}}+\ln \left(2 {\mathsf{π}} \tau_{\mathrm{B}, i}^{p}\right) . \end{gather*} $

(29)

至此，两个模块的目标函数构造完成。下面介绍如何利用目标函数进行算法步长选择。由于两个模块的步长选择采用相同的策略，仅目标函数与调整的具体变量有所不同。因此，在下面有关步长选择策略的描述中，与步长选择有关的变量不再区分两个模块，用J(t)来统一描述，而不单独区分模块A目标函数J_A(t)或模块B目标函数J_B(t)。设时刻t目标函数取值为J(t)，则时刻t处迭代步长β(t) 的选择规则如下：1) 根据窗长度Win，选择最近的目标函数值共Win个，并求取其中最小值。2) 若当前时刻目标函数J(t)大于上面选取序列的最小值，则认为算法仍在正常迭代，可以增加步长以加快算法收敛速度，步长增量由上一次步长β(t-1)与一个大于1的常数Inc确定，即β(t)=Inc· β(t－1)；若不满足上述条件，则认为算法振荡或即将收敛，需要减小步长，步长减少量按照上一次步长β(t-1)与一个小于1的常数Dec确定，即β(t)=Dec·β(t－1)。3) 增大或减小步长均不会超过预设的步长最大值β_max或步长最小值β_min，直至算法收敛到一定精度或者迭代一定次数后结束迭代。

GUAMP算法的详细步骤请参考文[15]。将上述自适应步长选择规则耦合到GUAMP算法中，即可得到AD-GUAMP算法，如图 2所示。图中：g_x($\hat{r}$, τ^r)为输入估计函数，输入参数为GAMP算法迭代过程中的伪线性观测值与方差，输出结果为变量x的后验估计值；g_z($\hat{p}$, τ^p)为输出估计函数，输入参数为GAMP算法迭代过程中隐变量z先验均值与方差的估计值，输出结果为变量z的后验估计值。根据先验分布与似然分布以及估计方法的不同，输入估计与输出估计函数分别有不同的解析表达式。以最小均方误差(minimum mean squared error，MMSE)估计为例，当先验分布为p(x)、似然分布为p(y|z)时，输入估计与输出估计函数可以分别表示为：

$ g_{x}\left(\hat{r}, \tau^{r}\right) =\int x \frac{p(x) \mathcal{N}\left(x ; \hat{r}, \tau^{r}\right)}{X\left(\hat{r}, \tau^{r}\right)} \mathrm{d} x, $

(30)

$ g_{z}\left(\hat{p}, \tau^{p}\right)=\int z \frac{p(y \mid z) \mathcal{N}\left(z ; \hat{p}, \tau^{p}\right)}{D\left(\hat{p}, \tau^{p}\right)} \mathrm{d} z . $

(31)

其中：X($\hat{r}$, τ^r)和D($\hat{p}$, τ^p)分别是归一化常数，保证后验分布积分为1。本文对模块A中变量τ_A^p、τ_A^s、τ_A^r、$\hat{\boldsymbol{S}}_{\mathrm{A}}$、$\hat{\boldsymbol{x}}$进行阻尼衰减调整，模块B中则对变量τ_B^p、τ_B^s、τ_B^r、$\hat{\boldsymbol{S}}_{\mathrm{B}}$、$\hat{\boldsymbol{b}}$进行阻尼衰减调整。

2 仿真实验

本章将通过数值仿真实验来验证所提AD-GUAMP算法的有效性。下面共考虑3种测量矩阵的场景，分别为低秩矩阵、条件数病态矩阵和相关矩阵。

1) 低秩矩阵。

本文使用矩阵秩与其最小维度的比值r，即秩比，来描述矩阵的低秩程度。该值越大表明矩阵越接近满秩，矩阵各行或各列相关性越弱，算法重构性能越好。

矩阵构造方式如下：A=UV。其中：U∈$\mathbb{R}^{M \times R}$，V∈$\mathbb{R}^{R \times N}$，矩阵U、V各元素均从标准正态分布中抽样而来，且有R＜min{M, N}。此时易知矩阵A的秩为R。

2) 条件数病态矩阵。

本文使用条件数κ来刻画矩阵的病态特性。条件数越大，表明算法重构问题越困难，信号估计性能越差。矩阵构造方式如下：A=UΣV^T。其中：U、V为Gauss矩阵(矩阵各元素从Gauss分布中抽样得到)经奇异值分解产生，U为左奇异矩阵，V为右奇异矩阵。对角矩阵Σ对角线上的元素满足Σ_i，i/Σ_i+1，i+1=κ^1/min{M，N}。

3) 相关矩阵。

本文使用相关系数ρ来描述一类相关矩阵的相关性。相关系数越大，矩阵各列相关性越强，算法的重构性能越差。相关矩阵构造方式如下^[20]：A=R_LHR_R。其中：R_L=R₁^1/2∈$\mathbb{R}^{M \times M}$，R_R=R₂^1/2∈$\mathbb{R}^{N \times N}$，矩阵R₁和R₂在位置(i, j)处的元素值均为ρ^|i-j|；矩阵H∈$\mathbb{R}^{M \times N}$，其各元素均服从独立的标准正态分布。

在低秩测量矩阵和条件数病态测量矩阵情况下，理论上可以证明GVAMP算法最优^[8]。因此，在这两种情况下，本文所设计的AD-GUAMP算法能够逼近GVAMP算法性能即可表明AD-GUAMP算法的有效性。

仿真条件设置如下：信号x先验服从Bernoulli-Gauss分布，即p(x|q)=$\prod\limits_{j=1}^N$(1－λ)δ(x_j)+λ $\mathcal{N}$(x_j; 0，σ_x²)。过采样情况下稀疏度λ=0.15，欠采样情况下稀疏度λ=0.05。Gauss分布方差σ_x²=1/λ，此时等效Gauss分布方差为1，信号长度N=512。隐变量z由待估计变量x经线性变换矩阵A得到。噪声方差σ²由信噪比SNR=||Ax||₂²/(Mσ²)确定，在仿真实验中分别设置为20和40 dB。无量化观测数据经1 bit和2 bit量化得到。过采样情况下信号长度为M=2 048，欠采样情况下信号长度为M=410。对于2 bit量化模型，信号动态范围设定在[-3σ_z, +3σ_z]，其中σ_z²=||A||_F²/M。仿真中对矩阵A进行归一化使得||A||_F²=N。本文使用归一化均方误差(normalized mean squared error，NMSE)$\buildrel \Delta \over =\|\boldsymbol{z}-\hat{\boldsymbol{z}}\|_2^2 /\|\boldsymbol{z}\|_2^2$衡量2 bit量化情况下算法的重构性能。对于1 bit量化模型，由于无法估计信号幅度信息，因此利用去偏归一化均方误差(debiased NMSE，dNMSE)$\buildrel \Delta \over = \min\limits_c\|\boldsymbol{z}-c \hat{\boldsymbol{z}}\|_2^2 /\|\boldsymbol{z}\|_2^2$衡量1 bit量化下算法的估计性能，其中c为待估计的常数，用于修正信号x的幅度。最大迭代次数T_max=100，模块A最小步长β_min=0.05，最大步长β_max=1，步长增加项IncInc=1.15，步长衰减项Dec=0.5，窗长度Win=1。所有绘制曲线都经过500次Monte Carlo实验结果平均得到。下面首先数值计算目标函数随着迭代次数的变化，再通过数值仿真评估AD-GUAMP算法在不同矩阵场景下的性能。

2.1 目标函数

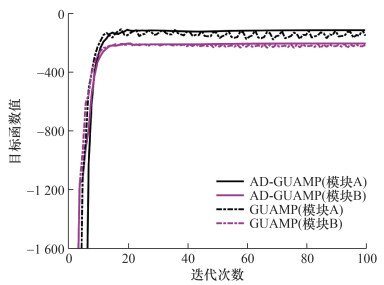
AD-GUAMP算法为两个消息传递模块分别设计了目标函数。下面以相关测量矩阵为例说明目标函数的收敛情况。仿真条件设置如下：信噪比SNR=40 dB，2 bit量化，过采样因子δ=0.8，测量矩阵的相关系数ρ=0.1，其他仿真参数与之前设置的仿真参数保持一致。图 2绘制的函数曲线为-J_A(t)与-J_B(t)，可见目标函数值会随着迭代次数的增加而不断上升。从图 3可以看出，GUMAP算法由于没有进行步长自适应调整，两个模块对应的目标函数值(虚线)会在平衡点附近不断振荡。AD-GUAMP算法则由于增加步长调整机制，两个模块的目标函数值(实线)均稳定上升，经一定迭代次数最后收敛到某个值。此外，从图 2还可以看到，对同样的仿真场景，GUAMP算法两个模块的目标函数值均低于AD-GUAMP算法的两个对应模块。可以预见，采用自适应步长方法后，AD-GUAMP算法性能将优于GUAMP算法性能。

2.2 低秩矩阵

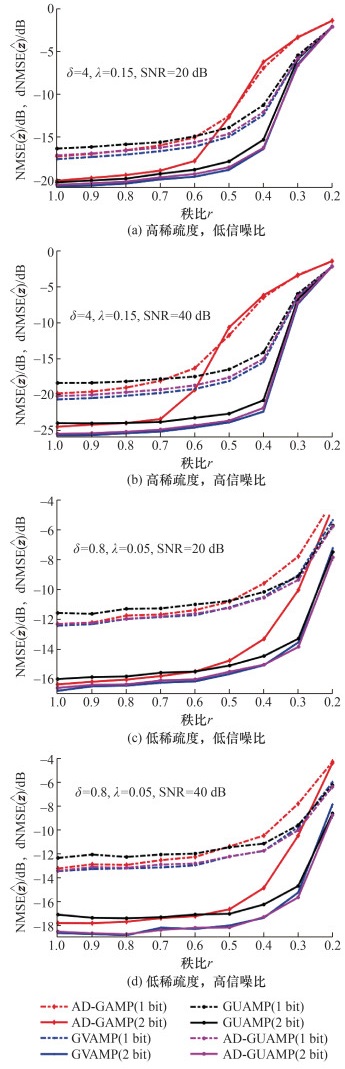
图 4展示了随着矩阵秩比的变化算法NMSE(2 bit量化)或dNMSE(1 bit量化)的结果。图 4a和4c中，信噪比为20 dB；图 4b和4d中，信噪比为40 dB。图 4a和4b对应于过采样，过采样因子为δ=4，稀疏度λ=0.15。图 4c和4d对应于欠采样，过采样因子为δ=0.8，稀疏度λ=0.05。从图 4a可以看出，在1 bit量化下，GVAMP算法的NMSE相对于AD-GUAMP算法低约0.4 dB，表明GVAMP算法的性能最佳，AD-GUAMP算法略逊于GVAMP算法，但优于GUAMP和AD-GAMP算法。当秩比r＞0.6时，AD-GAMP算法优于GUAMP算法。然而，随着秩比的减小，即矩阵变得更低秩，AD-GAMP算法的发散现象严重，此时GUAMP算法的性能优于AD-GAMP算法。在2 bit量化下，GVAMP算法的NMSE相对于AD-GUAMP算法低约0.25 dB，表明GVAMP算法稍优于AD-GUAMP算法，但GUAMP算法仍优于AD-GAMP算法。图 4b、4c和4d的结果与图 4a基本一致，即矩阵接近满秩时，GUAMP算法的性能仍高于AD-GAMP算法，随着矩阵秩比的减小，GUAMP算法的性能略低于AD-GAMP算法。在欠采样情况下，AD-GUAMP算法和GVAMP算法的性能非常接近。总之，随着秩比的减小，所有算法的性能都会恶化，但在低秩情况下，AD-GAMP算法的恶化现象更为严重，其性能明显低于其他算法，而其他算法在不同秩比下的性能相近。相对于GVAMP和AD-GUAMP算法，GUAMP算法有轻微的性能损失。

2.3 条件数病态矩阵

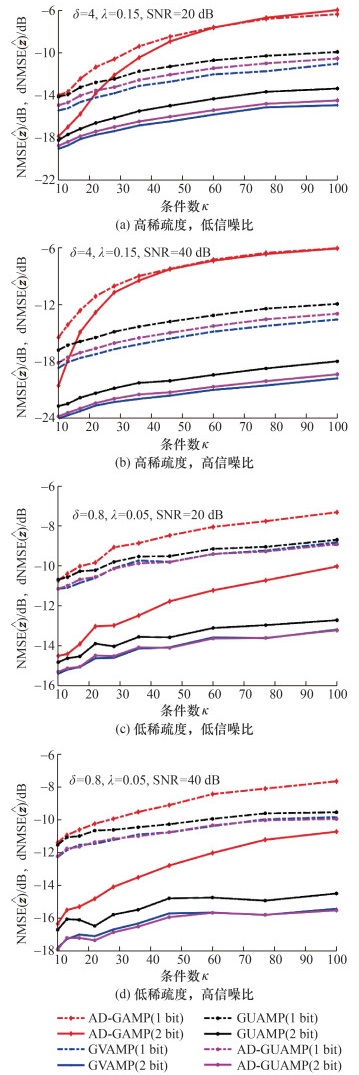
图 5展示了随着条件数κ的变化算法NMSE或dNMSE的变化曲线。图 5a和5c中，信噪比为20 dB；图 5b和5d中，信噪比为40 dB。图 5a和5b对应于过采样，过采样因子为δ=4，稀疏度λ=0.15。图 5c和5d对应于欠采样，过采样因子为δ=0.8，稀疏度λ=0.05。从图 5a可以看出，在1 bit量化下，GVAMP算法的dNMSE相对于AD-GUAMP算法低约0.6 dB，其重构性能最佳。其次是AD-GUAMP算法，两者的性能相近，并且均优于AD-GAMP和GUAMP算法。对于所有测试条件数，GUAMP算法的性能均优于AD-GAMP算法。在2 bit量化下，结果与1 bit量化场景类似。图 5b(过采样、高信噪比)、5c(欠采样、低信噪比)和5d(欠采样、高信噪比)的结果与图 5a基本一致。在欠采样情况下，AD-GUAMP算法和GVAMP算法的性能非常接近。同时，在高信噪比情况下，AD-GAMP算法相对于其他算法的性能恶化更为严重。总之，随着条件数κ的增加，所有算法的重构性能都变差，其中AD-GAMP算法最不稳健，其次是GUAMP算法。AD-GUAMP算法的重构性能非常接近GVAMP算法，尤其在低过采样因子和低稀疏度的情况下，两者的重构性能几乎完全一致。

2.4 相关矩阵

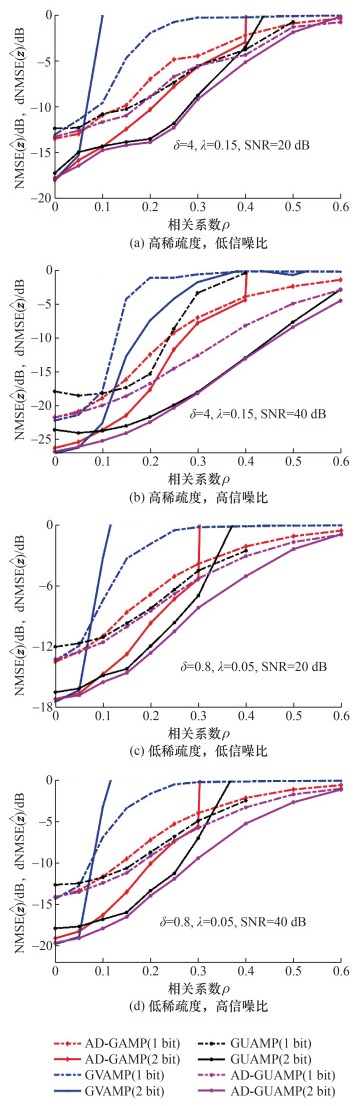
图 6给出了算法NMSE或dNMSE随相关系数ρ的变化曲线。各分图仿真设置与图 5情况相同。从图 6a可以看出，在过采样和1 bit量化的情况下，AD-GUAMP算法和GUAMP算法的性能相当，均优于AD-GAMP算法和GVAMP算法。此外，当测量矩阵的相关性较低时，GUAMP算法的性能略逊于AD-GAMP算法。随着测量矩阵的相关性增加，AD-GAMP算法的性能急剧恶化，而GUAMP算法的性能优于AD-GAMP算法。当矩阵相关系数ρ＞0.1时，GVAMP算法的性能开始急剧恶化。在2 bit量化下，AD-GUAMP算法的性能优于GUAMP算法，且两者均优于GVAMP算法。当测量矩阵相关系数为0＜ρ＜0.1时，GVAMP算法发散。图 6b(过采样、高信噪比)、6c(欠采样、低信噪比)和6d(欠采样、高信噪比)的结果与图 6a基本一致。总之，当相关系数ρ较小时(ρ＜0.05)，所有算法的估计性能相近。随着测量矩阵相关性的增加，GUAMP和AD-GUAMP算法的稳健性最高，并且在大多数情况下，AD-GUAMP算法优于GUAMP算法。这表明本文所提出的AD-GUAMP算法的自适应步长衰减机制提升了GUAMP算法的稳健性。

2.5 运行时间

表 1给出了在特定条件下各算法的平均运行时间。仿真设置在欠采样场景，其中欠采样因子与之前的仿真设置相同，信噪比为40 dB。不同测量矩阵的参数设置为：低秩矩阵中秩比r=0.8，条件数矩阵中条件数κ=10，相关矩阵中相关系数ρ=0.1。除了上述条件外，其他仿真参数与之前的仿真参数相同。表 1中的时间是通过进行50次Monte Carlo实验并取平均值得到的。

表 1中的数据表明，AD-GUAMP算法的平均运行时间大约是AD-GAMP算法的2倍。这是由于AD-GUAMP算法需要同时运行GAMP模块和AMP模块，相比之下AD-GAMP算法只需要运行单个GAMP模块，因此AD-GUAMP算法的运行时间会更长。此差异可能是由于AD-GUAMP算法的复杂性和额外的计算步骤所致。在实际应用中，需要综合考虑算法的性能和运行时间之间的权衡，并根据测量矩阵性质选择合适的算法。

3 结论

为了解决GUAMP算法容易振荡且在某些情况下性能略低于AD-GAMP算法和GVAMP算法的问题，本文针对GUAMP算法的两个模块分别构建了近似目标函数。通过监测目标函数的下降情况，并按照预设规则对两个模块的参数进行阻尼衰减调整，提出了AD-GUAMP算法，以提升算法的稳健性。通过大量的仿真试验，本文验证了AD-GUAMP算法的有效性。结果显示，在低秩或高条件数测量矩阵的情况下，AD-GUAMP算法的性能几乎与GVAMP相当，并且优于AD-GAMP和GUAMP算法。在相关矩阵场景下，AD-GUAMP算法的性能也优于AD-GAMP、GUAMP和GVAMP算法。本研究结果表明，AD-GUAMP算法在改进GUAMP算法的稳健性方面取得了显著效果。通过引入近似目标函数和参数调整机制，AD-GUAMP算法能够更好地适应不同的场景，并具有出色的性能表现。本文的研究为Bayes稀疏信号重构算法在稳健性和准确性提升方面提供了有益的补充。