2. 燕山大学 河北省信息传输与信号处理重点实验室, 秦皇岛 066004
2. Hebei Key Laboratory of Information Transmission and Signal Processing, Yanshan University, Qinhuangdao 066004, China
磁共振成像(magnetic resonance imaging,MRI)以非接触、非电离、无需造影剂的优点,成为了医学辅助诊疗领域的一项关键技术。传统MRI设备利用单线圈获得全采样的测量数据,采样时间长,不利于实际应用,因此探索高效采样方式十分必要。近年来,结合并行采样和欠采样这2种快速采样策略可构建并行压缩感知磁共振成像(parallel compressive sensing magnetic resonance imaging,p-CSMRI)[1]。p-CSMRI对应的算法需解决的问题是如何通过采集到的多线圈部分(欠采样)k域数据恢复原始信号。该恢复问题是一个病态问题,通常需要利用图像先验来限制解空间。如何利用先验来恢复高精度磁共振图像成为一大挑战。
传统基于模型的p-CSMRI算法首先通过正则化模型表征原始图像的先验信息,例如梯度域[2]和小波变换域[3]的稀疏性,然后通过合适的求解器求解相应的优化模型。如Block等[4]提出了从多线圈径向欠采样数据中重建原始磁共振(magnetic resonance,MR)图像的算法,由惩罚线圈边缘轮廓信息和整幅图像的梯度稀疏性来引入先验知识。在梯度域和小波变换域利用全局稀疏变换法引入图像的全局稀疏先验,通常是固定的且非最优的。此外,上述先验忽略了图像的局部先验信息。为解决这些问题,Weller等[5]提出了将自适应字典学习与L1-SPIRiT[6]相结合的快速MRI算法,该算法利用了图像在自适应字典下的稀疏性,获得了比全局稀疏变换法更好的重建结果。另一种常用的先验是非局部相似性[7-8],如Zhang等[9]提出了STDLR-SPIRiT算法,利用k域空间双向低秩特性和多线圈数据之间的相关性,通过无奇异值分解的数值算法解决优化问题。在这些方法中,基于全局稀疏变换的方法重建速度快但重建质量较差,特别是在低采样率下,重建图像存在严重伪影。相比利用全局先验的方法,基于自适应字典下稀疏性或非局部相似性的方法重建的图像质量更高,但重建速度慢。
随着人工智能的兴起,深度学习方法在图像处理任务中的应用引起广泛关注[10]。深度学习方法通过深度神经网络(deep neural network,DNN)从大量数据中学习有效的特征或映射以刻画图像的潜在分布[11]。这种方法可以充分利用数据集的分布信息,避免过度依赖人工经验设计的先验。将DNN用于p-CSMRI后研究出的诸多算法解决了传统方法重建速度慢、效果差的问题,如Wang等[12]设计并训练了卷积神经网络以学习零填充(zero filled,ZF)重建和真实图像之间的映射关系,该数据驱动的端到端DNN能够克服基于传统先验的p-CSMRI算法的缺点,实现较好的重建质量,但其模型架构是不可解释的。架构不可解释不利于算法的收敛性分析,而收敛性会影响网络的稳定性。因此,研究者提出将迭代算法展开成模型驱动的DNN[13-16],如Wang等[17]提出的PARCEL算法是一个展开的并行网络架构,从增强的多线圈部分采样k域数据中对比学习网络2个分支中的参数,并且2个网络训练时的损失函数相同;Yang等[18]基于半二次分裂算法提出MD-DAN网络,该网络通过学习相应的近端算子来学习交叉对比度先验。研究表明,利用事先训练好的模型驱动DNN能够完成快速成像且取得较好的重建效果。虽然上述模型驱动的DNN在p-CSMRI任务上取得了一定的效果,但仍存在以下不足:1) 现有模型驱动的并行MRI网络利用深度神经网络学习了隐式的正则化项,但其先验网络架构缺乏模型可解释性;2) 由于网络架构的复杂性,现有模型驱动的p-CSMRI网络没有显式地给出对应迭代算法的收敛性分析。
针对上述问题,受Chan等[19]提出的利用有界去噪器分析算法收敛性的启发,本文基于对偶标架提出了一种模型架构可解释且可证明有界的深度去噪器,并将其作为先验模块融入到模型驱动的p-CSMRI网络中,构建了收敛性可分析的模型驱动p-CSMRI算法。首先,本文基于对偶标架并结合深度阈值网络,构建满足有界条件的深度去噪器;其次,构建了基于对偶标架的p-CSMRI优化模型,并将迭代求解步骤展开成了一个可端到端有监督训练的深度神经网络;最后,利用构建的有界深度去噪器作为先验模块,提出了收敛性可分析的模型驱动p-CSMRI成像算法。通过利用有界去噪器作为先验网络构建可证明收敛的模型驱动p-CSMRI算法,网络的稳定性得到保证,同时实现了低采样率下的高质量图像重建。
1 基于可训练对偶标架的去噪器有界去噪器的定义如下所示。
定义1 对于任意输入x∈
| $ \left\|D_{\sigma}(\boldsymbol{x})-\boldsymbol{x}\right\|_{2}^{2} / N \leqslant \sigma^{2} C . $ |
则该去噪器为有界去噪器。其中C是独立于N和σ的通用常数。
有界Gauss去噪器[19]是指任意一幅图像与该图像通过该Gauss去噪器后的差值能量有界且该边界与噪声方差呈线性关系。在噪声强度逐渐降低的前提下[20],有界Gauss去噪器对即插即用成像算法的收敛性保证至关重要[19, 21]。然而Gauss去噪器的网络结构通常使用深度神经网络并根据经验设计,引入了很多深度学习的技巧,比如残差连接、批归一化等,属于深度去噪器。因此很难显式地证明设计的先验网络满足有界条件。为解决这些问题,本文基于对偶标架表示模型提出了一个可证明有界的深度去噪器,并首次尝试分析基于学习的模型驱动p-CSMRI算法的收敛性。
在成像算法中,标架和字典通常被用于稀疏表示的基。其中,紧标架能够表示整幅图像且稀疏编码速度较快[22]。紧标架学习所对应的优化问题可描述为
| $ \left\{\begin{array}{l} \min\limits_{\boldsymbol{W}, \boldsymbol{a}}\|\boldsymbol{a}-\boldsymbol{W} \boldsymbol{x}\|_{2}^{2}+\lambda\|\boldsymbol{a}\|_{1}\\ \text { s. t. } \boldsymbol{W}^{\mathrm{T}} \boldsymbol{W}=\boldsymbol{I} . \end{array}\right. $ | (1) |
其中:x∈
| $ D_{\varepsilon}(\bullet ; \sigma)=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} T_{\varepsilon(\sigma)}[\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}(\bullet)] . $ |
其中:Ψ∈
| $ D_{\varepsilon}(\bullet ; \sigma)=\hat{d}=\underset{d}{\operatorname{argmin}}\left\{\frac{1}{2}\|d-\bullet\|_{2}^{2}+\lambda R_{\text {dual }}(d)\right\}. $ |
其中Rdual(d)表示可学习的隐式正则化项。
图像像素在空域具有相关性,并且在优化过程中估计图像包含的噪声通常是空间变化的,因此阈值也应该是空间变化且与噪声相关的。本文设置阈值与噪声标准差σ呈线性相关[25]。
| $ \varepsilon_{l}=\sigma c_{l} . $ |
其中:εl是待处理特征图的第l个通道的阈值,cl是相应的比例常数。不同于Isogawa等[25]提出的利用反向传播算法来学习比例常数的思想,本文构建深度阈值网络从输入图像中确定这些常数,该方式能够有效提取空间变化的cl。阈值向量e可以表示为
| $ \boldsymbol{e}=\left[\varepsilon_{1}, \varepsilon_{2}, \cdots, \varepsilon_{q}\right]^{\mathrm{T}}=\boldsymbol{c} \otimes \boldsymbol{m}. $ |
其中:⊗表示逐元素乘积;c表示由cl组成的比例常数向量;q表示通道的个数;m表示一个由噪声标准差σ扩展为与c相同大小的矩阵,称为噪声水平强度图。为了避免任意性,cl的大小被限制为[cmin, cmax]。深度阈值网络的具体架构如图 1所示,该网络主要由卷积层(convolutional layer,Conv)、线性整流函数(rectified linear unit,ReLU)和拼接(Concat)操作构成。为了进一步有效提取常数,本文引入了稠密残差连接和通道注意力机制(对应图 1中的SE[26]模块)。相关描述在2.2节中结合算法作详细展开。
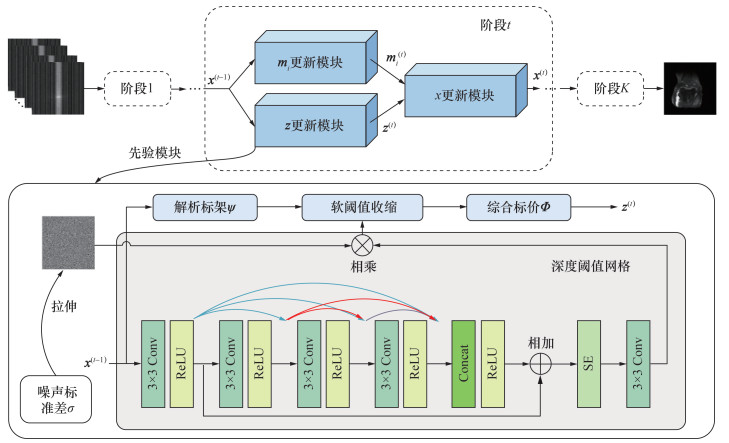
|
| 图 1 CSMRI-Dual算法的网络架构图 |
本文将有界去噪器满足的条件(即有界且该界为噪声强度的线性函数)定义为有界条件。满足有界条件的深度去噪器有利于收敛性保证。引理1表明构建的深度去噪器满足有界条件。
引理1 对于任意输入x∈
| $ \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant M \sigma^{2} L. $ |
本文假设通过所提出的先验网络学习到的解析标架和综合标架是满足严格对偶性质的。在实验中,上述2个标架可能不满足严格对偶条件,而是满足松弛的对偶条件。基于此种情况,本文在2.3节的推论1进行了算法的收敛性分析,并给出了相应证明。在此,假设学习到的解析标架和综合标架满足严格的对偶约束,即有ΦΨ=I。因此,
| $ \begin{gather*} \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2}= \\ \left\|\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \\ \|\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}\|_{2}^{2}\left\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \end{gather*} $ | (2) |
由于||Φ||22=λmax(ΦTΦ)≤τ0(此处λmax(·)表示最大特征值),式(2)的上界可以进一步被定义为
| $ \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \tau_{0}\left\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2}. $ | (3) |
式(3)可以被改写为
| $ \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \tau_{0}\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}, \boldsymbol{e})\|_{2}^{2}. $ | (4) |
其中:阈值向量e的元素被用于收缩Ψx。令(Ψx)m和εm分别代表Ψx和e的第m个元素,εm为非负值,则软阈值算子T[(Ψx)m, εm]可以定义为
| $ \begin{array}{*{20}{c}} T\left[(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})_{m}, \boldsymbol{\varepsilon}_{m}\right]= \\ \begin{cases}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})_{m}+\varepsilon_{m}, & (\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})_{m}<-\varepsilon_{m} ; \\ 0, & \left|(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})_{m}\right| \leqslant \varepsilon_{m} ; \\ (\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})_{m}-\varepsilon_{m}, & (\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})_{m}>\varepsilon_{m} .\end{cases} \end{array} $ |
收缩过程T(Ψx, e)会发生以下4种情况之一:
C1:Ψx的任意元素满足(Ψx)m < -εm,则T(Ψx, e)=Ψx+e。因此有
| $ \|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}, \boldsymbol{e})\|_{2}^{2}=\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\boldsymbol{e}\|_{2}^{2}=\|\boldsymbol{e}\|_{2}^{2}. $ | (5) |
C2:Ψx的任意元素满足|(Ψx)m|≤εm,则T(Ψx, e)=0。因此有
| $ \|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}, \boldsymbol{e})\|_{2}^{2}=\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\mathbf{0}\|_{2}^{2} \leqslant\|\boldsymbol{e}\|_{2}^{2}. $ | (6) |
C3:Ψx的任意元素满足(Ψx)m>εm,则T(Ψx, e)=Ψx-e。因此有
| $ \|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}, \boldsymbol{e})\|_{2}^{2}=\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}+\boldsymbol{e}\|_{2}^{2}=\|\boldsymbol{e}\|_{2}^{2}. $ | (7) |
C4:上述3种情况的任意2种,或C1—C3均发生。
因此当C4情况发生时,||Ψx-T(Ψx, e)||22的上界是C1—C3情况下该值的最大上界。基于式(5)—(7)可得
| $ \|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}, \boldsymbol{e})\|_{2}^{2} \leqslant\|\boldsymbol{e}\|_{2}^{2}. $ | (8) |
根据阈值向量的定义e=c⊗m,其中比例常数向量c的每一个元素的范围均为cl∈[cmin, cmax]。令εmax=σcmax表示e的最大元素,则有
| $ \|\boldsymbol{e}\|_{2}^{2} \leqslant M \varepsilon_{\max }^{2} \leqslant M c_{\max }^{2} \sigma^{2}. $ | (9) |
根据式(4)、(8)和(9)可得
| $ \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \tau_{0} M \sigma^{2} c_{\max }^{2} \leqslant M \sigma^{2} L. $ |
其中L=τ0cmax2。
2 基于对偶标架的模型驱动p-CSMRI网络 2.1 优化问题p-CSMRI的采样模型可以描述为
| $ \boldsymbol{y}=\sum\limits_{i=1}^{n_{\mathrm{c}}} \boldsymbol{M F S}_{i} \boldsymbol{x}+\boldsymbol{n}. $ |
式中,x∈
根据最大后验概率准则和Bayes理论,从测量数据y中重建原始图像x的优化模型可以表示为
| $ \min\limits_{\boldsymbol{x}} \frac{1}{2} \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{M F S}_{i} \boldsymbol{x}-\boldsymbol{y}_{i}\right\|_{2}^{2}+\lambda R_{\text {dual }}(\boldsymbol{x}). $ | (10) |
式中,yi∈
为求解式(10)定义的优化问题,引入辅助变量z∈
| $ \left\{\begin{array}{l} \min\limits_{z, \boldsymbol{m}_i, \boldsymbol{x}} \frac{1}{2} \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{M F m}_i-\boldsymbol{y}_i\right\|_2^2+\lambda R_{\text {dual }}(\boldsymbol{z}) \\ \text { s. t. } \boldsymbol{m}_i=\boldsymbol{S}_i \boldsymbol{x}, \boldsymbol{z}=\boldsymbol{x} . \end{array}\right. $ | (11) |
利用半二次分裂算法求解式(11)定义的优化问题,可将式(11)转化为
| $ \begin{array}{*{20}{c}} & \min\limits_{z, \boldsymbol{m}_{i}, \boldsymbol{x}} \frac{1}{2} \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{M F} \boldsymbol{m}_{i}-\boldsymbol{y}_{i}\right\|_{2}^{2}+\lambda R_{\text {dual }}(\boldsymbol{z})+ \\ & \frac{\alpha}{2} \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{m}_{i}-\boldsymbol{S}_{i} \boldsymbol{x}\right\|_{2}^{2}+\frac{\beta}{2}\|\boldsymbol{z}-\boldsymbol{x}\|_{2}^{2} . \end{array} $ | (12) |
其中α和β为惩罚参数。
式(12)通过交替优化z、m、x进行求解,在第t次迭代中,交替迭代式(13)—(15)。
| $ \boldsymbol{z}^{(t)}=\underset{z}{\operatorname{argmin}}\left\{\frac{\beta}{2}\left\|\boldsymbol{z}-\boldsymbol{x}^{(t-1)}\right\|_{2}^{2}+\lambda R_{\text {dual }}(\boldsymbol{z})\right\} . $ | (13) |
| $ \begin{array}{*{20}{c}} \boldsymbol{m}_{i}^{(t)}= & \underset{\boldsymbol{m}_{i}}{\operatorname{argmin}}\left\{\frac{1}{2} \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{M F m}_{i}-\boldsymbol{y}_{i}\right\|_{2}^{2}+\right. \\ & \left.\frac{\alpha}{2} \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{m}_{i}-\boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}\right\|_{2}^{2}\right\} .\\ & \boldsymbol{x}^{(t)}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\left\{\frac{\alpha}{2} \sum\limits_{i=1}^{n_{c}} \| \boldsymbol{m}_{i}^{(t)}-\right. \end{array} $ | (14) |
| $ \left.\boldsymbol{S}_{i} \boldsymbol{x}\left\|_{2}^{2}+\frac{\beta}{2}\right\| \boldsymbol{z}^{(t)}-\boldsymbol{x} \|_{2}^{2}\right\} . $ | (15) |
具体步骤如下:
1) 固定mi和x,更新辅助变量z
式(13)可通过满足有界条件的对偶标架去噪器进行近似求解。
| $ \boldsymbol{z}^{(t)}=\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}\left[\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}\left(\boldsymbol{x}^{(t-1)}\right)\right]. $ | (16) |
由于估计图像包含的噪声随着迭代次数增加而降低,因此输入到去噪器的噪声强度也应逐渐降低。本文给定σ的初始值,并按照σ(t)=ξσ(t-1) (0 < ξ < 1)进行更新。为了满足这样的变化趋势,在实验中给定σ的初始值σinit和最终值σfinal,使其随着展开次数的增长呈指数级衰减。此外,由于本文最后将迭代算法展开成网络,因此将求解辅助变量z所对应的网络称为先验模块。
2) 固定z和x,更新辅助变量mi
式(14)的目标函数包括2个关于mi的简单二次项,可对其求导并令导数等于0,对应的闭式解满足
| $ \left(\boldsymbol{F}^{H} \boldsymbol{M}^{H} \boldsymbol{M} \boldsymbol{F}+\alpha \boldsymbol{I}\right) \boldsymbol{m}_{i}^{(t)}=\boldsymbol{F}^{H} \boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}. $ |
其中F作为一个酉矩阵,满足FHF=FFH=I。因此上述方程可以写为
| $ \left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha \boldsymbol{I}\right) \boldsymbol{F} \boldsymbol{m}_{i}^{(t)}=\boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{F} \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)} . $ |
即
| $ \boldsymbol{F m}_{i}^{(t)}=\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha \boldsymbol{I}\right)^{-1}\left(\boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{F} \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}\right) . $ | (17) |
其中:MHM表示N×N的对角矩阵,其对角线上的元素为0和1,值为1的位置表示k域中对应变换系数被采样,值为0的位置表示未被采样;MHyi表示ZF重建的k域测量数据。
令(ku, kv)表示k域的二维索引值,Ω表示被采样到的像素点索引值的集合,则在k域中mi的更新可表示为
| $ \boldsymbol{F m}_{i}^{(t)}\left(k_{u}, k_{v}\right)=\left\{\begin{array}{l} P^{(t)}\left(k_{u}, k_{v}\right), \left(k_{u}, k_{v}\right) \notin \mathit{\boldsymbol{ \boldsymbol{\varOmega}}} ; \\ \frac{P^{(0)}\left(k_{u}, k_{v}\right)+\alpha P^{(t)}\left(k_{u}, k_{v}\right)}{1+\alpha}, \\ \left(k_{u}, k_{v}\right) \in \mathit{\boldsymbol{ \boldsymbol{\varOmega}}} . \end{array}\right. $ |
其中P(0)=MHyi,P(t)=FSix(t-1)。对式(17)进行Fourier反变换,可以得到mi(t)。
3) 固定z,mi,更新图像x
式(15)同样也包含2个关于x的二次项,对代价函数求导并令导数等于0得到其闭式解为
| $ \boldsymbol{x}^{(t)}=\left(\beta \boldsymbol{I}+\sum\limits_{i=1}^{n_{{\rm{c}}}} \alpha \boldsymbol{S}_{i}^{H} \boldsymbol{S}_{i}\right)^{-1}\left(\beta \boldsymbol{z}^{(t)}+\alpha \sum\limits_{i=1}^{n_{{\rm{c}}}} \boldsymbol{S}_{i}^{H} \boldsymbol{m}_{i}^{(t)}\right) $ | (18) |
通过交替更新图像x、辅助变量mi和z这3个步骤求解式(12)以优化模型。为获得更高的重建质量,本文将上述迭代过程展开成网络,每次迭代对应深度展开网络的一个阶段(Stage),且每一个阶段都包含上述每一步的更新过程,网络总的展开次数即总的阶段数记为K。将所提算法记为CSMRI-Dual算法,其具体实现步骤如算法1所示。
算法1 CSMRI-Dual算法.
1) 输入:测量数据y,线圈灵敏度Si,掩膜M,噪声标准差的初始值σinit和最终值σfinal
2) FOR t=1∶K
3) 根据式(16)更新辅助变量z
4) 根据式(17)更新辅助变量mi
5) 根据式(18)更新图像x
6) 结束
7) 输出:重建图像
算法具体的数据流程图如图 1所示。图中展示了第t个阶段的具体架构,包含辅助变量mi更新模块、辅助变量z更新模块(先验模块)和图像x更新模块。
2.3 CSMRI-Dual算法的收敛性分析收敛的p-CSMRI算法有益于算法稳定且获得较高的重建质量。基于先验模块的有界性,本文分析当K→∞时,即迭代次数趋于无限次的时候,算法是否收敛。定理1表明所提出的CSMRI-Dual算法是收敛的。
定理1 对于p-CSMRI的采样模型y=
证明:对于所有t,令Θ表示x(t)的域。在域Θ中,定义一个距离函数d:Θ×Θ→
| $ d\left(\boldsymbol{x}^{(t)}, \boldsymbol{x}^{(j)}\right)=\frac{1}{\sqrt{N}}\left\|\boldsymbol{x}^{(t)}-\boldsymbol{x}^{(j)}\right\|_{2}. $ |
Θ⊆
根据上述定义,可构建
| $ \begin{array}{*{20}{c}} {\left\|\boldsymbol{x}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2}=\left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}+\boldsymbol{z}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant}\\ {\left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}\right\|_{2}+\left\|\boldsymbol{z}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2}}. \end{array} $ | (19) |
由于z(t)=Dε[x(t-1); σ],且根据引理1中可训练对偶标架去噪器的边界,可得
| $ \begin{gather*} \left\|\boldsymbol{z}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2}=\| D_{\varepsilon}\left[\boldsymbol{x}^{(t-1)} ; \sigma\right]- \\ \boldsymbol{x}^{(t-1)} \|_{2} \leqslant \sqrt{M L} \sigma^{(t-1)} . \end{gather*} $ | (20) |
将式(20)代入式(19),可得
| $ \begin{gather*} \left\|\boldsymbol{x}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant\left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}\right\|_{2}+ \\ \left\|\boldsymbol{z}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant\left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}\right\|_{2}+\sqrt{M L} \sigma^{(t-1)} . \end{gather*} $ | (21) |
令
| $ f(\boldsymbol{x})=\frac{\alpha}{2} \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{m}_{i}^{(t)}-\boldsymbol{S}_{i} \boldsymbol{x}\right\|_{2}^{2} . $ | (22) |
则式(15)可改写为
| $ \boldsymbol{x}^{(t)}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\left\{f(\boldsymbol{x})+\frac{\beta}{2}\left\|\boldsymbol{z}^{(t)}-\boldsymbol{x}\right\|_{2}^{2}\right\}. $ | (23) |
对式(23)定义的代价函数求导并令导数等于0,可以得到
| $ \nabla f(\boldsymbol{x})+\beta\left[\boldsymbol{x}-\boldsymbol{z}^{(t)}\right]=0 . $ |
即
| $ \boldsymbol{x}-\boldsymbol{z}^{(t)}=-\frac{\nabla f(\boldsymbol{x})}{\beta}. $ |
对于第t次迭代,可得
| $ \boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}=-\frac{\nabla f\left(\boldsymbol{x}^{(t)}\right)}{\beta}. $ |
即
| $ \left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}\right\|_{2}=\frac{\left\|\nabla f\left(\boldsymbol{x}^{(t)}\right)\right\|_{2}}{\beta} . $ | (24) |
由式(22)可以求得,f(x(t))在点x(t)的梯度▽f(x(t))为
| $ \nabla f\left(\boldsymbol{x}^{(t)}\right)=\alpha \sum\limits_{i=1}^{n_{\mathrm{c}}} \boldsymbol{S}_{i}^{H}\left[\boldsymbol{S}_{i} \boldsymbol{x}^{(t)}-\boldsymbol{m}_{i}^{(t)}\right]. $ |
因此,
| $ \begin{gather*} \left\|\nabla f\left(\boldsymbol{x}^{(t)}\right)\right\|_{2}=\left\|\alpha \sum\limits_{i=1}^{n_{{\rm{c}}}} \boldsymbol{S}_{i}^{H}\left[\boldsymbol{S}_{i} \boldsymbol{x}^{(t)}-\boldsymbol{m}_{i}^{(t)}\right]\right\|_{2} \leqslant \\ \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i} \boldsymbol{x}^{(t)}-\boldsymbol{m}_{i}^{(t)}\right\|_{2} \leqslant \\ \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+ \\ \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{m}_{i}^{(t)}\right\|_{2} . \end{gather*} $ | (25) |
将式(17)代入式(25),可得
| $ \begin{array}{*{20}{c}} & \left\|\nabla f\left(\boldsymbol{x}^{(t)}\right)\right\|_{2} \leqslant \alpha \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+ \\ & \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2} \| \boldsymbol{F}^{H}\left[\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha I\right)^{-1} \cdot\right. \\ & \left.\left(\boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{F} \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}\right)\right] \|_{2} \leqslant \\ & \alpha \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+ \\ & \alpha\left\|\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha \boldsymbol{I}\right)^{-1}\right\|_{2} \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2} \\ & \left\|\boldsymbol{F}^{H}\left[\boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{F} \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}\right]\right\|_{2} . \end{array} $ | (26) |
其中,MHM是一个N×N的对角矩阵,其对角线元素为0或1,所以MHM+αI是一个N×N的对角矩阵,其对角线元素为α或α+1。由此可推导出
| $ \begin{array}{*{20}{c}} {\left\|\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha \boldsymbol{I}\right)^{-1}\right\|_{2}=}\\ {\sqrt{\lambda_{\max }\left\{\left[\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha \boldsymbol{I}\right)^{-1}\right]^{H}\left[\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha \boldsymbol{I}\right)^{-1}\right]\right\}}=}\\ {\sqrt{\left(\frac{1}{\alpha}\right)^{2}}=\frac{1}{\alpha} .} \end{array} $ | (27) |
式(27)代入式(26)可得
| $ \begin{array}{*{20}{c}} \left\|\nabla f\left(\boldsymbol{x}^{(t)}\right)\right\|_{2} \leqslant \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+ \\ \alpha\left\|\left(\boldsymbol{M}^{H} \boldsymbol{M}+\alpha I\right)^{-1}\right\|_{2} \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2} \cdot \\ \left\|\boldsymbol{F}^{H}\left[\boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{F} \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}\right]\right\|_{2} \leqslant \\ \alpha \sum\limits_{i=1}^{n_{\mathrm{c}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+\\ \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{F}^{H} \boldsymbol{M}^{H} \boldsymbol{y}_{i}+\alpha \boldsymbol{S}_{i} \boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant \\ \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+ \\ \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{F}^{H} \boldsymbol{M}^{H}\right\|_{2}\left\|\boldsymbol{y}_{i}\right\|_{2}+ \\ \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t-1)}\right\|_{2}. \end{array} $ | (28) |
其中x(t)与x(t-1)分别表示第t次与第t—1次迭代过程中的重建图像,其大小被限制为
| $ \|\boldsymbol{x}\|_{2} \leqslant C_{0}. $ | (29) |
考虑到采样模型yi=MFSix+n中||n||2≤κ,且||MFSix||2≤||FSix||2=||Six||2≤||Si||2||x||2。因此,
| $ \begin{array}{*{20}{c}} \left\|\boldsymbol{y}_{i}\right\|_{2}=\left\|\boldsymbol{M F S}_{i} \boldsymbol{x}+\boldsymbol{n}\right\|_{2} \leqslant\left\|\boldsymbol{M F S}_{i} \boldsymbol{x}\right\|_{2}+ \\ \|\boldsymbol{n}\|_{2} \leqslant\left\|\boldsymbol{S}_{i}\right\|_{2}\|\boldsymbol{x}\|_{2}+ \\ \|\boldsymbol{n}\|_{2} \leqslant C_{0}\left\|\boldsymbol{S}_{i}\right\|_{2}+\kappa . \end{array} $ | (30) |
由于||FHMH||2=
| $ \left\|\boldsymbol{F}^{H} \boldsymbol{M}^{H}\right\|_{2}=\sqrt{\lambda_{\max }\left(\boldsymbol{M F} \boldsymbol{F}^{H} \boldsymbol{M}^{H}\right)}=1 . $ | (31) |
将式(29)、(30)和(31)代入式(28)中,可得
| $ \begin{array}{*{20}{c}} \left\|\nabla f\left(\boldsymbol{x}^{(t)}\right)\right\|_{2} \leqslant \alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t)}\right\|_{2}+ \\ \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{F}^{H} \boldsymbol{M}^{H}\right\|_{2}\left\|\boldsymbol{y}_{i}\right\|_{2}+\\ {\alpha \sum\limits_{i=1}^{n_{{\rm{c}}}}\left\|\boldsymbol{S}_{i}^{H}\right\|_{2}\left\|\boldsymbol{S}_{i}\right\|_{2}\left\|\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant C_{1}+C_{2}+C_{3}.} \end{array} $ |
其中C1=αC0
| $ \begin{gather*} \left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}\right\|_{2}=\frac{\left\|\nabla f\left(\boldsymbol{x}^{(t)}\right)\right\|_{2}}{\beta} \leqslant \\ \frac{C_{1}+C_{2}+C_{3}}{\gamma^{t-1} \beta^{(0)}}=\frac{C_{4}}{\gamma^{t-1}} . \end{gather*} $ | (32) |
其中C4=
根据输入噪声标准差的更新准则σ(t)=ξσ(t-1)(0 < ξ < 1)并将式(32)代入式(21),可得
| $ \begin{gather*} \left\|\boldsymbol{x}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant\left\|\boldsymbol{x}^{(t)}-\boldsymbol{z}^{(t)}\right\|_{2}+\sqrt{M L} \sigma^{(t-1)} \leqslant \\ \frac{C_{4}}{\gamma^{t-1}}+\sqrt{M L} \xi^{t-1} \sigma^{(0)} \leqslant \frac{C_{4}}{\gamma^{t-1}}+C_{5} \xi^{t-1} . \end{gather*} $ | (33) |
其中C5=
综上所述,对于任意t和常数C4、C5,{x(t)}t=1∞序列总满足
| $ d\left(\boldsymbol{x}^{(t)}, \boldsymbol{x}^{(t-1)}\right) \leqslant \frac{C_{4}}{\gamma^{t-1}}+C_{5} \xi^{t-1}(\gamma>1, 0<\xi<1). $ |
因此,对于任意有限的j和t(j>t),总满足
| $ \begin{array}{*{20}{c}} {d\left(\boldsymbol{x}^{(j)}, \boldsymbol{x}^{(t)}\right) \leqslant \sum\limits_{n=t+1}^{j} \frac{C_{4}}{\gamma^{n-1}}+\sum\limits_{n=t+1}^{j} C_{5} \xi^{n-1}=}\\ {C_{4} \frac{\gamma^{j-t}-1}{\gamma^{j-1}(\gamma-1)}+C_{5} \xi^{t} \frac{1-\xi^{j-t}}{1-\xi} .} \end{array} $ |
而
| $ \begin{aligned} & \lim _{\substack{j \rightarrow \infty \\ t \rightarrow \infty \\ j>t}} C_{4} \frac{\gamma^{j-t}-1}{\gamma^{j-1}(\gamma-1)}+C_{5} \xi^{t} \frac{1-\xi^{j-t}}{1-\xi}= \\ & \lim _{\substack{j \rightarrow \infty \\ t>\infty \\ j>t}} \frac{1}{\gamma^{t-1}(\gamma-1)}-\frac{1}{\gamma^{j-1}(\gamma-1)}+ \\ & \xi^{t}-\xi^{j}=0(\gamma>1, 0<\xi<1) . \end{aligned} $ |
由于j>t且γ>1,0 < ξ < 1, 所以t→∞时,d(x(j), x(t))→0。因此{x(t)}t=1∞是一个Cauchy序列。又因为在完备空间
| $ d\left(\boldsymbol{x}^{(t)}, \boldsymbol{x}^{*}\right) \rightarrow 0 . $ |
因此可得||x(t)-x*||2→0。
推论1 在定理1中,本文分析了当通过先验网络学习到的标架是满足严格的对偶性质时,算法会收敛到一个不动点。然而,通过损失函数对标架进行的对偶约束,经验上并不是严格对偶。在近似对偶约束的条件下,对偶约束项不是0,但有一个上界,即||ΦΨ-I||F2≤τ1 (此处τ1是一个很小的正值),此时随着迭代次数增加,即t→∞,有||x(t)-x(t-1)||2→C6。
证明:由于||ΦΨ-I||F2≤τ1,进而可得||ΦΨx-x||22≤τ2,则有下式:
| $ \begin{gathered} \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2}= \\ \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}+\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \\ \|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}\|_{2}^{2}+\left\|\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \\ \tau_{2}+\|\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}\|_{2}^{2}\left\|\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x}-T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} . \end{gathered} $ |
根据引理1的证明,可证明下式成立:
| $ \left\|\boldsymbol{x}-\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} T_{\varepsilon(\sigma)}(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}} \boldsymbol{x})\right\|_{2}^{2} \leqslant \tau_{2}+M \sigma^{2} L . $ |
在近似对偶约束的条件下,将式(33)改写,可得
| $ \left\|\boldsymbol{x}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant \frac{C_{4}}{\gamma^{t-1}}+\left(\sqrt{M L} \sigma^{(t-1)}+\sqrt{\tau_{2}}\right) . $ | (34) |
根据输入噪声标准差的更新准则σ(t)=ξσ(t-1) (0 < ξ < 1),式(34)可以改写为
| $ \begin{gathered} \left\|\boldsymbol{x}^{(t)}-\boldsymbol{x}^{(t-1)}\right\|_{2} \leqslant \frac{C_{4}}{\gamma^{t-1}}+\left(\sqrt{M L} \xi^{t-1} \sigma^{(0)}+\sqrt{\tau_{2}}\right) \leqslant \\ \frac{C_{4}}{\gamma^{t-1}}+C_{5} \xi^{t-1}+C_{6} . \end{gathered} $ |
其中,C6=
本文从纽约大学的膝盖磁共振数据集(http://mridata.org)中分别随机选取了500、100、100张不同的图片作为训练、验证和测试数据集。原始数据由15个通道的k域数据组成,尺寸大小为320×320。本文通过ESPIRiT[27]算法,从全采样k空间中心的大小为30×30的数据块中预先计算线圈灵敏度图。采用2倍、4倍和6倍加速因子(acceleration factor,AF)对原始k空间数据进行了Déscartes采样,对于不同加速因子采用相同的全采样k空间中心进行估计。训练的轮数(Epoch)设置为100,使用ADAM作为优化器,学习率初始值设置为0.000 5,每经过50个Epoch的优化,学习率衰减10%。损失函数定义为
| $ \text { Loss }=\left\|\boldsymbol{x}_{\mathrm{gt}}-\hat{\boldsymbol{x}}\right\|_{2}^{2}+\frac{\eta}{K G} \sum\limits_{t=1}^{K}\|\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}}-\boldsymbol{I}\|_{\mathrm{F}}^{2} . $ |
式中,
针对100幅测试图像在不同倍数(2、4、6)AF情况下进行图像重建,将本文提出的CSMRI-Dual算法与Modl[13]、VN[15]和VS-Net[14]算法在模型参数量、平均每张图片的推断时间上进行比较。如表 1所示,在参数量方面,VN算法采用梯度下降方法结合变分模型进行图像重建,算法简单,参数量最少;CSMRI-Dual算法在提升算法性能与模型稳定性的前提下具有较高的模型参数量,这是因为深度阈值网络和对偶紧标架采用非共享的方式,如何减小这些参数量且保证算法的重建性能有待进一步研究。在推断时间方面,CSMRI-Dual算法用时少于Modl算法与VN算法,略多于VS-Net算法,计算复杂度适中;Modl算法用时最长,这是因为其展开层数为10,迭代次数最多。
| 算法 | 模型参数量/M | 平均每张图片推断时间/s |
| Modl | 0.34 | 0.69 |
| VN | 0.13 | 0.21 |
| VS-Net | 0.57 | 0.15 |
| CSMRI-Dual | 12.12 | 0.20 |
为了对算法重建性能进行客观评估,本文采用了多种指标评价,包括:平均峰值信噪比(peak signal-to-noise ratio,PSNR),结构相似性指数(structure similarity index measure,SSIM)和归一化均方误差(normalized mean squared error,NMSE),结果如表 2所示。由表可知,通过Modl算法重建的图像的SSIM在所有采样率的情况下都比ZF重建法要低,但是其PSNR和NMSE远高于ZF重建法,这是因为Modl算法首次将深度展开技术应用于p-CSMRI算法中,网络架构较简单。VN算法使用变分模型结合梯度下降算法,能够获得优于Modl算法的重建质量,但仍略逊于VS-Net算法。VS-Net算法采用交替优化的方式更新辅助变量和重建图像,能够获得优于VN算法和VS-Net算法的重建质量,但参数量在上述3种对比算法中最大。CSMRI-Dual算法由于使用了基于对偶标架的先验网络且可证明收敛,能够取得最优的重建质量,在4倍AF情况下,其图像重建的平均PSNR比Modl算法、VN算法和VS-Net算法分别有1.70、1.45和0.46 dB的提升。
| 算法 | 2倍AF | 4倍AF | 6倍AF | ||||||||
| 平均 PSNR/dB |
SSIM | NMSE | 平均 PSNR/dB |
SSIM | NMSE | 平均 PSNR/dB |
SSIM | NMSE | |||
| ZF | 36.51 | 0.946 5 | 0.010 1 | 33.78 | 0.912 9 | 0.018 5 | 32.78 | 0.896 0 | 0.023 1 | ||
| Modl | 38.61 | 0.928 8 | 0.007 4 | 35.88 | 0.892 8 | 0.012 5 | 34.46 | 0.891 5 | 0.016 5 | ||
| VN | 38.27 | 0.938 6 | 0.007 3 | 36.13 | 0.922 2 | 0.011 3 | 34.58 | 0.903 7 | 0.015 6 | ||
| VS-Net | 40.57 | 0.963 2 | 0.005 0 | 37.12 | 0.933 1 | 0.009 7 | 35.65 | 0.915 1 | 0.012 9 | ||
| CSMRI-Dual | 40.91 | 0.964 4 | 0.004 8 | 37.58 | 0.935 1 | 0.009 1 | 36.10 | 0.918 6 | 0.012 0 | ||
为进一步评估本文提出的CSMRI-Dual算法的重建效果,图 2和图 3分别展示了在4倍和6倍AF时,不同算法重建图像的区域放大图。由图可知,ZF重建图像非常模糊,并且图像过于平滑,缺少细节信息;Modl算法恢复出的重建图像同样丢失了很多的细节信息;VN算法和VS-Net算法重建图像类似,比Modl算法恢复出的重建图像有明显提升,但是细节信息依旧有部分丢失;CSMRI-Dual算法重建图像在4倍AF下视觉效果较好,有效消除了噪声,获得了更多细节,且保留了丰富的纹理信息;在6倍AF下,重建细节更接近原始图像,重建图像较为清晰。由此可见,CSMRI-Dual算法表现出了良好的重建效果。
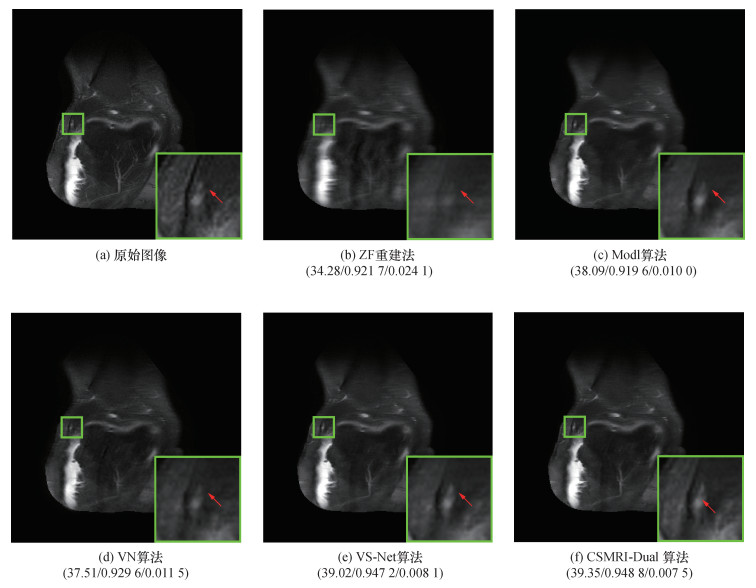
|
| 图 2 4倍AF下不同算法重建图像的对比(平均PSNR/SSIM/NMSE) |
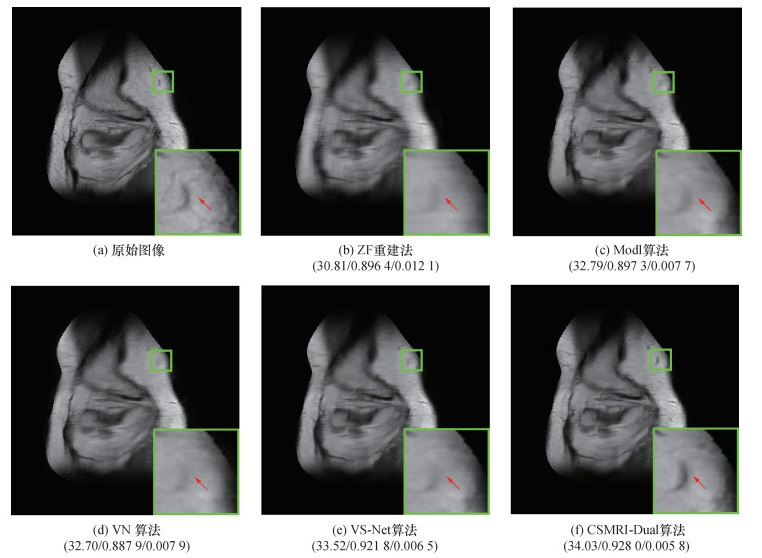
|
| 图 3 6倍AF下不同算法重建图像的对比(平均PSNR/SSIM/NMSE) |
4 结论
本文基于可训练对偶标架提出了可证明收敛的模型驱动并压缩感知磁共振成像算法。针对现有的模型驱动p-CSMRI网络,其先验网络架构不可解释,算法收敛性难以分析的问题,本文构建了基于可训练对偶标架的深度有界去噪器,并提出了在噪声强度逐渐下降的条件下可证明收敛的并行压缩感知磁共振成像算法框架。本文将满足有界条件的去噪器作为先验模块引入到所构建的模型驱动并行压缩感知磁共振成像网络中,在理论上证明了所提出的深度去噪器满足有界条件,分析了提出模型驱动网络的收敛性,保证了网络的稳定性。仿真实验表明,提出的算法能够取得高质量的MR图像重建。
| [1] |
LIANG D, LIU B, WANG J, et al. Accelerating SENSE using compressed sensing[J]. Magnetic Resonance in Medicine, 2009, 62(6): 1574-1584. DOI:10.1002/mrm.22161 |
| [2] |
CHEN C, LI Y Q, HUANG J Z. Calibrationless parallel MRI with joint total variation regularization [C]// Proceedings of the 16th International Conference on Medical Image Computing and Computer-Assisted Intervention. Nagoya, Japan: Springer, 2013: 106-114.
|
| [3] |
CHARI L, PESQUET J C, BENAZZA-BENYAHIA A, et al. A wavelet-based regularized reconstruction algorithm for SENSE parallel MRI with applications to neuroimaging[J]. Medical Image Analysis, 2011, 15(2): 185-201. DOI:10.1016/j.media.2010.08.001 |
| [4] |
BLOCK K T, UECKER M, FRAHM J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint[J]. Magnetic Resonance in Medicine, 2007, 57(6): 1086-1098. DOI:10.1002/mrm.21236 |
| [5] |
WELLER D. Reconstruction with dictionary learning for accelerated parallel magnetic resonance imaging [C]// Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation. Santa Fe, NM, USA: IEEE, 2016: 105-108.
|
| [6] |
LUSTIG M, ALLEY M, VASANAWALA S, et al. Fast L1-SPIRiT Compressed Sensing Parallel Imaging MRI: Scalable Parallel Implementation and Clinically Feasible Runtime[J]. IEEE Transactions on Medical Imaging, 2012, 31(6): 1250-1262. DOI:10.1109/TMI.2012.2188039 |
| [7] |
HALDAR J P, ZHUO J W. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data[J]. Magnetic Resonance in Medicine, 2016, 75(4): 1499-1514. DOI:10.1002/mrm.25717 |
| [8] |
KIM T H, SETSOMPOP K, HALDAR J P. LORAKS makes better SENSE: Phase-constrained partial fourier SENSE reconstruction without phase calibration[J]. Magnetic Resonance in Medicine, 2017, 77(3): 1021-1035. DOI:10.1002/mrm.26182 |
| [9] |
ZHANG X L, GUO D, HUANG Y M, et al. Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI[J]. Medical Image Analysis, 2020, 63: 101687. DOI:10.1016/j.media.2020.101687 |
| [10] |
王尧. 基于深度学习的脑部多模态核磁共振影像研究[D]. 长春: 吉林大学, 2022. WANG Y. Multi-modality brain magnetic resonance images recognition with deep learning [D]. Changchun: Jilin University, 2022. (in Chinese) |
| [11] |
施伟成, 金朝阳, 叶铮. 基于PCAU-Net的快速多通道磁共振成像方法[J]. 波谱学杂志, 2023, 40(1): 39-51. SHI W C, JIN Z Y, YE Z. Fast multi-channel magnetic resonance imaging based on PCAU-Net[J]. Chinese Journal of Magnetic Resonance, 2023, 40(1): 39-51. (in Chinese) |
| [12] |
WANG S S, SU Z H, YING L, et al. Accelerating magnetic resonance imaging via deep learning [C]// Proceedings of the IEEE 13th International Symposium on Biomedical Imaging. Prague, Czech Republic: IEEE, 2016: 514-517.
|
| [13] |
AGGARWAL H K, MANI M P, JACOB M. MoDL: Model-based deep learning architecture for inverse problems[J]. IEEE Transactions on Medical Imaging, 2019, 38(2): 394-405. DOI:10.1109/TMI.2018.2865356 |
| [14] |
DUAN J M, SCHLEMPER J, QIN C, et al. VS-Net: Variable splitting network for accelerated parallel MRI reconstruction [C]// Proceedings of the 22nd International Conference on Medical Image Computing and Computer Assisted Intervention. Shenzhen, China: Springer, 2019: 713-722.
|
| [15] |
HAMMERNIK K, KLATZER T, KOBLER E, et al. Learning a variational network for reconstruction of accelerated MRI data[J]. Magnetic Resonance in Medicine, 2018, 79(6): 3055-3071. DOI:10.1002/mrm.26977 |
| [16] |
MENG N, YANG Y, XU Z B, et al. A prior learning network for joint image and sensitivity estimation in parallel MR imaging [C]// Proceedings of the 22nd International Conference on Medical Image Computing and Computer Assisted Intervention. Shenzhen, China: Springer, 2019: 732-740.
|
| [17] |
WANG S S, WU R Y, LI C, et al. PARCEL: Physics-based unsupervised contrastive representation learning for multi-coil MR imaging[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2023, 20(5): 2659-2670. |
| [18] |
YANG Y, WANG N, YANG H R, et al. Model-driven deep attention network for ultra-fast compressive sensing MRI guided by cross-contrast MR image [C]// Proceedings of the 23rd International Conference on Medical Image Computing and Computer Assisted Intervention. Lima, Peru: Springer, 2020: 188-198.
|
| [19] |
CHAN S H, WANG X R, ELGENDY O A. Plug-and-play ADMM for image restoration: Fixed-point convergence and applications[J]. IEEE Transactions on Computational Imaging, 2017, 3(1): 84-98. DOI:10.1109/TCI.2016.2629286 |
| [20] |
TERRIS M, REPETTI A, PESQUET J C, et al. Enhanced convergent PnP algorithms for image restoration [C]// Proceedings of the International Conference on Image Processing. Anchorage, AK, USA: IEEE, 2021: 1684-1688.
|
| [21] |
YUAN X, LIU Y, SUO J L, et al. Plug-and-play algorithms for large-scale snapshot compressive imaging [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Seattle, WA, USA: IEEE, 2020: 1444-1454.
|
| [22] |
CAI J F, JI H, SHEN Z W, et al. Data-driven tight frame construction and image denoising[J]. Applied and Computational Harmonic Analysis, 2014, 37(1): 89-105. DOI:10.1016/j.acha.2013.10.001 |
| [23] |
CAI J F, CHOI J K, WEI K. Data driven tight frame for compressed sensing MRI reconstruction via off-the-grid regularization[J]. SIAM Journal on Imaging Sciences, 2020, 13(3): 1272-1301. DOI:10.1137/19M1298524 |
| [24] |
SHI B S, WANG Y X, LI D. Provable general bounded denoisers for snapshot compressive imaging with convergence guarantee[J]. IEEE Transactions on Computational Imaging, 2023, 9: 55-69. DOI:10.1109/TCI.2023.3241551 |
| [25] |
ISOGAWA K, IDA T, SHIODERA T, et al. Deep shrinkage convolutional neural network for adaptive noise reduction[J]. IEEE Signal Processing Letters, 2018, 25(2): 224-228. DOI:10.1109/LSP.2017.2782270 |
| [26] |
HU J, SHEN L, SUN G. Squeeze-and-excitation networks [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA: IEEE, 2018: 7132-7141.
|
| [27] |
UECKER M, LAI P, MURPHY M J, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA[J]. Magnetic Resonance in Medicine, 2014, 71(3): 990-1001. DOI:10.1002/mrm.24751 |


