航空飞机等大型航空装备制造技术的发展对产品的制造精度、检测精度和控制精度提出了更高的要求[1], 以数字化工艺设计、产品数字化建模和实时数据测量反馈为代表的数字化测量和制造技术成为推进航空制造业发展的关键技术[2]。在飞机数字化装配过程中,需要对飞机位姿和机身部件形位公差等进行精确测量[3-4],对飞机机身零部件工装等进行运动控制和力控制[5-6],这对飞机数字化制造方案设计和验证,自动化测量设备和控制设备的选型、布置和规划提出了很高的要求。飞机数字化仿真技术可以实现飞机装配工艺的生成、飞机装配方案的验证和飞机制造过程中各个测控环节的评估,对控制飞机制造质量和提高制造效率发挥着至关重要的作用[7-8]。
目前针对数字化航空装配测控仿真的常用软件如下:1) DELMIA:具备完整的数字化设计、制造和数字化生产线解决方案,主要通过导入3-D模型进行产品工艺的开发和验证。但是由于其不具备测量传感器模块和控制模块,因此无法实施测控算法的验证和测量设备的智能规划。2) CATIA:提供了产品机械设计、机械加工、分析模拟等功能和完整的2-D、3-D、参数化混合建模及数据管理手段,可以实现从单个零件的设计到最终整机的装配。但其无法实现运动控制分析和测量分析,只能根据装配模型按工程经验进行静态的测量设备位置规划和调姿机构位置布置。3) SA:航空装备制造过程中常用的三维测量仿真分析软件,可以实现针对激光跟踪仪等大范围测量仪器的测量场建立、测量结果分析计算和测量精度检验等功能,但是其内核为数据支撑,无法导入3-D模型进行测量遮挡分析,且无法进行运动控制等,功能过于单一。综上所述,现有软件在实现测量、控制、规划、模型分析中各具特点,但是存在模型设计、方案规划验证和测量控制仿真脱节的情况,无法一体化地实现各个要素的统一结合,导致复杂环境下的测量/控制仿真(例如,在某飞机测量场中布置多个激光跟踪仪站位使得其无遮挡地对大量目标点进行测量并优化测量精度)难以实现。因此,本文希望提出一种全新的仿真思路,利用机器人仿真平台,将场景中的核心测控设备构建为机器人模型,实现多要素结合的一体化、高效率、可视化仿真。
机器人仿真技术结合了机器人学、计算机图形学和计算机技术,利用几何图形实现3-D可视化地完成机器人本体及其周围环境的仿真[9]。随着机器人仿真技术的发展,大量优秀的机器人仿真平台相继问世,如Microsoft Robotic Studio[10]、Webots[11]、THROBSM[12]、RIDE[13]、RVIZ[14]、Gazebo、V-REP[15]等, 其具备以下共同特点:1) 集成了大量的传感器(如相机、激光雷达、力传感器、位置传感器等) 数据包,可以轻易仿真实际传感器采集数据;2) 可自主搭建机器人模型,且具备完整的机器人坐标转换、正逆运动学、动力学运算模块和机器人关节控制器,以实现机器人控制;3) 具备和3-D建模软件的通用接口格式,可以导入3-D模型,可视化地构建整体环境信息。由此可见机器人仿真平台具有综合测量、控制、建模和规划等多要素的仿真能力,本文尝试将机器人仿真平台用于航空装备装配过程中的测控综合仿真。
针对复杂航空装配环境的测量和控制一体化仿真,本文提出了基于机器人建模的航空装配测控仿真分析方法。首先,对航空装备数字化装配场景下的各机构进行模块化建模。随后,在仿真过程中实时获取图像、距离和力等传感信息,控制所建机器人模型进行运动,从而进行综合分析计算和优化,辅助工程人员实现集建模、测量和控制一体化的综合性仿真;基于该方法,进一步实现了高遮挡环境下的多个激光跟踪仪对大量测量点的联合测量可达性仿真分析、测量场测量精度分析和多激光跟踪仪站位仿真规划(现有方法无法准确高效实现)。最后,搭建了某飞机数字化实际测量仿真环境,验证了该方法的有效性。
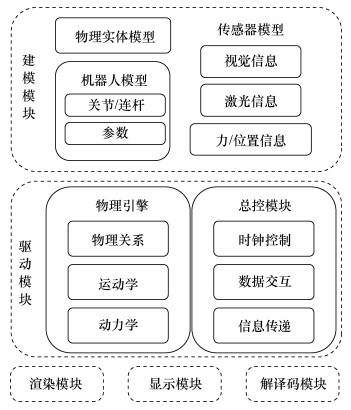
1 基于机器人建模的测控仿真方法 1.1 机器人仿真平台组成架构常见机器人仿真平台架构如图 1所示,机器人仿真平台的核心模块是建模模块和驱动模块,同时还配置基于计算机图形学的显示模块、增强图像可视化质量的渲染模块以及解译码模块。
|
| 图 1 机器人仿真平台架构 |
建模模块需要物理实体、机器人和传感器3类对象进行建模。其中物理实体模型通常在3-D造型软件(CATIA、Solidworks等)中进行设计,然后导入仿真平台中。机器人模型需要根据物理模型和运动逻辑进行建模,具体包括关节、连杆及DH(Denavit-Hartenberg)参数等的设计。传感器模型是机器人仿真平台中测量的核心模块,其给仿真对象添加虚拟传感器,使仿真对象能够通过虚拟传感器获取仿真场景中的信息,使得仿真可以涉及到图像信息、激光信息和力/位置信息等。
驱动模块是仿真动态运行的核心部分。其中,物理引擎可以模拟现实物理世界的运行情况,在仿真中为物体设置质量、动量、弹性、摩擦系数等物理属性,并对上述参数按物理规律进行运动学和动力学运算,使得物体实现平移、旋转、碰撞等功能; 总控模块则负责控制仿真平台的运行,使得系统按一定逻辑关系按顺序运行,并协调和传递系统中的数据信息和消息信息。
1.2 航空装配测控仿真分析方法本节将分析航空装配测控仿真在机器人仿真平台中的具体搭建方法,即建立航空装备测控过程的零件及其工装、调姿运动机构、数字化测量机构和集控系统等元素与机器人仿真平台主要组成架构和功能模块之间的对应关系。当完成机器人仿真平台中的各部分建模后,系统已等价于实际航空装配系统,可进一步根据需求编程进行测量、控制、工艺流程、站位规划等方面仿真。
通常航空飞机装配环境非常复杂,环境中通常包含加工和装配的零部件、装配工位的辅助工装、人工操作所需要的工作梯和工作区、自动导引运输车(automated guided vehicle,AGV)和天梯等运输设备、POGO柱和千斤顶等组成的并联调姿机构、工业机械臂等串联调姿机构和激光跟踪仪等高精度测量设备,为了保证仿真的真实性和有效性,各部分环境物体均需在机器人仿真平台中分别进行建模。根据航空飞机装配环境中物体的运动性能,将其分为运动控制机构和静态刚性物体,其建模类型和方式不同。
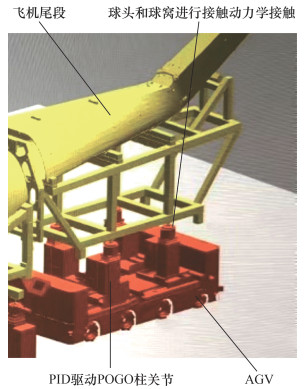
在仿真平台中对运动控制机构建模。AGV运输车和天梯等运输设备通常建立为3自由度移动机器人,通常只需关注其运动学性能来表征运输位置,而无需关注动力学性能。串并联调姿态机构可直接按照其构型在机器人仿真平台中进行机器人建模,为其配置关节驱动器和关节控制器,其动力学特性可以用于调姿控制算法的验证和分析。该类调姿态机构具备动力学特性,仿真引擎可直接对调姿机构进行力空间的PID控制,从而驱动设备在仿真环境中执行接触动力学交互。图 2为一个由AGV搭载的4个3自由度POGO柱组成的并联调姿系统,通过球窝和飞机舱段工装球头进行动力学交互和调姿控制的仿真示意图,可通过仿真程序预先执行调姿轨迹,检验POGO柱控制算法有效性。高精度测量设备可以将其可运动部分建立为机器人关节,并在其机器人末端附加测量传感器,如激光跟踪仪可以建立为底座具备3个平动自由度和末端具备2个转动自由度的5自由度机器人,并且在其末端附加一个激光雷达,以仿真其激光测距性能,并辅助站位规划。
|
| 图 2 AGV搭载POGO柱组成的并联调姿系统 |
针对静态刚性物体,其模型结构通过3-D造型软件设计形成,本身不具备运动能力,根据其发挥的作用不同,分为2类物体:制造主体和环境物体。制造主体主要指代加工装配的零部件和装配工位的辅助工装,其在数字化制造过程中通过连接件安装在运动控制机构中,因此在机器人仿真平台中,将导入的零件和工装模型随动安装在运动机器人末端,并可根据实际安装精度设置一定的安装误差;环境物体指不主动参与运动控制和加工制造的物体,如人工操作所需要的工作梯和工作区,其在数字化装配环境中有时候可能形成运动障碍区域或遮挡测量光路,因此对其建模仿真也必不可少,环境物体可以直接按3-D模型导入并固定于仿真环境中,需要合理设定其站位。
按上述步骤完成机器人仿真平台搭建后,按需求和工艺流程编写控制程序,即可开始航空装配测控过程。仿真运行过程中,可以采集运行中各个传感器的数据进行制造方案的分析评价,进一步构建一系列优化问题,设置目标函数,以实现参数优化、站位规划或工艺流程优化。
1.3 激光跟踪仪测量可达性分析与站位规划案例激光跟踪仪的测量原理是发射一束激光并接收来自测量点的反射光,通过距离和转角信息计算测量点的空间三维坐标[16]。因此,激光跟踪仪在使用过程中,必须保证测量点和设备之间形成一条无遮挡的光线,这就是激光跟踪仪测量的可达性。然在飞机数字化装配环境中,产品尺寸大,测量特征点数量多,且环境中除了产品部件本身,还包括工作梯、工装型架等多种复杂物体,可能对测量光路进行遮挡,导致测量不可达,使得飞机数字化装配误差大或者装配失败。
激光跟踪仪的测量光路可达性仿真分析具有下列难点:1) 由于测量环境模型复杂,采用数学方式将模型建立为离散点云的代价无法接受,需要探索理论建模外的方法;2) 目前仍缺乏可直接用于仿真测量仪器光路可达性的任何软件或平台,大多数分析方法基于工程经验,缺乏理论支撑;3) 测量现场环境复杂且可能发生变化,因此需要快速地对测量光路可达性进行分析,从而对测量站位进行重规划,对方法的速度和简易度提出了很高要求。
不同于传统物体碰撞检测或干涉检查 [17-18],激光跟踪仪测量可达性分析需要检测光路遮挡。部分研究从理论层面分析了测量光路的可达性判断方法。Woo [19]提出可视图形法的概念,源自于几何体的检测规划,用于求解光学仪器测量光线能测量的目标点得一系列位置集合,平面被测点得可视性图为半球集合。Chen等[20]运用了可视性图形法判断经纬仪测量是否可达,同时考虑到空间大型干涉区域形成可视性图。可视图形法原理简单,但是由于其通过理论数学计算,难以建立复杂的测量环境模型,只适用于简单环境。Kong等[21]提出了一种基于屏幕空间变换的分析方法,把空间线与多面体的相交问题转化为平面上点与多边形的交集问题,该方法试图降维简化分析,但是其需要针对每个测量点对空间所有物体进行屏幕空间变换,计算量仍然很大,且难以建立复杂真实环境模型。
近年来,部分学者试图通过利用仿真平台替代理论计算以实现复杂环境中的光路可达性分析。杨晓辉[22]基于CATIA提出了一种测量可达性分析方法,通过从测量设备和待测量点间建立一条线段或一个细长圆柱体模拟光路,进而检测该线段/圆柱体和空间中所有模型的碰撞干涉点,观察最近的干涉点是否位于测量点附近来检测测量可达性。石循磊等[23]对DELMIA软件进行二次开发,从跟踪仪发射一个小实体球到测量靶标位置,在小球运动过程中如果发生碰撞则认为光线被实物遮挡,以此判断测量点的光路可达性。然而,上述研究的核心是进行3-D模型全局动态干涉检查或运动碰撞检测,因而计算量比较大且耗时长,并且人机交互友好性差,无法实现测量点光路可视化观察。而目前对于激光雷达的仿真比较成熟,其根据场景信息,采用光线追踪的原理生成光线,随后仅需计算射线和目标的交点即可实现测距,计算量小,速度快(每秒数十次)。
结合所提出的基于机器人建模的航空装配测控仿真分析方法,本文提出了一种系统化激光跟踪仪测量可达性分析仿真方法。将激光跟踪仪建模为平移机器人模型,在其末端附加转动关节和激光雷达,在机器人仿真平台中可视化地模拟出实际测量设备。给定测量点后,通过进行机器人逆运动学计算,控制激光方向指向测量点,分析测量距离和理论距离之差以判断测量点的可达性。基于前述可达性分析理论,定义评估指标,最终实现多激光跟踪仪的全场站位规划,完成针对某个测量环境的激光跟踪仪最优组合站位布置。该方法的优点如下:1) 将测量设备建模为机器人模型,方法简单快速,且实现了人工光路可视化;2) 真实地模拟测量设备和复杂环境的光路交互,且计算代价小;3) 若环境发生改变,只需对环境模型重新导入,无需重配置机器人模型,可以快速进行重规划。
1.4 激光跟踪仪测量仿真系统架构激光跟踪仪测量可达性仿真方法的核心思路是其机器人仿真模型的搭建和运动建模,以及激光与环境的交互作用,因此仿真系统中包含3类系统结构元素:1) 3-D建模软件如Solidworks, Catia等:主要用于构建待测量部件、测量环境和激光跟踪仪的物理模型,用作仿真平台中的模型实体;2) 机器人仿真平台如Gazebo, V-rep等:可仿真激光雷达传感器,允许导入建模软件生成的物理模型,可以搭建多自由度机器人模型,并具备动力学仿真功能以控制机器人各个关节的运动;3) 集控系统:用于与机器人仿真引擎通信,控制测量设备关节运动,计算测量可达性并进行测量设备站位优化等。
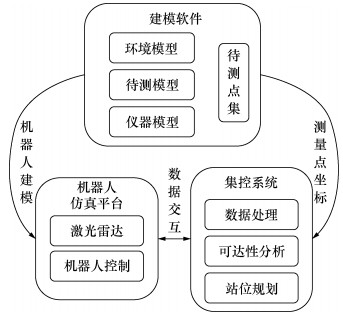
仿真系统中各个元素的动态交互关系如图 3所示:建模软件中进行待测量部件模型,测量环境模型和测量仪器模型的建模,待测量部件模型上提取测量点的三维坐标(xi, yi, zi), i=1, 2, …, n;机器人仿真平台将直接导入待测量部件模型和测量环境模型,并完成激光雷达机器人模型的搭建和关节驱动器的控制;集控系统包含测量可达性分析算法,接受仿真平台的实时数据和建模软件提供的测量点的三维坐标,进行测量可达性分析;可以在测量可达性分析算法的基础上,设计激光跟踪仪组合站位优化算法,利用网格化分析和计算,寻找具有最优指标的测量组合站位。
|
| 图 3 仿真系统结构元素 |
仿真系统搭建和仿真流程如下:1) 静态测量环境构建:向仿真环境中导入待测量部件模型和环境模型,使得世界坐标系与待测量部件坐标系重合;2) 激光跟踪仪机器人模型设计:完成激光跟踪仪机器人模型的建立、机器人运动学模型的计算和关节驱动器的配置;3) 初始测量状态布置:根据工艺方案或工程经验预先给定一个激光跟踪仪站位布置方案,该方案目前可能无法实现所有测量点可达;4) 测量可达性分析:针对现有站位方案控制机器人关节运动,分析各个测量点的可达性;5) 站位优化:在初始站位附近沿x、y、z轴方向布置一定数量的空间离散网格点,分析各个激光跟踪仪在各个网格点的测量可达性,最终以测量全部可达和测量精度最高(测量距离最短)为优化目标进行组合站位设计。
2 激光跟踪仪机器人建模和测量 2.1 机器人建模和逆运动学分析激光跟踪仪其底座部位具备3个平移自由度Tx、Ty、Tz,表征其可以摆放在空间中任意位置;激光跟踪仪测量头用于发射激光和接受反射激光,具备2个转动自由度Ry、Rz,表征其可以通过旋转指向空间中任意一点;激光跟踪仪测量头与底座之间具有固定的连接关系。激光跟踪仪机器人结构形式如图 4所示。
|
| 图 4 激光跟踪仪机器人结构形式 |
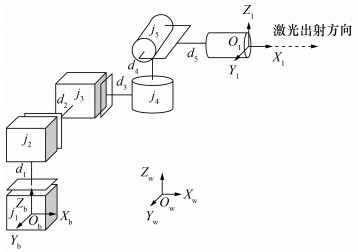
世界坐标系为Ow-XwYwZw,机器人基座坐标系Ob-XbYbZb固定于地面上,其到世界坐标系的齐次变换矩阵为Tw, b。机器人从基座到末端执行器依次具备沿Zb方向的平动关节j1、沿Yb方向的平动关节j2、沿Xb轴方向的平动关节j3、绕Zb方向的转动关节j4和绕Yb方向的转动关节j5,末端执行器为激光发射装置和测量头,在激光发射装置末端中心固定坐标系Ol-XlYlZl,机器人关节j1与j2、j2与j3、j3与j4、j4与j5、j5与末端执行器之间的连杆长度分别为d1、d2、d3、d4、d5。为了方便后续运动学计算和关节控制,设置激光从Ol点沿Xl方向出射,d1=d2=d4=d5=0。由于激光跟踪仪测量头的2个转动关节通常位于整体设备的垂直轴线上且彼此重合,因此将其3个平动关节都设置于激光跟踪仪底部中心,则j3和j4之间的齐次变换矩阵T3, 4仅包含平移变换,即
| $ \boldsymbol{T}^{3, 4}=\left(\begin{array}{cccc} 1 & 0 & 0 & l_{x}^{3, 4} \\ 0 & 1 & 0 & l_{y}^{3, 4} \\ 0 & 0 & 1 & l_{z}^{3, 4} \\ 0 & 0 & 0 & 1 \end{array}\right). $ | (1) |
其中:lx3, 4、ly3, 4、lz3, 4为d3的3个分量,具体数值可以根据激光跟踪仪的物理尺寸计算或读取仿真中的数据获取。将上述机器人结构关系配置到实际的机器人3-D物理模型中,得到机器人模型及其运动自由度表征如图 5所示,机器人5个关节的平动/转动量按顺序分别表示为t1, x、t2, y、t3, z、r4, z、r5, y。

|
| 图 5 激光跟踪仪机器人模型 |
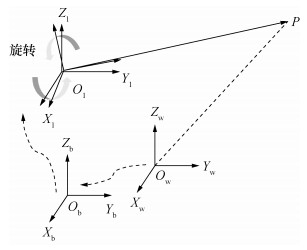
下面进行机器人关节逆运动学分析,以使得机器人末端激光可以按照需求指向各个测量点。本文所定义的机器人需完成的逆运动学解算如下:给定一个空间待测量点P在世界坐标系下的三维坐标(Pxw, Pyw, Pzw),计算在给定激光跟踪仪基座位置Tw, b和激光跟踪仪平移关节运动量t1, x、t2, y、t3, z时的2个转动关节j4和j5的转动角度r4, z、r5, y,从而使得末端执行器发射的激光可以指向点P。
图 6中,由机器人的构型可知,当给定t1, x、t2, y、t3, z时坐标系Ol-XlYlZl只是随着关节j4和j5的转动绕其自身原点发生坐标系旋转,因此为了计算关节转动角度与(Pxw, Pyw, Pzw)的关系,先按式(2)计算点P在坐标系Ol-XlYlZl的坐标:
| $ \begin{align*} \left(\begin{array}{c} P_{x}^{1} \\ P_{y}^{1} \\ P_{z}^{1} \\ 1 \end{array}\right)=\boldsymbol{T}^{\mathrm{b}, 1} \boldsymbol{T}^{\mathrm{w}, \mathrm{b}}\left(\begin{array}{c} P_{x}^{\mathrm{w}} \\ P_{y}^{\mathrm{w}} \\ P_{z}^{\mathrm{w}} \\ 1 \end{array}\right), \\ \boldsymbol{T}^{\mathrm{b}, 1}=\left(\begin{array}{cccc} 1 & 0 & 0 & -t_{1, x}-l_{x}^{3, 4} \\ 0 & 1 & 0 & -t_{2, y}-l_{y}^{3, 4} \\ 0 & 0 & 1 & -t_{3, z}-l_{z}^{3, 4} \\ 0 & 0 & 0 & 1 \end{array}\right). \end{align*} $ | (2) |
|
| 图 6 坐标系示意图 |
其中Tb, l为坐标系Ob-XbYbZb到Ol-XlYlZl的齐次变换矩阵。
根据旋转坐标变换,要使得Xl轴指向点P,按式(3)计算关节j4、j5的转动角度:
| $ \left\{\begin{array}{l} r_{4, z}={\mathsf{π}} \operatorname{sgn}\left(P_{y}^{1}\right)-\operatorname{atan}\left(\frac{P_{y}^{1}}{P_{x}^{1}}\right), \\ r_{5, y}=\operatorname{atan}\left(\frac{P_{z}^{1}}{\sqrt{\left(P_{y}^{1}\right)^{2}+\left(P_{x}^{1}\right)^{2}}}\right) . \end{array}\right. $ | (3) |
其中sgn()为符号函数。
在仿真平台中为机器人5个关节配置PID位置控制器,为了使得激光快速指向测量点,调整控制参数KP、KI、KD以实现各关节快速且无超调地跟踪阶跃输入信号。进而按式(3)计算关节转动角度,即可对任意给定空间中测量点P,机器人末端执行器转动使得激光出射方向指向该点,完成本节所定义的机器人逆运动学解算。
2.2 单跟踪仪测量可达性分析方法假设环境中仅存在1个激光跟踪仪,按上述机器人建模方法将该跟踪仪建模为机器人laser。设n为待测量零部件上测量点的总数。预先设定激光跟踪仪在仿真空间中在世界坐标系的相对位姿关系为Tw, b,t1, x=t2, y=t3, z=0,此状态为仿真初始状态。这本质上是根据环境和测量模型,人为给定了一个激光跟踪仪的站位,需要分析该站位可以测量到哪些测量点,即进行激光测量可达性分析。激光测量可达性分析包含2步:分析测量点是否位于激光跟踪仪视野范围外,分析激光跟踪仪的测量头到测量点Pi是否存在障碍物遮挡光路。
单激光测跟踪仪测量可达性分析的流程如下:从待测量部件三维模型中读取一个待测量点坐标Piw(i=1, 2, …, n),按式(2)计算该测量点在Ol-XlYlZl坐标系下的三维坐标Pil,按式(3)计算r4, z、r5, y。首先判断关节转动角度是否超出激光跟踪仪转角限位(通常激光跟踪仪绕z轴旋转角度可以覆盖0~360°,但是绕y轴俯仰角度绝对值在45°以内),如果|r5, y|≥45°,认为点Pi测量不可达。如果旋转关节j5位于角度限位之内,则须判断由激光跟踪仪的测量头到测量点Pi之间是否存在障碍物遮挡光路。利用仿真平台驱动PID控制器,控制laser的j4和j5关节分别旋转r4, z和r5, y角度(此时激光指向测量点),读取激光雷达实测距离值dm,按式(4)计算其与点Pi和测量头的理论距离dt之间的差值绝对值,如果小于阈值tdist(可取0.01dt),则认为测量头到测量点Pi之间光路通畅,无遮挡,认为点Pi测量可达;否则认为其受到了某种障碍物的遮挡,认为点Pi测量不可达。由此完成了针对一个测量点的测量可达性分析,按上述方法依次遍历n个测量点,即可分析出laser在目前位姿下的测量可达性。
| $ \left|d_{\mathrm{m}}-d_{\mathrm{t}}\right|=\left|d_{\mathrm{m}}-\sqrt{\left(P_{x}^{1}\right)^{2}+\left(P_{y}^{1}\right)^{2}+\left(P_{z}^{1}\right)^{2}}\right|. $ | (4) |
如果环境中仅存在1台激光跟踪仪,在测量点选择合理的情况下,必须通过调整激光跟踪仪站位以保证其对所有测量点均测量可达。如果laser在初始基座位置Tw, b和初始关节运动量(t1, x=t2, y=t3, z=0)下不能满足测量可达性要求,则可以进一步构造如式(5)所示的优化问题:在给定的范围内,通过移动机器人laser关节j1—j3以调整激光跟踪仪位置,最大化可测量点数。
| $ \begin{gather*} m=\max _{t_{1, x}, t_{2, y}, t_{3, z}} f\left(t_{1, x}, t_{2, y}, t_{3, z}, \right. \\ \left.P_{1}, P_{2}, \cdots, P_{n}, E\right), \\ \text { s. t. }\left(\boldsymbol{T}^{\mathrm{w}, \mathrm{b}}\right)^{-1}\left(t_{1, x}, t_{2, y}, t_{3, z}, 1\right)^{\mathrm{T}} \in \text { Region. } \end{gather*} $ | (5) |
其中:m为laser测量可达点数的最大值;f()代表给定n个测量点和测量环境E情况下,laser在当前站位下测量可达点的数量,为隐函数,通过本节前述仿真方法获取;Region代表为世界坐标系下激光跟踪仪的可行站位区域,通常与实际环境有关。可以通过遗传算法、粒子群优化算法等优化算法求解该优化问题。如果m=n,则找到了一个合理的站位;如m始终无法收敛到n,则证明Region内无法寻找一个跟踪仪布置方案,使得所有测量点都可测到,此时则需要通过调整跟踪仪姿态(将姿态Rw, b也加入优化问题)或增加跟踪仪数量来进行优化。
3 多跟踪仪组合站位规划方法在实际飞机数字化测量环境中,由于测量范围广,测量障碍物复杂且测量特征多,单一激光跟踪仪几乎不能测量到所有目标点。通常做法是设置多个激光跟踪仪布置于不同位置,通过一组增强参考系统(enhanced reference system,ERS)点将其测量结果统一到一个坐标系中,实现多跟踪仪组合站位,协同建立测量场。本节基于提出的激光跟踪仪测量可达性仿真分析方法,从测量可达性和测量精度2方面讨论构建的多跟踪仪组合站位的测量性能,进而提出一种基于网格搜索的激光跟踪仪组合站位优化方法,该方法将寻找所有测量点可达情况下,测量精度相对最优的激光跟踪仪组合站位。
3.1 测量精度表征指标定义定义多个激光跟踪仪组合站位形成测量场的测量性能包含如下2方面:1) 所有测量点的测量可达性,即确保每个测量点至少有一个激光跟踪仪对其测量可达;2) 所有测量点的全局平均测量精度最高,即在所设计精度衡量指标下,依次求取每个测量点的测量精度,n个测量点整体测量精度达到最优。
假设场景中存在k个激光跟踪仪,待测量部件上存在n个测量点。将激光跟踪仪按2.1节的方法分别建模为机器人laseri (i=1, 2, …, k)。
定义laseri的测量可达性向量Mi和激光跟踪仪组合测量可达性向量Mall如下:
| $ \boldsymbol{M}_{i}=\left(m_{i}^{1}, m_{i}^{2}, \cdots, m_{i}^{n}\right); $ |
| $ m_{i}^{j}= \begin{cases}1, & \text { 若laser }{ }_{i} \text { 对 } P_{j} \text { 测量可达; } \\ 0, & \text { 若laser }{ }_{i} \text { 对 } P_{j} \text { 测量不可达; }\end{cases} $ | (6) |
| $ \boldsymbol{M}_{\mathrm{all}}=\sum\limits_{i=1}^{k} \boldsymbol{M}_{i}. $ | (7) |
其中:mij表示laseri对Pj的测量可达性。当进行多跟踪仪组合站位规划时,必须保证每个测量点至少有1个激光跟踪仪对其测量可达,即Mall的每个分量mallj≥1。
在测量可达性满足的基础上,希望激光跟踪仪对全场测量精最优化。根据下列标准来分析激光跟踪仪测量精度:1) 针对工艺给定的需求测量精度最高的g个点,其必须被2个以上激光跟踪仪测量可达,从而降低测量误差正态分布的方差,大幅度提高测量精度;2) 针对工艺给定的需求测量精度较低的其余(n—g)个测量点,其只需对某个激光跟踪仪测量可达;3) 在满足上述情况基础上,希望尽可能减小激光跟踪仪测量头与测量点的距离,因为激光跟踪仪测量误差分为测距误差和测角误差,随着测量距离增大,测角误差会更明显地反映到测量点3-D坐标的综合测量误差上,因此激光跟踪仪测量误差随测量距离的增大而增大,通常与距离成线性正相关[24-25]。
进一步定义激光跟踪仪组合对每个点的最小测量距离向量Dall为:
| $ \begin{gather*} \boldsymbol{D}_{\text {all }}=\left(d_{1}, d_{2}, \cdots, d_{n}\right), \\ d_{j}=\min \left(\operatorname{dist}\left(\text { laser }_{i}, P_{j}\right)\right), i=1, 2, \cdots, k . \end{gather*} $ | (8) |
其中:dist(laseri, Pj)为laseri到Pj的距离;dj代表目前激光跟踪仪组合站位下,对Pj的最小测量距离。可以认为dj越小,则目前测量场对Pj的测量数据精度越高。
综合测量可达性和测量精度,定义测量精度表征指标I如下:
| $ I= \begin{cases}\operatorname{norm}\left(\boldsymbol{D}_{\text {all }}\right), & \forall m_{\text {all }}^{j} \geqslant 1(j=1, 2, \cdots, n) \text { 且 } \\ & \forall m_{\text {all }}^{g}>1 ; \\ +\infty, & \exists m_{\text {all }}^{j}=0(j=1, 2, \cdots, n) \text { 或 } \\ & \exists m_{\text {all }}^{g} \leqslant 1 .\end{cases} $ | (9) |
式(9)中存在3种情况:1) 对每个测量点均有至少1个跟踪仪可执行测量,且对于每个测量关键点有多个跟踪仪可执行测量;2) 对于n个测量点,该测量场对部分测量点无法进行测量;3) 对于部分期望被多个跟踪仪同时测量的关键点,仅有不多于1个激光跟踪仪可以执行测量。针对情况1,定义其测量精度表征指标为norm(Dall);针对情况2和3定义其测量精度表征指标定义为+∞,表示测量场完全不可用。
I越小,则多激光跟踪仪组合站位所构建的测量场精度越高。
3.2 基于网格搜索的跟踪仪站位规划方法多激光跟踪仪组合站位规划的思路是在给定的离散网格范围内,为每个跟踪仪选取合适的站位,使得构建的测量场的达到最小,即测量场性能最优。可以描述为如下优化问题:
| $ \frac{\min }{t_{1, x . \text { laser }_i}, t_{2, y, \text { laser }_i}, t_{3, z, \text { laser }_i}} I, $ |
| $ \begin{array}{l} {\rm{s.\;t.}}\\ \begin{gathered} \left(\boldsymbol{T}_{\text {laser }_1}^{\mathrm{w}, \mathrm{b}}\right)^{-1}\left(t_{1, x, \text { laser }_1}, t_{2, y, \text { laser }_1}, t_{3, z, \text { laser }_1}, 1\right)^{\mathrm{T}} \in \text { Region }_{\text {laser }_1}, \\ \left(\boldsymbol{T}_{\text {laser }_2}^{\mathrm{w}, \mathrm{b}}\right)^{-1}\left(t_{1, x, \text { laser }_2}, t_{2, y, \text { laser }_2}, t_{3, z, \text { laser }_2}, 1\right)^{\mathrm{T}} \in \text { Region }_{\text {laser }_2}, \\ \vdots \\ \left(\boldsymbol{T}_{\text {laser }_k}^{\mathrm{w}, \mathrm{b}}\right)^{-1}\left(t_{1, x, \text { laser }_k}, t_{2, y, \text { laser }_k}, t_{3, z, \text { laser }_k}, 1\right)^{\mathrm{T}} \in \text { Region }_{\text {laser }_k} . \end{gathered} \end{array} $ |
其中:Tlaseriw, b表示laseri的基座坐标系到世界坐标系的齐次变换矩阵;t1, x, laseri、t2, y, laseri、t3, z, laseri分别表示laseri的j1、j2、j3关节平移量;Regionlaseri为世界坐标系下laseri的可行站位区域,与测量环境有关。该优化问题的各个约束的物理意义是使得各个激光跟踪仪位置仅可在预先给定范围内进行优化。
该优化问题维度为3k,当k较大时维度较高,使用智能优化算法直接进行高维空间优化需要进行大量仿真实验,效率低且难以收敛。因此考虑本文构建仿真环境的特点和激光跟踪仪实际应用场景,对问题进行简化,提高站位规划效率。
仿真过程中主要耗费时间的环节为控制机械臂运动到所需的关节角度(如果对该关节采用运动学一步设置位置而非动力学控制,则该部分时间可忽略,仿真将大大加速),其余的数据读取和计算环节耗费的时间可忽略不计。使用智能优化算法的本质是反复通过改变激光跟踪仪前3个关节移动量,反复生成大量的激光跟踪仪不同的组合站位,再对每一个组合站位分别进行检验,这样每一个组合站位都需要进行一次可达性分析,耗费时间不可接受。考虑到每个激光跟踪仪在同一个位置的测量精度表征指标始终保持不变且小范围移动对激光跟踪仪测量性能影响不大,因此如果将每个激光跟踪仪的站位预先离散到空间中一些预设离散点,则一次仿真实验可以测量并记录每个激光跟踪仪在每个离散站位上的测量精度表征指标,随后再脱离仿真平台进行数据处理,分析激光跟踪仪组合站位测量精度表征指标,即可实现数据加速优化。
给定一组激光跟踪仪基座位姿(Tlaser1w, b, Tlaser2w, b, …, Tlaserkw, b),基于网格搜索的跟踪仪站位规划算法如下:
1) 网格离散:图 7中,利用空间3-D均匀网格的方式,为每个激光跟踪仪关节j1—j3的位置生成多种组合情况(由于激光跟踪仪基座位姿已给定,仿真中关节j1—j3处于不同位置将表征激光跟踪仪在实际环境下的站位),假设生成的组合总数为num=nxnynz,其中nx、ny、nz分别表示沿关节j1—j3运动方向生成网格离散点的数量;

|
| 图 7 空间三维均匀网格 |
2) 仿真实验:将k个激光跟踪仪的关节j1—j3分别运动到一个未仿真的位置,计算各激光跟踪仪关节j4、j5的转角,仿真并记录各激光跟踪仪在该站位的测量可达性向量Mi。由于同时对k个激光跟踪仪进行并行仿真,则共需进行num组仿真实验,即可记录k个激光跟踪仪在每个离散站位的单一测量性能;
3) 数据组合分析:将k个激光跟踪仪的测量可达性向量进行组合,共生成numk个激光跟踪仪组合站位,计算每个激光跟踪仪组合站位的Mall和I,选择I最小值对应的组合站位即为最终的组合站位;
4) 分析测量裕度:将激光跟踪仪调整到最终组合站位,控制各个机器人关节j4和j5转动角度使得激光依次指向各个测量点,在激光跟踪仪和测量点之间发生较小位置偏差(如现场布置出现误差,部件变形等)后,仍旧能够测量可达,使得构建的测量场具备一定鲁棒性。在规划到最优测量站位后,赋予激光跟踪仪站位一定范围内随机的位置误差(如10 mm,20 mm,…,100 mm),进而仿真所有测量点是否仍然可以被测量到,从而得出测量裕度,指导实际测量场构建。
本节提出的基于网格搜索的跟踪仪站位规划方法利用num次仿真实验,即可得到numk种激光跟踪仪组合站位下的测量精度表征指标I,大大提高了规划效率。
4 某飞机测量场的测量分析实例 4.1 仿真环境介绍仿真使用Ubuntu20.04系统环境,采用建模软件Solidworks导出仿真所需的飞机舱段模型和激光跟踪仪模型,机器人仿真引擎选用Gazebo,基于python和ROS编写节点文件对系统仿真进行运作和控制。计算机配置如下:第13代Intel i7-13700F处理器,16 GB系统内存,NVIDIA GeForce RTX 3060(12 GB显存) 显卡。显卡配置仅影响仿真交互界面的流畅性,不影响规划速度和效率。
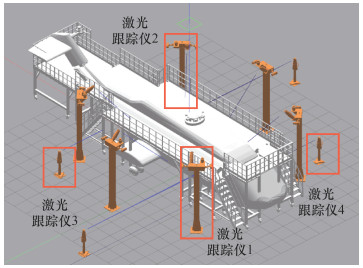
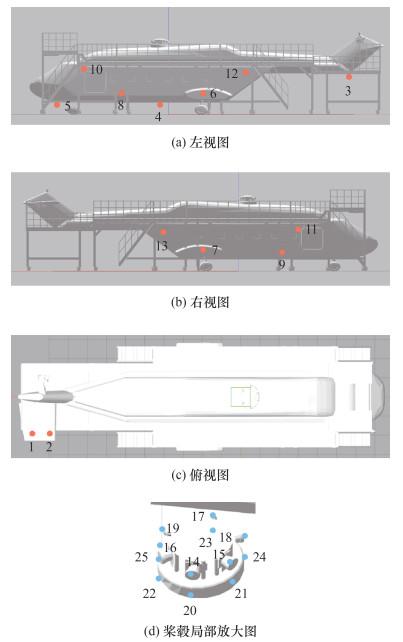
4.2 测量环境介绍图 8给出了测量场整体环境,测量场中包含一架某型号直升机,其附近安装了一圈工作梯。图 9表示机身上测量点的分布信息,其中直升机的平尾下部、机身底部蒙皮、短翼蒙皮和机身蒙皮和桨毂上分别布置测量点1—2、测量点3—5、测量点6—9、测量点10—13、测量点14—25。场景中共10台激光跟踪仪,其中4台激光跟踪仪(激光跟踪仪1—4)用于测量这25个测量点,其余跟踪仪用于其他用途(已预先布置好),因此只需要对这4台跟踪仪进行测量可达性分析和站位规划。为了保证系统能够测量到桨毂上的测量点,为其中2台激光跟踪仪设计了4 m高的支架,通过地脚螺栓固定于地面,另外2台激光跟踪仪用其自身支架固定于地面上。
|
| 图 8 测量场环境(初始站位) |
|
| 图 9 机身待测量点分布 |
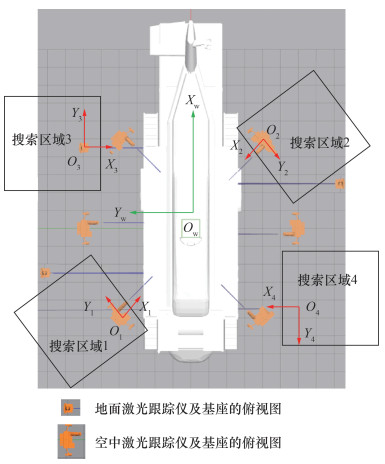
由于机身测量点数量较多且分布较为离散,激光跟踪仪的初始给定站位如图 10所示,4个激光跟踪仪基座均匀分布在飞机四周,基座中心在Ow-XwYwZw下坐标分别为(4 m, 4 m, 0)、(—4 m, 4 m, 0)、(4 m, —4 m, 0)、(—4 m, —4 m, 0)。
|
| 图 10 激光跟踪仪初始站位和搜索区域 |
为了保证测量场搭建的合理性,下面分析激光跟踪仪目前组合站位下能否测量到所有测量点,并进一步进行激光跟踪仪组合站位规划,以实现最优测量性能。
4.3 测量可达性分析4个跟踪仪在目前组合站位下,运行一次可达性检测仿真实验。在组合站位给定的情况下,针对某个测量点运行一次测量可达性耗费实际时间约为1 s,针对共25个测量点运行一次测量可达性分析耗费时间约为30 s。计算M1~M4和Mall:
M1=(1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0),
M2=(0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1),
M3=(1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
M4=(0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
Mall=(2, 2, 0, 1, 1, 1, 2, 2, 2, 0, 0, 1, 0, 2, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1).
由Mall可知,目前组合站位下,可以测量21个测量点,有4个测量点测量不可达,需要进行激光跟踪仪站位规划。
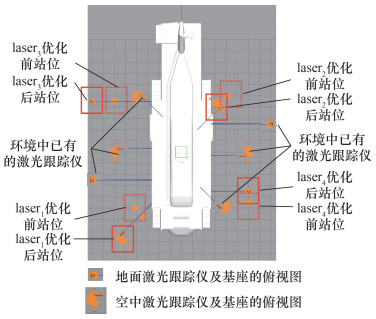
4.4 激光跟踪仪组合规划根据实际环境中可放置跟踪仪的位置范围,为每个跟踪仪设置离散网格的站位(即j1—j3运动量的离散取值范围),用以为每个激光跟踪仪搜索最优站位。考虑到图 10所示的测量点分布于机身的前后左右上下,因此初步将4个激光跟踪仪网格搜索区域分布于机身的4个方位,考虑到机身底部的测量点较难无遮挡地测量,给予每个跟踪仪较大范围的水平面可搜索空间(j1和j2可运动范围均为5 m,共25 m2的搜素空间),但是又需要保证该4个激光跟踪仪与现在已有的6个激光跟踪仪保持一定距离。于是生成的网格搜索区域如图 11所示,其中2个空中激光跟踪仪的j1、j2、j3的运动范围均分别为[—4, 1]、[—1, 4]、[0, 0] m;2个地面激光跟踪仪的j1、j2、j3运动范围均分别为[0, —5]、[—3, 2]、[0, 0] m。
|
| 图 11 优化后的激光跟踪仪测量站位 |
为了验证不同网格密度对于最优站位的规划时间效率和最优站位的测量精度的影响,将4个激光跟踪仪组合站位优化过程中的网格间距分别设置为5.0、2.5、1.6、1.0、0.5 m,仿真规划结果如表 1所示。
| 网格间距/ m |
仿真时间/ s |
寻优时间/ s |
总时间/ s |
精度指标 | 平均测量距离/m |
| 5.0 | 151.0 | 0.01 | 151.0 | — | — |
| 2.5 | 336.6 | 0.1 | 336.7 | 43.81 | 8.76 |
| 1.6 | 595.9 | 1.3 | 597.2 | 39.65 | 7.96 |
| 1.0 | 1 368.0 | 33.5 | 1 401.5 | 34.07 | 6.81 |
| 0.5 | 4 485.9 | 4 146.5 | 8 632.4 | 33.32 | 6.66 |
表 1中仿真时间代表仿真引擎运行的时间,与网格点数量基本呈线性相关;寻优时间代表对仿真运行得到的结果进行组合排布从而寻找得到最优组合站位精度指标所需时间,与网格点数量呈非线性增长(与激光跟踪仪数量有关,本文讨论4台跟踪仪组合站位规划的寻优时间与网格点数量的4次方近似呈线性相关);平均测量距离指根据精度指标进行平均还原得到的每个测量点的近似测量距离,由于激光跟踪仪测量精度随测量距离增长而线性下降,因此该指标可用于评估测量精度。
从仿真结果可见,当网格站位较为稀疏(网格间距小于或等于1.0 m)时,站位规划可在几百秒内实现,且测量精度随网格密度增加提升较大;而当网格站位较为密集(网格间距大于1.0 m)时,随网格密度增加,规划效率显著提升,而规划结果精度提升不显著。这与航空测量场的范围较大有关,对于数十米的航空测量场,小于0.5 m的测量站位离散意义不大。仿真结果显示,当网格间距从1.6 m减小到1.0 m时,仍可显著提升测量精度(测量精度表征指标减小约14.4%),因此选用1.0 m的网格间距是本次实验的最优解,该结果可直接适用于小型航空飞机(长度约十几米)的测量场布置。最终按该方案寻找4台激光跟踪仪的组合站位共需1 401.5 s,相比基于建模软件的方法[22]效率高得多,且具备较好的可视性。
图 11中,实线方框代表优化后的4个激光跟踪仪的站位,虚线方框代表优化前的4个激光跟踪仪的站位,未框出的激光跟踪仪为环境中已有激光跟踪仪(站位已预先设定)。优化得到的激光跟踪仪1的j1—j3的关节移动量分别为1、—3、0 m;激光跟踪仪2的j1—j3的关节移动量分别为0、1、0 m;激光跟踪仪3的j1—j3的关节移动量分别为0、—2、0 m;激光跟踪仪4的j1—j3的关节移动量分别为—1、0、0 m,此即为规划出的激光跟踪仪最优组合站位。
表 2为该站位下各个激光跟踪仪可达测量点序号(表中√代表可达,加红表示选用该激光跟踪仪测量精度更高)。
| 测量点序号 | 激光跟踪仪1 | 激光跟踪仪2 | 激光跟踪仪3 | 激光跟踪仪4 |
| 1(平尾下部) | √ |  |
||
| 2(平尾下部) | √ |  |
||
| 3(机身底部蒙皮) |  |
|||
| 4(机身底部蒙皮) |  |
|||
| 5(机身底部蒙皮) |  |
|||
| 6(短翼蒙皮) |  |
|||
| 7(短翼蒙皮) | √ |  |
||
| 8(短翼蒙皮) |  |
|||
| 9(短翼蒙皮) |  |
|||
| 10(机身蒙皮) |  |
|||
| 11(机身蒙皮) |  |
|||
| 12(机身蒙皮) |  |
|||
| 13(机身蒙皮) |  |
√ | √ | |
| 14(桨毂) | √ |  |
√ | |
| 15(桨毂) |  |
√ | ||
| 16(桨毂) |  |
√ | ||
| 17(桨毂) |  |
|||
| 18(桨毂) | √ |  |
√ | |
| 19(桨毂) |  |
√ | ||
| 20(桨毂) |  |
√ | ||
| 21(桨毂) |  |
|||
| 22(桨毂) |  |
|||
| 23(桨毂) |  |
√ | ||
| 24(桨毂) |  |
|||
| 25(桨毂) |  |
4.5 最优站位下测量裕度分析
对4个激光跟踪仪基座x、y轴方向分别施加范围为e的随机扰动误差,然后再次执行测量仿真程序,观察是否仍可对25个测量点全部测量成功。e依次选为(0, 10]、(10, 20]、…、(90, 100] mm共10组,每组执行100次仿真,计算测量成功率,如表 3所示。对于小于或等于50 mm的随机扰动误差,该站位仍可以实现对25个测量点全部可测。而当扰动误差大于50 mm时,测量成功率下降,检查发现主要是飞机底部测量点受到飞机和工作梯遮挡导致不易测量,可进一步将测量点通过T型探头(T-Probe)设备引出进行测量。该测量组合站位的测量裕度为50 mm,现场布置时只要测量点扰动不超过50 mm,均可实现全部测量点可测,而50 mm的误差是很容易通过手工放置测量点保障的。
| e/mm | 对全部测量点的测量成功率/% |
| (0, 10] | 100 |
| (10, 20] | 100 |
| (20, 30] | 100 |
| (30, 40] | 100 |
| (40, 50] | 100 |
| (50, 60] | 78 |
| (60, 70] | 78 |
| (70, 80] | 74 |
| (80, 90] | 52 |
| (90, 100] | 44 |
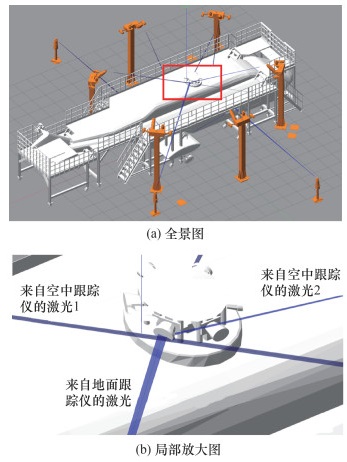
图 12给出了激光跟踪仪在仿真过程中对桨毂上某个测量点进行测量的示意图,可见该方法具备较好的人机交互友好性和可见性。
|
| 图 12 仿真测量桨毂某点 |
5 结论
本文提出了基于机器人建模的航空装配测控仿真分析方法。通过将航空装配中各关键要素在机器人仿真平台中进行建模,可以充分模拟复杂的综合测控环境;进行了激光跟踪仪仿真机器人模型构建、单激光跟踪仪对目标点测量可达性仿真分析、多激光跟踪仪测量场仿真精度评估和组合站位优化,并通过某飞机实际测量场景仿真验证了该方法的有效性。该方法可以实现规划、运动控制和测量的综合仿真,解决航空装配测控仿真领域多类问题。
该方法具备较好的扩展性和重规划性能。例如,激光跟踪仪测量可达性分析与组合站位规划不仅仅使用于激光跟踪仪,还适用于一切利用光路进行测量的设备如室内定位系统(indoor global positioning system,IGPS)等。当测量环境发生改变时,该方法仅需要进行模型重导入即可实现快速重规划,使用简单且效率高。
| [1] |
冯子明. 基于三维模型的飞机数字化快速检测技术研究[J]. 航空制造技术, 2011(21): 32-35. FENG Z M. Research on digital and rapid inspection technology based on 3D model for aircraft[J]. Aeronautical Manufacturing Technology, 2011(21): 32-35. DOI:10.3969/j.issn.1671-833X.2011.21.003 (in Chinese) |
| [2] |
王永栓, 王晓丽, 向颖, 等. 航空工业数字化协同现状与发展[J]. 航空制造技术, 2009(11): 62-65. WANG Y S, WANG X L, XIANG Y, et al. Current status and development of digital collaboration in aviation industry[J]. Aeronautical Manufacturing Technology, 2009(11): 62-65. (in Chinese) |
| [3] |
邱宝贵, 蒋君侠, 毕运波, 等. 大型飞机机身调姿与对接试验系统[J]. 航空学报, 2011, 32(5): 908-919. QIU B G, JIANG J X, BI Y B, et al. Posture alignment and joining test system for large aircraft fuselages[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 908-919. (in Chinese) |
| [4] |
巴晓甫, 薛红前, 李西宁. 飞机部件数字化调姿定位测量点的优选与构造算法[J]. 航空学报, 2022, 43(5): 625514. BA X F, XUE H Q, LI X N. Optimization and construction algorithm of measuring points for digital attitude adjusting and positioning of aircraft components[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(5): 625514. (in Chinese) |
| [5] |
陈文亮, 潘国威, 王珉. 基于力位协同控制的大飞机机身壁板装配调姿方法[J]. 航空学报, 2019, 40(2): 522403. CHEN W L, PAN G W, WANG M. High precision positioning method for aircraft fuselage panel based on force/position control[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(2): 522403. (in Chinese) |
| [6] |
岳烜德, 安鲁陵. 力控制技术在飞机数字化装配中的应用[J]. 航空制造技术, 2016(5): 47-51. YUE X D, AN L L. Application of force control technology in digital assembly of aircraft[J]. Aeronautical Manufacturing Technology, 2016(5): 47-51. (in Chinese) |
| [7] |
何胜强. 飞机数字化装配技术体系[J]. 航空制造技术, 2010(23): 32-37. HE S Q. Digital assembly technology system of aircraft[J]. Aeronautical Manufacturing Technology, 2010(23): 32-37. (in Chinese) |
| [8] |
毕利文, 唐晓东, 杨红宇. 飞机数字化装配工艺仿真技术[J]. 航空制造技术, 2008(20): 48-50. BI L W, TANG X D, YANG H Y. Digital assembly process simulation technology for aircraft[J]. Aeronautical Manufacturing Technology, 2008(20): 48-50. (in Chinese) |
| [9] |
衣勇, 宋雪萍. 机器人仿真研究的现状与发展趋势[J]. 机械工程师, 2009(7): 63-65. YI Y, SONG X P. The present situation and developing trend of robot simulation research[J]. Mechanical Engineer, 2009(7): 63-65. (in Chinese) |
| [10] |
CEPEDA J S, CHAIMOWICZ L, SOTO R. Exploring microsoft robotics studio as a mechanism for service-oriented robotics [C]// 2010 Latin American Robotics Symposium and Intelligent Robotics Meeting. Sao Bernardo do Campo, Brazil: IEEE, 2010: 7-12.
|
| [11] |
MAGYAR B, FORHECZ Z, KORONDI P. Developing an efficient mobile robot control algorithm in the Webots simulation environment [C]// IEEE International Conference on Industrial Technology. Maribor, Slovenia: IEEE, 2003: 179-184.
|
| [12] |
孙增圻. 机器人系统仿真及应用[J]. 系统仿真学报, 1995, 7(3): 23-29. SUN Z Y. Robotic system simulation and its application[J]. Acta Simulata Systematica Sinica, 1995, 7(3): 23-29. (in Chinese) |
| [13] |
渠瀛. 机器人模块化可重用仿真平台的设计与研究[D]. 沈阳: 东北大学, 2010. QU Y. Design and research of modular reconfigurable simulation platform for robot [D]. Shenyang: Northeastern University, 2010. (in Chinese) |
| [14] |
IÑIGO-BLASCO P, DIAZ-DEL-RIO F, ROMERO- TERNERO C. Robotics software frameworks for multi-agent robotic systems development[J]. Robotics and Autonomous Systems, 2012, 60(6): 803-821. DOI:10.1016/j.robot.2012.02.004 |
| [15] |
FREESE M, SINGH S, OZAKI F, et al. Virtual robot experimentation platform V-REP: A versatile 3D robot simulator [C]// Second International Conference on Simulation, Modeling, and Programming for Autonomous Robots. Darmstadt, Germany: Springer, 2010: 51-62.
|
| [16] |
李广云. LTD500激光跟踪测量系统原理及应用[J]. 测绘工程, 2001, 10(4): 3-8. LI G Y. The principle and application of the LTD500 laser tracker system[J]. Engineering of Surveying and Mapping, 2001, 10(4): 3-8. (in Chinese) |
| [17] |
黄娟, 顾寄南. 装配仿真中碰撞干涉检查研究的综述[J]. 江苏大学学报(自然科学版), 2002, 23(2): 17-21. HUANG J, GU J N. Summary of the research in collision and interference detection in assembly simulation[J]. Journal of Jiangsu University (Natural Science), 2002, 23(2): 17-21. (in Chinese) |
| [18] |
何朝良. 基于CATIA/CAA平台的虚拟装配路径规划的研究[D]. 南京: 南京航空航天大学, 2005. HE C L. The research on path planning of virtual assembly on the basis of CATIA/CAA platform [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005. (in Chinese) |
| [19] |
WOO T C. Visibility maps and spherical algorithms[J]. Computer-Aided Design, 1994, 26(1): 6-16. DOI:10.1016/0010-4485(94)90003-5 |
| [20] |
CHEN H K, HU S J, WOO T C. Visibility analysis and synthesis for assembly fixture certification using theodolite systems[J]. Journal of Manufacturing Science & Engineering, 2001, 123(1): 83-89. |
| [21] |
KONG Z Y, HUANG W Z, CEGLAREK D. Visibility analysis for assembly fixture calibration using screen space transformation[J]. Journal of Manufacturing Science and Engineering, 2005, 127(3): 622-634. DOI:10.1115/1.1947209 |
| [22] |
杨晓辉. 面向飞机大部件的数字化测量站位规划方法[D]. 南京: 南京航空航天大学, 2016. YANG X H. Reserch on station planning technology of digital measuring metrology for aircraft large component [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. (in Chinese) |
| [23] |
石循磊, 邓健健, 盖宇航, 等. 基于DELMIA的飞机大部件调姿对接仿真方法[J]. 航空制造技术, 2020, 63(23-24): 24-28. SHI X L, DENG J J, GAI Y H, et al. Simulation method of posture alignment and docking of large aircraft components based on DELMIA[J]. Aeronautical Manufacturing Technology, 2020, 63(23-24): 24-28. (in Chinese) |
| [24] |
饶建华, 梁静. 测距测角对激光跟踪仪精度影响的实验与分析[J]. 城市勘测, 2019(4): 160-162. RAO J H, LIANG J. Experimental analysis of the distance and angle measuring effect on laser tracking[J]. Urban Geotechnical Investigation & Surveying, 2019(4): 160-162. (in Chinese) |
| [25] |
甘霖, 李晓星. 激光跟踪仪现场测量精度检测[J]. 北京航空航天大学学报, 2009, 35(5): 612-614. GAN L, LI X X. Site measuring accuracy testing of laser tracker[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(5): 612-614. (in Chinese) |



