线激光视觉传感器是一种基于激光三角法的测量原理,通过相机采集图像获取照射在测量物体表面的激光线信息,并以此信息数字化重构物体三维轮廓的视觉传感器[1]。除了非接触测量,线激光视觉传感器还具备速度快、精度高和稳定性好等优势,被广泛应用于焊缝跟踪、缺陷检测和医疗健康等领域[2-3]。传统线激光视觉传感器受到相机景深的限制,只能采集有限范围的清晰图像。提高相机景深的一般解决方法是减小光圈、缩短焦距等,但这会显著降低视觉传感器的分辨率[4]。另一种解决思路是按照Scheimpflug定律[5-6]在传感器内搭建恒聚焦光路。该光路下,激光光平面上的所有可视检测点都能清晰聚焦。
基于恒聚焦光路设计新的线激光视觉传感器后,还需要建立并标定相应的数学测量模型才能在实际应用中进行有效检测。线激光视觉传感器的标定可以分为相机标定和光平面标定2部分。由于光路条件改变使原有的数学测量模型不足以描述新系统的检测原理,因此相应的标定方案也亟待优化。
满足Scheimpflug定律的倾斜相机成像模型,近年来受到诸多学者的关注。文[7-8]在保留传统相机的针孔成像模型的前提下,把Scheimpflug倾斜角作为一个特殊的畸变参数加入镜头畸变模型,但只在Scheimpflug倾斜角较小时模型才具有较高的标定精度。Louhichi等[9]假设了一个未发生倾斜的理想像平面,并以此为桥梁,通过一维Scheimpflug倾斜角描述实际倾斜像平面到理想像平面的转换关系,从而获得倾斜相机成像模型。Zhang等[10]将Scheimpflug倾斜角由一维扩展为二维,并证明了二维Scheimpflug倾斜角能更准确地描述倾斜相机成像模型。考虑二维Scheimpflug倾斜角时,根据不同的成像思想建立的成像模型不同。其中,文[11-12]利用光沿直线传播的原理,分别获得了物点所在光线与理想像平面和倾斜像平面的相交点,借助物点与2个相交点的转换关系建立了成像模型。文[13]利用二维Scheimpflug倾斜角对应的旋转矩阵建立了成像模型。文[6]通过理论推导和对比实验指出,旋转矩阵建立的倾斜相机成像模型更灵活且适用性强。
尽管倾斜相机成像模型不断涌现,但倾斜相机在线激光视觉传感器应用环境下的标定方案仍未获得妥善解决。同时,传感器成像光路的改变也使传统光平面标定时所用标定靶物和算法不再满足实际应用需求。
因此,本文在阐述基于恒聚焦光路的线激光视觉传感器的原理和建立相应的数学检测模型的基础上,提出了一种高效可靠的标定方案。针对倾斜相机的标定,建立了基于旋转矩阵的成像模型,并提出新的初值获取方法和非线性优化流程,这为倾斜相机在恒聚焦光路中的标定提供了思路;针对光平面的标定,设计了双台阶形状的标定靶物,只需要采集一次标志物轮廓信息,就能获取大量光平面上的非共线点,并通过最优化求解获得光平面方程系数。
1 线激光视觉传感器中的恒聚焦光路在传统线激光视觉传感器建立的光路中,透镜和光敏元件(像平面)始终保持平行关系,测量过程中仅参考基准面处的检测点就能在像平面上清晰聚焦。这是因为在不改变透镜的情况下(焦距f固定),检测点成像需满足如下规则:
| $ \frac{1}{a_{t}}+\frac{1}{b_{t}}=\frac{1}{f}. $ | (1) |
其中at和bt分别为第t个检测点的物距和像距。
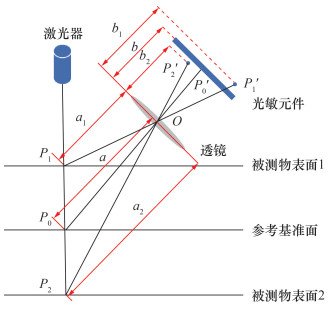
传统线激光视觉传感器调试好后传感器有限聚焦,如图 1所示。其中,参考基准面上的测量点P0对应的清晰像点P'0位于像平面上。受式(1)所述规则的约束,其余位置的测量点P1、P2对应清晰像点P'1、P'2均不会落在像平面上。此外,测量点离参考基准面越远,采集到的像点越不清晰,这极大地限制了传统线激光视觉传感器的高精度检测范围。
|
| 图 1 传统线激光视觉传感器有限聚焦 |
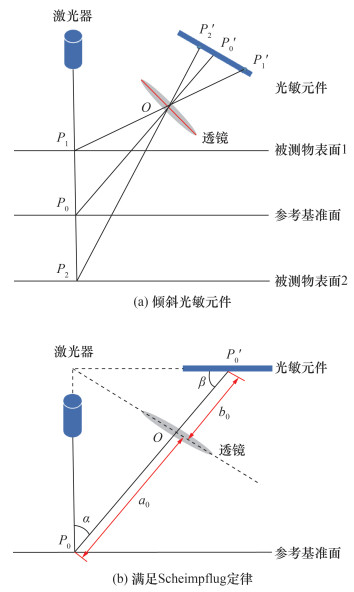
针对上述问题,可通过倾斜光敏元件使测量点P1、P2对应的像点P'1、P'2也聚焦到像平面上,如图 2a所示。当光敏元件的倾斜满足Scheimpflug定律时,即限制激光光平面、透镜平面、光敏元件(像平面)三者交于一条直线,从而建立起恒聚焦光路[14-15],此时传感器中所有可视的测量点都能准确聚焦,如图 2b所示。从几何角度分析,线激光视觉传感器建立恒聚焦光路需要满足的条件表示如下:
| $ a_{0} \tan \alpha=b_{0} \tan \beta. $ | (2) |
|
| 图 2 线激光视觉传感器恒聚焦原理 |
其中:a0和b0分别为参考基准面处P0的物距和像距;α为激光平面与透镜主光轴的夹角;β为光敏元件的倾斜角。
为说明恒聚焦光路的优越性,对2种光路的传感器进行对比实验。传统线激光视觉传感器成像情况如图 3a所示,传统线激光视觉传感器在采集图像时,中心聚焦处能清晰成像,但成像的清晰程度随着偏离中心逐渐降低。当传感器需要大范围检测时,图片两端区域由于偏离中心过多,成像质量很难满足高精度检测需求。而基于恒聚焦光路设计的线激光传感器成像情况如图 3b所示,可视范围内均能清晰成像。

|
| 图 3 不同光路线激光视觉传感器成像对比情况 |
2 倾斜相机标定原理 2.1 倾斜相机成像模型
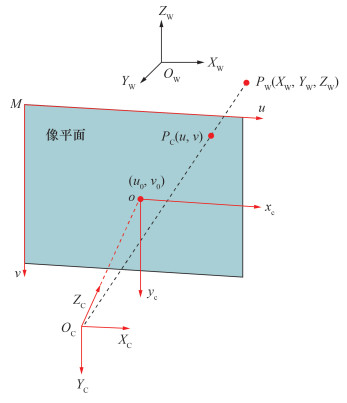
针孔模型是传统相机应用最广泛的成像模型,它是基于小孔成像的物理思想描述三维空间中的一点到像平面上二维像素点的转换关系。传统相机针孔模型成像图如图 4所示。针孔模型涉及4个坐标系的转换,分别是世界坐标系OW-XWYWZW、以相机镜头光心OC为原点的相机坐标系OC-XCYCZC、像平面上以像主点o为原点的图像物理坐标系o-xcyc和以像平面左上角M点为原点的图像像素坐标系M-uv。
|
| 图 4 传统相机针孔模型成像图 |
世界坐标系中的一点PW(XW, YW, ZW)沿着一束光线通过OC,在像平面上投影成点PC,PC在图像像素坐标系下的坐标为(u, v)。传统相机的成像模型表示如下:
| $ \lambda_{0}\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\boldsymbol{K}\left(\boldsymbol{R}\left[\begin{array}{l} X_{\mathrm{W}} \\ Y_{\mathrm{W}} \\ Z_{\mathrm{W}} \end{array}\right]+\boldsymbol{T}\right) ; $ | (3) |
| $ \begin{gather*} \boldsymbol{K}=\left[\begin{array}{ccc} f_{x} & 0 & u_{0} \\ 0 & f_{y} & v_{0} \\ 0 & 0 & 1 \end{array}\right], \\ f_{x}=\frac{f}{\Delta x}, \\ f_{y}=\frac{f}{\Delta y} . \end{gather*} $ | (4) |
其中:λ0为尺度因子,与投影深度有关;旋转矩阵R(3×3)和平移向量T(3×1)为OW-XWYWZW到OC-XCYCZC的刚体变换关系;K为相机固有属性决定的内参矩阵;Δx和Δy分别为每个像素在xc和yc方向的物理尺寸;fx和fy分别为相机沿xc和yc方向的等效焦距;u0和v0为像主点在图像像素坐标系下的坐标。
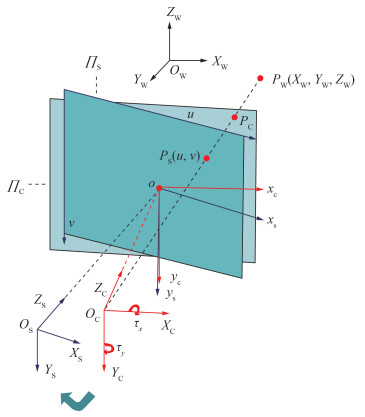
倾斜相机成像模型可由传统相机成像模型改进而来。倾斜相机模型成像图如图 5所示,实际的倾斜像平面ΠS可由一个理想像平面ΠC围绕o点旋转得到,此旋转关系Rτ可以分解为绕o-xcyc的xc轴和yc轴的连续旋转[2],旋转角度分别为τx和τy,表示如下:
| $ \boldsymbol{R}_{\tau}=\left[\begin{array}{ccc}\cos \tau_{y} & 0 & \sin \tau_{y} \\ 0 & 1 & 0 \\ -\sin \tau_{y} & 0 & \cos \tau_{y}\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos \tau_{x} & -\sin \tau_{x} \\ 0 & \sin \tau_{x} & \cos \tau_{x}\end{array}\right]. $ | (5) |
|
| 图 5 倾斜相机模型成像图 |
此时点PW (XW, YW, ZW)将沿着光线,分别与ΠC和ΠS相交于PC、PS。由PW、PC、PS这3个点的共线关系和Rτ,可以得到PW在倾斜相机坐标系OS-XSYSZS下的坐标(XS, YS, ZS)和OC-XCYCZC下的坐标(XC, YC, ZC)的转换关系[13],表示如下:
| $ \begin{gather*} X_{\mathrm{S}}^{\prime}=\frac{X_{\mathrm{S}}}{Z_{\mathrm{S}}}, \quad Y_{\mathrm{S}}^{\prime}=\frac{Y_{\mathrm{S}}}{Z_{\mathrm{S}}}, \quad X_{\mathrm{C}}^{\prime}=\frac{X_{\mathrm{C}}}{Z_{\mathrm{C}}}, \quad Y_{\mathrm{C}}^{\prime}=\frac{Y_{\mathrm{C}}}{Z_{\mathrm{C}}}, \\ \lambda_{1}\left[\begin{array}{c} X_{\mathrm{S}}^{\prime} \\ Y_{\mathrm{S}}^{\prime} \\ 1 \end{array}\right]={{\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}}} \boldsymbol{R}_{\tau}^{\mathrm{T}}\left[\begin{array}{c} X_{\mathrm{C}}^{\prime} \\ Y_{\mathrm{C}}^{\prime} \\ 1 \end{array}\right] ; \end{gather*} $ | (6) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}}}=\left[\begin{array}{ccc} \cos \tau_{x} \cos \tau_{y} & 0 & \sin \tau_{y}\\ 0 & \cos \tau_{x} \cos \tau_{y} & -\sin \tau_{x} \cos \tau_{y} \\ 0 & 0 & 1 \end{array}\right]. $ | (7) |
其中:X'S、Y'S、X'C和Y'C均为归一化坐标;λ1为式(6)中的尺度因子,由等式两边坐标的归一化决定;Λ为推导出的Scheimpflug[13]矩阵。
把式(6)代入式(3),可得点PW (XW, YW, ZW)与点PS(u, v)的成像关系,表示如下:
| $ \lambda_{2}\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\boldsymbol{K} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}}} \boldsymbol{R}_{\tau}^{\mathrm{T}}\left(\boldsymbol{R}\left[\begin{array}{l} X_{\mathrm{W}} \\ Y_{\mathrm{w}} \\ Z_{\mathrm{w}} \end{array}\right]+\boldsymbol{T}\right) . $ | (8) |
其中:λ2为尺度因子,由等式两边坐标的归一化决定。
上述建立的倾斜相机成像模型是在忽略镜头畸变情况下建立的理想模型。实际应用中,镜头的设计、制造和安装等过程不可避免地存在缺陷,因此镜头畸变引起的图像点变形情况显著存在。考虑常用畸变模型的定义,若要去除存在耦合情况的切向畸变[16],则需要在OC-XCYCZC的归一化坐标中加入径向畸变和薄棱镜畸变,表示如下:
| $ \begin{gather*} r^{2}=X_{\mathrm{C}}^{\prime 2}+Y_{\mathrm{C}}^{\prime 2}, \\ \left\{\begin{array}{l} X_{\mathrm{d}}^{\prime}=\left(1+k_{1} r^{2}+k_{2} r^{4}\right) X_{\mathrm{C}}^{\prime}+g_{1} r^{2}+g_{2} r^{4}, \\ Y_{\mathrm{d}}^{\prime}=\left(1+k_{1} r^{2}+k_{2} r^{4}\right) Y_{\mathrm{C}}^{\prime}+g_{3} r^{2}+g_{4} r^{4} . \end{array}\right. \end{gather*} $ | (9) |
其中:X'd和Y'd分别为X'C和Y'C畸变后的值;k1和k2为径向畸变的前二阶系数;g1和g2为OC-XCYCZC下XC向的薄棱镜畸变系数,g3和g4为OC-XCYCZC下YC向的薄棱镜畸变系数。
根据式(8)和(9)可建立包含镜头畸变的倾斜相机成像模型。
2.2 倾斜相机成像模型初值获取相机的成像模型是一个复杂的非线性模型,多利用非线性优化算法求解。获取合适的初值是该类算法快速收敛的关键。传统相机标定采用以单应分解求初值的方法[17],能简单快速地获取相机内外参数初值。倾斜相机模型更复杂,目前常用的初值获取方法主要基于以下2种思路:1) 直接选择相机理论参数作为初值[13-14],但初值精度差;2) 借助额外的辅助工具获取[16],但操作较复杂。
本文通过分析和比较基于旋转矩阵的倾斜相机成像模型和传统相机成像模型的异同之处,改进了以单应分解求初值的方法[17],使倾斜相机标定也能简单快速地获取参数初值。
对式(8)进行合并运算,可以得到:
| $ \lambda_{2}\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\boldsymbol{K}_{\eta}\left(\boldsymbol{R}_{\eta}\left[\begin{array}{l} X_{\mathrm{W}} \\ Y_{\mathrm{W}} \\ Z_{\mathrm{W}} \end{array}\right]+\boldsymbol{T}_{\eta}\right); $ | (10) |
| $ \begin{gather*} \boldsymbol{R}_{\eta}=\boldsymbol{R}_{\tau}^{\mathrm{T}} \boldsymbol{R}, \boldsymbol{T}_{\eta}=\boldsymbol{R}_{\tau}^{\mathrm{T}} \boldsymbol{T}, \\ \boldsymbol{K}_{\eta}=\boldsymbol{K} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}}}=\left[\begin{array}{ccc} F_{x} & 0 & U_{0} \\ 0 & F_{y} & V_{0} \\ 0 & 0 & 1 \end{array}\right], \\ F_{x}=f_{x} \cos \tau_{x} \cos \tau_{y}, \\ F_{y}=f_{y} \cos \tau_{x} \cos \tau_{y}, \\ U_{0}=u_{0}+f_{x} \sin \tau_{y}, \\ V_{0}=v_{0}-f_{y} \sin \tau_{x} \cos \tau_{y} . \end{gather*} $ | (11) |
改进后的初值获取步骤如下:
步骤1 不考虑相机倾斜和镜头畸变,因为式(3)和(10)具有相似表达,所以可直接采用以单应分解求初值的方法[17]得到倾斜相机模型带偏差的内外参初值Kη、Rη、Tη。
步骤2 根据设计值确定τx、τy的初值,τx由满足Scheimpflug定律的倾斜角决定,τx=6°,τy由轻微的装配误差决定,通常τy=0°。
步骤3 将τx、τy的值代入式(5)和(7)可计算得到RτT和Λ的初值。
步骤4 根据式(10)和(11)所描述的转换关系,利用RτT和Λ从Kη、Rη、Tη中分解得到K、R、T的初值。
2.3 倾斜相机标定流程倾斜相机标定算法主要包括2个环节:一是通过粗略分解,获得相机内外参数的初值;二是基于极大似然准则,通过数值迭代的方法对各参数进行非线性优化。具体流程如下:
1) 使用倾斜相机拍摄不同位姿的棋盘格并将棋盘格黑白条纹的角点作为标定的靶点。
2) 采用Harris算法[18]提取处于第j个位姿的棋盘格的第i个角点的实际像素坐标pi, j(u, v)。
3) 按照2.2节描述的方法,利用pi, j(u, v)和其对应的世界坐标系下的点Pi, j(XW, YW, ZW)求得倾斜相机的初始内参矩阵K、Λ、RτT,以及第j个位姿棋盘格的初始外参矩阵Rj、Tj。
4) 在不考虑畸变的情况下,利用式(8)将Pi, j(XW, YW, ZW)映射成靶点的理论像素坐标
| $ \min \sum\limits_{j=1}^{m} \sum\limits_{i=1}^{n}\left\|p_{i, j}(u, v)-\hat{p}_{i, j}(\hat{u}, \hat{v})\right\|^{2} . $ | (12) |
采用Levenberg-Marquardt非线性优化算法迭代求解式(12),从而不断优化内外参数,直至结果收敛。
5) 考虑畸变影响,利用式(8)和(9)描述的倾斜相机成像模型和上一步骤优化得到的内外参,再次将Pi, j(XW, YW, ZW)映射成靶点的理论像素坐标
由第2章可知,PS(u, v)经过倾斜相机成像模型的映射,能获得点PW在OC-XCYCZC下的归一化坐标(X'C, Y'C, 1),但该坐标缺失了深度信息。进一步,利用点PW在光平面上这一约束,可将光平面在OC-XCYC ZC下的方程AplXC+BplYC+DplZC+Epl=0作为补充条件以获得深度信息。为方便理解,方程的转换形式表示如下:
| $ A_{\mathrm{pl}} X_{\mathrm{C}}^{\prime}+B_{\mathrm{pl}} Y_{\mathrm{C}}^{\prime}+D_{\mathrm{pl}}+\frac{E_{\mathrm{pl}}}{Z_{\mathrm{C}}}=0. $ | (13) |
其中Apl、Bpl、Dpl、Epl为光平面参数。
由式(13)可知,当已知归一化坐标(X'C, Y'C, 1)和光平面参数后,可以得到ZC的值,从而获得PW在OC-XCYCZC下的完整坐标(XC, YC, ZC)。
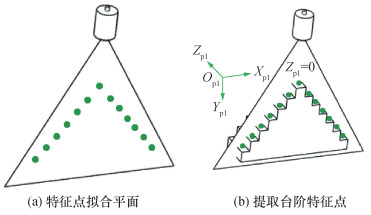
特征点拟合平面如图 6a所示,为获得光平面参数,可以利用h个光平面上不共线的特征点qpl, e在OC-XCYCZC的坐标(XC, e, YC, e, ZC, e),构建所有点到平面距离和最小的目标函数,并通过SVD分解等方式[19]进行求解,即
| $ \begin{gather*} G\left(A_{\mathrm{pl}}, B_{\mathrm{pl}}, D_{\mathrm{pl}}, E_{\mathrm{pl}}\right)= \\ \min \sum\limits_{e=1}^{h} \frac{\left|A_{\mathrm{pl}} X_{\mathrm{C}, e}+B_{\mathrm{pl}} Y_{\mathrm{C}, e}+D_{\mathrm{pl}} Z_{\mathrm{C}, e}+E_{\mathrm{pl}}\right|}{\sqrt{A_{\mathrm{pl}}^{2}+B_{\mathrm{pl}}^{2}+D_{\mathrm{pl}}^{2}}} \end{gather*} $ | (14) |
|
| 图 6 光平面标定原理图 |
提取台阶特征点如图 6b所示,本文将光平面投射至双边台阶,采集光平面与每层台阶交线的中点作为光平面拟合所需点。为了获得qpl, e在OC-XCYCZC下的坐标,首先,建立台阶坐标系Opl-Xpl Ypl Zpl,并令光平面位于Zpl=0处;其次,将qpl, e对应的像点(ue, ve)进行去畸变处理[17],获得无畸变的像素坐标(uud, e, vud, e);最后,可根据式(8)得到像素坐标系到台阶坐标系的单应性关系, 表示如下:
| $ \lambda_{2}\left[\begin{array}{c}u_{\mathrm{ud}, e} \\ v_{\mathrm{ud}, e} \\ 1\end{array}\right]=\boldsymbol{H}\left[\begin{array}{c}X_{\mathrm{pl}, e} \\ Y_{\mathrm{pl}, e} \\ 1\end{array}\right]=\boldsymbol{K} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}}} \boldsymbol{R}_{\tau}^{\mathrm{T}}\left[\begin{array}{ll}\boldsymbol{R}_{\mathrm{pl}} & \boldsymbol{T}_{\mathrm{pl}}\end{array}\right]\left[\begin{array}{c}X_{\mathrm{pl}, e} \\ Y_{\mathrm{pl}, e} \\ 1\end{array}\right]. $ | (15) |
其中:H为单应性矩阵, 可由直接线性变换法(direct linear transform, DLT)[20]获得;Rpl和Tpl为Opl-Xpl Ypl Zpl到OC-XC YC ZC的刚体变换关系,可先利用相机内参标定得到K、Λ、RτT,再根据式(15)从H中分解获得;(Xpl,e, Ypl, e, 0)为qpl, e在Opl-Xpl Ypl Zpl下的坐标,由Rpl和Tpl可以将qpl, e在Opl-Xpl Ypl Zpl下的坐标(Xpl,e, Ypl, e, 0)转换为OC-XC YC ZC下的坐标(XC, e, YC, e, 0),从而根据式(14)求得光平面参数。
4 实验验证 4.1 实验布置为了验证标定算法可行,设计和加工了一款基于恒聚焦光路的线激光视觉传感器。恒聚焦线激光视觉传感器主要由采集图像的镜头和相机、调整光路的倾斜连接座、产生激光平面的线激光发射器及提高激光成像质量的滤光片构成,如图 7所示。根据应用需求,上述关键元件的选型或加工如下:相机选择型号为MV-CB016-10GM-C的海康威视公司板级CMOS相机(分辨率为1 440×1 080,像元尺寸为3.45 μm×3.45 μm);镜头选用12 mm焦距的定焦镜头;根据恒聚焦光路的几何限制,加工了倾角为6°的倾斜连接座;分析应用场景中杂光的最弱波段,线激光发射器发射的激光波长选择658±5 nm,并在镜头前安装相应波长段的窄带滤光片。

|
| 图 7 恒聚焦线激光视觉传感器 |
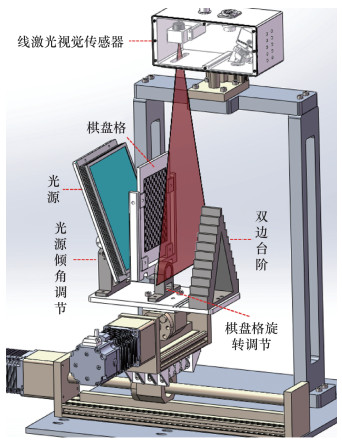
本文标定方案中,线激光视觉传感器需要棋盘格、双边台阶分别标定相机内参、光平面参数。此外,为提高算法的鲁棒性,标定过程还需不断调整传感器与标定物间的相对位姿[17]。为精简操作步骤、减少人工干预,设计了一体化的自动标定装置,如图 8所示。
|
| 图 8 一体化的自动标定装置 |
标定装置的外框由三轴丝杆滑台按梁架式组合而成,可在工作空间内沿标定装置的x、y、z这3个方向调整传感器和标定物的相对位置。传感器固定在标定装置z轴上,并沿该方向向下投射光平面;棋盘格通过旋转法兰安装在与标定装置xy面平行的联动平台上,能同时调整其相对于传感器的位置和姿态;双边台阶固定在联动平台上,并通过定位销确保与光平面垂直;光源通过倾斜角调整机构安装在联动平台上,根据采集图片的明暗程度能自动调整光源倾角[21],此外光源发光波长为特定的660 nm,避免了传统相机标定时需要拆卸传感器滤光片的问题[21]。标定时,在嵌入式系统控制下,装置能按照预设方案,自动有序地完成所有标定步骤。
4.2 相机标定相机标定采用的棋盘格尺寸为150.0 mm×100.0 mm,单个格子大小为5.0 mm×5.0 mm,横纵排列为22×15,精度为±0.1 mm。采集棋盘格图像时,首先,需要移动棋盘格至棋盘格图案面与光平面重合的位置;其次,在保证采集的棋盘格图像完整且清晰的条件下,旋转棋盘格或调节传感器位置,采集12组不同位姿的棋盘格图像;最后,分别提取每张棋盘格图像的黑白角点,如图 9所示。

|
| 图 9 棋盘格图像采集和角点提取 |
提取角点后,参照2.3节的流程完成倾斜相机的标定。此外,为说明倾斜相机成像模型具有有效性和优越性,增加了一组利用传统相机模型标定的对比实验。2种成像模型的标定结果如表 1所示。其中,l1和l2为传统相机成像模型使用的切向畸变系数。
| 相机参数 | 成像模型 | |
| 倾斜相机 | 传统相机 | |
| fx | 3 575.443 8 | 3 271.696 1 |
| fy | 3 410.314 6 | 2 815.888 3 |
| u0 | 604.037 2 | 736.762 5 |
| v0 | 495.782 4 | 503.408 8 |
| k1 | -0.096 3 | -0.090 1 |
| k2 | -0.599 8 | 0.214 1 |
| l1 | — | 0.005 5 |
| l2 | — | -0.001 6 |
| g1 | -0.005 4 | -0.005 7 |
| g2 | 0.235 8 | 0.252 9 |
| g3 | 0.001 6 | 0.002 3 |
| g4 | 0.139 2 | 0.137 6 |
| τx/(°) | 5.647 3 | — |
| τy/(°) | 0.718 8 | — |
| 重投影偏差 | 0.129 | 0.487 |
使用倾斜相机模型标定,获得的τx和τy分别为5.647 3°和0.718 8°,这与设计值τx=6°,τy=0° 非常接近,并且使用倾斜相机模型的重投影偏差仅为0.129,具有较高的标定精度。上述实验结果说明倾斜相机成像模型有效。
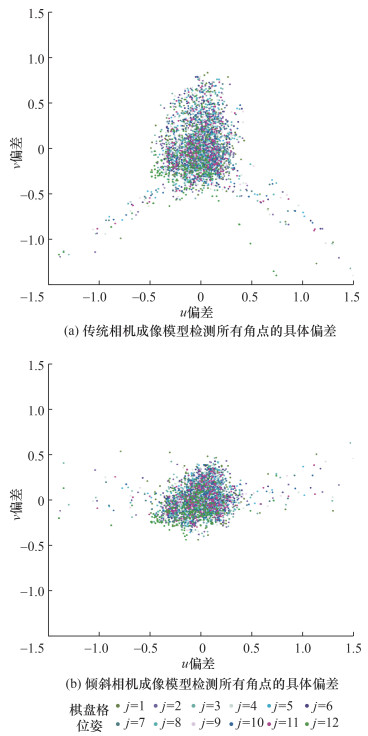
由2.1节所述和表 1可知,l1和l2在一定程度上能补偿相机倾斜带来的影响。实验结果也表明传统相机模型的重投影偏差为0.487,该偏差在实际中尚能接受,但远大于倾斜相机模型的0.129。尤其是当相机的倾斜角度更大时,使用传统相机成像模型进行标定,精度会显著下降[16]。针对相同的多张棋盘格图像,分别使用2种模型完成标定后,计算每张棋盘格图像的角点的重投影误差情况,角点重投影后在u、v方向上的偏差如图 10所示。上述对比结果说明倾斜相机成像模型具有优越性。
|
| 图 10 角点重投影后在u、v方向上的偏差 |
4.3 光平面标定
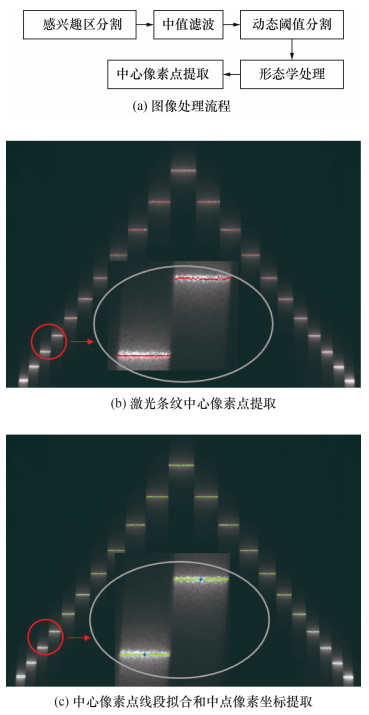
完成相机标定后,还需进行光平面的标定。首先,需要移动标定装置,使光平面投影到双边台阶;其次,采集投影形成的激光条纹图像,此时图像存在反光干扰、环境光噪声等缺陷,并且采集的激光条纹具有一定宽度。经过如图 11a所示的图像处理流程后,可获得如图 11b所示的每条光条纹的中心像素点。为提高光平面标定算法的鲁棒性,通常不是直接选择中心像素点作为标定时的特征点,而是先对这些中心像素点进行线段拟合,再选择每条线段的中点的像素坐标作为光平面标定时qpl, e的像素坐标(ue, ve),结果如图 11c所示。对比结果表明,光平面标定算法拟合后选取特征点比直接选取特征点精度更高。进一步比较极值法、重心法、形态学边缘法和Steger算法等4种光条中心提取算法[2]对光平面标定结果的影响,结果表明,不同算法获得的特征点的亚像素坐标相差小于0.050,最终标定得到的光平面参数相差小于0.5%,因此上述4种光条中心提取算法对光平面标定结果的影响不显著。
|
| 图 11 光平面特征点像素坐标提取 |
利用qpl, e的像素坐标和台阶坐标,参照第3章中的方案进行光平面标定,能够获取Rpl和Tpl,表示如下:
| $ \begin{gather*} \boldsymbol{R}_{\mathrm{pl}}=\left[\begin{array}{ccc} 0.999\;2 & 0.999\;2 & 0.019\;9 \\ 0.000\;6 & 0.000\;6 & -0.847\;7 \\ -0.039\;1 & -0.039\;1 & 0.493\;4 \end{array}\right], \\ \boldsymbol{T}_{\mathrm{pl}}=\left[\begin{array}{c} -43.657\;6 \\ -13.639\;3 \\ 186.790\;0 \end{array}\right]. \end{gather*} $ | (16) |
利用求得的外参矩阵可以对qpl,e进行坐标转换,并根据式(14)拟合求得光平面的方程,表示如下:
| $ -0.000\;2 X_{\mathrm{C}}+0.008\;5 Y_{\mathrm{C}}+Z_{\mathrm{C}}-0.004\;8=0. $ | (17) |
为了评估标定方案的效果,使用完成标定的线激光视觉传感器测量一个高度为(35.000 0±0.000 1) mm的标准陶瓷量块。恒聚焦线激光传感器测量标准陶瓷量块如图 12所示。图 12a为标准陶瓷量块,量块位于已校准好的平面上,可控制视觉传感器投影光平面到量块上。由于量块和平面间存在高度差,激光将被分成阶梯状的2段条纹。通过计算2段条纹的高度差可获得量块的检测结果。

|
| 图 12 恒聚焦线激光传感器测量标准陶瓷量块 |
为获得可信度更高的评估结果,在保持测量条件不变的情况下,需要改变量块的位置,使量块产生的阶梯条纹成像在图像中的不同方位。在满足激光条纹成像清晰且尽可能覆盖整个图像视野的前提下,采集并测算量块在多个位置的高度,标准陶瓷量块测量图像如图 12b所示。为定量评估传感器的检测精度,先用传感器的检测值减去陶瓷量块高度的标称值35.000 0 mm,再取差值的绝对值(绝对偏差值)作为定量依据,并以所有测量组的绝对偏差值的均值作为最终评估指标。标准陶瓷量块检测结果如表 2所示。由表 2的实验数据可知,传感器检测的平均高度为34.989 1 mm,检测数据的标准差为0.038 1 mm,绝对偏差值的均值约为0.030 2 mm。结果表明,按本文方法完成标定后的线激光视觉传感器具有较高的检测精度和稳定性,符合实际应用需求。
| 测量组号 | 检测值/mm | 绝对偏差值/mm |
| 1 | 35.046 2 | 0.046 2 |
| 2 | 34.936 2 | 0.063 8 |
| 3 | 34.971 7 | 0.028 3 |
| 4 | 34.996 4 | 0.003 6 |
| 5 | 34.950 9 | 0.049 1 |
| 6 | 35.002 7 | 0.002 7 |
| 7 | 34.999 9 | 0.000 1 |
| 8 | 34.969 9 | 0.030 1 |
| 9 | 35.027 9 | 0.027 9 |
| 平均值 | 34.989 1 | 0.028 0 |
5 结论
本文针对基于恒聚焦光路的线激光视觉传感器,提出了一套完整且有效的标定方案。通过引入二维Scheimpflug倾斜角建立了更适合该线激光视觉传感器的倾斜相机成像模型,并详细阐述了模型参数的初值求解和非线性优化的具体流程。通过使用双边台阶作为标志物,方便快速地获取了光平面上的大量非共线点,并有效地拟合了光平面在理想相机坐标下的平面方程。设计了一套一体化的自动标定装置,能在满足成像限制的情况下,高效完成线激光视觉传感器的标定实验。
从线激光视觉传感器对已知尺寸的标准陶瓷量块的检测结果看,该线激光视觉传感器测量的平均偏差约为0.028 0 mm。这表明,本文所提标定方案能够保证基于恒聚焦光路的线激光视觉传感器检测精度高和重复性好,可满足实际应用需求。
| [1] |
XU X B, FEI Z W, YANG J, et al. Line structured light calibration method and centerline extraction: A review[J]. Results in Physics, 2020, 19: 103637. DOI:10.1016/j.rinp.2020.103637 |
| [2] |
郭吉昌, 朱志明, 于英飞, 等. 焊接领域激光结构光视觉传感技术的研究及应用[J]. 中国激光, 2017, 44(12): 7-16. GUO J C, ZHU Z M, YU Y F, et al. Research and application of visual sensing technology based on laser structured light in welding industry[J]. Chinese Journal of Lasers, 2017, 44(12): 7-16. (in Chinese) |
| [3] |
STEGER C. A comprehensive and versatile camera model for cameras with tilt lenses[J]. International Journal of Computer Vision, 2017, 123(2): 121-159. DOI:10.1007/s11263-016-0964-8 |
| [4] |
孙聪, 刘海波, 陈圣义, 等. 基于广义成像模型的Scheimpflug相机标定方法[J]. 光学学报, 2018, 38(8): 114-122. SUN C, LIU H B, CHEN S Y, et al. A general imaging model based method for Scheimpflug camera calibration[J]. Acta Optica Sinica, 2018, 38(8): 114-122. (in Chinese) |
| [5] |
MEI Q, GAO J, LIN H, et al. Structure light telecentric stereoscopic vision 3-D measurement system based on Scheimpflug condition[J]. Optics and Lasers in Engineering, 2016, 86: 83-91. DOI:10.1016/j.optlaseng.2016.05.021 |
| [6] |
SUN C, LIU H B, JIA M N, et al. Review of calibration methods for Scheimpflug camera[J]. Journal of Sensors, 2018, 2018: 3901431. |
| [7] |
PENG J Z, WANG M, DENG D N, et al. Distortion correction for microscopic fringe projection system with Scheimpflug telecentric lens[J]. Applied Optics, 2015, 54(34): 10055-10062. DOI:10.1364/AO.54.010055 |
| [8] |
KUMAR A, AHUJA N. Generalized radial alignment constraint for camera calibration [C]// Proceedings of 201422nd International Conference on Pattern Recognition. Stockholm, Sweden: IEEE, 2014: 184-189.
|
| [9] |
LOUHICHI H, FOURNEL T, LAVEST J M, et al. Self-calibration of Scheimpflug cameras: An easy protocol[J]. Measurement Science and Technology, 2007, 18(8): 2616-2622. DOI:10.1088/0957-0233/18/8/037 |
| [10] |
ZHANG X, ZHOU T. Generic Scheimpflug camera model and its calibration [C]// Proceedings of 2015 IEEE International Conference on Robotics and Biomimetics. Zhuhai, China: IEEE, 2015: 2264-2270.
|
| [11] |
LEGARDA A, IZAGUIRRE A, ARANA N, et al. A new method for Scheimpflug camera calibration [C]// Proceedings of 201110th International Workshop on Electronics, Control, Measurement and Signals. Liberec, The Czech Republic: IEEE, 2011: 1-5.
|
| [12] |
LEGARDA A, IZAGUIRRE A, ARANA N, et al. Comparison and error analysis of the standard pin-hole and Scheimpflug camera calibration models [C]// Proceedings of 2013 IEEE 11th International Workshop of Electronics, Control, Measurement, Signals and Their Application to Mechatronics. Toulouse, France: IEEE, 2013: 1-6.
|
| [13] |
CORNIC P, ILLOUL C, CHEMINET A, et al. Another look at volume self-calibration: Calibration and self-calibration within a pinhole model of Scheimpflug cameras[J]. Measurement Science and Technology, 2016, 27(9): 094004. DOI:10.1088/0957-0233/27/9/094004 |
| [14] |
王平江, 吴娟娟. 基于Scheimpflug定律的线结构光系统摄像机标定方法[J]. 制造业自动化, 2017, 39(10): 10-14, 19. WANG P J, WU J J. Calibration method of line structure optical system camera based on Scheimpflug's law[J]. Manufacturing Automation, 2017, 39(10): 10-14, 19. (in Chinese) |
| [15] |
蔡逸, 刘常杰. 激光三角法测距传感器的参数优化[J]. 传感技术学报, 2017, 30(10): 1472-1477. CAI Y, LIU C J. Parameters optimization of laser range sensor based on triangulation[J]. Chinese Journal of Sensors and Actuators, 2017, 30(10): 1472-1477. (in Chinese) |
| [16] |
柳升龙, 孙聪, 刘海波, 等. 一种新的移轴相机两步标定方法[J]. 中国科学: 技术科学, 2018, 48(8): 836-844. LIU S L, SUN C, LIU H B, et al. A new two-step method for tilt/shift camera self-calibration[J]. Scientia Sinica: Technologica, 2018, 48(8): 836-844. (in Chinese) |
| [17] |
ZHANG Z Y. Flexible camera calibration by viewing a plane from unknown orientations [C]// Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra, Greece: IEEE, 1999: 666-673.
|
| [18] |
HARRIS C, STEPHENS M. A combined corner and edge detector [C]// Proceedings of the 4th Alvey Vision Conference. Manchester, UK: Alvety Vision Club, 1988: 147-151.
|
| [19] |
LIU Z, LI X J, LI F J, et al. Calibration method for line-structured light vision sensor based on a single ball target[J]. Optics and Lasers in Engineering, 2015, 69: 20-28. DOI:10.1016/j.optlaseng.2015.01.008 |
| [20] |
吴剑, 王广志, 丁海曙, 等. 三维测量系统中线性CCD相机的直接线性变换[J]. 清华大学学报(自然科学版), 2004, 44(6): 860-863. WU J, WANG G Z, DING H S, et al. Direct linear transformation of linear charge-coupled device cameras in a 3-D measurement system[J]. Journal of Tsinghua University (Science and Technology), 2004, 44(6): 860-863. DOI:10.3321/j.issn:1000-0054.2004.06.037 (in Chinese) |
| [21] |
SHEHZAD M, LAWRENCE S, ATKINSON C, et al. On assuring the accurate parallel alignment of a laser sheet for planar and stereoscopic particle image velocimetry[J]. Experiments in Fluids, 2021, 62(10): 208. DOI:10.1007/s00348-021-03307-3 |



