2. 瑞能赛特(深圳)科技有限公司, 深圳 518118;
3. 江苏费尔曼安全科技有限公司, 徐州 221100
2. Ruinengsaite Technology (Shenzhen) Co., Ltd., Shenzhen 518118, China;
3. Jiangsu Firemana Safety Technology Co., Ltd., Xuzhou 221100, China
热释放速率(heat release rate,HRR)是指在规定的试验条件下单位时间内材料燃烧所释放的热量。热释放速率的增加会导致燃烧过程中向材料表面传递热量的增加,从而使材料的热解速度提升,进而加速火焰传播速度。对热释放速率的准确测量是深入理解火灾发展过程的关键[1]。
目前,科研工作者已提出了很多测量热释放速率的方法,比如质量损失法[2]、氧耗法[3]等,其中氧耗法被广泛使用。氧耗法的基本原理为物质完全燃烧每消耗单位质量的氧气就会产生一定量的热量。Huggett[4]利用常见可燃物对这一原理进行了精确测算,发现燃烧每消耗1kg的氧气就会产生约13.2MJ的热量,其精度在5%左右。ISO 9705标准下的锥形量热仪系统就是利用这一原理制成的,该量热仪主要有6部分:燃烧室、载重台、氧分析仪、烟气测量系统、通风装置及其他装置[5]。氧分析仪是核心部件,物质燃烧时热释放速率的测量精度很大程度上取决于氧分析仪的测量精度。然而,氧分析仪对被测气体的压力和流量相当敏感,一台高精度的氧分析仪市场购买价格约4万美元。此外,构建大型量热仪系统程序繁琐,导致大型量热仪市场价格约20万美元,这样昂贵的价格不利于装置的推广,更不利于科研工作者开展热释放速率相关的研究工作。
根据能量守恒原理,室内火灾中可燃物产生的能量等于使烟气层温度升高和通过壁面传导或辐射损失的能量,以及通过开口对流损失的能量之和。房间内温度的升高由所处环境的热量传递所致,故单位时间内材料燃烧所释放的热量与房间内温度的升高密切相关。
机器学习方法在揭示若干自变量与若干因变量之间关系的研究中具有相当大的潜力[6-10]。该方法通过训练学习来建立已有的自变量和与之对应的因变量之间的耦合关系。Deng等[11]基于油池大小、燃料深度和燃烧时间等参数特征,利用遗传算法结合反向传播神经网路预测了不同时间段隧道油池火灾燃烧的质量损失速率。Saeed等[12]从烟雾和热量中提取特征,然后应用卷积神经网络算法进行火灾探测。刘全义等[13]选取燃烧产物中质量浓度迅速升高的粒径小于10μm的颗粒物(particulate matter with particle size below 10μm, PM10)及CO作为分类的特征参数,建立了6种常见的机器学习算法进行火灾探测。上述研究分别根据预测目标选择合适的特征参数,展现了较好的预测效果。
基于目前较成熟且设备价格便宜的温度传感器技术,将火灾中最重要的数据之一——温度数据——作为机器学习模型的输入,进行火灾参数的预测,已有一些相关的尝试性研究。Zhang等[14-16]基于温度时间序列特征建立大型隧道火灾数据库,并搭建了预测隧道火源位置、危险来临时间和温度场等参数的机器学习模型。Hodges等[17]基于温度特征建立转置卷积神经网络预测房间内的温度分布。在已有研究的基础上,本文将温度数据作为机器学习模型的输入,最终输出火灾的热释放速率,同时创新性地引入特征筛选技术,得到对热释放速率预测作用最大的关键位置温度数据。
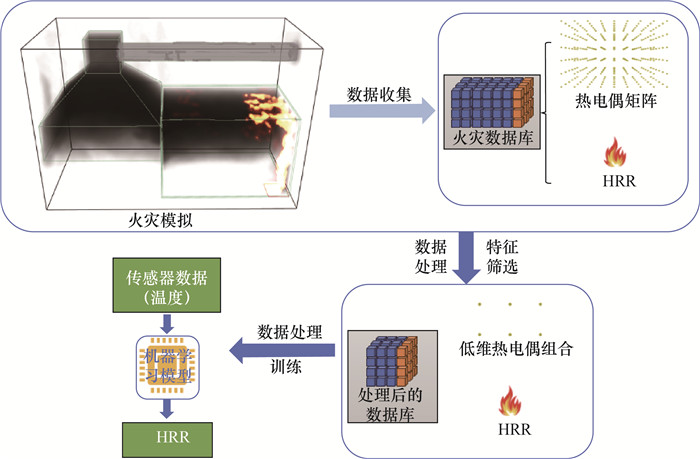
1 预测方法的框架为预测ISO 9705标准房间内火源热释放速率,本文提出了基于机器学习的综合性框架,如图 1所示。首先,使用火灾动力学模拟(fire dynamics simulator, FDS)软件进行火灾模拟,并基于生成的数据建立数据库。其次,通过特征筛选方法,得到低维度的热电偶组合。最后,基于上一步所产生的低维度特征子集,利用机器学习模型进行热释放速率的预测。
|
| 图 1 基于机器学习的综合性框架 |
2 数据生成
人工智能模型的训练需要足量的能反映真实客观世界规律的数据,因此数据样本的全面性非常重要[15]。数据的来源应当是真实火灾试验或者能反映真实火灾场景的火灾模拟两种途径,本文采用基于FDS的火灾模拟来生成火场数据。
2.1 量热仪的FDS建模 2.1.1 火灾场景基于ISO 9705标准,在美国国家标准与技术研究院研发的FDS 6.7版中建立量热仪数值模型[18]。FDS是开源的计算流体力学工具,已经得到了广泛验证,并被大量用于火灾模拟中[19-20]。
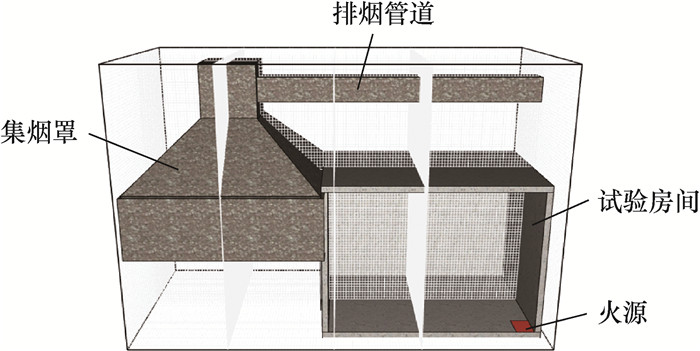
数值模型参照ISO 9705房间尺寸建立:长3.6m、宽2.4m、高2.4m;试验房间的门设在一侧短边墙的中心,尺寸(宽×高)为0.8m×2.0m;其他墙体、地板以及顶板无通风口。试验房间门外正上方安装有锥形集烟罩,集烟罩与排烟管道相连。所建立的模型如图 2所示。
|
| 图 2 ISO 9705量热仪FDS建模图 |
2.1.2 模型设置
为验证所提出的特征筛选和机器学习模型相结合的热释放速率预测方法,本研究设置固定的火灾场景,将火源放置在与门相对角落的地面上,且优先考虑火源表面积、最大热释放速率两个参数。房间的墙壁材料设置为混凝土,排烟风速设置为1m/s,压差为500Pa。形成了60个火灾工况,参数设置如表 1所示。后续研究可以考虑更多的参数,如火源的位置、火源的几何形状等,从而扩大数据库。
| 参数 | 取值 |
| 火源表面积/m2 | 0.16, 0.25, 0.36, 0.49, 0.64, 0.81 |
| 最大热释放速率/MW | 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 |
火源表面积不同会导致燃烧面积不同,影响释放和传递的热量、热辐射损失量等。最大热释放速率反映了火源本身的燃烧强度。
假定房间内火灾模型中火源使用非稳态火中的t2火,具体公式为[21]
| $ \mathrm{HRR}=\alpha t^2 . $ | (1) |
其中:HRR为热释放速率;α为火灾增长率,这里按照超快速火取值0.1878[22];t为燃烧时间。
网格大小是影响FDS建模的准确性和计算速度的关键参数。无量纲式D*/δx是评估网格设置质量的标准,其中D*为火源特征直径,δx为网格尺寸[23]。研究表明,D*/δx的推荐取值范围为4~16[24],故本研究的网格尺寸可取范围是0.0238~0.0952m。因此,本文将火源附近区域,沿X轴、Y轴、Z轴的网格设置为0.05m。
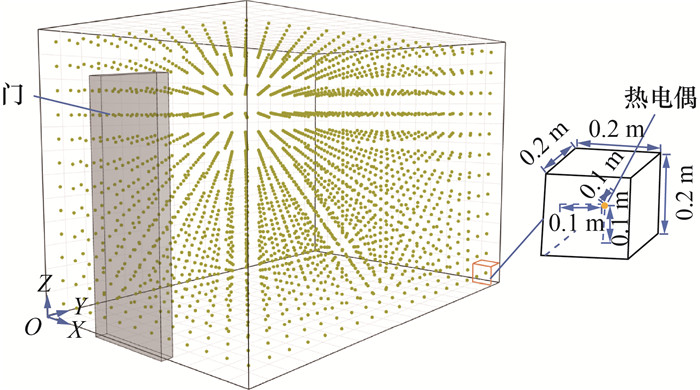
为了获取房间内不同位置的温度数据,如图 3所示,将试验房间内空间进行网格划分,每个网格的大小为0.2m×0.2m×0.2m,在网格中心布置热电偶。本研究受计算资源所限,网格尺寸选取0.2m,下一步的研究中可选取更加精细的网格,以获取与火源热释放速率的预测更加相关的温度特征子集。基于上述传感器布置,每个火灾工况分别生成2632个温度传感器数据。每个工况模拟时间为200s,温度数据生成频率为1Hz。
|
| 图 3 热电偶布置 |
2.2 数据库建立
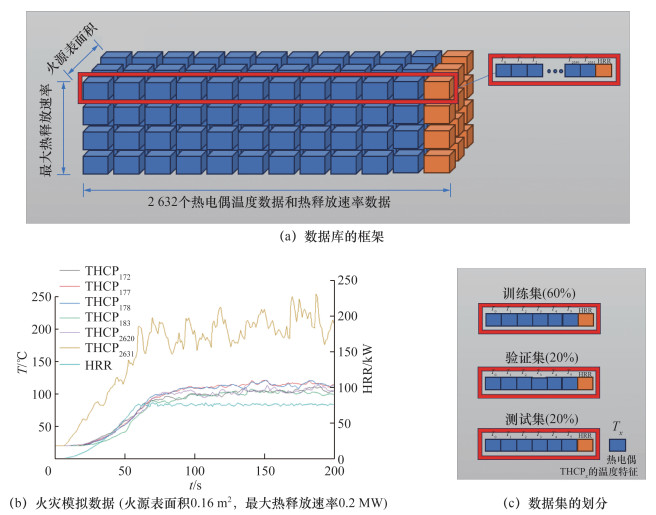
基于FDS模拟结果,生成了一个具有不同火源表面积和最大热释放速率的数据库,以支持机器学习模型的训练。数据库的框架如图 4a所示。样本空间由3个维度组成:1) 火源表面积,包含不同表面积的火源;2) 最大热释放速率,包含不同最大热释放速率的火源;3) 参数数据,包含热电偶温度数据和热释放速率数据,图 4b展示了其中一种工况下6个热电偶温度数据和对应的热释放速率数据。对于每个数据样本,某一时刻n若干热电偶THCP0, THCP1, …, THCPm测量的温度数据储存为机器学习模型的输入信息,因此模型的输入数据可以写为Xn=[T0, T1, …, Tm]。其中:T表示温度,下标1, 2, …, m为热电偶序数。
|
| 图 4 数据库的建立 |
为了训练机器学习模型,所有输入数据都应在数据库中标记预期输出。在本文中,输出是输入数据时刻的热释放速率。因此,模型的输出写为Yn=HRR。
基于上述描述生成的最终数据样本中,每个样本包含该时刻的热电偶温度数据和对应的热释放速率数据,共生成了12060个样本。将样本数据集按照3∶1∶1比例划分为训练集、验证集和测试集。为确保数据划分的随机性和代表性,每种火源表面积随机抽取2个工况的数据样本作为测试数据,如图 4c所示,且保证相同最大热释放速率的工况数量不超过3个。选取的测试数据工况如表 2所示,对应于2412个样本。其余48个工况的数据样本则分别为训练数据和验证数据,对应于9648个样本,并基于五折交叉验证进行分割。
| 序号 | 火源表面积/m2 | 最大热释放速率/kW |
| 1 | 0.16 | 100 |
| 2 | 0.16 | 800 |
| 3 | 0.25 | 100 |
| 4 | 0.25 | 300 |
| 5 | 0.36 | 300 |
| 6 | 0.36 | 1 000 |
| 7 | 0.49 | 200 |
| 8 | 0.49 | 300 |
| 9 | 0.64 | 200 |
| 10 | 0.64 | 800 |
| 11 | 0.81 | 600 |
| 12 | 0.81 | 1 000 |
3 特征筛选
特征筛选是删除不相关和冗余特征并选择一小组具有代表性信息特征的过程。特征筛选一直是机器学习和统计学研究的活跃领域[25-26]。本文采用两种基于递归特征消除(recursive feature elimination, RFE)法的特征筛选方法,从2632个热电偶温度特征中筛选出6个特征。通过特征筛选,可以尝试通过布置较少的热电偶来获取低维度的温度特征集。为了便于描述所筛选出的热电偶的位置,本研究采用图 3中的空间坐标系,即O点为原点(0,0,0),X、Y、Z轴方向如图 3所示。
3.1 递归特征消除法RFE由Guyon等[27]基于支持向量机提出。该方法使用一个基模型来进行多轮训练,每轮训练后,消除若干具有一定权值系数的特征,并基于新的特征集进行下一轮训练。RFE在本文中的实现步骤可概括如下:
步骤1 训练一个机器学习基模型,本研究中基模型分别为最小绝对收缩和选择算子(least absolute shrinkage and selection operator, Lasso)模型、随机森林(random forest, RF)模型;
步骤2 计算不同的热电偶温度数据在回归预测中的重要性;
步骤3 消除重要性较低的热电偶温度数据;
步骤4 重复步骤1至3,直至筛选出最终的热电偶温度数据组合。
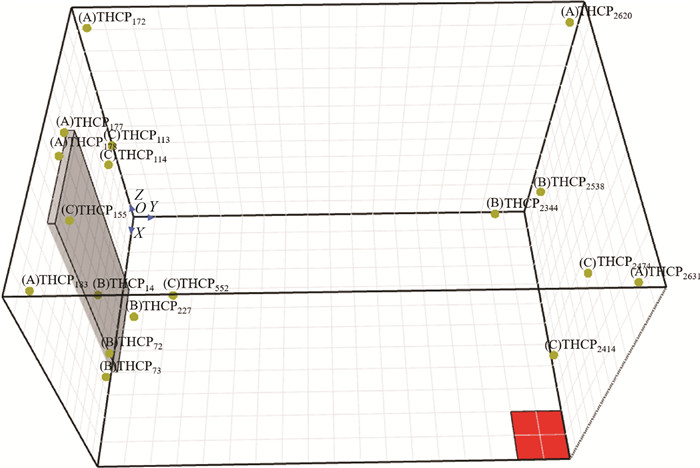
3.2 对照组(A组)为了验证特征筛选出的热电偶温度数据对预测性能的提高作用,本研究设置对照组,即人工选择位于房间关键区域的热电偶。考虑到热电偶在实际火灾场景的测量代表性,在房间顶部设置6个热电偶构成对照组,分别位于房间天花板角落处和门口上方,其分布位置如表 3和图 5所示。
| 热电偶 | THCP172 | THCP177 | THCP178 | THCP183 | THCP2620 | THCP2631 |
| 位置/m | (0.1, 0.1, 2.3) | (1.1, 0.1, 2.3) | (1.3, 0.1, 2.3) | (2.3, 0.1, 2.3) | (0.1, 3.5, 2.3) | (2.3, 3.5, 2.3) |
|
| 图 5 筛选后A、B、C各组热电偶布置 |
3.3 基于Lasso模型的RFE特征筛选(B组) 3.3.1 模型原理
Lasso回归通过构造惩罚函数得到较为精炼的模型[28],训练过程采用正则化线性回归(LR)将对预测贡献最小或无贡献的特征系数降为零,从而实现特征筛选。该模型在高维数据中表现出色[29]。
在本研究的热释放速率预测的特征筛选中,给定有m个热电偶温度数据的特征向量T=[T1, T2, …, Ti, …, Tm],其中Ti为第i个热电偶的温度,取m个热电偶温度数据的线性组合来进行热释放速率的预测,即
| $ f(\boldsymbol{T})=w_1 T_1+w_2 T_2+\cdots+w_i T_i+\cdots+w_m T_m . $ | (2) |
系数w1,w2,…,wm构成系数向量w。
损失函数定义为[28]
| $ \operatorname{loss}(\boldsymbol{w})=\|f(\boldsymbol{T})-\boldsymbol{y}\|+\alpha\|\boldsymbol{w}\| . $ | (3) |
式中: y表示热释放速率真实值,
在原始数据集上利用Lasso回归进行特征筛选,设置参数“max_iter”为10000,同时通过网格搜索选择超参数“alpha”。每轮训练去除一个特征,记该筛选过程为Lasso-RFE。通过特征筛选,得到6个热电偶,其分布位置如表 4和图 5所示。
| 热电偶 | THCP14 | THCP72 | THCP73 | THCP227 | THCP2344 | THCP2538 |
| 位置/m | (1.3, 0.0, 0.7) | (1.7, 0.1, 0.5) | (1.9, 0.1, 0.5) | (1.5, 0.3, 0.7) | (0.1, 3.3, 0.1) | (0.5, 3.5, 0.9) |
3.4 基于RF模型的RFE特征筛选(C组) 3.4.1 模型原理
随机森林(RF)是由多棵决策树集成的机器学习模型,其输出值是模型中所有决策树结果的平均值。
在本文的热释放速率预测中,以房间中获取的热电偶温度数据建立特征向量作为输入,以该特征向量对应的热释放速率作为预测结果,通过训练样本进行拟合得到预测模型。随机森林计算特征重要度的过程如下[30]:
1) 记FDS模拟数据集的每个样本所包含的特征为Tx,x=1,2,…,i,…,m。根据Boostrap自助法从样本集中随机抽取n次,每个子集记为Di,每个子集的剩余样本集即袋外样本集记为Bk,i,k=1,2,…,n。
2) 对于特征Tx,利用式(4)和(5)计算加入噪声干扰前后每个袋外样本集Bk对应的袋外误差,记未加入噪声干扰的袋外误差为ERRBk,加入噪声干扰后的袋外误差为ERR′Bk。
| $ \mathrm{ERR}_{B_k}=\frac{1}{2} \sum\limits_{i=1}^n\left(p_i-{\overset\frown{p}}_i\right)^2, $ | (4) |
| $ \operatorname{ERR}_{B_k}^{\prime}=\frac{1}{2} \sum\limits_{i=1}^n\left(p_i-{\overset\frown{p}}_i^{\prime}\right)^2 . $ | (5) |
其中:pi表示袋外样本集中第i个温度数据对应的HRR真实值;
3) 利用式(6)计算特征Tx对应的重要度。
| $ \text { Feature }_x=\frac{1}{n} \sum\limits_{k=1}^n\left(\mathrm{ERR}_{B_k}-\mathrm{ERR}_{B_k}^{\prime}\right) . $ | (6) |
4) 重复上述步骤2)和3),计算所有特征Tx对应的重要度。
进一步,将所有特征Tx按照重要度由大到小排序,保留重要度靠前的特征,完成特征筛选。
3.4.2 模型应用在原始数据集上利用随机森林模型进行特征筛选。由于数据量较大且随机森林模型训练时间较长,若每轮特征筛选后重新对模型进行调参则需要大量的时间。为节约计算资源和时间,针对原始数据集所建立的随机森林模型的参数“n_estimators”“max_depth”“min_samples_split”“min_samples_leaf”“bootstrap”进行随机调参,得到最佳参数组合,每轮固定采用该调参结果进行特征筛选。每轮训练去除一个特征,记该筛选过程为RF-RFE。通过特征筛选,得到6个热电偶,其分布位置如表 5和图 5所示。
| 热电偶 | THCP113 | THCP114 | THCP2474 | THCP155 | THCP2414 | THCP552 |
| 位置/m | (0.3, 0.1, 1.3) | (0.5, 0.1, 1.3) | (2.1, 3.3, 2.1) | (1.5, 0.1, 1.9) | (2.1, 3.3, 1.1) | (1.7, 0.7, 1.3) |
4 数据预测
本节通过输入3种特征筛选方法得到的低维特征子集(A、B、C组热电偶分别对应数据集A、B、C),研究了LR、K最近邻(K-nearest neighbor, KNN)、轻量级梯度提升机(light gradient boosting machine, LightGBM) 3个代表性机器学习模型对ISO 9705房间内火源热释放速率的预测结果。给定一个训练集{(Xi, Yi)},i=1,2,…,n,n是训练样本数。这些机器学习模型的输入是X=[Tj], j=1, 2, …, 6,即经过特征筛选得到的6维特征向量,而输出为Y,即对应时刻的热释放速率。
4.1 模型的评估指标对于机器学习的回归模型,根均方误差(root mean square error, RMSE)和均绝对误差(mean absolute error, MAE)通常用于评估预测结果和真实数据之间的近似程度。此外,决定系数(coefficient of determination, R2)通常用于表征预测值与真实值的拟合度。RMSE、MAE和R2分别定义如下:
| $ \text { RMSE }=\sqrt{\frac{\sum\limits_{i=1}^n\left(y_i^{\text {pre }}-y_i^{\text {exp }}\right)^2}{n}} \text {, } $ | (7) |
| $ \text { MAE }=\frac{\sum\limits_{i=1}^n\left|y_i^{\text {pre }}-y_i^{\text {exp }}\right|}{n} \text {, } $ | (8) |
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(y_i^{\mathrm{pre}}-y_i^{\mathrm{exp}}\right)^2}{\sum\limits_{i=1}^n\left(y_i^{\mathrm{exp}}-\bar{y}\right)^2} . $ | (9) |
其中: n是样本数,yipre是预测值,yiexp是真实值,y是真实值的平均值。
本研究基于RMSE和MAE,使用降低比值δ表示来评估改进后的模型相对于原模型预测性能的提升,δ越高,表明RMSE和MAE降低程度越大,模型预测性能提升越大。
| $ \delta=\frac{E_0-E_1}{E_0} \times 100 \% . $ | (10) |
其中:E1表示改进后的模型的评估指标,E0表示原模型的评估指标。
4.2 线性回归模型 4.2.1 模型原理线性回归(LR)函数f表示将输入变量即热电偶温度数据[T1, T2, …, Ti, …, Tm]映射到输出变量即热释放速率y的函数,
| $ f(\boldsymbol{x})=\theta_0+\theta_1 x_1+\theta_2 x_2+\cdots+\theta_m x_m . $ | (11) |
LR模型需求得系数{θ0, θ1, …, θm}的解,使得函数值尽可能接近热释放速率真实值y。
4.2.2 模型应用使用Pyhton语言环境下的Sklearn包的LinearRegression模型,建立基于LR的热释放速率预测模型。采用数据集A、B、C分别训练后得到3个不同的LR模型,然后输入测试数据得到预测结果。计算所得结果的RMSE、MAE、R2,并进行比较,如表 6所示。
| 数据集 | RMSE/kW | MAE/kW | R2 |
| 数据集A(人工) | 61.82 | 50.58 | 0.94 |
| 数据集B(Lasso-RFE) | 42.64 | 27.84 | 0.97 |
| 数据集C(RF-RFE) | 50.98 | 40.06 | 0.96 |
表 6显示了不同特征子集输入训练后的LR模型预测性能:相较于对照组,即人工选择的数据集A,基于Lasso模型RFE筛选后的数据集B训练的LR模型预测性能最佳,预测结果的RMSE和MAE分别降低了31.02%和44.95%,决定系数R2增加了3%。这主要是因为基于Lasso模型RFE筛选得到线性相关性更高的特征子集,该高线性相关性的特征子集用于训练,线性回归模型学习到了更加准确的权重系数{θ0, θ1, …, θm},从而提升预测性能,数据集B和数据集C的预测结果也验证了特征筛选对LR模型预测性能有重要影响。
4.3 K最近邻模型 4.3.1 模型原理K最近邻(KNN)不仅适用于分类,也可用于回归问题。该算法通过找出某个样本的K个最近邻居,并将这些邻居在某些属性上的平均值赋予该样本,从而获得该样本对应属性的值[31]。
4.3.2 模型应用使用Python语言环境下Sklearn包的KNeighborsRegressor模型,建立基于KNN的热释放速率预测模型,通过网格搜索确定最佳参数。KNN需要调节的参数为“n_neighbors”,该参数是KNN模型中的K值,即回归中数据预测所需的参考样本的数量。其他参数采用默认设置。
3个数据集分别训练后得到3个不同的KNN模型,输入测试数据得到预测结果。计算所得结果的RMSE、MAE、R2并进行比较,如表 7所示。
| 数据集 | RMSE/kW | MAE/kW | R2 |
| 数据集A(人工) | 44.99 | 29.27 | 0.970 2 |
| 数据集B(Lasso-RFE) | 57.03 | 33.44 | 0.952 2 |
| 数据集C(RF-RFE) | 30.06 | 18.35 | 0.986 7 |
表 7显示了不同特征子集输入训练后的KNN模型预测性能:相较于对照组,基于RF模型RFE筛选后的数据集C训练的KNN模型预测性能最佳,预测结果的RMSE和MAE分别减少了33.18%和37.30%,决定系数R2提升了1.65%。这主要是因为基于RF模型的RFE选择了对热释放速率预测作用更大的特征子集,使得该特征子集中相似的训练样本在特征空间中更加接近,基于该数据集KNN算法能够更好地反映自变量与目标变量的真实关系,从而预测效果优于其他数据集。
4.4 LightGBM模型 4.4.1 模型原理梯度提升决策树(gradient boosting decision tree,GBDT)是一种机器学习模型,其主要思想是利用多棵弱回归树(决策树)迭代训练得到最优模型,通过将弱学习器线性组合得到强学习器[32],
| $ F(\boldsymbol{x})=\sum\limits_{m=1}^M f_m(\boldsymbol{x}) . $ | (12) |
其中:F(x)为最终输出,fm(x)为第m个弱回归树的输出。
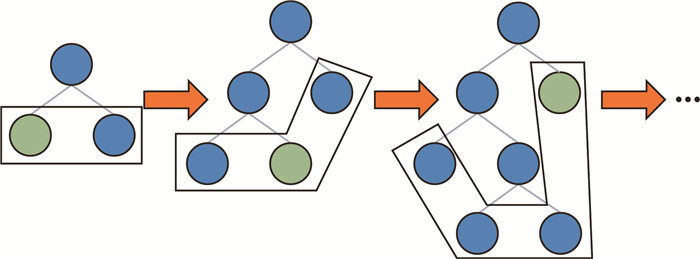
LightGBM是一个用于实现GBDT的框架,相较于原始的GBDT方法,具有更快的训练速度和更高的效率。LightGBM相对于传统的GBDT算法的主要改进在于引入了直方图算法和采用了基于Leaf-wise的深度限制生长策略[33]。直方图算法将连续数据划分成k个整数间隔,形成宽度为k的直方图;在遍历过程中,将离散化后的值累计在直方图中作为索引,然后在直方图中搜索最优的决策树分裂点。带有深度限制的Leaf-wise生长策略,每次从当前所有叶子节点中选择具有最大分裂增益的叶子节点进行分裂,如图 6所示。其中:灰框内圆点为当前所有叶子节点,绿色圆点为当前所有叶子节点中切分增益最大的叶子节点。这个过程不断循环,直至达到设定的深度限制。Leaf-wise策略具有很高的效率,并且可以通过限制树的深度和叶子节点的数量,降低模型的复杂度,有效防止过拟合的发生。
|
| 图 6 基于Leaf-wise的生长策略 |
LightGBM具有准确率高、训练速度快、支持分布式计算、内存占用率低等优点,因此被广泛用于大规模数据集的回归预测[33-34]。
4.4.2 模型应用使用Python语言环境下的LightGBM包,建立基于LightGBM的热释放速率预测模型。LightGBM的参数较为复杂,且训练时间较长,故先采用随机调参确定参数范围,然后利用网格搜索找到最佳参数。表 8为需要调节的主要参数。
| 参数 | 参数说明 |
| n_estimators | 基学习器数量,即迭代次数 |
| max_depth | 树的最大深度 |
| min_child_samples | 最小子节点的所有样本权重总和 |
| learning_rate | 学习率,即梯度提升步长 |
| reg_alpha | L1正则,用于控制模型的复杂度 |
| reg_lamba | L2正则,用于控制模型的复杂度 |
3个数据集分别训练后得到3个不同的LightGBM模型,迭代次数分别为88、615、111。输入测试数据得到预测结果,计算所得结果的RMSE、MAE、R2并进行比较,如表 9所示。
| 数据集 | RMSE/kW | MAE/kW | R2 |
| 数据集A(人工) | 44.69 | 31.40 | 0.970 6 |
| 数据集B(Lasso-RFE) | 28.71 | 18.37 | 0.987 8 |
| 数据集C(RF-RFE) | 23.89 | 15.49 | 0.991 6 |
表 9显示了不同特征子集输入训练后的LightGBM模型预测性能: 相较于对照组,数据集C训练的LightGBM模型预测性能最佳,预测结果的RMSE和MAE分别减少了46.54%和50.66%,决定系数R2提升了2.1%。这是由于基于RF模型的RFE选择了对目标值预测作用更强的特征子集,LightGBM的决策树可以充分利用这些特征的交互信息。同时,LightGBM通过Leaf-wise策略选择信息增益最大的特征,并控制树深度防止过拟合,更好地学习了这些温度特征与热释放速率之间的复杂非线性关系,从而提升了预测的准确率。
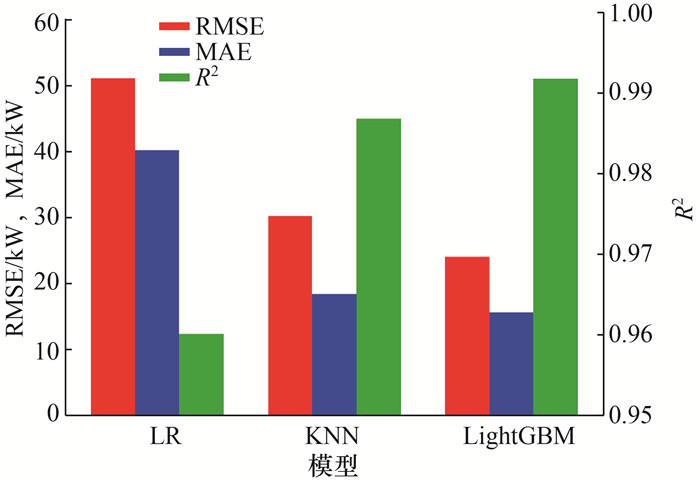
4.5 不同模型的比较由4.2.2、4.3.2和4.4.2节的结果比较可得:基于RF模型的RFE筛选得到最优的热电偶组合,即该热电偶组合所测得数据组成的数据集,特征表达合理,能够满足训练需求,使模型取得更好的性能。图 7为该数据集的3种模型预测性能的对比。
|
| 图 7 基于数据集C的不同模型预测性能对比 |
从图 7可以看出,LightGBM模型取得了最佳的RMSE和MAE值,分别为23.89kW和15.49kW,说明该模型的预测值与实际观测值的偏差最小。从R2指标看,LightGBM模型达到了0.9916的最高值,接近于1,表明该模型拟合能力非常强。这主要是由于训练集中温度数据和热释放速率数据具有复杂的非线性关系,相较于KNN模型和LR模型,LightGBM的直方图算法和深度可控的Leaf-wise生长策略能够充分发挥其优势。
此外,KNN模型的预测误差低于LR模型,RMSE和MAE分别减少了41.03%和54.19%,决定系数R2提升了2.67%。这是由于KNN算法本身的非线性和非参数假设使得该算法能建模目标变量更为复杂和灵活的非线性关系,因此训练后的KNN模型更好地拟合了目标变量中包含的非线性关系。
综上所述,LightGBM模型在该预测任务中拟合程度最高,预测误差最小,具有强大的非线性拟合能力。LR和KNN作为非迭代算法,具有较快的训练速度,但预测性能较低。相比之下,LightGBM是一种基于梯度提升的迭代算法,在大型和高维数据集上表现出更高的预测精度。由于通过温度特征预测热释放速率是个复杂的非线性预测问题,数据特征之间存在复杂的高阶交互,KNN模型无法捕捉这些交互关系,而LightGBM作为树基模型,可以分裂特征来捕捉交互特征和非线性关系,预测效果最佳。故后续若在算法模型方面进行改进,可以继续采用LightGBM和XGBoost等树基模型,也可考虑深度学习模型,如多层全连接网络、卷积神经网络等,以实现复杂映射关系的拟合。
5 结论本研究提出了一种基于机器学习的综合性框架对火源热释放速率进行预测。首先通过FDS火灾模拟获取热电偶温度数据,然后将特征筛选(Lasso-RFE和RF-RFE)和预测模型(LR、KNN和LightGBM)与热释放速率预测结合起来。
研究结果表明,基于随机森林的递归特征消除算法(RF-RFE)筛选得到的特征子集训练后的LightGBM模型预测结果的RMSE和MAE分别为23.89kW和15.49kW,决定系数R2为0.991 6,相较于人工特征子集训练LightGBM模型所得的预测结果,RMSE和MAE分别降低46.54%和50.66%,决定系数R2提升了2.1%,验证了该特征筛选方法较人工特征选择可显著提高预测精度。本文提出的基于机器学习的综合性框架具有理论和实践价值,为预测热释放速率参数开拓了有效途径。后续研究可通过构建更全面的数据库、增加其他特征参数或探索算法组合以进一步提高模型的预测性能。
| [1] |
BABRAUSKAS V, PEACOCK R D. Heat release rate: The single most important variable in fire hazard[J]. Fire Safety Journal, 1992, 18(3): 255-272. DOI:10.1016/0379-7112(92)90019-9 |
| [2] |
程远平, 陈亮, 张孟君. 火灾过程中火源热释放速率模型及其实验测试方法[J]. 火灾科学, 2002, 11(2): 70-74. CHENG Y P, CHEN L, ZHANG M J. The models and experimental testing method of heat release rate of fuel during the development of fire[J]. Fire Safety Science, 2002, 11(2): 70-74. (in Chinese) |
| [3] |
THORNTON W M.XV. The relation of oxygen to the heat of combustion of organic compounds[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1917, 33(194): 196-203. DOI:10.1080/14786440208635627 |
| [4] |
HUGGETT C. Estimation of rate of heat release by means of oxygen consumption measurements[J]. Fire and Materials, 1980, 4(2): 61-65. DOI:10.1002/fam.810040202 |
| [5] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 火灾试验表面制品的实体房间火试验方法: GB/T 25207—2010[S]. 北京: 中国标准出版社, 2010. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Fire tests: Full-scale room test for surface products: GB/T 25207—2010[S]. Beijing: Standards Press of China, 2010. (in Chinese) |
| [6] |
孙利民, 尚志强, 夏烨. 大数据背景下的桥梁结构健康监测研究现状与展望[J]. 中国公路学报, 2019, 32(11): 1-20. SUN L M, SHANG Z Q, XIA Y. Development and prospect of bridge structural health monitoring in the context of big data[J]. China Journal of Highway and Transport, 2019, 32(11): 1-20. (in Chinese) |
| [7] |
乔莹莹. 基于数值预测的机器学习相关算法综述[J]. 安阳工学院学报, 2017, 16(4): 71-74. QIAO Y Y. Summarization of machine learning based on numerical prediction[J]. Journal of Anyang Institute of Technology, 2017, 16(4): 71-74. (in Chinese) |
| [8] |
林岚, 王婧璇, 付振荣, 等. 脑老化中脑年龄预测模型研究综述[J]. 生物医学工程学杂志, 2019, 36(3): 493-498. LIN L, WANG J X, FU Z R, et al. A review on brain age prediction in brain ageing[J]. Journal of Biomedical Engineering, 2019, 36(3): 493-498. (in Chinese) |
| [9] |
高超, 林红蕾, 胡海清, 等. 我国林火发生预测模型研究进展[J]. 应用生态学报, 2020, 31(9): 3227-3240. GAO C, LIN H L, HU H Q, et al. A review of models of forest fire occurrence prediction in China[J]. Chinese Journal of Applied Ecology, 2020, 31(9): 3227-3240. (in Chinese) |
| [10] |
吴浩, 牛风雷. 高温球床辐射传热中的机器学习模型[J]. 清华大学学报(自然科学版), 2023, 63(8): 1213-1218. WU H, NIU F L. Machine learning model of radiation heat transfer in the high-temperature nuclear pebble bed[J]. Journal of Tsinghua University (Science and Technology), 2023, 63(8): 1213-1218. DOI:10.16511/j.cnki.qhdxxb.2023.25.015 (in Chinese) |
| [11] |
DENG L, SHI C L, LI H R, et al. Prediction of energy mass loss rate for biodiesel fire via machine learning and its physical modeling of flame radiation evolution[J]. Energy, 2023, 275: 127388. DOI:10.1016/j.energy.2023.127388 |
| [12] |
SAEED F, PAUL A, HONG W H, et al. Machine learning based approach for multimedia surveillance during fire emergencies[J]. Multimedia Tools and Applications, 2020, 79(23-24): 16201-16217. DOI:10.1007/s11042-019-7548-x |
| [13] |
刘全义, 朱博, 邓力, 等. 基于机器学习的双参数火灾探测方法[J]. 中国安全科学学报, 2022, 32(5): 90-96. LIU Q Y, ZHU B, DENG L, et al. Double parameters fire detection method based on machine learning[J]. China Safety Science Journal, 2022, 32(5): 90-96. (in Chinese) |
| [14] |
WU X Q, ZHANG X N, HUANG X Y, et al. A real-time forecast of tunnel fire based on numerical database and artificial intelligence[J]. Building Simulation, 2022, 15(4): 511-524. DOI:10.1007/s12273-021-0775-x |
| [15] |
ZHANG X N, WU X Q, PARK Y, et al. Perspectives of big experimental database and artificial intelligence in tunnel fire research[J]. Tunnelling and Underground Space Technology, 2021, 108: 103691. DOI:10.1016/j.tust.2020.103691 |
| [16] |
WU X Q, PARK Y, LI A, et al. Smart detection of fire source in tunnel based on the numerical database and artificial intelligence[J]. Fire Technology, 2021, 57(2): 657-682. DOI:10.1007/s10694-020-00985-z |
| [17] |
HODGES J L, LATTIMER B Y, LUXBACHER K D. Compartment fire predictions using transpose convolutional neural networks[J]. Fire Safety Journal, 2019, 108: 102854. DOI:10.1016/j.firesaf.2019.102854 |
| [18] |
MCGRATTAN K B, MCDERMOTT R, WEINSCHENK C. Fire dynamics simulator technical reference guide volume 1: Mathematical model[EB/OL]. (2021-11-20)[2023-03-14]. https://www.nist.gov/publications/fire-dynamics-simulator-technical-reference-guide-volume-1-mathematical-model.
|
| [19] |
杨晓菡, 何学超, 邓玲. ISO 9705房间实体火灾试验及FDS模拟研究[J]. 消防科学与技术, 2016, 35(7): 920-924. YANG X H, HE X C, DENG L. Research of ISO 9705 room fire test and FDS simulation[J]. Fire Science and Technology, 2016, 35(7): 920-924. (in Chinese) |
| [20] |
朱五八. 不同通风状况下典型软垫家具火灾特性研究[D]. 合肥: 中国科学技术大学, 2007. ZHU W B. The study on effect of ventilation on fire behavior of typical upholstered furniture[D]. Hefei: University of Science and Technology of China, 2007. (in Chinese) |
| [21] |
DRYSDALE D. An introduction to fire dynamics[M]. 3rd ed. New York, USA: John Wiley & Sons, 2011.
|
| [22] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 消防安全工程第4部分: 设定火灾场景和设定火灾的选择: GB/T 31593.4—2015[S]. 北京: 中国标准出版社, 2015. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Fire safety engineering Part 4: Selection of design fire scenarios and design fires: GB/T 31593.4—2015[S]. Beijing: Standards Press of China, 2015. (in Chinese) |
| [23] |
MCGRATTAN K, HOSTIKKA S, FLOYD J, et al. Fire dynamics simulator user's guide[EB/OL]. (2021-11-20) [2023-03-14]. https://pages.nist.gov/fds-smv/manuals.html.
|
| [24] |
BAUM H R, MCCAFFREY B J. Fire induced flow field-theory and experiment[J]. Fire Safety Science, 1989, 2: 129-148. DOI:10.3801/IAFSS.FSS.2-129 |
| [25] |
YU L, LIU H. Efficient feature selection via analysis of relevance and redundancy[J]. The Journal of Machine Learning Research, 2004, 5(12): 1205-1224. |
| [26] |
KOHAVI R, JOHN G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1-2): 273-324. DOI:10.1016/S0004-3702(97)00043-X |
| [27] |
GUYON I, WESTON J, BARNHILL S, et al. Gene selection for cancer classification using support vector machines[J]. Machine Learning, 2002, 46(1-3): 389-422. |
| [28] |
TIBSHIRANI R. Regression shrinkage and selection via the Lasso: A retrospective[J]. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2011, 73(3): 273-282. DOI:10.1111/j.1467-9868.2011.00771.x |
| [29] |
李根, 邹国华, 张新雨. 高维模型选择方法综述[J]. 数理统计与管理, 2012, 31(4): 640-658. LI G, ZOU G H, ZHANG X Y. Model selection for high-dimensional data: A review[J]. Journal of Applied Statistics and Management, 2012, 31(4): 640-658. (in Chinese) |
| [30] |
VERIKAS A, GELZINIS A, BACAUSKIENE M. Mining data with random forests: A survey and results of new tests[J]. Pattern Recognition, 2011, 44(2): 330-349. DOI:10.1016/j.patcog.2010.08.011 |
| [31] |
张晓利, 陆化普. 非参数回归方法在短时交通流预测中的应用[J]. 清华大学学报(自然科学版), 2009, 49(9): 1471-1475. ZHANG X L, LU H P. Non-parametric regression and application for short-term traffic flow forecasting[J]. Journal of Tsinghua University (Science and Technology), 2009, 49(9): 1471-1475. (in Chinese) |
| [32] |
曹莹, 苗启广, 刘家辰, 等. AdaBoost算法研究进展与展望[J]. 自动化学报, 2013, 39(6): 745-758. CAO Y, MIAO Q G, LIU J C, et al. Advance and prospects of AdaBoost algorithm[J]. Acta Automatica Sinica, 2013, 39(6): 745-758. (in Chinese) |
| [33] |
KE G L, MENG Q, FINLEY T, et al. LightGBM: A highly efficient gradient boosting decision tree[C]//31st Conference on Neural Information Processing Systems. Long Beach, USA: NIPS, 2017: 3146-3154.
|
| [34] |
FAN J L, MA X, WU L F, et al. Light gradient boosting machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data[J]. Agricultural Water Management, 2019, 225: 105758. DOI:10.1016/j.agwat.2019.105758 |



