2. 南京工业大学 安全科学与工程学院, 南京 211800
2. College of Safety Science and Engineering, Nanjing Tech University, Nanjing 211800, China
城市是污染物泄漏等危险事件的多发地区,研究污染物在城市的扩散规律有助于应对紧急泄漏突发事故。城市内部的建筑群会改变流场结构,使得污染物的分布更加复杂,因此有必要开展建筑物影响下的污染物扩散[1]研究。计算流体力学(com-putational fluid mechanics, CFD)是一种常见的污染物扩散模拟方法,然而高计算成本限制了其应用。对于城市社区规模的突发泄漏事件(例如,有毒气体泄漏、气溶胶排放),有必要短时间内提供关于污染物扩散的信息以及对可能危害的评估,为快速应急决策提供依据[2]。因此,亟需开发一种快速、高精度、低计算成本的方法来模拟城市建筑物周围的污染物扩散。
为了快速计算大量建筑周围污染物扩散的浓度场,学者们结合Markov链、机器学习等方法提出了多种模型。其中,响应因子法(response factor method, RFM)[3-5]计算室内浓度场和温度场时表现优良且高效,在空调负荷计算中被广泛应用,近年来引起了学界的普遍关注。浓度响应因子法的原理是:当流场处于稳态时,污染物的对流-扩散方程是线性的,输入函数与脉冲响应之间的卷积积分可用于计算线性系统的输出,因此利用CFD计算有限时间脉冲释放污染物对应的响应因子,并对响应因子进行卷积计算,可以获得准确的污染物浓度分布。Ishida等[6]首先将建筑冷负荷计算中常用的响应因子法应用于污染物扩散,提出了瞬态浓度计算方法,并考虑了空调回风的影响,较好地计算了室内污染物浓度的分布。Hiyama等[7-8]将浓度响应因子法集成到流动网络模型中模拟三维瞬态污染物扩散,证明了其有效性,并将该方法扩展到热模拟。此后,一些学者也将浓度响应因子法应用到污染物反演问题上。Zhang等[9]和Lei等[10]分别提出了一种结合Tikhonov正则化和最小二乘优化的反问题建模过程,利用浓度响应因子和热响应因子加快三维腔内的释放速率的计算,结果均表明该方法可以较好地反演室内环境中污染源和热源的释放速率。Liu等[11]将浓度响应因子法与Tikhonov正则化方法结合,对多隔间建筑内的污染物源强度进行反演计算。Hu等[12]将浓度响应因子法与Markov链模型耦合,以二维等温流场和三维通风室流场为例,针对不同污染源类型和释放强度进行计算,验证了该方法对空气污染物传输模拟较为准确。浓度响应因子法的计算负荷远低于直接利用CFD求解组分方程的计算负荷,因此便于进行大量假设事故场景的模拟。
目前浓度响应因子法的应用场景主要在室内,如果将该方法用于计算量更大的城市环境,能显著提高效率。Zhou等[13]将浓度响应因子法应用在室外环境中,与Markov链和深度神经网络模型结合反演污染源位置和强度,发现与简单二维室内环境相比,源位置准确率从83%下降到36%。这是因为建筑周围的流场结构较为复杂,有空腔区、尾流区等,流速和湍流强度也有明显变化,使得浓度分布非常复杂。
此外,在实际情况中,污染源的泄漏速率通常是未知的和暂时的。例如,化学气体的泄漏率往往随时间衰减。因此,本文将浓度响应因子法应用到室外污染物扩散模拟中,利用典型建筑结构的风洞实验数据验证模型的可靠性,并与CFD瞬态模拟方法对比,分析了随时间变化的污染源对该方法准确性的影响。
1 研究方法根据组分控制方程式(1),当污染源位置固定时,在稳态流场下各点浓度与污染源释放强度之间为线性关系,由此可以得到式(2)。
| $ \frac{\partial C}{\partial t}+\frac{\partial C u_{i}}{\partial x_{i}} =\frac{\partial}{\partial x_{j}}\left(v_{t} \frac{\partial C}{\partial x_{i}}\right)+q . $ | (1) |
| $ \boldsymbol{C} =\boldsymbol{A} \boldsymbol{q} . $ | (2) |
其中:C为气体浓度,t为时间,ui为速度分量,xi为空间坐标,ρ为空气密度,vt为湍流动力黏度,q为污染源某时刻的释放强度,下标i=1、2、3分别表示任意点坐标的x、y、z分量。C为浓度变化时间序列,A为污染源释放强度与浓度分布关系的组分传递矩阵,q为污染源释放强度的时间序列。
由线性系统的叠加特性可知,任意的输入函数可以分解为基元函数的线性组合。假设脉冲函数δ(t)为基元函数,则污染源释放函数可以表示为
| $ \begin{equation*} C(t)=\boldsymbol{A} \cdot q(t)=\int_{0}^{t} q(\tau)[\boldsymbol{A} \delta(t-\tau)] \mathrm{d} \tau . \end{equation*} $ | (3) |
式中: C(t)为t时刻某点的浓度,q(t)为t时刻污染源释放强度,而q(τ)为0~t间某一时刻的污染源释放强度,Aδ(t-τ)为脉冲释放污染物在t-τ时刻某点的浓度。将该卷积公式离散可以得到式(4),矩阵形式如式(5)所示。
| $ C_{n}=\sum\limits_{k=0}^{n} q_{k} F_{n-k}= \\ q_{0} F_{n}+q_{1} F_{n-1}+\cdots+q_{k} F_{n-k}+\cdots+q_{n} F_{0} . $ | (4) |
| $\left[\begin{array}{c} C_{0} \\ C_{1} \\ \vdots \\ C_{n} \end{array}\right]=\left[\begin{array}{cccc} F_{0} & 0 & \cdots & 0 \\ F_{1} & F_{0} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ F_{n} & F_{n-1} & \cdots & F_{0} \end{array}\right] \cdot\left[\begin{array}{c} q_{0} \\ q_{1} \\ \vdots \\ q_{n} \end{array}\right] . $ | (5) |
其中:Cn是第n个时间步的浓度,[q0, …, qk, …, qn]T为释放强度的时间序列,[F0, …, Fk, …, Fn]T为浓度响应因子的时间序列。由此可知,求解浓度响应因子的时间序列是构建组分传递矩阵A的核心。
基于浓度响应因子法对建筑物周围的污染物扩散进行快速数值模拟分为以下步骤:
1) 构建计算域,稳态求解流场;
2) 瞬态求解脉冲污染物释放下的浓度场,获得空间各点的浓度响应时间曲线,根据此序列构建组分传递矩阵A;
3) 由组分传递矩阵A和释放强度的时间序列计算得到任意时刻的浓度。
针对已知污染源位置的各种可能泄漏场景,浓度响应因子法只需利用一次脉冲释放获得的浓度响应因子矩阵进行卷积,即可获得各点浓度;相比于利用CFD多次模拟,可以大大降低计算量,节省计算资源和时间。
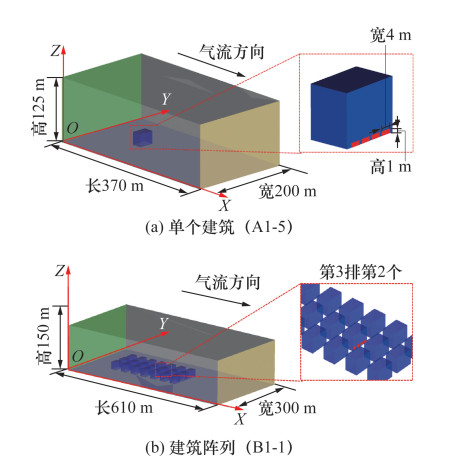
2 算例分析 2.1 场景描述为了检验CFD模拟的准确性,本文利用CFD软件ANSYS Fluent[14]对德国汉堡大学的风洞实验(http://www. mi. unihamburg. de/Category-A. 628. 0.html,下文简称CEDVAL)中的2个例子进行数值模拟。图 1a为实验编号A1-5的单个建筑物;图 1b为实验编号B1-1的3×7个建筑的阵列,每个建筑的尺寸均为30 m×20 m×25 m。位于建筑物背风侧近地面处有4个污染源出口,每个出口宽为4 m、高为1 m,释放速率为0.03 m/s。其中,建筑阵列的污染源在第3排中间建筑。在该风洞实验中,缩尺比为1∶200,结果采用归一化质量浓度K。
| $\begin{equation*} K=\frac{C \cdot U_{\mathrm{ref}} H^{2}}{Q_{\mathrm{s}}} . \end{equation*} $ | (6) |
|
| 图 1 算例的计算域 |
其中: C为测点的污染物浓度,Uref为实验中大气边界层顶部的速度6.36 m/s,H为建筑模型的高度25 m,Qs为泄漏源的污染物质量流量。
2.2 CFD模拟设置CFD数值模拟基于Realizable k-ε模型[15],采用二阶迎风格式以及SIMPLE算法。数值模拟边界条件设置如表 1所示。入口为指数边界层速度入口,出口为自由流出,顶部、两侧、地面与建筑物表面均采用无滑移壁面,污染源的质量流量与风洞实验一致。计算过程包括2个阶段:1) 稳态计算。在无污染物释放情景下获得稳定的流场,作为后续计算的初始条件。2) 瞬态计算。设置污染源为质量流量入口边界,获得浓度场。
| 边界 | 条件 |
| 入口 | 速度入口 |
| 出口 | 自由流出 |
| 顶部、两侧、地面、建筑物表面 | 无滑移壁面 |
| 污染源 | 阶段1无滑移壁面;阶段2质量流量入口 |
在单个建筑的模拟域中,参考COST[16]和AIJ[17]指南的建议,来流边界位于建筑物上游4H,流出边界位于建筑物的下游10H,两侧边界距离源建筑中心6H,顶部边界距地面5H。计算域尺寸为370 m×200 m×125 m,网格数为28万个。网格为正六面体网格,靠近建筑物的最内层的网格尺寸为1 m,最外层为5 m。在建筑阵列的模拟域中,参数设置与单个建筑基本相同,顶部边界距地面6H,计算域尺寸为610 m×300 m×150 m,网格数为236万个。
设置污染物的性质与空气相同,且流量较低,源动量效应可以忽略不计;气体浓度的输送近似认为是被动的,不影响流场。
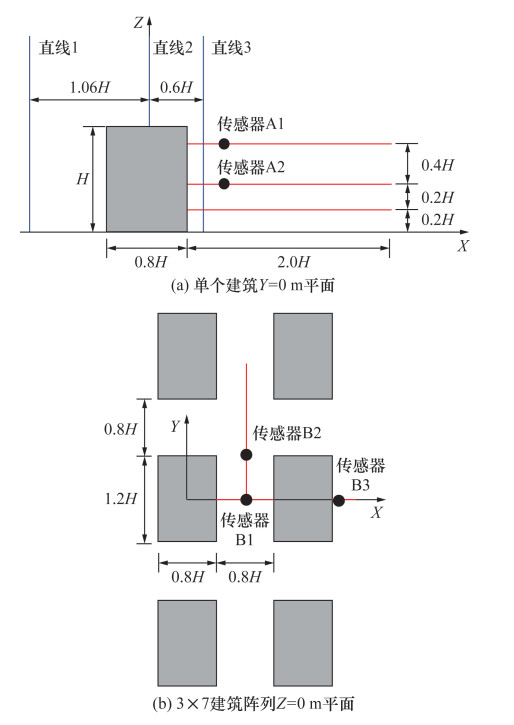
图 2为选取的传感器位置示意图。图 2a为单个建筑场景,在3条红线处共选取了230个传感器点,其中两个黑色实心点为建筑后侧不同高度的代表点,传感器A1坐标(0.8H, 0 m, 0.4H),传感器A2坐标(0.8H, 0 m, 0.8H)。图 2b为3×7建筑阵列场景,在两条红线处共选取了218个传感器点,其中3个黑色实心点为代表点,传感器B1坐标(0.8H, 0 m, 0.8H),传感器B2坐标(0.8H, 0.6H, 0.8H),传感器B3坐标(2H, 0 m, 0.8H)。
|
| 图 2 传感器布置方式 |
2.3 CFD模型验证
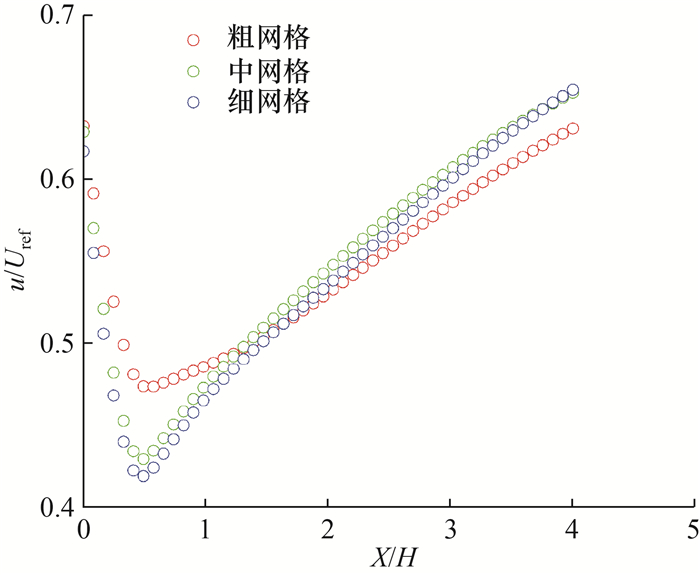
采用CEDVAL风洞实验数据验证所建立的CFD模型计算的准确性。为了保证模拟结果不受网格尺寸大小的影响,对单个建筑情况下3种网格尺寸大小进行无关性验证,粗、中、细3种网格划分下总网格数分别为67 516、284 250和953 533。图 3是高度为30 m沿中心线的无量纲速度图。可以看出,中网格和细网格的结果基本相同,因此本文选择中网格进行模拟。
|
| 图 3 网格无关性验证 |
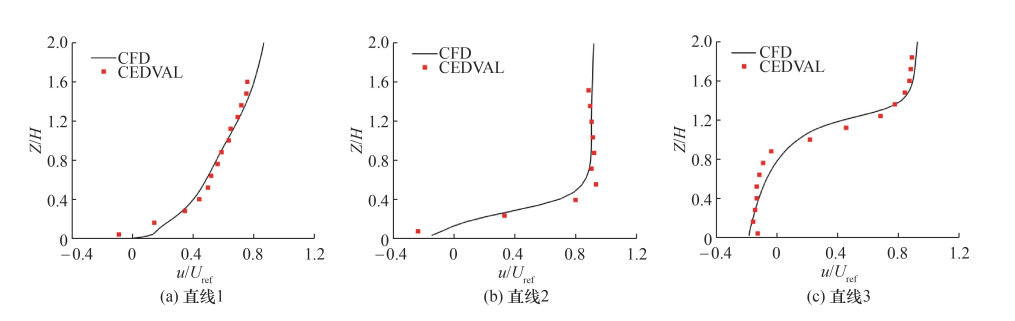
图 4是单个建筑在Y=0平面CFD数值模拟结果与风洞实验的速度对比。其中:图 4a是建筑前的直线1处(X=-1.06H)的结果对比,图 4b是建筑上方的直线2处(X=0 m)的结果对比,图 4c是建筑后侧的直线3处(X=0.6H)的结果对比。这3条直线即图 2中的蓝线。可以看出,数值模拟与风洞实验结果比较吻合,从计算域入口至建筑后侧处的剖面风速没有发生显著变化。
|
| 图 4 CFD数值模拟结果与风洞实验的速度对比 |
2.4 浓度响应因子法参数设置
为了研究在不同污染源释放场景下浓度响应因子法的准确性,分别使用CFD瞬态模拟方法和浓度响应因子法模拟了3种污染物泄漏场景,如图 5所示。设定释放时间为1 500 s,释放函数分别为稳定释放(1 kg/s)、周期释放((1-cos(π·t/20))kg/s)和三角释放(当t < 200 s时,(0.05t)kg/s)。
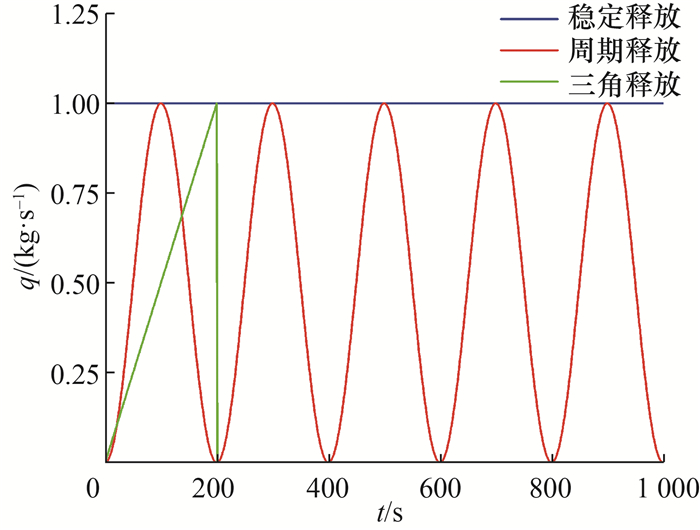
|
| 图 5 污染物释放函数 |
本研究采用CFD瞬态模拟脉冲污染物释放所形成的浓度场,以获得浓度响应因子的时间序列。根据Hu等的研究[12],选择三维空间、面源释放精度最高的矩形脉冲,浓度响应因子求解步长为1 s,总时间步长为1 500 s。图 6a为单个建筑代表点的浓度响应因子时程曲线。可以看出,浓度响应因子随时间变化呈现双峰,差异较大。图 6b为建筑阵列代表点的浓度响应因子时程曲线。可以看出,位于不同排的传感器处浓度响应因子有量级上的差异。由于500 s后的浓度响应因子较低,图 6中仅画出0~500 s的结果。
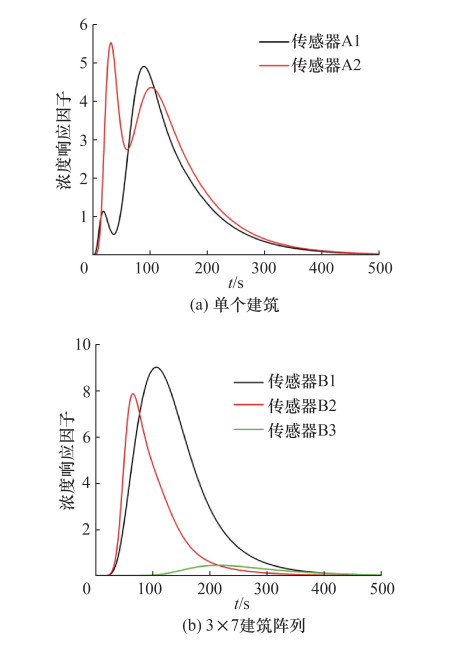
|
| 图 6 浓度响应因子时程曲线 |
3 结果与讨论
为了评估浓度响应因子法的准确性,本文使用以下常用的气体扩散精度统计指标对CFD和浓度响应因子法结果作对比,包括分数偏差(fractional bias,FB)、归一化均方误差(normalized mean squared error,NMSE)、比值在2之间的比率(fraction within a factor of two,FAC2)。对于一个理想的模型,FB和NMSE均为0.0,FAC2为1.0。由Chang等[18]的模拟效果评价实验可知,当|FB| < 0.3、NMSE < 1.5、FAC2>0.5时,模型的模拟表现较好。其中:FB提供了模型对浓度高估或低估的趋势的信息;NMSE提供了每个浓度值的偏差情况;FAC2不受极端数值的影响,直接反映了模拟效果。
| $ \left\{\begin{array}{l} \mathrm{FB}=\frac{\bar{C}_{\mathrm{C}}-\bar{C}_{\mathrm{R}}}{0.5\left(\bar{C}_{\mathrm{C}}+\bar{C}_{\mathrm{R}}\right)}, \\ \mathrm{NMSE}=\frac{\left(\bar{C}_{\mathrm{C}}-\bar{C}_{\mathrm{R}}\right)^{2}}{\bar{C}_{\mathrm{C}} \bar{C}_{\mathrm{R}}}, \\ \mathrm{FAC} 2 \text { 为满足 } 0.5 \leqslant \frac{C_{\mathrm{R}}}{C_{\mathrm{C}}} \leqslant 2.0 \\ \quad \text { 的数值在某一数值集合中的比例. } \end{array}\right. $ | (7) |
其中: CC表示CFD瞬态模拟的浓度,CR表示浓度响应因子法模拟的浓度。
3.1 单个建筑图 7是单个建筑在3种污染源释放场景下,使用浓度响应因子法和CFD瞬态模拟得到的传感器A1处的浓度-时间曲线。从整体来看,3种情况下浓度响应因子法的模拟结果与CFD模拟结果都比较吻合,表明浓度响应因子法能够很好地模拟有较大波动的周期释放和变化速度快的三角释放。在稳定释放场景下,500 s以后浓度没有变化,浓度响应因子法与CFD瞬态模拟结果保持一定的偏差,稳定在2.16%。在周期释放和三角释放场景下,随着时间变化,偏差也在变化,但都在可接受范围内。在此工况下,在Intel Core 2.40 GHz CPU的计算机上使用CFD瞬态模拟需要的运行时间为1 h左右,使用浓度响应因子法需要的运行时间为2 min,约为CFD瞬态模拟的1/30。
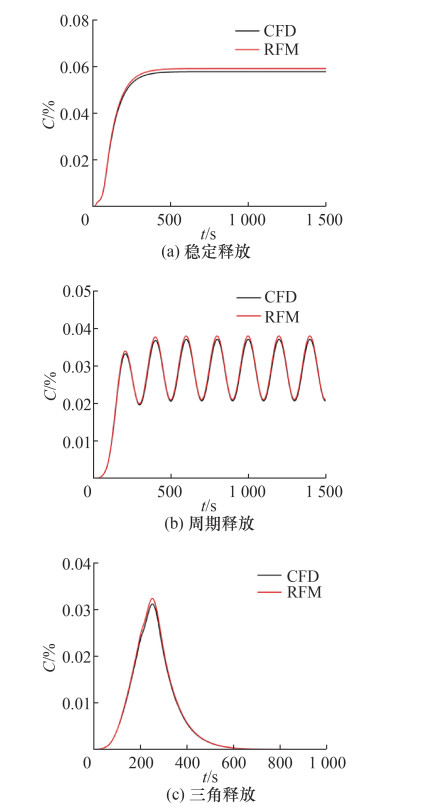
|
| 图 7 单个建筑的浓度响应因子法与CFD瞬态模拟的浓度-时间曲线 |
进一步分析不同点的模拟结果。表 2是单个建筑在3种污染源释放场景下,使用浓度响应因子法和CFD瞬态模拟得到的320个传感器处的结果评估。可以看出,浓度响应因子法表现良好,各指标数值都在可接受范围内。其中,在周期释放时FAC2的值为0.878,说明有部分点稍有偏差,但整体偏差很小。
| 释放函数 | FAC2 | NMSE | FB |
| 稳定释放 | 0.978 | 6.515×10-4 | -0.026 |
| 周期释放 | 0.878 | 5.784×10-4 | -0.024 |
| 三角释放 | 0.996 | 0.001 | -0.034 |
3.2 建筑阵列
图 8是3×7建筑阵列在3种污染源释放场景下,使用浓度响应因子法和CFD瞬态模拟得到的传感器B1处的浓度-时间曲线。对比单个建筑,建筑阵列的模拟效果更好,在3种释放场景下的浓度响应因子法模拟都更贴合CFD瞬态模拟。此外,从表 3中也可以看出,两种方法得到的结果基本一致。
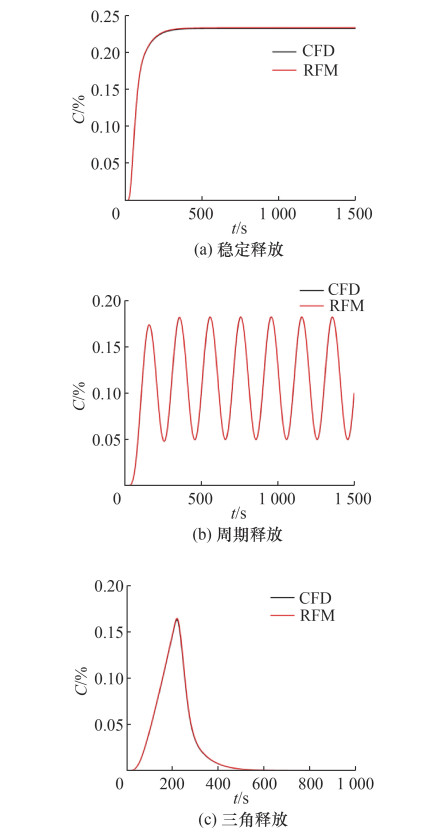
|
| 图 8 建筑阵列的浓度响应因子法与CFD瞬态模拟的浓度-时间曲线 |
| 释放函数 | FAC2 | NMSE | FB |
| 稳定释放 | 1.000 | 1.753×10-4 | 0.013 |
| 周期释放 | 1.000 | 5.224×10-4 | 0.022 |
| 三角释放 | 0.986 | 3.218×10-4 | 0.017 |
对比表 2和3,建筑阵列场景下的误差小于单个建筑物,这是因为受周围建筑的阻挡时,气流流速更小,污染物扩散更慢。结合图 6中的浓度响应因子随时间的变化,建筑阵列时的浓度响应因子变化也更平缓,因此模拟结果优于单个建筑。此外,建筑阵列中采用相同的建筑,使得流场结构相较实际情况更简单。
4 结论本文将浓度响应因子法应用于城市建筑周围污染物扩散场景,通过与CFD瞬态模拟结果的对比,分析了典型流场结构和污染源释放函数的影响。主要结论如下:
1) 浓度响应因子法能较好地模拟建筑周围的污染物扩散,浓度的变化趋势与CFD瞬态模拟结果相吻合,FAC2值基本在0.95以上,且能够节约大量求解时间。
2) 对于时变的污染源释放函数,浓度响应因子法能很好地模拟浓度场,且能够很好地模拟过程中任何时刻的浓度。
本文选取的是稳定流场条件下单个建筑和建筑阵列模型,但真实的城市风环境是不断变化的,需要考虑风向、温度场等的影响,而且建筑群结构更复杂。此外,浓度响应因子法是建立在流场稳定且各点浓度为线性关系的基础之上,如果要进一步扩展应用场景,一方面需要建立随流场变化的时变浓度响应因子矩阵,另一方面应采用多点集合计算方法,降低非线性的影响。
| [1] |
LAMER K, LUKE E P, MAGES Z, et al. The impact of heat and inflow wind variations on vertical transport around a supertall building: The One Vanderbilt field experiment[J]. Science of the Total Environment, 2022, 851: 157834. DOI:10.1016/j.scitotenv.2022.157834 |
| [2] |
WANG J Y, YU X Y, ZONG R W. A dynamic approach for evaluating the consequences of toxic gas dispersion in the chemical plants using CFD and evacuation modelling[J]. Journal of Loss Prevention in the Process Industries, 2020, 65: 104156. DOI:10.1016/j.jlp.2020.104156 |
| [3] |
STEPHENSON D G, MITALAS G P. Cooling load calculations by thermal response factor method[J]. ASHRAE Transactions, 1967, 73(1): 1-7. |
| [4] |
LU I, FISHER D E. Application of conduction transfer functions and periodic response factors in cooling load calculation procedures[J]. ASHRAE Transactions, 2004, 110(2): 829-841. |
| [5] |
MITALAS G P, STEPHENSON D G. Room thermal response factors[J]. ASHRAE Transactions, 1967, 73(1): 1-10. |
| [6] |
ISHIDA Y, KATO S. Method for coupling three-dimensional transient pollutant transport into one-dimensional transport simulation based on concentration response factor[J]. ASHRAE Transactions, 2008, 114(1): 259-272. |
| [7] |
HIYAMA K, ISHIDA Y, KATO S. Coupling 3D transient pollutant transport in a room into a flow network model with concentration response factor method[J]. ASHRAE Transactions, 2008, 114(2): 119-129. |
| [8] |
HIYAMA K, KATO S, ISHIDA Y. Thermal simulation: Response factor analysis using three-dimensional CFD in the simulation of air conditioning control[J]. Building Simulation, 2010, 3(3): 195-203. DOI:10.1007/s12273-010-0009-0 |
| [9] |
ZHANG T F, YIN S, WANG S G. An inverse method based on CFD to quantify the temporal release rate of a continuously released pollutant source[J]. Atmospheric Environment, 2013, 77: 62-77. DOI:10.1016/j.atmosenv.2013.04.057 |
| [10] |
LEI L, XUE Y, ZHENG W H, et al. An inverse method based on CFD to determine the temporal release rate of a heat source in indoor environments[J]. Applied Thermal Engineering, 2018, 134: 12-19. DOI:10.1016/j.applthermaleng.2018.01.097 |
| [11] |
LIU X R, LI F, CAI H, et al. Dynamical source term estimation in a multi-compartment building under time-varying airflow[J]. Building and Environment, 2019, 160: 106162. DOI:10.1016/j.buildenv.2019.106162 |
| [12] |
HU Q M, YAN L, LIU H, et al. Rapid simulation of airborne contaminant transport: Coupling concentration response factor method into a Markov chain model[J]. International Journal of Heat and Mass Transfer, 2022, 185: 122389. DOI:10.1016/j.ijheatmasstransfer.2021.122389 |
| [13] |
ZHOU Y D, AN Y T, HUANG W J, et al. A combined deep learning and physical modelling method for estimating air pollutants' source location and emission profile in street canyons[J]. Building and Environment, 2022, 219: 109246. DOI:10.1016/j.buildenv.2022.109246 |
| [14] |
ANSYS. ANSYS Fluent user's guide[R]. Canonsburg, USA: ANSYS, 2020.
|
| [15] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG F J. Computational fluid dynamics analysis: Principle and application of CFD software[M]. Beijing: Tsinghua University Press, 2004. (in Chinese) |
| [16] |
FRANKE J. Recommendations of the COST action C14 on the use of CFD in predicting pedestrian wind environment[C]// Proceedings of the Fourth International Symposium on Computational Wind Engineering (CWE 2006). Yokohama, Japan, 2006.
|
| [17] |
TOMINAGA Y, MOCHIDA A, YOSHIE R, et al. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1749-1761. |
| [18] |
CHANG J C, HANNA S R. Air quality model performance evaluation[J]. Meteorology and Atmospheric Physics, 2004, 87(1-3): 167-196. |



