2. 陕西省工业过程安全与应急救援工程技术研究中心, 西安 710054
2. Shaanxi Engineering Research Center for Industrial Process Safety and Emergency Rescue, Xi'an 710054, China
中国是全球产煤量和耗煤量最大的国家,同时也是受煤火危害最严重的国家。据统计,煤火灾害每年烧毁了中国2 000万余t的煤炭资源,导致2亿余t煤炭资源无法开采,直接经济损失高达20亿元以上[1],还释放出大量的有毒物质(如氮氧化合物、多环芳香烃、汞、砷和氟等)[2-5],造成大面积地表下沉[6],严重污染、破坏环境和生态系统,危害人类健康安全。煤自燃是煤矿开采和储存过程中可能发生的灾害之一,且煤自燃过程伴随复杂的放热反应。已有许多研究人员致力于通过各种实验方法来了解煤自燃机理以及煤自燃过程中温度和释放的气体产物浓度的变化,从而合理解释和早期探测煤自燃状态。
煤自燃指标气体已被广泛用作矿井火灾的指标。煤自燃的早期检测主要通过分析煤自燃发火过程中的温度、气体的浓度及比值等特征的变化来进行。比如,肖旸等[7]利用大型煤自燃发火实验台确定了指标气体与特征温度的对应关系,得到了各阶段气体特征变化。邓军等[8]为准确预测不同阶段的煤自燃发火状态,利用自制的程序升温实验台分析煤样在低温阶段的气体组分及其体积分数并建立指标体系。Chen等[9]通过煤自燃绝热氧化实验系统分析了煤自燃的3个过程(缓慢氧化、加速氧化和燃烧阶段),得到的CO、CO2产生率可作为煤自燃预测指标。CO2和CO是煤自燃低温阶段的主要产物,但是受到煤炭的吸附作用以及柴油机废气和煤层气的影响,空气中的CO2浓度值与实际煤自燃产生的CO2浓度值存在一定差异,从而影响到对煤自燃状态的判断。尽管从CO的绝对浓度中获得的煤自燃状态信息较少,但CO的产生趋势通常反映了煤自燃的持续发展状况。因此,随着时间的推移获取CO的产生趋势对于煤自燃的预测和状态判断至关重要。
近年来,学者们将煤自燃指标气体与机器学习方法相结合进行数据挖掘,融合煤自燃特征与指标气体,进而实现对煤自燃危险性的预测。邓军等[10]扩大数据来源,基于实验研究、现场观测以及专家经验的数据,利用人工神经网络(artificial neural network,ANN) 和灰色关联分析法建立了煤自燃预警指标体系,实现了煤自燃程度的预测。Zhao等[11]基于72组样本建立了反向传播神经网络(backpropagation neural network,BPNN)模型,利用煤的动力学参数和外部因素预测了煤自燃温度和CO浓度,并且利用BPNN在训练完成后随机产生的40组数据验证模型,但是随机产生的数据并不一定能反映真实的煤自燃反应过程。Meng等[12]利用180组数据,运用支持向量机(support vector machine,SVM)和径向基函数神经网络(radial basis function neural network,RBF-NN),建立了煤自燃过程中气体浓度和煤的性质之间的关系。Guo等[13]基于遗传算法的支持向量回归(support vector regression,SVR)模型,利用低温氧化实验数据建立了煤温与CO浓度的关系,并与SVR和BPNN模型进行了性能比较。许多学者已经应用机器学习方法来建立煤自燃温度与气体浓度的关系模型,但是这些模型为静态模型,无法获取随着时间的推移温度与气体浓度的变化情况,且模型很大程度上围绕影响因素、煤温与指标气体浓度之间的相互关系,忽略了变量的时间行为。并且,已有研究[14]表明,当涉及时间序列数据的训练和预测时,动态模型总是比静态模型具有更高的预测精度。
因此,本文选择陕西彬长大佛寺煤矿作为实验基地,获取40105综放工作面不同距离的采空区的多种气体的体积分数数据285组,利用循环神经网络(recurrent neural network,RNN)、长短期记忆(long short-term memory,LSTM)网络和门控循环单元(gated recurrent unit,GRU) 3种算法,建立CO体积分数动态序列预测模型,实现对未来时刻CO体积分数变化趋势的预测。最后, 对模型预测结果采用平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)和确定系数(determination coefficient,R2) 3个指标进行统计分析。
1 实验与数据处理 1.1 原位观测实验为了验证RNN、LSTM和GRU模型在实际现场应用中的性能,选择陕西彬长大佛寺煤矿作为实验基地,观测了40105综放工作面不同距离的采空区的O2、CO、CO2、CH4和C2H6,获得了各气体组分的体积分数。40105工作面走向长1 855 m,倾向长200 m,面积37 100 m2,煤层底板标高580.8~ 620.6 m,埋藏深度324.6~460.9 m。40105综放工作面通风方式如图 1所示。
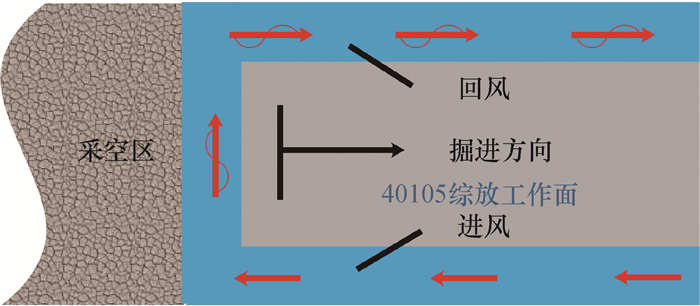
|
| 图 1 40105综放工作面通风系统示意图 |
1.2 现场数据
本研究通过束管监测系统获取40105综放工作面不同距离测点的CO、O2、CO2、CH4和C2H6的体积分数值。束管监测的工作面采样器布置安排如下:分别在架后束管保护管50#、70#、90#及上隅角共埋设4个测点,并将测点分别编号为50支架、75支架、105支架和135支架,为一组;随工作面推采,每60 m埋设一组测点,每日进行早、午、晚3次测点取样。但是,随着工作面的开采和推进,当煤和岩石从顶板坍塌时,一些测点被损坏,导致50支架、75支架和135支架出现无气压现象,故在本研究中统一选择105支架的早班数据建立模型的数据集。通过285 d的监测获取285组连续的气体体积分数测量值。
如图 2所示,采空区不同测点位置的O2、CO、CO2、CH4和C2H6的体积分数(φO2、φCO、φCO2、φCH4和φC2H6)构成了9个循环。图 2中L表示测量点与工作面之间的距离(m)。从图 2可知,在每一个循环中,随着L的逐渐增大,CO、CO2、CH4和C2H6的体积分数出现相同变化趋势,即逐渐升高达到峰值;而O2的体积分数呈现相反趋势,即逐渐下降到达本循环最小值。该结果主要是由于随着采空区工作面的推进,煤体氧化程度增大,O2逐渐消耗,产生大量的CO、CO2、CH4和C2H6。另外,从图 2可知,随着时间的推移,CO与其他气体产物以及采空区工作面距离表现出复杂的非线性关系,CO的变化可能受到其他气体产物的影响,造成测量值出现偏差。因此,本研究在建模过程中选择O2、CO2、CH4和C2H6的体积分数以及L作为输入变量,以CO体积分数作为模型输出目标。
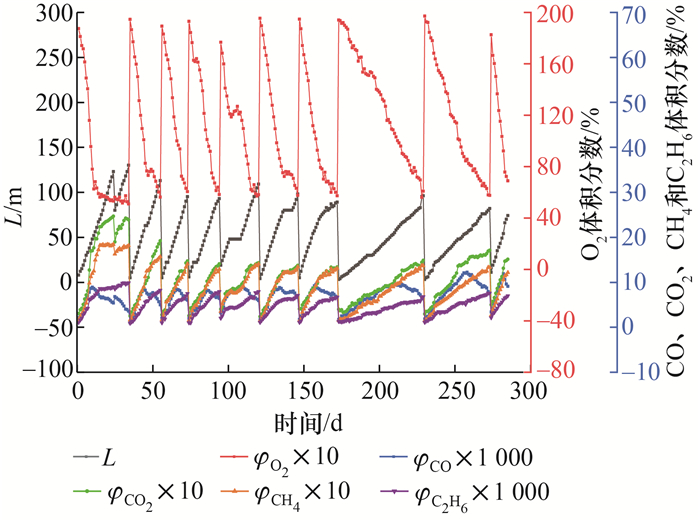
|
| 图 2 随着时间的推移采空区不同位置测点的各气体体积分数的变化情况 |
O2、CO、CO2、CH4和C2H6体积分数的均值、标准差、最小值、第1四分位数、第2四分位数、第3四分位数和最大值见表 1的现场实验数据的描述统计。此外,将285组样本分为171组(60%)样本、57组(20%)和57组(20%)样本,分别作为训练集、验证集和测试集。
| 统计量 | O2体积分数/% | CO2体积分数/% | CH4体积分数/% | C2H6体积分数/% | L/m | CO体积分数/% |
| 均值 | 11.273 | 1.076 | 0.902 9 | 0.004 9 | 53.281 | 0.006 8 |
| 标准差 | 4.462 | 0.521 | 0.441 8 | 0.002 2 | 29.172 | 0.002 4 |
| 最小值 | 5.091 | 0.236 | 0.146 3 | 0.000 9 | 3 | 0.001 0 |
| 第1四分位数 | 7.213 | 0.707 | 0.550 6 | 0.003 2 | 29 | 0.005 5 |
| 第2四分位数 | 10.678 | 1.022 | 0.899 6 | 0.005 1 | 52 | 0.007 2 |
| 第3四分位数 | 15.292 | 1.362 | 1.220 4 | 0.006 4 | 77 | 0.008 4 |
| 最大值 | 19.702 | 2.470 | 1.842 4 | 0.009 9 | 130 | 0.012 2 |
1.3 数据集预处理 1.3.1 数据分布检验
为了提高预测模型的拟合和泛化能力,利用核密度估计得到数据集的特征变量分布情况,如图 3所示。核函数选择Gauss核函数,带宽(h)选择20。此外,对于非正态分布数据采用对数变换使数据趋于正态分布[15]。
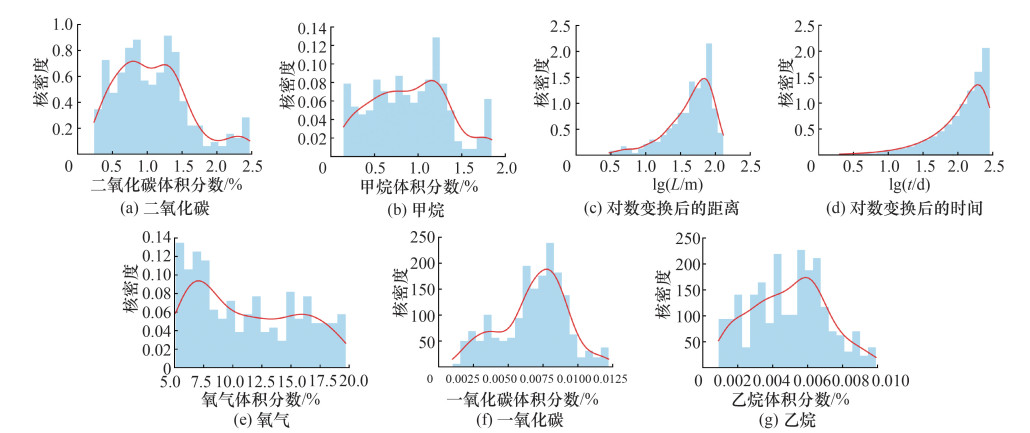
|
| 图 3 模型特征变量分布情况 |
由于时间(t)和L呈非正态分布,使用对数变换公式(3)使其趋于正态分布,以稳定方差并提高模型训练速度和预测精度。此外,由图 3a和3e可知,CO2和O2体积分数也是非正态分布的,但由于CO2和O2值分布较为集中,对数变换对这2个特征变量的分布影响较小,对模型预测结果的影响也较小,故O2和CO2体积分数不进行对数转换。
1) 核密度估计。
| $ K(x)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{1}{2} x^{2}\right). $ | (1) |
| $ f_{h}(x)=\frac{1}{n} \sum\limits_{i=1}^{n} K_{h}\left(x-x_{i}\right)=\frac{1}{n h} \sum\limits_{i=1}^{n} K\left(\frac{x-x_{i}}{h}\right) . $ | (2) |
其中:K(x)是Gauss核函数,fh(x)是核密度函数值,xi是来自总体x的样本,n为样本数量。
2) 对数变换。
| $ \begin{equation*} y=\log _{c}(1+\lambda x) . \end{equation*} $ | (3) |
其中:y为对数变换后的变量,x为原始变量,λ通常设置为1,c通常设置对数变换特征的最大值。
1.3.2 数据归一化处理本研究采用最大最小归一化方法(式(4))对数据集的特征变量进行归一化处理。该方法将特征变量归一化在[-1, 1]的范围内,不会改变变量的分布状态。最大最小归一化公式为[16]
| $ \begin{equation*} P^{\prime}=\frac{2\left(P-P_{\min }\right)}{\left(P_{\max }-P_{\min }\right)}-1 . \end{equation*} $ | (4) |
其中:P′和P分别是归一化参数值与实际参数值,Pmax和Pmin分别是P的最大和最小值。
2 煤自燃CO动态预测模型为了评估RNN、LSTM和GRU模型对CO体积分数的预测性能,使用以下指标来定量判断模型的预测性能。
1) MAE。MAE取值范围为[0, +∞),预测值与实验值的误差越小,MAE数值越小,表明预测模型的精度越高。
2) RMSE。RMSE反映样本的分散程度,数值越小,表明模型的预测能力越好。
3) R2。R2取值范围为[0, 1],越接近1,表明模型的拟合和泛化能力越好。
3个指标的计算公式如下:
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{j=1}^{n}\left|\hat{y}_{j}^{k}-y_{j}^{k}\right| , $ | (5) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{j=1}^{n}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)^{2}} , $ | (6) |
| $ R^{2}=1-\frac{\sum\limits_{j=1}^{n}\left(y_{j}^{k}-\hat{y}_{j}^{k}\right)^{2}}{\sum\limits_{j=1}^{n}\left(y_{j}^{k}-\bar{y}\right)^{2}} . $ | (7) |
其中:n是样本数据的总数量,yjk是实验值,
RNN是一种用于处理序列数据的神经网络结构[17]。相较于传统神经网络中的“层”,RNN的“层”是指单个时间步长的循环单元[18]。给定序列数据X=(X1, X2, …, Xτ),RNN的展开长度为τ。待处理的序列通常为时间序列,序列的演进方向的长度被称为时间步长,并且为了有效地映射序列数据,RNN通过将循环层输出反馈到自身作为下一个时间步长计算的输入[19]。
基于数据集,选择CO体积分数作为模型的输出特征和标签,实现对CO体积分数的动态预测。在Python工具箱中,选择Numpy、Pandas、Sklearn、Keras、Matplotlib库以及Sequential、SimpleRNN、Dropout、Dense、Compile类构建RNN模型。添加Sequential类以确保添加的类的正确顺序;SimpleRNN类是模型的主要层;Dropout类用于从数据集中删除一些随机样本并反馈到下一层,在每次训练后从原始训练集中随机丢弃一定数量的数据点,以避免过拟合;Dense层为“全连接”层,前一层的所有单元都连接到当前层的所有单元,用于定义模型的输出节点数;Compile函数使用Adam、SGD、RMSprop等优化算法训练模型。基于RNN算法的煤自燃CO体积分数预测模型结构示意图如图 4所示,下面对该模型进行简单的阐述。
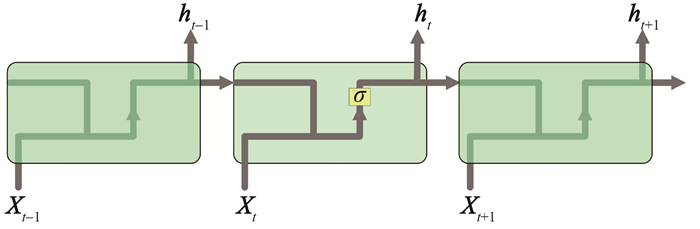
|
| 图 4 基于RNN算法的煤自燃CO体积分数预测模型结构示意图 |
1) 在每一步的时间步长中,激活值(ht)和输出值(ot)如下:
| $ \begin{equation*} \boldsymbol{h}_{t}=\sigma_{h}\left(\boldsymbol{W}_{h} \boldsymbol{X}_{t}+\boldsymbol{U}_{h} \boldsymbol{h}_{t-1}+b_{h}\right) . \end{equation*} $ | (8) |
| $ \begin{equation*} \boldsymbol{o}_{t}=\sigma_{o}\left(\boldsymbol{W}_{o} \boldsymbol{h}_{t}+b_{o}\right) . \end{equation*} $ | (9) |
其中:Xt为输入向量;ht为隐藏层向量;ot为输出向量;Wh、Wo、Uh为模型权重矩阵;bh和bo为模型调整系数;σh和σo分别为隐藏层和输出层激活函数。
2) 损失函数。
选择反向传播训练模型。在特定时间中,损失函数与权重矩阵(W)的导数表示为
| $ \begin{equation*} L_{i}^{t}=\left.\sum\limits_{t=1}^{T} \frac{\partial L}{\partial \boldsymbol{W}}\right|_{t} . \end{equation*} $ | (10) |
其中:Lit是随着时间累计的模型损失总和,T为模型时间步长的数量。
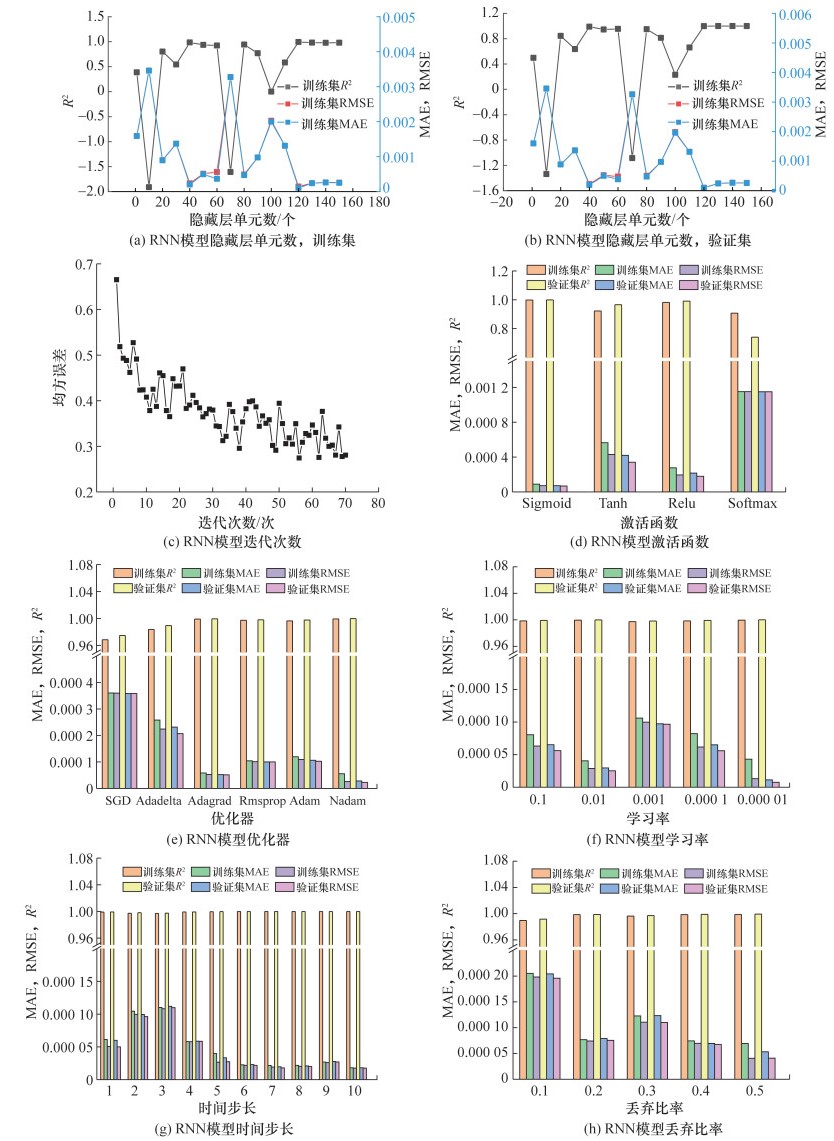
2.1.2 参数优化在模型训练过程中,需要对其参数进行优化,获取CO体积分数序列模型参数的最优取值,从而使其预测结果达到最优。由于CO体积分数序列模型输入特征维度低,因此RNN模型隐藏层为单层网络。其次,利用均方误差(mean square error,MSE)确定RNN模型的迭代次数。RNN模型的迭代次数和MSE的关系如图 5c所示。从图 5c中可知,随RNN模型的迭代次数的增加,MSE前期迅速下降,后期变化平缓,因此确定模型的迭代次数为50。另外,通过训练集和验证集的MAE、RMSE和R2确定RNN模型的隐藏层单元数、激活函数、优化器、学习率、时间步长和丢弃比率。RNN模型的训练集和验证集的MAE、RMSE和R2如图 5所示。由于调参过程中模型波动幅度过大,RNN模型可能发生了过拟合现象,因此出现了R2为负值的情况。
|
| 图 5 基于RNN算法的CO体积分数预测模型参数优化 |
1) 隐藏层单元数。在模型训练过程中,隐藏层单元数很大程度上影响模型是否会发生欠拟合或者过拟合。从图 5a和5b可知,RNN模型的MAE、RMSE与R2在隐藏层单元数为120时趋于平稳,且R2>0.99,MAE、RMSE均小于0.000 5,模型拟合能力较强,因此确定RNN模型的隐藏层单元数为120个。
2) 激活函数。常用的激活函数有Sigmoid、Tanh、ReLU和Softmax。如图 5d所示,激活函数为Sigmoid时,RNN模型的MAE、RMSE和R2较稳定,模型性能最佳。
3) 优化器。优化器在模型训练过程中,指引损失函数的各个参数更新为最优取值,使得更新后的损失函数值趋于全局最小。图 5e显示了几种常用的优化器, 包括:不含动量的随机梯度下降法(stochastic gradient descent, SGD);添加了二阶动量的自适应学习率优化法, 有Adagrad算法、Rmsprop算法、Adam算法和Adadelta算法;以及基于Newton梯度动量下降(NAG)和Adam的Nadam算法。从图 5e中可以看到,当RNN模型的优化器为Nadam算法时,模型的MAE、RMSE和R2达到理想状态。
4) 学习率。学习率控制训练中网络梯度更新的量级,影响模型的有效容限能力。根据常用的学习率大小对模型进行训练,得到的MAE、RMSE和R2如图 5f所示。随着学习率的降低, RNN模型的MAE、RMSE和R2呈现先降后升再降低的趋势,降低学习率会导致训练误差增加,最终确定学习率为0.01。
5) 时间步长。时间步长是序列模型特有的参数。图 5g显示了在1~10时间步长下模型的MAE、RMSE和R2的变化。结果表明,对于RNN模型,随预测的时间步长增大,模型误差趋于平稳,当时间步长为6时,模型性能逐渐稳定。
6) 丢弃比率。丢弃比率指在模型训练过程中,对隐藏层单元按照一定比率将其暂时从模型中丢弃,从而降低模型出现过拟合的概率,一般设定其取值范围为[0, 0.5]。如图 5h所示,当丢弃比率为0.5时,RNN模型的MAE、RMSE最低,选择该值用于开发模型。
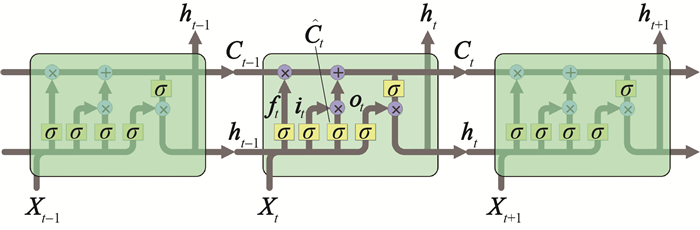
2.2 长短期记忆网络模型 2.2.1 模型配置LSTM模型是RNN模型的一种变体。RNN模型由于梯度消失的原因只存在短期记忆,LSTM模型通过门控制将短期记忆与长期记忆相结合,抑制有害的梯度更新,并且实现更好的长期依赖性学习[20]。一个典型的LSTM单元由输入、遗忘和输出门组成。与标准RNN不同,每个LSTM层不仅接收前一序列层的输出,还接收前一单元状态(Ct-1)。其中:输入门(it)控制单元的主层输出的哪些部分应该被添加到长期单元状态(Ct);输出门(ot)控制读取长期单元状态(Ct),并生成当前时间步长输出;遗忘门(ft)控制长期单元状态(Ct)的哪些部分应当被删除[17]。
LSTM模型与RNN模型同样选择CO体积分数作为模型的输出特征和标签。在Python工具箱中,选择同样的库和类构建LSTM模型。LSTM输入门的数据是当前时刻的输入Xt和前一个时刻的隐藏状态ht-1,Xt由一个全连接层和一个计算输入门、遗忘门和输出门的激活函数进行处理。基于LSTM算法的煤自燃CO体积分数预测模型结构示意图如图 6所示,下面对该模型进行简单的阐述。
|
| 图 6 基于LSTM算法的煤自燃CO体积分数预测模型结构示意图 |
1) 在每一步的时间步长中,it、ft和ot计算公式如下:
| $ \boldsymbol{i}_{t} =\sigma_{i}\left(\boldsymbol{W}_{i} \boldsymbol{X}_{t}+\boldsymbol{U}_{i} \boldsymbol{h}_{t-1}+b_{i}\right) . $ | (11) |
| $\boldsymbol{f}_{t} =\sigma_{f}\left(\boldsymbol{W}_{f} \boldsymbol{X}_{t}+\boldsymbol{U}_{f} \boldsymbol{h}_{t-1}+b_{f}\right) . $ | (12) |
| $ \boldsymbol{o}_{t} =\sigma_{o}\left(\boldsymbol{W}_{o} \boldsymbol{X}_{t}+\boldsymbol{U}_{o} \boldsymbol{h}_{t-1}+b_{o}\right) . $ | (13) |
其中:it为输入门结果;ft为遗忘门结果;ot为输出门结果;σi、σf和σo分别为输入层、隐藏层和输出层的激活函数;Wi、Wf、Wo或Ui、Uf、Uo为模型的权重矩阵;bi、bf、bo为模型的调整系数。
2) 细胞状态的更新。在LSTM模型中,首先在遗忘门中选择细胞状态中丢弃的信息,通过读取ht-1和Xt,输出[0, 1] 之间的值反馈到旧状态Ct-1;其次,确定存放在细胞状态中的新信息
| $\check{\boldsymbol{C}}_{t}=\sigma_{c}\left(\boldsymbol{W}_{c} \boldsymbol{X}_{t}+\boldsymbol{U}_{c} \boldsymbol{h}_{t-1}+b_{c}\right) . $ | (14) |
| $ \boldsymbol{C}_{t}=\boldsymbol{f}_{t} \cdot \boldsymbol{C}_{t-1}+\boldsymbol{i}_{t} \cdot \check{\boldsymbol{C}}_{t} . $ | (15) |
| $ \boldsymbol{h}_{t}=\boldsymbol{o}_{t} \cdot \sigma_{c}\left(\boldsymbol{C}_{t}\right) . $ | (16) |
其中:σc为激活函数;Wc和Uc为模型权重矩阵;bc为模型调整系数。
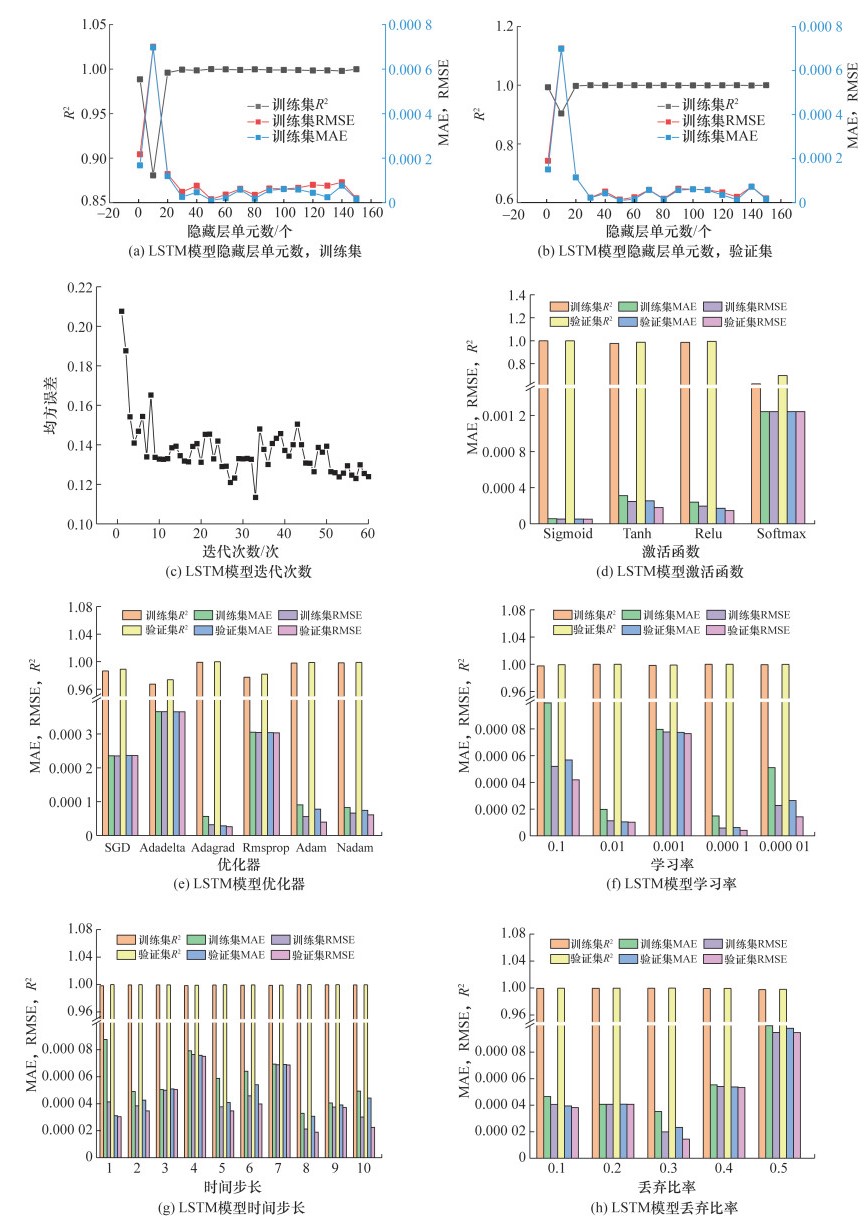
2.2.2 参数优化设置LSTM模型为单层网络,模型的迭代次数和MSE的关系如图 7c所示。在LSTM模型训练过程中,随着迭代次数的增加,MSE前期迅速下降,当迭代次数接近50时,MSE趋于最小值且下降速度平缓,因此确定模型的迭代次数为50。其次,通过训练集和验证集的MAE、RMSE和R2确定LSTM模型的最佳隐藏层单元数、激活函数、优化器、学习率、时间步长和丢弃比率,如图 7所示。
|
| 图 7 基于LSTM算法的CO预测模型参数优化 |
1) 隐藏层单元数。从图 7a和7b可知,模型的MAE和RMSE随着隐藏层单元数的增加逐渐降低,R2随着隐藏层单元数的增加逐渐升高。当隐藏层单元数为30时,模型的MAE和RMSE趋于最小值,R2趋于最大值,选择30个隐藏层单元用于LSTM模型开发。
2) 激活函数。在LSTM模型训练过程中,基于4种激活函数选择模型的最佳激活函数。如图 7d所示,当激活函数为Sigmoid时,模型的MAE和RMSE趋于最小值,R2趋于最大值,LSTM模型的性能最佳。
3) 优化器。图 7e显示了基于几种常用的优化器的模型性能。可见,当模型的优化器为Adagrad算法时,LSTM模型的MAE、RMSE和R2值达到理想状态。
4) 学习率。如图 7f所示,模型性能较稳定,学习率对模型误差影响较小。由于在0.000 1学习率下,模型出现了过拟合,且模型收敛缓慢,计算成本高,因此不选择0.000 1。当学习率为0.01和0.1时,模型均未出现过拟合。学习率为0.01时,模型收敛速度稍高于0.1。综合考量收敛速度以及模型误差,最终确定LSTM的学习率为0.01。
5) 时间步长。图 7g显示了在1~10时间步长下模型的MAE、RMSE和R2的变化。结果表明,对于LSTM模型,当时间步长为8时,模型的性能最稳定,模型的MAE和RMSE值最低。
6) 丢弃比率。如图 7h所示,在LSTM模型中,丢弃比率对模型性能影响较小,误差波动较小。当丢弃比率为0.3时,模型误差最低。
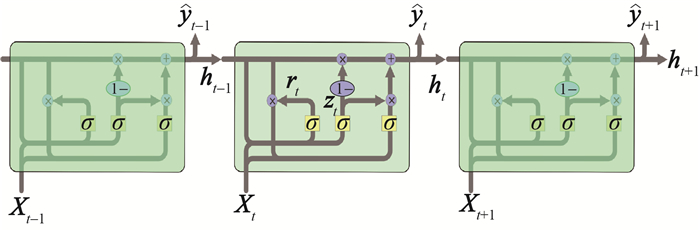
2.3 门控循环单元模型 2.3.1 模型配置模型GRU模型同样是RNN模型的一种变体。与LSTM模型不同,GRU模型有两个门:重置门(rt)决定了如何将新的输入信息与前面的记忆结合;更新门(zt) 定义了前面记忆保存到当前时刻的量,并将两个状态向量合并为一个向量,把该向量传递到下一个时刻和输出层[17]。GRU模型与LSTM模型一致,利用门控机制学习长期依赖关系的基本思想,而且研究表明,GRU和LSTM模型在多种任务中表现相似,没有明显差异[21]。基于此原因,在本研究中使用了两种RNN模型的变体。
基于GRU算法的煤自燃CO预测模型结构示意图如图 8所示,GRU模型同样选择CO作为模型的输出特征并作为标签。在Python工具箱中,构建GRU模型。LSTM与GRU模型的区别在于后者只有rt和zt,不存在输出门,并且GRU模型使用单个门来同时控制信息单元状态的更新,以及将两个状态向量合并为一个向量,传递到下一个时刻和输出层。下面对GRU模型进行简单的阐述。
|
| 图 8 基于GRU算法的煤自燃CO预测模型结构示意图 |
在每一个时间步长中,zt、rt、输入过程
| $\boldsymbol{z}_{t}=\sigma_{z}\left(\boldsymbol{W}_{z} \boldsymbol{X}_{t}+\boldsymbol{U}_{z} \boldsymbol{h}_{t-1}+b_{z}\right). $ | (17) |
| $ \boldsymbol{r}_{t}=\sigma_{r}\left(\boldsymbol{W}_{r} \boldsymbol{X}_{t}+\boldsymbol{U}_{t} \boldsymbol{h}_{t-1}+b_{r}\right) . $ | (18) |
| $ \hat{\boldsymbol{h}}_{t}=\sigma_{h}\left(\boldsymbol{W}_{h} \boldsymbol{X}_{t}+\boldsymbol{U}_{h}\left(\boldsymbol{r}_{t} \cdot \boldsymbol{h}_{t-1}\right)+b_{h}\right) . $ | (19) |
| $ \boldsymbol{h}_{t}=\left(1-\boldsymbol{z}_{t}\right) \cdot \boldsymbol{h}_{t-1}+\boldsymbol{z}_{t} \cdot \hat{\boldsymbol{h}}_{t} . $ | (20) |
| $\boldsymbol{y}_{t}=\boldsymbol{h}_{t} . $ | (21) |
其中:σz、σr和σh分别为更新门、重置门和隐藏层的激活函数;Wz、Wr、Wh或Uz、Ur、Uh为模型的权重矩阵;bz、br、bh为模型的调整系数。
2.3.2 参数优化设置模型隐藏层为单层网络,模型的迭代次数和MSE的关系如图 9c所示。在GRU模型训练过程中,随着迭代次数的增加,MSE迅速下降,当迭代次数为10时,MSE趋于最小值且下降速度平缓,因此确定GRU模型的迭代次数为10。其次,通过训练集和验证集的MAE、RMSE和R2确定GRU模型的最佳隐藏层单元数、激活函数、优化器、学习率、时间步长和丢弃比率,如图 9所示。
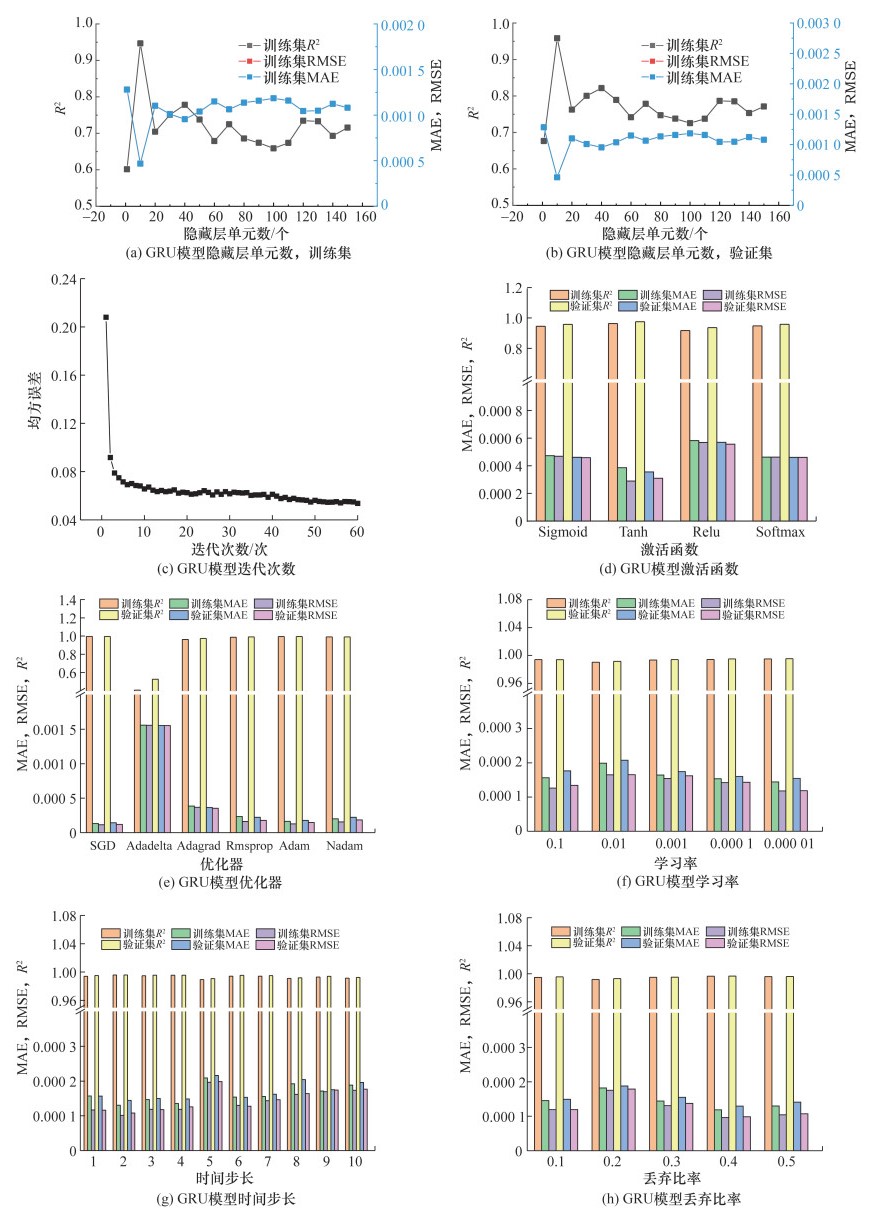
|
| 图 9 基于GRU算法的CO预测模型参数优化 |
1) 隐藏层单元数。图 9a和9b显示了随着隐藏层单元数的增加,GRU模型的MAE、RMSE和R2的变化情况。模型的MAE和RMSE随着隐藏层单元数的增加逐渐增大,R2随着隐藏层单元数的增加逐渐减小。该结果表明,隐藏层单元数越大,GRU模型的性能越差,故选择10个隐藏层单元用于开发模型。
2) 激活函数。本研究对比了4种激活函数对GRU模型的MAE、RMSE和R2的影响。从图 9d中可知,当激活函数为Tanh时,模型的MAE和RMSE趋于最小值,R2趋于最大值,模型的性能最佳。
3) 优化器。图 9e显示了几种常用的优化器在GRU模型中的模型性能指标结果。当优化器为SGD算法时,GRU模型的MAE和RMSE值最小,R2值最大。
4) 学习率。如图 9f所示,GRU模型性能较稳定,学习率对模型误差影响较小。当学习率为0.000 1时GRU模型的MAE和RMSE值最小,R2值最大。
5) 时间步长。图 9g显示了在1~10时间步长下模型的MAE、RMSE和R2的变化。结果表明,随着时间步长的增大,GRU模型的MAE和RMSE变化幅度较小,当时间步长为2时模型误差最低。
6) 丢弃比率。如图 9h所示,在GRU模型中,丢弃比率对模型性能影响较小,误差波动较小。当丢弃比率为0.4时,模型误差最低。
3 模型评估基于285组现场数据数据建立了RNN、LSTM和GRU模型。利用MAE、RMSE和R2定量判断模型的预测性能,结果见表 2。3种模型均能成功实现对CO体积分数的动态预测,且预测精度高达99%。LSTM模型预测性能最佳,其次是RNN模型和GRU模型。这表明利用时间序列模型对CO体积分数进行预测是可行的,模型构建过程以及参数优化过程可以作为开发其他指标气体时间序列预测模型的基础。
| 模型 | 训练集 | 测试集 | |||||
| MAE | RMSE | R2 | MAE | RMSE | R2 | ||
| RNN | 1.20×10-5 | 1.76×10-5 | 0.999 | 1.17×10-5 | 1.43×10-5 | 0.999 | |
| LSTM | 4.72×10-6 | 9.62×10-6 | 0.999 | 4.66×10-6 | 5.80×10-6 | 0.999 | |
| GRU | 8.32×10-5 | 9.14×10-5 | 0.997 | 8.50×10-5 | 9.68×10-5 | 0.997 | |
4 结果与讨论
本文基于171组现场数据建立了RNN、LSTM和GRU模型,利用57组数据验证了模型的性能,并基于57组数据测试了模型的泛化能力。图 10显示了3个模型对CO体积分数动态预测的结果。从图 10可知,3个模型均成功预测随着时间的推移煤自燃CO体积分数的变化情况,CO的实验值与预测值高度吻合,预测误差低于1%。LSTM模型预测精度最高,其次是RNN模型和GRU模型。导致该结果的原因有两方面:1) 3个模型均为动态模型,已有研究[14]表明在序列数据中动态模型预测精度要高于静态模型;2) 3个模型预测精度的不同主要与模型结构有关,LSTM模型可以通过门控制将短期记忆与长期记忆相结合,抑制有害的梯度更新并且实现更好的长期依赖性学习,但LSTM模型的结构与参数要比RNN和GRU模型更复杂。
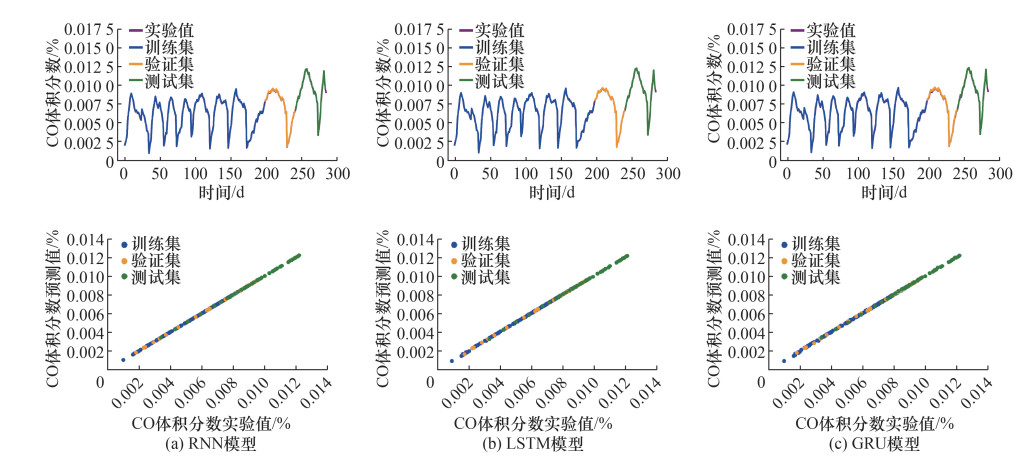
|
| 图 10 煤自燃CO模型预测结果与实验结果对比 |
5 结论
1) 基于陕西彬长大佛寺煤矿现场数据建立了CO体积分数时间序列数据集。采用核密度估计检验了特征变量的分布状态,并对非正态分布数据进行了对数变换,提高了模型拟合能力和泛化能力。其次,对特征变量归一化处理加快了模型的收敛速度,缩短了训练时间。
2) 利用285组现场数据,提出了基于RNN、LSTM和GRU算法的CO体积分数预测模型,CO体积分数的实验值与预测值高度吻合,预测误差低于1%,实现了CO体积分数连续动态趋势预测。可见,相较于传统静态模型,利用序列模型对CO体积分数进行动态时间序列预测是可行的。通过训练集和验证集的MAE、RMSE和R2得到了3个模型的最佳参数,并使用模型性能评估指标对比研究了同一序列数据下3个模型的预测精度,发现LSTM模型预测精度最高,其次是RNN模型和GRU模型。
由于煤矿火灾现场的局限性,很难同时获取煤自燃反应过程中指标气体和温度的变化。在未来研究中,将针对某发火煤矿进行现场调研,同时设置温度与气体传感器获得随时间推移的CO体积分数与温度数据,以改进所建立的动态时序模型。
| [1] |
VAN DIJK P, ZHANG J Z, JUN W, et al. Assessment of the contribution of in-situ combustion of coal to greenhouse gas emission; Based on a comparison of Chinese mining information to previous remote sensing estimates[J]. International Journal of Coal Geology, 2011, 86(1): 108-119. DOI:10.1016/j.coal.2011.01.009 |
| [2] |
LIANG Y C, LIANG H D, ZHU S Q. Mercury emission from coal seam fire at Wuda, Inner Mongolia, China[J]. Atmospheric Environment, 2014, 83: 176-184. DOI:10.1016/j.atmosenv.2013.09.001 |
| [3] |
LIU S Q, WANG C H, ZHANG S J, et al. Formation and distribution of polycyclic aromatic hydrocarbons (PAHs) derived from coal seam combustion: A case study of the Ulanqab lignite from Inner Mongolia, northern China[J]. International Journal of Coal Geology, 2012, 90-91: 126-134. DOI:10.1016/j.coal.2011.11.005 |
| [4] |
O'KEEFE J M K, HENKE K R, HOWER J C, et al. CO2, CO, and Hg emissions from the Truman Shepherd and Ruth Mullins coal fires, eastern Kentucky, USA[J]. Science of the Total Environment, 2010, 408(7): 1628-1633. DOI:10.1016/j.scitotenv.2009.12.005 |
| [5] |
ENGLE M A, RADKE L F, HEFFERN E L, et al. Gas emissions, minerals, and tars associated with three coal fires, Powder River Basin, USA[J]. Science of the Total Environment, 2012, 420: 146-159. DOI:10.1016/j.scitotenv.2012.01.037 |
| [6] |
KUENZER C, STRACHER G B. Geomorphology of coal seam fires[J]. Geomorphology, 2012, 138(1): 209-222. DOI:10.1016/j.geomorph.2011.09.004 |
| [7] |
肖旸, 王振平, 马砺, 等. 煤自燃指标气体与特征温度的对应关系研究[J]. 煤炭科学技术, 2008, 36(6): 47-51. XIAO Y, WANG Z P, MA L, et al. Research on correspondence relationship between coal spontaneous combustion index gas and feature temperature[J]. Coal Science and Technology, 2008, 36(6): 47-51. (in Chinese) |
| [8] |
邓军, 白祖锦, 肖旸, 等. 煤自燃指标体系试验研究[J]. 安全与环境学报, 2018, 18(5): 1756-1761. DENG J, BAI Z J, XIAO Y, et al. Experimental investigation and examination for the indexical system of the coal spontaneous combustion[J]. Journal of Safety and Environment, 2018, 18(5): 1756-1761. (in Chinese) |
| [9] |
CHEN J C, LI L, JIANG D Y, et al. Experimental study on the spatial and temporal variations of temperature and indicator gases during coal spontaneous combustion[J]. Energy Exploration & Exploitation, 2021, 39(1): 354-366. |
| [10] |
邓军, 肖旸, 陈晓坤, 等. 矿井火灾多源信息融合预警方法的研究[J]. 采矿与安全工程学报, 2011, 28(4): 638-643. DENG J, XIAO Y, CHEN X K, et al. Study on early warning method of multi-source information fusion for coal mine fire[J]. Journal of Mining and Safety Engineering, 2011, 28(4): 638-643. DOI:10.3969/j.issn.1673-3363.2011.04.026 (in Chinese) |
| [11] |
ZHAO J Q, YANG D G, WU J X, et al. Prediction of temperature and CO concentration fields based on BPNN in low-temperature coal oxidation[J]. Thermochimica Acta, 2021, 695: 178820. DOI:10.1016/j.tca.2020.178820 |
| [12] |
MENG Q, WANG H Q, WANG Y S, et al. SVM based prediction of spontaneous combustion in coal seam[C]// Proceedings of 2008 International Symposium on Computational Intelligence and Design. Wuhan: IEEE, 2008: 254-257.
|
| [13] |
GUO Q, REN W X, LU W. A method for predicting coal temperature using CO with GA-SVR model for early warning of the spontaneous combustion of coal[J]. Combustion Science and Technology, 2022, 194(3): 523-538. DOI:10.1080/00102202.2020.1772767 |
| [14] |
SAFDARNEJAD S M, TUTTLE J F, POWELL K M. Dynamic modeling and optimization of a coal-fired utility boiler to forecast and minimize NOx and CO emissions simultaneously[J]. Computers & Chemical Engineering, 2019, 124: 62-79. |
| [15] |
ZHAO H Q, LU L, HE Z Y, et al. Adaptive recursive algorithm with logarithmic transformation for nonlinear system identification in α-stable noise[J]. Digital Signal Processing, 2015, 46: 120-132. DOI:10.1016/j.dsp.2015.08.004 |
| [16] |
FENG Q H, ZHANG J Y, ZHANG X M, et al. Proximate analysis based prediction of gross calorific value of coals: A comparison of support vector machine, alternating conditional expectation and artificial neural network[J]. Fuel Processing Technology, 2015, 129: 120-129. DOI:10.1016/j.fuproc.2014.09.001 |
| [17] |
LAUBSCHER R. Time-series forecasting of coal-fired power plant reheater metal temperatures using encoder-decoder recurrent neural networks[J]. Energy, 2019, 189: 116187. DOI:10.1016/j.energy.2019.116187 |
| [18] |
GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M]. Cambridge, USA: MIT Press, 2016.
|
| [19] |
SCHMIDHUBER J. Deep learning in neural networks: An overview[J]. Neural Networks, 2015, 61: 85-117. |
| [20] |
GÉRON A. Hands-on machine learning with scikit-learn and tensorflow: Concepts, tools, and techniques for building intelligent systems[M]. Beijing: O'Reilly Media, 2017.
|
| [21] |
GREFF K, SRIVASTAVA R K, KOUTNÍK J, et al. LSTM: A search space odyssey[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(10): 2222-2232. DOI:10.1109/TNNLS.2016.2582924 |


