2. 安徽理工大学 化工与爆破学院, 淮南 232001
2. School of Chemical and Blasting Engineering, Anhui University of Science and Technology, Huainan 232001, China
大多数火蔓延模型假设燃料具有一个连续表面或是均匀多孔介质[1-6],然而在实际火灾中,火焰通常在离散燃料之间传播,并且无法将这些燃料元件视为均质。为了更准确地预测火焰传播行为,需要进一步改进火灾建模理论和方法。为模拟离散燃料火焰传播现象,木条常常被用作现实燃料的替代物,同时实验通常在水平静止状态[7-8]或在风洞中[9]进行,以模拟野火情况。水平火焰传播时,火焰的传播方向与浮力气体的流动方向垂直,在没有风的情况下,相邻木棍受到稳定的辐射热量,因此火焰可以达到稳定的传播状态,并且这种辐射热量的大小是由木棍之间的距离决定的[7]。在真实火场中,不同的燃料间距、外界风等条件下,离散燃料床上的火焰前锋的形状差异很大,例如形状相反的“A”形和“V”形。由于前人对离散固体燃料燃烧的火焰前锋形状研究比较有限,因此分析火焰在不同环境条件下的传播方式和前锋形状,深入研究其形成的条件和机理具有重要意义,并将有助于采取更有效的控制措施以减少火灾对人类和自然环境造成的损害。此外,离散燃料火蔓延前锋形状的研究还可以为火灾模拟和消防技术的发展提供重要的理论基础,为真实火灾中的火势蔓延趋势预测提供参考。
离散燃料火焰传播研究大多使用不同尺寸的木条进行缩尺寸实验。当火焰通过非连续的水平燃料阵列传播时,其蔓延受多种因素影响,例如燃料尺寸[7, 10-12]、阵列间距[7, 11-12]、阵列宽度[10]和环境风速[13-15]等。Vogel和Williams[7]利用垂直的火柴棒模拟了水平离散燃料火焰传播,并通过改变火柴棒的长度和间距确定了离散燃料火焰传播的必要条件。他们提出了基于恒定火焰温度和熄灭距离的对流控制理论,并且理论的计算结果与实验结果吻合较好。Prahl和Tien[13]研究了火焰在垂直方向上水平传播现象,通过在火柴棒和纸条上添加方向相反的风来进行实验,探讨了火焰蔓延、风速、燃料间距和燃料高度之间的相关性。研究结果表明,当风速较小时,火焰的传播速度主要取决于燃料间距和燃料高度;而当风速较大时,火焰的传播速度受到风速的显著影响,且随着风速的增加,火焰传播速度逐渐增加。Wolff等[14-15]研究了有风条件下火焰在离散燃料元件阵列上的传播,发现火焰的传播速度与风速和燃料质量分布的比值成正比。火蔓延速度受燃料间距和环境风速的影响,而受燃料长度的影响不明显[7, 13, 16]。随着燃料间距的增加,火蔓延速度先增加后降低[7, 10, 12]。一些学者认为这是由于对流传热主导逐渐转变为辐射传热主导所导致的。He等[17]通过测量辐射和对流热通量,探讨了不同间距下火焰蔓延的传热行为,结果发现在较大间距下火焰蔓延是由辐射传热主导的。Bu等[10]的实验发现,密集阵列火焰蔓延过程中,狭小的木条间距会限制空气卷吸。然而,目前仅有稀疏阵列传热过程的相关理论研究,而密集阵列的传热过程尚不清晰。
近些年来,火蔓延热解前锋形状引起了不少学者的关注。Qi等[18]对倾斜木板的双面并发火焰蔓延行为进行了实验和理论研究,对不同倾角下木板上表面的热解前沿呈倒“V”形夹角变化进行了分析。谢小冬[19]的上坡火实验和理论研究表明,当上坡角大于25°时火焰前锋会逐渐呈现“V”形,并保持稳定的形状;当上坡角小于或等于20°时,火焰前锋呈现弧形。
上述前人研究侧重于离散燃料火蔓延的影响因素或单一热解前锋形状,而对火焰蔓延前锋的形状差异现象缺乏理论分析和深入研究。本文主要针对不同燃料间距下火焰前锋形状差异的形成展开研究,为火蔓延行为的精准预测提供理论方法。
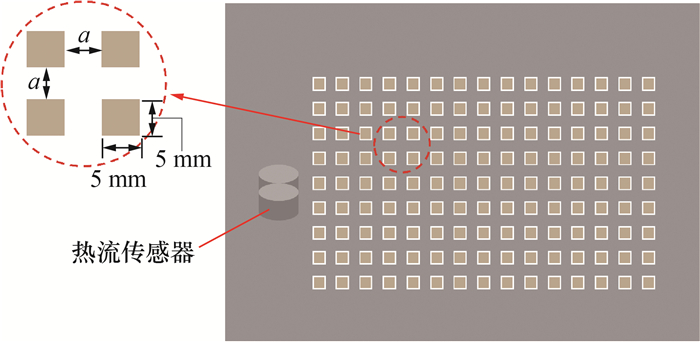
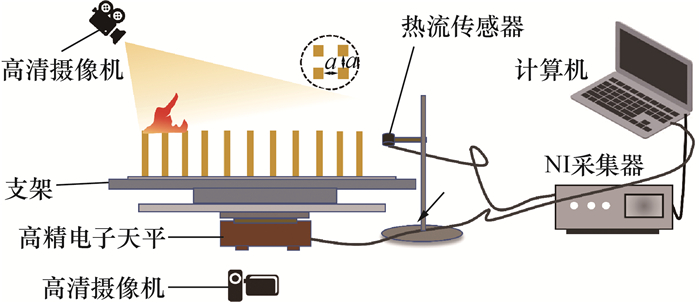
1 实验装置与测量方法 1.1 实验装置本实验选择5 mm(长)×5 mm(宽)×60 mm(高)的松木条作为燃料。实验设计了如图 1所示的铝制组合板(包括孔距a分别为3、5、7 mm的开孔板和3 mm厚的支撑板)来固定燃料,可用于进行3、5、7 mm 3个不同间距组别的实验。开孔板的厚度为2 mm,即松木条的嵌入深度为5 mm,暴露的松木条长度为55 mm。实验装置平台如图 2所示。
|
| 图 1 实验开孔布置示意图(俯视图) |
|
| 图 2 实验装置平台 |
1.2 测量方法
采用2台60帧/s高清摄像机来拍摄燃料燃烧过程, 其中一台摄像机位于燃料台正前上方,另一台则位于侧方。在实验开始之前,需要调节摄像机的高度和焦距,确保摄像机能够拍摄到整个火焰和燃料台。将一台高精电子天平放置在燃料台的底部,以1 Hz采样频率记录燃烧过程中的质量变化。2个Schmidt-Boelter式热流传感器(STT-25-10-R/WF)并列安装在阵列末端的木条间距处,其量程为10 kW/m2,采集频率为5 Hz。一个用作总热流计,测量火焰蔓延过程中的总热通量;另一个用作辐射热流计,测量火焰蔓延过程中的辐射热通量,测量时取下仪器表面的蓝宝石窗口。对流热通量的值可以通过总热通量减去辐射热通量得到。质量损失和热通量的测量信号均通过NI采集器采集,采集频率为100 Hz。本实验使用线点火器点燃,在点燃时,在第1和第2行木条之间插入一块薄的隔热板以避免点火带来的影响。
2 结果与讨论 2.1 火焰发展与火焰形状 2.1.1 火焰发展过程将木条按照一定的间距固定在开孔板上,利用线点火器均匀点燃第1行,正前上方摄像机可以直观、清晰地记录木条燃烧火焰蔓延的过程。
图 3展示了间距为7 mm时表面火焰形状的发展过程,大致可分为4个阶段:Ⅰ)火焰聚合阶段,Ⅱ)热解前锋形状发展阶段,III)稳定火焰形状阶段,IV)燃尽阶段。点火后,在宽度方向上呈现出几个高度接近的小火焰(5 s),然后这些小火焰逐渐向中心汇聚(40 ~70 s)。随着火焰向中心汇聚,离散木条形成的上表面中心线区域接收到更多的热量,形成一束相对较高的火焰。木条的热解过程伴随着炭化[18-19],在记录的视频中可以清晰地识别出表面黑色烧焦和热解的木条,因此在本文中将黑色木条区域的外部轮廓连线定义为热解前锋(图 3和4中的红色虚线轮廓线)。在这个阶段,热解前锋的形状呈现出近似直线形,向前蔓延的趋势不明显。70 s以后,热解前锋开始明显向前移动,前侧木条顶部达到热解温度,然后火焰开始扩散。在此阶段,热解前锋逐渐从直线形发展为弧形(150 s)。150 s后聚集的火焰导致更大程度的热解和更高的表面温度上升,从而造成中心线上的热解速率逐渐增加。最后,火焰热解前锋显示出明显的“A”形(180 s)。这与传统火焰以直线形热解前锋传播的现象完全不同。180 s后,具有“A”形热解前锋的火焰形状基本不再改变,火焰以稳定的形状向前扩散。当“A”形热解前锋到达燃料末端(270 s)时,火焰无法继续向前扩散并逐渐燃烧殆尽。

|
| 图 3 7 mm间距木柴燃烧蔓延情况 |

|
| 图 4 5 mm间距木柴燃烧蔓延情况 |
图 4展示了间距为5 mm时表面火焰形状的发展过程,同样大致可分为4个阶段。完成点火后,由于单个木条燃烧,每个木条上出现小火焰(5 s),然后这些小火焰逐渐融合,火焰高度逐渐增大(20~50 s)。在此阶段,火焰热解前锋呈现出近似直线形的形状,向前蔓延的趋势不明显。随着时间的推移(50~100 s),前方木条顶部到达热解温度,热解前锋开始向前移动,火焰发生扩散。在此阶段,中间木条燃烧卷吸受限,导致火焰形状开始发生变化,两边木条燃烧过程中因为和空气发生对流,火焰燃烧蔓延速度相对较快,热解前锋逐渐从直线形发展为弧形。不同于7 mm间距时的情况,5 mm间距时两侧火焰各自融合,中间火焰燃烧较弱,呈现出火焰分叉现象。100 s以后,两侧汇聚的火焰导致更大程度的热解和更高的表面温度上升,造成两侧火焰蔓延速度增加,而中心线上的木条燃烧卷吸受限,加上中部木条不能及时完全燃烧导致引燃状态堆积,进一步限制了扩散速率。最后,热解前锋呈现出明显的“V”形(180 s)。180 s后,火焰形状和“V”形热解前锋基本不再改变,火焰以稳定的形状向前扩散。当“V”形热解前锋到达燃料末端(330 s)时,火焰无法继续向前扩散并逐渐燃烧殆尽。
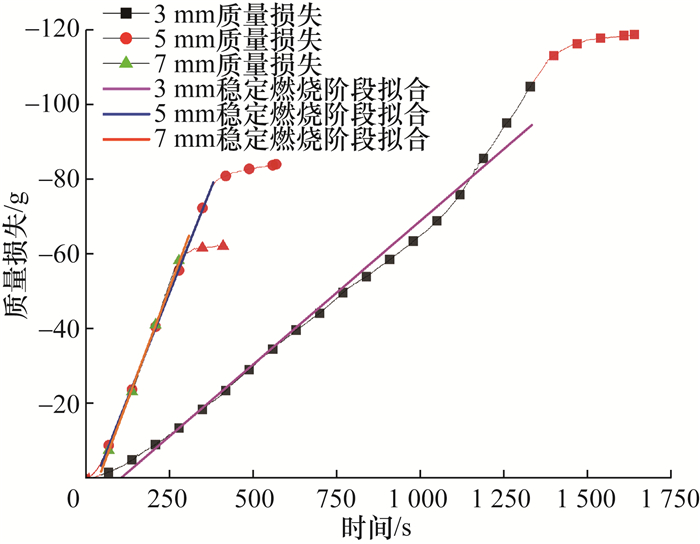
2.1.2 质量损失速率分析质量损失速率描述了物质在不同温度下随时间的质量变化情况。在分析物体燃烧时,质量损失速率表征了物质的热释放速率,反映了燃料燃烧的剧烈程度。图 5所示为不同间距木条阵列的质量损失曲线。取稳定燃烧阶段(即图中黑色线条部分;红色线条为非稳定阶段,拟合时忽略此部分数据)的质量损失进行线性拟合。由图 5可以发现,拟合线与实验结果较为吻合,因此由拟合线的斜率即可得到燃烧的质量损失速率。3 mm间距阵列时的质量损失速率小于7和5 mm间距阵列。通过实验的燃烧过程可以发现,由于3 mm间距过窄,阵列燃烧受阻,火焰蔓延速度较慢,会直接导致质量损失较慢。同时,5和7 mm间距阵列时的质量损失速率近似相等,而两阵列燃烧时呈现不同形状的火焰前锋,由此可以初步判断火焰前锋形状的差异与燃烧热释放速率无关。
|
| 图 5 不同间距木条阵列的质量损失曲线及稳定燃烧阶段拟合线 |
2.1.3 热通量分析
对传热机理的分析需要进行热通量的测量,本文使用总热流计和辐射热流计测量火蔓延前锋的热通量分布。2个热流计的响应时间略有不同,但影响十分微弱,因此在本次分析中忽略不计,近似认为用总热通量值减去辐射热通量值等于对流热通量值。
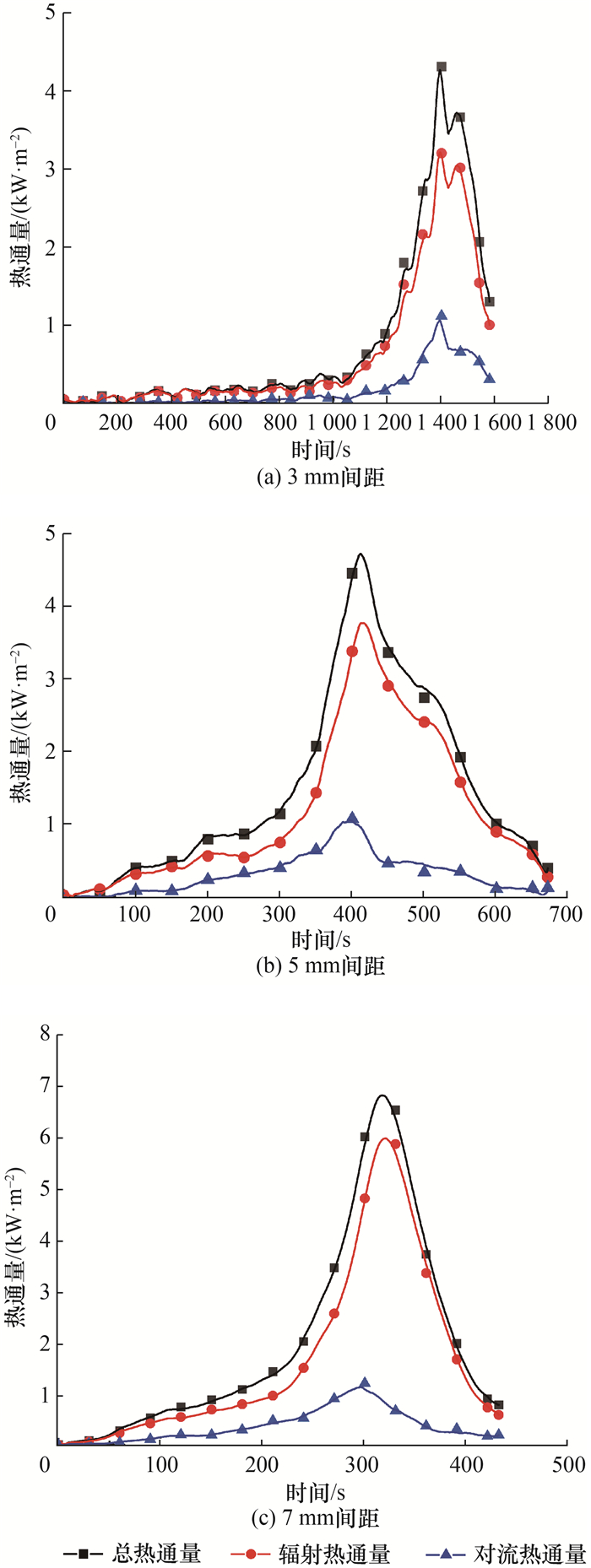
图 6为“V”形(间距S=3,5 mm)和“A”形(S=7 mm)火焰前锋的木条阵列火蔓延过程中,热流计测量的未燃区木条接收到的来自火焰加热以及高温热流等产生的热通量随时间变化的曲线图。可以看出,稳定燃烧阶段,当火蔓延到末端时热通量达到峰值,并且随着间距的增加,同一阶段总热通量峰值增加。如图 6a所示,对于3 mm间距阵列,木条间距较窄,燃烧时空气卷吸受制,火焰向未燃区的传热较弱,火焰蔓延速率与5和7 mm间距阵列工况相比明显较慢。在t ≤900 s时,辐射和对流热通量没有发生明显的变化;当t >900 s时,随着火焰的蔓延,辐射热通量快速增加,而对流热通量没有明显的变化,并且当火焰蔓延到阵列末端时,辐射热通量明显高于对流热通量。如图 6b、6c所示,5、7 mm间距阵列的辐射热通量明显高于3 mm间距阵列,而对流热通量峰值几乎持平,说明不同间距阵列间总热通量差异主要是由辐射传热造成的。5、7 mm间距阵列未燃区接收的辐射热通量更早地升高,在第Ⅱ阶段,未燃区接收到的辐射热通量快速增加,说明5、7 mm间距工况下辐射加热区域更大。5 mm较7 mm间距阵列火焰热通量曲线波动较大,主要是因为阵列两侧燃烧较快,中线部分卷吸受限,火焰微弱,从而导致整体火焰融合程度较差,火焰断断续续。
|
| 图 6 未燃区热通量随时间变化曲线 |
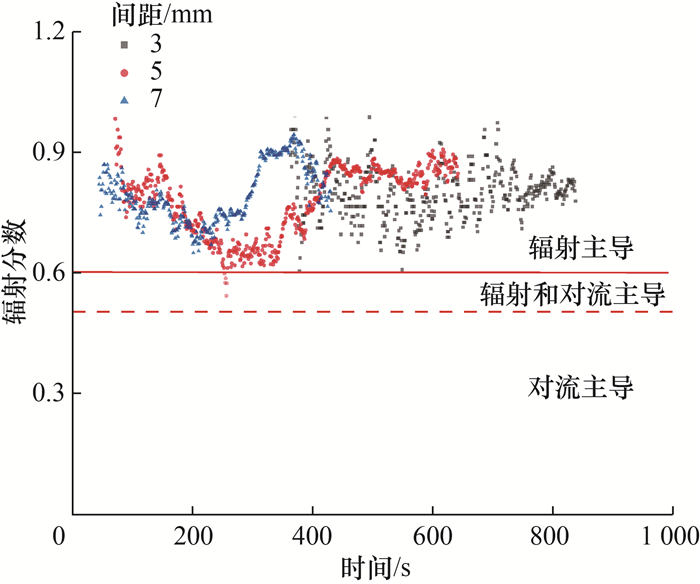
为进一步明晰辐射和对流传热的竞争关系,引入辐射分数χrad[20]进行讨论。辐射分数可以理解为辐射热通量占总热通量的比例。截取稳定燃烧阶段的热通量数据,假设有±20%的浮动范围,可以认为辐射分数χrad>0.6的加热过程是由辐射传热主导的,而χrad<0.4是由对流传热主导的。3个间距阵列工况下,稳定蔓延过程中的辐射分数χrad的变化如图 7所示。随着火焰的蔓延,辐射分数并非稳定的常数,但整体的辐射分数大于0.6,可以认为火焰蔓延是由辐射传热主导的。
|
| 图 7 阵列间距对辐射分数的影响 |
2.2 离散燃料火蔓延模型
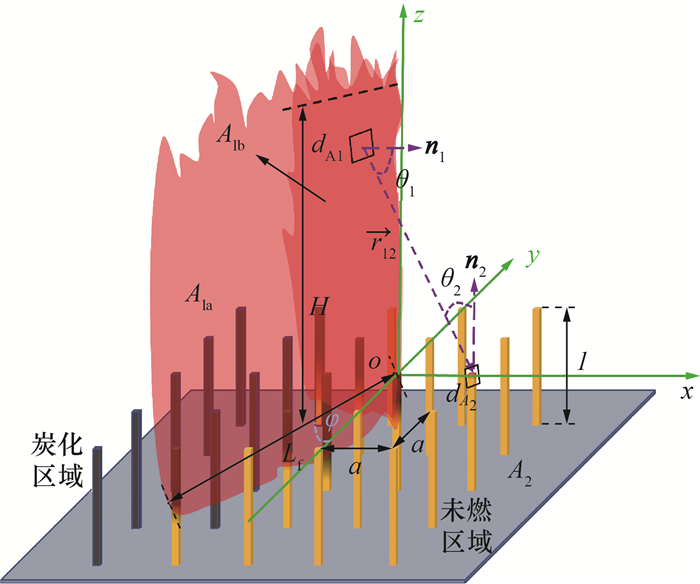
火焰到未燃区的辐射传热是影响火焰传播的关键因素。为量化未燃区接收的辐射传热,本文建立了图 8所示的离散燃料火蔓延传热模型。本研究中表面的火焰在7 mm间距下呈现“A”形,这与森林火灾中上坡火的形状相似,并且上坡火的建模思想也可应用到“V”形火焰蔓延上。因此,本文应用上坡火中的传热分析方法建立离散燃料火蔓延传热模型。
|
| 图 8 离散燃料火蔓延传热模型示意图 |
如图 8所示,“A”形火焰被视为两个相同的相交火焰面(A1a,A1b)。辐射热流传感器的位置被选择为燃料表面A2,这是中心线上最具代表性的区域。A2从火焰中接收到的辐射热通量可以表示为[20]
| $\dot{q}_{\mathrm{r}}^{\prime \prime}=\left(A_1 / A_2\right) \sigma \varepsilon F_{12}\left(T_{\mathrm{f}}^4-T_{\mathrm{s}}^4\right).$ | (1) |
其中F12是从火焰面A1到燃料表面A2的视角因子。基于火焰面等温和等发射率假设,视角因子就是一个几何因子,与火焰面及燃料表面的温度和发射率没有关系。σ是Boltzmann常数,取5.67×10-8 W·m-2·K-4;ε是火焰发射率,取ε=0.5。Tf是火焰温度,下标f表示火焰;Ts是燃料温度,下标s表示固体燃料;取Tf=735 ℃,Ts=28 ℃。
火焰向未燃材料顶表面传热的视角因子F12可以表示为[19]
| $F_{12}=F_{A_1 \rightarrow A_2}=\frac{1}{A_1} \int_{A_1} \int_{A_2} \frac{\cos \theta_1 \cos \theta_2}{\pi R^2} \mathrm{~d} A_2 \mathrm{d} A_1.$ | (2) |
θ1和θ2分别是表面A1和A2的极角。
如图 8所示,垂直火焰面与未燃燃料的距离(R)和极角可以表示为:
| $R^2=\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2+\left(z_1-z_2\right)^2, $ | (3) |
| $\cos \theta_1=\left(z_1-z_2\right) / R, $ | (4) |
| $\cos \theta_2=\left(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\right) / R.$ | (5) |
其中:x、y和z是建立在火焰前锋中心线点和火焰面高度H的空间坐标轴, (x1,y1,z1)和(x2,y2,z2)分别表示火焰面微元和燃料面微元中心点的坐标。
为了简化计算,根据火焰平板假设:火焰为具有均匀发射率的等温片;火焰面可以简化为矩形,并被认为垂直于木条表面。因此,可以定义无量纲辐射热通量[19]:
| $\begin{gathered}\dot{q}_{\mathrm{r}}^{\prime \prime *}=\frac{\dot{q}_{\mathrm{r}}^{\prime \prime}}{\sigma \varepsilon\left(T_{\mathrm{f}}^4-T_{\mathrm{s}}^4\right)}=\frac{A_1}{A_2} F_{12}=F_{21}= \\ \frac{1}{A_1} \int_{A_1} \int_{A_2} \frac{\cos \theta_1 \cos \theta_2}{\pi R^2} \mathrm{d} A_2 \mathrm{d} A_1 ;\end{gathered}$ | (6) |
| $F_{21}=F_{2, 1 \mathrm{a}}+F_{2, 1 \mathrm{b}}.$ | (7) |
可以看出,
对于式(6),如果燃料表面A2的面积足够小,那么
| $\dot{q}_{\mathrm{r}}^{\prime \prime *}=\int_{A_1} \frac{\cos \theta_1 \cos \theta_2}{\pi R^2} \mathrm{d} A_1.$ | (8) |
对于无量纲辐射热通量
| $\dot{q}_{\mathrm{r}}^{\prime \prime *}=\frac{-1}{\pi} \sum\limits_{i=1}^N \frac{\left(r_{12} \cdot\left|\boldsymbol{n}_1\right|\right)\left(r_{12} \cdot\left|\boldsymbol{n}_2\right|\right)}{R^4} \Delta A_i$. | (9) |
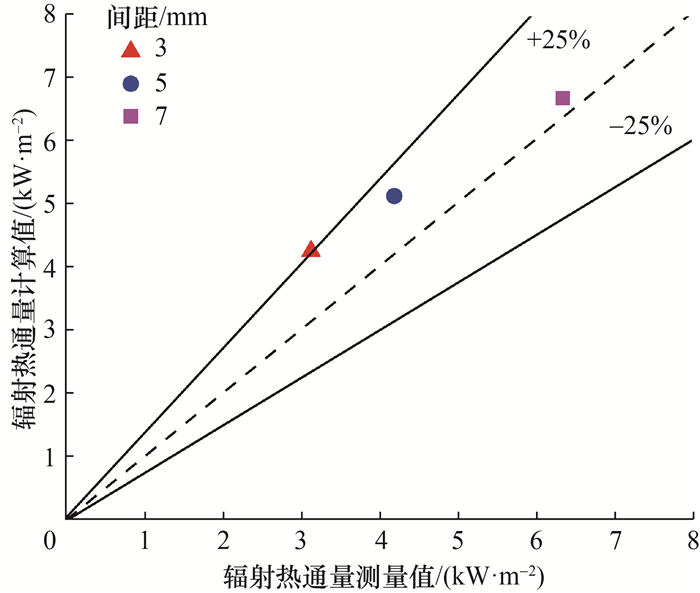
结合式(1)—(9)计算未燃区辐射热通量,并将计算值与测量值进行对比,如图 9所示。结果显示, 误差在25%区间内,表明模型较为合理。同时,计算值整体大于测量值,主要是由于本模型假设火焰是理想的等温面,而在实际情况中, 火焰时刻处于不均匀的波动状态,火焰面积要小于假设情况。
|
| 图 9 辐射热通量计算值与测量值结果比较 |
3 结论
本文开展了不同木条间距下离散燃料床的火蔓延实验。以5 mm(长)×5 mm(宽)×60 mm(高)的规则松木条为燃料,按照一定间距固定在均匀开孔板上,通过对火蔓延过程中的热通量、质量损失的测量,结合理论分析,研究了离散燃料水平火蔓延的前锋形状变化规律以及传热机理,主要结论如下:
1) 3和5 mm间距的密集木条阵列火蔓延火焰前锋呈现“V”形,而7 mm间距的稀疏木条阵列呈现“A”形。稳定燃烧阶段,质量损失速率近似恒定,5和7 mm间距的质量损失速率接近,且均大于3 mm间距阵列质量损失速率,反映出火焰形状的形成可能与其燃烧热释放速率关系不紧密。
2) 从3 mm到7 mm间距的木条阵列,随着间距的增加,木条阵列燃烧释放的总热通量峰值依次增大。不同间距下辐射分数整体大于0.6,火蔓延由辐射传热主导。
3) 本文综合考虑了非连续火蔓延和双火焰面共同作用下的复杂状况,基于火焰平板假设,应用上坡火传热分析理论,建立了离散燃料水平火蔓延传热模型。
此外,本研究尚存在一定的局限性:由于实验设计的间距较大且组数较少,无法得到形状变化的临界间距和普适性规律;造成不同间距木条阵列火焰前锋形状的差异可能主要由于卷吸是否受限,但本实验缺乏相应的测量数据。以上问题将在未来的研究中进行探究。
| [1] |
GOLLNER M J, HUANG X, COBIAN J, et al. Experimental study of upward flame spread of an inclined fuel surface[J]. Proceedings of the Combustion Institute, 2013, 34(2): 2531-2538. DOI:10.1016/j.proci.2012.06.063 |
| [2] |
JIANG L, MILLER C H, GOLLNER M J, et al. Sample width and thickness effects on horizontal flame spread over a thin PMMA surface[J]. Proceedings of the Combustion Institute, 2017, 36(2): 2987-2994. DOI:10.1016/j.proci.2016.06.157 |
| [3] |
JIANG L, HE J J, SUN J H. Sample width and thickness effects on upward flame spread over PMMA surface[J]. Journal of Hazardous Materials, 2018, 342: 114-120. DOI:10.1016/j.jhazmat.2017.08.022 |
| [4] |
FERNANDEZ-PELLO A C, HIRANO T. Controlling mechanisms of flame spread[J]. Combustion Science and Technology, 1983, 32(1-4): 1-31. DOI:10.1080/00102208308923650 |
| [5] |
WILLIAMS F A. Urban and wildland fire phenomenology[J]. Progress in Energy and Combustion Science, 1982, 8(4): 317-354. DOI:10.1016/0360-1285(82)90004-1 |
| [6] |
TAKENO K, HIRANO T. Flame spread over porous solids soaked with a combustible liquid[J]. Symposium(International)on Combustion, 1988, 21(1): 75-81. |
| [7] |
VOGEL M, WILLIAMS F A. Flame propagation along matchstick arrays[J]. Combustion Science and Technology, 1970, 1(6): 429-436. DOI:10.1080/00102206908952223 |
| [8] |
GOLLNER M J, XIE Y X, LEE M, et al. Burning behavior of vertical matchstick arrays[J]. Combustion Science and Technology, 2012, 184(5): 585-607. DOI:10.1080/00102202.2011.652787 |
| [9] |
FINNEY M A, COHEN J D, FORTHOFER J M, et al. Role of buoyant flame dynamics in wildfire spread[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(32): 9833-9838. |
| [10] |
BU R W, ZHOU Y, SHI L, et al. Experimental study on combustion and flame spread characteristics in horizontal arrays of discrete fuels[J]. Combustion and Flame, 2021, 225: 136-146. DOI:10.1016/j.combustflame.2020.10.049 |
| [11] |
JIANG L, ZHAO Z, TANG W, et al. Flame spread and burning rates through vertical arrays of wooden dowels[J]. Proceedings of the Combustion Institute, 2019, 37(3): 3767-3774. DOI:10.1016/j.proci.2018.09.008 |
| [12] |
BU R W, SHI L, ZHOU Y. Identifying the criterion for discrete flame spread over single-row birch rods[J]. Fire Safety Journal, 2021, 120: 103116. DOI:10.1016/j.firesaf.2020.103116 |
| [13] |
PRAHL J M, TIEN J S. Preliminary investigations of forced convection on flame propagation along paper and matchstick arrays[J]. Combustion Science and Technology, 1973, 7(6): 271-282. DOI:10.1080/00102207308952367 |
| [14] |
WOLFF M F, CARRIER G F, FENDELL F E. Wind-aided firespread across arrays of discrete fuel elements. Ⅱ. Experiment[J]. Combustion Science and Technology, 1991, 77(4-6): 261-289. DOI:10.1080/00102209108951731 |
| [15] |
CARRIER G F, FENDELL F E, WOLFF M F. Wind-aided firespread across arrays of discrete fuel elements. Ⅰ. Theory[J]. Combustion Science and Technology,, 1991, 75(1-3): 31-51. DOI:10.1080/00102209108924077 |
| [16] |
WEBER R O. A model for fire propagation in array[J]. Mathematical and Computer Modelling, 1990, 13(12): 95-102. DOI:10.1016/0895-7177(90)90103-T |
| [17] |
HE Q Q, LIU N A, XIE X D, et al. Experimental study on fire spread over discrete fuel bed-part Ⅰ: Effects of packing ratio[J]. Fire Safety Journal, 2021, 126: 103470. DOI:10.1016/j.firesaf.2021.103470 |
| [18] |
QI Z Y, HU H W, JI J. Investigation on the double-sided concurrent flame spread behavior of log planks[J]. Proceedings of the Combustion Institute, 2023, 39(3): 3889-3898. DOI:10.1016/j.proci.2022.08.096 |
| [19] |
谢小冬. 上坡地表火蔓延的实验和理论研究[D]. 合肥: 中国科学技术大学, 2014. XIE X D. Experimental and theoretical research on upslope surface fire spread[D]. Hefei: University of Science and Technology of China, 2014. (in Chinese) |
| [20] |
卜蓉伟, 范传刚, 周洋. 燃料分布特征对非连续水平火蔓延传热行为的影响机制[J]. 工程热物理学报, 2022, 43(6): 1702-1709. BU R W, FAN C G, ZHOU Y. Mechanism of the fuel distribution characteristics on heat transfer for horizontal flame spread over discrete fuels[J]. Journal of Engineering Thermophysics, 2022, 43(6): 1702-1709. (in Chinese) |



