2. 中南大学 土木工程学院, 长沙 410075
2. School of Civil Engineering, Central South University, Changsha 410075, China
随着公路隧道建设规模迅猛发展,中国已成为世界上公路隧道规模最大、数量最多的国家[1]。截至2021年末,中国公路隧道达到23 268处、2 469.89万m,且中国隧道数量在世界范围内增长最显著[2]。随着隧道数量及机动车保有量的增加,相关研究表明,隧道火灾数量呈逐年上升趋势[3]。隧道属于狭长且半封闭的管状结构,一旦发生火灾容易造成严重的灾难性后果[4-6]。隧道火灾持续时间长,火场及烟气容易迅速蔓延,消防救援和人员疏散工作困难[7]。若隧道火灾处置不当或救援不及时,往往会造成隧道内被困人员的大量伤亡以及财产损失[8]。因此,隧道人员疏散安全性一直是隧道安全领域的研究热点[9-10]。
疏散仿真模拟是目前隧道疏散研究最常用的方法[11],具有计算速度快、应用便捷、使用成本低等特点。疏散仿真模拟常采用的软件有:火灾动力学模拟器(fire dynamics simulator,FDS)、人员应急疏散仿真工程软件Pathfinder、人流运动及疏散仿真工具(simulation of transient evacuation and pedestrian movements,STEPS)等[12-14]。李霞等[15]采用FDS和Pathfinder研究了公路隧道火灾时横洞口车辆停靠随机性对被困人员逃生概率的影响,结果表明横洞口有车辆停靠会影响被困人员疏散路径并降低门流率。陈诗明等[16]通过建立隧道横通道人员疏散模型,研究了不同人员荷载密度、车辆位置对人员疏散时间的影响。Król等[17]利用FDS和Pathfinder软件进行隧道火灾模拟和人员疏散模拟,分析了火灾探测时间、通风系统类型、交通状况、火灾位置对人员疏散的影响。李森生[18]利用FDS进行火灾数值模拟,并采用Pathfinder软件模拟人员疏散,分析了湖底双层隧道共用疏散楼梯间距设置对人员疏散安全性的影响。Wang等[19]利用FDS和Pathfinder软件构建隧道模型,模拟不同纵向风速下的火灾场景和疏散场景。章庭瑞等[20]对多组横通道参数取值情况下共计25种疏散场景进行模拟,获得了横通道间距及宽度对人员疏散时间的影响规律。郭志杰等[21]采用Pathfinder建立了隧道人员疏散仿真模拟平台,研究在高海拔条件下人员疏散速度折减以及隧道内环境能见度对人员疏散决策及人员疏散运动时间的影响。综上所述,现有研究通常会考虑火灾规模、火源位置、通风排烟等对可用安全疏散时间的影响,还会考虑疏散设施类型、间距、宽度、人员荷载、车辆位置等对必需安全疏散时间的影响,而鲜有考虑不同车型在各车道的分布差异及车辆随机分布对疏散时间的影响[22]。
实际上,不同类型的车辆偏向行驶在不同的车道上,如大型货车及大客车偏向于在慢车道行驶,小汽车则更多是在超车道行驶。不同类型车辆的体积和人员荷载相差很大,如大型货车长度和高度都远超小汽车,而人员荷载仅有2人。隧道火灾时,滞留的大型货车及大客车占用了逃生空间,使得逃生路径变得曲折且延长。大客车及小汽车的人员密度大,可对人员荷载造成显著影响。隧道内的人行横通道多位于左侧,不同车道的人员疏散距离及疏散时间也会不同。显然,隧道火灾时,车道车型分布差异及车辆停靠位置的随机性可对疏散时间造成显著影响。若在公路隧道疏散仿真模型中布置车辆,需对各车辆依次进行计算和设定模型代码,会存在计算复杂、容易出错、布置不合理等问题。对于上述问题,前人开展公路隧道火灾及疏散仿真模拟时,常忽略或者简化车辆布置,致使模拟结果存在一定偏差。为提高公路隧道火灾及疏散仿真的建模效率,以及提高模拟结果精准性,有必要根据隧道数值模型(车道)空间坐标、车辆尺寸、车型比例、不同车型的车道分布差异等参数来布置车辆。
本文提出了基于车道车型分布差异来随机布置车辆的算法,并开发了公路隧道火灾及疏散模拟车辆随机布置(randomly arranging vehicle types, RAVT)系统。该系统可以输出车辆模型FDS代码,高效准确地布置公路隧道火灾及疏散数值模型中的车辆。最后,应用该系统生成的代码建立了两车道和三车道隧道疏散模型,分析了车道车型分布差异及车辆随机分布对人员疏散的影响。
1 隧道车辆随机布置算法及系统 1.1 算法实现流程本文针对公路隧道火灾及疏散模拟建模过程中车辆布置的需求及难点,提出了一种基于隧道数值模型空间坐标、车辆尺寸、车型比例、不同车型的车道分布差异等参数来随机布置车辆的方法。隧道车辆随机布置算法的实现流程如图 1所示。

|
| 图 1 隧道车辆随机布置算法实现流程 |
1.2 算法实现具体步骤
算法实现具体步骤如下:
1) 设置车辆类型参数。
假定有m种车辆类型(V1, V2, …, Vm-1, Vm), 第i种类型车辆的长、宽、高、人员荷载、占比分别用LVi, WVi, HVi, PVi, RVi表示。设置的各车型占比应满足式(1)的约束条件,即各车型占比之和等于1。
| $R_{V_1}+R_{V_2}+\cdots+R_{V_{m-1}}+R_{V_m}=1.$ | (1) |
2) 设置人员类型参数。
假定有n种人员类型(P1, P2, …, Pn-1, Pn),第j种类型人员的占比为RPj。设置的各类型人员占比需满足式(2)的约束条件,即各人员类型占比之和等于1。
| $R_{P_1}+R_{P_2}+\cdots+R_{P_{n-1}}+R_{P_n}=1.$ | (2) |
3) 设置公路隧道数值模型空间参数。
设公路隧道数值模型长度方向为X轴方向、宽度方向为Y轴方向、高度方向为Z轴方向。根据隧道X起始坐标(Xs)及结束坐标(Xe)、隧道路面的Z坐标(Z0),可得到公路隧道的长度为|Xe-Xs|。假定公路隧道数值模型共l条车道,需设定各车道中线的Y坐标(Y1, Y2, …, Yl-1, Yl)。各车道的车辆平均间距为(S1, S2, …, Sl-1, Sl)。
4) 设置不同车型的车道分布差异。
不同车型的车道分布差异即不同车型在不同车道的数量占该车型总数的比例。第i种类型车辆在第k条车道的数量占第i种类型车辆总数的比例为R(RVi, Lk),需满足式(3)的约束条件,即第i种类型车辆在各车道的数量占第i种类型车辆总数的比例之和等于1。
| $\begin{aligned} & R\left(R_{V_i}, L_1\right)+R\left(R_{V_i}, L_2\right)+\cdots+ \\ & R\left(R_{V_i}, L_{l-1}\right)+R\left(R_{V_i}, L_l\right)=1 .\end{aligned}$ | (3) |
5) 算法开始进行计算,生成车辆的FDS代码。
按照式(4)计算第i种类型车辆在第k条车道的数量占所有类型车辆总数NT的比例R(RVi, Lk, NT)。
| $R\left(R_{V_i}, L_k, N_{\mathrm{T}}\right)=R\left(R_{V_i}, L_k\right) \cdot R_{V_i} \cdot$ | (4) |
按照式(5)计算第k条车道的车辆数量Nk。
| $N_k=\frac{\left|X_{\mathrm{e}}-X_{\mathrm{s}}\right|}{S_k+R\left(R_{V_1}, L_k, N_{\mathrm{T}}\right) \cdot L_{V_1}+R\left(R_{V_2}, L_k, N_{\mathrm{T}}\right) \cdot L_{V_2}+\cdots+R\left(R_{V_{m-1}}, L_k, N_{\mathrm{T}}\right) \cdot L_{V_{m-1}}+R\left(R_{V_m}, L_k, N_{\mathrm{T}}\right) \cdot L_{V_m}}.$ | (5) |
按照式(6)计算公路隧道数值模型中所有类型车辆的总数NT。
| $N_{\mathrm{T}}=N_1+N_2 \cdots+N_{l-1}+N_l.$ | (6) |
按照式(7)计算第k条车道的第i种类型车辆的数量Nk, Vi。
| $N_{k, v_i}=N_k \cdot R\left(R_{V_i}, L_k, N_{\mathrm{T}}\right).$ | (7) |
计算并输出公路隧道数值模型的人员荷载参数。按照式(8)计算第k条车道的第i种类型车辆的人员荷载P(RVi, Lk)。按照式(9)计算第k条车道的人员荷载总数PLk。按照式(10)计算公路隧道数值模型的人员荷载总数P。按照式(11)计算公路隧道第j种类型人员的人员荷载总数Pj。
| $P\left(R_{V_i}, L_k\right)=N_{k, V_i} \cdot P_{V_i}.$ | (8) |
| $\begin{gathered}P_{L_k}=P\left(R_{V_1}, L_k\right)+P\left(R_{V_2}, L_k\right)+\cdots+ \\ P\left(R_{V_{m-1}}, L_k\right)+P\left(R_{V_m}, L_k\right) .\end{gathered}$ | (9) |
| $P=P_{L_1}+P_{L_2}+\cdots+P_{L_{l-1}}+P_{L_l}.$ | (10) |
| $P_j=P \cdot R_{P_j}.$ | (11) |
在式(1)—(7)的基础上,构建第k条车道车辆排列的集合(或数组)VArray(Lk),数组的长度等于第k条车道的车辆数量Nk。VArray(Lk)的元素包含:Nk(V1)个V1,Nk(V2)个V2,……, Nk(Vm-1)个Vm-1,Nk(Vm)个Vm。使用数组随机排列算法对VArray(Lk)中的元素进行随机排序得到新的集合NVArray(Lk)。显然,VArray(Lk)与NVArray(Lk)的差异在于元素(车辆类型)的排列顺序不一样。
以Xs为起点,以Sk为间距,依次根据NVArray(Lk)中元素(车辆类型)来排列布置车辆。令排列的第a辆车的X结束坐标为Xa, e。假设排列的第a+1辆车的类型为Vi,那么第a+1辆车的X、Y、Z的起止坐标Xa+1, s、Xa+1, e、Ya+1, s、Ya+1, e、Za+1, s、Za+1, e可分别按照式(12)—(17)计算。
| $X_{a+1, \mathrm{~s}}=X_{a, \mathrm{e}}+S_k, $ | (12) |
| $X_{a+1, \mathrm{e}}=X_{a, \mathrm{e}}+S_k+L_{V_i}.$ | (13) |
| $Y_{a+1, s}=Y_k-\frac{W_{V_i}}{2}, $ | (14) |
| $Y_{a+1, \mathrm{e}}=Y_k+\frac{W_{V_i}}{2}.$ | (15) |
| $Z_{a+1, \mathrm{~s}}=Z_0, $ | (16) |
| $Z_{a+1, \mathrm{e}}=Z_0+H_{V_i}.$ | (17) |
算法输出第k条车道的第a+1辆车的FDS代码为“&OBST XB=Xa+1, s, Xa+1, e, Ya+1, s, Ya+1, e, Za+1, s, Za+1, e/”。对车辆类型进行多次随机排列,输出各车道各辆车的FDS代码,直至所有车道的所有车辆代码均输出完成。
6) 建立公路隧道火灾和疏散数值模型。
将第5)步生成的FDS代码导入到Pyrosim和Pathfinder软件中,可用来快速建立包含车辆布置的公路隧道火灾数值模型和疏散数值模型;还可在第5)步计算的结果及生成的FDS代码基础上,添加其他必要的FDS代码。按照本步骤建立的火灾数值模型及疏散数值模型,均将不同类型车辆在不同车道的分布差异性考虑在内,与实际情况更接近,因此模型得到的模拟结果更加准确。
7) 生成多组随机代码。
鉴于不同类型车辆的分布位置对于火灾烟气蔓延及输运、人员疏散逃生都有影响,可在设置同样的隧道数值模型空间坐标、车辆尺寸、车型比例、不同车型的车道分布差异等参数情况下,随机生成满足上述参数要求的多组FDS代码。然后,参照第6)步,以上述FDS代码为依托建立多组火灾模拟模型或人员疏散模型进行模拟。对各组模型的模拟结果进行数学统计处理(如求平均值、最大值与最小值相差百分比、方差、标准差等),可为评估隧道火灾安全性提供更加充分的数据支撑。
1.3 系统开发应用1.2节的算法流程,本文基于HTML5、CSS、JavaScript开发了对应的RAVT系统(如图 2所示)。应用该系统可快速计算出车辆布置的参数及人员荷载参数,并自动生成相应的车辆模型FDS代码,可实现高效准确地布置公路隧道火灾及疏散数值模型中的车辆。FDS代码可用于直接建立火灾模型,也可导入到Pyrosim和Pathfinder中进行火灾模拟和疏散模拟。该系统界面由4个模块构成,分别为工程项目参数设置模块、车辆类型参数设置模块、人员类型参数设置模块及车辆随机布置计算模块。
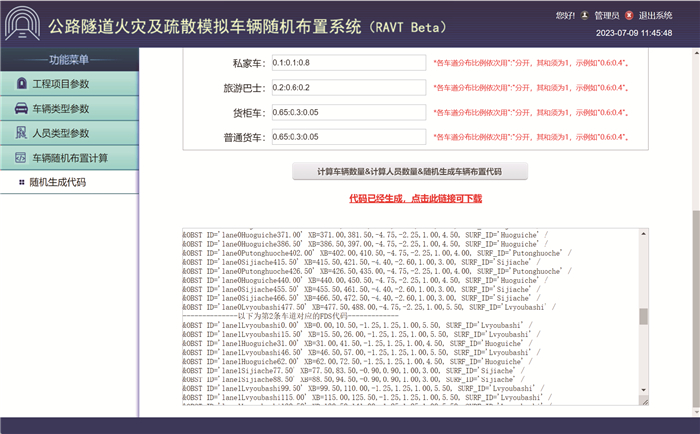
|
| 图 2 RAVT系统界面 |
2 模拟场景设置 2.1 隧道疏散模型参数
为研究车道车型分布差异及车辆随机分布对隧道火灾人员疏散的影响及验证RAVT系统的可行性,本文拟建立隧道人员疏散模型,分别考虑两车道、三车道两种车道场景。隧道模型长度设为500 m,即X起始值为0.0 m,X结束值为500.0 m。两车道隧道模型宽度为7.5 m,各车道宽为3.5 m,依次为慢车道、超车道。各车道中线Y值分别为-1.75和1.75 m;三车道隧道模型宽度为11 m,依次为慢车道、行车道和超车道。各车道中线Y值分别为-3.5、0.0和3.5 m。两车道隧道和三车道隧道于超车道一侧均设置了宽为0.5 m的检修平台。人行横通道净高为2.5 m,净宽为2.0 m,分别设置于隧道长123与373 m处,依次为1#人行横通道和2#人行横通道,间隔为250 m。两车道隧道模型与三车道隧道模型的Z起始值均为1.0 m。隧道模型的车道平面示意图如图 3所示。

|
| 图 3 隧道模型车道平面示意图 |
2.2 车辆及人员组成
根据《道路交通管理 机动车类型》(GA 802—2019)并结合实际情况,设置隧道内车辆类型分类、车辆尺寸、载客量和车型比例如表 1所示。本文考虑的是所有车辆均坐满乘客。
| 车辆类型 | (长/m)×(宽/m)× (高/m) | 载客量/人 | 车型比/% |
| 私家车 | 6×1.8×2 | 4 | 54.0 |
| 旅游巴士 | 10.5×2.5×4.5 | 36 | 17.3 |
| 货柜车 | 10.5×2.5×3.5 | 2 | 17.4 |
| 普通货车 | 8.5×2.5×3 | 2 | 11.3 |
根据美国消防工程师协会(Society of Fire Protection Engineers,SFPE)《消防工程手册》和相关文献资料[23],设置隧道内疏散人员类型为成年男性、成年女性、儿童和老人。各人员类型的构成比例、疏散速度和肩宽尺寸见表 2。
| 人员类型 | 所占比例/% | 疏散速度/ (m·s-1) | 肩宽尺寸/m |
| 成年男性 | 40 | 1.2 | 0.4 |
| 成年女性 | 35 | 1.0 | 0.35 |
| 儿童 | 15 | 0.8 | 0.3 |
| 老人 | 10 | 0.6 | 0.4 |
2.3 疏散模拟场景
在实际情况中,隧道内超车道私家车等小型车辆较多,而慢车道旅游巴士、货柜车、普通货车等大型车辆较多。因此,本文按照各车道车型比例均匀分布和非均匀分布(接近于实际情况)各设置相应比例,从而建立疏散模拟场景。各车道车型比例依次用比例号“∶”分开,且各比例之和为1,如表 3所示。其中两车道隧道车型比例顺序依次为慢车道∶超车道,三车道隧道车型比例顺序依次为慢车道∶行车道∶超车道。
| 车道数 | 车道车型比例分布 | 私家车 | 旅游巴士 | 货柜车 | 普通货车 |
| 两车道 | 均匀分布 | 0.50∶0.50 | 0.50∶0.50 | 0.50∶0.50 | 0.50∶0.50 |
| 非均匀分布 | 0.20∶0.80 | 0.80∶0.20 | 0.90∶0.10 | 0.90∶0.10 | |
| 三车道 | 均匀分布 | 0.33∶0.33∶0.33 | 0.33∶0.33∶0.33 | 0.33∶0.33∶0.33 | 0.33∶0.33∶0.33 |
| 非均匀分布 | 0.10∶0.10∶0.80 | 0.20∶0.60∶0.20 | 0.65∶0.30∶0.05 | 0.65∶0.30∶0.05 |
考虑车辆极度拥堵、拥堵和非拥堵情形将车距分别设置为1.5、5和60 m。根据车道数、车辆间距和各车道车型比例共设置了12种模拟场景(如表 4所示)。考虑到车辆停靠位置的随机性,本文对12种模拟场景各进行20次车辆随机布置和疏散模拟,共计240次疏散模拟。通过在RAVT系统中输入以上参数,点击随机生成车辆布置代码即可进行相应计算并生成FDS代码。FDS代码中会显示车辆总数和人员总数(见表 4)。将FDS代码导入Pathfinder软件进行疏散仿真模拟,计算各场景下车辆随机布置后的人员疏散时间。
| 场景 | 车道数 | 车间距/m | 车道车型比例分布 | 车数/辆 | 人数/人 |
| S1 | 2 | 1.5 | 均匀分布 | 108 | 940 |
| S2 | 2 | 1.5 | 非均匀分布 | 109 | 922 |
| S3 | 2 | 5 | 均匀分布 | 78 | 716 |
| S4 | 2 | 5 | 非均匀分布 | 78 | 694 |
| S5 | 2 | 60 | 均匀分布 | 14 | 112 |
| S6 | 2 | 60 | 非均匀分布 | 15 | 150 |
| S7 | 3 | 1.5 | 均匀分布 | 162 | 1 410 |
| S8 | 3 | 1.5 | 非均匀分布 | 157 | 1 520 |
| S9 | 3 | 5 | 均匀分布 | 117 | 1 074 |
| S10 | 3 | 5 | 非均匀分布 | 115 | 1 086 |
| S11 | 3 | 60 | 均匀分布 | 21 | 168 |
| S12 | 3 | 60 | 非均匀分布 | 22 | 236 |
Pathfinder软件是目前隧道与地下空间人员疏散模拟常用的软件之一。本文疏散模拟均选用Steering模式,在该模式中门不会限制人群的流动,且人与人之间会保持一个合理的间距,能够较为真实地反映隧道内的人流速度和疏散时间[24]。在使用Pathfinder软件进行疏散模拟时,设置疏散人员随机分布,且根据各车道人数分别在各车道布置疏散人员。
3 结果与分析 3.1 疏散结果必需安全疏散时间(required safe evacuation time, RSET)指起火时刻至人员疏散到安全区域的时间,如式(18)所示。其中:Ta、Tr为报警探测时间、人员响应时间,分别取为60、120 s[25]。Tm为疏散仿真模拟所得人员疏散行走时间。
| $\operatorname{RSET}=T_{\mathrm{a}}+T_{\mathrm{r}}+T_{\mathrm{m}}.$ | (18) |
由于车辆停靠位置的随机性,每个场景对应的20次模拟结果都不一样。表 5中统计了各场景中20次疏散模拟得到的行走时间(Tm)的平均值、最大值、最小值、最大值与最小值相差百分比、方差和均方差,进而对疏散结果进行统计分析。
| 场景 | 平均值/s | 最大值/s | 最小值/s | 最大值与最小值相差百分比/% | 方差/s2 | 均方差/s |
| S1 | 288.96 | 341.00 | 219.30 | 55.49 | 955.28 | 30.91 |
| S2 | 245.45 | 331.00 | 212.80 | 55.55 | 1 294.51 | 35.98 |
| S3 | 221.28 | 240.00 | 202.50 | 18.52 | 166.36 | 12.90 |
| S4 | 212.73 | 232.50 | 201.80 | 15.21 | 50.14 | 7.08 |
| S5 | 190.73 | 209.80 | 153.00 | 37.12 | 249.65 | 15.80 |
| S6 | 192.28 | 208.00 | 157.30 | 32.23 | 151.42 | 12.31 |
| S7 | 418.54 | 479.30 | 304.50 | 57.41 | 2 387.24 | 48.86 |
| S8 | 389.58 | 517.30 | 323.80 | 59.76 | 3 528.91 | 59.41 |
| S9 | 303.45 | 344.80 | 252.80 | 36.39 | 923.88 | 30.40 |
| S10 | 278.53 | 360.80 | 241.30 | 49.52 | 1 587.38 | 39.84 |
| S11 | 197.40 | 211.00 | 168.50 | 25.22 | 150.95 | 12.29 |
| S12 | 198.49 | 209.30 | 169.00 | 23.85 | 100.10 | 10.01 |
选取各场景中与该场景疏散时间平均值最接近的一次随机模拟作为典型模拟。图 4和5分别为模拟场景S1—S6、场景S7—S12中的典型疏散模拟情形时,疏散人数随疏散时间的变化。
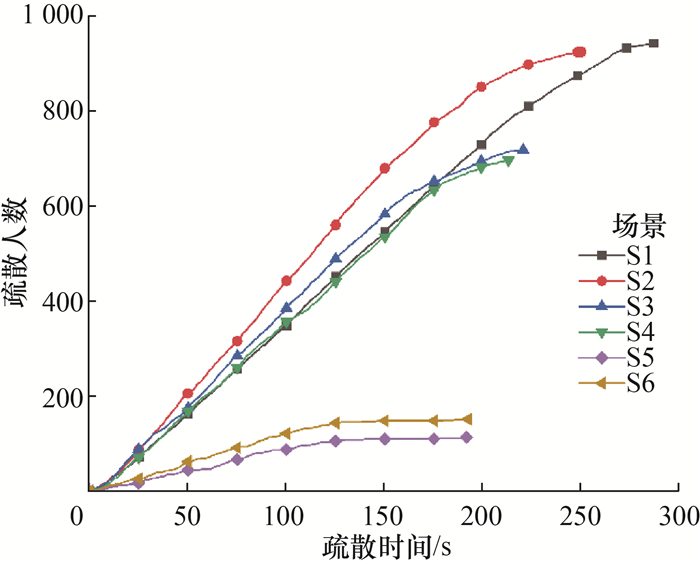
|
| 图 4 场景S1—S6典型模型中疏散人数变化 |
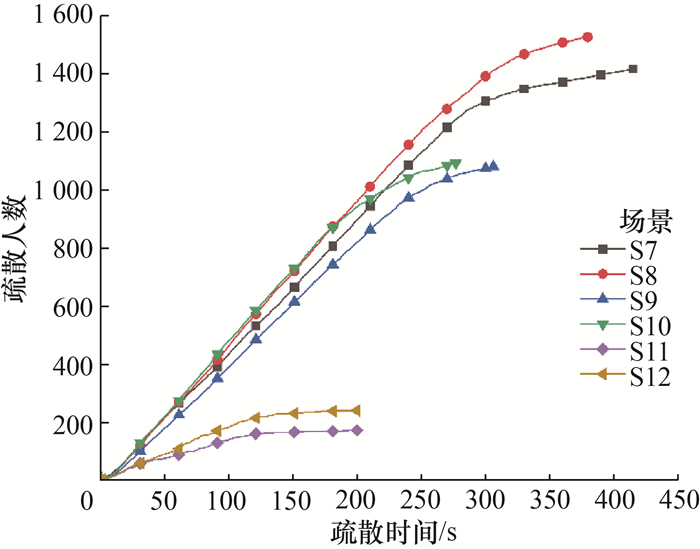
|
| 图 5 场景S7—S12典型模型中疏散人数变化 |
3.2 疏散结果分析 3.2.1 车道车型分布差异对疏散时间的影响
由表 5可知,当车辆极度拥堵(车距为1.5 m)和车辆拥堵(车距为5 m)时,各车道车型比例均匀分布时所用的疏散时间平均值远大于各车道车型比例非均匀分布时所用的疏散时间平均值。尤其当车辆极度拥堵时,两者疏散时间平均值的差异性更为显著,差值最大达到43.51 s。由图 4和5也可以看出,场景S1所用疏散时间整体上大于场景S2所用疏散时间,场景S7所用疏散时间整体上大于场景S8所用疏散时间。这说明车辆极度拥堵和车辆拥堵时,车道车型分布差异对疏散时间的影响很大。
当车辆极度拥堵和车辆拥堵时,各车道车型比例均匀分布时人员疏散所需时间普遍较长,即平均值较大。这可能是由于各车道车型比例均匀分布时,超车道大型车辆比实际情况多,车辆滞留在横通道入口的可能性增大,易造成疏散时人员拥堵。被困人员必须穿过车辆间的间隙才能进入人行横通道,疏散距离大幅增加,导致疏散时间大幅增加。横通道入口滞留大型车辆导致人员拥堵的典型情况如图 6所示。该典型场景为S7场景下疏散时间最长的场景,即三车道隧道、车距为1.5 m、各车道车型比例均匀分布。疏散时间取为150.0 s。Exited表示该时刻已疏散人数为486,该场景总疏散人数为1 410。
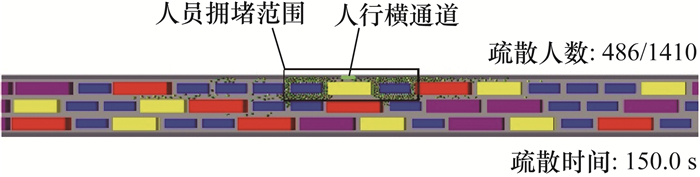
|
| 图 6 横通道入口滞留大型车辆的情形 |
由图 4和5可知,场景S5和S6、场景S11和S12所用疏散时间相差很小,曲线变化趋势也基本一致。这说明当车辆非拥堵(车距为60 m)时,各车道车型比例均匀分布和非均匀分布时所用的疏散时间平均值相差较小,即各车道车型分布差异对疏散时间平均值影响不大。但是,各车道车型比例均匀分布会增大疏散时间的波动范围,即方差相差较大。
3.2.2 车辆随机分布对疏散时间的影响当车辆极度拥堵时,各车道车型比例均匀分布和非均匀分布时,各次疏散模拟中疏散时间最大值与最小值相差百分比均超出55.00%。其中,S8场景下,疏散时间最大值与最小值相差百分比达到了59.76%。此外,在S8场景下,各次疏散模拟时间方差最大,达到了3 528.91 s2,且S8场景下的方差与S7场景下的方差相差了1 141.67 s2。这说明车辆极度拥堵时,各车道车型比例非均匀分布情形下,随着车辆布置发生变化,疏散结果存在很大差异,即车辆极度拥堵时,同一场景下车辆的分布对疏散时间的影响最大。其余各场景下,随着车辆布置发生变化,疏散结果也发生了相应的变化。本研究结果表明,各车道相同车型分布比例和相同车距时,随着车辆布置不同,疏散结果也会不同。尤其当车辆极度拥堵时,车辆分布对疏散时间的影响程度更大。
4 结论本文提出了隧道车辆随机布置算法并开发了对应系统RAVT。该系统充分考虑了车道车型分布差异和车辆随机分布对疏散时间的影响,能准确地计算出人员数量和车辆数量,并对车辆位置进行布置,具有较强的适用性和可行性。本文综合应用RAVT及Pathfinder软件,研究了在两车道和三车道隧道内,车辆极度拥堵、车辆拥堵和车辆非拥堵情形下,车道车型分布差异及车辆随机分布对疏散时间的影响。主要研究结论如下:
1) 车辆极度拥堵和车辆拥堵时,各车道车型分布差异对疏散时间的影响很大,疏散时间平均值相差最大达到43.51 s;
2) 车辆非拥堵时,各车道车型分布差异对疏散时间平均值影响不大,但各车道车型比例均匀分布会增大疏散时间的波动范围;
3) 人行横通道入口处很有可能滞留大型车辆,尤其当车辆拥堵、各车道车型比例均匀分布时,超车道大型车辆相对较多,更易造成疏散时人员拥挤,导致疏散时间变长;
4) 即使各车道具有相同车型分布比例和相同车距,随着车辆布置不同,疏散结果也会不同,疏散时间最大值与最小值相差百分比达到了59.76%。
鉴于上述结论,建议学者或工程师开展隧道疏散仿真模拟时须考虑车道车型分布差异及车辆随机停靠性的影响。本文对两车道和三车道隧道进行了多组不同车距、不同车型分布比例场景下的疏散模拟,后续研究还可以考虑其他影响因素及参数组合,如研究超大断面隧道(四车道隧道)疏散时间变化规律。此外,还可以将RAVT系统导出的FDS代码进行火灾数值模拟,研究车道车型分布差异及车辆随机分布对隧道火灾模拟结果的影响。
| [1] |
洪开荣, 冯欢欢. 中国公路隧道近10年的发展趋势与思考[J]. 中国公路学报, 2020, 33(12): 62-76. HONG K R, FENG H H. Development trends and views of highway tunnels in China over the past decade[J]. China Journal of Highway and Transport, 2020, 33(12): 62-76. (in Chinese) |
| [2] |
PERVEZ A, LEE J, HUANG H L. Exploring factors affecting the injury severity of freeway tunnel crashes: A random parameters approach with heterogeneity in means and variances[J]. Accident Analysis & Prevention, 2022, 178: 106835. |
| [3] |
REN R, ZHOU H, HU Z, et al. Statistical analysis of fire accidents in Chinese highway tunnels 2000—2016[J]. Tunnelling and Underground Space Technology, 2019, 83: 452-460. DOI:10.1016/j.tust.2018.10.008 |
| [4] |
杨宇轩, 刘畅, 仇培云, 等. 含坡度隧道车辆阻塞下全尺寸火灾实验[J]. 清华大学学报(自然科学版), 2020, 60(12): 1030-1038. YANG Y X, LIU C, QIU P Y, et al. Full-scale experimental study of a fire under a vehicle in a sloped tunnel[J]. Journal of Tsinghua University(Science and Technology), 2020, 60(12): 1030-1038. DOI:10.16511/j.cnki.qhdxxb.2020.25.028 (in Chinese) |
| [5] |
LI Y Z, INGASON H. Overview of research on fire safety in underground road and railway tunnels[J]. Tunnelling and Underground Space Technology, 2018, 81: 568-589. DOI:10.1016/j.tust.2018.08.013 |
| [6] |
岳顺禹, 龙增, 仇培云, 等. 独头隧道火灾全尺寸实验研究[J]. 清华大学学报(自然科学版), 2023, 63(6): 917-925. YUE S Y, LONG Z, QIU P Y, et al. Full-scale experimental study on single-end tunnel fires[J]. Journal of Tsinghua University(Science and Technology), 2023, 63(6): 917-925. (in Chinese) |
| [7] |
王星, 屈建荣, 夏永旭, 等. 单洞双向公路隧道火灾人员疏散救援研究[J]. 地下空间与工程学报, 2020, 16(3): 944-954. WANG X, QU J R, XIA Y X, et al. Study on the human evacuation and rescue in single highway tunnel for subtended traffic with fire[J]. Chinese Journal of Underground Space and Engineering, 2020, 16(3): 944-954. (in Chinese) |
| [8] |
赵文忠, 罗宇, 戎贤. 基于FDS的高速公路隧道火灾人员疏散研究[J]. 消防科学与技术, 2020, 39(12): 1683-1687. ZHAO W Z, LUO Y, RONG X. Study on evacuation from highway tunnel fire based on FDS[J]. Fire Science and Technology, 2020, 39(12): 1683-1687. DOI:10.3969/j.issn.1009-0029.2020.12.017 (in Chinese) |
| [9] |
戎贤, 许家杰, 张新宇, 等. 特长公路隧道火灾烟气沉降特性对人员疏散影响的研究[J]. 中国安全生产科学技术, 2023, 19(2): 128-135. RONG X, XU J J, ZHANG X Y, et al. Research on influence of fire smoke descent characteristics on personnel evacuation in extra-long highway tunnel[J]. Journal of Safety Science and Technology, 2023, 19(2): 128-135. (in Chinese) |
| [10] |
胥旋, 史聪灵, 李建, 等. 考虑绕行效应的人员疏散元胞自动机模型研究[J]. 中国安全生产科学技术, 2018, 14(2): 20-25. XU X, SHI C L, LI J, et al. Study on cellular automata model of personnel evacuation considering detour effect[J]. Journal of Safety Science and Technology, 2018, 14(2): 20-25. (in Chinese) |
| [11] |
胡卫, 黄亚东, 蒋云刚, 等. 隧道横纵向通道组合模式下的人员疏散特性[J]. 消防科学与技术, 2022, 41(8): 1073-1078. HU W, HUANG Y D, JIANG Y G, et al. Evacuation characteristics of the transverse and longitudinal channel combination mode in tunnel[J]. Fire Science and Technology, 2022, 41(8): 1073-1078. DOI:10.3969/j.issn.1009-0029.2022.08.011 (in Chinese) |
| [12] |
沈卓恒, 马杰, 钱芳, 等. 盾构隧道火灾人员纵向疏散模拟[J]. 消防科学与技术, 2019, 38(1): 92-94. SHEN Z H, MA J, QIAN F, et al. Simulation on longitudinal evacuation in shield tunnel under fire[J]. Fire Science and Technology, 2019, 38(1): 92-94. (in Chinese) |
| [13] |
王明年, 胡萧越, 于丽, 等. 公路隧道动态火灾规模及人员疏散研究[J]. 消防科学与技术, 2020, 39(2): 203-207. WANG M N, HU X Y, YU L, et al. Research on dynamic fire scale and personnel evacuation of urban road tunnel[J]. Fire Science and Technology, 2020, 39(2): 203-207. (in Chinese) |
| [14] |
刘松涛, 赵金龙, 卫文彬, 等. 隧道内不同间距双火源火灾试验及模拟研究[J]. 中国公路学报, 2022, 35(7): 193-202. LIU S T, ZHAO J L, WEI W B, et al. Experimental and simulation study on double fire source tunnels with different spacings[J]. China Journal of Highway and Transport, 2022, 35(7): 193-202. (in Chinese) |
| [15] |
李霞, 郭梦婷, 王海鹏, 等. 基于车辆停靠随机性的公路隧道火灾逃生概率研究[J]. 安全与环境学报, 2023, 23(5): 1689-1698. LI X, GUO M T, WANG H P, et al. Study on personnel escape probability in road tunnel based on randomness of vehicle parking[J]. Journal of Safety and Environment, 2023, 23(5): 1689-1698. (in Chinese) |
| [16] |
陈诗明, 张玉春, 杜晟, 等. 车辆-人员荷载条件对隧道人员疏散时间的影响[J]. 武汉理工大学学报(信息与管理工程版), 2016, 38(6): 662-666. CHEN S M, ZHANG Y C, DU S, et al. Effect of vehicle-personnel load condition on personnel evacuation time in tunnel[J]. Journal of Wuhan University of Technology(Information & Management Engineering), 2016, 38(6): 662-666. (in Chinese) |
| [17] |
KRÓL A, KRÓL M. The factors determining the number of the endangered people in a case of fire in a road tunnel[J]. Fire Safety Journal, 2020, 111: 102942. |
| [18] |
李森生. 湖底双层超大直径盾构隧道火灾人员疏散分析[J]. 中国安全生产科学技术, 2022, 18(5): 199-204. LI S S. Analysis on personnel evacuation in fire of a double-layer super-large diameter shield tunnel at bottom of lake[J]. Journal of Safety Science and Technology, 2022, 18(5): 199-204. (in Chinese) |
| [19] |
WANG K, HU J W, CHEN R D, et al. A study on the evacuation of an extra-long highway tunnel fire: A case study of Chengkai tunnel[J]. Sustainability, 2023, 15(6): 4865. |
| [20] |
章庭瑞, 李维, 闫治国. 长大公路隧道纵向排烟与人员疏散特性研究[J]. 现代隧道技术, 2020, 57(S1): 651-661. ZHANG T R, LI W, YAN Z G. Research on performance of longitudinal smoke extraction strategy and personnel evacuation in road tunnel[J]. Modern Tunnelling Technology, 2020, 57(S1): 651-661. (in Chinese) |
| [21] |
郭志杰, 张奥宇, 鲁水涛, 等. 高海拔隧道防烟策略及疏散通道间距探讨[J]. 地下空间与工程学报, 2021, 17(5): 1671-1678. GUO Z J, ZHANG A Y, LU S T, et al. Discussion on the smoke prevention strategy of high-altitude tunnel and the evacuation channel spacing[J]. Chinese Journal of Underground Space and Engineering, 2021, 17(5): 1671-1678. (in Chinese) |
| [22] |
惠豫川, 肖益民, 黄浩天, 等. 单向长隧道极端条件下火灾安全疏散研究[J]. 地下空间与工程学报, 2020, 16(6): 1826-1835, 1848. HUI Y C, XIAO Y M, HUANG H T, et al. Research on fire safety evacuation in unidirectional and long tunnel under extreme conditions[J]. Chinese Journal of Underground Space and Engineering, 2020, 16(6): 1826-1835, 1848. (in Chinese) |
| [23] |
李强, 王峻, 方青青, 等. 大直径城市水下盾构公路隧道人员疏散模式研究[J]. 现代隧道技术, 2022, 59(S1): 666-675. LI Q, WANG J, FANG Q Q, et al. Research on personnel evacuation modes in large-diameter urban underwater shield highway tunnels[J]. Modern Tunnelling Technology, 2022, 59(S1): 666-675. (in Chinese) |
| [24] |
马燕平, 郑学林, 臧建彬. 单洞双层超大直径城市盾构隧道逃生优化模拟[J]. 科学技术与工程, 2021, 21(11): 4641-4647. MA Y P, ZHENG X L, ZANG J B. Optimization simulation of single tunnel double layer and super large diameter urban shield tunnel escape[J]. Science Technology and Engineering, 2021, 21(11): 4641-4647. (in Chinese) |
| [25] |
徐志胜, 谢宝超, 张焱, 等. 公路隧道通风排烟及人员疏散[M]. 北京: 机械工业出版社, 2021. XU Z S, XIE B C, ZHANG Y, et al. Road tunnel ventilation and evacuation[M]. Beijing: China Machine Press, 2021. (in Chinese) |



