隧道为现代交通及地下资源开采提供了便利,然而隧道内的各类灾害一旦发生,就会对人类生命和财产造成严重损失,因而确保安全是隧道运营面临的非常重要的问题。火灾是隧道中常见的灾害类型[1-3]。隧道内发生火灾时释放的热量和有害组分在热浮力和通风作用的驱动下,导致高温有害气体实现热质同步输运,从而在隧道内扩散蔓延,严重威胁隧道安全。为降低隧道火灾造成的危害,必须厘清隧道内物理场信息的演化规律。
为此,很多学者对通风作用下的隧道火灾进行了研究。卢平等[4]通过实验研究了纵向通风水平隧道火灾烟气流动特性,得到了控制火灾烟气逆流的通风条件。陈长坤等[5]通过缩尺寸模型隧道火灾实验和大涡模拟方法研究了不同火源面积下隧道火灾温度场,得到了火灾在不同阶段的演化规律。安伟光等[6]研究了油罐车行驶速度对隧道火灾温度及烟气蔓延的影响,得到了移动火焰下隧道火灾各参数的演化规律。传统的实验和模拟方法所得结果可以为隧道安全设计和救援决策提供理论依据。除此之外,通过人工智能的方法也可以基于数据或模型获得隧道火灾中各关键控制参数的一般规律。Hong等[7]通过大量数值模拟结果,利用机器学习算法预测了隧道火灾中的烟气流动状态和烟气回流长度。Zhang等[8]通过时序神经网络模型成功反演了隧道火灾中热释放速率等参数。Hu等[9]通过神经网络模型预测了隧道火灾中顶棚最高温度的一般规律。以上方法均为隧道火灾的一般规律的总结提供了有利的依据。
然而,以上方法均无法实现隧道火灾全物理场信息的预测,也无法实现已知数值模拟全物理场信息下火灾中关键控制参数的预测。事实上,火灾全物理场信息的预测目前仅可通过计算流体力学的方式获得,但计算速度极为缓慢。通过全物理场信息预测火灾的控制条件属于反演预测的范畴,虽然有学者对此进行了研究,但物理场信息和隧道火灾关键控制参数信息(标量信息)之间的双向预测仍未能实现。本文提出一种深度学习模型用于实现物理场信息和标量关键控制参数信息间的双向快速预测。
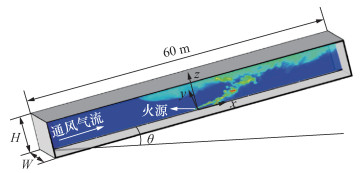
1 场景与预测方法 1.1 火灾场景本文所考察的隧道火灾场景如图 1所示。除了隧道长度设为固定值60 m外,隧道高度(H)、宽度(W)、倾斜角度(θ)、火源功率(
|
| 图 1 隧道火灾场景示意图 |
本文基于火灾动力学模拟器(fire dynamics simulator,FDS)[10]采用高分辨率数值模拟手段获取隧道火灾数据库。模拟过程中,混凝土材料的比热容、热导率、传热厚度分别设为1.04 kJ/(kg·K)、1.8 W/(m·K)、2 m。隧道内壁和墙内的导热在计算时使用一维导热方程模拟内壁边界上格点的温度变化。隧道入口处施加垂直于整个截面的均匀分布的速度边界条件,其大小为v0。隧道出口处施加恒动压出口边界条件。燃料的一氧化碳的质量产率假定为0.01 kg/kg,烟气的质量产率假定为0.037 kg/kg,烟气中氢体积占比假定为10%[11]。为使系统可达统计意义的准稳态,数值模拟时间定为从火源点燃推进至300 s时结束。
1.2 数据集所形成的数据集包含1 000组不同隧道火灾场景中的演化过程,每组案例中均受到上文中6项物理和几何条件的控制,各项控制参数从以下变化范围内均匀随机选取:H∈{2, 2.5, 3, 3.5, 4} m,W∈{3, 3.5, 4, 4.5, 5}m,T∞∈[10, 30] ℃,θ∈[-15, 15] (°),
每组案例在确定6项控制参数后,使用数值模拟的方式进行计算,本文采用D*判据[12]保证网格精度[1],即单元网格尺寸小于D*/10,以确保在能捕捉流场精细结构的同时保证计算速度。在各项参数均取最极端值的情形下,以0.062 5 m为边长的网格仍符合判据要求,因此选取该精度的网格进行计算。
为使研究结果具有统计上的代表意义,物理场信息的计算结果均处理为准稳态下的时均结果。物理场信息可以为直接的数值张量,也可以间接为经过上下限和颜色栏统一后物理场的图像。每一类物理场均有与之对应的6项控制参数,因此数据集中每个样本可以表示为S={ x, z }。其中:x为物理场张量,z =(H, W, T∞, θ,
数据集中共含有1 000个样本,随机选取其中700个组成训练集,剩余300个组成测试集。
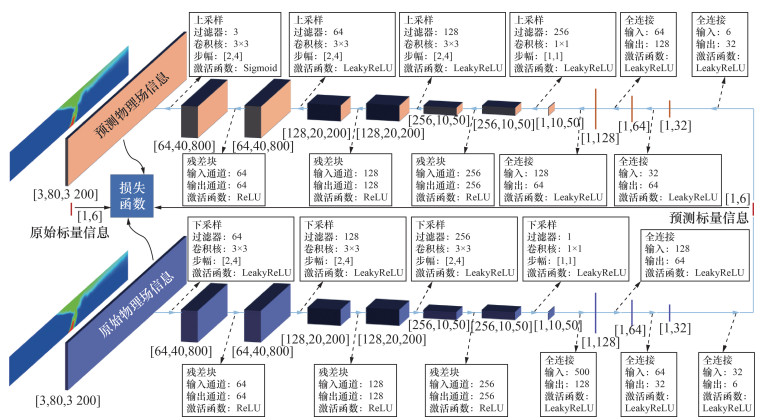
1.3 深度学习模型的构建为实现隧道火灾中物理场信息和关键控制参数(标量信息)间的相互快速预测,提出如图 2所示的深度学习网络模型。图 2的下半部分为编码部分,上半部分为解码部分。编码部分[13]包含4个交替进行的下采样层和残差块层以及4个全连接层,其中前3个下采样层的零填充数为1×1,而最后1个下采样层的补充层数为0;卷积核及其移动步幅信息如图 2所示,第1个全连接层之前的张量在连接前需展成1×500大小的向量。解码部分包含4个交替进行的上采样层和残差块层以及4个全连接层,顺着数据的流动方向上的前3个上采样层的输出零填充数为1×3,最后1个上采样层的输出零填充数为1×1;卷积核及其移动步幅信息如图 2所示,最后1个全连接层的输出向量在进行上采样操作之前需展成1×10×50大小的张量。网络结构中的其他信息可直接在图 2中读取。网络结构中的残差块[14]起到防止梯度消失的作用,每个残差块内部均为类似的结构,依次为:卷积层(卷积核3×3,零填充数1×1,输出通道数等于输入通道数)、激活层(ReLU函数[15])、卷积层(卷积核3×3,零填充数1×1,输出通道数等于输入通道数)、叠加层(上一层卷积层结果与原始输入相加)、激活层(ReLU函数)。
|
| 图 2 双向预测网络模型结构示意图 |
网络损失函数(
| $ \mathcal{L}=\underbrace{\frac{1}{3 N} \sum\limits_{c=1}^3 \sum\limits_{n=1}^N\left(x_{c, n}-x_{c, n}^{\prime}\right)^2}_{\mathcal{L}_1}+ \\ \;\;\;\;\;\;\;\;\;\;\underbrace{\frac{10}{6} \sum\limits_{k=1}^6\left(z_k-z_k^{\prime}\right)^2}_{\mathcal{L}_2} . $ | (1) |
其中:xc, n是第c个通道中第n个像素点的值,zk是第k个控制标量的值。图像的原始通道总数为3,原始像素点数为80×3 200,控制标量的个数为6 (如1.2节所述)。为平衡两部分损失函数的大小,将
模型训练超参数设置为:训练批尺寸大小为8,优化求解器为Adam[16],求解器的β1、β2参数分别为0.9和0.999,学习率为1.5×10-4,避免分母为0的小参量为1.5×10-8,训练周期数为500。
模型训练完成后,通过网络结构中的解码部分(图 2中上半部分),以6项控制参数作为网络输入,即可以实现标量信息到物理场信息的预测;通过网络结构中的编码部分(图 2中下半部分),以物理场信息图片作为输入,即可实现物理场信息到标量关键控制参数的预测。
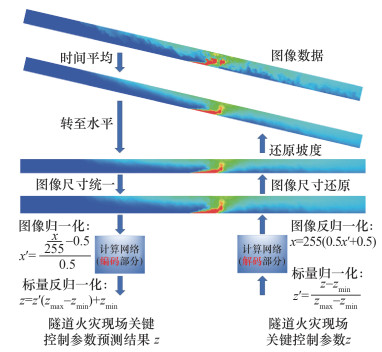
1.4 数据预处理为规范化计算网络的输入和输出信息,并使网络易于训练和收敛,对数据集进行相应的数学处理[17]。如图 3所示,对于图像数据,在输入网络进行预测之前,先将所有的瞬态结果进行时间平均得到时均场结果,接着将时均场结果旋转至水平,之后将时均场信息的图像进行图像尺寸的统一(尺寸为网络的输入尺寸,即80×3 200),最后按照均匀缩放的原则将像素点的RGB[18]值放缩到[-1, 1]的区间范围内。经过编码部分的计算之后,获得归一化后的标量信息,因此需要进行一次反归一化即可获得最终隧道火灾现场关键控制参数的预测结果。对于6项火灾的标量信息,使用最小最大归一化方法,将其等比例缩放到[0, 1]的区间范围内。对于给出隧道火灾现场关键控制参数来预测物理场信息的情况,则与上述顺序相反,首先将现场关键控制参数进行最小最大归一化,之后输入解码部分的网络中进行计算,输出的物理场信息进行反归一化并按照标量信息中的几何信息将图像尺寸进行还原,最后再根据标量信息中的几何信息将隧道坡度进行还原。具体流程如图 3所示。
|
| 图 3 数据预处理细节示意图 |
2 结果分析与讨论 2.1 模型训练过程分析
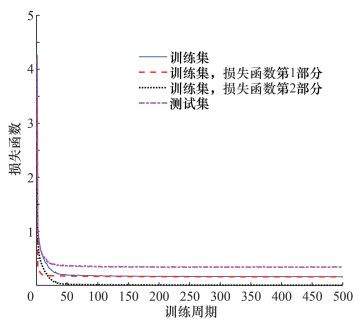
图 4给出了模型训练过程中损失函数随训练周期的演化情况。可以看出,训练集的损失函数在50个训练周期内急剧下降,而测试集的损失函数在25个周期内就急剧下降至接近收敛的状态。图 4中还分别绘制了损失函数中第1部分和第2部分的演化曲线。损失函数的第2部分(
|
| 图 4 训练过程损失函数演化曲线 |
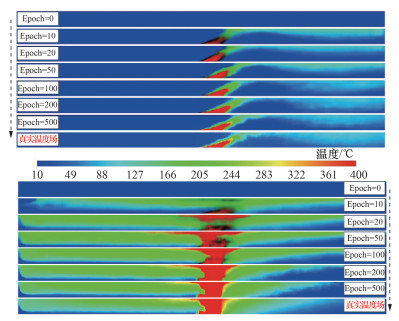
图 5显示了训练过程中模型对物理场信息预测能力的增强过程。该结果为从训练集中随机选取的2个案例,所演示的预测物理场为温度场。可以看到,当训练周期(Epoch)为0时,整个模型无任何预测能力,在对解码网络输入6项控制参数后,所获得的温度场图像无法观察到任何火灾发生后的温度变化。当训练周期到10以后,已经可以大致预测出温度场的轮廓,但火焰周围的温度场依然误差比较大。在训练周期达到100时,可以看到模型基本具备了预测能力,整个温度场与真实温度场已经非常接近。当训练周期达到500时,尽管预测结果在烟气轮廓的位置表现得不如真实温度场那样平滑,但预测温度场和真实温度场已经几乎一致,表明本文提出的网络模型具备较强的对物理场信息的预测能力。
|
| 图 5 训练集中随机选取的2个案例在训练过程中由标量信息预测温度场信息的预测结果演化情况 |
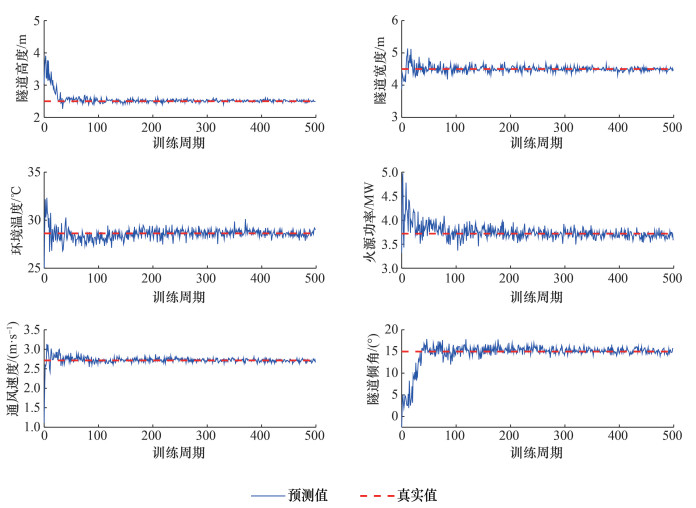
图 6显示了训练过程中模型对控制参数标量信息预测能力的增强过程。该结果为从训练集中随机选取的某案例的结果。图 6中红色直线为案例的真实值,蓝色曲线为训练过程中的预测值。可以看出,各控制参数预测值在训练初期都没有接近真实值,在训练周期达到50左右时,基本上所有参数都近似收敛到真实值。隧道高度、隧道宽度、通风速度和隧道倾角在训练周期达到100以后的振荡程度非常小,说明模型对这些变量的辨识程度非常高;而环境温度和火源功率的预测结果随训练周期的振荡程度相对强一些,说明模型对环境温度和火源功率的辨识难度相对更高,这可能是因为环境温度对整个温度场的影响能力较弱,而且由于燃烧的不稳定性,火源功率也不易确定。但总体而言,6项关键控制参数的预测结果都展现了模型良好的预测能力。
|
| 图 6 训练集中随机选取的案例在训练过程中由物理场信息预测标量关键控制参数信息的预测结果演化情况 |
2.2 模型预测能力评估分析
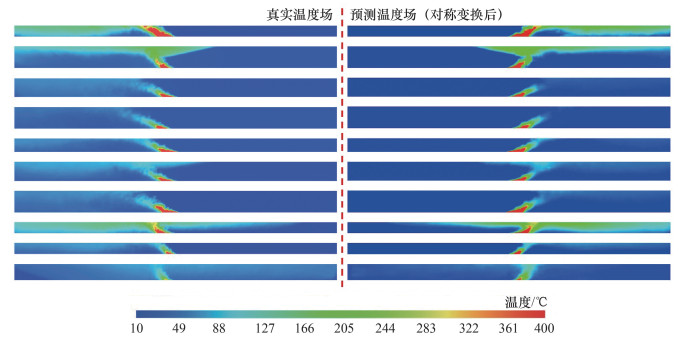
2.1节中已经展现了模型在训练过程中对于训练集的学习能力,但在训练完成后依然需要通过测试集中的数据进一步评估其预测能力。为评估由标量信息预测物理场信息的能力,图 7从预测集中的300个案例中挑选出一些案例作为对比,其中左侧为真实温度场,右侧为预测温度场(为更容易对比,对其作了左右对称变换)。温度场颜色栏所标记的温度范围均统一为10~400 ℃。图 7中结果的良好对称展现了模型具有优越的物理场信息预测能力。此外,为说明模型在任何控制参数下的预测能力,所挑选的预测案例中的各项控制参数都是不同的,图 7中的高度和倾斜角度就可以清晰地表明这一点。可见,模型预测具有较强的鲁棒性。
|
| 图 7 测试集中所选取不同控制参数下的真实温度场与预测温度场(经过左右对称变换)对比 |
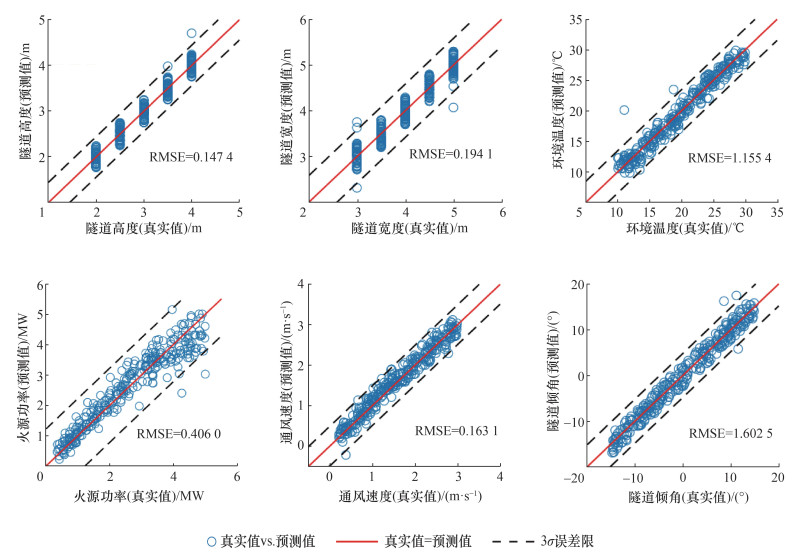
此外,由物理场信息预测控制参数等标量信息同样重要。图 8为网络中编码器所预测的结果和真实结果的对比。可以看出,均方根误差(root mean square error, RMSE)总体而言相对真实值的量级较小,预测效果较好。然而,模型对隧道宽度的预测效果相对弱一些,可能是由于隧道宽度对温度场的影响相对较弱。此外,火源功率的预测效果也相对较弱,其原因与之前的分析类似,这可能是由于火源功率是相对敏感的参数,燃烧本身的不稳定性[20]导致该指标难以预测。其他指标如隧道高度、通风速度、倾斜角度等都获得了相对较好的预测效果。
|
| 图 8 测试集中真实关键控制参数与预测关键控制参数对比 |
3 结论
本文开展隧道火灾关键控制参数和物理场信息间快速双向预测方法研究,主要结论如下:
1) 提出了基于隧道火灾特点的深度学习网络模型,可用于各类物理信息场以及火灾现场关键控制参数的预测。阐明了物理场信息图像和标量关键控制参数的处理方式,使得快速预测模型的训练更易收敛,预测效果更好。
2) 基于所设计的网络损失函数,分析了快速预测模型的训练过程,确定了模型达到近似收敛的训练周期,明确了模型对数据集的学习能力。
3) 评估了双向预测模型的预测能力,定性分析和对比了预测集的真实物理场和预测物理场,定量分析和对比了隧道火灾真实关键控制参数和预测关键控制参数。结果表明,隧道火灾的平均温度场和6项隧道火灾的关键控制参数得到了基本的预测,预测结果同时涵盖了隧道的几何信息和物理信息。
| [1] |
CARVEL R. A review of tunnel fire research from Edinburgh[J]. Fire Safety Journal, 2019, 105: 300-306. DOI:10.1016/j.firesaf.2016.02.004 |
| [2] |
CASEY N. Fire incident data for Australian road tunnels[J]. Fire Safety Journal, 2020, 111: 102909. DOI:10.1016/j.firesaf.2019.102909 |
| [3] |
田向亮, 钟茂华, 刘畅, 等. 不同阻塞条件下的隧道火灾全尺寸试验研究[J]. 煤炭科学技术, 2021, 49(2): 93-101. TIAN X L, ZHONG M H, LIU C, et al. Experimental study on safety full-scale of tunnel fire disaster under different blocking conditions[J]. Coal Science and Technology, 2021, 49(2): 93-101. (in Chinese) |
| [4] |
卢平, 丛北华, 廖光煊, 等. 纵向通风水平隧道火灾烟气流动特性研究[J]. 中国工程科学, 2004, 6(10): 59-64. LU P, CONG B H, LIAO G X, et al. Study of fire smoke flow characteristics of horizontal tunnel using longitudinal ventilation[J]. Strategic Study of CAE, 2004, 6(10): 59-64. (in Chinese) |
| [5] |
陈长坤, 王玮玉, 康恒, 等. 不同火源面积下隧道火灾温度场试验与数值模拟分析[J]. 中国公路学报, 2018, 31(6): 235-243. CHEN C K, WANG W Y, KANG H, et al. Experimental and numerical simulation analysis of temperature field of tunnel fire with different fire source areas[J]. China Journal of Highway and Transport, 2018, 31(6): 235-243. (in Chinese) |
| [6] |
安伟光, 广大庆, 陈凡宝. 油罐车行驶速度对隧道火灾温度及烟气蔓延的影响[J]. 消防科学与技术, 2023, 42(6): 742-746. AN W G, GUANG D Q, CHEN F B. The effect of tank truck speed on the temperature distribution and smoke spread of tunnel fire[J]. Fire Science and Technology, 2023, 42(6): 742-746. (in Chinese) |
| [7] |
HONG Y, KANG J H, FU C J. Rapid prediction of mine tunnel fire smoke movement with machine learning and supercomputing techniques[J]. Fire Safety Journal, 2022, 127: 103492. DOI:10.1016/j.firesaf.2021.103492 |
| [8] |
ZHANG X N, WU X Q, HUANG X Y. Smart real-time forecast of transient tunnel fires by a dual-agent deep learning model[J]. Tunnelling and Underground Space Technology, 2022, 129: 104631. DOI:10.1016/j.tust.2022.104631 |
| [9] |
HU P, PENG X Y, TANG F. Prediction of maximum ceiling temperature of rectangular fire against wall in longitudinally ventilation tunnels: Experimental analysis and machine learning modeling[J]. Tunnelling and Underground Space Technology, 2023, 140: 105275. DOI:10.1016/j.tust.2023.105275 |
| [10] |
MCGRATTAN K B, BAUM H R, REHM R G, et al. Fire dynamics simulator: Technical reference guide: NISTIR 6467[R]. Gaithersburg, USA: National Institute of Standards and Technology, 2000.
|
| [11] |
HURLEY M J, GOTTUK D, HALL J R, et al. SFPE handbook of fire protection engineering[M]. 5th ed. New York, USA: Springer, 2016.
|
| [12] |
MCGRATTAN K B, MCDERMOTT R, WEINSCHENK C, et al. Fire dynamics simulator technical reference guide volume 1: Mathematical model[R]. Gaithersburg, USA: National Institute of Standards and Technology, 2013.
|
| [13] |
AGHDAM H H, HERAVI E J. Guide to convolutional neural networks[M]. New York, USA: Springer, 2017: 51.
|
| [14] |
ZHANG K, SUN M, HAN T X, et al. Residual networks of residual networks: Multilevel residual networks[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 28(6): 1303-1314. DOI:10.1109/TCSVT.2017.2654543 |
| [15] |
YAROTSKY D. Error bounds for approximations with deep ReLU networks[J]. Neural Networks, 2017, 94: 103-114. DOI:10.1016/j.neunet.2017.07.002 |
| [16] |
YAZAN E, TALU M F. Comparison of the stochastic gradient descent based optimization techniques[C]// Proceedings of 2017 International Artificial Intelligence and Data Processing Symposium. Malatya, Turkey, 2017: 1-5.
|
| [17] |
SARANYA C, MANIKANDAN G. A study on normalization techniques for privacy preserving data mining[J]. International Journal of Engineering and Technology, 2013, 5(3): 2701-2704. |
| [18] |
SÜSSTRUNK S, BUCKLEY R, SWEN S. Standard RGB color spaces[C]// Proceedings of the 7th Color Imaging Conference. Scottsdale, USA, 1999: 127-134.
|
| [19] |
HOCHREITER S. The vanishing gradient problem during learning recurrent neural nets and problem solutions[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 1998, 6(2): 107-116. DOI:10.1142/S0218488598000094 |
| [20] |
SIRIGNANO W A. Driving mechanisms for combustion instability[J]. Combustion Science and Technology, 2015, 187(1-2): 162-205. DOI:10.1080/00102202.2014.973801 |



