2. 国网山东省电力公司, 济南 250001;
3. 中国标准化研究院, 北京 100191
2. State Grid Shandong Electric Power Company, Jinan 250001, China;
3. China National Institute of Standardization, Beijing 100191, China
2023年6月国家能源局发布《新型电力系统发展蓝皮书》,强调了新型电力系统要以确保能源电力安全为基本前提,以满足经济社会高质量发展的电力需求为首要目标[1]。有序开展电力作业对于确保新型电力系统的长期稳定运行至关重要。但是,电力作业受人员、设备、环境和管理等多种因素的耦合影响,使得电力作业的风险识别要素日趋复杂,且具有高度随机性和时空耦合性。因此,面向电力行业安全监测的作业风险识别领域正面临严峻挑战。
近年来,技术水平的不断提高推动了新理论、新理念、新方法在新型电力系统中的广泛应用。为进一步提升电力作业的规范要求、降低人员安全事故的发生频率,研究人员聚焦于从电力事故中提取风险要素。高阳等[2]构建了一套新型电力作业安全管理系统,并通过层次分析法(analytic hierarchy process,AHP)对安全管理系统中各关键风险要素进行定量分析,旨在强化电力作业的安全性。然而,电力作业的风险要素多源且时空关系复杂,单纯依赖人工分析方法来识别电力作业风险不仅准确度难以保证,而且主观分析方法往往带来主观偏颇性和偶然性因素。许永刚等[3]针对于电力作业特征构建了一个智能预警系统框架,实时监控作业人员的操作规范和作业场景,并评估作业风险,但缺乏具体实施流程,亟需结合新技术和新规范来完善与发展不相协调的风险因素。陈碧云等[4]提取电力作业事故数据库中的作业风险数据作为训练集,并使用云自适应粒子群算法优化脉冲神经网络以实现对电力作业风险态势感知。但是,神经网络对数据规模和质量的要求较高,实际上电力作业事故数据库的统计信息并不完善,高维历史数据的获取难度较高,难以兼顾多种典型空间。
整体来看,典型场景下电力作业的风险识别模型可划分为风险因子体系和风险因子权重机制两部分,而风险因子体系的构建存在诸多挑战:1) 作业风险要素多源且难以量化。例如,电力行业中电击、电弧闪和触电等电气风险,人员坠落、物体坠落、大风等高空作业风险,爆炸、泄漏和中毒等化学风险,电弧、短路和高温等火灾风险,不当操作引起的夹伤、碰撞和切割等机械伤害风险[5]。作业风险的多源特性对风险因子体系的全面性提出了严峻挑战,因此亟需研制一套全方位、易量化的电力作业风险因子库。2) 风险因子体系固定,但典型作业场景多样。由于带电、近电、高空、有限空间等典型空间对于不同风险因子的重视程度各异,因此风险因子体系需要具备普适性,因子库应覆盖不同典型作业场景的特征,最终由因子权重机制基于自适应准则通过动态调整权重分布来兼容不同作业空间[6]。3) 现有的技术标准过于精细,导致不同标准对于同一技术要求的表述存在差异;各专业、各时期的技术标准与管理规定存在矛盾,过于冗余的条例造成执行不便,为电力作业人员带来诸多困扰[7];国内的细分标准与国外标准在形式上存在不利于对接的问题,致使作业指导书未能引用最新技术标准。因此,亟需融合现有的标准规范,以确保风险因子体系与时俱进,并建立通用的电力行业典型作业风险识别机制,强化技术标准的落地执行。
对于如何确定风险因子权重机制的问题,典型方法可划分为主观识别方法、客观识别方法以及综合识别方法,其中综合识别方法可进一步细化为组合风险识别方法和自适应风险识别(adaptive risk identification, ARI)方法[8],具体如下:1) 主观识别方法在权重结果中融入了不同专家对风险因子的主观认知,从而使识别结果更贴合风险管控专家的侧重点[9],但不同专家对不同风险因子的重视程度存在偏差,可能导致识别结果的不稳定或存在偏颇[10]。主流的主观识别方法包括区间层次分析法(interval analytic hierarchy process,IAHP)[9]、模糊层次分析法[10]、二项系数法[11]、AHP[12]等。2) 客观识别方法则是通过分析客观数据的分布来判断风险因子间的数学关系,但对事故风险数据的规模和精度有更高的要求,且单纯依赖客观权重将缺失专家主观意见对其的修正,风险识别结果容易偏离实际需求。目前主流的客观识别方法包括熵权法[13]、主成分分析法[14]、多目标规划法[15]等。3) 综合识别方法可以降低单一识别方法造成的偏颇风险,其中组合识别方法是通过固定形式的数学运算来组合主观识别结果和客观识别结果,可归纳为线性加权和乘法合成两种形式[16],但组合识别方法的本质是简单加权组合主客观识别结果,未将客观和主观结果有机融入一个完整模型中,并且主观和客观结果的各自所占比例缺乏理论支撑,使识别结果难以让人信服。近期,自适应(自学习)方法开始兴起,但仅初步应用于极个别领域。张宏博等[17]率先提出权重自适应的概念,以极大熵准则为导向,以Bayes优化为途径,构建自适应的赋权方法,但没有将主观结果融入自适应模型中,过度依赖指标数据的客观分布;Ge等[18]以主观专家认知为基础,在迭代过程中不断降低权重信息熵使权重分布更为均衡,进而提升评估的容错率,但采用的退火模拟算法在某些场景下的寻优效果较主流的群智能算法、商用求解器仍存在一定差距,且未能充分利用动态调节机制。综上,文[17-18]的两种策略均未体现ARI方法可通过配置约束调节机制来兼容多种典型场景的动态识别特性,也未能基于高效的优化方法来融合主观和客观评价结果。
总体来看,ARI方法既具备组合识别方法的主客观融合优点,又规避了主客观权重各自占比难以确定的缺点,可通过约束调节机制动态适应不同的典型作业空间,在风险识别领域具备广阔的发展空间和应用潜力。因此,本文首先构建了电力行业典型作业的风险识别总体框架,接着建立了典型作业多源要素全域风险因子体系,根据风险管控专家意见计算基于IAHP的风险因子的主观权重区间,以极大熵准则为客观基准融合风险管控专家的意见,引入约束调节机制为作业空间的灵活调整提供实施途径,提出渐进式蜜獾算法为自适应权重的求解提供优化手段。最后,案例结果验证了本文的ARI模型可有效量化电力行业典型空间下的作业风险。
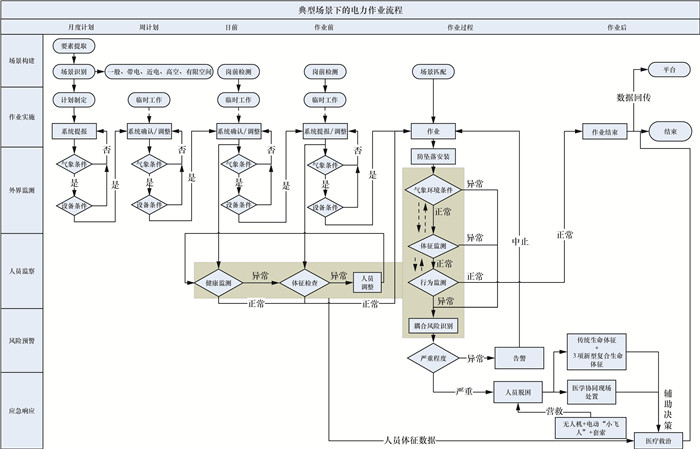
1 电力行业典型场景作业风险识别框架 1.1 电力行业典型场景作业流程电力行业典型场景作业流程涵盖了场景构建、作业实施、外界监测、人员监察、风险预警和应急响应等关键环节,其中电力作业风险的识别贯穿于流程始终。典型场景下的电力作业流程图如图 1所示,具体流程如下:
|
| 图 1 典型场景下的电力作业流程图 |
1) 场景构建是电力作业的数据觉察阶段。通过全面了解作业目标、地理位置、周围环境、工作条件、人员配置,提取作业场景的关键信息要素[7],确定此次作业场景所隶属的典型空间类型(一般、带电、近电、高空、有限空间),获取风险识别所需的客观数据,从而为后续工作提供数据支撑。
2) 作业实施是电力作业的核心环节。根据事先构建的作业场景制定下一步作业计划,并提交系统审核,等待确认和调整;审核通过后开展作业,完成相关设备的安装、调试、检修、维护以及作业验收。在此过程中,需要严格遵守安全规范和标准规定,以确保作业过程的安全、高效、质量可控。
3) 外界监测是作业安全防控的外围防线。根据所属的典型空间,指导防坠落装置安装,严格监测相关的气象和设备条件,取消异常作业计划。
4) 人员监察是作业安全防控的自我防线。人员监察主要从生命体征和行为习惯2个维度来评价作业人员的风险状态,建立实时的管理机制和监测系统,以及时发现和解决潜在问题,保障电力作业安全。
5) 风险预警是全域要素风险的耦合识别环节。基于全域风险要素,通过既定的风险识别模型耦合识别当前典型空间下引发事故的风险,量化当前或未来的作业风险等级,并对异常状况及时告警,确保电力作业的安全开展。
6) 应急响应是紧急情况下的生命保障措施。基于风险识别状况制定电力作业的应急预案,以最大限度地降低潜在事故风险。当严重事故发生时启动应急预案,开展人员营救、医学协同现场处置、生命体征诊断等医疗救治行动,尽量保障作业人员的生命安全。
1.2 电力行业典型作业风险类别纵观近几年的电力作业事故,作业风险大多源自作业风险辨识不完善、作业风险管控不到位、个人防护措施不到位、安全设施运维管理不到位等。为量化电力作业风险的严重程度,提供风险识别的判别尺度,本文构建了表 1所示的电力行业典型作业风险类别。
| 风险等级 | 风险后果 |
| 低风险 | 电力作业风险可控,可在遵守标准的前提下进行 |
| 较低风险 | 电力作业存在较低风险,低概率发生人身轻微伤事故 |
| 中风险 | 电力作业存在一定风险,低概率发生人身轻伤事故 |
| 较高风险 | 电力作业存在较高风险,低概率发生人身较重伤事故 |
| 高风险 | 电力作业存在高度风险,低概率发生人身重伤事故 |
| 极高风险 | 电力作业存在极高风险,低概率发生多人重伤事故 |
根据不同风险等级,制定作业计划时需基于风险因子数据有针对性地完善现场作业人员的防护措施。较低风险需分配专人指导并监督现场作业安全;中风险需由部门负责人或委托人指导、检查并监督作业安全;较高风险需由上级单位负责人或委托技术人员进行指导、检查并监督作业安全;高风险需暂停作业,公司负责人分析危险并采取科学防控措施后方可继续工作;极高风险则禁止电力作业,须制定严格的防控措施,将风险等级降至较高风险及以下后方可开展作业。
1.3 电力行业典型作业风险识别体系电力行业典型作业风险识别具有一套科学的体系。首先,需要收集并整合不同电力作业场景下的作业事故案例,融合雷达、气象站、现场记录等多源观测数据,对典型事故气象要素进行反演,获取作业事故发生时的气象要素数据;其次,提取作业事故发生时的风速、温度、湿度、降水等变化情况,分析它们与电力作业事故的关联程度,进而确定事故风险的关键气象影响因子;最后,结合多源监测、融合感知和气象预报,构建基于人工智能的典型电力作业的多源要素风险量化模型,以识别作业计划或现场的风险情况。
本文构建的电力行业典型作业风险识别体系主要包含两个部分:用于量化个体风险的典型作业多源要素全域风险因子体系、主客观动态融合的自适应赋权方法。最终,本文建立了基于渐进式蜜獾算法的典型作业多源要素风险的自适应识别模型。
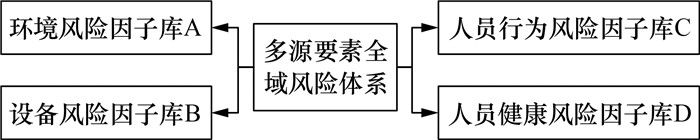
2 典型作业多源要素全域风险因子体系为实现作业现场和作业计划的全域风险量化,本文构建了图 2所示的多层次多维度的典型作业多源要素全域风险因子体系。该体系共包含51个风险因子,划分为环境风险因子库、设备风险因子库、人员行为风险因子库、人员健康风险因子库。为便于观察和应用,每个风险因子在数据获取后进行标准化,数值越高则代表风险越高。
|
| 图 2 多源要素全域风险因子体系 |
2.1 环境风险因子库
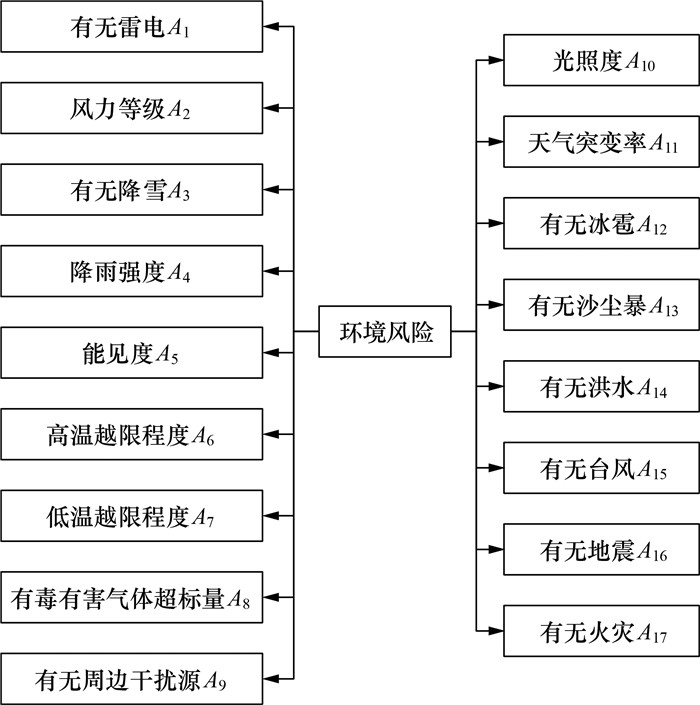
环境风险是带电、近电、高空、有限空间等典型空间下首要考虑的风险因素。首先,结合历史安全事故记录和电力作业安全规范,分析作业环境风险失控机理,构建涵盖强风、降水、雷电、高温、有毒有害气体、周边干扰源等关键环境指标的因子库,再结合作业位置风险隐患信息,量化作业环境风险。本文构建的环境风险因子库如图 3所示,共17个风险因子。
|
| 图 3 环境风险因子库 |
2.2 设备风险因子库
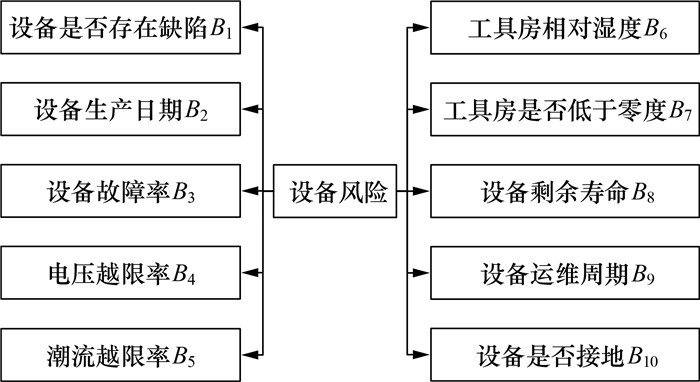
电力作业的设备风险分析与模型构建是现场亟待解决的难题。为了分析不同作业工具、平台、作业之间的设备风险差异,本文基于设备特性和运行参数,结合历史作业安全事故记录,构建了作业设备风险因子库,如图 4所示,共10个风险因子。
|
| 图 4 设备风险因子库 |
2.3 人员行为风险因子库
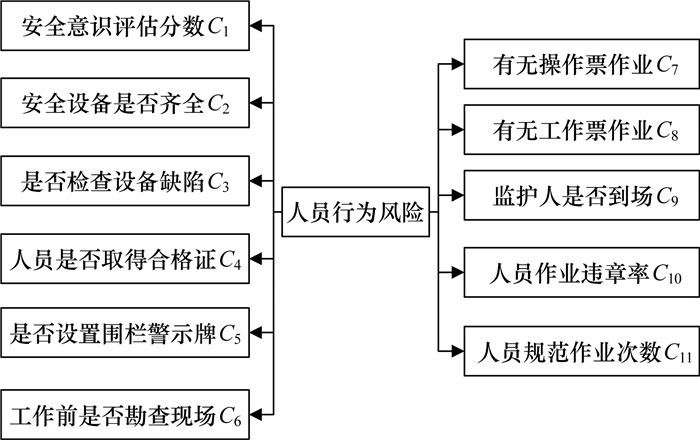
典型作业的人员行为风险是电力作业的重点监察对象。通过分析操作人员的熟练度、作业行为的规范性对作业安全的影响,结合电力作业安全操作规定和现场监督人员评价,形成能够反映行为习惯安全隐患的人员行为风险因子库,如图 5所示,共包含11个风险因子。
|
| 图 5 人员行为风险因子库 |
2.4 人员健康风险因子库
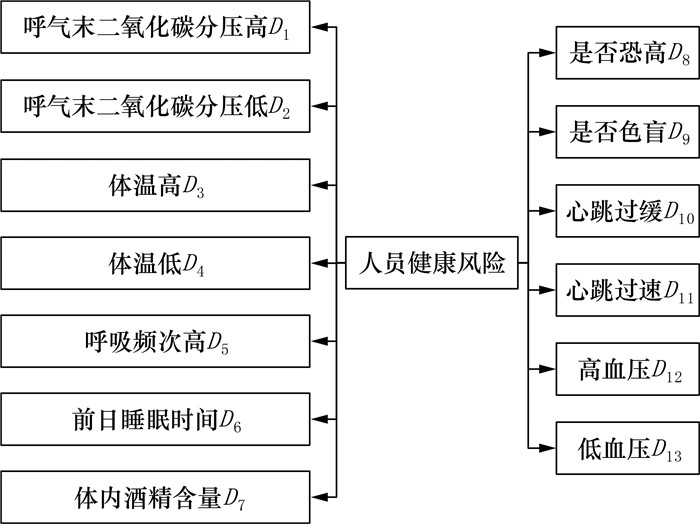
为了保证人身安全,现阶段典型作业场景下电力作业风险识别引入了对作业人员的健康风险分析。图 6所示的人员健康风险因子库基于不同作业条件对人体生理、心理耐受度的影响,量化生理风险和心理风险对安全作业的影响,共包含13个风险因子。
|
| 图 6 人员健康风险因子库 |
3 渐进式蜜獾算法
构建动态适应多种典型空间的ARI模型,亟需一种强搜索能力的优化算法根据作业场景特征的变化对因子权重分布进行动态调整,因此本文提出了渐进式蜜獾算法(progressive honey badger algorithm, PHBA)作为ARI模型的通用求解算法。PHBA借鉴蜜獾群体的觅食行为,通过对蜜獾的挖掘阶段和寻蜜阶段进行渐进式引导从而改进了传统蜜獾算法(honey badger algorithm, HBA),提升了蜜獾的决策准确度。在挖掘阶段,蜜獾利用嗅觉来估测猎物(目标)位置,并在目标周围徘徊,选择合适的挖掘地点;在寻蜜阶段中,在响蜜指引下蜜獾直接定位目标位置,使受控随机化,在保持充沛种群多样性的同时保持优秀局部探索能力。具体步骤如下:
步骤1 初始化阶段。初始化蜜獾的数量(候选解的种群数量) NPHBA,并根据式(1)确定蜜獾所处位置xi,
| $ x_i=\mathrm{lb}_i+r_1 \cdot\left(\mathrm{ub}_i-\mathrm{lb}_i\right), \quad r_1 \in[0, 1] . $ | (1) |
式中:xi是第i个蜜獾(候选解)的位置,而lbi和ubi分别是第i个蜜獾的狩猎空间下界和上界。
步骤2 定义适应度函数。适应度函数f(·)是量化蜜獾群体进化状态的函数,引导蜜獾的搜索方向。
步骤3 定义行动强度。行动强度I与目标气味强度以及蜜獾与目标的距离有关。目标越近,目标气味越强烈,蜜獾行动越迅速,反之亦然:
| $ I_i=r_2 \cdot \frac{L}{4 \pi d_i^2}, \quad r_2 \in[0, 1], $ | (2) |
| $ L=\left(x_i-x_{i+1}\right)^2, $ | (3) |
| $ d_i=x_{\text {prey }}-x_i . $ | (4) |
式中:Ii是第i个蜜獾的行动强度,L是目标的气味强度,di代表目标与第i个蜜獾之间的距离,xprey是目标的位置(迄今为止的全局最优解)。
步骤4 更新密度因子α,实现从挖掘阶段的粗略估计到寻蜜阶段精细搜索的平稳过渡。
| $ \alpha=C_\alpha \cdot \mathrm{e}^{-\frac{C_{\mathrm{PHBA}}}{C_{\mathrm{PHBA}-\mathrm{max}}}} \cdot $ | (5) |
式中:递减影响因子Cα是一个不小于1的常数,CPHBA是当前迭代次数,CPHBA-max是最大迭代次数。伴随着α随迭代次数依次递减,PHBA的随机化程度同步降低。
步骤5 更新蜜獾群体的位置。为降低陷入局部最优的风险,本文提出一种渐进式引导策略以协助蜜獾高效扫描狩猎空间。蜜獾位置的更新策略被分为“渐进式挖掘阶段”和“渐进式寻蜜阶段”。如果范围在[0, 1]的随机数ra小于0.5,则进入渐进式挖掘阶段;反之则进入渐进式寻蜜阶段。
步骤5-1:渐进式挖掘阶段。蜜獾的行动轨迹将类似心形,并基于式(6)模拟心形运动,
| $ \begin{gathered} x_{\text {new }}=x_{\text {prey }}+F \beta I x_{\text {prey }}+ \\ F r_3 \alpha d_i\left|\cos \left(2 \pi r_4\right) \cdot\left[1-\cos \left(2 \pi r_5\right)\right]\right| . \end{gathered} $ | (6) |
式中:xnew指蜜獾的新位置;觅食参数β代表蜜獾觅食能力,恒大于1;r3、r4和r5是范围在[0, 1] 的随机数。F作为改变搜索方向的标志,通过式(7)确定:
| $ \begin{gathered} F= \begin{cases}1, & r_6 \leqslant 0.5 ; \\ -1, & \text { 其他. }\end{cases} \\ r_6=1-0.8 C_{\mathrm{AHBA}} / C_{\mathrm{AHBA}-\max } . \end{gathered} $ | (7) |
式中r6是PHBA的渐进式搜索指向数。得益于渐进式的思想,PHBA能在搜索初期开展大范围探索以搜寻全局最优解的大致位置,在搜索后期则将更注重于对局部最优解的精度提升。若新位置的蜜獾具有更好的适应度f(xnew),则全局最优解将被替换为xnew。
步骤5-2:渐进式寻蜜阶段。蜜獾跟随响蜜寻找蜂巢的过程可模拟为
| $ x_{\text {new }}=x_{\text {prey }}+F r_7 \alpha d_i \text {. } $ | (8) |
式中:r7是0到1的随机数,F和α通过式(7)和(5)确定。根据距离信息,蜜獾群体将围绕目前的目标位置xprey附近进行搜寻。若新位置的蜜獾具有更好的适应度f(xnew),则全局最优解将被替换为xnew。此过程中,PHBA能够有效应对复杂空间搜索问题,保证在勘探与开发之间的平衡性。
步骤6 当PHBA达到最大迭代次数CPHBA-max,算法结束。
4 基于渐进式蜜獾算法的典型作业多源要素风险的自适应识别方法为了分析一般、带电、近电、高空、有限空间等典型空间下多源要素对电力作业安全的影响,风险识别方法需能自适应电力作业场景的变化;另外,由于电力作业风险量化的特殊性,传统的主观、客观、组合赋权方法并不适用。因此,本文提出了基于PHBA的典型作业多源要素风险的自适应识别方法,主要包括:赋予主观认知的IAHP、实现客观平衡的极大熵准则、随作业场景动态变化的约束调节机制、基于PHBA求解的风险识别流程。
4.1 IAHPIAHP是一种用于量化风险状态的主观模糊赋权方法。ARI模型通过IAHP融入风控专家的认知,估测各风险因子的主观权重区间,流程如下:
1) 构建区间判断矩阵A。基于典型作业多源要素全域风险因子体系,邀请N位风控专家对每一层的不同风险因子进行重要性比较,构建区间判断矩阵A为:
| $ \boldsymbol{A}=\left[\begin{array}{cccc} {\left[a_{11}^{\prime}\right]} & {\left[a_{12}^{\prime}\right]} & \cdots & {\left[a_{1 n}^{\prime}\right]} \\ {\left[a_{21}^{\prime}\right]} & {\left[a_{22}^{\prime}\right]} & \cdots & {\left[a_{2 n}^{\prime}\right]} \\ \vdots & \vdots & & \vdots \\ {\left[a_{n 1}^{\prime}\right]} & {\left[a_{n 2}^{\prime}\right]} & \cdots & {\left[a_{n n}^{\prime}\right]} \end{array}\right], \\ \left[a_{i j}^{\prime}\right]=\left[a_{i j}-\mu, a_{i j}+\mu\right], \quad 0<\mu<1 . $ | (9) |
式中:n表示所选因子层次中的风险因子数量;i和j是取值范围从1到n的整数;[aij′]是由专家提供的重要差异程度aij和不确定裕度μ组成的区间数,其中aij表征了因子i和因子j之间的基础重要性差异大小,μ代表因子重要性差异的不确定裕度,是取值范围(0, 1)的实数。
2) 推导区间互反性标度。
当风险因子i被认为比风险因子j更重要时,aij>1,i≠j;当因子i和j被认为同等重要时,aij=1,i≠j;当因子j被认为比因子i更重要时,1/aij>1,i≠j。区间互反性的1—9标度如表 2所示。
| 不同风险因子间重要性差距 | 重要差异程度aij |
| 因子i与因子j同等重要 | 1, 2 |
| 因子i比因子j稍微重要 | 3, 4 |
| 因子i比因子j更为重要 | 5, 6 |
| 因子i比因子j明显重要 | 7, 8 |
| 因子i比因子j格外重要 | 9 |
3) 特征向量推导。
区间判断矩阵A采用数值算法求解。本文通过幂法[19]计算判断矩阵A的最大特征根λmax及其对应的特征向量P。
4) 一致性校验。
为了校验A的合理性,引入一致性校验:
| $ \mathrm{CR}=\frac{\mathrm{CI}}{\mathrm{RI}}, $ | (10) |
| $ \mathrm{CI}=\left(\lambda_{\max }-n\right) /(n-1) . $ | (11) |
式中:RI是自由度指标,其值可根据表 3确定[20];如果A的校验值CR小于0.1,则A通过一致性校验并转入下一步;若A没有通过一致性校验则返回步骤1)重新收集专家意见。
5) 提取每位专家的区间特征向量Pj。
当第j位专家比较风险因子重要性并通过一致性校验后,将该专家的权重特征向量记作Pj,其每一个元素分别对应每一个风险因子的权重区间。事实上,不同的专家对于风险因子的重要性可能有截然不同的看法。通过重复上述流程,即可根据N位专家的意见获取对应的N个区间特征向量Pj,i=1, 2, …, N。每个区间特征向量Pj包含n个因子的权重区间,
| $ \boldsymbol{P}_j=\left[\left[\omega_{j-1}\right], \left[\omega_{j-2}\right], \cdots, \left[\omega_{j-i}\right], \cdots, \left[\omega_{j-n}\right]\right] . $ | (12) |
式中[ωj-i]表示专家j给出的因子i的权重区间,全部专家共计N×n个权重区间。
4.2 极大熵准则为了提升风险识别的客观性,需要构建一个可量化的适应度目标,因此本文将适应度函数设为极大熵准则。极大熵准则是一种选择最能满足随机变量统计特征的客观数据分布标准。信息熵理论的宗旨是丰富从数据中获取的信息以降低结果的不确定性[18]。因此,本文采用因子权重特征向量(ω)的信息熵H(ω)来量化风险识别结果的弹性,在已知的约束条件下通过最大化权重信息熵H(ω)来有效降低由于客观数据偏差造成的系统不稳定和识别偏颇风险[17],减少因客观参数缺失导致的不合理主观假设,并提升ARI的鲁棒性和兼容度;此外,将极大熵准则作为ARI的目标函数也可规避传统风险识别方法直接对不同专家评分进行简单加权平均的弊端,同时可将IAHP获取的不确定的因子权重区间转化为确定的数值。权重信息熵H(ω)的计算方法如下:
| $ \begin{aligned} H(\boldsymbol{\omega}) & =\sum\limits_{i=1}^n-\omega_i \ln \omega_i, \\ \text { s.t. } \quad \sum\limits_{i=1}^n \omega_i & =1 \quad\left(0 \leqslant \omega_i \leqslant 1\right) . \end{aligned} $ | (13) |
式中ωi为因子i的权重数值。当生成新的因子权重特征向量ω时,可将其代入式(13)来计算新的权重信息熵H(ω)。
4.3 约束调节机制当作业场景或技术装备发生变化时,通常需要管理部门重新邀请相关领域专家对风险因子的重要程度进行评定,但这将需要双倍的人力成本,而额外约束的设立辅以PHBA的快速求解能够实现ARI模型的低成本动态调整。因此,针对于本文提出的风险因子体系,在自适应过程中添加电力作业风险约束可以人为干预权重的数值分布。例如,当作业空间转移至典型高空场景时,应提升风力等级的重要程度,因此可添加“风力等级A2的因子权重应保持在0.03以上”的约束。基于极大熵理论和IAHP权重区间,最终约束条件所引起的权重调整均通过PHBA来求解。由此,约束调节机制可以根据场景变化来动态制定约束条件,能够适应不同的典型空间,无须重复IAHP邀请专家评分的繁琐过程以及客观赋权方法对于因子数据的数值分析,从而实现了不同典型空间下低实施成本的风险动态识别。
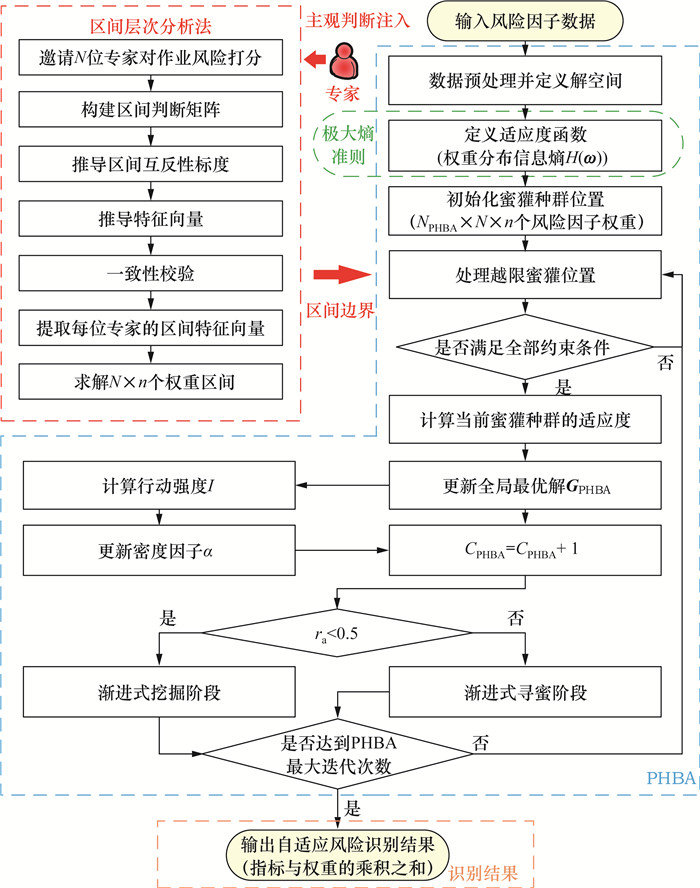
4.4 基于PHBA求解的自适应风险识别流程作为联合上述边界条件、目标函数、约束调节机制的求解方法,PHBA以IAHP获取的主观权重区间为边界条件,在全部约束条件满足的情况下引导模型向着权重信息熵升高的方向搜索。本文构建的基于PHBA求解的ARI流程如图 7所示,步骤如下:
|
| 图 7 基于PHBA求解的自适应风险识别流程 |
1) 邀请N位专家对不同作业风险因子的重要性进行比较打分。
2) 通过IAHP计算N个区间特征向量Pj,包括N×n个权重区间[ωj-i]。
3) 定义权重信息熵H(ω)作为适应度函数。
4) 初始化蜜獾的数量为NPHBA,根据由专家提供的N×n个权重区间[ωj-i]分别初始化NPHBA×N×n个风险因子权重,每只蜜獾的位置信息包含了所有专家提出的多源要素全域风险因子的N×n个权重数值。
5) 检查蜜獾位置是否满足权重边界条件和约束条件。如果满足全部约束,则进行下一步;否则,处理越限变量并重新生成蜜獾位置。
6) 定义适应度函数为典型空间下风险因子的权重信息熵。
7) 计算当前蜜獾种群的适应度fk。
8) 根据fk的变化更新对应全局最优解GPHBA。
9) 计算行动强度I。
10) 更新密度因子α。
11) 迭代次数CPHBA=CPHBA+1。
12) 若随机数ra<0.5,则进入渐进式挖掘阶段。在该阶段模拟蜜獾的心形运动来搜索全局最优解。
13) 若随机数ra≥0.5,则进入渐进式寻蜜阶段。在该阶段模拟蜜獾追随响蜜寻找蜂巢的过程来搜索全局最优解。
14) 判断PHBA当前的迭代次数CPHBA是否达到最大迭代次数CPHBA-max:如果CPHBA<CPHBA-max,则返回步骤5)继续迭代;如果CPHBA=CPHBA-max,则进行下一步输出计算结果。
15) 输出全局最优解GPHBA,求解GPHBA中蕴含的n个自适应因子权重:
| $ \boldsymbol{\omega}=\left[\omega_1, \omega_2, \cdots, \omega_i, \cdots, \omega_n\right], $ | (14) |
| $ \omega_i=\frac{1}{N} \sum\limits_{j=1}^N \omega_{j-i}, $ | (15) |
| $ \boldsymbol{G}_{\mathrm{PHBA}}=\left[\omega_{j-1}, \omega_{j-2}, \cdots, \omega_{j-i}, \cdots, \omega_{j-n}\right] . $ | (16) |
16) n个风险因子值分别乘以n个因子权重,加权求和得到最终的风险识别分数。
5 案例分析 5.1 算例描述本文根据已有的风险事件记录,结合电气领域专家意见,构建了当地电力作业风险数据库,针对某市的典型空间生成了风险因子数据,并对所有风险因子数据进行标准化。本文邀请了5位电力专责人员作为专家对风险因子重要程度进行打分,根据4.1节的IAHP步骤求解基于每一位专家评分结果的主观因子权重区间,其中每位专家分5轮分别对全域风险因子体系的环境风险因子库、设备风险因子库、人员行为风险因子库、人员健康风险因子库进行重要性判断,标准化后每位专家给出51个因子的权重区间,5位专家则共计给出51×5个电力作业风险因子权重区间,因此PHBA的输入变量维度为255,以此确定所有专家给出的对应风险因子的自适应权重。
5.2 风险因子分析根据历史风险事件记录以及专家的评估意见,本文针对一般、带电、近电、高空、有限空间等典型空间生成了区域A和区域B的风险因子数据。其中风险因子C2、C3、C4、C5、C6、C7、C8、C9、D7、D8、D9、A14、A15、A16、A17无论在不同区域还是不同典型空间的数值皆为0,这是由于《电力安全工作规程》对不可作业的条件进行了严格规定,以上风险因子只要出现不合格,均应立刻叫停作业,因此不存在违规的电力作业场景。
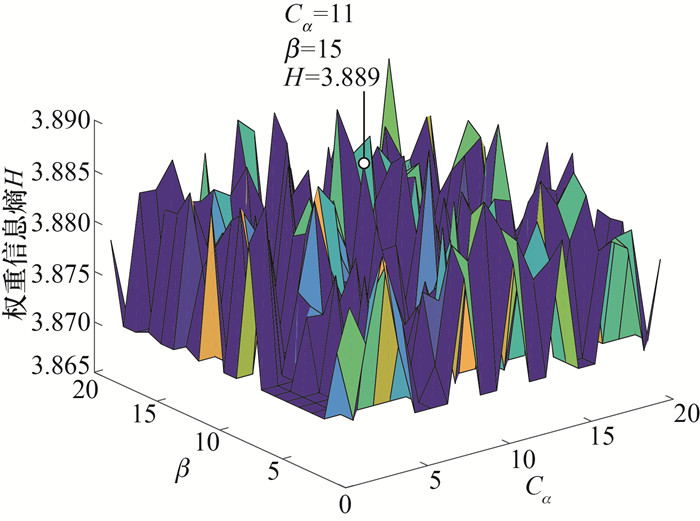
5.3 超参数配置基于PHBA的ARI模型涉及超参数的配置,合理的超参数可有效提高风险因子权重的自适应调节效果,进而保证风险识别结果的均衡性和鲁棒性。对于PHBA,递减影响因子Cα和觅食参数β是影响收敛性能的关键超参数。在保证充分的蜜獾种群数量(NPHBA=30)和PHBA最大迭代次数(CPHBA-max=300)的前提下,本文对不同取值下的递减影响因子Cα和觅食参数β进行探索,以一般空间为例的数值仿真结果如图 8所示。经测试,当Cα=11、β=15时,权重信息熵达到最大值3.889,此时风险因子权重的分布更均衡。
|
| 图 8 自适应风险识别模型的超参数配置 |
5.4 优化方法对比
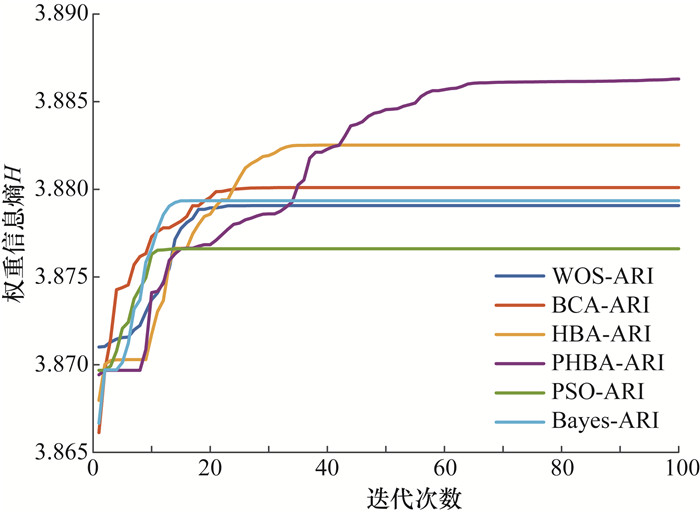
为了验证PHBA适用于ARI模型,本文选取了数种优秀的基准优化算法作为对比,求解相同风险因子区间下的因子权重分布,包括基于凝血算法[21]的自适应风险识别(BCA-ARI)、基于鲸鱼算法[22]的自适应风险识别(WOS-ARI)、基于粒子群算法[4]的自适应风险识别(PSO-ARI)、基于蜜獾算法的自适应风险识别(HBA-ARI)和基于Bayes优化[17]的自适应风险识别(Bayes-ARI)。将基于渐进式蜜獾算法的自适应风险识别(PHBA-ARI)与这些算法模型进行效果对比。各模型的迭代曲线如图 9所示,计算结果如表 4所示。PHBA-ARI的权重信息熵分别比WOS-ARI、BCA-ARI、HBA-ARI、PSO-ARI、Bayes-ARI高0.186%、0.159%、0.097%、0.249%、0.179%,且重复实验下出现不收敛的情况最少。另外,由于ARI模型计算复杂度不高,因此不同优化算法的计算速度差异不大,说明所有基准模型中具有最高权重信息熵的PHBA最适于本文提出的ARI模型,能有效保证风险因子权重的均衡分布,降低因客观数据不准确导致的识别偏颇风险并提升识别结果的鲁棒性。
|
| 图 9 自适应风险识别的优化方法对比 |
| 算法模型 | 权重信息熵 | 计算时间/s |
| WOS-ARI | 3.879 073 | 2.56 |
| BCA-ARI | 3.880 106 | 1.35 |
| HBA-ARI | 3.882 525 | 1.22 |
| PHBA-ARI | 3.886 296 | 1.29 |
| PSO-ARI | 3.876 614 | 1.60 |
| Bayes-ARI | 3.879 351 | 0.89 |
5.5 风险识别方法对比
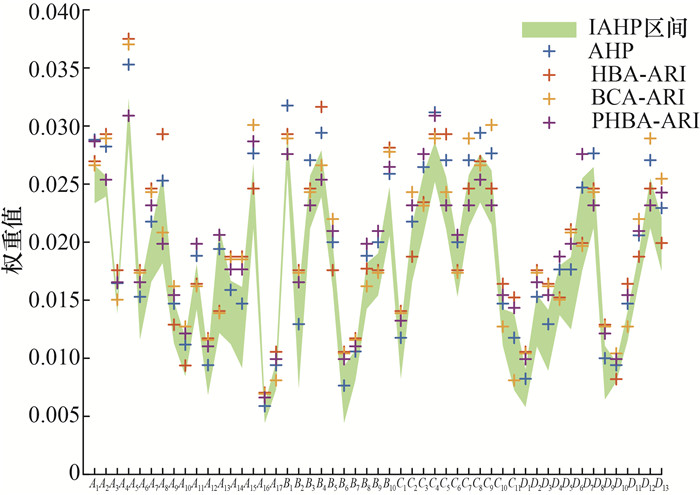
由于客观统计的事故数据规模不足,直接对历史数据分布进行分析的客观赋权方法不适于ARI模型。为了体现ARI模型与常见风险识别模型的区别,本文引入主流风险识别方法AHP,以及ARI识别方法BCA-ARI、HBA-ARI、PHBA-ARI,并以IAHP的权重区间作为基准参考,探索主观认知在ARI中所发挥的作用。以一般空间为例的风险识别方法对比结果如图 10所示。
|
| 图 10 以一般空间为例的风险识别方法对比结果 |
整体来看,各风险识别方法所求得的权重分布趋势类似,风险因子权重大多位于IAHP的权重区间之内。但单纯基于主观方法的风险识别难免会增加评估偏颇风险,而ARI方法为了提高权重分布的信息熵和风险识别鲁棒性,使部分风险因子的权重跳脱出IAHP主观区间的束缚,并对纯主观的风险识别结果进行修正。PHBA-ARI比其他基准模型的权重分布更为均衡,对应着更高的权重信息熵,因此当个别客观数据失准时能有效均摊不良信息影响,从而具有更高的鲁棒性。
5.6 风险因子权重分析针对不同的典型空间,本文算法可通过约束调节机制实现风险因子权重的自适应调整,即在不同的典型空间下根据风险重视程度的差异,通过设置约束条件提升某些关键风险的权重,以突出该风险因子在本次识别结果中所占的比重。本文针对一般、带电、近电、高空、有限空间等典型空间设置了表 5所示的额外约束。
| 典型空间 | 额外约束设置 |
| 一般空间 | 无约束 |
| 带电空间 | 是否检查设备缺陷C3不小于0.034 |
| 近电空间 | 降雨强度A4不小于0.039 |
| 高空空间 | 风力等级A2不小于0.030 |
| 有限空间 | 有毒有害气体超标量A8不小于0.017 |
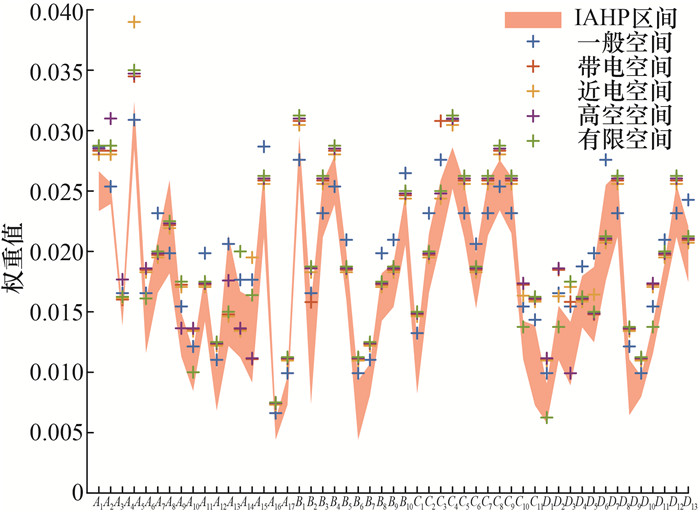
基于本文提出的PHBA-ARI模型,各典型空间下的电力作业风险因子权重分布如图 11所示。在约束调节机制的限制之下,ARI模型通过PHBA实现了针对不同典型空间特征的自适应调整,对应特征的风险因子侧重性比一般空间有显著提升,相应风险因子权重值也达到所有空间中的最高。但由于额外约束条件的增加,各典型空间的权重分布均衡性比一般空间有所下降,且分布波动性更强。
|
| 图 11 各典型空间下电力作业风险因子权重分布 |
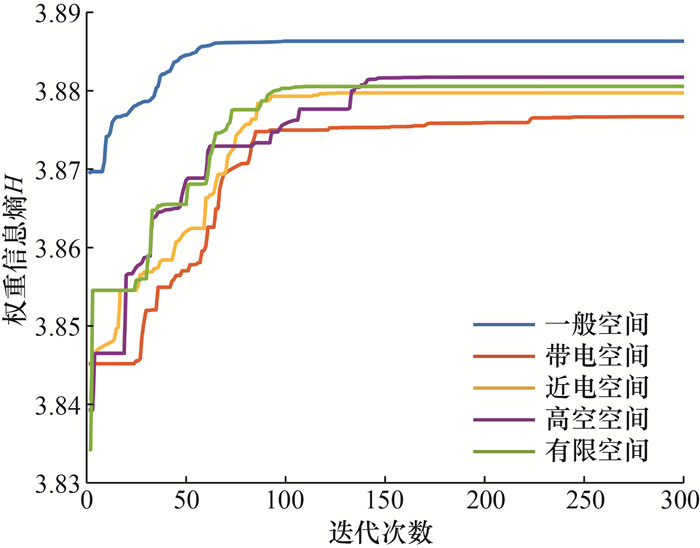
为了观察约束调节机制的设置对ARI模型的影响,本文基于PHBA-ARI模型对比了不同典型空间下的权重信息熵迭代曲线,如图 12所示。由于额外约束条件的设置,带电、近电、高空、有限空间下的权重信息熵比一般空间分别下滑0.248%、0.170%、0.117%、0.149%,且收敛速度有所下降。总体来看,因地制宜的约束调节机制仅在牺牲少量权重信息熵和计算速度的前提下,就能实现针对不同典型空间下电力作业的自适应调整,相比于传统风险识别方法在切换作业场景时需要重新邀请专家再次评估风险的繁琐流程,节省了大量人力和物力。
|
| 图 12 典型空间作业风险识别的权重信息熵迭代曲线 |
5.7 评估结果与案例分析
本文基于PHBA-ARI分别获取一般、带电、近电、高空、有限空间等典型空间的风险因子权重后,分别与对应的风险因子数据加权求和,得到各典型空间下电力作业的风险识别结果。
选取A和B两个实际区域,采用PHBA-ARI进行评估,结果如表 6所示。区域A的带电、近电、高空空间作业风险相比区域B升高了8.5%、0.2%、13%,但是有限空间的作业风险降低了5.5%。有关部门可针对作业风险较高的场景进行强化管控,结合具体风险因子数据制定相应措施来消除安全隐患,保障作业人员的人身安全。
| 区域 | 带电空间 | 近电空间 | 高空空间 | 有限空间 |
| A | 0.055 406 | 0.054 012 | 0.057 226 | 0.050 653 |
| B | 0.050 681 | 0.053 894 | 0.049 751 | 0.053 429 |
综上所述,相比于传统的风险识别方法,ARI模型通过融合客观准则可有效减弱主观臆断影响;更均衡的权重分布可减少因客观风险数据失准所导致的偏颇风险;当典型空间发生变化也无须邀请专家重新评估风险,而是基于PHBA和约束调节机制根据空间特征来自适应调整因子权重分布,从而实现动态低成本的典型空间下电力作业的自适应风险识别。
6 结论面向电力作业风险识别及应急救援的重大需求,本文提出了一种典型空间下电力作业多源要素风险的自适应识别模型。首先构建了全流程的电力行业典型作业风险识别框架,建立了多维度的典型作业多源要素全域风险因子体系,然后提出了基于渐进式蜜獾算法、极大熵准则、约束调节机制的电力作业风险自适应识别方法,实现了主客观动态融合的风险自适应识别。案例结果证明了本文方法可有效识别电力作业在典型空间下的多源要素风险,并在鲁棒性能、实施成本、偏颇风险方面具备明显优势。
| [1] |
李湃, 黄越辉, 张金平, 等. 多能互补发电系统电/热/氢储能容量协调优化配置[J/OL]. (2023-08-31)[2023-12-15]. 中国电机工程学报. https://link.cnki.net/urlid/11.2107.TM.20230830.1851.007. LI P, HUANG Y H, ZHANG J P, et al. Capacity coordinated optimization of battery, thermal and hydrogen storage system for multi-energy complementary power system[J/OL]. (2023-08-31)[2023-12-15]. Proceedings of the CSEE. https://link.cnki.net/urlid/11.2107.TM.20230830.1851.007. (in Chinese) |
| [2] |
高阳, 朱坤双, 黄海静, 等. 我国电力作业安全管理体系构建及分析研究[J]. 武汉理工大学学报(信息与管理工程版), 2022, 44(6): 894-898. GAO Y, ZHU K S, HUANG H J, et al. Research on the construction of safety management system for electric power operation in China[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2022, 44(6): 894-898. (in Chinese) |
| [3] |
许永刚, 朱坤双, 王立峰, 等. 电力作业风险智能预警设计与实现[J]. 数字通信世界, 2023(6): 54-56. XU Y G, ZHU K S, WANG L F, et al. Design and implementation of intelligent early warning for electric power operation risk[J]. Digital Communication World, 2023(6): 54-56. (in Chinese) |
| [4] |
陈碧云, 李弘斌, 李滨. 基于数据挖掘和CAPSO-SNN的电力作业风险态势感知[J]. 电力自动化设备, 2020, 40(1): 148-155. CHEN B Y, LI H B, LI B. Power operation risk situation awareness based on data mining and CAPSO-SNN[J]. Electric Power Automation Equipment, 2020, 40(1): 148-155. (in Chinese) |
| [5] |
何敏, 秦亮, 赵峰, 等. 面向电力系统现场作业的安全风险管控智能检测算法[J]. 高电压技术, 2023, 49(6): 2442-2457. HE M, QIN L, ZHAO F, et al. Intelligent detection algorithm of security risk management and control for power system on-site operation[J]. High Voltage Engineering, 2023, 49(6): 2442-2457. (in Chinese) |
| [6] |
葛磊蛟, 李元良, 陈艳波, 等. 智能配电网态势感知关键技术及实施效果评价[J]. 高电压技术, 2021, 47(7): 2269-2280. GE L J, LI Y L, CHEN Y B, et al. Key technologies of situation awareness and implementation effectiveness evaluation in smart distribution network[J]. High Voltage Engineering, 2021, 47(7): 2269-2280. (in Chinese) |
| [7] |
马富齐, 王波, 董旭柱, 等. 电力工业安全影像解译: 基本概念与技术框架[J]. 中国电机工程学报, 2022, 42(2): 458-474. MA F Q, WANG B, DONG X Z, et al. Safety image interpretation of power industry: Basic concepts and technical framework[J]. Proceedings of the CSEE, 2022, 42(2): 458-474. (in Chinese) |
| [8] |
葛磊蛟, 李元良, 汪宇倩. 智能配电网态势感知实现效果综合评估模型[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(11): 1101-1111. GE L J, LI Y L, WANG Y Q. Comprehensive evaluation model for situational awareness effects of a smart distribution network[J]. Journal of Tianjin University (Science and Technology), 2020, 53(11): 1101-1111. (in Chinese) |
| [9] |
WANG S X, GE L J, CAI S X, et al. Hybrid interval AHP-entropy method for electricity user evaluation in smart electricity utilization[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(4): 701-711. DOI:10.1007/s40565-017-0355-3 |
| [10] |
ARMAN H, HADI-VENCHEH A, ARMAN A, et al. Revisiting the approximated weight extraction methods in fuzzy analytic hierarchy process[J]. International Journal of Intelligent Systems, 2021, 36(4): 1644-1667. DOI:10.1002/int.22355 |
| [11] |
程明熙. 处理多目标决策问题的二项系数加权和法[J]. 系统工程理论与实践, 1983, 3(4): 23-26. CHENG M X. Binomial coefficient weighted sum method for dealing with multi-objective decision-making problems[J]. Systems Engineering: Theory & Practice, 1983, 3(4): 23-26. (in Chinese) |
| [12] |
WANG J S, DENG X C. Comprehensive economic benefit evaluation method of coastal enterprises based on AHP[J]. Journal of Coastal Research, 2020, 103(S1): 24-28. |
| [13] |
LI M, WANG J L, LI Y, et al. Evaluation of sustainability information disclosure based on entropy[J]. Entropy, 2018, 20(9): 689. DOI:10.3390/e20090689 |
| [14] |
王依宁, 解大, 王西田, 等. 基于PCA-LSTM模型的风电机网相互作用预测[J]. 中国电机工程学报, 2019, 39(14): 4070-4080. WANG Y N, XIE D, WANG X T, et al. Prediction of interaction between grid and wind farms based on PCA-LSTM model[J]. Proceedings of the CSEE, 2019, 39(14): 4070-4080. (in Chinese) |
| [15] |
GE L J, LI Y L, LI S X, et al. Evaluation of the situational awareness effects for smart distribution networks under the novel design of indicator framework and hybrid weighting method[J]. Frontiers in Energy, 2021, 15(1): 143-158. DOI:10.1007/s11708-020-0703-2 |
| [16] |
张华一, 文福拴, 张璨, 等. 基于前景理论的电网建设项目组合多属性决策方法[J]. 电力系统自动化, 2016, 40(14): 8-14. ZHANG H Y, WEN F S, ZHANG C, et al. Prospect theory based multiple-attribute decision-making method for determining portfolio of construction projects in power systems[J]. Automation of Electric Power Systems, 2016, 40(14): 8-14. (in Chinese) |
| [17] |
张宏博, 陈伟炯, 闫明. 多式联运路径优化模型中的贝叶斯极大熵权重自学习方法研究[J]. 计算机应用与软件, 2018, 35(10): 28-32, 44. ZHANG H B, CHEN W J, YAN M. The Bayesian maximun entropy weight self-learning method in the multimodal transport path optimization model[J]. Computer Applications and Software, 2018, 35(10): 28-32, 44. (in Chinese) |
| [18] |
GE L J, LI Y L, ZHU X S, et al. An evaluation system for HVDC protection systems by a novel indicator framework and a self-learning combination method[J]. IEEE Access, 2020, 8: 152053-152070. DOI:10.1109/ACCESS.2020.3017502 |
| [19] |
WANG Y Q, GE L J, ZHANG N. Hybrid evaluation method for dispatching control level of smart distribution network[J]. Journal of Electrical Engineering & Technology, 2019, 14(6): 2263-2275. |
| [20] |
阿辽沙·叶, 祝恩国, 成倩, 等. 用电设备安全评估的改进区间层次分析法[J]. 电力系统及其自动化学报, 2015, 27(1): 32-36. ALIAOSHA Y, ZHU E G, CHENG Q, et al. Improved interval analytic hierarchy process method for electrical equipment safety assessment[J]. Proceedings of the CSU-EPSA, 2015, 27(1): 32-36. (in Chinese) |
| [21] |
YADAV D. Blood coagulation algorithm: A novel bio-inspired meta-heuristic algorithm for global optimization[J]. Mathematics, 2021, 9(23): 3011. DOI:10.3390/math9233011 |
| [22] |
许德刚, 王再庆, 郭奕欣, 等. 鲸鱼优化算法研究综述[J]. 计算机应用研究, 2023, 40(2): 328-336. XU D G, WANG Z Q, GUO Y X, et al. Review of whale optimization algorithm[J]. Application Research of Computers, 2023, 40(2): 328-336. (in Chinese) |



