飞机离地姿态是指飞机由滑跑开始至主轮离地为止的全过程飞行姿态。飞机离地过程是起飞阶段的关键过程,离地姿态安全与否直接决定了飞机起飞阶段的安全水平。
国内外学者对于飞机离地的分析主要集中在离地超轮速和起飞擦机尾事件。飞机在起飞离地过程中,超轮速会造成轮胎损伤甚至爆胎[1],严重危及飞行安全。钱宇等[2]、Alligier[3]筛选飞机离地速度影响参数,对运输飞机超轮速诱因进行了定量研究。张一山等[4]对高温、高海拔机场环境下的起飞超轮速事件进行风险分析,并提出了改进措施。当飞机起飞时,如果持续增加姿态仍不足以使飞机离地,就会导致擦机尾事件。孙瑞山等[5]基于快速存取记录器(quick access recorder, QAR)数据,利用Kolmogorov-Smirnova (K-S)检验方法模拟飞机起飞离地仰角值的概率分布,对飞机起飞时擦机尾事件的风险概率进行预测。杨星月等[6]基于飞行员模型建立民用飞机擦机尾人因操作分析模型,分析了驾驶杆与俯仰角之间的相位差及飞行员模型参数变化对俯仰角的影响。Noh[7]与Wang等[8]采用定性与定量相结合的方法计算飞机擦机尾风险,确定擦机尾事件的风险等级和主要危险因素。在应对飞机离地风险过程中,还有学者对影响离地姿态的风向、跑道、重量/重心进行研究[9-11]。Chen等[12]与Huijbrechts等[13]利用决断速度v 1研究飞机在污染跑道和侧风情景中的可控性问题。
上述研究以“离地时刻风险状态”为核心,旨在降低离地姿态异常导致后果的严重性,强调通过提升风险识别和分析等方法的准确性来实现有效的风险管理,也被称为“安全Ⅰ”模式。但是,突发事件本身发生发展的未知性、随机性导致了飞行任务实施的高度不确定性,加之飞行环境、飞机性能等客观因素多变难测,使得飞行任务实施风险难以被完全准确地预测。以韧性理论为基础的“安全Ⅱ”模式表明风险应对的关键在于:系统如何在环境多变条件下实现多项风险与目标之间的均衡,最终实现可持续安全飞行[14]。
根据“安全Ⅱ”模式,安全本身即构成一个系统,由安全的主体、客体及斡体3个基本要素嵌套耦合、分形迭代构成具体的安全功能体系[15]。客体未知、不确定风险普遍存在,且无法准确预测,只有从主体角度提高主体自身应对风险冲击与扰动的能力,即提高主体安全韧性,才是实现安全系统的必由之路。黄浪等[16]提出安全系统韧性是指系统在一定时空内面对风险的冲击与扰动时,维持、恢复和优化系统安全状态的能力。张秀艳等[17]针对安全系统应对不确定风险问题,提出了“主体韧性-客体风险”应对思想,以突发事件演化过程为主线,构建了“预防-应急-进化(prevention-emergency-evolutionary, PEE)”动态韧性模型,提出了一套用于指导如何从提高主体韧性的角度应对客体风险,进而实现安全系统的研究方法与理论体系。
飞机离地姿态安全与否取决于飞行任务自身的动态韧性水平,准确识别飞行任务动态韧性特征因素之间的关联关系则是提高风险应对能力的关键。
本文以“安全Ⅱ”模式为指导,从飞行任务主体应对客体风险的角度,关注飞机离地的全过程表现,基于国内某航空公司A319机队飞行QAR数据,运用动态Bayes网络,借助Genie软件进行参数学习和建模,建立飞机离地姿态、飞行操作、飞机性能、飞行环境耦合模型,深入挖掘和充分利用日常飞行数据,揭示了飞行操作与飞机离地姿态“因果-时序”耦合机理,最终为飞机离地过程中飞行员的操作提供指导,从而提高飞行员在飞机离地过程中的风险应对能力。
1 Bayes网络与动态Bayes网络 1.1 Bayes网络Bayes网络(Bayesian networks, BN)是一个有向无环图,由代表变量的节点及连接这些节点的有向边构成[18]。节点代表随机变量,有向边代表节点关系,变量间依赖关系用条件概率表达。Bayes推理是通过Bayes公式实现的。一旦在有向图中提供了先验概率,输入的先验概率就会在2个方向上传播[19]。对于随机事件A和B,P(A)、P(B)是A、B事件发生的先验概率,P(A|B)是在B发生的情况下A发生的可能性,则
| $ P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)} . $ | (1) |
当变量超过2个或更多的时候,Bayes公式也同样成立,如式(2)所示,
| $ \begin{gathered} P(A \mid B, C)= \\ \frac{P(A) P(B \mid A) P(C \mid A, B)}{P(B) P(C \mid B)} \text {. } \end{gathered} $ | (2) |
基于Bayes公式,以飞机离地姿态影响因素为自变量预测飞机离地姿态概率,构建Bayes网络可以分为2个主要步骤。
1) 结构学习。基于已有文献和离地姿态相关影响因素,确定BN节点[20];基于飞机离地姿态各项参数之间的关联关系构建因果拓扑结构。
2) 参数学习。采用最大期望算法(expectation-maximization, EM)对离散化数据集进行训练学习[21],得到不同节点的概率分布。
1.2 动态Bayes网络动态Bayes网络(dynamic Bayesian networks, DBN)是BN在时间维度上的扩展,可用一个二元组〈A0, A〉来表示。其中:A0表示初始网络,即初始时间片的BN,定义了同一时间片网络节点的先验概率分布;A表示转移网络,由2个以上时间片的BN组成,定义了不同时间片节点间的转移概率分布。设变量集X={X1,…,XN},时间片为[0, 1, …,T],则P(X0, …, XT)的联合概率分布为
| $ \begin{gathered} P\left(X^0, \cdots, X^T\right)= \\ P\left(X^0\right) \cdot \prod\limits_{i=1}^T \prod\limits_{i=1}^N P\left[X_i^t \mid P_{\mathrm{a}}\left(X_i^t\right)\right] . \end{gathered} $ | (3) |
式(3) 中:Xit为第t时间片上的第i个节点;Pa(Xit)为Xit的父节点,与Xit既可以存在于同一时间片内,也可以为前一时间片与其有因果关系的节点。相邻时间片之间可进行连续的概率推理。采用最大期望算法进行参数学习,对初始化的条件概率分布进行迭代修正以预测得到不同时间片节点的概率分布[22]。
DBN在描述变量之间的因果关系的同时,也能够对变量在时间序列上状态的变化过程进行描述,因此该网络模型可用于飞机离地姿态全过程分析。构建基于DBN的飞机离地姿态模型时,在确定DBN的节点后,需构建因果拓扑结构,包括初始网络和转移网络[23]。
2 飞机离地姿态与飞行操作“因果-时序”耦合模型 2.1 飞机离地姿态分析飞机离地姿态由飞机主轮离地时刻tvD的飞行姿态直接决定,但是与飞机离地全过程均相关,某时刻与主轮离地时刻越接近,其与飞机离地姿态的相关性也越强[24]。从系统安全的角度,QAR参数可以划分为飞行姿态(飞机的运动状态)、飞机性能(飞机系统工作状态)、飞行操作(飞行员操作行为)、飞行环境(飞行气象状态) 4类,分别对应飞行姿态类参数集{q1i}、飞机性能类参数集{q2i}、飞行操作类参数集{q3i}、飞行环境类参数集{q4i},如表 1所示。
| 飞行参数 | 参数集 | 决断时刻(tv1) | 抬前轮时刻(tvR) | 离地时刻(tvD) |
| 飞行姿态(q1i) | 速度(q11) | 决断速度(q11[tv1]) | 抬前轮速度(q11[tvR]) | 离地速度(q11[tvD]) |
| 俯仰角(q12) | 离地仰角(q12[tvD]) | |||
| 飞机性能(q2i) | 飞机重量(q21) | 滑跑重量(q21[tv1]) | 抬前轮重量(q21[tvR]) | 离地重量(q21[tvD]) |
| 发动机排气温度(q22) | 滑跑发动机排气温度(q22[tv1]) | 抬前轮发动机排气温度(q22[tvR]) | 离地发动机排气温度(q22[tvD]) | |
| 飞行操作(q3i) | 油门指令(q31) | 滑跑油门指令(q31[tv1]) | 抬前轮油门指令(q31[tvR]) | 离地油门指令(q31[tvD]) |
| 襟翼位置(q32) | 襟翼位置(q32[tvR]) | |||
| 俯仰指令(q33) | 俯仰指令(q33[tvD]) | |||
| 飞行环境(q4i) | 风速(q41) | 决断风速(q41[tv1]) | 抬前轮风速(q41[tvR]) | 离地风速(q41[tvD]) |
| 风向(q42) | 决断风向(q42[tv1]) | 抬前轮风向(q42[tvR]) | 离地风向(q42[tvD]) |
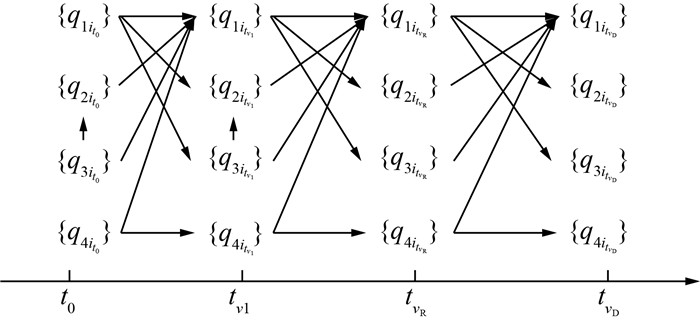
飞机离地姿态由飞行姿态类参数集{q1i}直接表征,但是会受到其他3类参数状况的影响,具有“因果”关联性;同时,每个时刻的飞行参数也会受到上一时刻飞行参数的影响,具有“时序”关联性。根据飞行操作手册,将飞机离地过程划分为滑行至决断速度t0→tv1、决断至抬前轮tv1→tvR、抬前轮至离地tvR→tvD3个关键阶段。每个阶段涉及的飞行参数不同,将4类飞行参数按照关键阶段进行因果-时序分解,如图 1所示。
|
| 图 1 飞行参数因果-时序分解 |
2.2 模型构建
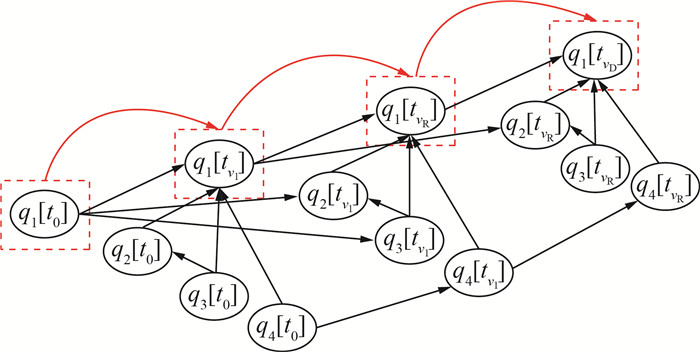
飞机离地姿态各项参数之间的关联关系,既具有时序耦合复杂性,又具有因果耦合复杂性。图模型因能更有效地反映系统的复杂性,适用于解决飞行姿态关联关系问题[22],但节点的不确定性、节点之间的相关性和权重分配是目前确定性图模型无法解决的关键问题[25]。概率图模型能够有效解决不确定性与相关性问题,且更加贴近实际情况[26]。DBN模型是一种高度可视化的概率图模型,在问题的分析和推理方面有更好的表现,在量化描述变量因果关系的同时,还能够对变量在时间序列上状态的变化过程进行概率预测,多用于交通、电力、航空航天等领域的事故风险预测[27-29]。因此,本文采用DBN图模型构建飞机离地姿态与飞行操作“因果-时序”耦合(“causal-time series” coupling,CTC)模型,如图 2所示,对飞行操作与飞机离地姿态之间的耦合机理进行研究。
|
| 图 2 飞机离地姿态与飞行操作“因果-时序”耦合模型 |
2.3 模型量化
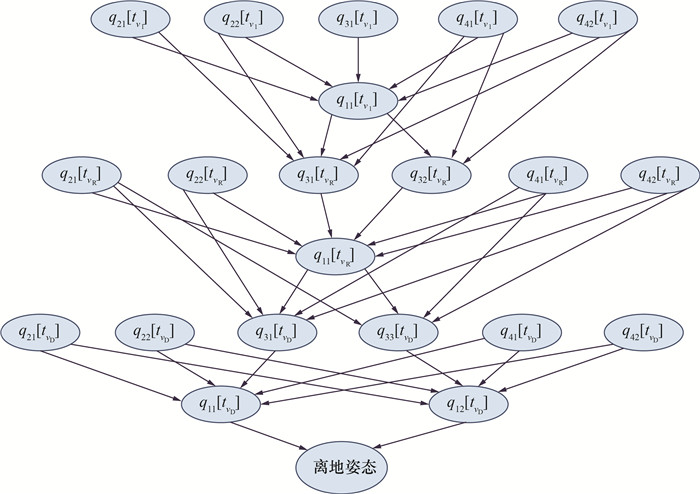
基于国内某航空公司A319机队飞行QAR数据,借助Genie软件进行参数学习和建模,如图 3所示。
|
| 图 3 飞机离地姿态与飞行操作CTC-DBN模型 |
针对453个航班,按照CTC模型进行因果-时序分解,得到1 359个航段。对航段飞行数据中tv1、tvR、tvD 3个时刻的关键参数进行整理与合并,对其中参数缺失或异常的部分航段进行处理,最终获得1 023个有效航段。将每个航段21个关键参数作为样本数据。通过飞行参数进行等级划分,对QAR数据进行参数离散化,以确定网络节点状态。数值型参数(风速、温度、重量等)按数值大小进行排序,均分为3个区间;属性型参数(风向、襟翼位置)按照种类分布,分为2或3个区间,如表 2所示。
| 参数 | 决断时刻(tv1) | 抬前轮时刻(tvR) | 离地时刻(tvD) | ||||||
| 飞行姿态参数(q1i) | 速度/(km·h-1) | 决断速度小 | <272 | 抬前轮速度小 | <274 | 离地速度小 | <292 | ||
| 决断速度较大 | [272,278) | 抬前轮速度较大 | [274,290) | 离地速度较大 | [292,307) | ||||
| 决断速度大 | ≥278 | 抬前轮速度大 | ≥290 | 离地速度大 | ≥307 | ||||
| 俯仰角/(°) | 仰角小 | <8 | |||||||
| 仰角较大 | [8,12) | ||||||||
| 仰角大 | ≥12 | ||||||||
| 飞机性能参数(q2i) | 重量/N | 重量小 | <588 000 | 重量小 | <588 000 | 重量小 | <588 000 | ||
| 重量较大 | [588 000,637 000) | 重量较大 | [588 000,637 000) | 重量较大 | [588 000,637 000) | ||||
| 重量大 | ≥637 000 | 重量大 | ≥637 000 | 重量大 | ≥637 000 | ||||
| 排气温度/℃ | 温度低 | <500 | 温度低 | <550 | 温度低 | <550 | |||
| 温度高 | [500,750) | 温度高 | [550,750) | 温度高 | [550,750) | ||||
| 温度过高 | ≥750 | 温度过高 | ≥750 | 温度过高 | ≥750 | ||||
| 飞行操作参数(q3i) | 油门指令 | 滑跑油门小 | <84 | 抬前轮油门小 | <84 | 离地油门小 | <84 | ||
| 滑跑油门较大 | [84,90) | 抬前轮油门较大 | [84,90) | 离地油门较大 | [84,90) | ||||
| 滑跑油门大 | ≥90 | 抬前轮油门大 | ≥90 | 离地油门大 | ≥90 | ||||
| 襟翼位置 | 位置1 | 1 | 俯仰指令/(°) | 慢 | <6 | ||||
| 位置2 | 2 | 较快 | [6,8) | ||||||
| 位置3 | 3 | 快 | ≥8 | ||||||
| 飞行环境参数(q4i) | 风速/(km·h-1) | 风速小 | <7.4 | 风速小 | <5.5 | 风速小 | <7.4 | ||
| 风速较大 | [7.4,16.6) | 风速较大 | [5.5,14.8) | 风速较大 | [7.4,18.5) | ||||
| 风速大 | ≥16.6 | 风速大 | ≥14.8 | 风速大 | ≥18.5 | ||||
| 风向/(°) | 逆风 | <0 | 逆风 | <0 | 逆风 | <0 | |||
| 顺风 | ≥0 | 顺风 | ≥0 | 顺风 | ≥0 | ||||
2.4 模型验证
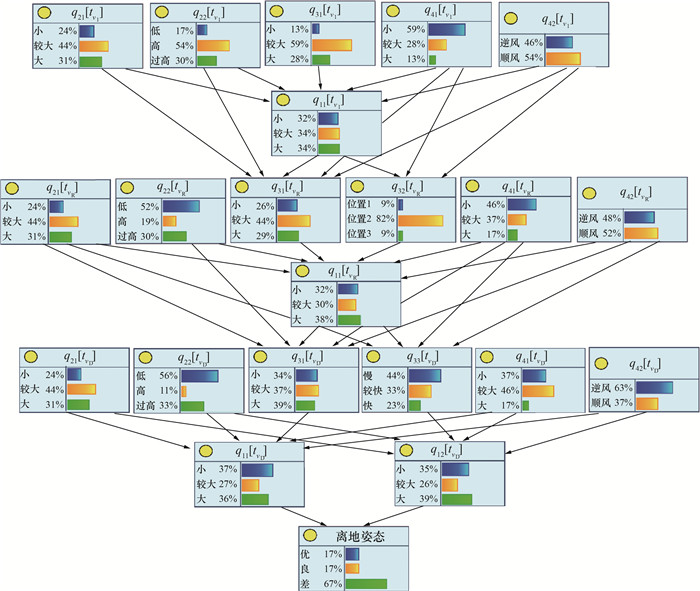
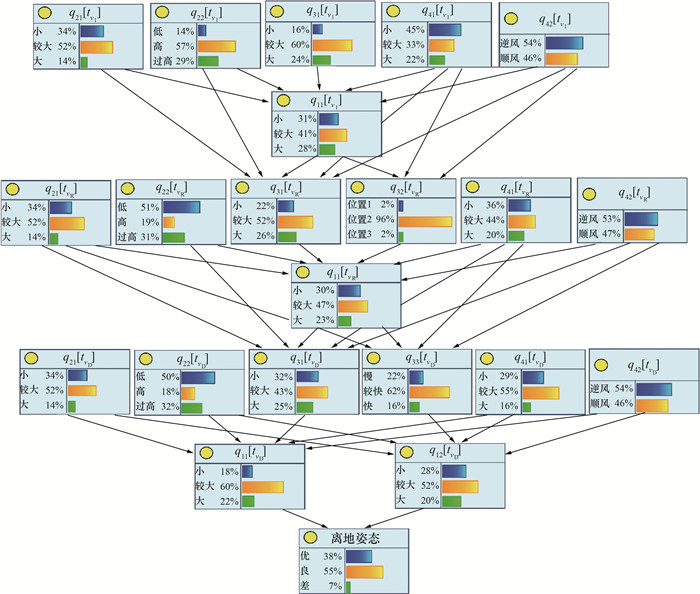
将触发离地俯仰角大和离地速度大/小等超限事件的航段称为超限航段(165段),其余称为正常航段(858段)。将超限航段数据与正常航段数据分别代入“因果- 时序”耦合模型,得到节点分布,如图 4、5所示。
|
| 图 4 超限航段节点分布 |
|
| 图 5 正常航段节点分布 |
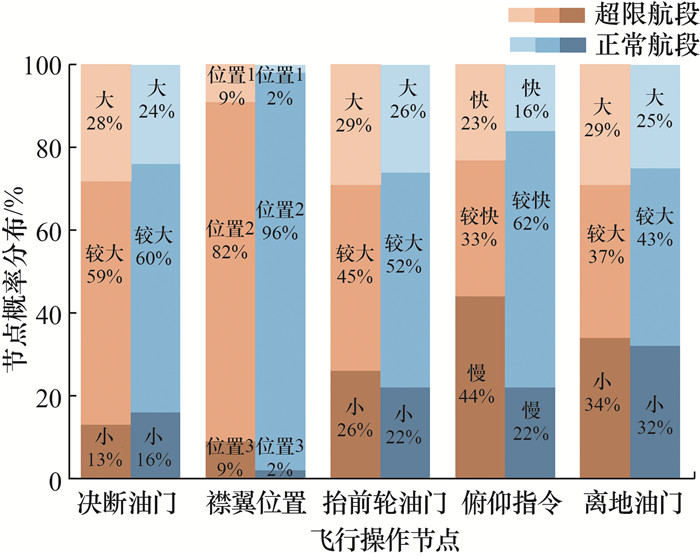
正常航段飞行姿态节点等级为优的概率明显高于超限航段,且不同时刻的飞行操作节点的概率分布也存在显著差异,如图 6所示。其中:棕色渐变柱状条为超限航段,蓝色渐变柱状条为正常航段。超限航段的所有飞行操作节点在较大/快这一区间的分布概率均明显低于正常航段,即超限航段飞行操作总体更为滞后迟缓,正常航段飞行操作总体表现出预先反应的特征,这与《飞行操作手册》中关于预先判断与应对的要求相符,验证了“因果-时序”耦合动态Bayes网络(CTC-DBN)模型的合理性与有效性。
|
| 图 6 超限航段与正常航段飞行操作节点概率分布对比 |
3 实例分析 3.1 情景分析
飞行姿态受到飞行操作、飞行环境、飞机性能等多种因素影响,但飞行操作是飞行员在飞行过程中进行风险应对的唯一可控因素[30]。因此,以飞机性能类参数和飞行环境类参数为情景变量,对比分析不同情景下飞行操作与飞机离地姿态的“因果-时序”耦合机理。
在飞机性能参数中,发动机相关参数短时间内趋于稳定,不同航班差异较小,飞机重量随载客、加油等因素变化较大,因此选择飞机重量作为情景变量,针对“重载”(飞机重量≥637 000 N)与“轻载”(飞机重量<588 000 N)情景进行验证分析。在飞行环境参数中,风向与风速是飞机在任何环境条件下飞行均会考虑的影响因素,因此选择风向与风速作为情景变量,针对“顺风”(风向≥0°)、“逆风”(风向 < 0°)、“大风”(风速≥18.5 km/h)和“小风”(风速<7.4 km/h)情景进行验证分析。
3.2 不同情景最佳飞行操作模式根据表 2飞行参数等级划分,筛选出符合以上情景的航段,并通过调节飞行操作节点进行分析。如图 6可知,襟翼位置在航班起飞阶段处于位置2的占比过大,其概率变化不显著,因此仅调节油门指令q31与俯仰指令q33 2个关键飞行操作节点在tv1、tvR、tvD3个时刻的节点分布概率,将飞机离地姿态优的概率由低逐步增高,最终确定不同情景最佳飞行操作模式。
3.2.1 单一情景的最佳飞行操作模式1) “重载”情景。筛选出飞机重量大于或等于637 000 N的“重载”情景航段共计231条。如图 7a所示,“重载”情景最佳飞行操作模式为:飞行员在决断时刻(tv1)增大油门,在抬前轮时刻(tvR)增大油门,在离地时刻(tvD)通过快速发布俯仰指令、减小油门,完成最后时刻飞机离地姿态的建立。

|
| 图 7 不同情景最佳飞行操作模式下关键节点概率变化 |
2) “轻载”情景。筛选出飞机重量小于588 000 N的“轻载”情景航段共计327条。如图 7b所示,“轻载”情景最佳飞行操作模式为:飞行员在决断时刻(tv1)增大油门,在抬前轮时刻(tvR)较大增加油门,在离地时刻(tvD)通过较快发布俯仰指令、减小油门,完成最后时刻飞机离地姿态的建立。
3) “顺风”情景。筛选出风向大于或等于0°的“顺风”情景航段共计309条。如图 7c所示,“顺风”情景最佳飞行操作模式为:飞行员在决断时刻(tv1)较大增加油门,在抬前轮时刻(tvR)减小油门,在离地时刻(tvD)通过较快发布俯仰指令、减小油门,完成最后时刻飞机离地姿态的建立。
4) “逆风”情景。筛选出风向小于0°的“逆风”情景航段共计714条。如图 7d所示,“逆风”情景最佳飞行操作模式为:飞行员在决断时刻(tv1)增大油门,在抬前轮时刻(tvR)较大增加油门,在离地时刻(tvD)通过较快发布俯仰指令、较大增加油门,完成最后时刻飞机离地姿态的建立。
5) “大风”情景与“小风”情景。筛选出风速大于或等于18.5 km/h的“大风”情景航段共计174条,筛选出风速小于7.4 km/h的“小风”情景航段共计360条。由图 7e和7f可知,“大风”情景与“小风”情景最佳飞行操作模式一致,均为飞行员在决断时刻(tv1)较大增加油门,在抬前轮时刻(tvR)较大增加油门,在离地时刻(tvD)通过较快发布俯仰指令、较大增加油门,完成最后时刻飞机离地姿态的建立。
3.2.2 组合情景的最佳飞行操作模式由于“大风”情景与“小风”情景的最佳飞行操作模式一致,因此仅考虑飞机重量与风向2个情景变量,确定组合情景为“重载顺风”情景与“轻载逆风”情景。组合情景的变量取值如表 3所示。
1) “重载顺风”情景。筛选出“重载顺风”情景航段共计192条。如图 7g所示,“重载顺风”情景最佳飞行操作模式为:飞行员在决断时刻(tv1)减小油门,在抬前轮时刻(tvR)增大油门,在离地时刻(tvD)通过较快发布俯仰指令、减小油门,完成最后时刻飞机离地姿态的建立。
2) “轻载逆风”情景。筛选出“轻载逆风”情景航段共计213条。如图 7h所示,“轻载逆风”情景最佳飞行操作模式为:飞行员在决断时刻(tv1)较大增加油门,在抬前轮时刻(tvR)较大增加油门,在离地时刻(tvD)通过较快发布俯仰指令、减小油门,完成最后时刻飞机离地姿态的建立。
3.3 讨论将不同情景最佳飞行操作模式汇总为表 4,可发现:
| 情景 | 时刻 | 油门指令 | 俯仰指令 | |||||
| 小 | 较大 | 大 | 慢 | 较快 | 快 | |||
| 重载 | tv1 | ● | ||||||
| tvR | ● | |||||||
| tvD | ● | ● | ||||||
| 轻载 | tv1 | ● | ||||||
| tvR | ● | |||||||
| tvD | ● | ● | ||||||
| 顺风 | tv1 | ● | ||||||
| tvR | ● | |||||||
| tvD | ● | ● | ||||||
| 逆风 | tv1 | ● | ||||||
| tvR | ● | |||||||
| tvD | ● | ● | ||||||
| 重载顺风 | tv1 | ● | ||||||
| tvR | ● | |||||||
| tvD | ● | ● | ||||||
| 轻载逆风 | tv1 | ● | ||||||
| tvR | ● | |||||||
| tvD | ● | ● | ||||||
1) 根据飞机重量不同,最佳飞行操作模式主要表现为飞机抬前轮时刻油门指令不同和离地时刻俯仰指令不同。飞机重量越大,抬前轮时刻油门越大、离地时刻俯仰指令越快,以快速提高速度与俯仰角,获得足够的飞机升力。
2) 根据风向不同,最佳飞行操作模式主要表现为3个时刻的油门指令不同。“逆风”情景3个时刻的油门均大于“顺风”情景,以克服风速获得足够的空速,最终保证飞机升力充足。
3) 将2种组合情景与4种单一情景的最佳飞行操作模式相比可发现,重量大、逆风使油门指令呈现增大趋势;重量小、顺风则使油门指令呈现减小趋势。各种情景下的离地时刻俯仰指令以较快为主要模式。
4 结论本文针对飞机离地过程风险应对问题,以飞机离地时刻飞行姿态为核心,根据“安全Ⅱ”模式,运用动态Bayes网络方法,构建了飞机离地姿态与飞行操作“因果-时序”耦合模型。利用国内某航司A319机队实际飞行QAR数据进行模型验证与情景分析,得出“重载”“轻载”“顺风”“逆风”等单一情景和组合情景的最佳飞行操作模式,有助于提高飞行员的离地风险应对能力。
本研究结果表明,飞机离地姿态与飞行操作“因果-时序”耦合动态Bayes网络模型可对飞机离地风险问题进行合理量化与科学分析。后续将结合地形、气象、飞行员特征等其他数据,针对不同类型的起降场、飞行员、气象环境等情景变量,研究最佳飞行操作模式,进一步完善CTC-DBN模型。
| [1] |
黄正. 防止高原机场超轮速[J]. 科技创新导报, 2013(17): 81. HUANG Z. Preventing excessive wheel speed at high altitude airports[J]. Science and Technology Innovation Herald, 2013(17): 81. (in Chinese) |
| [2] |
钱宇, 龙涛. 基于主成分回归的运输飞机超轮速诱因研究[J]. 计算机仿真, 2022, 39(10): 34-39, 65. QIAN Y, LONG T. Study on the inducement of transport aircraft exceeding tire speed rating based on principal component regression[J]. Computer Simulation, 2022, 39(10): 34-39, 65. (in Chinese) |
| [3] |
ALLIGIER R. Predictive distribution of mass and speed profile to improve aircraft climb prediction[J]. Journal of Air Transportation, 2020, 28(3): 114-123. DOI:10.2514/1.D0181 |
| [4] |
张一山, 余江. 民航飞机起飞超轮速的分析与研究[J]. 民航学报, 2021, 5(2): 79-84. ZHANG Y S, YU J. Analysis and research on excessive wheel speed in civil aircraft take-off[J]. Journal of Civil Aviation, 2021, 5(2): 79-84. (in Chinese) |
| [5] |
孙瑞山, 杨绎煊. 飞机起飞擦机尾事件的风险预测研究[J]. 安全与环境工程, 2016, 23(2): 153-156. SUN R S, YANG Y X. Risk prediction of aircraft tail strike events during take-off phase[J]. Safety and Environmental Engineering, 2016, 23(2): 153-156. (in Chinese) |
| [6] |
杨星月, 汪磊. 基于飞行员模型的民机擦机尾事件分析[J]. 飞行力学, 2022, 40(5): 89-94. YANG X Y, WANG L. Analysis of civil aircraft tail striking event based on pilot model[J]. Flight Dynamics, 2022, 40(5): 89-94. (in Chinese) |
| [7] |
NOH K S. A study on B737NG aircraft tail strike during takeoff[J]. Journal of the Korean Society for Aviation and Aeronautics, 2009, 17(4): 70-75. |
| [8] |
WANG X, WANG H F, YU L L. Aircraft tail strike events during take-off phase: A risk evaluation model[C]//Proceedings of the 12th International Conference on Reliability, Maintainability, and Safety. Shanghai, 2018: 142-145.
|
| [9] |
DRESSLER R F. New approach to air safety statistics[J]. Journal of Aircraft, 1967, 4(4): 347-355. DOI:10.2514/3.43847 |
| [10] |
MOSLEH A, GROTH K M, WANG C, et al. Methodology and software platform for multi-layer causal modeling[C]//Proceedings of 2008 Annual Conference of the European Society for Reliability. Valencia, Spain, 2008: 3-12.
|
| [11] |
ORIOLA A O, ADEKUNLE A K. Assessment of runway accident hazards in Nigeria aviation sector[J]. International Journal for Traffic and Transport Engineering, 2015, 5(2): 82-92. DOI:10.7708/ijtte.2015.5(2).01 |
| [12] |
CHEN Y Q, HOU Y J, HU D F, et al. Research about optimizing the wake turbulence separation for takeoff of CSPRs under crosswind conditions[C]//Proceedings of the 2nd International Conference on Smart Vehicular Technology, Transportation, Communication and Applications. Cham, Switzerland: Springer, 2018: 457-464.
|
| [13] |
HUIJBRECHTS E J A M, KOOLSTRA H J, MULDER J A. Using Vmcg-limited V1 controllability issues on contaminated runways and in crosswind[J]. Journal of Aircraft, 2019, 56(4): 1342-1352. DOI:10.2514/1.C035222 |
| [14] |
HAM D H. Safety-Ⅱ and resilience engineering in a nutshell: An introductory guide to their concepts and methods[J]. Safety and Health at Work, 2021, 12(1): 10-19. DOI:10.1016/j.shaw.2020.11.004 |
| [15] |
李升友. 安全系统思想及其理论核心研究[J]. 中国安全科学学报, 2016, 26(1): 28-33. LI S Y. Research on core theories of safety system thoughts[J]. China Safety Science Journal, 2016, 26(1): 28-33. (in Chinese) |
| [16] |
黄浪, 吴超, 杨冕, 等. 韧性理论在安全科学领域中的应用[J]. 中国安全科学学报, 2017, 27(3): 1-6. HUANG L, WU C, YANG M, et al. Application of resilience theory in field of safety science[J]. China Safety Science Journal, 2017, 27(3): 1-6. (in Chinese) |
| [17] |
张秀艳, 王琪. 基于PEE动态韧性模型的安全系统风险应对机制[J]. 综合运输, 2023, 45(12): 71-76, 165. ZHANG X Y, WANG Q. The risk response mechanism of safety system based on PEE dynamical resilience model[J]. China Transportation Review, 2023, 45(12): 71-76, 165. (in Chinese) |
| [18] |
刘洋. 基于独立性验证和因果推理的贝叶斯网络结构学习[D]. 长春: 吉林大学, 2021. LIU Y. Structure learning of Bayesian networks based on independence verification and causal inference[D]. Changchun: Jilin University, 2021. (in Chinese) |
| [19] |
张少中, 章锦文, 张志勇, 等. 面向大规模数据集的贝叶斯网络参数学习算法[J]. 计算机应用, 2006, 26(7): 1689-1691. ZHANG S Z, ZHANG J W, ZHANG Z Y, et al. Parameter learning for Bayesian networks with large data set[J]. Computer Applications, 2006, 26(7): 1689-1691. (in Chinese) |
| [20] |
TABANDEH A, GARDONI P, MURPHY C, et al. Societal risk and resilience analysis: Dynamic Bayesian network formulation of a capability approach[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2019, 5(1): 04018046. |
| [21] |
周毅, 胡锡健. 动态贝叶斯网络在战争身份识别中的应用[J]. 山西师范大学学报(自然科学版), 2014, 28(3): 9-13. ZHOU Y, HU X J. Application of dynamic Bayesian network in combat identification[J]. Journal of Shanxi Normal University (Natural Science Edition), 2014, 28(3): 9-13. (in Chinese) |
| [22] |
钱宇, 龙涛. 基于云贝叶斯网络的运输飞机超轮速风险评估[J]. 航空工程进展, 2022, 13(3): 171-178. QIAN Y, LONG T. Risk assessment on transport aircraft exceeding tire speed rating based on cloud Bayesian network[J]. Advances in Aeronautical Science and Engineering, 2022, 13(3): 171-178. (in Chinese) |
| [23] |
李明, 洪梅. 基于动态贝叶斯网络的海战场自然环境评估与预测[J]. 军事运筹与系统工程, 2018, 32(1): 37-43. LI M, HONG M. Assessment and forecast of sea-battlefield natural environment based on dynamic Bayesian network[J]. Military Operations Research and Systems Engineering, 2018, 32(1): 37-43. (in Chinese) |
| [24] |
汪磊, 孙景陆, 王文超, 等. 基于QAR数据的着陆超限风险贝叶斯网络分析模型[J]. 安全与环境学报, 2023, 23(1): 26-34. WANG L, SUN J L, WANG W C, et al. Bayesian network analysis model on landing exceedance risk based on flight QAR data[J]. Journal of Safety and Environment, 2023, 23(1): 26-34. (in Chinese) |
| [25] |
任佳, 高晓光, 茹伟. 目标数据缺失下离散动态贝叶斯网络的参数学习[J]. 系统工程与电子技术, 2011, 33(8): 1885-1890. REN J, GAO X G, RU W. Parameter learning of discrete dynamic Bayesian network with missing target data[J]. Systems Engineering and Electronics, 2011, 33(8): 1885-1890. (in Chinese) |
| [26] |
KAMMOUH O, GARDONI P, CIMELLARO G P. Probabilistic framework to evaluate the resilience of engineering systems using Bayesian and dynamic Bayesian networks[J]. Reliability Engineering & System Safety, 2020, 198: 106813. |
| [27] |
SUN J, SUN J. A dynamic Bayesian network model for real-time crash prediction using traffic speed conditions data[J]. Transportation Research Part C: Emerging Technologies, 2015, 54: 176-186. |
| [28] |
于培永, 郭志刚, 刘月浩. 基于动态贝叶斯网络的三维电力检修系统[J]. 自动化技术与应用, 2023, 42(9): 180-182. YU P Y, GUO Z G, LIU Y H. Three dimensional power maintenance system based on dynamic Bayesian network[J]. Techniques of Automation and Applications, 2023, 42(9): 180-182. (in Chinese) |
| [29] |
刘浩, 王昊, 孟光磊, 等. 基于动态贝叶斯网络和模糊灰度理论的飞行训练评估[J]. 航空学报, 2021, 42(8): 525838. LIU H, WANG H, MENG G L, et al. Flight training evaluation based on dynamic Bayesian network and fuzzy gray theory[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(8): 525838. (in Chinese) |
| [30] |
BERINGER D B, WILLIGES R C, ROSCOE S N. The transition of experienced pilots to a frequency-separated aircraft attitude display: A flight experiment[J]. Proceedings of the Human Factors Society Annual Meeting, 1974, 18(1): 62-70. |


