2. 长沙理工大学 道路灾变防治及交通安全教育部工程研究中心, 长沙 410114
2. Engineering Research Center of Catastrophic Prophylaxis and Treatment of Road and Traffic Safety of Ministry of Education, Changsha University of Science and Technology, Changsha 410114, China
中国是世界上自然灾害最严重的国家之一,发生自然灾害的种类多、分布区域广、频率高,灾害损失严重。据应急管理部发布的2022年全国自然灾害基本情况,2022年有1.12亿人次受灾,554人因灾死亡失踪,直接经济损失达到2 386.5亿元[1]。应急物资作为应对突发事件的重要保障,其配送科学性和送达时效性关系到民众生命安全和基本生活保障,对受灾地区的经济发展和社会稳定具有重要意义[2]。据统计,在突发事件造成的严重人员伤亡和经济损失中,由于应急物资配送不当造成的损失约占总损失的15%~20%[3]。现实情况下,救援中心的应急物资有限,经常无法同时满足所有受灾区域的应急需求,并且每个受灾点由于地理环境位置和受灾时段不同,其物资需求紧迫度存在一定的差异[4]。灾后救援面临紧张的物资流和运输流的双重压力,致使灾区在短时间内迫切需要医疗救援和生活物资[5]。因此,考虑受灾点的需求紧迫度,开展适用于突发自然灾害事件的约束性应急物资车辆路径研究,对于提高应急物资的送达时效和应急救援的效率具有重要意义。
由于应急物资配送过程中需要处理车载量、服务时间、服务优先级等现实问题,应急物资车辆路径规划中通常会考虑多种约束条件,如时间窗约束、优先约束、路径约束、容量约束等[6]。目前国内外学者针对约束性应急物资车辆路径问题进行了大量研究,这些研究各有侧重,主要从物资配送过程中的配送条件和外部环境因素两个角度来设定约束条件。从配送条件入手,针对灾后激增的应急物资需求和时效要求,可以引申出配送次数约束、车辆配送形式约束和时间窗约束等。例如,但兵兵等[7]基于需求可拆分条件建立了多目标的应急物资调度模型,允许每辆车服务多个需求点。谭洁等[8]根据灾后需求的不确定性,在模糊需求与单边软时间窗的约束条件下建立了开放式应急物资车辆路径模型。吕伟等[9]考虑软硬时间窗综合约束条件,引入软时间窗的惩罚成本和硬时间窗的不满足率,构建了多目标应急物资配送车辆路径规划模型。从外部环境因素入手,针对救援过程中的物资竞争和供求矛盾,优先约束被纳入约束范围,每个受灾点的需求紧迫度成为车辆调度顺序的决策参考[10-12]。针对道路通行性能对应急物资车辆路径产生的影响,部分学者将道路损毁程度、道路复杂程度作为道路约束,但这些研究大多假设条件相对严格且约束单一[13-15]。
通过上述文献梳理发现,应急物资车辆路径研究受到单目标、单车场、单次配送、无差别化供给、闭合式调度等多方面限制。为进一步满足应急救援的实际需要,本文运用层次分析法对需求紧迫度进行量化分级,兼顾整体效率与重点处置。以总调度服务时间最短、配送延误惩罚最小和需求未满足率最小为目标,提出基于需求紧迫度的约束性应急物资车辆路径模型,并设计需求拆分策略与两阶段遗传算法,实现开放式调度、软时间窗、需求拆分等综合性配送条件。本研究为灾后应急救援提供综合性的应急物资车辆路径的科学决策,对减灾救灾具有重要理论和实践意义。
1 问题表述 1.1 约束性车辆路径问题约束性车辆路径问题,即在一定的约束条件下,规划合理的行驶路线并达到一定的决策目标[16]。针对灾后救援工作的物资流向与时效要求,开展基于需求紧迫度的约束性车辆路径问题研究符合实际应急需求,可以确保薄弱受灾点优先得到应急物资,同时不失全局救援的一般效率。本文提出基于需求紧迫度的约束性应急物资车辆路径模型,根据需求拆分策略规划车队的路径和运送顺序,将应急物资由多个集中供应点配送到各受灾点,及时进行物资补给并投入循环调度。在物资配送过程中主要考虑载重量、软时间窗和行驶长度等约束性条件,使整个应急过程的总调度服务时间最短、配送延误惩罚最小、需求未满足率最小。约束性车辆路径问题求解步骤如图 1所示。
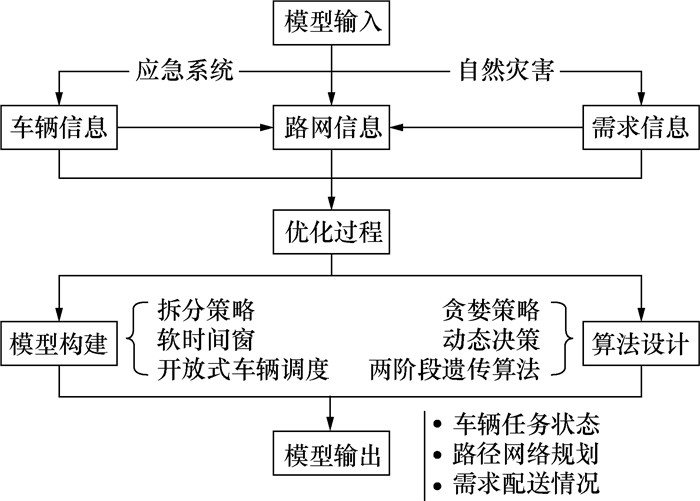
|
| 图 1 车辆路径问题求解步骤 |
1.2 受灾点需求拆分策略
基于车辆载重限制与受灾点阶段性需求的现实情况,设计受灾点的需求拆分策略如下:
| $ N= \begin{cases}0, & q_j \leqslant Q_m ; \\ {\left[\frac{q_j}{Q_m}\right], } & q_j>Q_m .\end{cases} $ | (1) |
式中:
各受灾点的受灾程度存在差异。考虑应急特征并结合已有研究成果[17],从人员、设施及其他维度考虑,使用层次分析法对受灾点需求紧迫度进行赋权分级。首先,建立表 1所示的需求紧迫度指标体系,通过指数标度法构造判断矩阵,由方根法得到判断矩阵的特征向量,再进行一致性检验。分析发现,准则层中,人员受灾情况(A1)的权重最高,反映灾后应急以“人民至上、生命至上”为第一救灾要素的决策性质。从指标层总权重结果可知,死亡人数(A1, 1)和紧急转移人数(A1, 4)的权重较大,分别影响当下与未来短期的灾情控制。
| 目标层 | 准则层 | 指标层 | 指标层总权重 | |||
| 内容 | 权重 | 内容 | 权重 | |||
| 受灾程度影响因素(T) | 人员受灾情况(A1) | 0.78 | 死亡人数(A1, 1) | 0.42 | 0.327 6 | |
| 受伤人数(A1, 2) | 0.15 | 0.117 0 | ||||
| 被困人数(A1, 3) | 0.05 | 0.039 0 | ||||
| 紧急转移人数(A1, 4) | 0.38 | 0.296 4 | ||||
| 基础设施情况(A2) | 0.07 | 道路损坏面积(A2, 1) | 0.23 | 0.016 1 | ||
| 房屋损坏间数(A2, 2) | 0.77 | 0.053 9 | ||||
| 其他指标(A3) | 0.15 | 自主抗灾能力(A3, 1) | 1.00 | 0.150 0 | ||
2 约束性应急物资车辆路径模型 2.1 模型构建
自然灾害下基于需求紧迫度的约束性应急物资车辆路径模型,考虑了软时间窗、车辆装载量、行驶上限对调度的影响,主要目标为尽可能提高物资供给率、行动时效性及减少灾害损失。相关假设如下:
1) 已知车辆额定装载量,受灾点经需求拆分接受多配送车辆的多次服务。
2) 基于需求紧迫度的单边软时间窗约束了配送任务在决策周期内完成。
3) 已知车辆的最长连续行驶时间,规划路径长度不能超过车辆单次调度行驶上限。
4) 车辆执行多条配送路径,完成当前任务后停靠最后一个服务点等待下次调度。
本研究建立的约束性应急物资车辆路径模型如式(2)—(13)所示,式中符号说明见表 2。其中:式(2)为目标函数1,表示车辆路径的总调度服务时间最小化;式(3)为目标函数2,表示配送延误惩罚最小化,由时间窗、延误时间和累积延误量决定;式(4)为目标函数3,表示系统需求未满足率最小化;式(5)表示车辆m配送路径上的物资总和不超过车辆的装载量Qm;式(6)表示车辆m在连接弧上通行时间不超过车辆的行驶时间上限Tm;式(7)确保车辆m从救援站出发,停靠路径末节点等待下次调度;式(8)表示指向受灾点j的路径至少存在一条;式(9)表示每个受灾点j至少被服务一次;式(10)表示只有车辆m服务的受灾点才经过其所在的弧;式(11)表示任意车辆m从车场出发的时刻为0;式(12)表示车辆到达不同受灾点的时间关系;约束(13)规定自变量xcmu, v、ycmj均为0-1变量。
| $ Z_1=\min \sum\limits_M \sum\limits_{C_m}\left[\sum\limits_V p_{u, v} O_{c_m}^{u, v} x_{c_m}^{u, v}+\sum\limits_J s_j y_{c_m}^j\right] . $ | (2) |
| $ \begin{aligned} & Z_2=\min \sum\limits_J\left[\sum _ { M } \sum _ { C _ { m } } \operatorname { min } \left\{\left(\max \left\{t_{j, c_m}-l_j, 0\right\}, \right.\right.\right. \\ & \left.\left.\left(t_{j, c_m}-t_{j, c_m-1}\right)\right\} \cdot\left(Q_j-\sum\limits_M \sum\limits_{C_m} y_{c_m}^j q_{j, c_m-1}\right)\right] . \end{aligned} $ | (3) |
| $ Z_3=\min \sum\limits_J \sum\limits_M \sum\limits_{C_m} \frac{Q_j-y_{c_m}^j q_{j, c_m}}{Q_j} . $ | (4) |
| $ \sum\limits_J q_{j, c_m} y_{c_m}^j \leqslant Q_m, \forall c_m \in C_m . $ | (5) |
| $ \sum\limits_V p_{u, v} x_{c_m}^{u, v} \leqslant T_m, u, v \in V, \forall c_m \in C_m . $ | (6) |
| $ x_{c_m}^{u, v}-x_{c_m}^{v, u}=\left\{\begin{array}{l} 1 \\ 0, \\ -1 \end{array}, c_m \in C_m, \forall u, v \in V .\right. $ | (7) |
| $ \sum\limits_V \sum\limits_{C_m} x_{c_m}^{v, j} \geqslant 1, \forall j \in J . $ | (8) |
| $ \sum\limits_{C_m} y_{c_m}^j \geqslant 1, \forall j \in J . $ | (9) |
| $ x_{c_m}^{v, j} \geqslant y_{c_m}^j, \quad \forall j \in J . $ | (10) |
| $ t_{i, c_m}=0, \quad \forall i \in I . $ | (11) |
| $ t_{j, c_m}=\sum\limits_{u, v \in c_m^j}\left(t_{u, c_m}+s_u+p_{u, v}\right) x_{c_m}^{u, v} . $ | (12) |
| $ x_{c_m}^{u, v}, y_{c_m}^j \in\{0, 1\}, u, v \in V, j \in J, c_m \in C_m . $ | (13) |
| 符号 | 说明 |
| I | 救援站集合 |
| J | 物资需求点集合 |
| V | 节点集合,包括救援站和需求点 |
| M | 车辆集合 |
| Cm | 车辆m行程集合 |
| Qm | 额定装载量,表示车辆m的最大装载能力 |
| Qj | 源需求量,表示受灾点j的需求总量 |
| qj, cm | 拆分需求量,表示受灾点j由行程cm供应的应急物资量 |
| cmj | 行程任务序列,表示行程cm服务的受灾点j及其之前的受灾点序列 |
| Tm | 行驶时间上限,表示车辆m在一次调度中的最长行驶时间 |
| sj | 服务时间,表示车辆在每个受灾点j卸载物资的停留时间 |
| [0, lj] | 物资送达受灾点j的软时间窗限制 |
| tj, cm | 行程cm到达需求点j的时刻 |
| pu, v | 表示任意两节点之间的行驶时间 |
| Ocmu, v | 行程cm途经节点u、v间的道路通行状态 |
| xcmu, v | 行程cm是否从节点u到节点v |
| ycmj | 行程cm是否服务节点j |
2.2 算法设计
考虑需求拆分、软时间窗、开放调度的约束性,应急物资车辆路径模型属于非确定性多项式(non-deterministic polynomial,NP)-hard问题,而遗传算法具有内在隐并行性和全局寻优能力,操作算子可加快算法收敛、提高解集质量,因此设计如图 2所示的两阶段遗传算法进行求解。第1阶段对受灾点进行需求拆分与初始聚类,基于受灾点的需求紧迫度确定物资配送的首轮调度;第2阶段完成车辆路径的动态规划,基于覆盖模型分配物资补给仓库,车辆循环投入调度。区别于受灾点分配和路径规划相互独立的一般方法,本研究所应用遗传算法的遗传算子(选择算子、交叉算子和变异算子,即图 2中的轮盘选择、OX交叉和两点变异)和车辆任务信息都进行了改进,能够更加灵活、动态地规划物资配送与车辆路径,从而跳出区域限制与局部最优解。
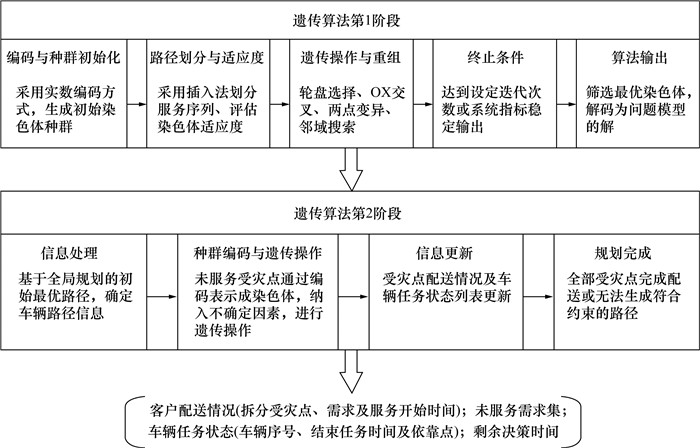
|
| 图 2 两阶段遗传算法流程 |
3 算例分析与结果讨论 3.1 情景介绍
选取河南省郑州市中原区的路网进行道路提取,如图 3所示。以2021年7月郑州特大暴雨后的应急物资配送为案例背景,选取3个储运便利的地点(工贸园A、郑州站B和高速服务站C)作为救援站,选取10个典型的居民区作为受灾点。依托层次分析法、全球定位系统(global positioning system,GPS)以及人口物资比例,10个受灾点的需求权重总排序以及相应物资需求量如表 3所示。考虑不同维度的灾情信息及需求紧迫度排序,得到各受灾点的送达软时间窗分别为:40、29、54、38、57、43、65、46、35、62 min。假设决策周期时间为150 min,车辆最长行驶时间为90 min。车辆装载量为200件,救援站A、B、C初始分别有2、3、1辆配送车辆。
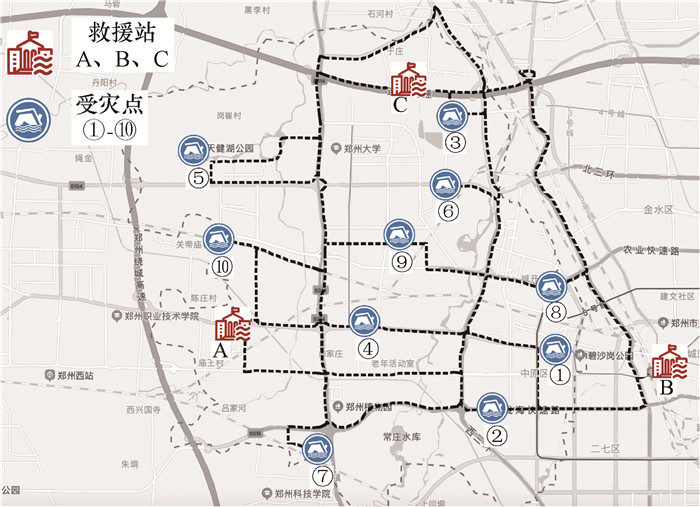
|
| 图 3 受灾区域物流网 |
| 受灾点 | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Z10 |
| 权重 | 0.145 | 0.209 | 0.035 | 0.153 | 0.034 | 0.116 | 0.025 | 0.098 | 0.157 | 0.028 |
| 权重排序 | 4 | 1 | 7 | 3 | 8 | 5 | 10 | 6 | 2 | 9 |
| 需求量/件 | 475 | 525 | 130 | 390 | 175 | 332 | 80 | 420 | 240 | 65 |
3.2 结果与讨论
运用MATLAB R2021a进行方案寻优。基于需求拆分策略,受灾点的拆分对应关系为{[1, 1, 2, 3],[2, 4, 5, 6],[3, 7],[4, 8, 9],[5, 10],[6, 11, 12],[7, 13],[8, 14, 15, 16],[9, 17, 18],[10, 19]}。其中[1, 1, 2, 3]表示受灾点1需求拆分后接受3次配送服务(分别定义为拆分受灾点1、2和3),[7, 13]为受灾点7需求拆分后接受1次配送服务(定义为拆分受灾点13)。各拆分受灾点的拆分需求量和配送情况如表 4所示。
| 受灾点序号 | 拆分受灾点序号 | 拆分需求量/件 | 开始服务时间/min |
| 1 | 1 2 3 | 200 200 75 | 17 61 110 |
| 2 | 5 4 6 | 200 200 125 | 21 73 86 |
| 3 | 7 | 130 | 60 |
| 4 | 9 8 | 190 200 | 18 111 |
| 5 | 10 | 175 | 71 |
| 6 | 11 12 | 200 132 | 18 117 |
| 7 | 13 | 80 | 116 |
| 8 | 15 16 | 200 200 | 22 81 |
| 9 | 17 18 | 200 40 | 33 127 |
| 10 | 19 | 65 | 99 |
第1阶段得到的初始配送路径为{[17, 18],[9, 8, 10, 19],[15, 14, 16],[1, 3, 2],[5, 4, 6, 13],[11, 12, 7]}。其中第1条路径上的服务节点为受灾点9需求拆分后的拆分受灾点17、18,即需求紧迫度高的受灾点得到了优先配送。随着第1阶段算法迭代,在不考虑配送能力限制下,方案种群的目标函数呈阶梯下降。违反时间窗约束的路径数为2。
将车辆任务状态表定义为[车序号, 完成时间, 停靠的拆分受灾点],则首轮车辆任务状态为{[1, 43, 17],[2, 28, 9],[3, 32, 15],[4, 27, 1],[5, 31, 5],[6, 28, 11]},结束配送任务的车辆重新投入调度,规划剩余需求物资的配送路径。图 4所示为最先结束首轮配送任务的车辆4进行动态路径规划的系统迭代过程。可以发现,随着车辆路径的执行,系统需求未满足率逐渐降低。在救援周期内,车辆循环开放调度于受灾点与救援站之间,车辆1至6的任务列表分别为:[17→救援站B→6、3],[9→救援站A→10→救援站A→13],[15→救援站B→14→救援站A→18],[1→救援站B→2→救援站B→8],[5→救援站B→4→救援站B→12],[11→救援站C→7、19]。各车辆的调度工作总量基本均衡,分别为[400, 445, 440, 600, 532, 395]。由车辆的任务列表分析发现,救援站A、B的工作负荷较大,可提前作出工作部署。受灾点8的拆分受灾点16因超出周期时间未配送,系统需求满足率为99.4%。
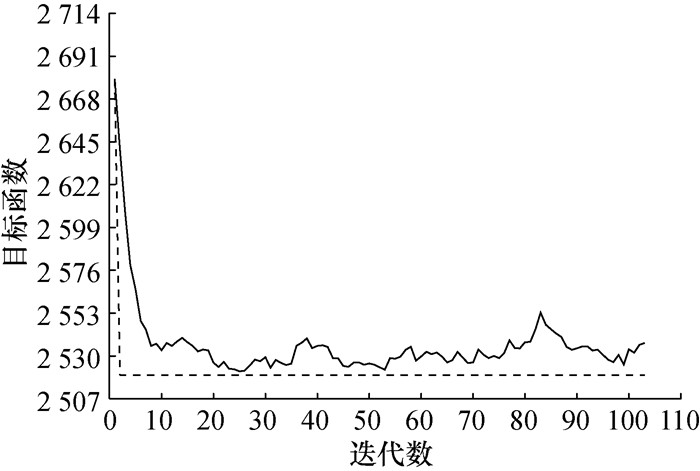
|
| 图 4 车辆4目标函数3的迭代曲线 |
图 5所示为车辆路径规划目标函数2的迭代曲线,即配送延误惩罚迭代曲线。随着车辆资源的循环投入,在算法规划完12条路径后,系统前期的配送延误惩罚逐渐降低,救援时间成本逐渐增加。虽然路线规划后期曲线有轻微波动上升,但配送延误惩罚依然较低。与初始配送延误惩罚相比,迭代后的最小配送延误惩罚下降了40.3%。受灾点的拆分配送情况取决于时间窗、需求量以及地理位置等因素,所提模型与算法能为决策者提供优化的可行路径方案,实现应急资源效能最大化。
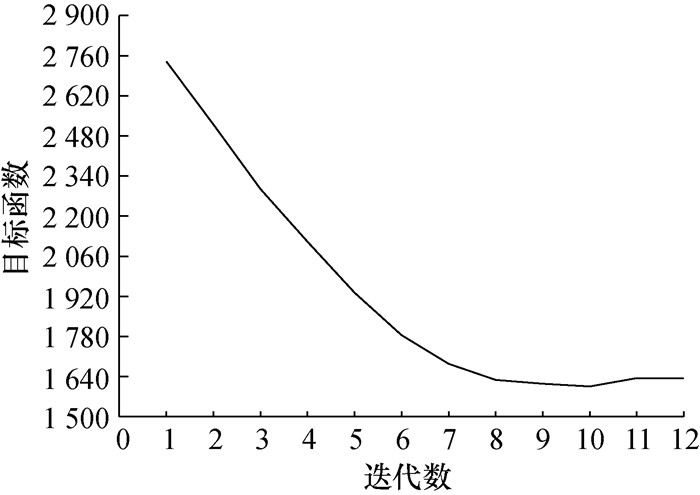
|
| 图 5 车辆路径规划目标函数2的迭代曲线 |
为验证模型、算法的适用性与灵活性,设置对照模拟条件。假设规划第3辆车的二次调度路径时,救援站B至拆分受灾点14的路线破坏。经算法迭代,车辆路径方案调整为{[17→救援站A→14],[9→救援站A→10→救援站A→13],[15→救援站B→6、3],[1→救援站B→2→救援站B→8],[5→救援站B→4→救援站B→12],[11→救援站C→7、19]}。在决策周期内,拆分受灾点16和18未被配送,需求量分别为[20, 40],系统需求满足率为97.9%,相对下降1.5%,配送延误惩罚上升,配送服务时间相对下降。
4 结论综合考虑需求紧迫度、需求拆分、软时间窗、开放式调度等灵活配送条件,构建了符合突发应急灾害事件的约束性应急物资车辆路径模型,并设计两阶段动态遗传算法,以最小化总调度服务时间、延误惩罚成本以及需求未满足率为目标,实现受灾点的多次服务和路径组合优化,兼顾重点灾区的需求紧迫性与全局救援的时效性。
通过对郑州市某区域突发暴雨灾害后应急物资调度的算例分析,所构建模型与算法不仅降低了40.3%的配送延误惩罚,还满足了99.4%的物资需求,充分发挥了应急物资和运输资源的时间效用价值。随着配送车辆的循环开放调度,受灾点的需求逐渐在决策周期内得到满足,所提出的模型可以形成科学合理的物资配送方案和车辆调度方案,并计算出各救援站与车辆的工作负荷。同时,所构建模型对突发道路状况也呈现出良好适应性,能以1.5%的最小化系统偏差动态调整路径方案。
本文的不足之处在于进行的是单决策周期的应急物资车辆路径研究,未考虑灾后路径损毁、修复情况及其影响。后续的研究方向拟针对目前研究模型与方法存在的不足进行完善与优化,拓展至多周期的决策研究,并结合路径可靠性理论,设计更为灵活的拆分策略。
| [1] |
中华人民共和国应急管理部. 应急管理部发布2022年全国自然灾害基本情况[EB/OL]. (2023-01-13)[2023-10-13]. https://www.mem.gov.cn/xw/yjglbgzdt/202301/t20230113_440478.shtml. Ministry of Emergency Management of the People's Republic of China. The Ministry of Emergency Management releases the basic situation of natural disasters in China in 2022[EB/OL]. (2023-01-13)[2023-10-13]. https://www.mem.gov.cn/xw/yjglbgzdt/202301/t20230113_440478.shtml. (in Chinese) |
| [2] |
胡晓伟, 宋浪, 杨滨毓, 等. 重大突发公共卫生事件下城市应急医疗物资优化调度研究[J]. 中国公路学报, 2020, 33(11): 55-64. HU X W, SONG L, YANG B Y, et al. Optimal matching of urban emergency medical supplies under major public health events[J]. China Journal of Highway and Transport, 2020, 33(11): 55-64. (in Chinese) |
| [3] |
赵彤. 我国突发自然灾害应急救灾物资配送系统优化研究[D]. 大连: 大连海事大学, 2011. ZHAO T. The study on optimized emergency logistics distribution system of burst natural disasters rescuing in China[D]. Dalian: Dalian Maritime University, 2011. (in Chinese) |
| [4] |
王英, 苏柏林, 闫鹏, 等. 基于改进TOPSIS的受灾点需求紧迫性分级研究[J]. 安全与环境学报, 2019, 19(1): 140-146. WANG Y, SU B L, YAN P, et al. Approach to the classification of the demand urgency of the affected points based on the improved TOPSIS[J]. Journal of Safety and Environment, 2019, 19(1): 140-146. (in Chinese) |
| [5] |
SHEU J B. Dynamic relief-demand management for emergency logistics operations under large-scale disasters[J]. Transportation Research Part E: Logistics and Transportation Review, 2010, 46(1): 1-17. DOI:10.1016/j.tre.2009.07.005 |
| [6] |
杨继军, 缪成, 许维胜. 应急救援物资运输与车辆路径规划[M]. 北京: 经济管理出版社, 2021. YANG J J, MIAO C, XU W S. Scheduling of rescure resources and planning of transportation path in emergency[M]. Beijing: Economy & Management Publishing House, 2021. (in Chinese) |
| [7] |
但兵兵, 朱万红, 桑杨阳, 等. 需求可拆分的应急物资调度问题的蚁群算法[J]. 指挥控制与仿真, 2013, 35(4): 81-83, 87. DAN B B, ZHU W H, SANG Y Y, et al. Ant colony optimization algorithm for split routing problem of dispatching emergency materials[J]. Command Control & Simulation, 2013, 35(4): 81-83, 87. (in Chinese) |
| [8] |
谭洁, 李文莉, 刘康康. 考虑二次灾害的开放式应急物流车辆路径问题[J]. 系统工程, 2021, 39(2): 61-71. TAN J, LI W L, LIU K K. The open vehicle routing problem of emergency logistics considering secondary disasters[J]. Systems Engineering, 2021, 39(2): 61-71. (in Chinese) |
| [9] |
吕伟, 李志红, 马亚萍, 等. 考虑受灾点需求时间窗的应急物资配送车辆路径规划研究[J]. 中国安全生产科学技术, 2020, 16(3): 5-11. LYU W, LI Z H, MA Y P, et al. Research on route planning of emergency materials distribution vehicles considering time window of requirements by disaster point[J]. Journal of Safety Science and Technology, 2020, 16(3): 5-11. (in Chinese) |
| [10] |
宋晓宇, 王建国, 常春光. 基于需求紧迫度的非线性连续消耗应急调度模型与算法[J]. 信息与控制, 2014, 43(6): 735-743. SONG X Y, WANG J G, CHANG C G. Nonlinear continuous consumption emergency material dispatching model based on demand urgency degrees and its algorithm[J]. Information and Control, 2014, 43(6): 735-743. (in Chinese) |
| [11] |
李华峰, 黄樟灿, 张蔷, 等. 求解需求可拆分车辆路径问题的改进的金字塔演化策略[J]. 计算机应用, 2021, 41(1): 300-306. LI H F, HUANG Z C, ZHANG Q, et al. Improved pyramid evolution strategy for solving split delivery vehicle routing problem[J]. Journal of Computer Applications, 2021, 41(1): 300-306. (in Chinese) |
| [12] |
宋英华, 白明轩, 马亚萍, 等. 考虑区域灾情分级的应急物资公平调度优化模型[J]. 中国安全科学学报, 2022, 32(1): 172-179. SONG Y H, BAI M X, MA Y P, et al. Optimal model for fair dispatch of emergency materials considering regional disaster classification[J]. China Safety Science Journal, 2022, 32(1): 172-179. (in Chinese) |
| [13] |
QI C M, HU L S. Optimization of vehicle routing problem for emergency cold chain logistics based on minimum loss[J]. Physical Communication, 2020, 40: 101085. DOI:10.1016/j.phycom.2020.101085 |
| [14] |
李军军, 黄有方, 许波桅. 道路修整与应急车辆路径的集成优化[J]. 工业仪表与自动化装置, 2013(5): 8-12. LI J J, HUANG Y F, XU B W. Integration optimization of road repair and emergency vehicle routing[J]. Industrial Instru-mentation & Automation, 2013(5): 8-12. (in Chinese) |
| [15] |
狄卫民, 张鹏阁, 杜慧莉. 考虑道路状况的应急配发站启用以及配送优化问题[J]. 中国安全生产科学技术, 2020, 16(9): 12-17. DI W M, ZHANG P G, DU H L. Opening of emergency distribution stations and optimization of distribution considering road conditions[J]. Journal of Safety Science and Technology, 2020, 16(9): 12-17. (in Chinese) |
| [16] |
兰奇. 考虑车型类别的车辆路径问题研究[D]. 北京: 北京交通大学, 2020. LAN Q. Study on vehicle routing problem considering vehicle type[D]. Beijing: Beijing Jiaotong University, 2020. (in Chinese) |
| [17] |
赵建有, 肖宇, 朱欣媛, 等. 考虑需求紧迫度的应急车辆路径优化方法[J]. 哈尔滨工业大学学报, 2022, 54(9): 27-34. ZHAO J Y, XIAO Y, ZHU X Y, et al. Route optimization method for emergency vehicles considering demand urgency[J]. Journal of Harbin Institute of Technology, 2022, 54(9): 27-34. (in Chinese) |



