2. 计算智能与信号处理教育部重点实验室(安徽大学), 合肥 230601
2. Ministry of Education Key Laboratory of Computational Intelligence and Signal Processing, Anhui University, Hefei 230601, China
现实世界中,许多复杂的实体关系均可以抽象为网络关系[1],对这些网络进行社区发现可以获得关系紧密的节点集合,从而发掘现实世界中潜在的模式和功能。社区发现极具实际意义,可用于详细追踪网络动态和社区影响,如谣言传播、病毒暴发和肿瘤演变等[2]。现实世界中,一个社区的参与者往往也是另一个社区的成员,重叠是现实世界社交网络的基本特征,Palla等[3]研究表明,重叠是网络结构内在的固有特征[4],实际网络中的社区往往由高度重叠的节点集合构成[5]。发现重叠社区对更好地理解和分析网络的结构和功能性质至关重要。
网络表示学习算法将网络信息转化为低维空间的向量并维持网络原有的结构和属性信息,以便应用于后续的链路预测[6]、节点分类[7]和社区发现等图形处理任务。因此,基于网络表示学习的社区发现方法可以有效融合网络结构和属性信息[8-9],过程一般为先得到网络节点的向量表示,再利用向量性质划分得到网络社区结果。
图自编码器模型作为网络表示学习的代表性方法,可以高效学习网络嵌入,在社区发现任务方面应用广泛。Qiu等[10]提出了一种基于图变分推理的社区发现方法,利用模块度矩阵和网络结构的联合优化实现非概率的社区发现。半监督的MRFasGCN算法[11]通过在图卷积网络(graph convolutional network, GCN)[12]框架中融入社区的Markov随机场(Markov random field,MRF)[11]进行建模,进而实现社区发现。基于GCN的无监督社区发现方法(gcn-based approach for unsupervised community detection, GUCD)[13]将MRFasGCN的网络建模方法整合到自编码器框架中,并引入一种可同时学习网络社区和节点语义的特殊神经网络体系结构,实现了无监督的社区发现。但是图自编码器模型通常只考虑节点连边恢复而忽略了社区结构作用,尤其是在多个社区包含重叠节点的情况下,难以准确判断节点归属关系和社区分布[14]。
针对该问题,本文提出了一种面向重叠社区发现的无监督模块度感知图自编码器模型(modularity-aware graph autoencoder model for overlapping community detection, GAME)。通过在图自编码器的基础上加入模块度最大化损失以保留模型在网络嵌入时的社区结构,以提高GAME处理重叠社区发现任务的性能,通过将编码器得到的节点向量矩阵处理为社区隶属度矩阵进行社区分配,以实现重叠社区发现。
1 模型算法 1.1 传统的重叠社区发现算法重叠社区发现是为了得到社区内部节点连接紧密而外部连接稀疏的节点集[15],传统算法大致可分为基于标签传播、图分割和局部优化算法等。重叠社区传播算法(community overlap propagation algorithm, COPRA)[16]是在标签传播算法(label propagation algorithm, LPA)[17]的基础上提出的重叠社区发现算法,该算法通过异步更新方式迭代节点标签,在达到迭代最大值或标签稳定时停止迭代,同一个节点可以包含多个标签,以实现重叠社区发现。基于派系过滤的算法(clique percolation method, CPM)[3]通过寻找、合并网络中的K阶完全子图实现社区发现,并且同一节点可能被多个K阶完全子图包含,从而实现重叠社区发现。但CPM算法复杂度较高,不适用于大规模网络。Whang等[18]以前K个度最高的节点为种子节点实现了重叠社区发现。该方法先选择初始种子节点并通过迭代扩展,再识别与种子节点紧密相关的重叠节点,从而实现大规模图社区发现,但该方法需要已知社区数量。半二元矩阵分解算法(semi-binary matrix factorization, SBMF)[19]可以理解为K-均值和非负矩阵分解的结合,与K-均值不同的是,SBMF算法既不限制每个个体仅属于一个社区,也不限制“软成员”值的总和为1。SBMF算法用张量分解的形式解决了最小二乘最优问题,实现了重叠社区发现。
传统的社区发现算法大多数基于统计推断和机器学习,在面对日益复杂的网络属性和网络规模时具有一定局限性[2]。
1.2 基于表示学习的重叠社区发现算法利用表示学习处理社区发现任务,需要先对网络数据进行降维,再对节点向量进行社区分配。相较于传统的社区发现算法,基于表示学习的重叠社区发现算法可以更灵活地编码网络信息,并且更易融合网络结构和属性信息[20]。网络表示学习的目的是将需要编码的网络信息转化为低维向量表示,同时保持原始的网络拓扑结构和节点属性的邻近性[21]。通过表示学习获得的低维向量表示更适用于网络分析的下游任务。
传统的网络表示学习算法主要有基于随机游走的算法[22]、基于矩阵分解的算法[23],以及深度学习被应用于网络表示学习的基于图神经网络[12]的算法等。Guo等[24]设计了一种基于节点中心性的行走策略,并开发了2种针对高低度节点的社区感知随机游走策略,通过上述策略捕捉社区中心和边界的特征并结合聚类算法实现了重叠社区发现。LookCom算法[20]通过联合框架学习最优网络拓扑结构和通过最优网络节点表示结果二者进行社区发现,并利用交替优化算法解决所提出的优化问题。自训练对抗性学习算法(self-training adversarial learning algorithm, ACNE-ST)[25]先在初始阶段采用一种游走策略以获得较多顶点的路径,采用所提出的对抗性学习方法进行网络表示学习,再使用简单分类器的分配结果作为软标签更新其中对抗性学习算法的参数,从而提高了算法的重叠社区发现性能。
基于图自编码器模型的社区发现算法使用编码器和解码器组件以无监管的方式学习网络表示,目标是最小化原始网络和重构网络之间的误差,以获得最佳的隐藏表示[2]。用于社区发现的变分图自动编码器(variational graph autoencoder for community detection, VGAECD)[26]算法通过引入以Gauss分布为基础的变分图自编码器,实现了社区发现。神经重叠社区发现(neural overlapping community detection, NOCD)[27]算法将GCN作为图表示模型编码器和将Bernoulli-Poisson图生成模型作为解码器构成自编码器模型,实现了重叠社区发现。上述基于图自编码器结构的社区发现算法大多致力于恢复网络节点连边,而忽略了社区结构对社区发现结果的影响,不利于充分挖掘网络潜在信息[28],以致上述算法在处理社区发现任务时表现欠佳[14]。
2 算法描述 2.1 问题定义本文使用的基本变量及其说明如表 1所示。对于一个节点包含属性信息的属性网络
| 基本变量 | 含义 |
| G | 属性网络 |
| N | G的节点数 |
| M | G的边数 |
| S | G的属性维数 |
| k | 社区数量 |
| γ | 模型迭代次数 |
| A∈N×N | 邻接矩阵 |
| A~∈N×N | 具有自环的邻接矩阵 |
| I∈N×N | 单位矩阵 |
| X∈N×S | 属性矩阵 |
| ϕ | 激活函数 |
| Wl | 模型权重矩阵 |
| B∈N×N | 模块度矩阵 |
| Zi | vi的向量表示 |
| F∈N×k | 社区隶属度矩阵 |
| 归一化后的矩阵F | |
| Ci | vi的预测社区编号 |
| C′i | vi的真实社区编号 |
| ρ | 社区划分阈值 |
社区发现的任务是将节点划分到社区
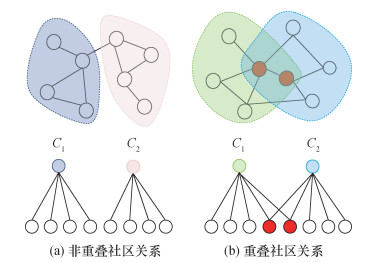
|
| 图 1 社区隶属关系 |
社区发现的目的是获得
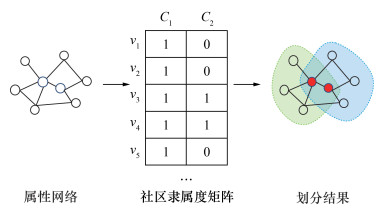
|
| 图 2 社区隶属度矩阵的社区分配 |
2.2 GAME模型
GAME的模型架构如图 3所示。其中:
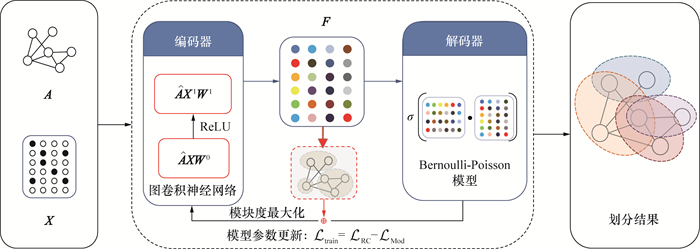
|
| 图 3 GAME的模型架构 |
2.2.1 图表示模块
GAME模型采用2层GCN[12]作为模块度图自编码器模块的编码器部分,通过在迭代损失中融入模块度最大化损失函数,并以端到端的方式学习社区隶属关系。其中,GCN的隐藏层为128维,输出k维,k的取值为数据集对应的真实社区数。
GAME通过直接拼接归一化后的A和X作为GCN的输入。表示如下:
| $ \boldsymbol{F}=\operatorname{GCN}_{\theta}(\boldsymbol{A}, \boldsymbol{X}) . $ | (1) |
其中θ表示负对数似然的参数。
层级之间的转换通过卷积函数
| $ \begin{gathered} & \boldsymbol{Z}^{l+1}=f_{\phi}\left(\boldsymbol{Z}^{l}, \boldsymbol{A} \mid \boldsymbol{W}^{l}\right)=\phi\left(\hat{\mathbf{A}} \boldsymbol{Z}^{l} \boldsymbol{W}^{l}\right) ,\\ & \hat{\boldsymbol{A}}=\widetilde{\boldsymbol{D}}^{-\frac{1}{2}} \widetilde{\boldsymbol{A}} \widetilde{\boldsymbol{D}}^{-\frac{1}{2}} ,\\ & \widetilde{\boldsymbol{A}}=\boldsymbol{A}+\boldsymbol{I} ,\\ & \widetilde{D}_{i i}=\sum\limits_{j} \widetilde{A}_{i j} . \end{gathered} $ | (2) |
其中:
GAME模型采用2层卷积神经网络作为编码器, 2个卷积层的激活函数均为ReLU, 模型输出为
| $ \;\;\;\;\;\;\;\boldsymbol{F}=\operatorname{GCN}_\theta(\boldsymbol{A}, \boldsymbol{X})= \\ \operatorname{ReLU}\left(\hat{\boldsymbol{A}} \operatorname{ReLU}\left(\hat{\boldsymbol{A}} \boldsymbol{X} \boldsymbol{W}^0\right) \boldsymbol{W}^1\right). $ | (3) |
模块度自编码器的解码器部分采用Bernoulli-Poisson图生成模型,该模型常用于重叠社区发现模型算法[27]。相比于传统的概率生成方法,Bernoulli-Poisson图生成模型不仅适用于多种社区结构,而且具有较高的计算效率[29]。相关计算表示如下:
| $ \boldsymbol{A}_{u v} \sim \operatorname{Bernoulli}\left(1-\exp \left(-\boldsymbol{F}_{u} \boldsymbol{F}_{v}^{\mathrm{T}}\right)\right) . $ | (4) |
其中:
| $ \begin{gather*} -\ln P(\boldsymbol{A} \mid \boldsymbol{F})= \\ -\sum\limits_{(u, v) \notin E} \ln \left(1-\exp \left(-\boldsymbol{F}_{u} \boldsymbol{F}_{v}^{\mathrm{T}}\right)\right)+\sum\limits_{(u, v) \in E} \boldsymbol{F}_{u} \boldsymbol{F}_{v}^{\mathrm{T}} . \end{gather*} $ | (5) |
其中
| $ \begin{gather*} \mathcal{L}_{\mathrm{RC}}=-E_{(u, v) \sim P_{E}}\left[\ln \left(1-\exp \left(-\boldsymbol{F}_{u} \boldsymbol{F}_{v}^{\mathrm{T}}\right)\right)\right]+ \\ E_{(u, v) \sim P_{N}}\left[\boldsymbol{F}_{u} \boldsymbol{F}_{v}^{\mathrm{T}}\right] . \end{gather*} $ | (6) |
其中
模块度是指通过比较实际观察到社区内边数与在随机网络中预期的社区内边数之间的差异衡量社区的显著性。如果模块度为正,表示图中的社区结构比随机网络更紧密。为进一步优化模型参数,本文提出了一种软模块度损失函数,利用网络的结构特征优化图自编码器参数,从而提升模型的社区发现性能。模块度Q表示如下:
| $ Q=\frac{1}{4 M} \sum\limits_{i, j}\left[\left(A_{i j}-\frac{\delta_{i} \delta_{j}}{2 M}\right) \tau(i, j)\right] . $ | (7) |
其中:
| $ b_{i j}=A_{i j}-\frac{\delta_{i} \delta_{j}}{2 M} . $ | (8) |
无论节点之间是否有连边, 均由
| $ \begin{gather*} Q=\frac{1}{4 M} \operatorname{tr}\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{F}\right) ,\\ \operatorname{tr}\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{F}\right)=N . \end{gather*} $ | (9) |
其中tr表示矩阵的迹。
式(9) 是一个非确定性多项式时间问题(nondeterministic polynomial-time hard, NP-hard), 为使式(9)达到最大, 引人
| $ \hat{F}_{i j}=\frac{\sqrt{N} \cdot \sqrt{F_{i j}}}{\sum\limits_{i} \sum\limits_{j} \sqrt{F_{i j}}} . $ | (10) |
其中
得到最终的模块度损失表示如下:
| $ \mathcal{L}_{\mathrm{Mod}}=\frac{1}{4 M} \operatorname{tr}\left(\hat{\boldsymbol{F}}^{\mathrm{T}} \boldsymbol{B} \hat{\boldsymbol{F}}\right) $ | (11) |
GAME模型通过反向传播优化编码器, 通过最小化
| $ \mathcal{L}_{\text {train }}=\mathcal{L}_{\mathrm{RC}}-\mathcal{L}_{\mathrm{Mod}} . $ | (12) |
GAME基于模块度自编码器和Bernoulli-Poisson模型进行训练,同时最大化模块度损失,从而优化模型得到初始的社区隶属度矩阵。图 4为GAME的算法流程。

|
| 图 4 GAME的算法流程图 |
使用Adam优化器[30]训练GCN和BernoulliPoisson模型, 设置学习率为0.001。训练过程中, 每迭代25次计算1次完整的损失, 若在100次迭代中损失不再下降, 或迭代达到最大次数, 则停止训练, 得到
模型训练中,使用梯度下降法更新
| $ \boldsymbol{W}^{l}=\boldsymbol{W}^{l}-\frac{\lambda}{N} \sum\limits_{i=1}^{N}\left(\frac{\partial \mathcal{L}_{\mathrm{RC}}}{\partial \boldsymbol{W}^{l}}-\frac{\partial \mathcal{L}_{\mathrm{Mod}}}{\partial \boldsymbol{W}^{l}}\right) . $ | (13) |
其中λ表示学习率。
社区分配:在完成训练任务后得到
为验证模型的性能,本文选取了2种类型(含有真实标签和人工标注标签的属性网络)的10个数据集进行实验。本文扩展了NOCD[27]的对比实验代码库,并选择主流重叠社区发现算法进行对比,包括传统方法和基于网络表示学习的算法,并采用广泛使用的归一化互信息(normalized mutual information,NMI)[31]对模型进行性能评估。
3.1 数据集表 2展示了本文使用的所有数据集信息。其中Facebook数据集(Facebook 348、Facebook 414、Facebook 686、Facebook 1684、Facebook 1912)[31]是含有人工标注标签的社交网络数据集,其中节点表示用户,边表示用户在社交网络中的好友关系,N为60~800。Computer Science、Engineering、Medicine、Chemistry这4个数据集是含有真实标签的协作者网络数据集[27],其中节点表示研究人员,边表示研究人员之间的合作关系,N为1.4×104~6.4×104。
| 数据集 | N | M | 网络 | 社区数 |
| Facebook 348 | 227 | 3 192 | 社交 | 14 |
| Facebook 414 | 159 | 1 693 | 社交 | 7 |
| Facebook 686 | 170 | 1 656 | 社交 | 14 |
| Facebook 698 | 66 | 270 | 社交 | 13 |
| Facebook 1684 | 792 | 14 024 | 社交 | 17 |
| Facebook 1912 | 755 | 30 025 | 社交 | 46 |
| Computer Science | 21 957 | 96 750 | 协作者 | 18 |
| Engineering | 14 927 | 49 305 | 协作者 | 16 |
| Medicine | 63 282 | 810 314 | 协作者 | 17 |
| Chemistry | 35 409 | 157 358 | 协作者 | 14 |
3.2 评估指标
NMI被广泛用于评估重叠社区[5],NMI的值越大表示模型性能越好。本文使用NMI测量真实社区和预测社区之间的相似性,NMI的计算表示如下:
| $ \begin{gather*} \mathrm{NMI}= \\ \frac{1}{2} \times \frac{H(C)+H\left(C^{\prime}\right)-H\left(C \mid C^{\prime}\right)-H\left(C^{\prime} \mid C\right)}{\max \left(H(C), H\left(C^{\prime}\right)\right)} . \end{gather*} $ | (14) |
其中:
基于表示学习的社区发现算法考验模型对网络结构和属性信息的融合能力,GCN能以简单高效的方式实现网络结构和属性信息融合。通过与主流重叠社区发现算法进行实验对比,验证模型的有效性。
非穷举、重叠K-均值(non-exhaustive, overlapping K-Means, NEO-K-均值) [32]算法(以下简称NEO):用易于理解的参数和直观的目标函数,以统一的方式捕获网络重叠程度。
DeepWalk算法(以下简称DW)[33]:先利用随机游走算法获取顶点序列,进而学习网络的隐藏信息,能够将图中的节点表示为一个包含潜在信息的向量。DeepWalk算法结合NEO-K-均值算法,可以实现重叠社区发现。
Graph2Gauss算法(以下简称G2G)[34]:每个节点的嵌入服从Gauss分布,提出的无监督个性化排序公式利于捕获多尺度网络结构的节点自然排序,可得到较好的网络嵌入性能。利用Graph2Gauss算法得到的嵌入结果并结合NEO-K-均值算法,可以实现重叠社区发现。
CESNA(communities from edge structure and node attributes)算法[35]:对网络结构和节点属性之间的交互作用进行统计建模,并结合Bernoulli-Poisson图生成模型优化网络的嵌入结果,从而实现重叠社区发现。
CDE算法[36]:该算法提出了一种新颖的社区嵌入矩阵,通过编码社区结构,并分解社区结构和网络节点属性,实现属性网络的重叠社区发现。
NOCD算法[27]:该算法基于图自编码器模型,利用GCN作为编码器,利用Bernoulli-Poisson图生成模型作为解码器,从而实现网络重构。
深度动态残差图卷积(deep dynamic residual graph convolutional, DynaResGCN)[4]算法:该算法提出一种动态扩展聚合机制和统一的基于编码-解码器的端到端框架,从而实现网络重叠社区划分。该算法以深层DynaResGCN模型作为编码器,以Bernoulli-Poisson图生成模型作为解码器。
基于社区视角和图卷积网络(community perspective and graph convolution network, CPGC) 的社区发现算法[37]:该算法基于图自编码器模型,将表示学习与聚类结合,获得了一种社区视角的相似性度量,能够同时处理重叠和非重叠社区发现任务。
3.4 实验设置与NOCD算法保持一致,GAME模型采用隐藏层为128维的GCN作为解码器,GCN的输出维度为真实社区数量k。学习率设置为0.001,使用默认参数的Adam[30]作为模型的优化器,通过L2正则化项以平衡模型的拟合和泛化能力,正则化系数设置为0.001。为更好地学习网络表示,本文设置最大迭代次数为1 000,并且设置停止优化的条件,即模型在100次迭代过程中
本文将GAME模型在各个数据集上获得的最佳得分作为最终结果,并将GAME的输入数据分为有属性和无属性输入,分别称为GAME-WA和GAME-NA。
表 3展示了GAME-WA模型与主流重叠社区发现算法的NMI对比结果。可以看出,GAME-WA在大多数数据集上的表现优于其他重叠社区发现算法;在Facebook数据集中,仅在Facebook 686和Facebook 1684上NMI略低于DynaResGCN-WA算法,在Facebook 348上NMI略低于CPGC-WA算法。此外,NOCD-WA、DynaResGCN-WA和GAME-WA算法的表现优于其他重叠社区发现算法,证明基于图自编码器的社区发现算法在处理社区发现任务时效果显著。图 5a展示了在考虑节点属性的情况下,GAME去除模块度最大化模块前后在社交网络数据集上的性能对比。可以看出,在所有的社交网络数据集上,去除模块度最大化模块的GAME(GAME-XO)性能下降1.1%~12.0%,这表明模块度最大化模块对GAME有较大贡献。
| 数据集 | CESNA | DW+NEO | G2G+NEO | CDE | NOCD-WA | DynaResGCN-WA | CPGC-WA | GAME-WA |
| Facebook 348 | 0.294 | 0.312 | 0.172 | 0.248 | 0.364 | 0.398 | 0.456 | 0.441 |
| Facebook 414 | 0.503 | 0.409 | 0.323 | 0.287 | 0.598 | 0.590 | 0.537 | 0.610 |
| Facebook 686 | 0.133 | 0.118 | 0.056 | 0.135 | 0.210 | 0.273 | 0.225 | 0.237 |
| Facebook 698 | 0.394 | 0.401 | 0.026 | 0.316 | 0.417 | 0.501 | 0.227 | 0.553 |
| Facebook 1684 | 0.280 | 0.372 | 0.099 | 0.288 | 0.261 | 0.410 | 0.413 | 0.390 |
| Facebook 1912 | 0.212 | 0.208 | 0.160 | 0.155 | 0.356 | 0.396 | 0.345 | 0.409 |
| Chemistry | 0.233 | 0.017 | 0.228 | — | 0.453 | — | — | 0.488 |
| Computer Science | 0.338 | 0.032 | 0.312 | — | 0.502 | 0.460 | 0.499 | 0.532 |
| Engineering | 0.243 | 0.047 | 0.334 | — | 0.391 | 0.390 | 0.484 | 0.411 |
| Medicine | 0.144 | 0.055 | 0.288 | — | 0.378 | 0.400 | — | 0.421 |
| 注:—表示文[36, 27, 4, 37]未给出结果,粗体表示最佳结果。 | ||||||||
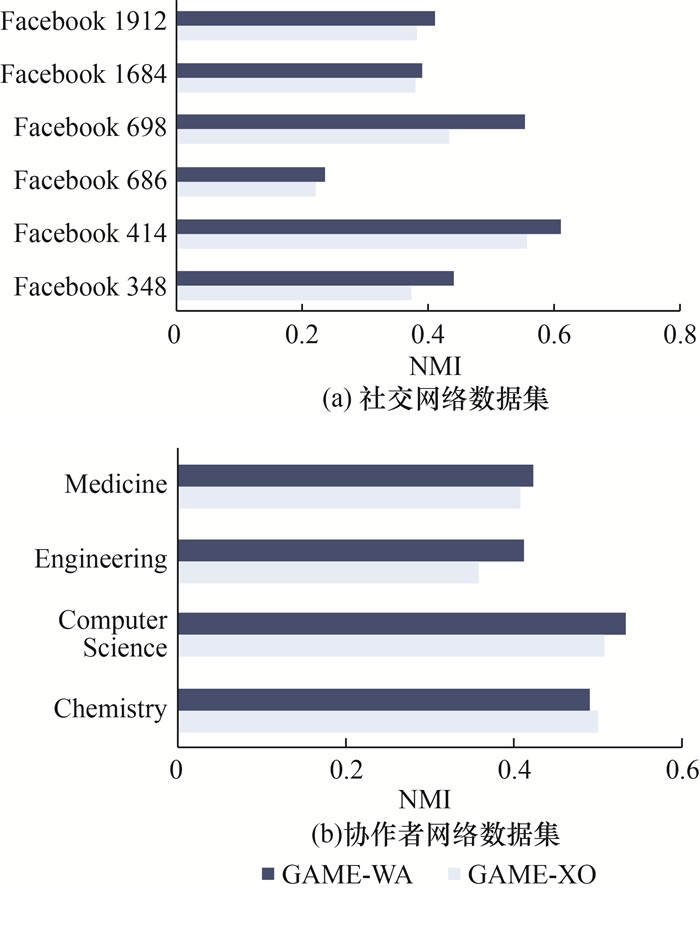
|
| 图 5 考虑节点属性时社交网络数据集和协作者网络数据集上的模型性能变化 |
协作者网络数据集中,GAME-WA在Chemistry、Computer Science和Medicine数据集上的性能表现均达到最优,仅在Engineering数据集上的NMI值低于CPGC-WA。图 5b展示了在考虑节点属性的情况下,GAME去除模块度最大化模块前后在协作者网络数据集上的性能对比。可以看出,同时考虑节点结构和属性时,GAME-WA的性能变化趋于稳定,GAME-WA仅在Chemistry数据集上的性能降低1.0%,在Computer Science、Engineering和Medicine数据集上的性能提升1.4%~5.4%。
相比于传统机器学习方法和两阶段图聚类算法,GAME-WA性能提升体现了基于表示学习的图自编码器模型在面对复杂属性网络时具有更好的处理能力。
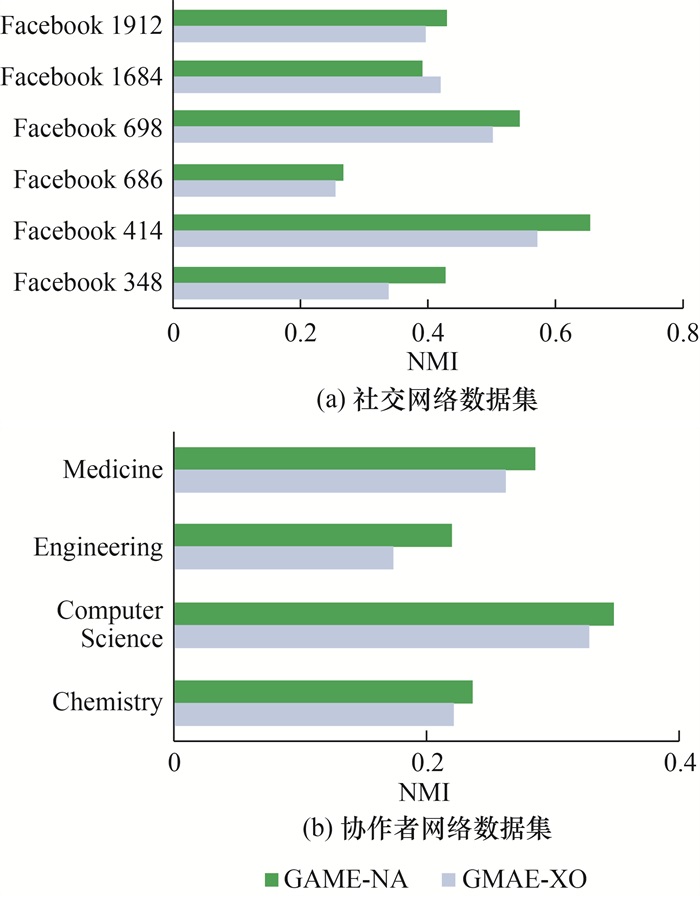
为验证GAME模型在面对网络属性缺失时的性能表现,本文将去除网络节点属性的模型命名为GAME-NA。表 4为GAME-NA模型与主流重叠社区发现算法的NMI对比结果。可以看出,GAME-NA在社交网络数据集上的综合性能优于NOCD-NA和DynaResGCN-NA算法,仅在Facebook 1684上表现低于DynaResGCN-NA算法,并且NOCD-NA算法的性能大幅度优于主流重叠社区发现算法。图 6a为社交网络数据集上仅考虑网络结构时模型的性能变化。可以看出,在Facebook 1684数据集上模型性能降低2.7%,而在其余5个数据集上模型性能均有提升。
| 数据集 | CESNA | DW+NEO | G2G+NEO | CDE | NOCD-NA | DynaResGCN-NA | CPGC-NA | GAME-NA |
| Facebook 348 | 0.294 | 0.312 | 0.172 | 0.248 | 0.347 | 0.398 | 0.427 | 0.428 |
| Facebook 414 | 0.503 | 0.409 | 0.323 | 0.287 | 0.563 | 0.581 | 0.596 | 0.655 |
| Facebook 686 | 0.133 | 0.118 | 0.056 | 0.135 | 0.206 | 0.254 | 0.236 | 0.267 |
| Facebook 698 | 0.394 | 0.401 | 0.026 | 0.316 | 0.493 | 0.510 | 0.494 | 0.545 |
| Facebook 1684 | 0.280 | 0.372 | 0.099 | 0.288 | 0.347 | 0.443 | 0.419 | 0.392 |
| Facebook 1912 | 0.212 | 0.208 | 0.160 | 0.155 | 0.368 | 0.401 | 0.372 | 0.430 |
| Chemistry | 0.233 | 0.017 | 0.228 | — | 0.226 | — | — | 0.238 |
| Computer Science | 0.338 | 0.032 | 0.312 | — | 0.342 | 0.374 | 0.232 | 0.348 |
| Engineering | 0.243 | 0.047 | 0.334 | — | 0.184 | 0.373 | 0.175 | 0.221 |
| Medicine | 0.144 | 0.055 | 0.288 | — | 0.274 | 0.373 | — | 0.287 |
| 注:—表示文[36, 27, 4, 37]未给出结果,粗体表示最佳结果。 | ||||||||
|
| 图 6 仅考虑网络结构时社交网络数据集和协作者网络数据集上的模型性能变化 |
图 6b为协作者网络数据集上仅考虑网络结构时模型的性能变化。可以看出,加入模块度最大化模块后模型的性能明显提升。由表 4可知,协作者网络数据集中,GAME-NA仅在Chemistry数据集上性能表现最好,这得益于动态图卷积机制,DynaResGCN-NA算法的性能表现优于NOCD-NA算法。此外,由表 4可知,GAME-NA在协作者网络数据集上的性能表现均优于NOCD-NA算法和CPGC-NA算法,而加入模块度最大化模块后模型的性能明显提升。这表明,GAME-NA在整合数据的结构和属性时性能表现较好,而面对单一的结构信息时性能表现欠佳。
3.6 参数分析本文实验中,根据社区隶属度矩阵中节点对社区的隶属度是否大于ρ,决定节点对所有社区的隶属关系。本文通过GAME-WA模型获取最优的ρ,区间为0~1,以0.1为步长。
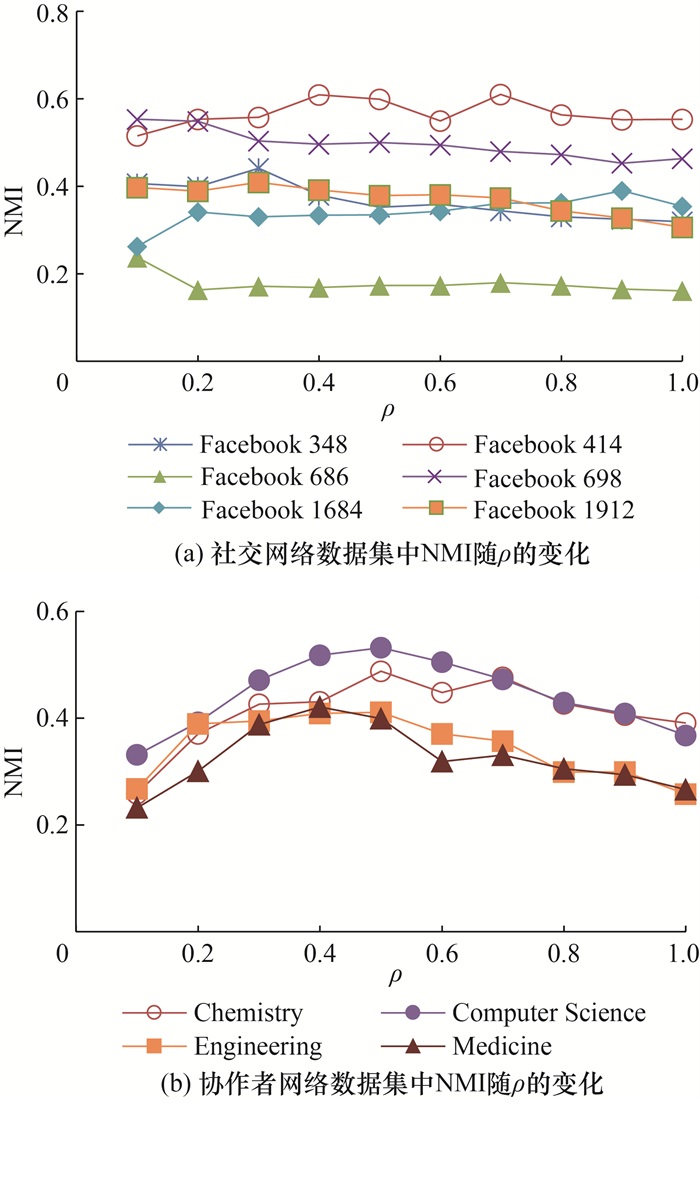
为评估ρ对GAME-WA的性能影响,GAME-WA性能在不同数据集上随ρ的变化如图 7所示。图 7a展示了GAME-WA在社交网络数据集上的性能变化,可以看出,当ρ取不同值时,6个数据集上GAME-WA的性能变化较平稳。这表明,在较小的数据集上,GAME-WA的性能对ρ的变化不敏感。因此求解实际问题时,ρ的取值在0.1~0.7内可获得较理想的性能表现。图 7b展示了GAME-WA在协作者网络数据集上的性能变化,当ρ=0.5时,GAME-WA在Chemistry、Computer Science和Engineering上均获得最佳性能,当ρ=0.4时,GAME-WA在Medicine数据集上获得最佳性能。这表明,属性网络较大(N≥1.4×104)的情况下,ρ的取值在0.5附近时GAME-WA可获得较理想的性能表现。
|
| 图 7 GAME-WA性能在不同数据集上随ρ的变化 |
3.7 模型收敛及复杂度分析
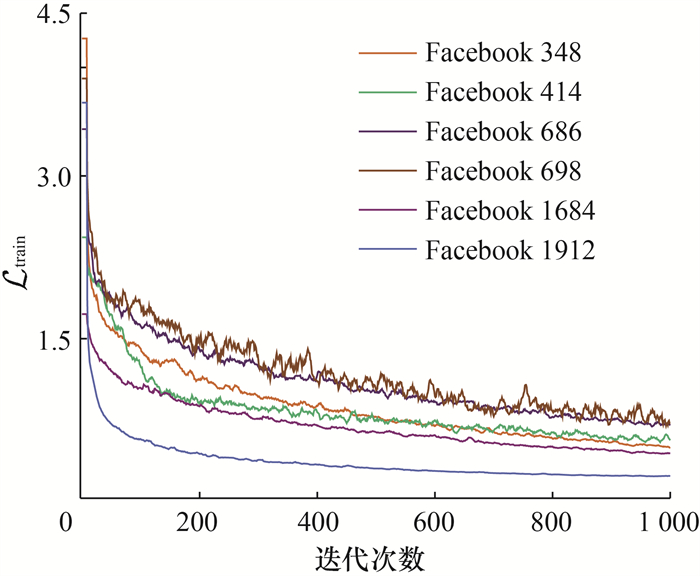
图 8展示了GAME-WA在社交网络数据集上迭代1 000次的收敛情况。可以看出,随着迭代次数增加,
|
| 图 8 社交网络数据集的损失收敛 |
GAME采用2层GCN作为编码器,Bernoulli-Poisson图生成模型作为解码器,并且GAME融入了模块度损失,加入模块度损失使GAME相较于NOCD算法复杂度提升。2层GCN的复杂度与网络边数和迭代次数线性相关,时间复杂度为O(h1γM),其中h1为常数;Bernoulli-Poisson图生成模型对有边节点和无边节点均匀随机抽样计算损失,时间复杂度为O(N+M);由式(9)可知模块度损失的时间复杂度为O(h2Nlog2N),h2为常数。因此GAME-WA的时间复杂度为O(h1γM+N+M+h2Nlog2N),与网络规模呈正相关。
4 结论本文提出了一种面向重叠社区发现的无监督模块度感知图自编码器模型(GAME)。首先,本文通过社区隶属度矩阵设置阈值以隶属关系进行社区分配,使用GCN图表示模型和Bernoulli-Poisson图生成模型组成自编码器;其次,在此基础上加入模块度最大化损失捕获模型信息传递时的社区结构,以提高GAME处理重叠社区发现任务的性能;最后,以6个含有人工标注标签的社交网络数据集和4个含有真实标签的协作者网络数据集作为输入数据,对比了GAME与主流方法的性能,在NMI评估指标下,GAME对2类数据集的性能平均提升2.1%,证明了GAME有效。
虽然本文通过增加模块度最大化模块提升了图自编码器模型在重叠社区发现任务的性能,但是处理数据集时融合网络结构和节点属性需要耗费大量内存,尤其是在小型属性网络(N ≤800)对ρ变化不敏感的情况下,GAME在面对现实场景时无法获得最佳性能。在未来工作中,将针对以上问题对GAME进行改进。
| [1] |
RADICCHI F, CASTELLANO C, CECCONI F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(9): 2658-2663. |
| [2] |
SU X, XUE S, LIU F Z, et al. A comprehensive survey on community detection with deep learning[J/OL]. IEEE Transactions on Neural Networks and Learning Systems. (2022-03-09)[2023-05-22]. DOI: 10.1109/TNNLS.2021.3137396.
|
| [3] |
PALLA G, DERÉNYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814-818. DOI:10.1038/nature03607 |
| [4] |
MUTTAKIN N, HOSSAIN I, RAHMAN S. Overlapping community detection using dynamic dilated aggregation in deep residual GCN[J/OL]. ArXiv. (2022-10-20) [2023-05-22]. https://doi.org/10.48550/arXiv.2210.11174.
|
| [5] |
LI H J, FENG Y H, XIA C Y, et al. Overlapping graph clustering in attributed networks via generalized cluster potential game[J]. ACM Transactions on Knowledge Discovery from Data, 2023, 18(1): 1-26. |
| [6] |
LIBEN-NOWELL D, KLEINBERG J. The link prediction problem for social networks[C]//Proceedings of the Twelfth International Conference on Information and Knowledge Management. New Orleans, USA: ACM, 2003: 556-559.
|
| [7] |
CAO S S, LU W, XU Q K. GraRep: Learning graph representations with global structural information[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. Melbourne, Australia: ACM, 2015: 891-900.
|
| [8] |
CHUNAEV P. Community detection in node-attributed social networks: A survey[J]. Computer Science Review, 2020, 37: 100286. DOI:10.1016/j.cosrev.2020.100286 |
| [9] |
LI D Y, ZHONG X X, DOU Z F, et al. Detecting dynamic community by fusing network embedding and nonnegative matrix factorization[J]. Knowledge-Based Systems, 2021, 221: 106961. DOI:10.1016/j.knosys.2021.106961 |
| [10] |
QIU C Y, HUANG Z C, XU W Z, et al. VGAER: Graph neural network reconstruction based community detection[J/OL]. arXiv. (2022-01-08)[2023-05-22]. https://arxiv.org/abs/2201.04066.
|
| [11] |
JIN D, LIU Z Y, LI W H, et al. Graph convolutional networks meet Markov random fields: Semi-supervised community detection in attribute networks[C]//Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Honolulu, USA: AAAI Press, 2019: 152-159.
|
| [12] |
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[J/OL]. arXiv. (2016-09-09)[2023-05-22]. https://doi.org/10.48550/arXiv.1609.02907.
|
| [13] |
HE D X, SONG Y, JIN D, et al. Community-centric graph convolutional network for unsupervised community detection[C]//Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. Yokohama, Japan: IJCAI. org, 2021: 486.
|
| [14] |
SALHA-GALVAN G, LUTZEYER J F, DASOULAS G, et al. Modularity-aware graph autoencoders for joint community detection and link prediction[J]. Neural Networks, 2022, 153: 474-495. DOI:10.1016/j.neunet.2022.06.021 |
| [15] |
GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. |
| [16] |
GREGORY S. Finding overlapping communities in networks by label propagation[J]. New Journal of Physics, 2010, 12(10): 103018. DOI:10.1088/1367-2630/12/10/103018 |
| [17] |
RAGHAVAN U N, ALBERT R, KUMARA S. Near linear time algorithm to detect community structures in large-scale networks[J]. Physical Review E, 2007, 76(3): 036106. DOI:10.1103/PhysRevE.76.036106 |
| [18] |
WHANG J J, GLEICH D F, DHILLON I S. Overlapping community detection using seed set expansion[C]//Proceedings of the 22nd ACM International Conference on Information & Knowledge Management. San Francisco, USA: ACM, 2013: 2099-2108.
|
| [19] |
S∅RENSEN M, SIDIROPOULOS N D, SWAMI A. Overlapping community detection via semi-binary matrix factorization: Identifiability and algorithms[J]. IEEE Transactions on Signal Processing, 2022, 70: 4321-4336. DOI:10.1109/TSP.2022.3200215 |
| [20] |
DONG Y X, LUO M N, LI J D, et al. LookCom: Learning optimal network for community detection[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(2): 764-775. DOI:10.1109/TKDE.2020.2987784 |
| [21] |
ZHAO S, DU Z W, CHEN J, et al. Hierarchical representation learning for attributed networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(3): 2641-2656. |
| [22] |
XIAO W Y, ZHAO H, ZHENG V W, et al. Vertex-reinforced random walk for network embedding[C]//Proceedings of the 2020 SIAM International Conference on Data Mining. Cincinnati, USA: SIAM, 2020: 595-603.
|
| [23] |
谢雨洋, 冯栩, 喻文健, 等. 基于随机化矩阵分解的网络嵌入方法[J]. 计算机学报, 2021, 44(3): 447-461. XIE Y Y, FENG X, YU W J, et al. Learning network embedding with randomized matrix factorization[J]. Chinese Journal of Computers, 2021, 44(3): 447-461. (in Chinese) |
| [24] |
GUO K, WANG Q Z, LIN J Q, et al. Network representation learning based on community-aware and adaptive random walk for overlapping community detection[J]. Applied Intelligence, 2022, 52(9): 9919-9937. DOI:10.1007/s10489-021-02999-8 |
| [25] |
CHEN J Y, GONG Z G, MO J Q, et al. Self-training enhanced: Network embedding and overlapping community detection with adversarial learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(11): 6737-6748. DOI:10.1109/TNNLS.2021.3083318 |
| [26] |
CHOONG J J, LIU X, MURATA T. Learning community structure with variational autoencoder[C]//Proceedings of 2018 IEEE International Conference on Data Mining. Singapore: IEEE, 2018: 69-78.
|
| [27] |
SHCHUR O, GÜNNEMANN S. Overlapping community detection with graph neural networks[J/OL]. arXiv. (2019-09-26)[2023-05-22]. https://arxiv.org/abs/1909.12201.
|
| [28] |
ZHOU X C, SU L T, LI X J, et al. Community detection based on unsupervised attributed network embedding[J]. Expert Systems with Applications, 2023, 213: 118937. DOI:10.1016/j.eswa.2022.118937 |
| [29] |
YANG J, LESKOVEC J. Overlapping community detection at scale: A nonnegative matrix factorization approach[C]//Proceedings of the Sixth ACM International Conference on Web Search and Data Mining. Rome, Italy: ACM, 2013: 587-596.
|
| [30] |
KINGMA D P, BA J. Adam: A method for stochastic optimization[J/OL]. arXiv. (2014-12-22)[2023-05-22]. https://doi.org/10.48550/arXiv.1412.6980.
|
| [31] |
SCHMIDHUBER J. Deep learning in neural networks: An overview[J]. Neural Networks, 2015, 61: 85-117. DOI:10.1016/j.neunet.2014.09.003 |
| [32] |
WHANG J J, DHILLON I S, GLEICH D F. Non-exhaustive, overlapping k-means[C]//Proceedings of the 2015 SIAM International Conference on Data Mining. Vancouver, Canada: SIAM, 2015: 936-944.
|
| [33] |
PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2014: 701-710.
|
| [34] |
BOJCHEVSKI A, GÜNNEMANN S. Deep gaussian embedding of graphs: Unsupervised inductive learning via ranking[J/OL]. arXiv. (2017-07-12)[2023-5-22]. https://arxiv.org/abs/1707.03815.
|
| [35] |
YANG J, MCAULEY J, LESKOVEC J. Community detection in networks with node attributes[C]//Proceedings of 2013 IEEE 13th International Conference on Data Mining. Dallas, USA: IEEE, 2013: 1151-1156.
|
| [36] |
LI Y, SHA C F, HUANG X, et al. Community detection in attributed graphs: An embedding approach[C]//Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, USA: AAAI Press, 2018: 338-345.
|
| [37] |
LIU H T, WEI J H, XU T Y. Community detection based on community perspective and graph convolutional network[J]. Expert Systems with Applications, 2023, 231: 120748. DOI:10.1016/j.eswa.2023.120748 |



