工程结构在运营过程中难免会遭受疲劳载荷作用,内部材料在低于静态极限载荷水平的疲劳载荷影响下会发生疲劳破坏,从而导致承载部位的整体失效。材料在疲劳加载和静态单调加载下的塑性演化存在差异,并且单次疲劳载荷产生的塑性或微裂纹影响着后续发展。Bauschinger[1]发现了金属软化现象:金属材料在塑性变形后再反向施加疲劳加载时的屈服强度会变低。金属材料在疲劳加载中也存在变形抗力发生增大的硬化现象[2]。材料的疲劳应力应变体现了材料在疲劳加载过程中的状态,研究者在疲劳准则与应力应变关系的方面取得了显著的成果。混凝土和岩石材料内部没有位错等微观结构[3-5],所以疲劳加载下微裂纹演化直接影响着材料应力应变响应。李庆斌等[6]通过疲劳加载全过程的研究,得到了混凝土疲劳损伤量与应力应变之间的关系。为方便工程应用,疲劳包络线的概念被提出并且用于研究混凝土和岩石材料的疲劳破坏问题[7-9]。Sinha等[7]认为混凝土在循环和静态载荷下的破坏机理一致,所以可以使用静态应力应变曲线表达任意路径的循环载荷下的疲劳包络线。Cachim等[8]和Kim等[9]分别针对纤维混凝土和高强混凝土展开的疲劳包络线研究表明,这2类混凝土的疲劳包络线与静态应力应变曲线相同。葛修润等[10]、蒋宇[11]、林卓英等[12]、郭印同等[13]、冯春林等[14]和卢高明等[15]在岩石材料的压缩疲劳试验中验证了疲劳包络线的适用性。以上研究表明了混凝土材料的疲劳破坏应力和应变规律可用其自身静态应力应变曲线中的峰后段来表示。
此外,材料在确定应力加载下的疲劳最大应变和疲劳循环次数之间的规律也引起了国内外学者的关注。Holmen[16]研究了混凝土材料在疲劳压缩加载下的变形性能,发现不同载荷水平下的疲劳最大应变均随疲劳循环次数增加单调增加,并呈现3个发展阶段。王瑞敏[17]、李朝阳等[18]、林燕清[19]验证了混凝土材料的疲劳最大应变与疲劳循环次数之间的关系呈现3个发展阶段的规律,并研究了二者的函数关系式。Huang等[20]提出了适用于混凝土及水泥基复合材料在疲劳压缩、拉伸等加载下的最大应变与疲劳循环次数的函数关系式。Xiao等[21]在岩石材料中也观察到疲劳最大应变随着疲劳循环次数增加呈现3个发展阶段。材料在确定应力加载下的最大应变与疲劳循环次数存在函数关系,所以疲劳应力应变的状态可以通过疲劳循环次数进行表达[22-23]。
然而,基于疲劳包络线的评估方法无法量化疲劳状态;基于应力应变疲劳准则的方法虽然反映了疲劳破坏过程中应力应变约束疲劳寿命的机制[24],但材料的应力应变与疲劳循环次数之间的关系仍有待进一步研究。基于等效疲劳循环次数的评估方法则有望克服上述2种评估方法的不足,解决现有疲劳状态评估中面临的问题。
本文研究了基于应力应变—疲劳准则的混凝土疲劳寿命分析方法。首先分析了混凝土材料疲劳加载曲面函数随疲劳循环次数的变化规律;之后建立了描述疲劳加载过程的等效方程,并提出了MRS(maximum R-square)算法来获取等效方程中的有效系数,进一步联立疲劳加载曲面函数和等效方程计算等效疲劳循环次数;最终利用等效疲劳循环次数量化了疲劳应力应变状态,为混凝土的疲劳寿命分析提供了借鉴。
1 疲劳状态的描述朱贺等[25-26]考虑了历时载荷作用下的变形对疲劳破坏的影响,进而提出了描述历时荷载下疲劳破坏的应力应变准则。该准则的函数形式为
| $ \begin{gather*} F\left(\sigma_{\mathrm{f}}, \varepsilon_{\mathrm{f}}, N_{\mathrm{f}}\right)=\left(\sigma_{\mathrm{f}}-\sigma_{\mathrm{m}}\right)+\left[\eta\left(\lg N_{\mathrm{f}}\right)^{2}+\right. \\ \left.\delta \lg N_{\mathrm{f}}+k_{0}\right] E_{\mathrm{m}}\left(\varepsilon_{\mathrm{f}}-\varepsilon_{\mathrm{m}}\right)=0 . \end{gather*} $ | (1) |
其中:σf和εf分别表示疲劳破坏应力和应变,Nf表示疲劳寿命,σm和εm分别表示静态破坏应力和应变,Em表示静态破坏应力和应变的比值,η、δ和k0表示系数。
该准则的表达方式为疲劳问题中的应力应变强度研究带来了启示。材料应力应变疲劳准则在几何形式上可表达为疲劳包络面,以疲劳破坏应力、应变为自变量,疲劳寿命为因变量。由于材料疲劳应力应变可以通过等效疲劳循环次数进行表达。因此,本文提出利用疲劳加载曲面函数描述疲劳应力应变与疲劳循环次数之间的关系:
| $ \begin{gather*} f\left(\sigma_{\max }, \varepsilon_{\max }, N\right)=\left(\sigma_{\max } / \sigma_{\mathrm{m}}-1\right)+\left[\eta(\lg N)^{2}+\right. \\ \left.\delta \lg N+k_{0}\right]\left(\varepsilon_{\max } / \varepsilon_{\mathrm{m}}-1\right) . \end{gather*} $ | (2) |
其中:σmax表示疲劳最大应力,εmax表示疲劳最大应变,N表示实际疲劳循环次数。
图 1中,材料在疲劳加载过程中的应力应变及疲劳循环次数所构成的几何曲面可定义为疲劳加载曲面,其几何形状主要由f(σmax, εmax, N)确定;疲劳破坏是疲劳加载过程的极限状态,而疲劳包络面可看作疲劳加载曲面随着疲劳发展的极限状态, 其几何形状主要由求解F(σf, εf, Nf)=0获得。混凝土材料的疲劳破坏与疲劳加载过程之间的关系,尤其是疲劳加载曲线函数的演化规律,是描述疲劳状态的关键。
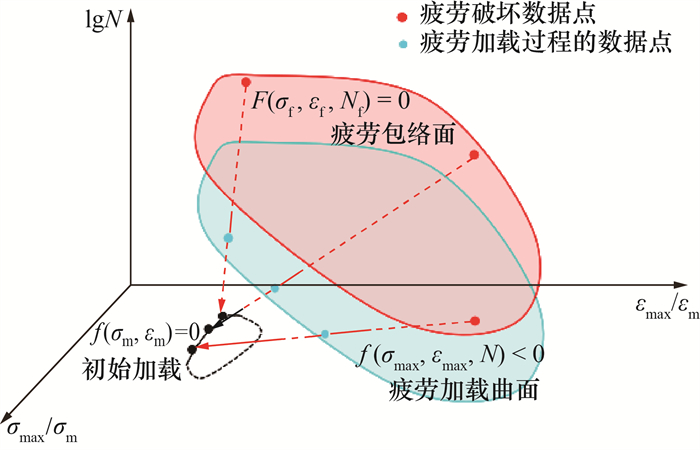
|
| 图 1 疲劳加载曲面与疲劳包络面的示意图 |
材料疲劳加载曲面函数值随疲劳加载过程的变化规律尚不明晰,需要通过疲劳试验作进一步探究。图 2中,无论是拉伸还是压缩加载条件下,混凝土材料的f(σmax, εmax, N)随着N的增加,逐渐从负值增长到0附近,呈现出单调递增的变化规律,该规律为不同载荷水平下疲劳试验结果的等效标定提供了基础。
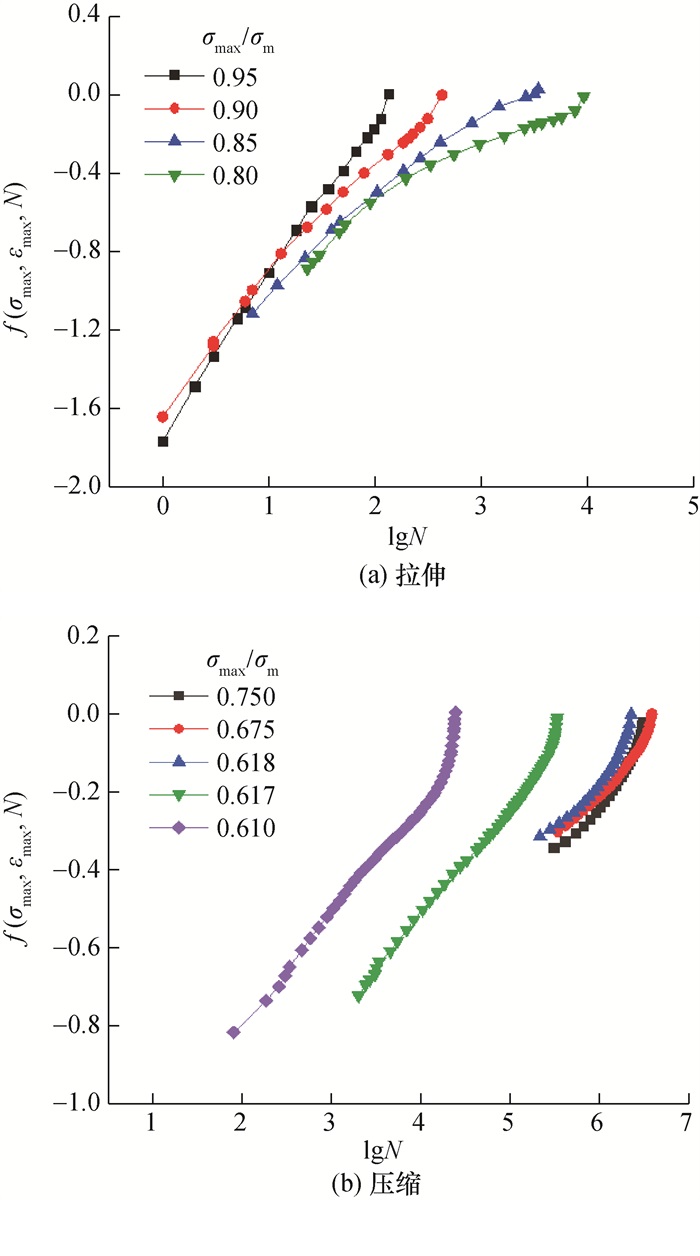
|
| 图 2 疲劳加载曲面函数值随疲劳循环次数的变化规律 |
疲劳加载曲面函数值是状态量,决定着疲劳加载曲面的几何形状。本文在材料拉伸和压缩状态下各选取f(σmax, εmax, N) 的3个特殊值,绘制出混凝土材料在不同加载条件下的疲劳加载曲面,如图 3所示。可以看出,疲劳加载曲面的几何形状随f(σmax, εmax, N)取值的不同发生明显变化;且取值越小,疲劳加载曲面的几何形状越接近疲劳包络面的形状,这也定性说明了应力应变与循环次数之间存在着对应关系。
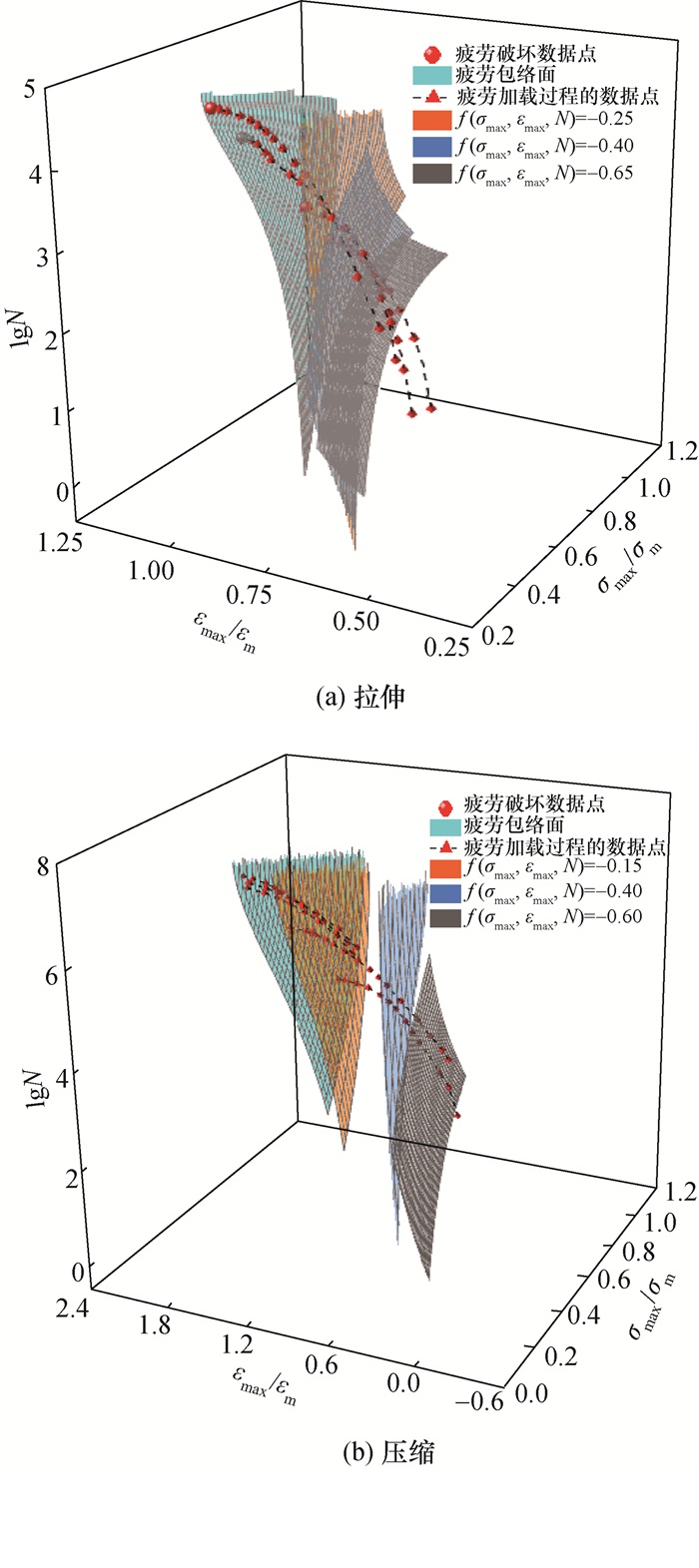
|
| 图 3 混凝土材料疲劳加载曲面、疲劳应力应变随疲劳循环次数的演化过程 |
2 疲劳状态的等效描述及分析
疲劳加载曲面函数值决定了疲劳加载曲面的位置,但该数值无法通过材料的疲劳应力应变来确定。研究疲劳加载曲面函数在疲劳试验结果中的等效标定方法,对于等效描述材料疲劳加载状态具有必要性。本文首先假设等效疲劳加载曲面函数的形式为
| $ \begin{gather*} g\left(\sigma_{\max }, \varepsilon_{\max }, N_{\mathrm{p}}\right)= \\ a_{\mathrm{c}}\left(\sigma_{\max } / \sigma_{\mathrm{m}}\right)+b_{\mathrm{c}}\left(\varepsilon_{\max } / \varepsilon_{\mathrm{m}}\right)+c_{\mathrm{c}}\left(\lg N_{\mathrm{p}}\right)+d_{\mathrm{c}} . \end{gather*} $ | (3) |
其中:Np表示等效疲劳循环次数,ac、bc、cc分别表示与σmax、εmax、Np相关系数,dc表示标定系数。
基于拉伸及压缩条件下实际的疲劳试验数据,对式(3)中的系数进行等效标定,引入R-square作为衡量等效标定结果有效性的重要指标。一般而言,R-square越接近于1则说明标定结果越好。
| $ \text { R-square }=1-\frac{\sum\left(N_{\mathrm{p}}-N\right)^{2}}{\sum(N-\bar{N})^{2}} . $ | (4) |
其中N表示实际疲劳循环次数的平均值。
图 4总结了本文提出MRS(maximum R-Square)算法的求解流程。首先提取疲劳试验结果中的特征点,然后按照等效标定所需要的特征点个数进行遍历分组,遍历计算Np,按照式(4)计算R-square,比较每组R-square的大小筛选出MRS并索引其对应的标定数组,最终得到g(σmax, εmax, Np)的最优系数值。
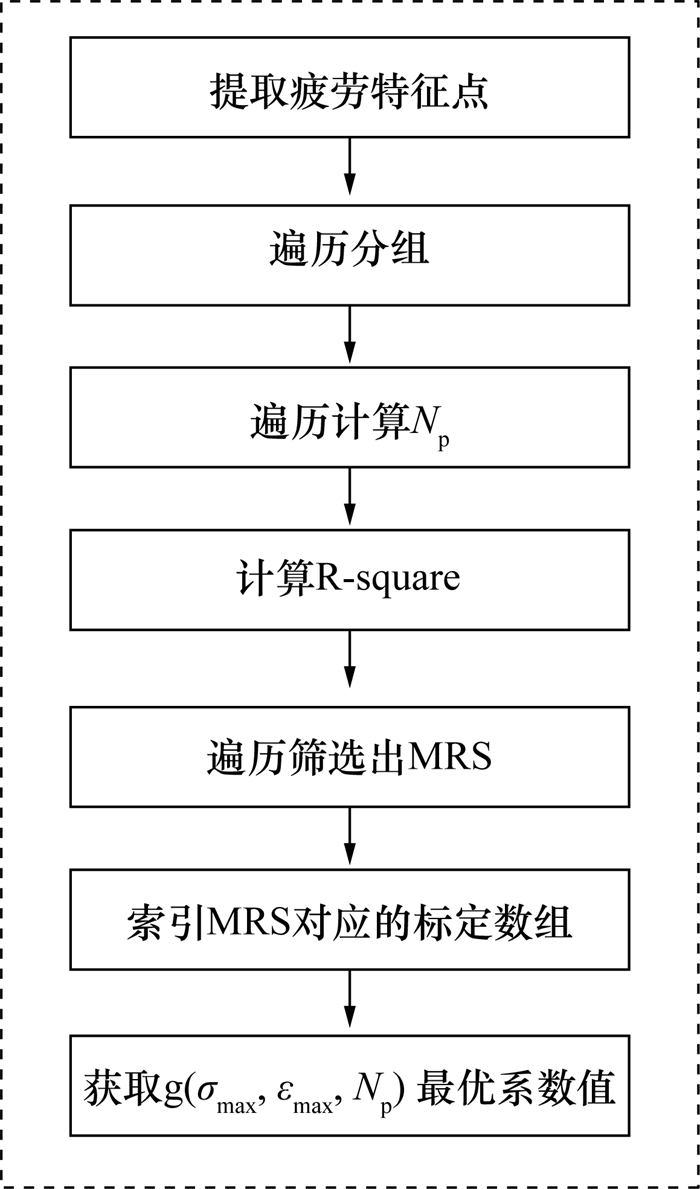
|
| 图 4 MRS算法的求解流程图 |
之后利用疲劳最小应力与静态破坏应力的比值(Smin=σmin/σm)对等效疲劳加载曲面函数的形式和系数标定结果进行验证。本文基于现有可查的数据(拉伸加载下Smin=0.013、压缩加载下Smin=0.050),计算出混凝土材料等效疲劳加载曲面函数的等效标定系数和MRS,如表 2所示。可以看出,混凝土材料在疲劳拉伸与压缩加载下的MRS均在0.930以上,说明等效标定结果较好。
| 加载类型 | ac | bc | cc | dc | MRS |
| 拉伸 | 4.384 | -0.115 | 0.341 | -4.772 | 0.968 |
| 压缩 | 3.319 | 0.159 | 0.206 | -3.724 | 0.937 |
因此,混凝土材料的Np可通过下式求解:
| $ f\left(\sigma_{\max }, \varepsilon_{\max }, N_{\mathrm{p}}\right)=g\left(\sigma_{\max }, \varepsilon_{\max }, N_{\mathrm{p}}\right) . $ | (5) |
图 5比较了混凝土材料在拉伸或压缩条件下,不同σmax/σm条件下的Np/Nf。可以看出,Np与Nf数值接近且在疲劳加载过程中呈现出的变化趋势一致。N/Nf与Np/Nf分别表达了混凝土材料实际与等效的疲劳破坏程度的物理意义,Np/Nf可作为疲劳预警值,是量化混凝土材料疲劳状态的重要指标。疲劳预警值被设定为2级:第1级为预防疲劳破坏发生的预警值,可取为0.30;第2级为临近疲劳破坏的预警值,可取为0.80。
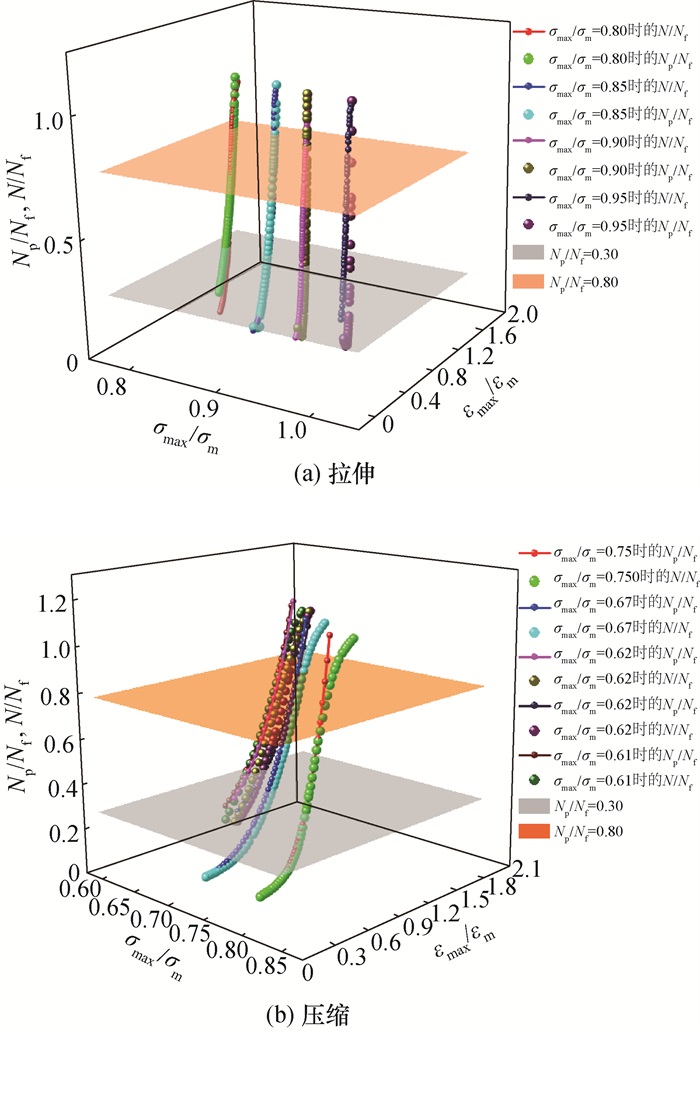
|
| 图 5 混凝土材料的Np值计算结果与疲劳预警范围 |
图 6中,混凝土材料的疲劳寿命分析过程分为3个步骤:1) 开展实际的疲劳实验,获得材料的疲劳应力、应变值和循环次数;2) 根据MRS算法和式(6)求解Np;3) 在材料应力应变疲劳准则中初步判断材料疲劳破坏与否,再根据Np/Nf来分析混凝土材料的疲劳状态,评估疲劳寿命。2级预警值将疲劳状态分为3种:正常运营、疲劳预警与临近疲劳破坏。通过Np/Nf分析可知,基于Np的寿命评估不应在完全达到Nf时进行预警,应该在临近疲劳破坏状态之前设定预警值。实际应用时的预警值还需要大量的疲劳实验结果和经济性分析结果来进一步确定。
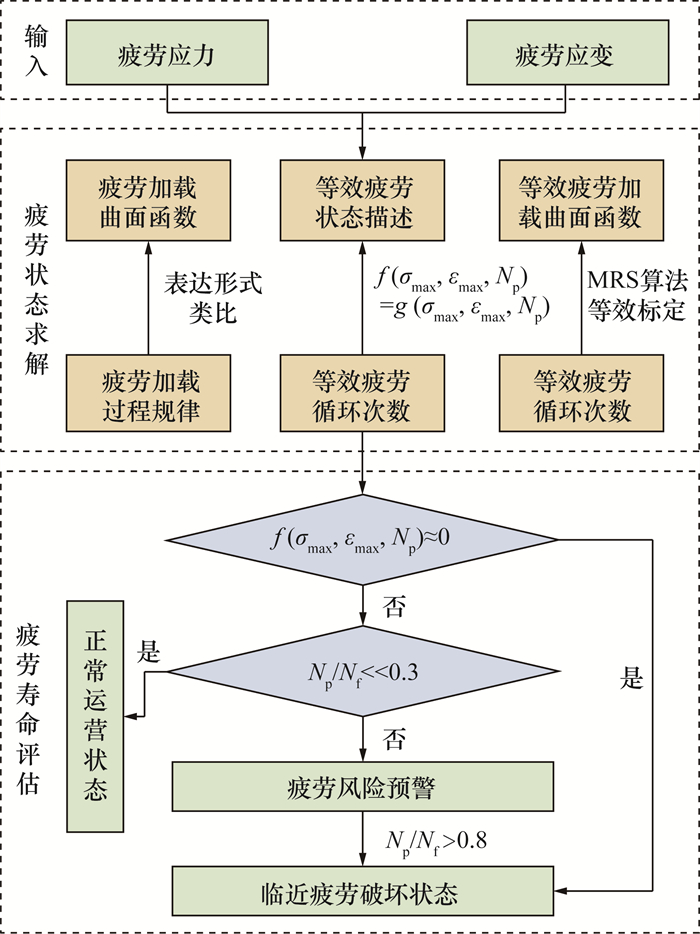
|
| 图 6 混凝土材料的疲劳状态分析的流程图 |
3 结论
本文研究了基于应力应变—疲劳准则的混凝土的疲劳寿命分析方法。根据混凝土材料疲劳加载曲面函数随疲劳循环次数的变化规律建立了描述疲劳加载过程的等效方程,提出了MRS算法来获取等效方程中的有效系数,联立疲劳加载曲面函数和等效方程计算等效疲劳循环次数,进而实现以等效疲劳循环次数来量化疲劳应力应变状态。结果表明,疲劳应力应变对疲劳循环次数的约束机制作用于整个疲劳加载过程。疲劳力学状态对应的等效疲劳循环次数与实际疲劳循环次数接近,验证了所提等效描述方法的有效性。建立的混凝土材料的疲劳状态分析流程实现了对材料疲劳状态的量化评估,为材料的疲劳寿命分析提供有效途径。
| [1] |
BAUSCHINGER J. Uber die veranderung der elasticitatagrenze und dea elasticitatamoduls verschiadener metalle[J]. Zivilingenieur, 1881, 27: 289-348. |
| [2] |
尚德广. 疲劳强度理论[M]. 北京: 科学出版社, 2017. SHANG D G. Fatigue strength theory[M]. Beijing: Science Press, 2017. (in Chinese) |
| [3] |
CHANG B, ZHANG Z. Cyclic deformation behavior in a nitrogen-alloyed austenitic stainless steel in terms of the evolution of internal stress and microstructure[J]. Materials Science and Engineering A, 2012, 556: 625-632. DOI:10.1016/j.msea.2012.07.037 |
| [4] |
PHAM M S, HOLDSWORTH S R. Change of stress-strain hysteresis loop and its links with microstructural evolution in AISI 316L during cyclic loading[J]. Procedia Engineering, 2011, 10: 1069-1074. DOI:10.1016/j.proeng.2011.04.176 |
| [5] |
ESTRIN Y, BRAASCH H, BRECHET Y. A dislocation density based constitutive model for cyclic deformation[J]. Journal of Engineering Materials and Technology, 1996, 118(4): 441-447. DOI:10.1115/1.2805940 |
| [6] |
李庆斌, 吕培印, 张立翔. 混凝土受压疲劳特性及损伤本构模型[J]. 水利学报, 2004, 35(4): 21-26. LI Q B, Lü P Y, ZHANG L X. Damage constitutive model for performance degradation of concrete due to compressive fatigue load[J]. Journal of Hydraulic Engineering, 2004, 35(4): 21-26. (in Chinese) |
| [7] |
SINHA B P, GERSTLE K H, TULIN L G. Stress-strain relations for concrete under cyclic loading[J]. ACI Structural Journal, 1964, 62(2): 195-210. |
| [8] |
CACHIM P B, FIGUEIRAS J A, PEREIRA P A A. Fatigue behavior of fiber-reinforced concrete in compression[J]. Cement and Concrete Composites, 2002, 24(2): 211-217. DOI:10.1016/S0958-9465(01)00019-1 |
| [9] |
KIM J K, KIM Y Y. Experimental study of the fatigue behavior of high strength concrete[J]. Cement and Concrete Research, 1996, 26(10): 1513-1523. DOI:10.1016/0008-8846(96)00151-2 |
| [10] |
葛修润, 蒋宇, 卢允德, 等. 周期荷载作用下岩石疲劳变形特性试验研究[J]. 岩石力学与工程学报, 2003, 22(10): 1581-1585. GE X R, JIANG Y, LU Y D, et al. Testing study on fatigue deformation law of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1581-1585. (in Chinese) |
| [11] |
蒋宇. 周期荷载作用下岩石疲劳破坏及变形发展规律[D]. 上海: 上海交通大学, 2003. JIANG Y. Fatigue failure and deformation development law of rock under cyclic load[D]. Shanghai: Shanghai Jiaotong University, 2003. (in Chinese) |
| [12] |
林卓英, 吴玉山. 岩石在循环荷载作用下的强度及变形特征[J]. 岩土力学, 1987, 8(3): 31-37. LIN Z Y, WU Y S. Srength and deformability of rock under cyclic loading[J]. Rock and Soil Mechanics, 1987, 8(3): 31-37. (in Chinese) |
| [13] |
郭印同, 赵克烈, 孙冠华, 等. 周期荷载下盐岩的疲劳变形及损伤特性研究[J]. 岩土力学, 2011, 32(5): 1353-1359. GUO Y T, ZHAO K L, SUN G H, et al. Experimental study of fatigue deformation and damage characeristics of salt rock under cyclic loading[J]. Rock and Soil Mechanics, 2011, 32(5): 1353-1359. (in Chinese) |
| [14] |
冯春林, 吴献强, 丁德馨, 等. 周期荷载作用下白砂岩的疲劳特性研究[J]. 岩石力学与工程学报, 2009, 28(增刊1): 2749-2754. FENG C L, WU X Q, DING D X, et al. Investigation on fatigue characteristics of white sandstone under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 2749-2754. (in Chinese) |
| [15] |
卢高明, 李元辉, 张希巍, 等. 周期荷载作用下黄砂岩疲劳破坏变形特性试验研究[J]. 岩土工程学报, 2015, 37(10): 1886-1892. LU G M, LI Y H, ZHANG X W, et al. Fatigue deformation characteristics of yellow sandstone under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1886-1892. (in Chinese) |
| [16] |
HOLMEN J O. Fatigue of concrete by constant and variable amplitude loading[C]//ACI Symposium Publication. Farmington Hills, USA: ACI, 1982, 75: 71-110.
|
| [17] |
王瑞敏. 混凝土结构的疲劳性能研究[D]. 大连: 大连理工大学, 1989. WANG R M. Study on fatigue properties of concrete structures[D]. Dalian: Dalian University of Technology, 1989. (in Chinese) |
| [18] |
李朝阳, 宋玉普, 赵国藩. 混凝土疲劳残余应变性能研究[J]. 大连理工大学学报, 2001, 3(3): 355-358. LI C Y, SONG Y P, ZHAO G F. Study of residual strain of concrete under fatigue loading[J]. Journal of Dalian University of Technology, 2001, 3: 355-358. (in Chinese) |
| [19] |
林燕清. 混凝土疲劳累积损伤与力学性能劣化研究[D]. 哈尔滨: 哈尔滨建筑大学, 1998. LIN Y Q. A Study on fatigue accumulative damage and behavior degradation of plain Concrete[D]. Harbin: Harbin University of Civil Engineering and Architecture, 1998. (in Chinese) |
| [20] |
HUANG B T, LI Q H, XU S L. Fatigue deformation model of plain and fiber-reinforced concrete based on the weibull function[J]. Journal of Structural Engineering, 2019, 145(1): 04018234. DOI:10.1061/(ASCE)ST.1943-541X.0002237 |
| [21] |
XIAO J Q, DING D X, XU G, et al. Inverted S-shaped model for nonlinear fatigue damage of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(3): 643-648. DOI:10.1016/j.ijrmms.2008.11.002 |
| [22] |
ONESCHKOW N. Fatigue behaviour of high-strength concrete with respect to strain and stiffness[J]. International Journal of Fatigue, 2016, 87: 38-49. DOI:10.1016/j.ijfatigue.2016.01.008 |
| [23] |
吕培印, 宋玉普, 吴智敏. 变速率加载下有侧压混凝土强度和变形特性[J]. 大连理工大学学报, 2001(6): 716-720. LÜ Y P, SONG Y P, WU Z M. Strength and deformation characteristics of concrete subjected to different loading rates combined with confined stress[J]. Journal of Dalian University of Technology, 2001(6): 716-720. (in Chinese) |
| [24] |
ZHANG S, MA R, HU Y, et al. Fatigue failure criterion of materials with static constitutive curve as the limit value[J]. Engineering Fracture Mechanics, 2023, 289: 109451. DOI:10.1016/j.engfracmech.2023.109451 |
| [25] |
朱贺, 胡昱, 李庆斌. 基于应力与变形的混凝土破坏准则[J]. 水力发电学报, 2018, 37(12): 1-10. ZHU H, HU Y, LI Q B. Stress-and-strain based failure criterion for concrete[J]. Journal of Hydroelectric Engineering, 2018, 37(12): 1-10. (in Chinese) |
| [26] |
ZHU H, HU Y, LI Q B, et al. Restrained cracking failure behavior of concrete due to temperature and shrinkage[J]. Construction and Building Materials, 2020, 244: 118318. DOI:10.1016/j.conbuildmat.2020.118318 |
| [27] |
余同希. 塑性力学[M]. 北京: 高等教育出版社, 1989. YU T X. Plastic mechanics[M]. Beijing: Higher Education Press, 1989. (in Chinese) |



