2. 中国运载火箭技术研究院,北京 100076
2. China Academy of Launch Vehicle Technology, Beijing 100076, China
火箭飞行阶段中,起飞阶段噪声环境最严酷。新一代大型火箭发射噪声测试表明,发射中心半径10 m内喷流噪声声压级不低于170.0 dB (参考声压2×10-5 Pa,下同)[1]。上述宽频随机噪声会引起结构高量级随机响应,可能导致箭体及地面发射系统的薄弱结构、卫星等有效载荷和仪器设备损坏[2]。随着新一代载人火箭的研制,火箭起飞噪声环境将更严酷。为保证箭体结构和仪器设备可靠,同时避免设计裕量过大而影响性能,噪声环境预示尤为重要。
火箭起飞噪声环境可先通过缩比试验测量[3-4],再利用缩比准则外推获得。但该类方法受条件和测点限制且费时费力,很难得到任意位置的噪声分布情况,因此,工程预示方法尤为重要。
Eldred[5]在20世纪70年代提出了2种预示火箭发动机喷流噪声环境的分布源方法(distributed source method,DSM),用一系列具有独立声功率和辐射特性的点声源代替实际喷流声源,并指出声源的功率、频谱特性和指向性是影响噪声预示精度的关键参数。Plotkin等[6]利用DSM-Ⅱ预测了Ares Ⅰ发射阶段噪声,给出了发射台附近声场分布。文[7-9]对DSM-Ⅱ中的喷流核心区长度(以下简称“喷流核长”)计算方法进行了改进,提高了预示精度。Haynes等[10]对DSM-Ⅱ进行了3点改进,即喷流核长计算系数减半、势流核心在导流偏转板处终止、试验测量一组新指向性,改进后方法的预示值增加约5.0 dB。Potter等[11]考虑了喷流沿导流板偏转的连续性,将喷流分为3段,分别计算了每段喷流的等效参数和辐射噪声。Zeng等[12]结合DSM-Ⅱ总声压级预示精度高和Potter方法[11]声压谱预示精度高的优点,利用前者的总声压级修正后者的声压级谱,修正后声压级谱吻合较好。以上方法对噪声声源和辐射特性均有较好的模拟,但未考虑火箭起飞时喷流与发射平台的相互作用,也较少关注导流槽对起飞噪声环境的影响。
文[13-14]详细分析了超音速喷流与水平偏转板相互作用时的声源特性。在此基础上,Kudryavtsev等[15]考虑了导流槽对起飞噪声环境的影响,建立了火箭起飞噪声环境预示模型,该模型考虑了火箭起飞的5个噪声来源,但弱化了自由喷流段噪声的辐射指向性,且未考虑发射平台和勤务塔对噪声的遮蔽。
国内火箭起飞噪声环境预示基础较薄弱,相关研究较少,通常依据以往发射遥测数据和发动机试车数据进行保守估计,总声压级和声压级谱精度难以保证。为满足国内火箭发射噪声环境预示需求,首先,本文在Kudryavtsev方法基础上,引入声源辐射指向性并重新分配自由喷流段噪声源声功率;其次,考虑发射平台和勤务塔对噪声的遮蔽效应,引入噪声遮蔽模型;再次,根据国内火箭发动机分布特征,修正火箭多喷流等效方法;最后,通过某型号火箭起飞实测噪声数据,验证修正方法的有效性。
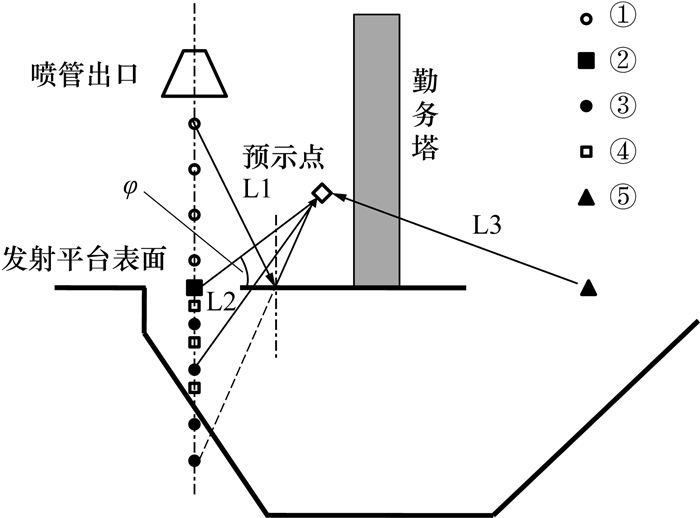
1 Kudryavtsev火箭起飞噪声模型和计算方法火箭起飞噪声模型如图 1所示,上方为发动机,下方为发射平台和导流槽。该模型共有5个噪声源,分别为未扰自由喷流噪声(①)、喷流与发射平台相互作用噪声(②)、反射噪声(③)、平台下受扰自由喷流噪声(④)和导流槽出口噪声(⑤),如图 1所示,L1为反射噪声传播路径;L2为平台下受扰自由喷流噪声传播路径;L3为导流槽出口噪声传播路径;φ为预示点方位角。
|
| 图 1 火箭起飞噪声模型 |
特征尺度Ym表示发动机喷口到等效完全膨胀喷流速度降低至0.75Uj横截面的距离,其中Uj为等效完全膨胀喷流出口速度。Ym表示如下:
| $\frac{Y_{\mathrm{m}}}{D_{\mathrm{j}}}=6\left(1+\frac{\gamma_{\mathrm{j}}-1}{2} M a_{\mathrm{j}}^2\right)\left(1+\frac{1}{2} \frac{H_{\mathrm{a}}}{H_{\mathrm{j}}}\right)-\frac{\gamma_{\mathrm{j}}-1}{3} M a_{\mathrm{j}}^2.$ | (1) |
其中:Dj为等效完全膨胀喷流出口直径;γj为等效完全膨胀喷流出口比热容比;Maj为等效完全膨胀喷流出口Mach数;Ha为环境气体总焓;Hj为等效完全膨胀喷流出口总焓。则喷流轴线坐标x可由Ym进行归一化,归一化坐标ξ表示如下:
| $\xi=x / Y_{\mathrm{m}}.$ | (2) |
发动机理想自由喷流总声功率WOA表示如下:
| $W_{\mathrm{OA}}=\eta_1 \frac{\pi}{8} \rho_{\mathrm{j}} U_{\mathrm{j}}^3 D_{\mathrm{j}}^2.$ | (3) |
其中:η1为发动机声效率,通常小于1%,与Uj有关[15];ρj为等效完全膨胀喷流出口密度。声功率沿喷流轴线分布密度表示如下:
| $\frac{\mathrm{d} W_{\mathrm{oa}}}{\mathrm{d} \xi}=g_1(\xi) W_{\mathrm{OA}}.$ | (4) |
其中:Woa为喷管出口到归一化坐标ξ之间喷流的声功率;g1(ξ)为功率分布经验曲线,由试验测试得出。
本文参考声功率为1×10-12 W,则点声源i在预示点辐射的总声压级SPLi表示如下:
| $\mathrm{SPL}_i=120+10 \lg W_{\mathrm{oa}, i}-10 \lg \left(4 \pi r_i^2\right).$ | (5) |
其中:Woa, i为点声源声功率;ri为i与预示点间的距离。得到SPLi后,根据经验曲线确定1/3倍频程声压级谱SPL1/3, i,相关计算表示如下:
| $\mathrm{SPL}_{1 / 3, i}-\mathrm{SPL}_i=g_2\left(Sr_1\right), $ | (6) |
| $S r_1=S r / S r_{\max }, $ | (7) |
| $S r=f D_{\mathrm{j}} / U_{\mathrm{j}}, $ | (8) |
| $S r_{\max }=f_{\max } D_{\mathrm{j}} / U_{\mathrm{j}}.$ | (9) |
其中:g2(Sr1)为未扰自由喷流噪声谱经验曲线,由试验测定;Sr1为峰值频率修正的Strouhal数(Sr),由Sr和峰值频率下的Strouhal数Srmax计算;f为频率;fmax为声压级谱峰值频率。累加所有点声源辐射的总声压级和1/3倍频程声压级谱,得到未扰自由喷流辐射总声压级。
1.2 喷流与发射平台相互作用噪声火箭起飞到一定高度时,由于喷流扩张,接近发射平台表面的喷流横截面直径大于发射孔直径,此时喷流与发射平台发生相互作用。该部分声源辐射的总声压级可由同等条件下喷流冲击无孔平板所产生的最大压力脉动Qmax计算,表示如下:
| $\mathrm{SPL}=0.7 Q_{\max }+10 \lg \left(F_{\mathrm{w}} / F_{\mathrm{j}}\right)-20 \lg \left(r_{\mathrm{h}} / D_{\mathrm{j}}\right)+38,$ | (10) |
| $F_{\mathrm{j}}=\rho_{\mathrm{j}} U_{\mathrm{j}}^2 A_{\mathrm{j}},$ | (11) |
| $F_{\mathrm{w}}=F_{\mathrm{j}}-\bar{\rho}_{\mathrm{w}} \bar{U}_{\mathrm{w}}^2 A_{\mathrm{w}} .$ | (12) |
其中:rh为发射孔中心与预示点之间的距离;Aj为等效完全膨胀喷流出口截面积;ρw为发射孔处喷流平均密度;Uw为发射孔处喷流平均速度;Aw为发射孔面积。1/3倍频程声压级谱由相互作用噪声谱经验曲线g3(Sr2)确定,其中Sr2为冲击修正的Strouhal数,表示如下:
| $S r_2=\frac{f D_{\mathrm{j}}}{M a_{\mathrm{j}} c_{\mathrm{a}}} \frac{1}{k_1(\varphi)} \frac{1}{k_2\left(r_{\mathrm{h}}\right)}.$ | (13) |
其中:ca为环境声速;k1和k2为经验参数,计算参考文[15]。
1.3 发射平台表面反射噪声发射台表面作为反射面会对未扰自由喷流噪声产生反射,因此采用镜面对称的“假想声源”模拟反射声源,“假想声源”具有与原声源相同的声功率和辐射特性。之后,由式(5)和(6)计算声压级和声压级谱,此部分噪声实际传播路径为L1,声源到目标点的距离需要根据“假想声源”位置重新计算。
1.4 发射平台入口与导流偏转器之间的受扰自由喷流噪声发射平台入口与导流偏转器之间的受扰自由喷流噪声的计算方法与1.1节基本一致,但需要考虑喷流与发射台相互作用后的损失,对Woa, i进行修正,修正后的点声源声功率W′oa, i表示如下:
| $W_{\text {oa }, i}^{\prime}=\left(1-\frac{F_{\mathrm{w}}}{F_{\mathrm{j}}}\right)^n W_{\mathrm{oa}, i}.$ | (14) |
其中:n为经验参数,一般取n=1.35。
1.5 导流槽出口噪声将导流槽内部噪声与出口亚音速流噪声统一等效为一个独立点声源,位于导流槽出口处。试验数据分析表明,该声源辐射的声功率Woa, out表示如下:
| $W_{\text {oa, out }}=\eta_2 \frac{\rho_2 U_2^8 D_2}{c_{\mathrm{a}}^5}+\eta_3 W_{\text {rem }}.$ | (15) |
其中:ρ2为导流槽出口喷流平均密度;U2为导流槽出口喷流平均速度;D2为导流槽出口等效直径;Wrem为导流槽内部剩余噪声的声功率;η2为导流槽出口亚音速流声效率,取值2×10-4;η3为导流槽内噪声声效率,取值0.05。导流槽出口噪声源主要为半球辐射,则预示点总声压级为:
| $\mathrm{SPL}=120+10 \lg W_{\text {oa, out }}-10 \lg \left(2 \pi r_{\text {out }}^2\right).$ | (16) |
其中rout为导流槽出口声源与预示点的距离。1/3倍频程声压级谱由导流槽出口噪声谱经验曲线g4(Sr3)确定,其中Sr3为导流槽出口参数修正的Strouhal数,表示如下:
| $S r_3=f D_2 / U_2.$ | (17) |
由式(5)—(9)可知,Kudryavtsev方法弱化了自由喷流段噪声辐射指向性,减小了各辐射方向声场差异,导致与实际情况不符;该方法未对发射台和勤务塔的噪声遮蔽衰减进行计算,可能导致火箭起飞时噪声预示值偏高;此外,该方法将火箭所有喷流等效为一个单喷流,与国内火箭实际情况有一定差异。本文针对以上问题,对Kudryavtsev方法进行修正。
2 噪声计算方法修正 2.1 自由喷流段噪声计算方法修正自由喷流段噪声主要影响图 1中声源1、3和4的计算。Kudryavtsev方法弱化了辐射角度对预示点声压级的影响,而文[5, 16-17]对自由喷流辐射特性的研究表明,不同角度声压级差异可能超过10.0 dB。本文利用DSM-Ⅱ进行指向性修正,并重新计算声功率和声功率分布,主要内容如下:
1) 采用Sutherland[18]提出的经验公式计算η1,表示如下:
| $\eta_1=K\left(\gamma_{\mathrm{j}} / \gamma_{\mathrm{a}}\right)\left(c_{\mathrm{t}} / c_{\mathrm{a}}\right)^3\left(c_{\mathrm{t}} / U_{\mathrm{j}}\right)^2.$ | (18) |
其中:K为经验系数;γa为环境气体比热容比;ct为发动机喉部声速。
2) 重新分配点声源声功率。喷流轴线由喷流核长Xco归一化,Xco的计算表示如下:
| $X_{\mathrm{co}}=1.75\left(1+0.38 M a_{\mathrm{j}}\right)^2 D_{\mathrm{j}}.$ | (19) |
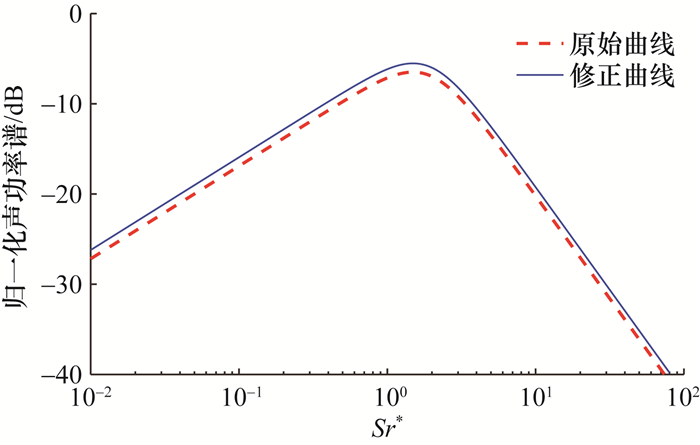
文[5]给出了声功率沿喷流轴线分布归一化曲线和点声源归一化声功率谱。分析文[5]中的经验曲线,发现积分结果均小于1,不符合归一化要求,可能造成预示值偏小。本文对经验曲线进行了拟合,并对拟合公式的系数进行修正,使曲线整体上移,满足归一化条件,修正后的点声源归一化声功率谱如图 2所示。修正后喷流轴线声功率分布和点声源归一化声功率谱的经验公式表示如下:
| $\frac{X_{\mathrm{co}} W(x)}{W_{\mathrm{OA}}}=\frac{0.352\left(x / X_{\mathrm{co}}\right)^{1.36}}{\left(1+0.005\left(x / X_{\mathrm{co}}\right)^{7.5}\right)^{0.91}}, $ | (20) |
| $\frac{W(f, x)}{W(x)} \cdot \frac{U_{\mathrm{j}} c_{\mathrm{a}}}{x c_{\mathrm{j}}}=\frac{0.272\left(S r^*\right)^{1.03}}{\left(1+0.124\left(S r^*\right)^{3.25}\right)^{1.02}}, $ | (21) |
| $S r^*=\frac{f x c_{\mathrm{j}}}{U_{\mathrm{j}} c_{\mathrm{a}}}.$ | (22) |
|
| 图 2 修正后点声源归一化声功率谱 |
其中:W(x)为沿喷流轴线声功率分布;W(f, x)为喷流轴线x位置处点声源归一化声功率谱;cj为等效完全膨胀喷流出口声速。
采用式(20)和(21)分配声功率,预示声压级提高约1.5 dB。
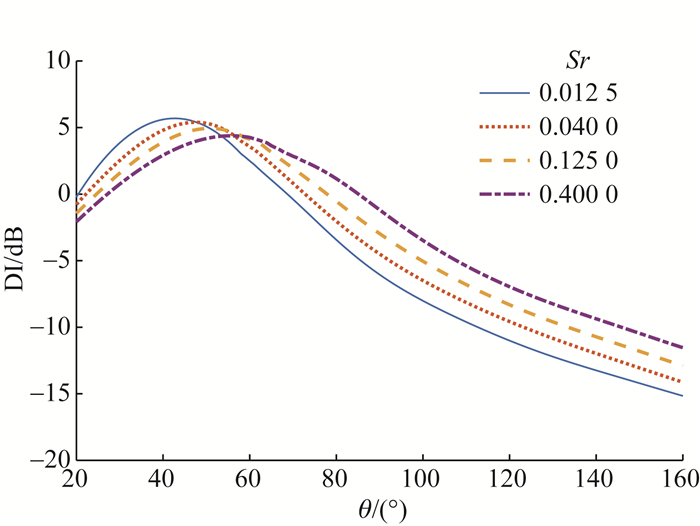
3) 修正声源指向性。以喷流下游轴线为0°方向,上游轴线为180°方向,不同St下各辐射角度θ的指向性修正系数DI(f, θ)如图 3所示,不同频率下噪声辐射峰值角度为40°~60°。
|
| 图 3 不同Sr下噪声指向性 |
每个点声源在预示点的声压级谱表示如下:
| $\mathrm{SPL}_{1 / 3, i}=120+10 \lg W_{1 / 3, i}-10 \lg \left(4 \pi r_i^2\right)+\mathrm{DI}(f, \theta).$ | (23) |
其中W1/3, i为i的1/3倍频程各频段声功率。
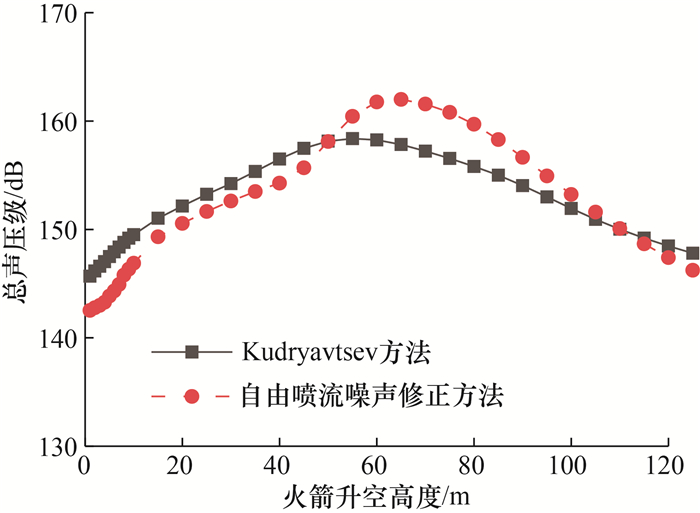
图 4比较了自由喷流噪声修正前后,不同火箭升空高度下预示点噪声总声压级。其中预示点高度40 m,距火箭轴线15 m。自由喷流噪声修正方法的预示点噪声总声压级峰值位置偏后且峰值更高,在火箭升空高度小于50 m和大于110 m时总声压级偏小。2种方法差异的原因主要是指向性不同,Kudryavtsev方法的总声压级变化趋势与火箭起飞过程中主要声源区域距预示点距离变化情况一致;自由喷流噪声修正方法除受距离影响外,还受指向性修正影响,当预示点位置处于主要声源区域下游附近时,受到指向性正修正,总声压级较高,否则会受到指向性负修正,总声压级较低。
|
| 图 4 自由喷流噪声修正前后预示点噪声总声压级 |
2.2 发射平台与勤务塔遮蔽衰减修正
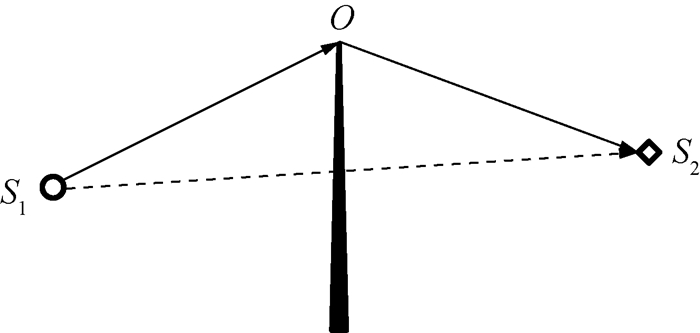
分析噪声传播路径,发射平台下方受扰自由喷流噪声会受到发射平台的遮蔽(图 1中路径L2),而导流槽出口噪声受到勤务塔遮蔽(图 1中路径L3)。火箭刚点火起飞时,大部分喷流位于发射平台下方,此时主要噪声源为发射平台受扰自由喷流噪声和导流槽出口噪声,因此遮蔽衰减估计对声压级预示尤为重要。本文遮蔽衰减估计采用Maekawa声遮蔽模型[19],如图 5所示,S1点为声源,S2点为目标点,O点为声障边缘。路径S1S2为无声障时噪声传播路径,路径S1O-OS2为有声障时噪声实际传播路径,则Fresnel数N表示如下:
| $N=\frac{2}{\lambda}\left(S_1 O+O S_2-S_1 S_2\right).$ | (24) |
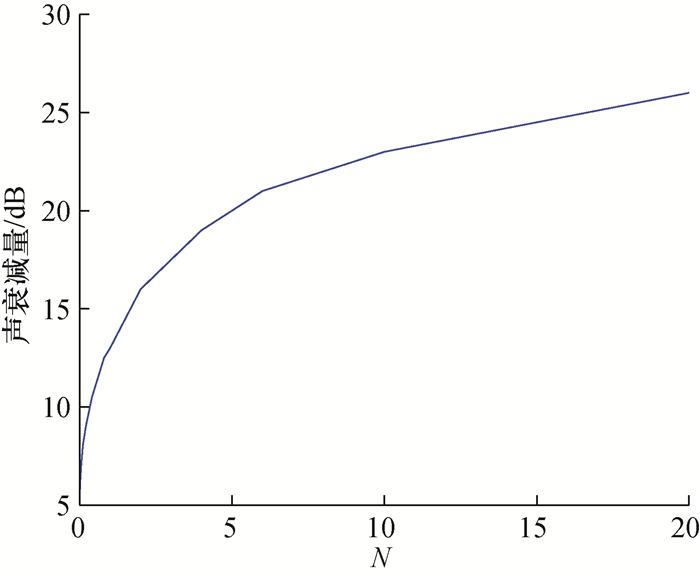
其中λ为声波波长。根据N及图 6声衰减经验曲线[19],即可估计各频段声衰减。
估计发射平台对发射平台下方受扰自由喷流噪声的遮蔽衰减时,发射平台作为声障,分别计算各频段声衰减SPLloss, 1/3,SPL1/3, i消除声衰减后得到修正声压级谱SPL′ 1/3, i,表示如下:
| $\mathrm{SPL}_{1 / 3, i}^{\prime}=\mathrm{SPL}_{1 / 3, i}-\mathrm{SPL}_{\text {loss }, 1 / 3}.$ | (25) |
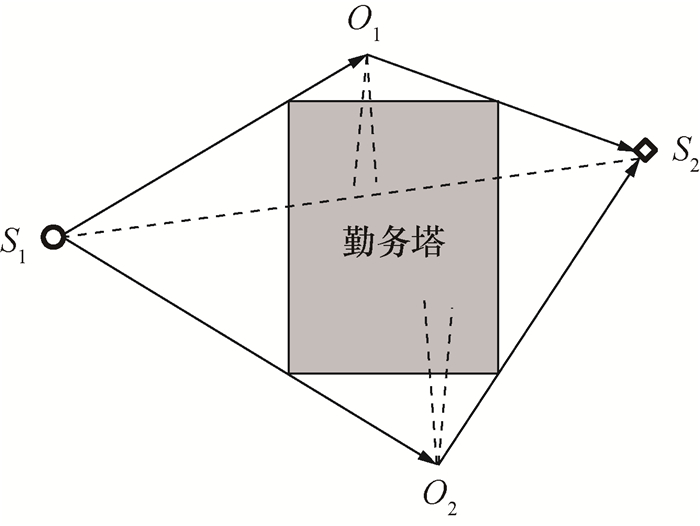
勤务塔厚度较大,需要根据噪声传播路径进行声障等效,等效的噪声遮蔽模型如图 7所示,其中O1和O2分别为2个等效声障边缘。由于勤务塔的高度远大于宽度,因此需要先采用式(24)和(25)分别估计两侧噪声声压级谱,再叠加获得修正声压级谱。
|
| 图 7 勤务塔噪声遮蔽模型 |
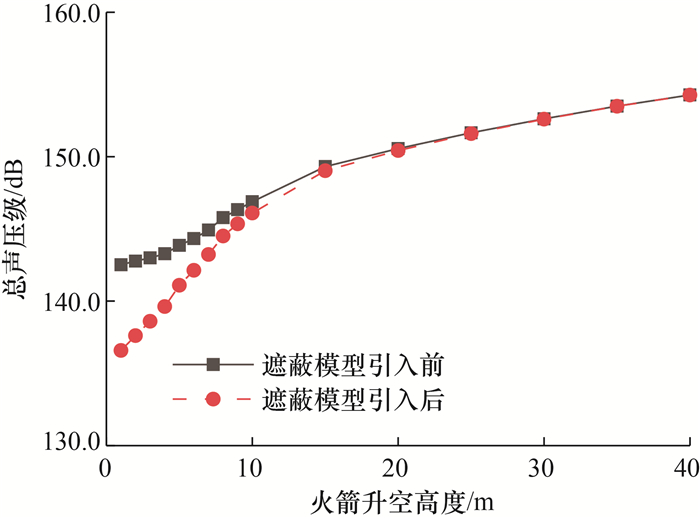
遮蔽模型引入前后预示点噪声总声压级变化情况如图 8所示。可以看出,在火箭升空高度10 m内,引入遮蔽模型使预示点噪声总声压级明显降低;随着火箭升空高度增大,主要声源移向发射平台上方,遮蔽模型影响逐渐减小。
|
| 图 8 遮蔽模型引入前后预示点噪声总声压级 |
2.3 多喷流并联等效方法修正
多喷流并联时,喷流形态发生变化,可能存在噪声叠加、噪声遮蔽等。目前多喷流等效方法取决于喷流间距:喷流间距较大时,先独立计算各喷流噪声,再叠加获得总噪声;喷流间距较小时,根据等效面积法,将所有喷流等效为一个单喷流进行计算;喷流间距适中时,混合区前各喷流噪声独立进行计算,混合区后将所有喷流等效为一个单喷流进行计算[20]。
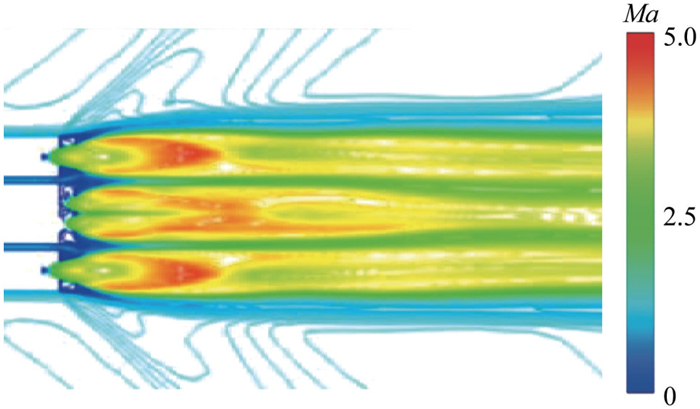
实际噪声预示时,发动机间距、参数不一致,助推发动机存在安装角等,都为喷流等效带来了困难。图 9为某多喷管火箭喷流外流场仿真结果,其中芯级喷流间距较小,互相掺混合为一股喷流,核心直径和长度明显增大;而助推喷流距芯级喷流的距离较远,表现为独立喷流。综合以上结果,本文采用的方法如下:芯级多喷流等效为单喷流计算、助推喷流独立计算,叠加两者获得总噪声。
|
| 图 9 多喷管火箭喷流外流场仿真结果 |
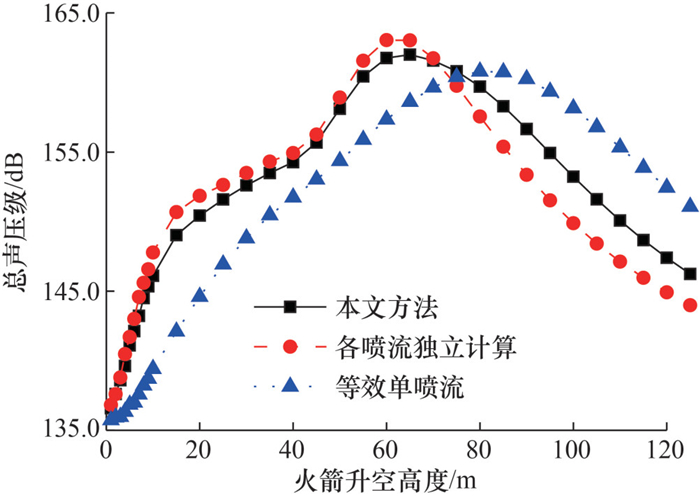
采用本文方法、各喷流独立计算方法及等效单喷流方法分别计算不同火箭升空高度下预示点噪声总声压级,多喷流不同等效方法对比如图 10所示。火箭芯级并联4台发动机,4个助推各分布1台发动机,所有发动机出口燃气参数一致。与各喷流独立计算方法相比,本文方法峰值位置偏后,峰值位置前总声压级较小,峰值位置后总声压级较大,且峰值范围较宽;与等效单喷流方法相比,本文方法峰值位置则靠前。原因如下:当各喷流独立计算时,各喷流核长一致且相对较短,声源分布密集且靠前;当全部等效为单喷流时,出口等效直径增大,以式(19)计算的核长增大,声源整体按比例向下游方向偏移,最大声源区域长度增大、位置靠后。本文方法避免了上述2种极端情况,更接近实际火箭喷流形态。
|
| 图 10 多喷流不同等效方法对比 |
3 火箭起飞噪声计算
某火箭芯级并联4台发动机,4个助推各分布1台发动机,所有发动机参数一致,具体计算参数见表 1。其中:Mae为出口燃气Mach数;Te为出口燃气温度;pe为出口燃气压力;γe为出口燃气比热容比;R为出口燃气气体常数。火箭起飞环境与图 1一致,噪声测点布置在勤务塔上,水平方向距火箭14 m,朝向火箭一侧,P1—P6共6个测点,各测点高度分别为12.5、24.0、29.8、36.1、42.2和48.3 m。
3.1 起飞不同时刻总声压级
首先计算火箭起飞不同时刻总声压级变化情况,以火箭起飞时刻(设定为0 s)开始,间隔为1 s,共计算9个不同时刻工况。图 11为修正方法和Kudryavtsev方法与测试数据在不同起飞时刻条件下的总声压级对比。修正方法考虑了自由喷流指向性并采用合适的多喷流等效方法,总声压级变化趋势与测试数据更接近,测点P2和P3的总声压级预示误差不超过3.0 dB,而Kudryavtsev方法在起飞初期和后期的总声压级偏大,峰值时刻的总声压级偏小;起飞2 s内,Kudryavtsev方法的总声压级最大预示误差接近15.0 dB,而修正方法考虑了发射平台和勤务塔的遮蔽,总声压级最大预示误差不超过5.0 dB,相比Kudryavtsev方法减小约10.0 dB;修正方法的总声压级峰值时刻更接近测试数据的峰值时刻,Kudryavtsev方法的总声压级峰值时刻相对靠前。

|
| 图 11 不同起飞时刻总声压级 |
表 2为峰值时刻附近2种方法预示总声压级的最大误差(预示值与测试值之差)。修正方法的最大误差不超过3.0 dB,而Kudryavtsev方法未进行指向性修正,预示值均偏小,最大误差超过3.0 dB。总体上,修正方法的总声压级预示精度更高。
| dB | |||||||||||||||||||||||||||||
| 方法 | 测点 | ||||||||||||||||||||||||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||||||||||||||||||||||
| 修正方法 | 0.98 | -0.05 | 1.40 | 1.64 | 0.99 | 2.22 | |||||||||||||||||||||||
| Kudryavtsev方法 | -1.33 | -3.67 | -2.50 | -2.12 | -2.74 | -3.75 | |||||||||||||||||||||||
从测点位置看,采用修正方法时,测点P1在起飞初期的预示值偏低,而测点P4—P6在起飞初期的预示值偏高,这是因为修正方法未考虑箭体对噪声的遮蔽及地面、箭体和勤务塔三者之间的复杂反射。箭体遮蔽主要影响向上辐射的噪声,因此较高位置测点的总声压级测试值更小;地面附近复杂反射对较低位置测点影响更大,因此测点P1的总声压级测试值比预示值更大。
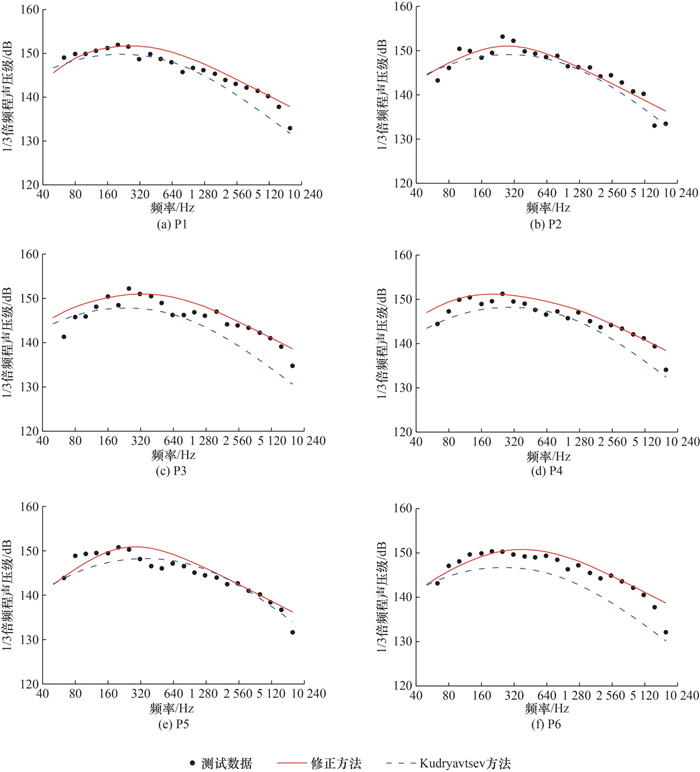
3.2 峰值时刻1/3倍频程声压级谱火箭起飞噪声为宽频噪声,不同箭体结构和有效载荷的噪声敏感频段有一定差异,因此噪声声压级谱预示也十分重要。在总声压级峰值时刻条件下,本文对比了测试值的1/3倍频程声压级谱与修正方法和Kudryavtsev方法的1/3倍频程声压级谱。各测点峰值时刻1/3倍频程声压级谱如图 12所示。可以看出,2种方法的声压级谱峰值频率预示能力接近,但Kudryavtsev方法的最大声压级预示值偏低,最大误差为4.0 dB,修正方法的最大声压级预示值较准确,误差在3.0 dB以内;修正方法在1~5 kHz频段的声压级预示值的最大误差小于3.0 dB,而Kudryavtsev方法在1~5 kHz频段的声压级预示值的最大误差超过6.0 dB;修正方法在全频段的最大声压级误差不超过6.0 dB,且最大误差集中在80 Hz以下低频频段和6 kHz以上高频频段,而此部分对总声压级作出的贡献有限。综上所述,修正方法的声压级谱预示精度明显提高,更适合工程应用。
|
| 图 12 各测点峰值时刻1/3倍频程声压级谱 |
4 结论
本文针对火箭起飞噪声环境预示问题,在Kudryavtsev方法基础上,修正自由喷流声源指向性并拟合经验公式重新分配声源功率,提高了Kudryavtsev方法在不同预示角度下的有效性;根据声遮蔽模型估计导流槽与勤务塔噪声遮蔽衰减,使噪声模型更接近真实环境,提高发射台下方噪声和导流槽出口噪声的预示精度;修正多喷流等效方法,提高Kudryavtsev方法对国内多喷管火箭喷流特征的适应性。
某火箭起飞后,不同升空高度和不同测点的测试数据与2种方法的预示值的对比结果表明:修正方法与Kudryavtsev方法相比,具有更高的总声压级和声压级谱预示精度。火箭起飞2 s内,修正方法的预示精度相较Kudryavtsev方法提高约10.0 dB;修正方法预示声压级峰值时刻更准确,且峰值时刻附近声压级最大误差不超过3.0 dB;修正方法的峰值时刻声压级谱全频段最大误差小于6.0 dB,峰值频率和频率1~5 kHz等关键频段声压级误差小于3.0 dB,优于Kudryavtsev方法。本文所提修正方法提高了预示精度,能更好地应用于实际工程。
火箭起飞噪声工程预示对载荷设计和噪声防护具有重要意义。本文方法虽然一定程度上提高了火箭起飞噪声预示精度,但仍存在一些不足,例如未考虑箭体对噪声的遮蔽和地面附近的复杂反射、对80 Hz以下低频频段和6 kHz以上高频频段噪声的预示误差较大等。未来可进一步完善模型,为载荷设计和噪声防护提供更有力的数据支撑。
| [1] |
陈劲松, 曾玲芳, 平仕良, 等. 大型火箭发射喷水降噪技术研究进展[J]. 导弹与航天运载技术, 2019(2): 94-100. CHEN J S, ZENG L F, PING S L, et al. Advances of water suppression technology for large rocket launching noise[J]. Missiles and Space Vehicles, 2019(2): 94-100. (in Chinese) |
| [2] |
王怀志, 于开平, 曾耀祥, 等. 能量有限元方法的双星整流罩中频声振环境预示[J]. 宇航总体技术, 2018, 2(5): 42-49. WANG H Z, YU K P, ZENG Y X, et al. Prediction for vibration environment of the double stars fairing structure based on energy finite element[J]. Astronautical Systems Engineering Technology, 2018, 2(5): 42-49. (in Chinese) |
| [3] |
COUNTER D, HOUSTON J. Ares Ⅰ scale model acoustic test lift-off acoustics[J]. The Journal of the Acoustical Society of America, 2011, 130(4): 2542. |
| [4] |
HOUSTON J, COUNTER D, GIACOMONI C. SLS scale model acoustic test liftoff results and comparisons: M15-4862[R]. Los Angels: National Aeronautics and Space Administration Marshall Space Flight Center, 2015.
|
| [5] |
ELDRED K M. Acoustic loads generated by the propulsion system: NASA SP-8072[R]. Washington, DC: National Aeronautics and Space Administration Technical Reports Server, 1971.
|
| [6] |
PLOTKIN K J, SUTHERLAND L C, VU B T. Lift-off acoustics predictions for the Ares Ⅰ launch pad[C]//Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference. Miami, USA: AIAA, 2009: 1-11.
|
| [7] |
VARNIER J. Experimental study and simulation of rocket engine freejet noise[J]. AIAA Journal, 2001, 39(10): 1851-1859. DOI:10.2514/2.1199 |
| [8] |
KOUDRIAVTSEV V, VARNIER J, SAFRONOV A. A simplified model of jet aerodynamics and acoustics[C]//Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference. Manchester, UK: AIAA, 2004: 898-910.
|
| [9] |
GRESKA B, KROTHAPALLI A, HORNE W C, et al. A near-field study of high temperature supersonic jets[C]//Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference. Vancouver, Canada: AIAA, 2008: 1-27.
|
| [10] |
HAYNES J, KENNY R J. Modifications to the NASA SP-8072 distributed source method Ⅱ for Ares Ⅰ lift-off environment predictions[C]//Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference. Miami, USA: AIAA, 2009: 1-12.
|
| [11] |
POTTER R C, CROCKER M J. Acoustic prediction methods for rocket engines, including the effects of clustered engines and deflected exhaust flow: NASA-CR-566[J]. Huntsville: National Aeronautics and Space Administration Technical Reports Server, 1966. |
| [12] |
ZENG Y X, WANG H X, RONG Y, et al. Improvement methodology of predicting engine jet noise in engineering application[J]. Journal of Physics: Conference Series, 2023, 2472(1): 012058. DOI:10.1088/1742-6596/2472/1/012058 |
| [13] |
VARNIER J, RAGUENET W, GELY D. Noise radiated from free and impinging hot supersonic jets[C]//Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference. Toulouse, France: AIAA, 1998: 1-15.
|
| [14] |
KOUDRIAVTSEV V. Acoustic environment at jet interaction with a plate[C/OL]. [2023-07-01]. http://www.conforg.fr/internoise2000/cdrom/data/articles/000775.pdf.
|
| [15] |
KUDRYAVTSEV V V, SAFRONOV A V. Acoustic environment resulting in interaction of launch vehicle main engines jets with a launch pad having closed long ducts like a tunnel[J]. Progress in Flight Physics, 2012, 3: 405-420. |
| [16] |
TAM C K W. Supersonic jet noise[J]. Annual Review of Fluid Mechanics, 1995, 27: 17-43. DOI:10.1146/annurev.fl.27.010195.000313 |
| [17] |
LUBERT C P, GEE K L, TSUTSUMI S. Supersonic jet noise from launch vehicles: 50 years since NASA SP-8072[J]. The Journal of the Acoustical Society of America, 2022, 151(2): 752-791. |
| [18] |
SUTHERLAND L C. Progress and problems in rocket noise prediction for ground facilities[C]//Proceedings of the 15th Aeroacoustics Conference. Long Beach, USA: AIAA, 1993: 1-11.
|
| [19] |
MAEKAWA Z. Noise reduction by screens[J]. Applied Acoustics, 1968, 1(3): 157-173. |
| [20] |
王国辉. 运载火箭喷流气动噪声[M]. 北京: 中国宇航出版社, 2019. WANG G H. Aerodynamic noise of launch vehicle jet[M]. Beijing: China Astronautic Publishing House, 2019. (in Chinese) |