2. 清华大学 天津高端装备研究院, 天津 300300
2. Tianjin Research Institute for Advanced Equipment, Tsinghua University, Tianjin 300300, China
工业流水线生产环境下,多种类小批次中小型零件在自动化喷涂作业等过程中,往往面临着因零件摆放位姿不固定而难以自动化测量和定位的问题。以中国民机零件喷涂为例,航空小零件种类繁多、无定位夹持装置,零件种类达五万余种,但目前仍以人工手动喷涂的方式为主。因此,具有智能识别零件的种类和位姿功能的零件定位系统是升级产线、实现智能生产的重要支撑。
目前二维(2D)视觉检测技术主要有2种:一是运用传统图像处理算法,实现前后景分割与模板建立[1];二是通过机器学习算法学习目标特征,通过特征匹配提取目标[2]。由于工业零件种类繁杂难以建立数据集,且工业环境存在各种不确定因素[3],因此可采用形态学运算和k-均值(k-means)聚类等传统图像处理方案,实现零件的粗分类、粗定位等信息提取。在航空零件喷涂生产中,往往是多种零件混线喷涂。由于零件种类丰富,且摆放方式多样,单纯依靠2D图像难以准确判断其位姿和种类,而三维(3D)相机的单幅拍摄范围有限,需要进行多位姿拍摄组合形成完整的点云数据。
在自动化流水线喷涂作业中,点云配准算法不仅需要精度,还需具有较快的运算速度以及对强干扰后景的鲁棒性,从而满足生产需求。受限于工业环境和零件种类的复杂性,以深度学习为主的3D点云匹配方法[4-9]并不适用于此类应用场景。对于传统点云配准算法,Besl等[10]提出的经典迭代最近点(iterative closest point, ICP)算法需要对配准点云的初始位姿有一个较好的估计量。Yang等[11-12]在此基础上改进的全局优化ICP (globally optimize ICP, Go-ICP)和其他ICP改进方案大多需要依靠从散乱的点云数据中提取关键特征点,或是构造新的表达向量等信息。因而存在某些情况下鲁棒性不够或计算效率低的问题。除了ICP系列算法外,基于点云特征,Frome等[13]提出了3D形状关联(3D shape context, 3Dsc)配准算法,以采样点为球心计算邻域点的对数极坐标,用以描述局部几何信息进行配准;Rusu等[14-15]又提出了点特征直方图(point feature histograms, PFH)和快速点特征直方图(fast PFH, FPFH)算法,应用点与邻域点法向量夹角等信息构建了特征直方图,取得了较好的配准效果。然而以上基于特征的算法均受限于难以处理的强后景噪声问题,不具有较好的鲁棒性。
基于特征的方法没有用点云中全部的点进行配准, 而是只选取点云中比较特殊的一部分进行配准, 这种方法可以不需要提供初始位姿, 并且具有鲁棒性。Yang等[16]使用超体素的方法, 考虑到了空间坐标、颜色值和局部几何特征, 以超体素的中心作为检测到的特征点。特征匹配的过程也是一个变换估计的过程,Jung等[17]利用3D点云生成不同视点的2D合成图像, 再生成不同分辨率的缩放图像, 这样产生大量重复的特征匹配关系, 然后投票选择重复多的匹配关系作为最终的特征匹配。
随着深度学习的发展, 基于学习的点云配准方法得到广泛研究和深入发展。在点云上进行学习的方法分为3类, 即基于体素的方法、基于多视图的方法和基于原始数据的方法。Zeng等[18]提出一种基于体素上学习关键点描述符的网络, 将关键点周围划分为体素并将其输入ConvNet网络, 学习的目标是对应关键点的描述符之间的距离应最小化, 同时拉开不对应关键点之间的距离。Kurobe等[19]使用PointNet获得特征, 然后再将源点云全局特征和目标点云全局特征与局部特征结合, 通过MLP获得对应关系, 使用SVD获得最终变换参数。
由于本文的3D点云数据是在流水线上动态实时采集,因传送链条的振动、酸洗后零件的高反光以及零件间的相互遮挡等问题,很难完整地获取到被测零件的全部3D特征。由于航空零件主要是钣金件,曲面特征并不明显。本研究在前期几乎没有生产线上零件点云数据积累,不适合采用学习等方式。综合考虑以上因素,采用改进粒子群算法进行流水线上零件点云配准,最大限度地利用被测点云的数据信息。
点云配准可以视为多变量的最优值求解问题。最优粒子群(particle swarm optimization,PSO) 算法[20]作为群智能优化算法具有结构简单、迭代速率快且兼顾全局和局部的特点,能够满足这一点云配准算法的需求。Ge等[21]将PSO算法与ICP算法融合,增强了配准算法的鲁棒性,表明了PSO算法在点云配准算法中的卓越成效;而韩贤权等[22]以法向量叉积代数和最小作为适应度函数,对相邻点云重叠区域内的所有数据进行高效的全局搜索,验证了PSO算法用于散乱点云精配准的可行性与稳定性。然而,标准的粒子群算法在进化过程中很容易陷入局部最优导致算法早熟收敛,使其在点云配准的过程中易导致位姿的误配准。为解决这一问题,潘峰等[23]通过标准粒子群算法中的全局最优、个体最优与普通粒子进行模型分析,得出了需要对全局最优粒子的运动形式加以改变,增加其多样性的结论;张顶学等[24]提出了随测度自适应变换的惯性权重,在多峰函数中得到了较好优化效果;王俊伟等[25]提出了一种带有梯度加速的粒子群算法,其对目标函数求解梯度以寻找函数值的最速下降方向。目前在点云配准的过程中并无明确的基于2D图像分割以及3D点云配准的粒子群算法的优化研究。
为满足测量效率需求,本文采用2D图像辅助进行零件初步定位和分类,根据零件初步定位信息自主规划3D扫描仪的扫描测量路径,以缩短3D扫描仪的拍摄时长,根据零件初步定位信息对点云数据进行分割,最后对测量点云与零件3D数模进行配准以确定零件的准确位姿。参考前人优化思路,为同时满足加工效率与精度的零件定位,本文应用基于自适应启发改进的粒子群算法。为解决粒子群算法收敛速度缓慢与易陷入局部最优以及较强的后景点云等问题,在应用随配准状态自适应的学习系数与惯性系数基础上,从局部搜索、全局搜索以及离群点智能剔除等方面进行优化。增强粒子的多样性和算法的全局搜索能力,实现分割后点云和理论数模的智能配准,获得零件摆放的精确位姿。
1 定位测量系统设计 1.1 硬件系统本文硬件系统的3D设计图和实际测量工位图分别如图 1a和1b所示。由图可知,当传送带某个网格筛盘到达2D相机测量工位后,2D相机采集零部件和网格筛盘图像;当筛盘到达3D扫描仪测量工位后,五轴测量机构根据2D图像处理所得的位置信息操纵3D扫描仪移动到指定位置进行拍摄,获取点云信息。五轴测量机构包含3个直线轴(X、Y、Z)以及2个旋转轴(A、C)。
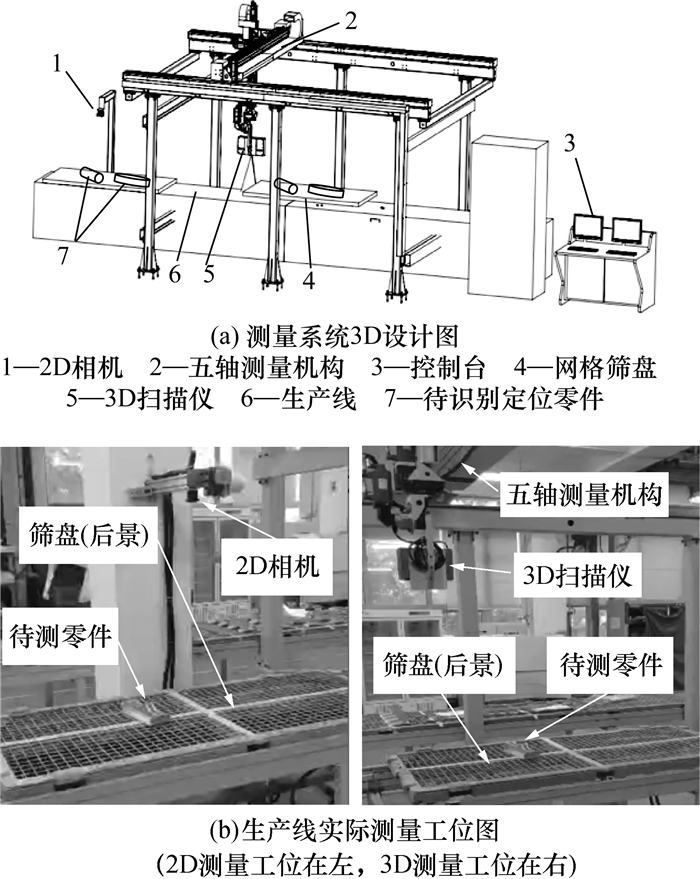
|
| 图 1 硬件系统 |
1.2 测量和计算流程
测量和计算流程分为预标定和实时计算2个部分。在预标定中完成坐标系标定、拍摄位姿标定等任务。实时计算的流程如下:
第一步,2D相机采集零部件和网格筛盘图像并进行图像处理,得到零件的粗分类、粗定位等信息。
第二步,五轴测量机构的运动路径根据零件的初步定位信息进行自主规划, 包含粗扫描轨迹和精确扫描轨迹。
第三步,系统对点云数据进行一定程度的前景提取后,依照零件边界信息进行并发分割。
第四步,对分割后的零件点云数据与零件的理论数模进行粗配准,以此确定每种零件对应的理论数模。
第五步,由于同类零件在筛盘上摆放大多处于同一姿态,因此对部分粒子继承粗配准所得Euler角作为初始旋转参数,进行并发精配准,最终获得每个零件的准确位姿。
2 平面图像处理与点云分割 2.1 平面图像处理对图像依次进行除畸变、滤波、灰度均衡化、二值化、形态学处理、小轮廓剔除、轮廓提取等处理,分割图像前景和背景,识别出图像中的零件。2D相机捕获的原始图像如图 2所示。

|
| 图 2 2D相机捕获的原始图像 |
为去除底部网格筛盘对图像造成的影响,分别使用“十”字形和椭圆形内核结构进行开运算操作。对开运算后的杂质点残余采用轮廓提取,并对面积小于阈值的轮廓进行填充。最后采用矩形内核结构对图像进行膨胀处理,处理后的图像如图 3所示。

|
| 图 3 处理后的图像 |
对膨胀处理后的图像进行轮廓提取作为目标零件,依次计算每个目标零件的轮廓面积、最小包含矩形面积、最小包含矩形长宽比、最小包含圆半径等数据作为维度信息,以此构建k-means聚类并通过直线拟合和最小曲率法计算得出最佳零件分类数。接着计算每个零部件的最小包含矩形顶点空间坐标、零件类别、零件中心点空间坐标,并根据零件中心点空间坐标自动规划五轴测量机构移动和测量路径。
2.2 点云分割当全部点云拍摄完毕后,需要对点云信息进行处理。由于拍摄的零件均位于筛盘上,因此首先对点云数据采用k-means聚类消除一部分后景中的杂质点,其次使用平面提取法找到筛盘网格构成的平面信息,最后使用条件滤波尽可能地将零件低噪点从复杂点云中剥离出来。接着根据2D图像处理后获得的零件坐标对点云进行并发分割。通过多线程同步运算在最高效率下将所有的零件点云单独存储完毕,并根据2D图像处理结果找到每一种零件的精拍点云。
3 位姿配准通过3D扫描模块得到了包括精拍和粗拍零件在内的所有零件点云信息。扫描点云与零件的理论数模点云进行配准可得零件位于筛盘坐标系上的真实位姿。
点云配准问题可以转化为旋转矩阵的多变量最优化计算问题,而旋转矩阵由6个参数变量计算得来,因此本文将点云配准所需的3个平移参数和3个旋转参数作为广义粒子维度。为解决粒子群算法收敛速度缓慢和易陷入局部最优问题,在应用随配准状态自适应的学习系数和惯性系数的基础上,从局部搜索和全局搜索2方面进行优化。为了减少后景点云对配准造成的影响,采用离群点剔除以解决后景点云对配准的影响。
本文配准算法主要分为初始化和迭代匹配2部分。
3.1 粒子群算法初始化为了提高计算效率,对测量的3D点云进行抽样参与配准计算。首先在扫描的点云中取X、Y、Z3个方向共计6个极大、极小值点,并对剩下的点云进行随机采样构建配准点云S={sk∈R3, k=1, 2, …, n}。与之相对应的,有理论数模点云Q={qj∈R3, j=1, 2, …, m}和PSO粒子群P={pi∈R6, i=1, 2, …, N}。初始粒子群以旋转参数(αi(t), βi(t), γi(t))和平移参数(xi(t), yi(t), zi(t))作为第i个粒子的广义维度参数,t表示第t次迭代。每个粒子的初始生成方法如下:
在(-π, π)范围内随机取值初始化旋转参数(αi(0), βi(0), γi(0)),并以此作为构建Z-Y-X Euler角旋转矩阵的依据。对于具有初始Euler角的,初始粒子群中一定比例的粒子以(α,β,γ)作为(αi(0), βi(0), γi(0))构建旋转矩阵的依据。旋转矩阵构造如下:
| $\boldsymbol{R}_i(t)=\left(\boldsymbol{R}_{i 1}(t), \boldsymbol{R}_{i 2}(t), \boldsymbol{R}_{i 3}(t)\right).$ | (1) |
其中:
| $\begin{gathered}\boldsymbol{R}_{i 1}(t)=\left(\begin{array}{c}\cos \beta_i(t) \cos \alpha_i(t) \\ \cos \beta_i(t) \sin \alpha_i(t) \\ -\sin \beta_i(t)\end{array}\right), \\ \boldsymbol{R}_{i 2}(t)=\left(\begin{array}{c}\sin \gamma_i(t) \sin \beta_i(t) \cos \alpha_i(t)-\cos \gamma_i(t) \sin \alpha_i(t) \\ \sin \gamma_i(t) \sin \beta_i(t) \sin \alpha_i(t)+\cos \gamma_i(t) \cos \alpha_i(t) \\ \sin \gamma_i(t) \cos \beta_i(t)\end{array}\right), \\ \boldsymbol{R}_{i 3}(t)=\left(\begin{array}{c}\cos \gamma_i(t) \sin \beta_i(t) \cos \alpha_i(t)+\sin \gamma_i(t) \sin \alpha_i(t) \\ \cos \gamma_i(t) \sin \beta_i(t) \sin \alpha_i(t)-\sin \gamma_i(t) \cos \alpha_i(t) \\ \cos \gamma_i(t) \cos \beta_i(t)\end{array}\right) .\end{gathered}$ |
将(αi(0), βi(0), γi(0))代入式(1)构建Ri(0)初始化旋转矩阵,求出以此角度进行旋转后配准点云的X、Y、Z方向上的极值。以理论数模的X、Y、Z方向上的极值与旋转后的配准点云的极值之差,作为平移矩阵参数的浮动范围。在浮动范围内随机取值作为初始平移参数(xi(0), yi(0), zi(0))。
| $\begin{gathered}p_i(0)=\left(\alpha_i(0), \beta_i(0), \gamma_i(0), \right. \\ \left.x_i(0), y_i(0), z_i(0)\right) .\end{gathered}$ | (2) |
以(αi(t), βi(t), γi(t), xi(t), yi(t), zi(t))作为粒子i当前位置的pi(t),构建转换矩阵对配准点云进行变换,粒子i代表的转换矩阵为
| $\mathbf{R} \mathbf{T}_i(t)=\left(\begin{array}{cc}\boldsymbol{R}_i(t) & \boldsymbol{T}_i(t) \\ 0 & 1\end{array}\right).$ | (3) |
其中Ti(t)=(xi(t), yi(t), zi(t))T。
将pi(0)代入式(3),构建RTi(0)初始化转换矩阵,对配准点云进行转换。
粒子群构建完毕后需要计算适应度值来评判出个体最优与粒子群最优。使用KD树(K dimensional tree,KD-Tree)来计算新姿态下第t次迭代时使用粒子i的参数变换配准点云后,配准点云上的点到理论数模点云上最近点的平均距离,即本文的适应度函数值Fi(t)。
| $F_i(t)=F\left(p_i(t)\right)=\frac{1}{n} \sum\limits_{k=1}^n f_i^k(t)=\frac{1}{n} \sum\limits_{k=1}^n f^k\left(\boldsymbol{p}_i(t)\right), $ | (4) |
| $\begin{gathered}f_i^k\left(p_i(t)\right)=\min \left(\left\|\boldsymbol{q}_1-\left(\boldsymbol{R}_i(t) \boldsymbol{s}_k+\boldsymbol{T}_i(t)\right)\right\|_1, \right. \\ \left.\cdots, \left\|\boldsymbol{q}_m-\left(\boldsymbol{R}_i(t) \boldsymbol{s}_k+\boldsymbol{T}_i(t)\right)\right\|_1\right)\end{gathered}.$ | (5) |
其中:i表示粒子群中的第i个粒子;fik(t)表示第t次迭代中,使用粒子i的参数变换配准点云后,配准点云上k点到理论数模点云上最近点的距离。在初始化过程中t=0,以当前粒子参数作为个体最优pb,选取Fi(t)值最小的粒子参数作为粒子群的全局最优pg。
3.2 迭代配准中的滞步和多样性增强初始化完毕后进入迭代配准过程。每次迭代过程中更新已经迭代的次数Td与剩余的迭代次数Tr直至达到迭代次数上限T,Tr=T-Td。根据相邻2次迭代中全局最优值的变化大小ΔF进行滞步状态的判定。
| $\begin{gathered}\Delta F=F\left(p_{\mathrm{g}}(t)\right)-F\left(p_{\mathrm{g}}(t-1)\right)< \\ \frac{F\left(p_{\mathrm{g}}(t)\right)}{20}\left(1-\exp \left(-T_{\mathrm{r}} /T_{\mathrm{d}}\right)\right) .\end{gathered}$ | (6) |
当式(6)成立时视为进入了滞步状态。
未进入滞步状态时,根据下列公式更新粒子群中每个粒子的参数:
| $\begin{gathered}p_i(t)=\left(\alpha_i(t), \beta_i(t), \gamma_i(t), \right. \\ \left.x_i(t), y_i(t), z_i(t)\right) ;\end{gathered}$ | (7) |
| $p_i(t+1)=v_i(t+1)+p_i(t);$ | (8) |
| $\begin{gathered}v_i(t+1)=\omega_i(t) \cdot v_i(t)+ \\ c_{1 i}(t) \cdot\left(p_{i \mathrm{~b}}(t)-p_i(t)\right) \cdot r_{1 i}(t)+ \\ c_{2 i}(t) \cdot\left(p_{\mathrm{g}}(t)-p_i(t)\right) \cdot r_{2 i}(t) ;\end{gathered}$ | (9) |
| $v_i(0)=p_i(0) \cdot r_i(0) ;$ | (10) |
| $p_{i b}(t)=\operatorname{argmin}\left(F_i(0), F_i(1), \cdots, F_i(t)\right) ;$ | (11) |
| $p_{\mathrm{g}}(t)=\operatorname{argmin}\left\{\begin{array}{c}F\left(p_{1 \mathrm{b}}(t)\right), \\ F\left(p_{2 \mathrm{b}}(t)\right), \\ \vdots \\ F\left(p_{N\mathrm{b}}(t)\right) .\end{array}\right\}.$ | (12) |
其中:vi(t)表示粒子i在第t次迭代时的速度值,vi(0)表示粒子i初始化的速度值,ωi(t)表示粒子i在第t次迭代时的惯性系数,pib(t)和pg(t)分别表示第t次迭代过程中粒子i的个体历史最优参数,以及粒子群p在t次迭代下的全局历史最优参数,c1i(t)和c2i(t) 分别表示t次迭代时针对于pib(t)和pg(t)的学习系数,r1i(t)和r2i(t)分别表示粒子i在t次迭代时针对于2个学习参数所取的0~1之间的随机数,ri(0)表示粒子i第0次迭代所取的0~1之间的随机数。
本文中,
| $\begin{gathered}\omega_i(t)=1-\exp \left(-\frac{F_i(t)}{0.1 T}\right), \\ c_{1 i}(t)=2-\exp \left(\frac{F\left(p_{i \mathrm{~b}}(t)\right)-F_i(t)}{0.05 T}\right), \\ c_{2 i}(t)=2-\exp \left(\frac{F\left(p_{\mathrm{g}}(t)\right)-F_i(t)}{0.05 T}\right) .\end{gathered}$ | (13) |
针对于因速度更新而导致pi(t)超出搜索范围限制的情况,将对超出范围的参数在允许范围内重新随机采样。旋转参数(αi(t), βi(t), γi(t))的允许范围为(-π, π),平移参数(xi(t), yi(t), zi(t))的允许范围在每次迭代后更新,为使用(αi(t), βi(t), γi(t))构建旋转矩阵旋转配准点云后,理论数模点云在X、Y、Z三个方向上的极值与旋转后配准点云的对应极值之差。
当滞步状态大于3次时,对一定比例粒子速度函数进行调整。即:
| $\omega_i(t)=\ln \left(0.1 T_{\mathrm{s}}+1\right)\left(1-\exp \left(-\frac{F_i(t)}{0.1 T}\right)\right) r_{\mathrm{s} i}(t).$ | (14) |
其中,Ts表示进入滞步状态的次数,rsi(t)表示粒子i在t次迭代时所取的—1~1之间的随机数。新增的滞步系数增大了惯性系数取值范围并引入随机数增加全局搜索能力,有助于飞跃局部收敛。与此同时,分别对一定比例的粒子绕着主成分分析(principal component analysis, PCA)计算出的扫描点云三个主方向进行旋转扰动。扰动角为(0, π)内随机取值以增加粒子多样性,同时防止错误位姿匹配而陷入局部最优。
3.3 类梯度下降运算与适应度离群值剔除在粒子群算法进行点云配准的过程中,旋转参数和平移参数(αi(t), βi(t), γi(t), xi(t), yi(t), zi(t))往往同时发生变化,从而影响Fi(t)的计算。为了对全局最优粒子进行更为精细化的参数迭代更新,采用类梯度下降运算对单个参数进行微量调整。针对pg(t)的6个参数分别进行微调如下:
针对旋转角,
| $\begin{gathered}\Delta v_{\mathrm{g}, \mathrm{r}}(t)=\Delta p_{\mathrm{g}, \mathrm{r}}(t) \cdot\left(1-\exp \left(-T_{\mathrm{r}} /T_{\mathrm{d}}\right)\right) \cdot \\ r_{\mathrm{d} 1}(t)+2 \times 10^{-4} \times F_{\mathrm{g}}(t) \cdot r_{\mathrm{d} 2}(t) .\end{gathered}$ | (15) |
若Δvg(t)>π, 则Δvg(t)=10-5·Fg(t)·rd(t)。
针对平移量,
| $\begin{gathered}\Delta v_{\mathrm{g}, \mathrm{t}}(t)=\Delta p_{\mathrm{g}, \mathrm{t}}(t) \cdot\left(1-\exp \left(-T_{\mathrm{r}} /T_{\mathrm{d}}\right)\right) \cdot \\ r_{\mathrm{d} 3}(t)+0.2 \times F_{\mathrm{g}}(t) \cdot r_{\mathrm{d} 4}(t) .\end{gathered}$ | (16) |
其中:Δvg, r(t)和Δvg, t(t)分别表示在第t次迭代下对旋转角和平移量的微动量,Δpg, r(t)和Δpg, t(t)分别表示全局最优粒子的旋转角和平移量参数上一次改变时的变换量,rd1(t), rd2(t), rd3(t), rd4(t), rd(t)均表示全局最优粒子在t次迭代下的0~1之间的随机数。以此为根据构建了三水平度独立参数正交试验来缩减计算次数,通过直观分析法反复测试后找到使适应度函数值减小最快的粒子参数变化趋势。
使用如上包括类梯度下降运算在内的方法更新粒子参数后,需要对适应度进行计算。由于筛盘等后景点云的影响,为剔除杂质点对适应度Fi(t)计算产生的影响,根据正态分布针对杂质比例设定置信度剔除适应度离群值。若应用粒子的转换参数进行变换后,个别配准点云上的点到理论数模的最近距离太远,则在计算适应度时剔除掉这些离群点以表示整体的匹配效果。即若式(17)成立,则剔除掉配准点云上的k点。
| $f_i^k(t)-F_i(t)>n_{\mathrm{C}} \cdot \sqrt{\frac{1}{n_{\mathrm{f}}-1} \sum\limits_{k=1}^{n_{\mathrm{f}}}\left(f_i^k(t)-F_i(t)\right)^2}.$ | (17) |
其中:nC表示根据杂质点数量设定的置信度系数,nf表示用于计算适应度的点数量,初始值等于配准点云的个数且随着剔除不断递减。重复上述过程,直至不再有点超出置信度区间。
根据计算后的适应度值更新粒子的个体历史最优值与粒子群的全局历史最优值。重复迭代过程直到达到期望配准精度或者达到迭代次数上限,记录具有全局最优值粒子的参数生成转换矩阵并求逆,作为理论数模点云到实际扫描点云的转换矩阵。最终实现了繁杂零件的检测、识别与定位。
4 实验分析与讨论以下实验中筛盘的长×宽尺寸为1.8 m×0.9 m,零件为多种类、多尺寸民机航空零件。计算所用工控机的参数为:Intel X-eon W1290 3.2 GHz CPU,32 G DDR4内存,Windows 10操作系统。软件使用C++语言的PCL 1.10和OpenCV 4.40在Visual Studio 2019环境下进行编译。软件界面如图 4所示。
|
| 图 4 软件界面 |
在本文中,粗配准迭代次数上限为25次,精配准迭代次数为100次,配准点云为分割后的扫描点云中抽样的100个点,PSO粒子数为100个。实际零件的扫描点云通常会出现残缺不全的情况,使得随机选取的配准点云并不能总是准确描述零件的总体特征,导致零件配准精度较差。因此置信度系数为2,根据正态分布2σ水平剔除适应度离群值。
民机的零件繁杂多样且多为钣金件或表面反光的零件。本文围绕分割过程中有较多杂质点、拍摄点云因反光等问题使扫描点云不全的零件, 以民机的机械加工零件(见图 3)为例进行分析,其3D点云扫描结果如图 5所示,左、右图分别为后景去除前、后的状态。该示例零件能够反映生产环境中零件的共性,对应的理论数模点云如图 6所示,由图可知,理论数模点云是在飞机的基坐标系上,而扫描点云数据是在测量坐标系上,与扫描点云相距甚远且姿态差异较大。
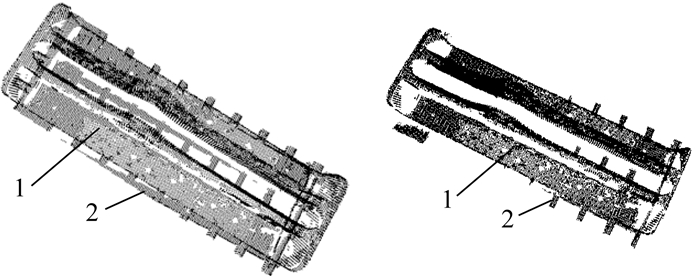
|
| 1—零件扫描点云 2—后景点云 图 5 示例零件的3D点云扫描结果(左、右图分别为后景去除前、后) |

|
| 图 6 示例零件的理论数模3D点云 |
4.1 各优化算法应用扰动粒子比例分析
为防止算法陷入局部最优,针对部分粒子本文采用应用滞步系数、进行大幅度扰动或二者叠加的方式;为节省配准时间并提高配准精度,将部分粒子继承同种零件粗配准所得Euler角作为初始旋转角。以示例零件为例,对每个优化算法应用的粒子比例进行分析。
该实验的步长为10%,每种算法优化方式所应用粒子的比例分别为0%,10%,20%,…,100%,共计11个水平。3种优化方式采取控制变量法进行实验,每个水平计算3次,共计进行3 993次实验。使用SPSS软件对实验结果进行方差分析,主体间效应检验结果如表 1所示。当显著性小于0.050时,认为对应因子的变化在0.050的水平下具有统计学意义,由表可知,示例零件的配准精度受到继承Euler角、应用滞步系数、大幅度扰动的应用比例的单独影响,还受到继承Euler角与大幅度扰动应用比例的交互作用的影响。
| 优化方式 | 状态数 | 均方 | F检验值 | 显著性 |
| 继承Euler角 | 10 | 34.816 | 32.673 | 0.000 |
| 应用滞步系数 | 10 | 7.632 | 7.162 | 0.000 |
| 大幅度扰动 | 10 | 126.675 | 118.876 | 0.000 |
| 继承Euler角×应用滞步系数 | 100 | 0.794 | 0.746 | 0.972 |
| 继承Euler角×大幅度扰动 | 100 | 1.396 | 1.310 | 0.023 |
| 应用滞步系数×大幅度扰动 | 100 | 1.172 | 1.100 | 0.237 |
| 继承Euler角×应用滞步系数×大幅度扰动 | 1 000 | 0.740 | 0.695 | 1.000 |
| 注:×表示同时优化多个参数 | ||||
对于不同比例的粒子应用滞步系数后,示例零件配准精度估算边际平均值如图 7所示。由图可知,随着应用滞步系数的粒子比例增加,示例零件的配准精度估算边际平均值前半段总体呈下降趋势;当对60%的粒子应用滞步系数后,估算边际平均值开始产生波动。综合考虑配准精度和粒子多样性,对60%的粒子应用滞步系数。
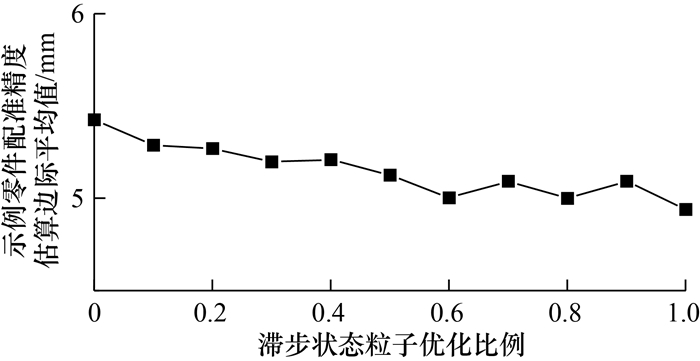
|
| 图 7 示例零件配准精度估算边际平均值随粒子优化(应用滞步系数)比例的变化 |
继承Euler角与大幅度扰动两者的应用比例交互作用影响下,示例零件配准精度估算边际平均值3D视图如图 8所示。由图可知,在继承Euler角与大幅度扰动的交互作用下,示例零件配准精度估算边际平均值发生剧烈变化。其在继承Euler角粒子占比为20%,大幅度扰动粒子占比20%时达到最小值, 对应图中底侧中央的黑点。
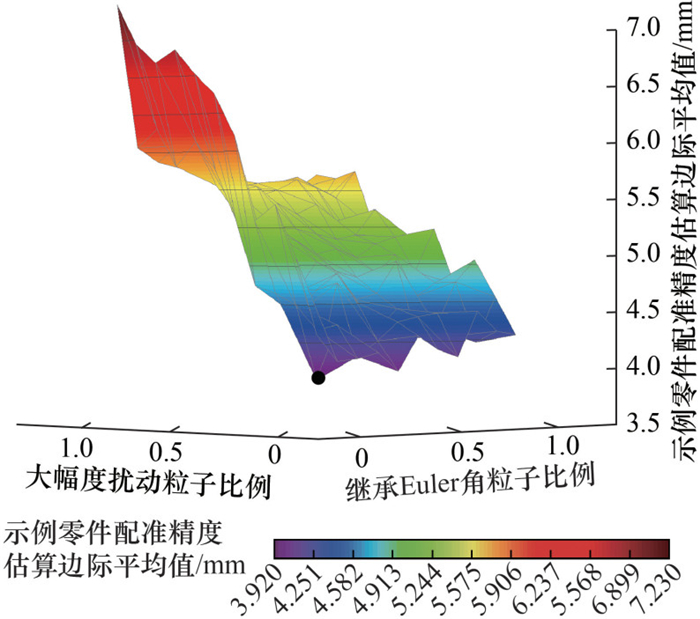
|
| 图 8 示例零件配准精度估算边际平均值3D视图 |
因此,对20%的PSO粒子继承同类零件粗配准Euler角,对60%的PSO粒子引入滞步系数,对20%的PSO粒子施加大幅度扰动,是兼顾零件定位精度以及配准效率的最佳参数组合。
4.2 多种类零件配准效果分析为验证应用优化措施应用粒子占比的匹配效果,特在一个筛盘上的不同位置摆放9种大小、颜色、形状均不同的零件各一个, 以验证算法鲁棒性。其2D图像检测效果如图 3所示,可以看出2D图像处理能够将零件准确分割;3D点云扫描结果与配准结果如图 9所示。虽然3D点云有很强的背景点云(网格筛盘)干扰,但自动分割后的扫描点云基本包络重构零件,展现了优良的配准效果。

|
| 图 9 3D点云扫描与配准结果 |
由于本算法存在一定的随机性,因此对配准精度进行Grubbs法双边异常值检验,显著性水平为0.050。剔除异常值后,9种不同零件在100次测试中保留有85次数据,其配准精度均值、标准差等信息如表 2所示。
| 序号 | 平均值/mm | 标准差/mm | 最小值/mm | 最大值/mm | Grubbs检验统计量 |
| 1 | 0.5977 | 0.1118 | 0.4550 | 0.9547 | 3.19 |
| 2 | 0.6081 | 0.0953 | 0.4702 | 0.8799 | 2.85 |
| 3 | 2.9985 | 0.4539 | 1.7586 | 3.9221 | 2.73 |
| 4 | 0.6989 | 0.0523 | 0.6107 | 0.8595 | 3.07 |
| 5 | 0.5352 | 0.0405 | 0.4783 | 0.6466 | 2.75 |
| 6 | 0.8695 | 0.2141 | 0.5399 | 1.4807 | 2.85 |
| 7 | 3.8750 | 0.9410 | 2.0060 | 6.0530 | 2.31 |
| 8 | 1.5810 | 0.3348 | 1.0946 | 2.4810 | 2.69 |
| 9 | 0.8352 | 0.1266 | 0.6298 | 1.2366 | 3.17 |
基于上述85次数据,分析了整盘零件的配准精度。如图 10所示,可以看出零件的配准精度均值为1.40 mm,均值95%置信区间为1.43~1.39 mm,整盘零件的平均配准精度有99.73%的概率在1.00~1.80 mm的范围内。这表明该系统对于多种大小、形状、颜色不同的零件均具有较强的鲁棒性。
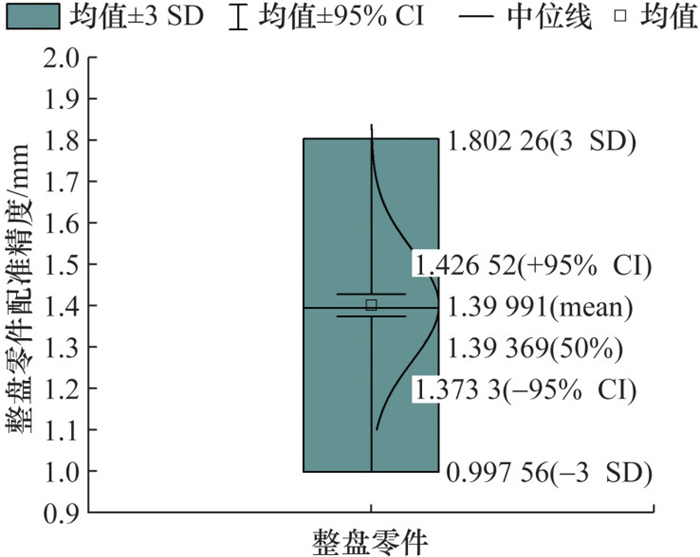
|
| 图 10 整盘零件平均配准精度箱线图 |
4.3 实际应用效果分析
在实际零件喷涂生产中,相同的零件通常尽量摆放在同一个筛盘上,筛盘上大多只摆放3~5种零件。由于精拍摄的幅数只与零件的种类相关,因此平均扫描时间的长度随着零件种类的增加而延长。配准时间同时受零件种类和数量的影响,因此出现了不同程度的波动。但由于零件数未超过CPU线程数,总平均配准时间稳定在2.5 min左右。本系统可以在3 min的节拍内完成3D点云的扫描,在2.5 min左右的节拍内实现多种繁杂零件的自动化配准且总平均精度为2.05 mm,能够满足自动化喷涂流水线的生产节拍和精度需求。
5 算法对比与优化效果分析进一步验证算法配准效果和各种措施的优化效果。本节中的计算均不继承粗配准所得的Euler角;示例零件分别对60%的PSO粒子引入滞步系数,对20%的PSO粒子施加大幅度扰动,使用类梯度下降运算并剔除离群适应度。运算得到的“迭代-适应度”配准曲线如图 11所示。由图可知,迭代100次后全局最优PSO粒子适应度由最初的12.57 mm降为3.17 mm, PSO粒子平均适应度由最初的41.14 mm降为8.73 mm;同时,算法具有短时间高响应的特点,且持续波动下行。当适应度长时间未随迭代进行变化时(如图中阶梯平稳处),滞步系数增加了全局最优搜索能力,大范围扰动使粒子参数阶跃,例如当粒子旋转参数产生大幅度变化时(如图 12中迭代8次时)。当迭代全局最优PSO粒子适应度下降而粒子参数仅有微小变化时,即类梯度下降运算产生的微动使粒子处于最优状态附近时,仍能振荡收敛于更优状态。由此可见上述措施均具有显著作用。
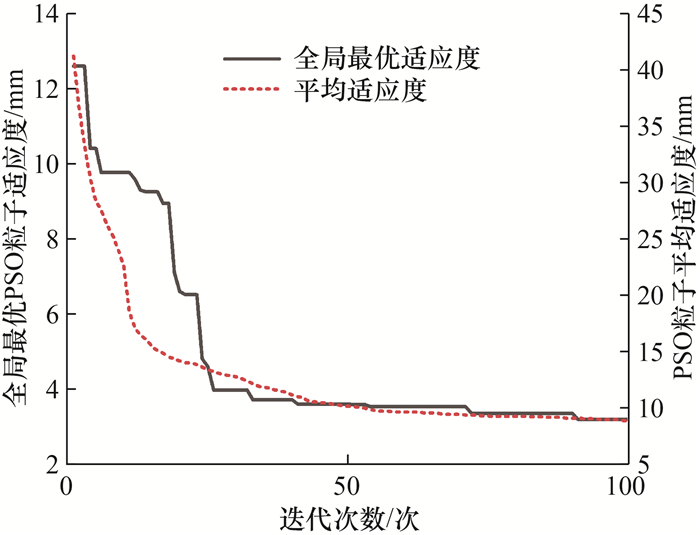
|
| 图 11 示例零件全局最优PSO粒子适应度随迭代次数的变化 |
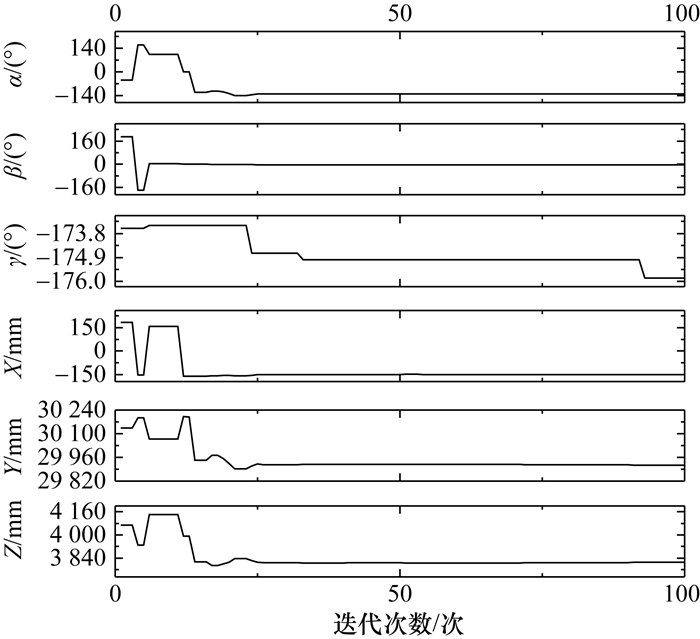
|
| 图 12 示例零件全局最优PSO粒子的旋转矩阵参数随迭代次数的变化 |
为独立地分析各措施产生的影响,针对机械加工零件使用控制变量法进行对比实验。即每次分析只针对于单个措施进行更改,其他保持优化算法不变。
5.1 应用滞步系数未应用滞步系数时,由于PSO算法的限制,很可能出现局部最优的情况。对60%的POS粒子应用滞步系数前后的“迭代次数-粒子适应度”变化曲线如图 13a所示。由图可知,曲线呈波动下降趋势且单次下降幅度较小,表明粒子的搜索能力较本算法有明显差距,算法的迭代收敛主要依靠类梯度下降运算。由PSO粒子平均适应度曲线的变化可知,尽管未应用滞步系数的粒子仍在向全局最优的位姿迭代,但最终的配准结果比引入滞步系数的存在超过2 mm的差距。这表明相同迭代次数下引入滞步系数后算法的响应能力更优。因此,当全局最优值的收敛速度连续多次低于预期的收敛速度时,将部分粒子的惯性系数乘滞步次数能够尽快跳出局部收敛状态。

|
| 图 13 优化措施前后的“迭代次数-粒子适应度”变化曲线对比 |
5.2 进行大幅度扰动
当算法较长时间处于滞步状态时,对20%的PSO粒子施加大幅度扰动前后的“迭代次数-粒子适应度”变化曲线如图 13b所示。由图可知,未进行大幅度扰动时,尽管收敛曲线波动下降展示了滞步系数与类梯度下降运算的性能,但仍旧缺乏强力脱离局部最优措施。相同迭代次数下,最终的配准适应度比施加大幅度扰动的存在约2 mm的差距。
5.3 使用类梯度下降运算已经达到近似处于全局收敛的PSO粒子仅需要改变其在算法中的部分参数,而粒子的6个参数变化速度在每次迭代中会同时改变。如图 13c所示,未使用类梯度下降运算时的由全局最优PSO粒子适应度下降速度比使用后慢,算法缺乏最速下降方向的指导。相同迭代次数下,未使用运算的最终配准适应度比使用的存在约1.5 mm差距。
5.4 剔除适应度离群值在实际应用中,即使通过滤波、聚类等方案进行了噪点去除,也无法使所有的零件从筛盘点云背景中完全独立出来。若不剔除适应度离群值,则算法无法准确描述匹配点云的主体,其中包含的噪点将严重影响匹配的效率与精度。如图 13d所示,全局最优PSO粒子适应度虽然下降,但到一定程度后速度变缓最后完全停滞。说明噪点的存在导致PSO粒子向着错误的方向迭代。由于配准方向错误,最后的全局最优适应度比剔除适应度离群值的结果存在约3 mm差距。
5.5 多次配准下各优化措施效果分析为了验证各优化措施在多次配准下的优化效果,对示例零件在不同情况下进行了10次配准,结果如表 3所示。可以看到对精度而言,滞步系数对于算法配准有1.6 mm的均值优化,大范围扰动仅有0.1 mm的均值优化但有超过0.4 mm的标准差优化,类梯度下降运算有0.2 mm的优化但同样有接近0.4 mm的标准差优化,离群适应度剔除有接近1.4 mm的均值优化。
| mm | |||||||||||||||||||||||||||||
| 缺少的优化措施 | 平均值 | 标准差 | 最小值 | 最大值 | |||||||||||||||||||||||||
| 无 | 4.010 | 0.965 | 2.920 | 5.696 | |||||||||||||||||||||||||
| 应用滞步系数 | 5.626 | 0.615 | 4.852 | 6.904 | |||||||||||||||||||||||||
| 进行大范围扰动 | 4.115 | 1.387 | 2.606 | 6.538 | |||||||||||||||||||||||||
| 使用类梯度下降 | 4.294 | 1.323 | 2.646 | 6.448 | |||||||||||||||||||||||||
| 剔除离群适应度 | 5.387 | 1.397 | 2.732 | 7.242 | |||||||||||||||||||||||||
5.6 不同算法配准效果对比
在本节中,使用与5.1节相同的机械加工零件点云作为配准目标点云,以理论数模点云作为待配准点云。使用已有的标准PSO算法、3Dsc算法、FPFH算法、PFH算法与本文算法进行配准结果的对比,结果如图 14所示,图中标记1为理论数模点云,标记2为扫描所得零件点云。由图可知,上述对比算法相较于本算法具有显著的匹配误差。
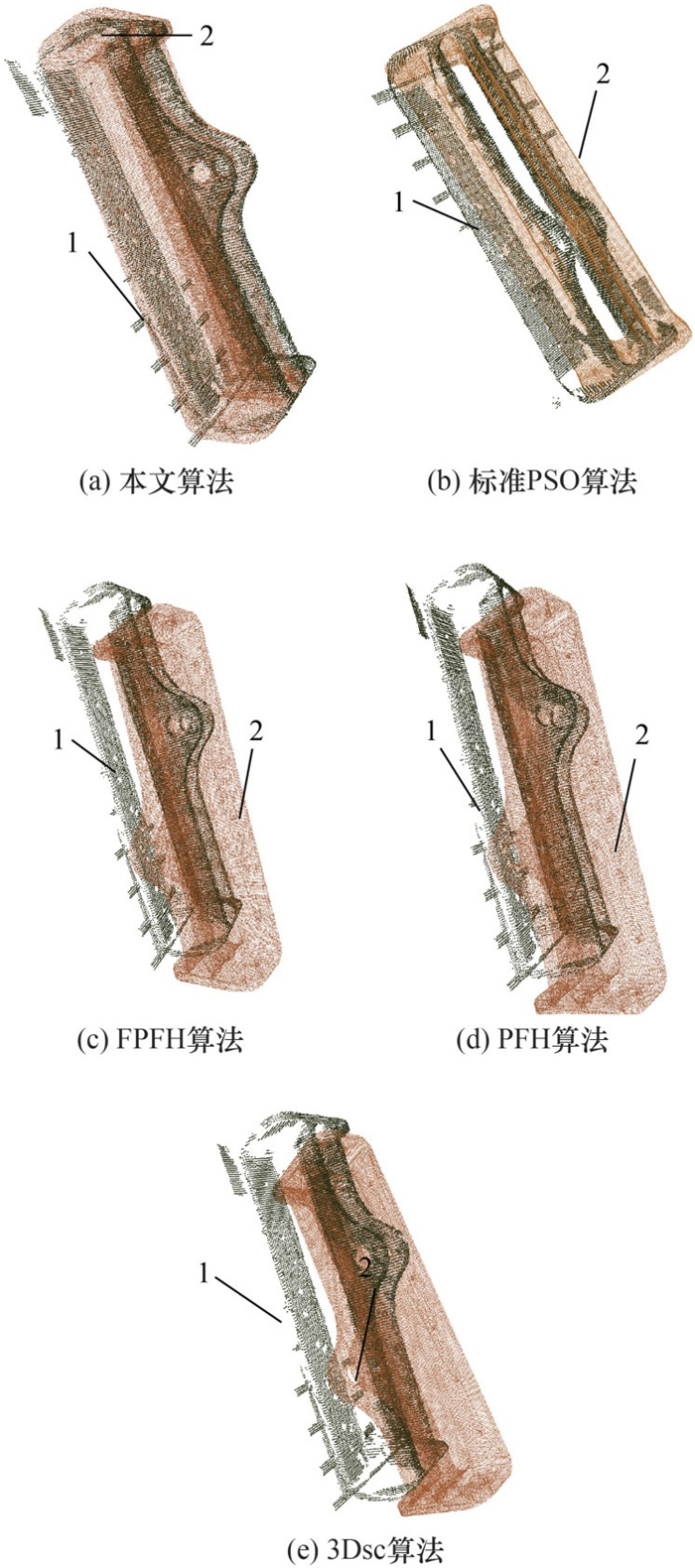
|
| 1—示例零件扫描点云 2—示例零件理论数模点云 图 14 示例零件不同算法配准效果图 |
进一步采用常用的均方差(mean square error, MSE)指标进行配准效果对比,如表 4可知,针对3次平均MSE指标,本文算法比标准PSO算法、PFH算法、FPFH算法与3Dsc算法分别有52.30%、39.76%、19.83%与11.92%的优化。
| 算法类别 | 配准后MSE/mm2 | 3次平均MSE/mm2 | ||
| 1 | 2 | 3 | ||
| 本文算法 | 47.932 | 48.584 | 55.076 | 50.531 |
| 标准PSO | 89.815 | 145.47 | 82.536 | 105.94 |
| PFH | 81.24 | 86.05 | 84.36 | 83.88 |
| FPFH | 66.09 | 62.26 | 60.75 | 63.03 |
| 3Dsc | 54.55 | 59.11 | 58.45 | 57.37 |
6 结论
为实现综合满足加工效率与精度的零件定位,本文将点云配准所需的3个平移参数以及3个旋转参数作为广义粒子维度,应用基于自适应启发改进的粒子群算法,实现了较强后景影响下快速地点云配准。为解决粒子群算法收敛速度缓慢与易陷入局部最优问题,在应用随配准状态自适应的学习系数与惯性系数基础上,从局部搜索与全局搜索两方面进行优化。基于正态分布置信度准则剔除适应度离群值降低了后景点云对配准的影响。经过实验与分析可以得到以下结论:
1) 针对示例零件的配准过程,在精度方面,滞步系数与离群适应度剔除对于算法配准有超过1 mm的均值优化,大范围扰动增加粒子多样性与类梯度下降运算在均值上优化较小,但具有约0.4 mm标准差优化。
2) 应用二维(2D)视觉减少测量时间、提供点云分割的依据,并多线程并发同步运算提高效率。在实际零件的测试中,能够在平均2.5 min节拍内实现整筛盘平均2 mm精度的多种零件自主配准定位。
3) 在针对同一片点云进行配准时,算法具有0.002 mm配准精度。尽管算法在具有强烈后景点云影响的情况下具有一定的鲁棒性,但配准精度仍受到较大影响。除此之外,本文中扫描点云与理论数模点云的采样一致性差异造成了约0.5 mm的固有误差也限制了配准精度的进一步提升。
本文实现了流水线生产线环境下,随机摆放航空零件的自动识别与定位,满足喷涂的定位精度与节拍要求。但一些特征少、尺寸小的航空零件容易误识别、姿态配准误差大,还需进一步深度结合2D图像、三维(3D)点云数据的优势,增强航空零件识别定位的鲁棒性。
| [1] |
WANG R Y, TANG L W, TANG T. Fast sample adaptive offset jointly based on HOG features and depth information for VVC in visual sensor networks[J]. Sensors, 2020, 20(23): 6754. DOI:10.3390/s20236754 |
| [2] |
张慧, 王坤峰, 王飞跃. 深度学习在目标视觉检测中的应用进展与展望[J]. 自动化学报, 2017, 43(8): 1289-1305. ZHANG H, WANG K F, WANG F Y. Advances and perspectives on applications of deep learning in visual object detection[J]. Acta Automatica Sinica, 2017, 43(8): 1289-1305. (in Chinese) |
| [3] |
赵继, 赵军, 张雷, 等. 焊缝磨抛机器人视觉算法实现及其试验研究[J]. 机械工程学报, 2013, 49(20): 42-48. ZHAO J, ZHAO J, ZHANG L, et al. Vision algorithm and experimental study on the robotic weld-bead grinding and polishing system[J]. Journal of Mechanical Engineering, 2013, 49(20): 42-48. (in Chinese) |
| [4] |
AOKI Y, GOFORTH H, SRIVATSAN R A, et al. PointNet LK: Robust & efficient point cloud registration using pointnet [C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Los Alamitos, USA: IEEE, 2019: 7163-7172.
|
| [5] |
LU W X, WAN G W, ZHOU Y, et al. Deep VCP: An end-to-end deep neural network for point cloud registration [C]//Proceedings of 2019 IEEE/CVF International Conference on Computer Vision. Seoul, Korea (South): IEEE, 2019: 12-21.
|
| [6] |
WANG Y, SOLOMON J. Deep closest point: Learning representations for point cloud registration [C]//Proceedings of 2019 IEEE/CVF International Conference on Computer Vision. Seoul, Korea (South): IEEE, 2019: 3523-3532.
|
| [7] |
CHARLES R Q, SU H, KAICHUN M, et al. PointNet: Deep learning on point sets for 3D classification and segmentation [C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE: 2017: 77-85.
|
| [8] |
LI J H, ZHANG C H, XU Z Y, et al. Iterative distance-aware similarity matrix convolution with mutual-supervised point elimination for efficient point cloud registration [C]//Proceedings of the 16th European Conference on Computer Vision. Glasgow, UK: Springer, 2020: 378-394.
|
| [9] |
YEW Z J, LEE G H. RPM-Net: Robust point matching using learned features [C]//Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle, USA: IEEE, 2020: 11824-11833.
|
| [10] |
BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 |
| [11] |
YANG J L, LI H D, CAMPBELL D, et al. Go-ICP: A globally optimal solution to 3D ICP point-set registration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(11): 2241-2254. DOI:10.1109/TPAMI.2015.2513405 |
| [12] |
YANG J L, LI H D, and JIA Y D. Go-ICP: Solving 3D registration efficiently and globally optimally [C]//Proceedings of the 2013 IEEE International Conference on Computer Vision. Los Alamitos: IEEE, 2013: 1457-1464.
|
| [13] |
FROME A, HUBER D, KOLLURI R, et al. Recognizing objects in range data using regional point descriptors [C]//Proceedings of the 8th European Conference on Computer Vision. Prague, Czech Republic: Springer, 2004: 224-237.
|
| [14] |
RUSU R B, BLODOW N, MARTON Z C, et al. Aligning point cloud views using persistent feature histograms [C]//Proceedings of 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice, France: IEEE, 2008: 3384-3391.
|
| [15] |
RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration [C]//Proceedings of 2009 IEEE International Conference on Robotics and Automation. Kobe, Japan: IEEE, 2009: 3212-3217.
|
| [16] |
YANG Y, Chen W L, Wang M Y, et al. Color point cloud registration based on supervoxel correspondence[J]. IEEE Access, 2020, 8: 7362-7372. DOI:10.1109/ACCESS.2020.2963987 |
| [17] |
JUNG S, SONG S, CHANG M, et al. Range image registration based on 2D synthetic images[J]. Computer-Aided Design, 2018, 94: 16-27. DOI:10.1016/j.cad.2017.08.001 |
| [18] |
ZENG A, SONG S R, NIEBNER M, et al. 2017. 3D match: Learning local geometric descriptors from RGB-D reconstructions [C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA: IEEE. 2017: 199-208.
|
| [19] |
E A, SEKIKAWA Y, ISHIKAWA K, et al. CorsNet: 3D point cloud registration by deep neural network[J]. IEEE Robotics and Automation Letters, 2020(3): 3960-3966. |
| [20] |
KENNEDY J, EBERHART R. Particle swarm optimization [C]//Proceedings of the ICNN'95- International Conference on Neural Networks. Perth, Australia: IEEE, 1995: 1942-1948.
|
| [21] |
GE Y Q, WANG B Y, NIE J H, et al. A point cloud registration method combining enhanced particle swarm optimization and iterative closest point method [C]//Proceedings of 2016 Chinese Control and Decision Conference. Yinchuan, China: IEEE, 2016: 2810-2815.
|
| [22] |
韩贤权, 朱庆, 丁雨淋, 等. 散乱点云数据精配准的粒子群优化算法[J]. 武汉大学学报(信息科学版), 2014, 39(10): 1214-1220. HAN X Q, ZHU Q, DING Y L, et al. Precise registration of scattered cloud data based on the particle swarm optimization[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1214-1220. (in Chinese) |
| [23] |
潘峰, 陈杰, 甘明刚, 等. 粒子群优化算法模型分析[J]. 自动化学报, 2006, 32(3): 368-377. PAN F, CHEN J, GAN M G, et al. Model analysis of particle swarm optimizer[J]. Acta Automatica Sinica, 2006, 32(3): 368-377. (in Chinese) |
| [24] |
张顶学, 关治洪, 刘新芝. 一种动态改变惯性权重的自适应粒子群算法[J]. 控制与决策, 2008, 23(11): 1253-1257. ZHANG D X, GUAN Z H, LIU X Z. Adaptive particle swarm optimization algorithm with dynamically changing inertia weight[J]. Control and Decision, 2008, 23(11): 1253-1257. (in Chinese) |
| [25] |
王俊伟, 汪定伟. 一种带有梯度加速的粒子群算法[J]. 控制与决策, 2004(11): 1298-1300, 1304. WANG J W, WANG D W. Particle swarm optimization algorithm with gradient acceleration[J]. Control and Decision, 2004(11): 1298-1300, 1304. (in Chinese) |



