2. 清华大学 机械工程系,高端装备界面科学与技术全国重点实验室,北京 100084;
3. 成都市排水有限责任公司 物资设备中心,成都 610039
2. State Key Laboratory of Tribology in Advanced Equipment, Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China;
3. Chengdu Drainage Co., Ltd., Material Equipment Center, Chengdu 610039, China
在航空航天等领域的关键设备中,密封是影响工作效率和使用寿命的关键因素之一,密封不严密造成的设备效率降低甚至故障将会导致巨大损失[1-2]。迷宫密封作为转轴密封的主要形式,具有结构简单、拆装方便及可承受高压等苛刻工作条件等优点,被广泛应用于离心式压缩机、航空发动机和膨胀透平机等旋转机械[3-4]。迷宫密封一旦存在固定间隙就会产生一定泄漏,并且工作过程中由转轴高速旋转产生的振动、温升等会导致迷宫密封变形和磨损,这将进一步增加间隙,引起额外泄漏。因此,研究如何减少迷宫密封泄漏量具有重要意义[5-8]。
泄漏量是评价迷宫密封性能最主要的指标之一。最初,基于气体在流道内流动的热力学分析计算泄漏量,并通过简化的条件和提出的假设推导了迷宫密封泄漏公式,泄漏公式中通常加入修正系数,该修正系数通过试验获得,通常被称为经验公式。对于迷宫密封流场及泄漏量的计算,早期较经典的公式是Egli[9]提出的采用热力学方程计算迷宫密封泄漏量的Egli公式。但是该公式主要基于理想迷宫的假设,即气体由空腔进入间隙后全部静压能转化为动能,并且气体由间隙再流入空腔后全部动能转化为静压能。其后,诸多学者在迷宫密封泄漏量计算方面做了许多改进,但是大部分都基于Egli公式发展而来。经验公式虽然计算简便、快捷,但是均基于宏观角度分析迷宫密封内部气体能量转化,具有局限性。此外,经验公式的许多系数都需要通过试验确定,极大地限制了经验公式的适用范围。
随着计算机计算能力提升,采用有限差分法和有限元法等数值计算方法研究迷宫密封泄漏量成为主流[10-13]。数值计算方法不仅可以计算迷宫密封泄漏量,还可以获得迷宫密封内部流场特征,这为分析新型结构的迷宫密封奠定了坚实的理论基础。随着计算流体动力学(computational fluid dynamics,CFD)数值计算方法被广泛应用于计算迷宫密封内部流场后,气体在迷宫密封内部流动的问题得到了较好的解决。文[14-17]在研究影响迷宫密封性能的因素时,考虑了密封齿结构、空腔形状和尺寸、介质流动方向等新因素。丁学俊等[18]采用CFD软件计算迷宫密封流场,研究了不同转速、密封间隙、密封长度和压差对泄漏量的影响,结果表明:密封间隙是影响泄漏量的最主要因素,增加密封长度有利于减小泄漏量。巴鹏等[19]通过对迷宫密封内部流场进行有限元仿真发现,虽然空腔面积对泄漏量的影响较大,但是当空腔面积达到一定程度时,其对泄漏量的影响将降为零。Whalen[20]等发现,与直通式迷宫密封结构相比,斜齿结构具有更小的泄漏量。
多样化结构和复杂实际工况使迷宫密封内部的气体流动和换热变得十分复杂。同时,影响迷宫密封泄漏量的因素较多,但大部分研究均基于单因素分析,并且假设密封长度随几何参数变化而发生改变。在实际工程应用中,密封长度为固定长度,若增加齿距和齿厚,则二者会产生交互影响,单因素分析无法准确体现泄漏特性。此外,由迷宫密封能量转化原理可知,空腔宽度和高度均通过改变空腔面积而改变内部气体流动,进而影响泄漏量,上述2项因素也具有交互影响。综上所述,在密封长度固定的情况下,如何避免迷宫密封多种齿形参数交互影响的研究较少。为满足现代旋转机械的发展需求,需要对迷宫密封性能展开更深入的研究。本文基于流场模型研究了迷宫密封的密封机理,通过多个齿形参数和多种齿形结构研究了其泄漏特性。研究成果对指导迷宫密封结构设计具有重要意义。
1 数学模型和几何模型 1.1 数学模型忽略气体重力,密封介质视为可压缩气体,迷宫密封的连续性方程、动量方程和能量方程分别表示如下:
| $ \nabla \rho \boldsymbol{v}=0, $ | (1) |
| $ \nabla \cdot(\rho \boldsymbol{v} \boldsymbol{v})=-\nabla p+\nabla \tau+\boldsymbol{S}_{\mathrm{M}} \text {, } $ | (2) |
| $ \nabla \cdot\left(\rho \boldsymbol{v} h_{\mathrm{tot}}\right)=\nabla \cdot(\lambda \nabla T+\boldsymbol{v} \mathit{\Omega })+\boldsymbol{v} \cdot \boldsymbol{S}_{\mathrm{M}}+S_{\mathrm{E}} . $ | (3) |
其中:▽为nabla算子;ρ为气体密度;v为速度矢量;p为压力;τ为应力张量大小;SM为质量的广义源项,是重力加速度与ρ的乘积;htot为总焓;λ为有效热传导率;T为温度;Ω为应变张量大小;SE为热能(内能)的广义源项。为保证计算精度及稳态结果稳定性,连续性方程、动量方程和能量方程的收敛精度均为1×10-6。
在迷宫密封中,气体在每一级密封间隙处进行加速,整个流动过程是熵增过程,在最后一级密封间隙处,气体速度可能超过声速。基于上述特点,本文采用k-ε湍流模型,湍动能k和能量耗散率ε表示如下:
| $ \nabla \rho k \boldsymbol{v}=\nabla\left(Z+\frac{\mu}{\sigma_k}\right) \nabla k+G_{\mathrm{ki}}+G_{\mathrm{bu}}-\rho \varepsilon-Y+S_k, $ | (4) |
| $ \begin{gathered} \nabla \cdot(\rho \varepsilon \boldsymbol{v})=\nabla\left(\left(Z+\frac{\mu}{\sigma_{\varepsilon}}\right) \nabla \varepsilon\right)+ \\ C_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{\mathrm{ki}}+C_{3 \varepsilon} G_{\mathrm{bu}}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^2}{k}+S_{\varepsilon}, \end{gathered} $ | (5) |
| $ \mu=\rho C_\mu k^2 / \varepsilon. $ | (6) |
其中:Z为气体黏度;μ为湍流黏度;Gki为由平均速度梯度产生的湍动能产生项;Gbu为由浮力产生的湍动能产生项;Y为可压缩湍流脉动对总耗散率的影响;C1ε、C2ε、C3ε和Cμ为经验常数,C1ε= 1.44,C2ε=1.92,C3ε=1.30,Cμ=0.09;σk和σε分别为k和ε的Prandtl常数,σk=1.0,σε=1.3;Sk和Sε分别为k和ε的源项。
1.2 几何模型及网格划分图 1为四齿直通式迷宫密封(齿形为直齿)二维流场模型。在非偏心工况下,可以将三维模型简化为二维模型。四齿直通式结构并不能应用于所有迷宫密封问题分析。因此,在后续计算过程中,将针对不同迷宫密封问题,通过建立多齿数、多种齿形和多种几何参数下的迷宫密封模型研究不同参数对泄漏量的影响。
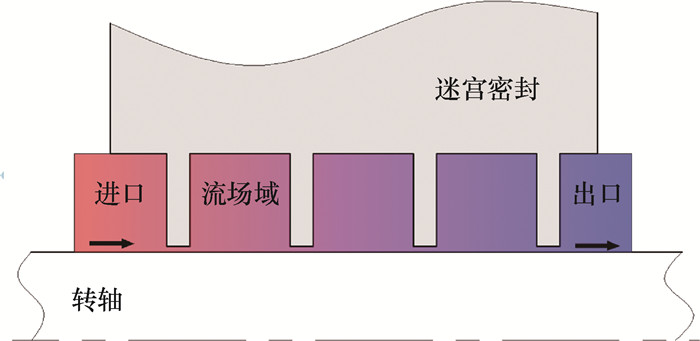
|
| 图 1 四齿直通式迷宫密封二维流场模型 |
迷宫密封内,气体流动区域主要为密封间隙和密封空腔。密封间隙内气体的动能越高,近轴表面气体速度越大,大量气体流经密封间隙时不易进入密封空腔,反而会迅速进入下一级密封间隙,从而降低气体在密封空腔内的热效应,上述现象也称为透气效应,透气效应不利于降低泄漏量。根据透气效应对迷宫密封整体流场域分区,并采用CFD-ICEM软件划分网格,同时在密封间隙和空腔近壁面区域进行网格加密。加密后密封间隙的网格有15层。此外,采用O-Block网格拓扑结构加密密封空腔内的网格,因为实际上气体在密封空腔内流动时主要沿壁面形成涡流。整体流场域网格均采用结构化网格,可以提高计算速度;近壁面y+范围为14.2~20.2,满足FLUENT的标准壁面法则。四齿直通式迷宫密封流场模型网格划分如图 2所示,整体网格质量大于0.9。
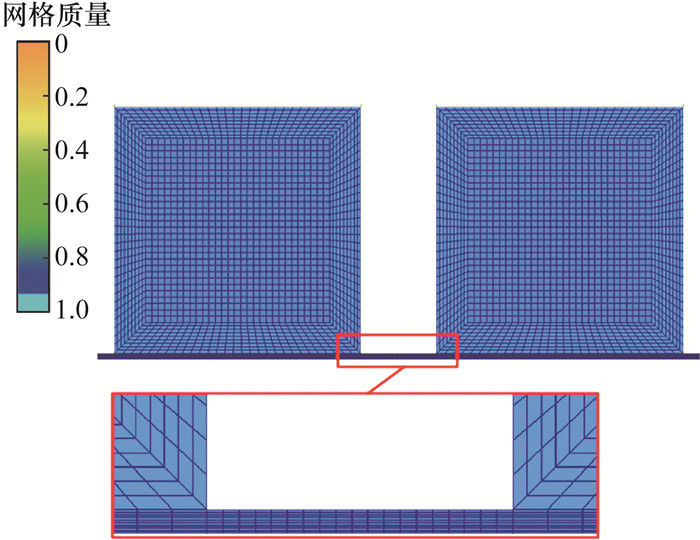
|
| 图 2 四齿直通式迷宫密封流场模型网格划分 |
2 迷宫密封泄漏实验系统
迷宫密封低压实验系统如图 3所示,主要包括电主轴系统、实验密封腔系统、流量测量系统和供气系统4部分。该实验系统可实现最高进气压力为0.6 MPa、实验转速为10 000 r/min的迷宫密封实验工况。实验密封腔内采用完全对称的双迷宫密封设计方式,该方式不仅可以解决气体在实验密封腔内部轴向压力不平衡问题,还可以实现两端实验数据对比并消除实验误差。空气压缩机可提供的最大工作表压为1.2 MPa,体积流量为4.5 m3/min。为防止气体压力在管道内部沿程损失过大,在空气压缩机出口与实验密封腔中间添加体积为1.0 m3的缓冲罐,并在缓冲罐出口安装压力调节阀和过滤阀。
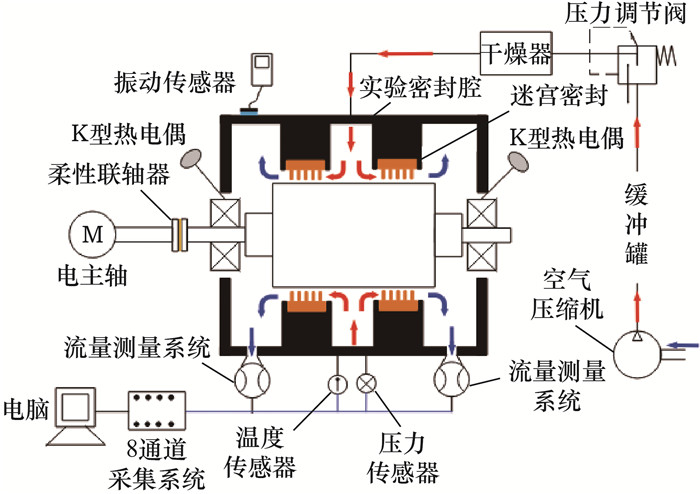
|
| 图 3 迷宫密封低压实验系统示意图 |
电主轴系统实物如图 4所示。电主轴的最大功率为47 kW,电主轴空转时最高转速可达24 000 r/min。采用油气润滑方式润滑电主轴轴承,逸散的油烟通过排油气扇排到外界。为提高输出转速、减小振动,联轴器采用双花键方式,花键连接有较大配合间隙,且允许小范围径向位移。电主轴输出端连接实验密封腔旋转轴,实验密封腔旋转轴最高转速为10 000 r/min。电主轴与实验转子端中间安装非接触扭矩传感器,用于监测转轴扭矩。

|
| 图 4 电主轴系统 |
实验密封腔系统实物如图 5所示,实验密封腔通过定位块安装在实验台架上。高压气体从实验密封腔中部进入,并且在实验密封腔中部布置2个进气口,其目的是使气体进入实验腔内,保持实验密封腔旋转轴的气流压力平衡,防止转轴产生额外振动。在实验过程中,将手持式振动传感器探头吸附在两侧端盖表面,用于测量实验台运转时的振动情况,一旦振动超出预警值就必须立即终止实验。

|
| 图 5 实验密封腔系统 |
进口压力和密封间隙不同,实验密封腔出口泄漏量不同,实验中泄漏量的变化范围为0~1 000 m3/h。若采用一个流量计,则无法满足全部量程的测量。本文设计了一套流量测量系统,如图 6所示。流量测量系统采用多组不同量程精度的流量计,通过串、并联方式进行连接,以此解决量程过大、单个仪表测量精度误差较大的问题。实验密封腔两侧出口的泄漏量分别进入流量测量系统,调节各处球阀,可以选择采用不同量程的流量计测量泄漏量。流量计均采用涡街流量计,该流量计具有温差补偿功能,可以解决由出口压力和温度导致泄漏量测量不准确的问题。为实现气体在出口处能够充分流动,实验中出口均采用DN50管道进行连接。此外,采用多通道采集卡收集所有传感器测量数据,并输出至电脑端,实时监测各个流量计、压力传感器和温度传感器的数据。
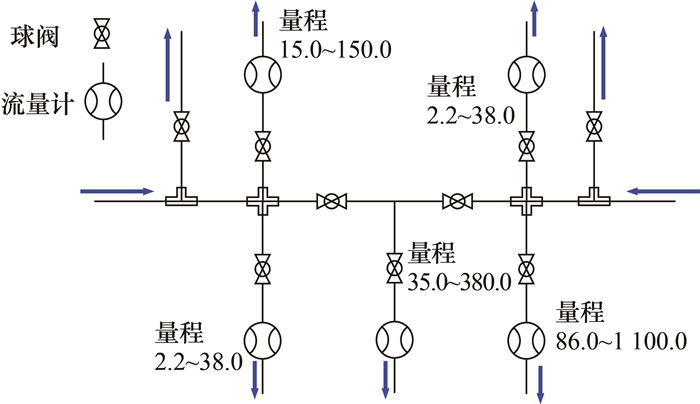
|
| 图 6 流量测量系统(单位:m3/h) |
3 结果与讨论 3.1 压差和转速对泄漏量的影响
四齿直通式迷宫密封(齿形为直齿,密封间隙为0.2 mm)在不同压差下的泄漏量如图 7所示,图中工况条件:出口为标准大气压。可以看出,泄漏量与进出口总压差呈正比,随着压差增加,泄漏量呈线性增加。
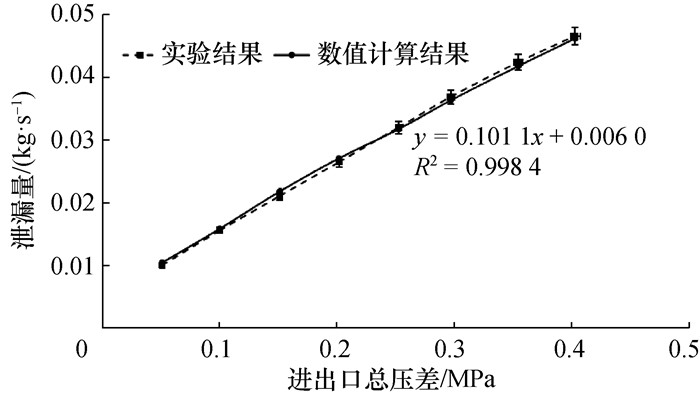
|
| 图 7 压差对泄漏量的影响 |
通过实验验证流场模型,最大误差为3%,表明流场模型具有准确性。
图 8为实验条件下得出的在不同压差下泄漏量随转速变化的趋势。可以看出,转速对泄漏量的影响非常小,并且随着转速提高,泄漏量会小幅度下降。原因如下:转轴高速旋转会使气体具有一定周向速度,从而增加周向的涡流强度,最终导致泄漏量下降;空气黏度较小,转轴旋转产生的气体周向速度较小,最终对泄漏量产生的影响有限。
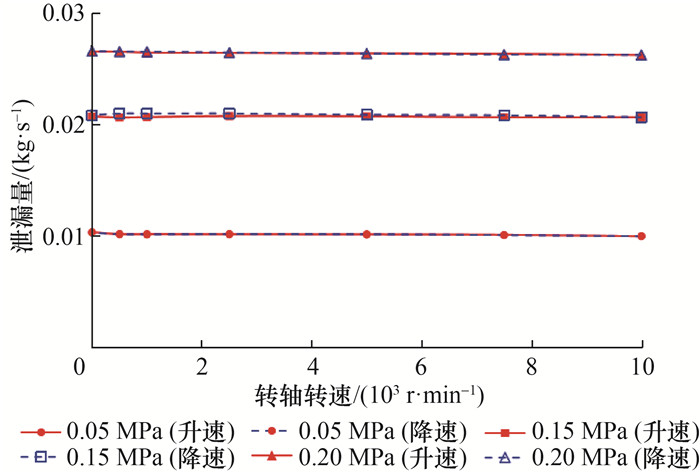
|
| 图 8 转速对泄漏量的影响 |
3.2 几何参数和齿形结构对泄漏量的影响
为设计密封性能更好的迷宫密封,分析迷宫密封几何参数和齿形结构对泄漏量的影响十分必要。对于直通式迷宫密封结构,影响泄漏量的主要几何参数为密封间隙、空腔高度、空腔宽度、齿厚和齿距。除此之外,迷宫密封齿形结构如直齿、梯形齿和斜齿等也会影响泄漏量。以下将分别深入研究几何参数和齿形结构对泄漏量的影响。
3.2.1 直通式迷宫密封几何参数对泄漏量的影响直通式迷宫密封几何参数对密封性能的影响较复杂,如何在最小的密封长度内设计泄漏量最低的迷宫密封结构具有重要意义。在密封长度固定的条件下,空腔宽度、齿厚、齿距和空腔高度四者存在交叉影响。改变空腔宽度、齿厚和齿距三者中任意一个参数,均会对其他2个参数产生影响,从而形成不同的密封机理;空腔宽度和空腔高度会改变空腔的面积和形状,空腔的面积和形状对泄漏量也具有显著影响。因此,仅采用某一种因素分析泄漏特性具有一定局限性。为了解决上述问题, 在各项尺寸之间存在某种协调的比例关系且有迹可循的前提下,本文引入占空比和深宽比这2个无量纲参数间接表达三者关系。占空比体现了齿厚与空腔宽度的比例搭配,深宽比体现了空腔形状。因此,占空比、深宽比、齿距三者即可清晰体现各项几何参数的关系,这简化了参数表示。直通式迷宫密封几何参数示意图如图 9所示。其中:g为齿厚,W为空腔宽度,H为空腔高度,q为密封间隙,L为齿距,η为占空比,ω为深宽比。
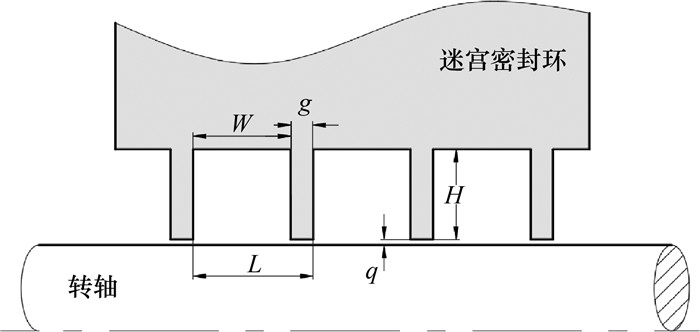
|
| 图 9 直通式迷宫密封几何参数示意图 |
采用CFD方法分析q、L、η和ω这4种几何参数对泄漏量的影响。η、ω和L的计算分别表示如下:
| $ \eta=g / W, $ | (7) |
| $ \omega=H / W, $ | (8) |
| $ L=W+g . $ | (9) |
为了研究q、L、η和ω这4个几何参数对迷宫密封性能的影响,设计了4水平4因素的正交实验表,如表 1所示。其中:4个几何参数的取值均在常规设计范围内;因素i=1, 2, 3, 4,分别表示间隙、齿距、占空比和深宽比;水平j=1, 2, 3, 4,分别表示表中各种因素选取的数值。
| i | j | |||
| 1 | 2 | 3 | 4 | |
| 1 | 0.15 | 0.20 | 0.25 | 0.30 |
| 2 | 7.1 | 7.6 | 8.1 | 8.6 |
| 3 | 0.3 | 0.5 | 0.7 | 0.9 |
| 4 | 0.4 | 0.8 | 1.2 | 1.6 |
正交试验方法是一种分析多因素影响的设计方法。该方法主要通过正交性从全面试验中挑选典型试验点进行试验测量,典型试验点具有“均匀分散、整齐可比”的特点。采用正交试验方法分析不同因素对泄漏量的影响过程如下:首先,根据需要分析的因素个数选择正确的正交分析表格,确定需要计算的典型试验数据;其次,通过对典型试验数据进行方差分析,获得不同参数对泄漏量的影响规律;最后,通过统计学方法对分析结果的准确性进行验证。需要指出的是,由于没有4水平4因素的正交试验表,通常采用4水平5因素正交试验表解决4水平4因素的正交计算问题。当采用4水平5因素正交试验表解决4水平4因素问题时,试验表会多出1列,在常规计算中,该列作为空列,不参与直接计算。本文为保证计算结果更准确,考虑了正交误差e对试验结果的影响,因此将空列作为正交误差列,该列实际是对试验进行重新排序,以方便对试验结果进行误差分析。选择4水平5因素的正交表L16(45),共需要16次试验,如表 2所示。若采用全面试验的方法,则共需要64次数值计算,而正交试验方法仅需要16次计算即可获得准确结果,极大地减少了工作量。通过上述4种几何参数,使用ANSYS Workbench软件建立迷宫密封流场模型,并计算各项几何参数下流场模型的泄漏量。
| 试验序号 | i | 正交误差列 | |||
| 1 | 2 | 3 | 4 | ||
| 1 | 0.15 | 7.1 | 0.3 | 0.4 | 1 |
| 2 | 0.15 | 7.6 | 0.5 | 0.8 | 2 |
| 3 | 0.15 | 8.1 | 0.7 | 1.2 | 3 |
| 4 | 0.15 | 8.6 | 0.9 | 1.6 | 4 |
| 5 | 0.20 | 7.1 | 0.5 | 1.2 | 1 |
| 6 | 0.20 | 7.6 | 0.3 | 1.6 | 2 |
| 7 | 0.20 | 8.1 | 0.9 | 0.4 | 3 |
| 8 | 0.20 | 8.6 | 0.7 | 0.8 | 4 |
| 9 | 0.25 | 7.1 | 0.7 | 1.6 | 1 |
| 10 | 0.25 | 7.6 | 0.9 | 1.2 | 2 |
| 11 | 0.25 | 8.1 | 0.3 | 0.8 | 3 |
| 12 | 0.25 | 8.6 | 0.5 | 0.4 | 4 |
| 13 | 0.30 | 7.1 | 0.9 | 0.8 | 1 |
| 14 | 0.30 | 7.6 | 0.7 | 0.4 | 2 |
| 15 | 0.30 | 8.1 | 0.5 | 1.6 | 3 |
| 16 | 0.30 | 8.6 | 0.3 | 1.2 | 4 |
泄漏量是评价迷宫密封性能的核心指标,计算表 2中试验1—16的泄漏量,其中进出口总压差为0.4 MPa,出口压力为标准大气压。不同几何参数对泄漏量的影响不同,通过极差和F值可以分析不同几何参数对泄漏量的影响程度,极差和F值越大,相应几何参数对泄漏量的影响就越显著。因素i的极差Ri表示如下:
| $ R_i=\max \left\{\bar{K}_i^j\right\}-\min \left\{\bar{K}_i^j\right\} . $ | (10) |
其中Kij为因素i水平j时计算所有泄漏量的均值。
因素i的F值表示如下:
| $ F=\frac{\mathrm{SS}_i / \mathrm{df}_i}{\mathrm{SS}_e / \mathrm{df}_e}, $ | (11) |
| $ \mathrm{SS}_i=\frac{1}{4} \sum\limits_{j=1}^4\left(K_i^j\right)^2-\frac{\left(\sum\limits_{j=1}^4 K_i^j\right)^2}{16}, $ | (12) |
| $ \mathrm{df}_i=m-1=3, m=4, $ | (13) |
| $ \mathrm{SS}_e=\frac{1}{4} \sum\limits_{j=1}^4\left(K_e^j\right)^2-\frac{\left(\sum\limits_{j=1}^4 K_e^j\right)^2}{16}, $ | (14) |
| $ \mathrm{df}_e=m-1=3, m=4. $ | (15) |
其中:SSi、dfi分别为因素i的离差平方和及自由度,SSe、dfe分别为误差e的离差平方和及自由度;Kij为因素i水平j时计算所得泄漏量,Kej为因素e水平j时计算所得泄漏量;m为因素个数。
查F分布表可知:显著性水平为0.10、0.05和0.01的临界值分别为F0.10(3, 3)=5.39,F0.05(3, 3)= 9.28和F0.01(3, 3)=29.46。显著性判断如下:若F≤5.39,则认为对泄漏量的影响不显著,无标记;若5.39<F≤9.28,则认为对泄漏量的影响轻微显著,标记为“*”;若9.28<F≤29.46,则认为因素对泄漏量的影响显著,标记为“* *”;若F>29.46,则认为对泄漏量的影响特别显著,标记为“* * *”。
几何参数对直通式迷宫密封泄漏量的影响如图 10所示。几何参数的极差和F值分析结果如表 3所示。各个因素对泄漏量的影响程度从大到小排序依次为间隙、占空比、齿距和深宽比。其中间隙对泄漏量的影响最显著,其他因素对泄漏量的影响不显著。原因如下:在迷宫密封中,间隙处的节流效应对减小泄漏起到了主导作用,并且间隙越小,泄漏量也越小。其他参数实际改变的是密封空腔的面积及形状,空腔的面积及形状主要影响空腔内周向涡流强度,周向涡流强度越大,气体在空腔中的能量损耗越大,出口泄漏量越小。
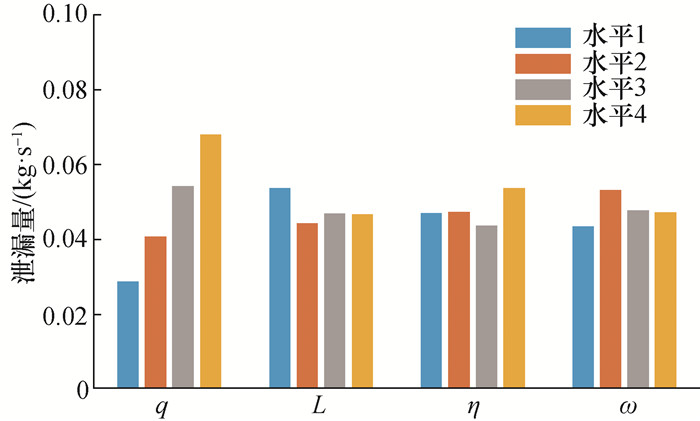
|
| 图 10 几何参数对泄漏量的影响 |
| 参数 | i | |||
| 1 | 2 | 3 | 4 | |
| Ri | 0.039 3 | 0.009 4 | 0.010 2 | 0.009 8 |
| F | 18.105 7** | 1.033 4 | 1.131 0 | 1.019 0 |
| 注:* *表示影响显著。 | ||||
3.2.2 齿数对泄漏量的影响
迷宫密封一般安装在固定静止件上,用于减小气体泄漏量;当用于平衡转轴轴向力时,迷宫密封也会安装在旋转轴上。不论是哪种装配条件,设备中被预留的密封长度均是有限的。目前在研究齿数对迷宫密封泄漏量的影响时,大部分研究均基于增加齿数不会改变空腔宽度和齿厚的假设展开,该假设与实际应用偏差较大。因此,本文在给定密封长度条件下,研究了密封齿数对泄漏量的影响规律。为保证建模过程中增加齿数的同时不改变密封长度,提出以下2点假设:一是保持占空比固定不变(η=0.3)和深宽比固定不变(ω=1),改变齿数时,齿距以固定比例随之变化;二是密封长度为定值,27.0 mm。在以上假设中,给定占空比和深宽比是为了保证齿数改变后的迷宫密封几何结构均为常见结构且易加工。
根据上述假设,采用FLUENT软件计算不同齿数下的泄漏量,结果如图 11所示。可以看出,在不同压差条件下,泄漏量随齿数增加而降低。在给定密封长度的情况下,增加密封齿数会减小齿厚和空腔宽度。从能量转化和结构变化角度考虑,该情况下迷宫密封的泄漏特性涉及2个因素:1) 从迷宫密封内部能量转化角度分析,减小齿厚和空腔宽度会降低气体在空腔内的涡流强度,从而降低涡流耗散,提高泄漏量;2) 虽然减小空腔宽度会使空腔面积减少,但是增加齿数不仅会增加空腔个数也会增加密封间隙个数,密封间隙增加有助于增加节流效应,从而降低泄漏量。由图 11的结果可知,当齿数较少时,齿数对泄漏量影响显著,此时第2个因素占主导地位;当齿数增加至一定程度,齿数对泄漏量的影响越来越弱,此时第1个因素占主导地位。此外,当进出口总压差为0.1 MPa时,齿数从11增加至12后,泄漏量变化幅度约为2%;当进出口总压差为0.5 MPa时,齿数从11增加至12后,泄漏量变化幅度约为9.8%。这说明齿数增加导致空腔面积减少,进出口压差增大有助于气体进入空腔内形成涡流,进而得出在大压差下齿数对泄漏量的影响仍较显著。
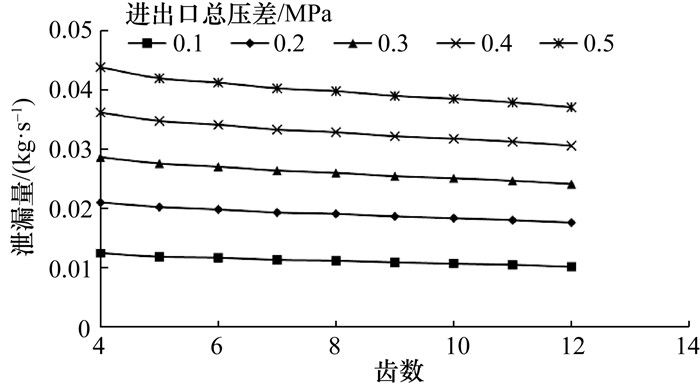
|
| 图 11 齿数对泄漏量的影响 |
3.2.3 齿形结构对泄漏量的影响
齿形结构也是影响迷宫密封泄漏量的关键因素之一,不同齿形会形成不同的空腔形状,从而影响空腔内的涡流强度,最终影响密封性能。通过研究直齿、梯形齿、斜齿、前齿面倾斜和后齿面倾斜等不同齿形下的泄漏量,对比分析齿形对泄漏量的影响。为防止其他几何参数对计算结果干扰,5种齿形下的齿厚、齿距、齿高、间隙和齿数都保持统一。不同齿形示意图如图 12所示。可以看出,常见迷宫密封齿形结构主要由前齿角α和后齿角θ交叉组合而来。各种齿形下的几何参数如表 4所示。
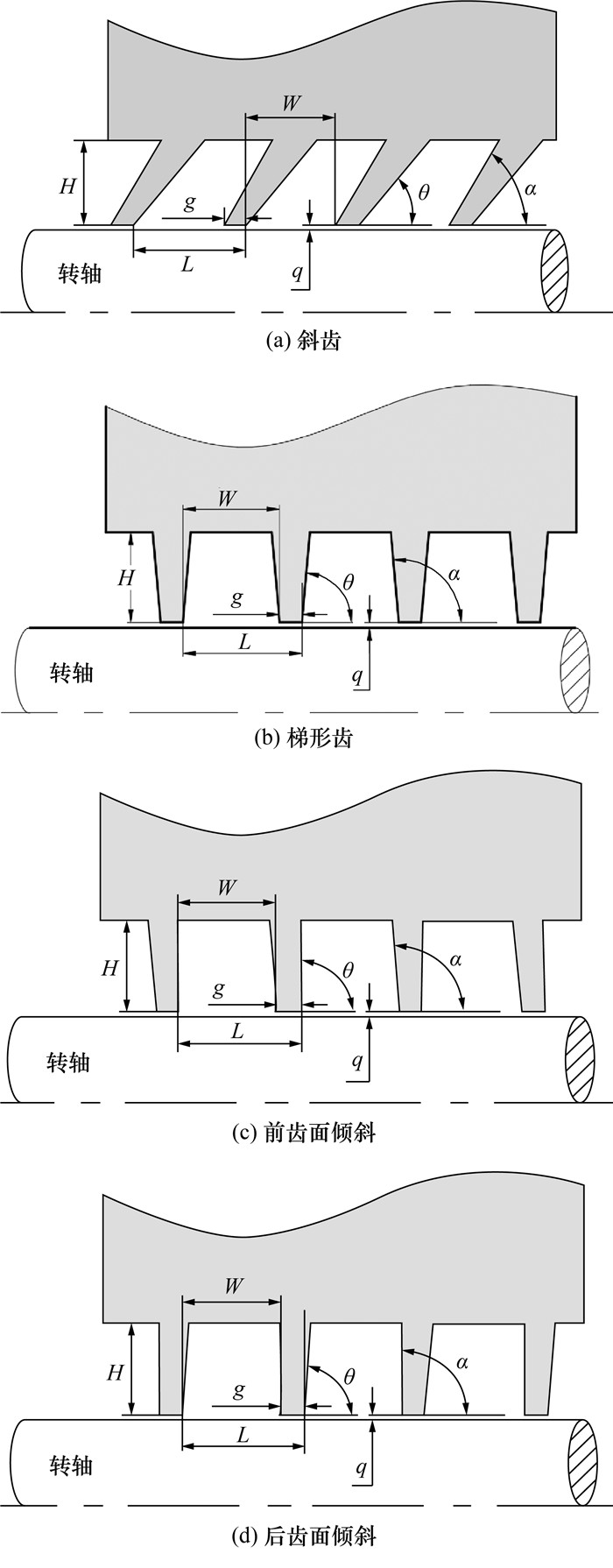
|
| 图 12 不同齿形示意图 |
| 齿形 | 参数 | ||||||||||||
| q | H | W | L | g | α | θ | |||||||
| mm | mm | mm | mm | mm | (°) | (°) | |||||||
| 直齿 | 0.15 | 6.23 | 6.23 | 8.1 | 1.87 | 90 | 90 | ||||||
| 斜齿 | 0.15 | 6.23 | 6.23 | 8.1 | 1.87 | 60 | 50 | ||||||
| 梯形齿 | 0.15 | 6.23 | 6.23 | 8.1 | 1.87 | 95 | 85 | ||||||
| 前齿面倾斜 | 0.15 | 6.23 | 6.23 | 8.1 | 1.87 | 95 | 90 | ||||||
| 后齿面倾斜 | 0.15 | 6.23 | 6.23 | 8.1 | 1.87 | 90 | 85 | ||||||
齿面倾斜变化会直接影响空腔结构,从而影响泄漏量。图 13为不同齿形对泄漏量的影响。可以看出,按泄漏量从小到大排列,齿形依次为斜齿、后齿面倾斜、直齿、梯形齿、前齿面倾斜,其中直齿和梯形齿下的泄漏量基本一致。通过分析流场结果,进一步讨论齿面倾斜角对内部流动机理的影响,以阐明结构对泄漏量的影响规律。第一级密封间隙流场云图如图 14所示。可以看出,前齿角越小,流束收缩效应越强,气体在间隙内的动能越大。迷宫密封内的流束收缩效应是指气体由较大空腔区域进入较小密封间隙时,气体在惯性作用下在间隙入口被压缩且流速增大。从图 14可以看出,前齿角越大,尤其是大于90°时,前齿迎风面会与齿顶形成一个有利于气流收缩的楔形结构,该结构更易使气体在空腔内的压力能转化为动能,提高了透气效应影响而不利于降低泄漏量。从图 14中还可以得出,在流束收缩效应存在的情况下,部分高速气体进入密封间隙后在惯性作用下产生回流,并形成涡流。该涡流区域会阻碍气体流动,减小气体流通间隙,表现为实际有效间隙小于设计间隙。通过分析其内部机理可以得出,前齿角减小可减弱流束收缩效应和透气效应,有利于降低泄漏量。在以Egli公式[9]为代表的热力学迷宫密封泄漏量经验公式均会引入流量系数,流量系数即为迷宫密封内部流束收缩效应的体现。
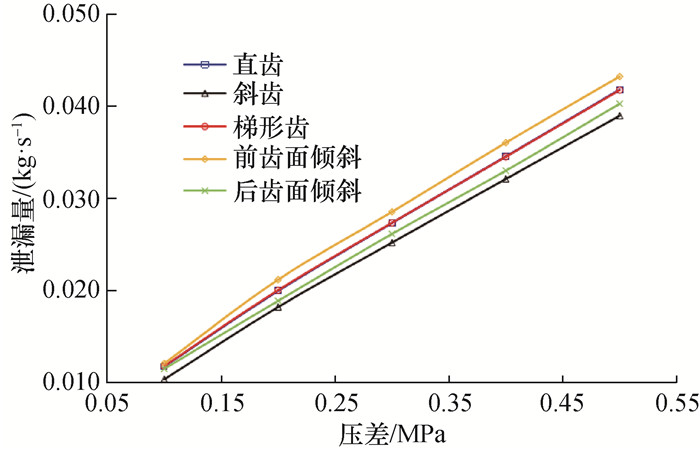
|
| 图 13 不同齿形对泄漏量的影响 |
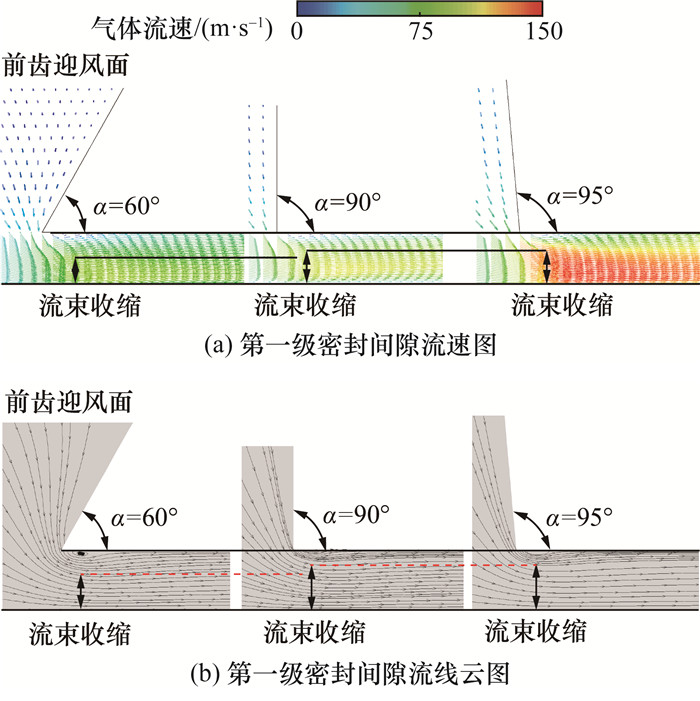
|
| 图 14 第一级密封间隙流场云图 |
对比前齿面倾斜泄漏量与直齿泄漏量可知,当前齿角大于90°时,泄漏量明显增加。该结果验证了上述机理分析,即前齿角增大将增大透气效应,从而增加泄漏量。对比后齿面倾斜泄漏量与直齿泄漏量可知,后齿面倾斜泄漏量明显小于直齿泄漏量。气体在第一级空腔内的流线云图如图 15所示。当后齿角小于90°时,气体会在空腔内形成除主涡流外的两团小涡流,增加了空腔内的能量耗散,从而达到降低泄漏量的效果。原因在于后齿角减小,有利于气体进入空腔形成涡流,且使涡流位置更接近上一级密封出口。对比直齿与梯形齿的泄漏量结果可知,虽然梯形齿后齿角具有一定倾斜度,有利于降低泄漏量,但是前齿角大于90°不利于降低泄漏量,两者影响效果相互抵消导致梯形齿与直齿的泄漏量结果相似。这种现象可以从侧面证明,前齿角和后齿角的角度变化时两者对泄漏量的影响能力接近。综上所述,迷宫密封前齿角和后齿角越小,越利于降低泄漏量,斜齿结构因兼具上述两点优势,相比其他齿形结构具有更优秀的密封性能。
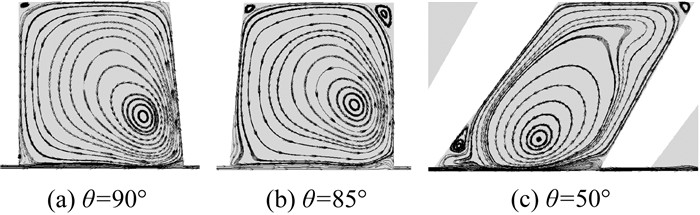
|
| 图 15 第一级空腔内流线云图 |
4 结论
本文通过实验与仿真相结合的方法研究了迷宫密封泄漏特性,并分析了不同因素对泄漏特性的影响规律,研究成果对迷宫密封结构设计工作具有重要意义。主要结论如下:
1) 建立了一种迷宫密封实验系统,该系统可以实现最高转速10 000 r/min、供气压力0.6 MPa下的迷宫密封实验工况,并且可以在线监测出口泄漏量、进出口压力、轴承温度、轴承振动和转速等实验参数。
2) 通过实验验证流场模型,流场模型最大误差为3%。实验和流场模型结果表明,压差会显著影响泄漏量,并且两者呈正比,转速基本不对泄漏量产生影响。
3) 针对四齿直通式(直齿)迷宫密封进行几何参数分析,考虑各项几何参数之间的耦合影响,定义了占空比、深宽比2种参数。通过正交试验分析了密封间隙、占空比、深宽比和齿距对泄漏量的影响。结果表明,密封间隙对泄漏量的影响显著,而占空比、深宽比和齿距对泄漏量的影响较小。
4) 在不增加轴向长度的前提下,针对不同齿数的直通式迷宫密封进行泄漏量分析。结果表明,增加齿数有利于降低泄漏量,并且随着压差增大,该现象更明显。同时,当进出口压差为定值时,增加齿数至一定数量后齿数对泄漏量的影响基本不会产生变化。
5) 针对不同齿形结构的迷宫密封进行泄漏量分析。结果表明,与直齿和梯形齿相比,斜齿具有更小的泄漏量,并且减小前齿与后齿角度倾斜角将利于降低泄漏量。
| [1] |
ASLAN-ZADA F E, MAMMADOV V A, DOHNAL F. Brush seals and labyrinth seals in gas turbine applications[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2013, 227(2): 216-230. DOI:10.1177/0957650912464922 |
| [2] |
ALIZADEH M, NIKKHAHI B, FARAHANI A S, et al. Numerical study on the effect of geometrical parameters on the labyrinth-honeycomb seal performance[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2018, 232(2): 362-373. DOI:10.1177/0954410017742227 |
| [3] |
汤赫男, 李赫, 王世杰. 热固耦合形变对BOG压缩机迷宫密封间隙的影响[J]. 润滑与密封, 2018, 43(11): 24-27, 35. TANG H N, LI H, WANG S J. Effect of thermal-solid interaction deformation on the sealing clearance of labyrinth of the BOG compressor[J]. Lubrication Engineering, 2018, 43(11): 24-27, 35. (in Chinese) |
| [4] |
KASZOWSKI P, DZIDA M, KRZYŚLAK P. Calculations of labyrinth seals with and without diagnostic extraction in fluid-flow machines[J]. Polish Maritime Research, 2013, 20(4): 34-38. DOI:10.2478/pomr-2013-0038 |
| [5] |
SUBRAMANIAN S, SEKHAR A S, PRASAD B V S S S. Influence of combined radial location and growth on the leakage performance of a rotating labyrinth gas turbine seal[J]. Journal of Mechanical Science and Technology, 2015, 29(6): 2535-2545. DOI:10.1007/s12206-015-0545-8 |
| [6] |
纪国剑, 吉洪湖. 直通篦齿封严结构压损规律和临界特性的研究[J]. 航空动力学报, 2008, 23(3): 415-420. JI G J, JI H H. Numerical and experimental investigation of pressure loss and critical sealing characteristics of straight-through labyrinth seals[J]. Journal of Aerospace Power, 2008, 23(3): 415-420. (in Chinese) |
| [7] |
SURYANARAYANAN S, MORRISON G L. Effect of tooth height, tooth width and shaft diameter on carry-over coefficient of labyrinth seals [C]// ASME Turbo Expo 2009: Power for Land, Sea, and Air. American Society of Mechanical Engineers. Orlando, USA: ASME, 2009: 1147-1152. .
|
| [8] |
KIRK G, GAO R. Influence of preswirl on rotordynamic characteristics of labyrinth seals[J]. Tribology Transactions, 2012, 55(3): 357-364. DOI:10.1080/10402004.2012.656880 |
| [9] |
EGLI A. The leakage of steam through labyrinth seals[J]. Journal of Fluids Engineering, 1935, 57(3): 115-122. |
| [10] |
赵炬颖, 陈义, 祝天一, 等. 螺旋槽对自适应迷宫密封的影响研究[J]. 润滑与密封, 2022, 47(1): 1-7. ZHAO J Y, CHEN Y, ZHU T Y, et al. Influence of spiral groove on the performance of adaptive labyrinth seal[J]. Lubrication Engineering, 2022, 47(1): 1-7. DOI:10.3969/j.issn.0254-0150.2022.01.001 (in Chinese) |
| [11] |
JIANG J, YANG Y Y, LI Y J, et al. Theoretical and experimental investigation on maximum pressure loads of labyrinth seal's teeth[J]. Advances in Mechanical Engineering, 2018, 10(10): 1687814018794348. |
| [12] |
JIANG J, YANG Y Y, HUANG W F, et al. Numerical and experimental investigation on uniformity of pressure loads in labyrinth seal[J]. Advances in Mechanical Engineering, 2017, 9(9): 1687814017728455. |
| [13] |
TANG H N, WANG S J, ZHAO J. Effect of fluid-structure interaction on sealed flow field and leakage rate based on computational fluid dynamics[J]. Journal of Shanghai Jiaotong University (Science), 2015, 20(3): 326-330. DOI:10.1007/s12204-015-1631-x |
| [14] |
白禄, 孙丹, 赵欢, 等. 转/静子齿对迷宫密封泄漏特性与动力特性影响机制研究[J]. 润滑与密封, 2022, 47(3): 40-48. BAI L, SUN D, ZHAO H, et al. Research on influence mechanism of rotor/stator teeth on leakage and dynamic characteristics of labyrinth seal[J]. Lubrication Engineering, 2022, 47(3): 40-48. (in Chinese) |
| [15] |
董振, 魏来, 汤赫男, 等. 轴向迷宫密封性能的流固耦合分析[J]. 润滑与密封, 2022, 47(1): 89-93. DONG Z, WEI L, TANG H N, et al. Fluid-structure interaction analysis on axial labyrinth seal[J]. Lubrication Engineering, 2022, 47(1): 89-93. (in Chinese) |
| [16] |
YANG S P, TAN B S, DENG X F. Numerical and experimental investigation of the sealing effect of a specific labyrinth seal structure[J]. Mathematical Problems in Engineering, 2019, 2019: 9851314. |
| [17] |
ASOK S P, SANKARANARAYANASAMY K, SUNDARARAJAN T, et al. Neural network and CFD-based optimisation of square cavity and curved cavity static labyrinth seals[J]. Tribology International, 2007, 40(7): 1204-1216. DOI:10.1016/j.triboint.2007.01.003 |
| [18] |
丁学俊, 杨彦磊, 黄来, 等. 直通式迷宫密封内可压缩流场的CFD数值模拟[J]. 流体机械, 2008, 36(6): 25-29. DING X J, YANG Y L, HUANG L, et al. Numerical simulation of compressible flow in straight through labyrinth seal by CFD[J]. Fluid Machinery, 2008, 36(6): 25-29. (in Chinese) |
| [19] |
巴鹏, 张雨薇, 吕忠阳, 等. 影响迷宫密封因素的分析[J]. 压缩机技术, 2016(2): 24-27, 30. BA P, ZHANG Y W, LÜ Z Y, et al. Analysis of the factors affecting labyrinth seal leakage[J]. Compressor Technology, 2016(2): 24-27, 30. (in Chinese) |
| [20] |
WHALEN J K, ALVAREZ E, PALLISER L P. Thermoplastic labyrinth seals for centrifugal compressors [C]// Proceedings of the Thirty-Third Turbomachinery Symposium. Houston, USA: Texas A&M University, 2004: 113-126.
|



