2. 北京动力机械研究所,北京 100074
2. Beijing Power Machinery Research Institute, Beijing 100074, China
机匣类工件目前主要应用于航空航天和核电等关乎国家安全的重大领域,此类工件所用材料的加工性能差、刚度不足且去除率高,易发生振动和变形,导致工件的机械加工表面质量大幅下降,甚至报废,这对工件加工工艺的可靠性和抗振性提出了较高的要求[1]。因此,针对包含五轴数控机床、刀具、工件及夹具的整体工艺系统进行刚度模型分析具有重要意义。
早期国内外学者通常将工艺系统的薄弱环节定位在刀具或工件[2],刀具和工件的结构相对简单,可采用理论计算、有限元分析或实验的方式进行研究,并已积累了较为丰富的研究成果[3-4];而机床因为刚度较大,常在该类研究中被忽略。
为了提高工艺系统刚度模型的精度,本文认为需要考虑五轴数控机床的影响。机床建模的方法主要有多体理论简化法[5]、有限元简化法[6]、动力学参数辨识简化法[7]和实验法[8]。多体理论简化法主要用于解决机器人多关节问题,针对机床各部件的简化较为困难;有限元简化法无需复杂的实验装置和仪器,但是需要通过实验校准重要参数;动力学参数辨识简化法可以与振动理论计算相结合,用以解释机床动力学参数和动刚度模型,但工程应用较为困难;实验法建立的模型精度最高,所以在工程中的应用也最为广泛。
动刚度的实验测量目前主要利用激振测试技术,根据激振方法的不同,可分为力锤激励[9]、接触式电磁激振器激励[10]、非接触式电磁激振器激励[11]、压电陶瓷促动器激励[12]4种方案。其中,力锤激励和接触式电磁激振器激励方案更适用于位姿多变的五轴工艺系统,但前者对工件和刀具等小型待测体的测量效果较好,后者则更适用于机床等大型待测体。
本文首先采用有限元分析和锤击实验,验证工件和刀具部分动刚度模型的准确性;接着采用接触式电磁激振器激振方案测量包含位姿信息的机床动刚度;再通过XGBoost模型建立包含机床位姿信息的机床动刚度模型,并利用刚度串联公式和空间坐标变换建立整体工艺系统的动刚度模型;最后利用铣削实验建立工艺系统动刚度模型的迭代和校准流程。
1 机匣工件和刀具部分的有限元仿真误差验证基于有限元仿真法建立的机匣工件和刀具部分的动刚度模型,本文设计了锤击实验,验证动柔度的仿真值与实验值之间的误差。
锤击实验中,机匣工件型号为sb1200,材质为铝合金,待测点为随机选择4个点,如图 1a所示;刀具的型号为R3*30*D10*90L*3F,材料为硬质合金,待测点为刀尖点,如图 1b所示。刀具和机匣的三维模型、材料性能等具体参数均由厂家提供。采用8778A500加速度传感器、9726A500力锤和NI-USB-9162信号采集器进行锤击实验,每组实验测量3次取平均值。

|
| 图 1 机匣工件和刀具的动柔度仿真值和实验值 |
数据处理方式以机匣位置1为例,如图 1c所示,由于固有频率附近的仿真误差较大,在实际加工时一般选择避开固有频率点,所以后续分析时删除附近频点。其他待测点的数据如图 1d—1h所示,处理方法和数据特性与图 1c相似。
采用仿真结果与实验结果的平均误差率M和最大误差率E来衡量仿真误差,计算方法如式(1)所示。
| $ \left\{\begin{array}{l} M=\frac{\sum\limits_{i=1}^n\left|\left(x_i-y_i\right) / y_i\right|}{n} \times 100 \%, \\ E=\max \left(\left|\left(x_i-y_i\right) / y_i \times 100 \%\right|\right) . \end{array}\right. $ | (1) |
其中:xi和yi分别为第i个仿真数据和实验数据,n为数据总量。
机匣和刀具的仿真误差如表 1所示,机匣和刀具的E值均小于10%,M值均小于6%。一般而言,动刚度仿真的M值在10%以下时,可以认为仿真结果可信[12-13]。因此,通过有限元仿真可以获得准确的刀具和机匣工件的动刚度模型。
| % | |||||||||||||||||||||||||||||
| 测量位置 | M | E | |||||||||||||||||||||||||||
| 机匣工件待测点1 | 5.3 | 9.8 | |||||||||||||||||||||||||||
| 机匣工件待测点2 | 4.5 | 9.5 | |||||||||||||||||||||||||||
| 机匣工件待测点3 | 5.1 | 9.1 | |||||||||||||||||||||||||||
| 机匣工件待测点4 | 4.5 | 9.6 | |||||||||||||||||||||||||||
| 刀具X方向 | 5.3 | 8.1 | |||||||||||||||||||||||||||
| 刀具Y方向 | 5.6 | 8.3 | |||||||||||||||||||||||||||
2 工艺系统动刚度建模 2.1 五轴数控机床动刚度测试系统设计
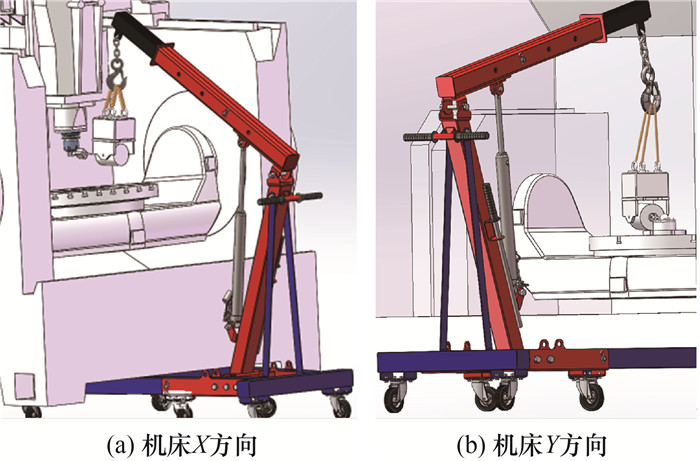
本文选择功率为20 W的VE-5102型电磁激振器。如图 2所示,采用小型液压吊车悬挂激振器,并设计质量为激振器10倍以上的配重块提供惯性质量,保证激振器的通电线圈有1~5 mm的行程。
|
| 图 2 五轴数控机床动刚度测试系统 |
2.2 五轴数控机床动刚度激振实验
为方便测量五轴数控机床在工作范围内的动刚度模型,对各轴的运动范围做分割处理,分割的节点如表 2所示。从X、Y、Z、A、C轴分割后的节点中随机选择并组合后,即可获得五轴数控机床工作空间内的任意一点。
| 编号 | X轴/mm | Y轴/mm | Z轴/mm | A轴/(°) | C轴/(°) |
| 1 | -208.3 | -208.3 | 92.0 | -60 | 0 |
| 2 | -148.8 | -148.8 | 124.5 | -45 | 40 |
| 3 | -89.3 | -89.3 | 157.0 | -30 | 80 |
| 4 | -29.8 | -29.8 | 189.5 | -15 | 120 |
| 5 | 29.8 | 29.8 | 222.0 | 0 | 160 |
| 6 | 89.3 | 89.3 | 254.5 | 15 | 200 |
| 7 | 148.3 | 148.3 | 287.0 | 30 | 240 |
| 8 | 208.3 | 208.3 | 319.5 | 45 | 280 |
| 9 | — | — | — | 60 | 320 |
正交实验可以根据各水平数据之间的关系。选择相互正交、有代表性且均匀分布的实验点,如表 3所示。机床动刚度测量的实验步骤为:首先开启五轴数控机床,安装激振器和液压小型吊车等实验装置;然后调节机床和激振器到指定位置;通过计算机上的LMS-Testlab软件设置扫频范围、通道、传感器灵敏度、采集频率等信息;启动激振器开始激振,并通过LMS-Testlab软件采集信号。以上过程在每组实验中重复3次,直至完成表 3中的所有实验。
| 编号 | X轴编号 | Y轴编号 | Z轴编号 | A轴编号 | C轴编号 |
| 1 | 1 | 5 | 4 | 9 | 2 |
| 2 | 3 | 1 | 3 | 1 | 5 |
| 3 | 5 | 5 | 6 | 5 | 5 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 79 | 5 | 4 | 7 | 9 | 5 |
| 80 | 2 | 3 | 6 | 9 | 3 |
| 81 | 1 | 3 | 4 | 1 | 9 |
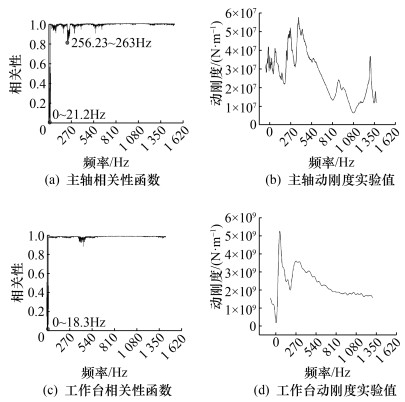
利用LMS-Testlab软件计算出机床的动刚度曲线和相关性曲线。以机床位姿为(-188 mm, 14 mm, 222 mm, 60°, 40°)时X方向的实验数据为例,如图 3所示,主轴和工作台的相关性基本接近1.0,只在固有频率附近出现较大波动。相关性曲线通常用于评价测量结果的信噪比,一般认为大于0.8时,数据的信噪比达标[8]。因此,除实验装置的固有频率点附近外,实验数据的信噪比均满足要求。
|
| (以机床位姿为-188 mm, 14 mm, 222 mm, 60°, 40°时X方向的数据为例) 图 3 机床动刚度实验 |
2.3 五轴数控机床动刚度模型建立
基于图 2的五轴数控机床动刚度测试系统和XGBoost模型,建立了五轴数控机床动刚度模型。
梯度下降树(gradient boosting decision tree, GBDT)算法是传统机器学习算法中对真实分布拟合较优的算法之一。XGBoost算法在GBDT算法的基础上优化了损失函数的计算方法,具有更快的收敛速度和更好的拟合效果。为了进一步优化XGBoost模型的收敛效果,采用Z-Score方法对全部数据集进行归一化处理和适当的特征缩放,计算表达式如下:
| $ p_j^{\prime}=\left(p_j-\mu\right) / \sigma . $ | (2) |
其中:pj为第j个机床在X、Y、Z 3个方向的动刚度实验数据,μ为多次实验数据的平均值,σ为多次实验数据的标准差。
为避免模型不收敛,还需要对刚度数据进行对数化处理,如式(3)所示。
| $ p_j^{\prime \prime}=\ln p_j^{\prime}. $ | (3) |
其中p′j为第j个经过式(2)处理后的刚度数据,即机床的动刚度值。
完成数据的归一化和特征缩放后,还需调节算法的超参数。本文采用Bayes优化法,通过梯度下降的方法对目标函数进行先验分布假设,从而以最小的计算量获得最佳的超参数组合。
为了衡量五轴数控机床动刚度模型的训练结果,对误差率(Ea)进行统计学分析。首先通过式(4)计算Ea。
| $ \mathrm{Ea}=(A-P) / A \times 100 \%. $ | (4) |
其中:A为机床动刚度实际值,P为对应的模型预测值。
再通过nσ原则评估模型的误差分布情况,如表 4所示。由表可知,采用XGBoost模型建立的、包含机床位姿信息的机床动刚度模型满足3σ原则,Ea分布在[-13.21%, 11.01%)的概率为96.83%,满足模拟的需求。
| nσ | Ea分布范围 | Ea分布概率/% |
| 1σ | [-7.16%, 4.95%) | 73.12 |
| 2σ | [-13.21%, 11.01%) | 96.83 |
| 3σ | [-19.26%, 17.07%) | 99.81 |
| 4σ | [-25.31%, 23.21%] | 99.93 |
2.4 工艺系统动刚度模型整合
本节暂时忽略机床和刀具之间、工件和夹具之间的装配动刚度,由此引起的误差由3.3节提出的动刚度校准和迭代方法消除。同时,忽略结构模态耦合是国内外学者常用的一种动刚度建模简化手段[14],且本研究通过预实验发现,各方向之间的耦合影响可以忽略。因此,本节只考虑工艺系统X、Y、Z方向的动刚度,忽略耦合导致的XY、XZ、YZ方向的动刚度。
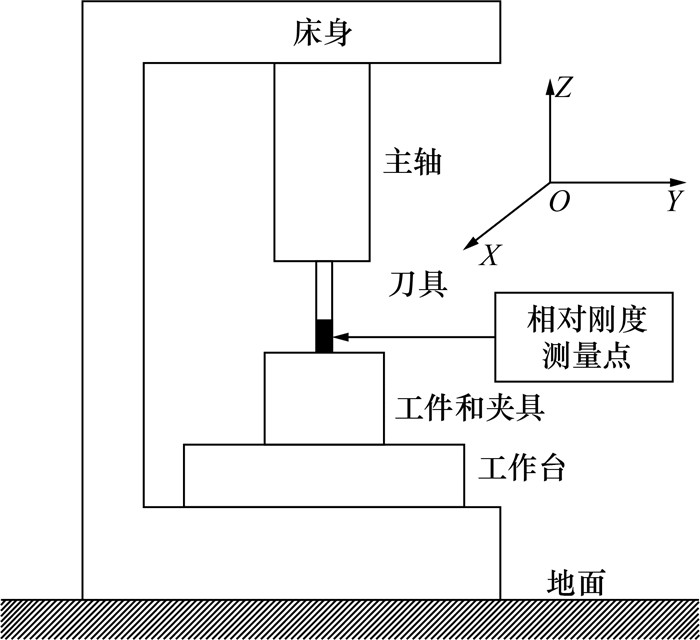
基于以上假设,可以将工艺系统简化为典型串联系统,包含五轴数控机床、刀具,工件和夹具,如图 4所示。
|
| 图 4 工艺系统简化图 |
如式(5)所示,可以通过主轴和工作台的刚度计算出机床的整体刚度。
| $ \left\{\begin{array}{l} \boldsymbol{M}_x=\frac{1}{1 / \boldsymbol{Z}_x+1 / \boldsymbol{G}_x}, \\ \boldsymbol{M}_y=\frac{1}{1 / \boldsymbol{Z}_y+1 / \boldsymbol{G}_y}, \\ \boldsymbol{M}_z=\frac{1}{1 / \boldsymbol{Z}_z+1 / \boldsymbol{G}_z} . \end{array}\right. $ | (5) |
其中:Mx, My, Mz、Zx, Zy, Zz和Gx, Gy, Gz分别为机床、主轴和工作台X, Y, Z方向的动刚度。
如式(6)所示,可以通过机床、刀具系统和工件与夹具系统计算工艺系统的整体刚度。
| $ \left\{\begin{aligned} \boldsymbol{K}_x & =\frac{1}{1 / \boldsymbol{M}_x+1 / \boldsymbol{J}_x+1 / \boldsymbol{D}_x}, \\ \boldsymbol{K}_y & =\frac{1}{1 / \boldsymbol{M}_y+1 / \boldsymbol{J}_y+1 / \boldsymbol{D}_y}, \\ \boldsymbol{K}_z & =\frac{1}{1 / \boldsymbol{M}_z+1 / \boldsymbol{J}_z+1 / \boldsymbol{D}_z} . \end{aligned}\right. $ | (6) |
其中:Mx, My, Mz、Kx, Ky, Kz、Dx, Dy, Dz和Jx, Jy, Jz分别为机床、工艺系统、刀具系统和工件与夹具系统X, Y, Z方向的动刚度。
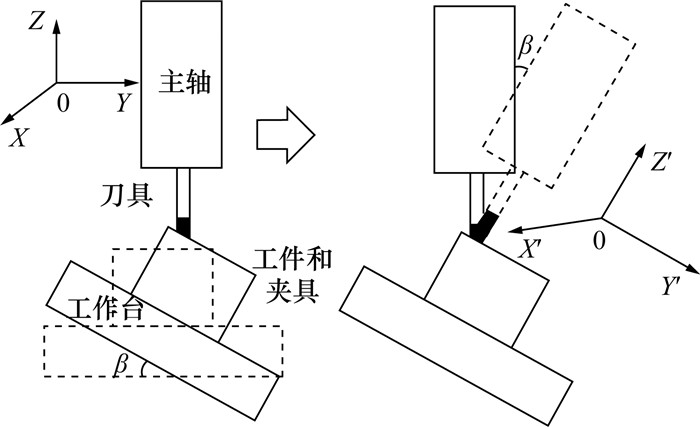
当机床的A轴发生变化后,工艺系统和机床的动刚度均不能直接通过动刚度串联公式获得,需要通过坐标变换,将XYZ地面坐标系下的机床主轴和刀具动刚度变化到X′Y′Z′工件坐标系下的动刚度,如图 5所示。
|
| 图 5 工艺系统坐标变换 |
将变换坐标系后的动刚度重新代入式(5)和(6),可获得机床整体和工艺系统整体的动刚度值,如式(7)所示。
| $ \left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta & 0 \\ 0 & \sin \beta & \cos \beta & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\left(\begin{array}{c} \boldsymbol{E}_{x i}^{\prime} \\ \boldsymbol{E}_{y i}^{\prime} \\ \boldsymbol{E}_{z i}^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{c} \boldsymbol{F}_{x i} \\ \boldsymbol{F}_{y i} \\ \boldsymbol{F}_{z i} \\ 1 \end{array}\right) . $ | (7) |
其中:β表示五轴数控机床A轴转动的角度,E′xi, E′yi, E′zi分别表示变换后X, Y, Z方向的机床主轴或刀具动刚度,Fx, Fy, Fz分别表示变换前X, Y, Z方向的机床主轴或刀具动刚度。
3 基于铣削实验的工艺系统动刚度模型迭代 3.1 工艺系统铣削实验实验设计如图 6所示,实验台底部为9255C型切削力测量仪,该仪器通过转接板与2根立柱相连,立柱上方放置用于切削的实验板;通过更换立柱将实验台高度h分别调整为92、206和320 mm,分别记为实验台1、2和3;为方便后续数据采集与处理,每隔10 mm确定一条走刀路线(切削线),将切削线从左往右依次编号为1—8(见图 6d)。刀具悬长可依次调节为56.5、42.6和33.5 mm,以实现在不更换刀具的前提下调节工艺系统动刚度。主轴转速、进给量和轴向切深分别为4 000 r/min、360 mm/min和0.4 mm。

|
| 图 6 工艺系统铣削实验台 |
基于搭建好的工艺系统铣削实验台,共进行30次有效铣削,实验参数组合的设计如表 5所示。
| 实验组编号 | 切削线编号 | 实验台编号 | 刀具悬长/mm | 实验组编号 | 切削线编号 | 实验台编号 | 刀具悬长/mm | |
| 1 | 1 | 1 | 56.5 | 16 | 6 | 2 | 56.5 | |
| 2 | 2 | 3 | 33.5 | 17 | 4 | 1 | 42.6 | |
| 3 | 3 | 2 | 42.6 | 18 | 5 | 3 | 56.5 | |
| 4 | 4 | 3 | 56.5 | 19 | 5 | 1 | 33.5 | |
| 5 | 5 | 2 | 33.5 | 20 | 6 | 3 | 56.5 | |
| 6 | 6 | 1 | 42.6 | 21 | 4 | 2 | 33.5 | |
| 7 | 7 | 2 | 56.5 | 22 | 8 | 3 | 42.6 | |
| 8 | 8 | 1 | 42.6 | 23 | 1 | 2 | 33.5 | |
| 9 | 1 | 3 | 56.5 | 24 | 7 | 1 | 42.6 | |
| 10 | 1 | 1 | 33.5 | 25 | 2 | 2 | 56.5 | |
| 11 | 7 | 3 | 56.5 | 26 | 3 | 1 | 42.6 | |
| 12 | 8 | 2 | 33.5 | 27 | 1 | 3 | 56.5 | |
| 13 | 3 | 3 | 42.6 | 28 | 4 | 1 | 33.5 | |
| 14 | 1 | 2 | 33.5 | 29 | 5 | 2 | 42.6 | |
| 15 | 2 | 1 | 42.6 | 30 | 6 | 3 | 56.5 |
对应的铣削结果如图 7所示,共有45条铣削痕迹,排除15条用于尝试加工参数的无效铣削,获得30条有效数据。在此基础上划分动刚度测量的采样点。从平板边缘到中心位置每隔25 mm均匀画出1条直线,共3条直线;将直线与铣削路径的交点设置为1个采样点,采样长度设置为3 mm,共计90组实验数据。需说明的是,本文选择锤击实验测量工艺系统在主轴转速一倍频率,即66.7 Hz处的动刚度。其他频率处的动刚度的研究方法类似。

|
| 图 7 铣削实验结果和动刚度测量采样点划分 |
针对包含实验台、刀具、五轴数控机床的工艺系统进行动刚度测量。如2.4节所述,只需要测量刀具部分(包含刀具、机床主轴)的动刚度和实验台部分(包含实验台和机床工作台)的动刚度,再对二者进行整合,即可获得整体工艺系统的动刚度。
由于刀具在Z方向的动刚度远远大于X和Y方向[4],因此本节只测量X和Y方向的动刚度。刀具部分的动刚度测量采用9726A500型力锤,加装型号为9926的配重块。依据表 5中的实验参数组合测量不同铣削位置处的不同刀具悬长条件下的刀具动刚度。实验台部分的动刚度测量同理,实验过程如图 8所示。再根据2.4节的方法将各部分的动刚度进行整合,求出工艺系统在66.67 Hz处的整体动刚度。

|
| 图 8 工艺系统动刚度测量 |
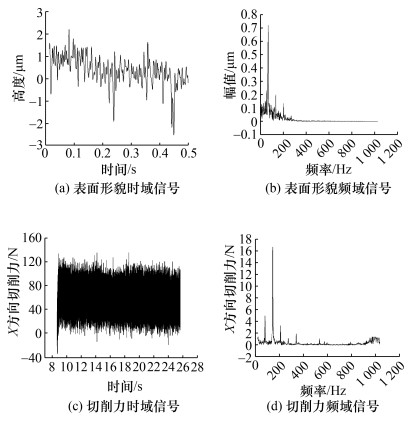
进一步采用ZYGO-Nexview白光干涉仪扫描工艺系统铣削实验台的上板的表面形貌,获得光镜图和三维形貌图。以表 5中的实验组1为例,观察并采集实验板的表面形貌和加工时X方向的切削力数据分别对应的时域和频域数据,结果如图 9所示。由图可知,表面形貌数据的主要信息分布在300.0 Hz内,且在66.7、133.3和200.0 Hz处均出现了明显尖峰;切削力数据在3个主要频点处也出现了明显尖峰,说明数据真实有效。针对表 5中其他29个实验组也采用相同方式进行处理,除了实验组25的数据的信噪比较低,频域内峰值被噪声淹没以外,其他实验组可获得与实验组1相似的结论,因此将实验组25对应的数据视为异常数据,不参与后续的数据分析。
|
| 图 9 实验组1中实验板的表面形貌和加工时的切削力数据的时域和频域信号 |
3.2 基于铣削实验的工艺系统动刚度测量模型建立
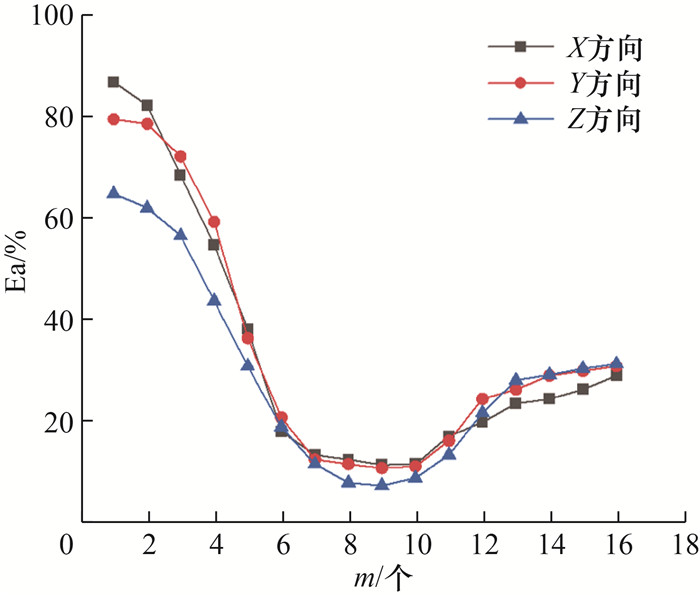
在获得FX、FY、FZ 3个方向的切削力数据和实验板表面形貌的时域和频域系列数据(如平均数、中位数、一阶频率处的峰值等)以后,从中提取出44组可用于XGBoost模型训练的时域和频域特征参数。在此基础上,以Person相关系数大于0.5为标准,进一步筛选出与工艺系统动刚度相关度高的16组特征参数。但在实际的模型训练时发现,16组特征参数仍然较多,会导致模型难以收敛。因此,利用XGBoost模型在训练时自动为特征参数分配权重的功能,对不同特征参数在5次模型训练后的权重取平均值,平均值越大代表该特征参数对模型准确率的影响越大。将平均值从大到小排列后,取前m个特征参数重新训练模型,并以Ea为指标评估模型的精度。如图 10所示,当m为9时,模型的Ea最低,所以选择前9个特征参数,分别为:FX一阶频率、FX二阶频率、FY一阶频率、FY二阶频率、FZ一阶频率、FZ二阶频率、表面形貌一阶频率、表面形貌二阶频率和表面形貌绝对平均值。
|
| 图 10 XGBoost模型训练选取的特征参数数量与平均误差率的关系 |
基于此,本文建立了可以通过切削力和表面形貌预测工艺系统动刚度的XGBoost模型,验证集共有18组数据,其平均值小于13%,最大值不超过18%,如表 6所示。
| % | |||||||||||||||||||||||||||||
| 数据编号 | Ea | ||||||||||||||||||||||||||||
| X方向 | Y方向 | Z方向 | |||||||||||||||||||||||||||
| 1 | -10.71 | -10.19 | 7.68 | ||||||||||||||||||||||||||
| 2 | -11.75 | -11.41 | -7.87 | ||||||||||||||||||||||||||
| 3 | 13.16 | -13.00 | -7.50 | ||||||||||||||||||||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ||||||||||||||||||||||||||
| 16 | 17.30 | 12.30 | -6.62 | ||||||||||||||||||||||||||
| 17 | -13.64 | -10.36 | -7.93 | ||||||||||||||||||||||||||
| 18 | 18.00 | 16.75 | -14.93 | ||||||||||||||||||||||||||
| 平均值 | 12.86 | 12.13 | 8.38 | ||||||||||||||||||||||||||
3.3 工艺系统动刚度模型迭代和验证
2.4节中建立工艺系统动刚度模型时忽略了各分系统之间的结合面,为了提高工艺系统动刚度的模型精度,需要对机床的动刚度模型进行迭代,从而消除结合面带来的误差。
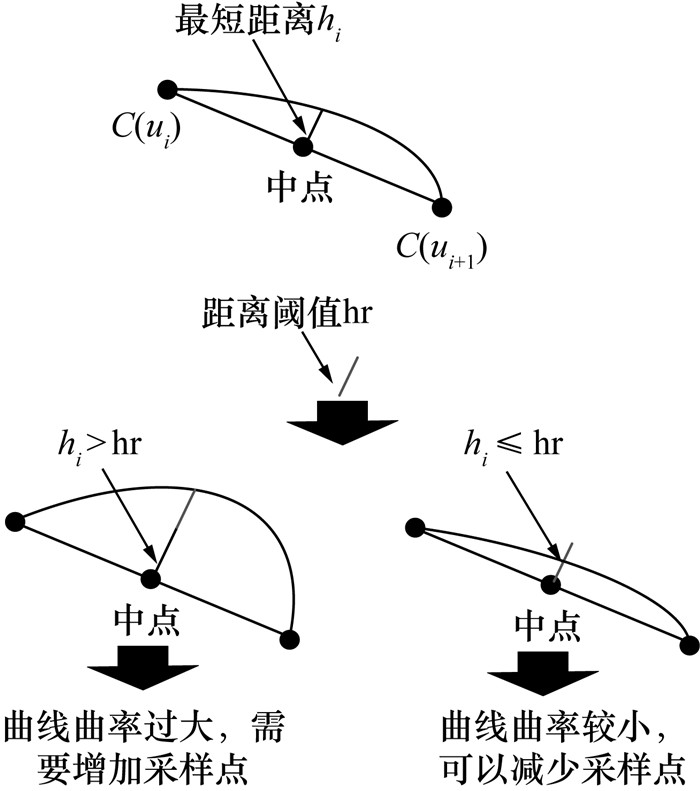
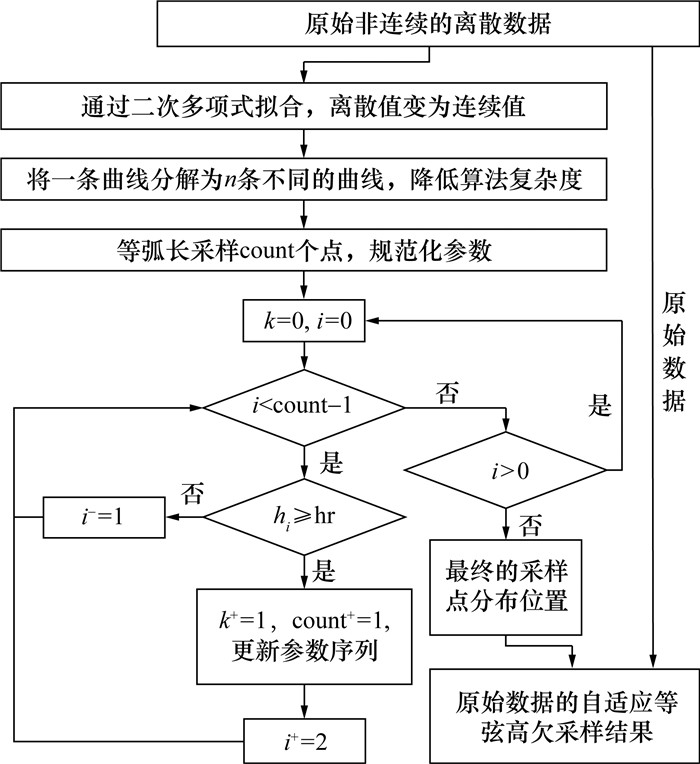
首先通过3.1节中的铣削实验获取工艺系统动刚度,利用2.4节中的式(5)和(6)反向计算出包括各系统间结合面的机床动刚度;然后通过等弦高自适应欠采样算法处理2.2节激振实验获取的动刚度数据,以平衡和通过铣削实验获取的机床动刚度数据之间的数据样本比例。等弦高自适应欠采样算法的原理如图 11所示,将每一小段曲线的最短距离与距离阈值hr进行比较,如果大于hr则添加采样点,反之减少,从而确保曲率大的曲线采样点多,曲率小的曲线采样点少。流程如图 12所示,首先对原始数据进行二次多项式拟合,将离散不可导的数据转化为处处连续可导的曲线,再将一条曲线分解为n条不同的曲线;然后根据所采样的曲线长度选择较小的初始采样点count并做等弧长采样;随后计算各采样点间弦长中点到曲线的最短距离值hi,与阈值hr比较后确定增加或减少采样点数量,并统计新增采样点数为k,不断重复该步骤,直至新增采样点数为0,完成自适应采样;最后利用XGBoost模型调整2种机床动刚度数据的权重,并重新训练机床动刚度模型,以完成对机床动刚度模型的迭代和校准。
|
| 图 11 自适应等弦高欠采样原理图 |
|
| 图 12 自适应等弦高欠采样流程图 |
之后分别利用2.2节激振实验获取的动刚度数据,以及切削实验获取的动刚度数据,验证动刚度模型经等弦高自适应欠采样算法迭代后的精度,结果分别如表 7和8所示。由表可知,机床动刚度模型在激振实验数据中的误差分布满足3σ原则,在铣削实验数据中各方向的Ea均小于9%,表明了该迭代方法提升模型精度的可行性。
| nσ | Ea分布范围 | Ea分布概率/% |
| 1σ | (-6.31%, 5.11%) | 74.22 |
| 2σ | (-12.03%, 10.83%) | 96.97 |
| 3σ | (-17.74%, 16.54%) | 99.81 |
| 4σ | (-23.46%, 22.26%) | 99.95 |
| % | |||||||||||||||||||||||||||||
| 数据编号 | Ea | ||||||||||||||||||||||||||||
| X方向 | Y方向 | Z方向 | |||||||||||||||||||||||||||
| 1 | -6.55 | 5.77 | 7.81 | ||||||||||||||||||||||||||
| 2 | -4.55 | 4.76 | 8.84 | ||||||||||||||||||||||||||
| 3 | -2.07 | 6.53 | -2.27 | ||||||||||||||||||||||||||
| 4 | -6.71 | 6.51 | -8.09 | ||||||||||||||||||||||||||
| 5 | 0.31 | -5.68 | -4.92 | ||||||||||||||||||||||||||
| 6 | 1.74 | 1.29 | 6.17 | ||||||||||||||||||||||||||
| 7 | -3.15 | -8.45 | -7.03 | ||||||||||||||||||||||||||
| 8 | -0.33 | -6.36 | 4.15 | ||||||||||||||||||||||||||
| 9 | 5.08 | 3.01 | -0.22 | ||||||||||||||||||||||||||
| 10 | 8.78 | -6.86 | 1.54 | ||||||||||||||||||||||||||
| 11 | 3.74 | 4.09 | -0.89 | ||||||||||||||||||||||||||
| 12 | 4.10 | 1.54 | 7.27 | ||||||||||||||||||||||||||
| 13 | 8.78 | 4.08 | 7.30 | ||||||||||||||||||||||||||
| 14 | 4.53 | 0.32 | 6.74 | ||||||||||||||||||||||||||
| 15 | -6.89 | -8.03 | 0.64 | ||||||||||||||||||||||||||
| 16 | -5.45 | 1.94 | -5.33 | ||||||||||||||||||||||||||
| 17 | -2.28 | 2.94 | 1.82 | ||||||||||||||||||||||||||
| 18 | -1.54 | 7.42 | 4.36 | ||||||||||||||||||||||||||
4 结论
本文首先基于悬挂式电磁激振器和XGBoost模型建立了包含位姿信息的机床动刚度模型,利用有限元仿真建立了刀具和工件及夹具的动刚度模型;然后暂时忽略各系统间结合面,利用动刚度串联公式和坐标变换公式建立了工艺系统动刚度模型;在此基础上建立了通过铣削实验测量工艺系统动刚度的XGBoost模型,并利用该模型获取新的工艺系统动刚度;最后使用等弦高自适应欠采样算法平衡数据样本后,重新训练出校准后的工艺系统动刚度模型,该模型经验证可满足3σ原则。本文通过仿真、实验和XGBoost模型构建的一种包含机床位姿信息的工艺系统动刚度模型,以及通过铣削实验校准和迭代工艺系统动刚度模型的流程,可为后续相关研究提供借鉴。
| [1] |
KAM M, DEMİRTAŞ M. Experimental analysis of the effect of mechanical properties and microstructure on tool vibration and surface quality in dry turning of hardened AISI 4340 steels[J]. Surface Review and Letters, 2021, 28(6): 2150041. DOI:10.1142/S0218625X21500414 |
| [2] |
SANTO D R, MENCIK J M, TANG B, et al. On the dynamic behavior of rods and beams with nonlinear boundary stiffness [C]//Latin American Congress on Computational Methods in Engineering. Paris, France: Université de Technologie de Compiègne, 2018.
|
| [3] |
孙孟琴, 王立臣. 球头铣刀动力学模型及其铣削加工稳定性的研究[J]. 机床与液压, 2012, 40(9): 52-54. SUN M Q, WANG L C. Research on dynamic model and milling stability of ball end milling cutter[J]. Machine Tool & Hydraulics, 2012, 40(9): 52-54. (in Chinese) |
| [4] |
邓聪颖, 刘蕴, 殷国富, 等. 基于响应面方法的数控机床空间动态特性研究[J]. 工程科学与技术, 2017, 49(4): 211-218. DENG C Y, LIU Y, YIN G F, et al. Research on machine tool spatial dynamic characteristics based on response surface method[J]. Advanced Engineering Sciences, 2017, 49(4): 211-218. (in Chinese) |
| [5] |
葛双好, 张蔚波, 王佩凤, 等. 基于模态实验的机床进给系统的分析[J]. 机床与液压, 2015, 43(1): 37-40. GE S H, ZHANG W B, WANG P F, et al. Analysis of machine tool feed system based on modal experiment[J]. Machine Tool & Hydraulics, 2015, 43(1): 37-40. (in Chinese) |
| [6] |
CHOWDHURY A R, PRASAD B, KUMAR V, et al. Design, modeling and open-loop control of a BCF mode bio-mimetic robotic fish [C]//2011 International Siberian Conference on Control and Communications. Krasnoyarsk, Russia: IEEE, 2011: 87-92.
|
| [7] |
姜越友. 五轴机床工作空间动刚度测试方法研究[D]. 成都: 电子科技大学, 2019. JIANG Y Y. Research on experimental method for evaluating dynamic stiffness of five-axis machine tool in workspace [D]. Chengdu: University of Electronic Science and Technology of China, 2019. (in Chinese) |
| [8] |
APPRICH S, WULLE F, LECHLER A, et al. Approach for a general pose-dependent model of the dynamic behavior of large lightweight machine tools for vibration reduction[J]. Procedia CIRP, 2016, 41: 812-817. DOI:10.1016/j.procir.2015.12.014 |
| [9] |
韩松林. 动态切削力模拟加载及误差在线测量装置的研究与开发[D]. 南京: 南京航空航天大学, 2016. HAN S L. Research and development of dynamic cutting force loading and online erro measureing device [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. (in Chinese. |
| [10] |
MATSUBARA A, TSUJIMOTO S, KONO D. Evaluation of dynamic stiffness of machine tool spindle by non-contact excitation tests[J]. CIRP Annals, 2015, 64(1): 365-368. DOI:10.1016/j.cirp.2015.04.101 |
| [11] |
KONO D, MORIYA Y, MATSUBARA A. Influence of rotary axis on tool-workpiece loop compliance for five-axis machine tools[J]. Precision Engineering, 2017, 49: 278-286. DOI:10.1016/j.precisioneng.2017.02.016 |
| [12] |
GUSEV A A. Time domain finite element estimates of dynamic stiffness of viscoelastic composites with stiff spherical inclusions[J]. International Journal of Solids and Structures, 2016, 88-89: 79-87. DOI:10.1016/j.ijsolstr.2016.03.021 |
| [13] |
MOHAMED N, CHONG P L, FARAJI F, et al. Stress analysis of various designs of centrifugal pump impellers using finite element method[J]. Journal of Engineering and Technological Advances, 2022, 7(1): 36-46. |
| [14] |
刘宗昊. 双柔性铣削系统动力学建模与叶片加工稳定性研究[D]. 北京: 北京交通大学, 2020. LIU Z H. Research on dynamic modeling of double flexible milling system and stability of blade processing [D]. Beijing: Beijing Jiaotong University, 2020. (in Chinese) |


