伴随着汽车电动化、智能化的浪潮,轮毂电机驱动即车轮内装电机的驱动形式受到越来越多的关注,并被认为是未来电动汽车的理想驱动方案。首先,轮毂电机驱动省掉了传动部件,既提高了驱动效率,又节省了底盘空间,便于底盘结构的模块化设计;其次,轮毂电机驱动可以灵活分配各车轮力矩,便捷地实现分布式驱动,显著提升车辆操纵性能[1-2]。
现有轮毂电机驱动的主流构型中,轮毂电机等动力系统全部集成在车轮内部,显著增加了车辆的簧下质量。簧下质量增加对车辆性能产生的影响就成为一个有待明确的问题。Vos等[3]在内燃机车辆的车轮上附加质量模拟轮毂电机,在不同路面上进行了道路试验。试验结果表明,簧下质量增加会恶化乘坐舒适性,且在轮毂电机前驱车辆中的负效应明显大于在轮毂电机后驱车辆中的。Protean公司[4-5]在传统福克斯车型的车轮上装载30 kg的质量并开展道路试验,期间进行驾驶员主观评价和客观振动测量,据此指出,簧下质量增加对车辆的平顺性和操纵性并无明显影响。
为了揭示簧下质量增加的影响规律,学者们也开展了大量仿真分析,其中大多数研究均基于1/4车辆模型。Nagaya [6]和Jin[7]发现轮毂电机驱动车辆的轮胎接地力和车身加速度均在簧下质量共振频率处增大,对车辆的接地性和舒适性均产生不利影响。Katsuyama等[8]指出簧下质量增加恶化了中频4~8 Hz内的振动。该频段正好处于人体最敏感的频率范围,因此会严重影响乘坐舒适性。Wang等[9]和童炜等[10]计算了随机路面激励下车辆平顺性指标的均方根值,发现对于轮毂电机驱动车辆,各指标的均方根值在不同等级路面和不同车速下均大于集中电机驱动车辆。
相对而言,基于半车模型和整车模型开展簧下质量增加的影响的研究较少。Terra等[11]建立了轮毂电机后驱车辆的半车模型,分析了前后路面同相和反相正弦输入下电机质量对车辆性能的影响,发现轮毂电机驱动的车身质心加速度、俯仰角加速度及轮胎动态力均大于集中电机驱动。Shi等[12]基于整车模型研究了随机路面上簧下质量对平顺性的影响,指出随着簧下质量的增加,座椅的加权加速度均方根值增大,车辆平顺性变差。李宁宁[13]研究了车辆以30 km/h通过脉冲路面时的平顺性,指出随着前轮质量的增加,前轮与车辆质心处的最大加速度反而逐渐减小。
显然,无论是试验还是计算研究,关于簧下质量增加带来的影响的结论并不统一。其中,计算研究多采用1/4车辆模型,结论是簧下质量增加会恶化车辆的平顺性。然而,1/4车辆模型无法体现多轮激励的差异,且不能反映车身不同位置处的振动。此外,基于半车和整车模型的计算研究大多在某些恒定车速下进行,且未考虑轮毂电机前驱、后驱和四驱的不同驱动方式的影响。
本文基于半车模型,综合考虑车速、车身位置、电机质量及轮毂电机驱动方式等因素,尝试系统分析轮毂电机驱动车辆中簧下质量增加对车辆平顺性的影响机理,为轮毂电机驱动车辆的设计提供动力学基础。
1 半车模型与车辆性能指标 1.1 半车模型假设汽车近似作为线性系统,本文研究的频率范围为0.1~30 Hz,可以将车身看作刚体,因此常采用刚体集中质量模型来表征车辆。假设车辆在水平路面上做匀速直线运动,描述车辆垂向动力学性能可采用图 1的半车模型。半车模型中有4个自由度,其中簧上运动可以用质心垂向位移z2c和车身俯仰角φ2,或者前和后轴上方的车身垂向位移z2f和z2r来描述;簧下运动可以用前和后簧下质量的垂向位移z1f和z1r表示。图中m2和I2分别为簧上质量和其俯仰转动惯量,m1f和m1r分别为前和后车轮质量,m3为电机(或动力系统)质量。k2f和k2r分别为前和后悬架弹簧刚度,c2f和c2r分别为前和后悬架减振器阻尼系数,k1f和k1r分别为前和后轮胎刚度。L为轴距,a和b分别为车身质心与前和后轴的距离,z0f和z0r分别为前和后车轮路面输入。
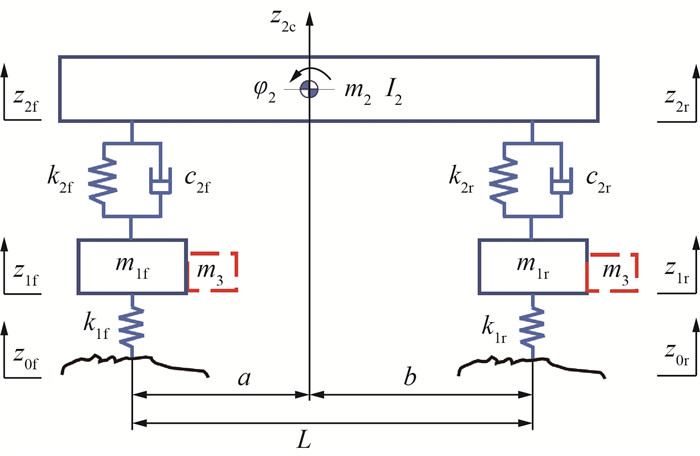
|
| 图 1 半车模型 |
应用Newton第二定律,系统的运动方程可表示为:
| $ \begin{gathered} m_2 \ddot{z}_{2 \mathrm{c}}+c_{2 \mathrm{f}}\left(\dot{z}_{2 \mathrm{f}}-\dot{z}_{1 \mathrm{f}}\right)+k_{2 \mathrm{f}}\left(z_{2 \mathrm{f}}-z_{1 \mathrm{f}}\right)+ \\ c_{2 \mathrm{r}}\left(\dot{z}_{2 \mathrm{r}}-\dot{z}_{1 \mathrm{r}}\right)+k_{2 \mathrm{r}}\left(z_{2 \mathrm{r}}-z_{1 \mathrm{r}}\right)=0, \end{gathered} $ | (1) |
| $ \begin{gathered} I_2 \ddot{\varphi}_2-a\left[c_{2 \mathrm{f}}\left(\dot{z}_{2 \mathrm{f}}-\dot{z}_{1 \mathrm{f}}\right)+k_{2 \mathrm{f}}\left(z_{2 \mathrm{f}}-z_{1 \mathrm{f}}\right)\right]+ \\ b\left[c_{2 \mathrm{r}}\left(\dot{z}_{2 \mathrm{r}}-\dot{z}_{1 \mathrm{r}}\right)+k_{2 \mathrm{r}}\left(z_{2 \mathrm{r}}-z_{1 \mathrm{r}}\right)\right]=0, \end{gathered} $ | (2) |
| $ \begin{gathered} \left(m_{1 \mathrm{f}}+m_3\right) \ddot{z}_{1 \mathrm{f}}+c_{2 \mathrm{f}}\left(\dot{z}_{1 \mathrm{f}}-\dot{z}_{2 \mathrm{f}}\right)+ \\ k_{2 \mathrm{f}}\left(z_{1 \mathrm{f}}-z_{2 \mathrm{f}}\right)+k_{1 \mathrm{f}}\left(z_{1 \mathrm{f}}-z_{0 \mathrm{f}}\right)=0, \end{gathered} $ | (3) |
| $ \begin{gathered} \left(m_{1 \mathrm{r}}+m_3\right) \ddot{z}_{1 \mathrm{r}}+c_{2 \mathrm{r}}\left(\dot{z}_{1 \mathrm{r}}-\dot{z}_{2 \mathrm{r}}\right)+ \\ k_{2 \mathrm{r}}\left(z_{1 \mathrm{r}}-z_{2 \mathrm{r}}\right)+k_{1 \mathrm{r}}\left(z_{1 \mathrm{r}}-z_{0 \mathrm{r}}\right)=0. \end{gathered} $ | (4) |
其中前和后车身的垂向加速度
| $ \ddot{z}_{2 \mathrm{f}}=\ddot{z}_{2 \mathrm{c}}-a \ddot{\varphi}_2, $ | (5) |
| $ \ddot{z}_{2 \mathrm{r}}=\ddot{z}_{2 \mathrm{c}}+b \ddot{\varphi}_2 \text {. } $ | (6) |
车身垂向加速度、车轮相对动载荷和悬架动挠度是评价车辆平顺性的常用指标[14]。车身垂向加速度影响舒适性;车轮相对动载荷反映车轮和路面的附着效果,影响行驶安全性;悬架动挠度与悬架限位行程有关,两者配合不当会增加撞击限位的概率。
在半车模型中,考虑车身不同位置垂向加速度以及前后轴各指标的差异,定义具体指标如下:
| $ \frac{F_{\mathrm{df}}}{G_{\mathrm{f}}}=\frac{k_{1 \mathrm{f}}\left(z_{1 \mathrm{f}}-z_{0 \mathrm{f}}\right)}{\left(m_{1 \mathrm{f}}+m_3+m_{2 \mathrm{f}}\right) g}, $ | (7) |
| $ f_{\mathrm{df}}=z_{2 \mathrm{f}}-z_{1 \mathrm{f}} . $ | (8) |
其中Fdf和Gf分别为前车轮的动载荷和静载荷。
下面简要推导各个指标的幅频特性。在半车模型中,前、后车轮均受到路面激励。假设前、后车轮位于同一车辙,则z0f和z0r只相差一个时间滞后量Δt。该值取决于L和车速u, Δt=L/u。因此,z0f和z0r满足:
| $ z_{0 \mathrm{r}}(t)=z_{0 \mathrm{f}}(t-\Delta t) . $ | (9) |
采用复指数表达,依据式(9)可得z0f和z0r的复振幅关系为
| $ \hat{z}_{0 \mathrm{r}}=\hat{z}_{0 \mathrm{f}} \mathrm{e}^{-\mathrm{j} \omega \Delta t} . $ | (10) |
对式(1)—(6)进行Fourier变换,计算各指标的复振幅
| $ \hat{x}=H_{x \sim \dot{z}_{0 \mathrm{f}}} \hat{\dot{z}}_{0 \mathrm{f}}+H_{x \sim \dot{z}_{0 \mathrm{r}}} \hat{\dot{\varepsilon}}_{0 \mathrm{r}} \text {. } $ | (11) |
其中Hx~
将式(10)代入式(11),则有
| $ \hat{x}=\left(H_{x \sim \dot{z}_{0 \mathrm{f}}}+H_{x \sim \dot{z}_{0 \mathrm{r}}} \mathrm{e}^{-\mathrm{j} \omega \Delta t}\right) \hat{\dot{z}}_{0 \mathrm{f}} . $ | (12) |
这样,双轮路面激励等效为前轮激励。各指标相对于单一前轮激励的等效幅频特性可以表示为
| $ \left|\frac{\hat{x}}{\hat{\dot{z}}_0}\right|=\left|H_{x \sim \dot{z}_{0 \mathrm{f}}}+H_{x \sim \dot{z}_{0 \mathrm{r}}} \mathrm{e}^{-\mathrm{j} \omega L / u}\right| . $ | (13) |
可以看出,半车模型中各指标的幅频特性不仅与车辆本身参数(质量、刚度、阻尼等)有关,还与前、后轮路面输入的相位差即轴距和车速有关。
汽车实际行驶的路面为等级随机路面,通常采用功率谱密度描述其统计特性。一般认为随机路面的速度功率谱密度为限带白噪声,可以表示为
| $ G_{\dot{z}_0}(n)=4 {\rm{ \mathsf{ π} }}^2 n_0^2 G_{z_0}\left(n_0\right) \text {. } $ | (14) |
其中:n为路面空间频率,范围为0.011~2.83 m-1[14];n0=0.1 m-1为参考空间频率;Gz0(n0)为路面不平度系数。
当近似把汽车看作线性系统,得到车辆系统的频响函数及路面输入的功率谱后,可得到各指标的功率谱密度:
| $ \begin{gathered} G_x(f)=\left|\frac{\hat{x}}{\hat{\dot{z}}_0}\right|^2 G_{\dot{z}_0}(f)= \\ 4 {\rm{ \mathsf{ π} }}^2 n_0^2 G_{z_0}\left(n_0\right) u\left|\frac{\hat{x}}{\hat{\dot{z}}_0}\right|^2 . \end{gathered} $ | (15) |
其中f=un为路面输入的时间频率。
在进行平顺性分析时,通常采用均方根(RMS)进行统计分析。各指标的均方根σx可由Gx (f)对频率积分得到:
| $ \sigma_x^2=\int_{f_1}^{f_{\mathrm{u}}} G_x(f) \mathrm{d} f . $ | (16) |
其中,fl和fu分别为下和上时间截止频率,由u和n共同决定。由于n的范围为0.011~2.83 m-1,车速较低时,应采用实际截止频率区间进行积分计算均方根;车速较高时,当上截止频率完全覆盖车辆系统固有频率时,可近似采用0.1~30 Hz的频率区间进行积分计算均方根。
根据ISO 2631-1振动标准[15],车身垂向加速度需经过频率加权。加权后车身加速度的均方根σ
| $ \sigma_{\ddot{z}}^2=\int_{0.5}^{80} W^2(f) G_{\ddot{z}}(f) \mathrm{d} f \text {; } $ | (17) |
| $ W(f)= \begin{cases}0.5, & 0.5 \mathrm{~Hz} \leqslant f <2 \mathrm{~Hz}; \\ f / 4, & 2 \mathrm{~Hz} \leqslant f <4 \mathrm{~Hz}; \\ 1, & 4 \mathrm{~Hz} \leqslant f <12.5 \mathrm{~Hz}; \\ 12.5 / f, & 12.5 \mathrm{~Hz} \leqslant f <80 \mathrm{~Hz}.\end{cases} $ | (18) |
其中:W(f)是频率加权函数,G
值得注意的是,由于路面速度激励为白噪声,各指标的均方根与幅频特性平方曲线和坐标轴所包围的面积成正比。后续分析中将结合幅频特性曲线对均方根进行讨论。
2 簧下质量增加的影响以某福特轿车[16]作为标准车辆模型,在每个车轮上增加30 kg质量来模拟轮毂电机驱动车辆模型。因此,除簧下质量外,2种车辆模型的其他所有参数均相同,如表 1所示。路面激励采用C级随机道路,其路面不平度系数Gz0(n0)=256×10-6 m3。虽然常用车速在35 m/s(126 km/h)以下,但为了全面理解汽车行驶速度的影响,仿真中选取车速范围为1~50 m/s(3.6~180 km/h)。
| 参数 | 数值 |
| m2 /kg | 690.0 |
| I2/(kg·m2) | 1 220.0 |
| m1f /kg | 40.5 |
| m1r /kg | 45.4 |
| m3 /kg | 30.0 |
| k1f /(N·m-1) | 192 000 |
| k1r /(N·m-1) | 192 000 |
| k2f /(N·m-1) | 17 000 |
| k2r /(N·m-1) | 22 000 |
| c2f/(N·s·m-1) | 1 500 |
| c2r/(N·s·m-1) | 1 500 |
| L/m | 2.76 |
| a/m | 1.25 |
| b/m | 1.51 |
2.1 两种车辆的性能对比
对于标准车辆和轮毂电机驱动车辆,根据式(15)—(18)分别在每个车速下计算各个指标的均方根,结果如图 2所示。
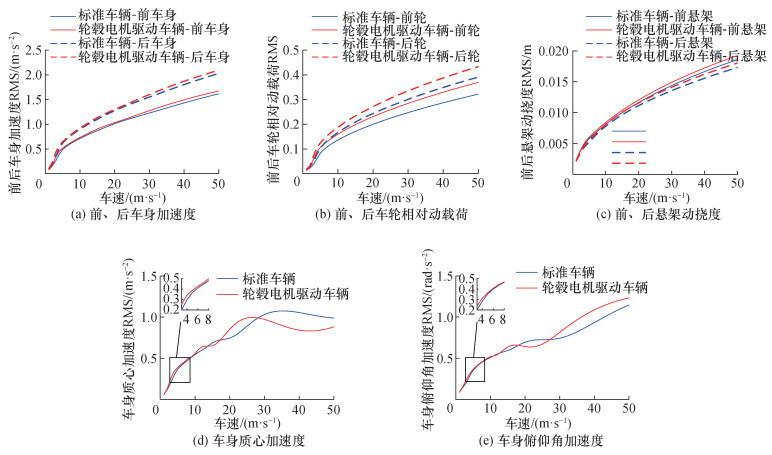
|
| 图 2 两种车辆各指标的RMS |
从图 2a、2b和2c可以看出,在1~50 m/s的车速范围内,轮毂电机驱动车辆的前、后车身加速度,前、后车轮相对动载荷,以及前、后悬架动挠度等指标的RMS均大于标准车辆的。这说明,簧下质量增加恶化了相关性能。其中,前、后车轮相对动载荷恶化程度最严重,前、后悬架动挠度恶化程度次之,前、后车身加速度恶化程度最小。并且随着车速增加,各指标的恶化越严重。这与基于1/4车辆模型得到的结论一致。
两种车辆的车身质心加速度和俯仰角加速度的RMS对比,则呈现出不同的复杂结果。由图 2d可以看出,在1~10 m/s的低速范围内,轮毂电机驱动车辆的质心加速度RMS略大于标准车辆的;在车速为10~14 m/s和18~28 m/s时,轮毂电机驱动车辆的质心加速度RMS大于标准车辆的;而在车速为14~18 m/s和28~50 m/s时,轮毂电机驱动车辆的质心加速度RMS则小于标准车辆的。换言之,在整个车速范围内,簧下质量增加交替恶化和改善车身质心加速度性能。需要注意的是,簧下质量增加显著改善质心加速度的车速区间为汽车不常使用的28~50 m/s (约100~180 km/h)的高速范围。在汽车经常行驶的18~28 m/s (约65~100 km/h)车速范围内,簧下质量增加对质心加速度的恶化程度远大于对前、后车身加速度的恶化程度。比如在车速为22 m/s (约80 km/h)处,质心加速度恶化了将近20%;而前、后车身加速度恶化程度不大于2%。图 2e显示:簧下质量增加对车身俯仰角加速度也有类似的影响规律,不过其改善或恶化对应的车速区间与质心加速度的情形刚好相反。这也意味着轮毂电机驱动恶化车身质心垂向振动时,会改善车身俯仰振动。
下面基于各指标的幅频特性,对上述结果进行讨论。本文主要研究0.1~30 Hz频段内的幅频特性。一般来说,前、后轴系统的垂向振动彼此几乎独立,因此,前、后轴的车身加速度,车轮相对动载荷及悬架动挠度的幅频特性几乎与车速无关。因此对这3个指标幅频特性的讨论均以车速20 m/s为例,如图 3所示。图中,为方便后续对比分析,将整个频带分为车身偏频附近的低频区(0.1~ 4.0 Hz)、车身偏频与车轮偏频之间的中频区(4.0~ 10 Hz)及车轮偏频之后的高频区(10~30 Hz)。
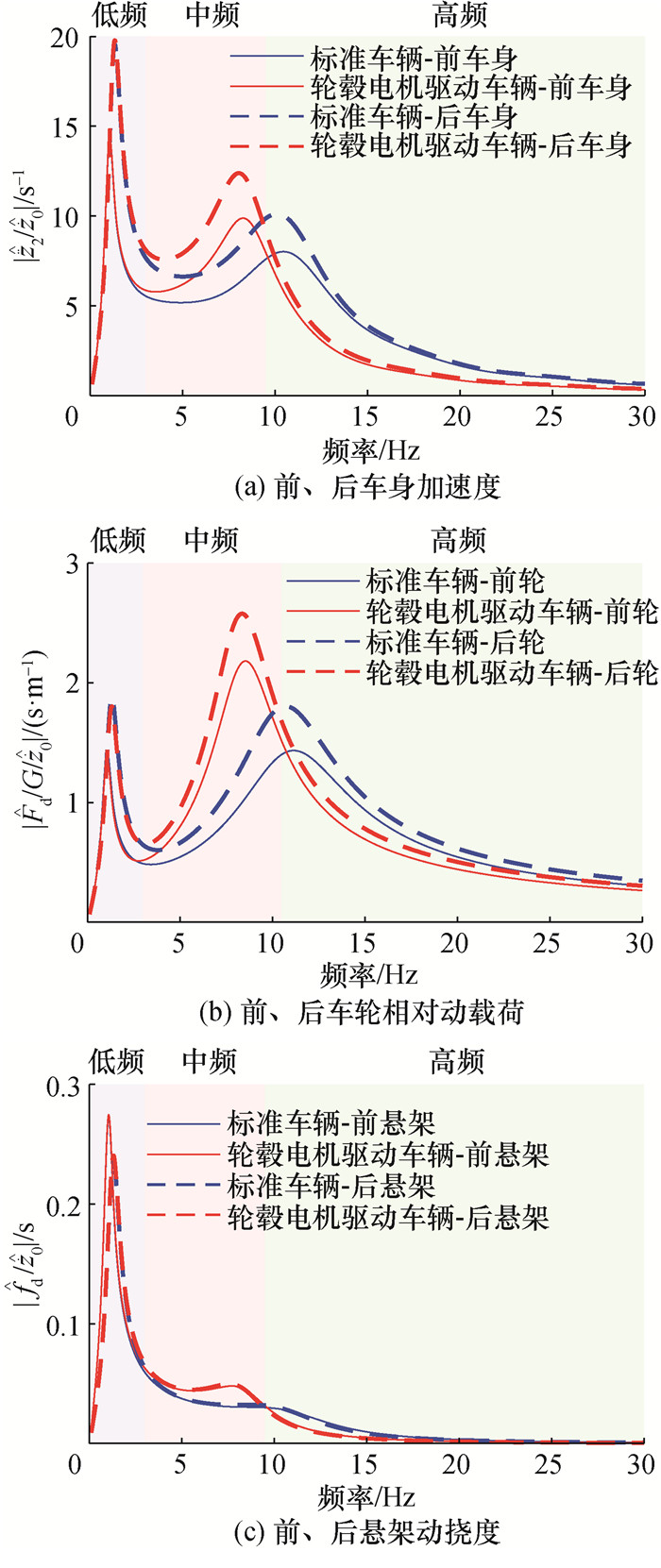
|
| 图 3 两种车辆前、后轴指标的幅频特性 |
从图 3可以看出,前、后车身加速度,前、后车轮相对动载荷和前、后悬架动挠度的幅频特性都呈现为双峰曲线。簧下质量增加对车身偏频1.0 Hz和低频区的幅频特性几乎没有影响,而对高频区域的幅频特性具有改善作用。对于中频4.0~10 Hz范围内的幅频特性,簧下质量增加则显著恶化了所有指标,尤其是在车轮偏频8.0 Hz处。
车身质心加速度和俯仰角加速度的幅频特性与车速相关。这里选取22和44 m/s两个车速的结果进行讨论。二者分别代表质心加速度和俯仰角加速度性能恶化和改善的车速区间,参见图 2d和2e。图 4和5分别展示了2种车速下前后车身相位差、质心加速度和俯仰角加速度的等效幅频特性。
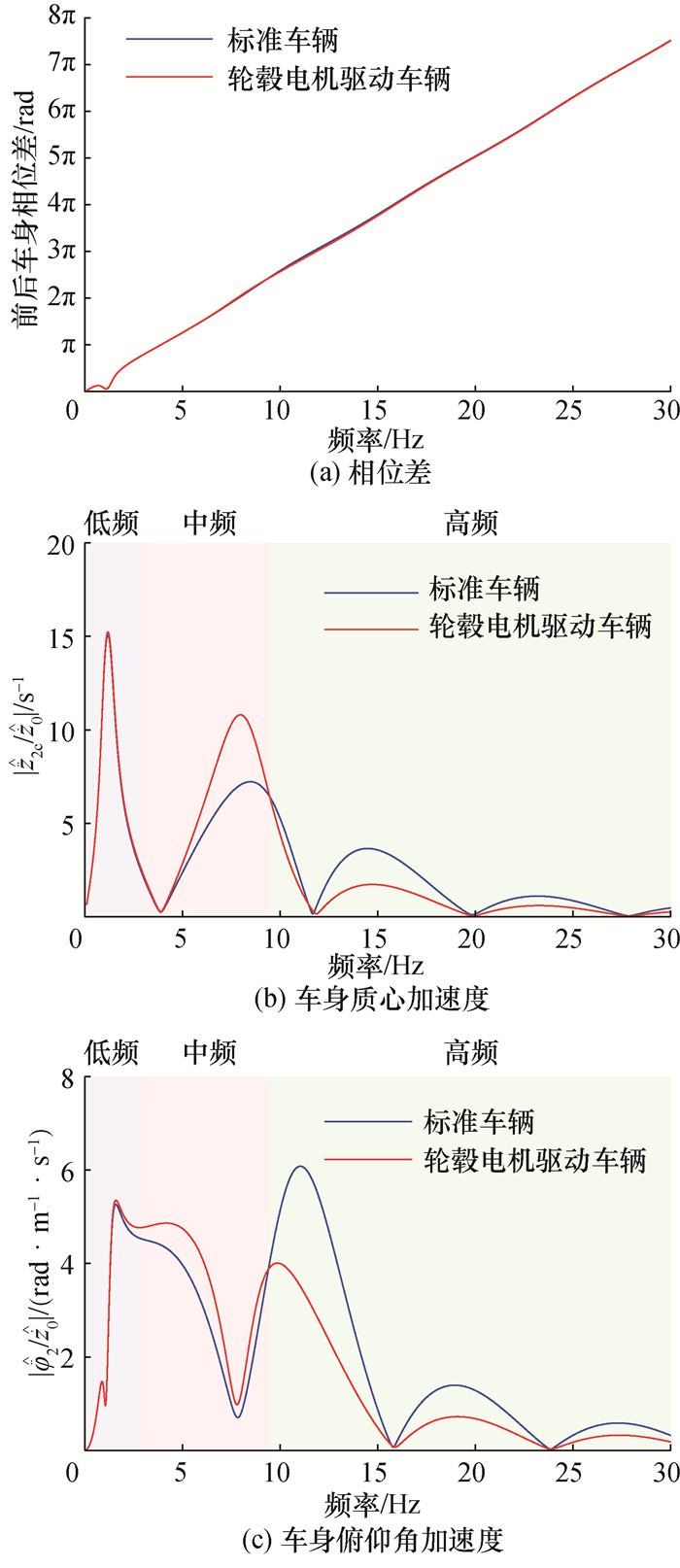
|
| 图 4 车速22 m/s下2种车辆的前后车身相位差、车身质心加速度和俯仰角加速度幅频特性 |
|
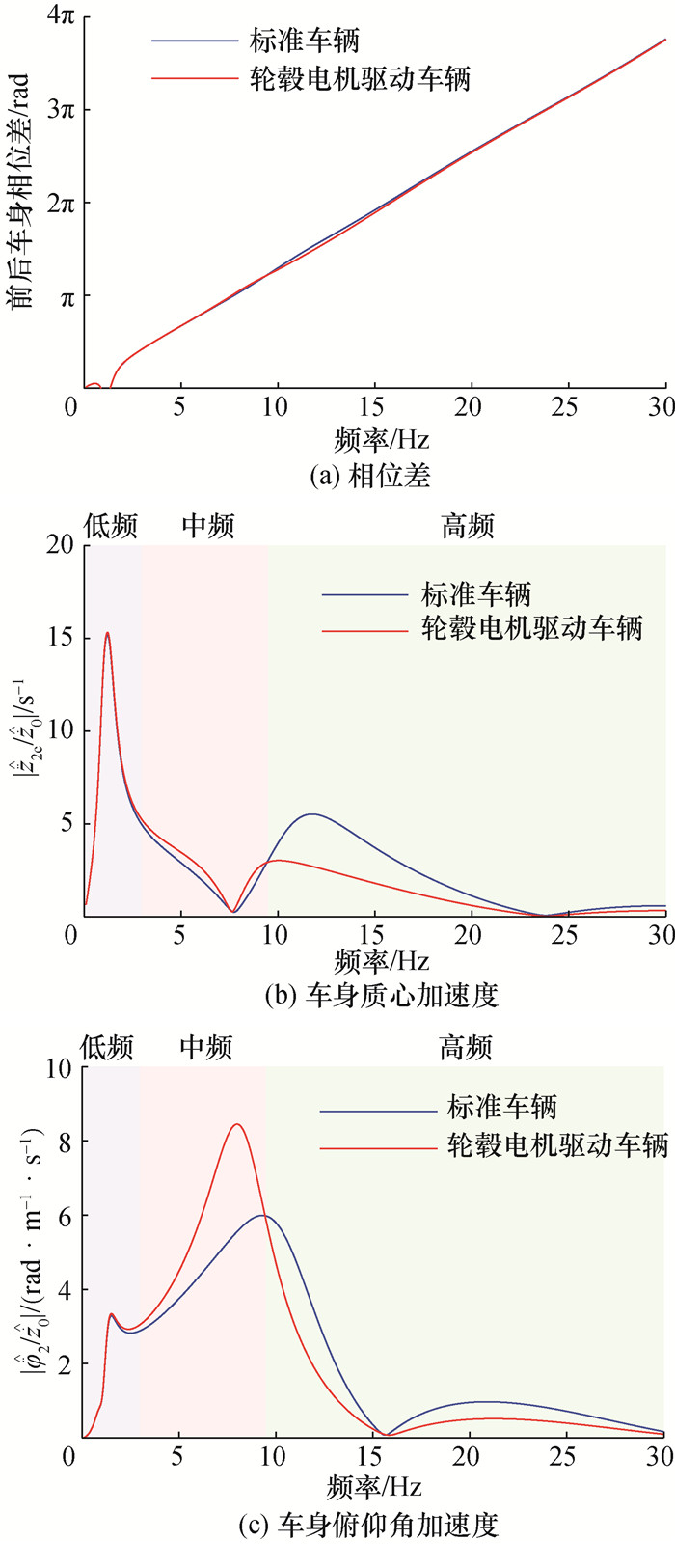
| 图 5 车速44 m/s下2种车辆的前后车身相位差、车身质心加速度和俯仰角加速度幅频特性 |
从图 4和5可以看出,不论标准车辆还是轮毂电机驱动车辆,车身质心加速度与车身俯仰角加速度的幅频特性并非双峰曲线,而是呈现为一种“花环曲线”。这是由于轴距滤波效应的影响[14]。轴距滤波效应主要与前、后车身加速度的相位差有关。当前、后轴系统近似对称且彼此独立时,前、后车身加速度的相位差近似等于前、后路面输入的相位差ωΔt。在相位差为2π的整数倍(ωΔt=2πfL/u=2kπ, k=1, 2, 3,…),即f=ku/L时,车身质心加速度幅频特性取极大值,而俯仰角加速度幅频特性取极小值。在相位差为π的奇数倍(ωΔt=2πfL/u=(2k-1)π, k=1, 2, 3,…),即f=(2k-1)u/2L时,车身质心加速度幅频特性取极小值,而俯仰角加速度幅频特性取极大值。
下面对比标准车辆和轮毂电机驱动车辆的相关幅频特性。从图 5b和5c可以发现,当车速为44 m/s时,由于轴距滤波效应,中频8.0 Hz处的车身质心加速度取得极小值,俯仰角加速度取得最大值,从而抑制了轮毂电机驱动车辆中簧下质量增加对质心加速度的恶化,但对俯仰角加速度的恶化则被放大。与此相反,当车速为22 m/s时,轴距滤波效应会放大轮毂电机驱动车辆中频8.0 Hz处簧下质量增加对质心加速度的恶化效果,而抑制对俯仰角加速度的恶化,如图 4b和4c所示。对于高频区域的幅频特性,在2种车速下,轮毂电机驱动车辆的2个指标均是改善的。
各指标RMS与幅频平方曲线和坐标轴所包围的面积呈正比。因此,对应车速44 m/s,轮毂电机驱动车辆的车身质心加速度RMS小于标准车辆的,而俯仰角加速度RMS则大于标准车辆的。对应车速22 m/s,结果刚好相反。
总结上述分析,可以推断出:在簧下质量增加导致车辆性能恶化的中频[f1, f2]范围内,当前、后轮路面激励的相位差为2kπ,即车速约在[f1L/k, f2L/k]时,簧下质量增加会增大车身质心加速度的RMS,而减小车身俯仰角加速度的RMS;当前、后轮路面激励的相位差为(2k-1)π,即车速约在[2f1L/(2k-1), 2f2L/(2k)-1)] 时,簧下质量增加将减小车身质心加速度的RMS,而增大车身俯仰角加速度的RMS。总体而言,在整个车速范围内,簧下质量增加对车身质心加速度和俯仰角加速度性能的影响均呈现出交替恶化和改善的特征,而且对这2个性能的影响趋势正好相反。
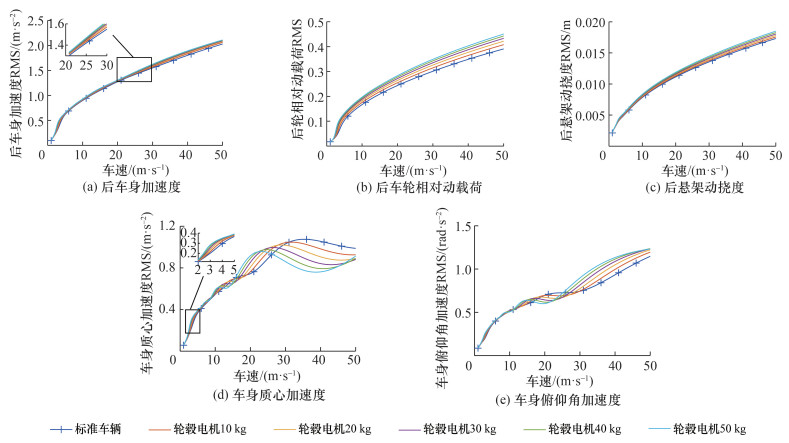
2.2 轮毂电机质量的影响2.1节的讨论中假设轮毂电机质量为30 kg,本节将分析轮毂电机质量对车辆性能的影响,以揭示电机或动力系统轻量化的潜力。为此,轮毂电机的质量分别取10、20、30、40和50 kg,各指标的RMS随车速的变化如图 6所示。对于对应前、后轴的3个指标即车身垂向加速度、车轮相对动载荷和悬架动挠度,因为前、后轴的结论类似,这里仅展示后轴各指标的变化曲线,如图 6a、6b和6c所示。
|
| 图 6 不同轮毂电机质量对应的各性能指标的RMS |
从图 6a、6b和6c可以看出,随着轮毂电机质量增加,前、后车身加速度,前、后车轮相对动载荷和前、后悬架动挠度的RMS在所有车速下均增加。换言之,簧下质量增加越多,3个车辆指标性能恶化越严重。
由图 6d和6e可以发现,随着轮毂电机质量增加,轮毂电机驱动车辆与标准车辆的车身质心加速度和俯仰角加速度RMS曲线的交点向左移动。这说明,簧下质量增加导致的车身质心加速度和俯仰角加速度性能恶化或改善的车速区间整体向低速方向偏移。当车速小于10 m/s时,轮毂电机驱动的质心加速度和俯仰角加速度RMS均随电机质量增大略有增加;在中速范围内(如20 m/s时),电机质量越大,则轮毂电机驱动车辆的质心加速度RMS越大,俯仰角加速度RMS越小,即表明质心加速度恶化越严重,俯仰角加速度改善越明显;而在高速范围内(如40 m/s时),电机质量越大,则轮毂电机驱动车辆的质心加速度改善越明显,俯仰角加速度恶化越严重。
3 轮毂电机驱动方式的影响根据轮毂电机位置的不同,轮毂驱动可以分为轮毂电机前驱、轮毂电机后驱以及轮毂电机四驱3种驱动方式。不同驱动方式对应的半车模型如图 7所示。
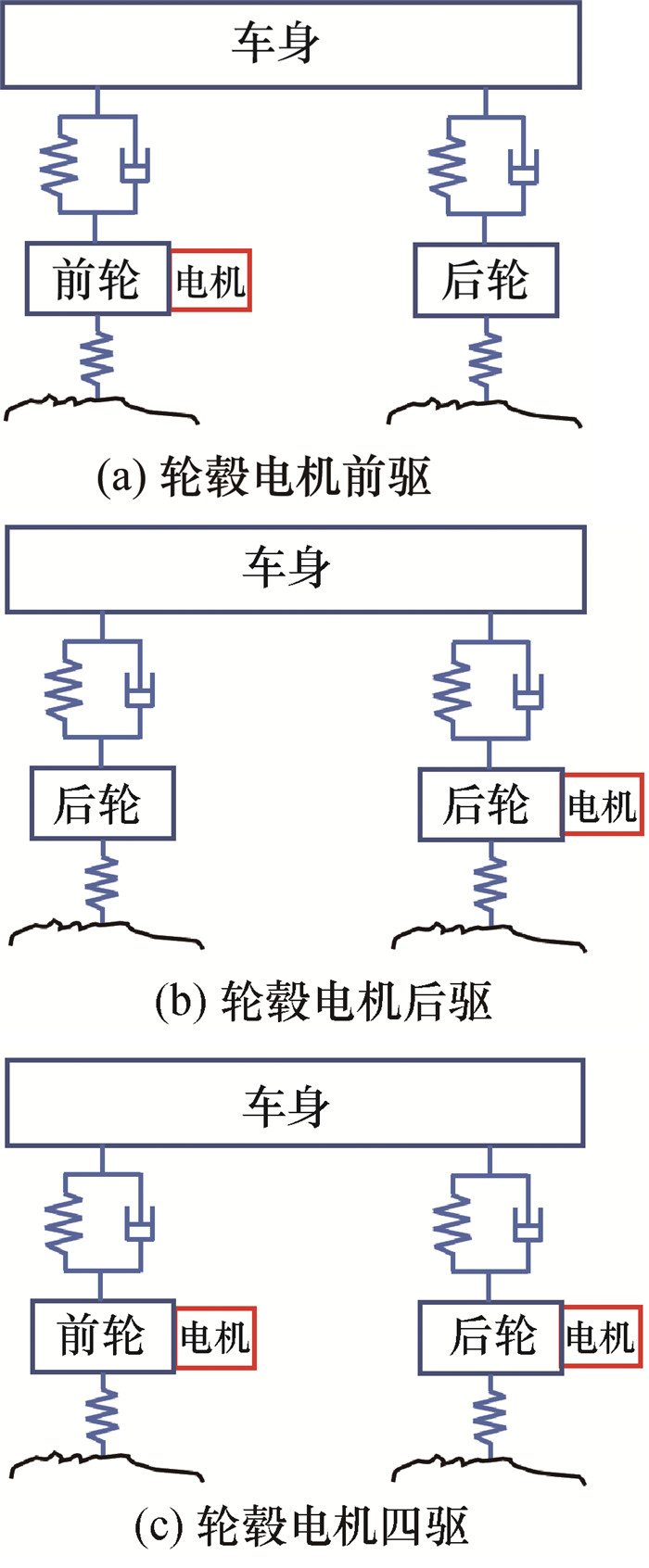
|
| 图 7 轮毂电机驱动方式简图 |
显然,不同轮毂电机驱动方式会影响前、后轴的轴荷分布,进而影响车辆动力学。因此,在分析不同轮毂电机驱动方式的影响之前,首先需要进行轴荷校核,确保3种驱动方式下整车的前、后轴荷分布满足车辆开发的相关要求。采用第2章中的算例数据,分别计算标准车辆与3种轮毂电机驱动车辆的前后轴荷,结果如表 2所示。为便于讨论,表中列出了乘用车常见的轴荷分布范围。
| % | |||||||||||||||||||||||||||||
| 车型 | 前轴轴荷 | 后轴轴荷 | |||||||||||||||||||||||||||
| 常用设计范围 | 51~56 | 44~49 | |||||||||||||||||||||||||||
| 标准车辆 | 53.82 | 46.18 | |||||||||||||||||||||||||||
| 轮毂电机前驱 | 55.64 | 44.36 | |||||||||||||||||||||||||||
| 轮毂电机后驱 | 51.70 | 48.30 | |||||||||||||||||||||||||||
| 轮毂电机四驱 | 53.53 | 46.47 | |||||||||||||||||||||||||||
表 2显示,对于本例中采用的轮毂电机质量30 kg,3种轮毂电机驱动车辆的前、后轴荷均处在常用的轴荷分配范围之内。下面对比3种驱动方式对车辆垂向动力学性能的影响,各指标的RMS随车速的变化曲线如图 8所示。
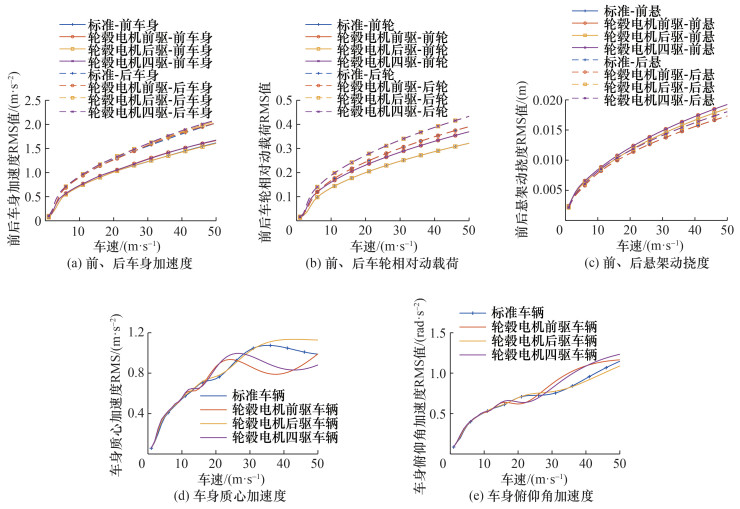
|
| 图 8 不同轮毂电机驱动方式车辆性能指标的RMS |
从图 8a、8b和8c可以发现:在所有车速下,对于车身加速度、车轮相对动载荷和悬架动挠度,轮毂电机四驱车辆的前、后轴对应的3个指标均有所恶化;而轮毂电机前驱、后驱车辆则只恶化对应车轴(前轴或后轴)的3个指标。
对于车身质心加速度和俯仰角加速度,不同驱动方式影响的规律则不同。图 8d和8e中,轮毂电机前驱和四驱车辆的结果相似,2个指标均呈现明显的交替恶化与改善趋势。不过在这2种驱动方式中,指标恶化的车速区间有所不同。以质心加速度指标为例,四驱车辆性能恶化的车速区间主要为18~ 28 m/s,而前驱车辆性能恶化的车速区间主要为18~26 m/s。值得注意的是,对于轮毂电机后驱车辆,其质心加速度RMS在车速32 m/s (约115 km/h)以下与标准车辆相差不大,仅在高于32 m/s的高速范围内有明显的增加。实际汽车常用的车速通常不超过35 m/s (126 km/h),因此可以认为轮毂电机后驱方式对车身质心加速度的负效应较小。由于质心位置通常靠近驾驶员和前排乘客的位置,因此轮毂电机后驱方式对乘坐舒适性的影响较小。这与文[3]中基于试验得到的结论一致。
为进一步阐明相关机理,下面以车身质心加速度为例,仍选取22和44 m/s两个代表车速,从幅频特性角度对3种轮毂驱动方式对应的动力学性能差别进行解释。图 9和10分别展示了2种车速下前、后车身加速度的相位差和车身质心加速度的幅频特性曲线。从图 9a和10a的相位差图中容易发现,不同轮毂电机驱动方式的前、后车身相位差在7~15 Hz的频带内有所不同。轮毂电机后驱车辆的前、后车身相位差在7~15 Hz频带内增加;轮毂电机前驱车辆的前、后车身相位差在该频率范围减小;而轮毂电机四驱车辆的相位差和标准车辆几乎相同,近似等于前、后路面输入的相位差。这主要是因为在轮毂电机前驱与轮毂电机后驱车辆中,前轮或后轮的簧下质量增加会使对应车轴(前轴或后轴)上方车身的加速度在车轮偏频附近出现相位滞后。
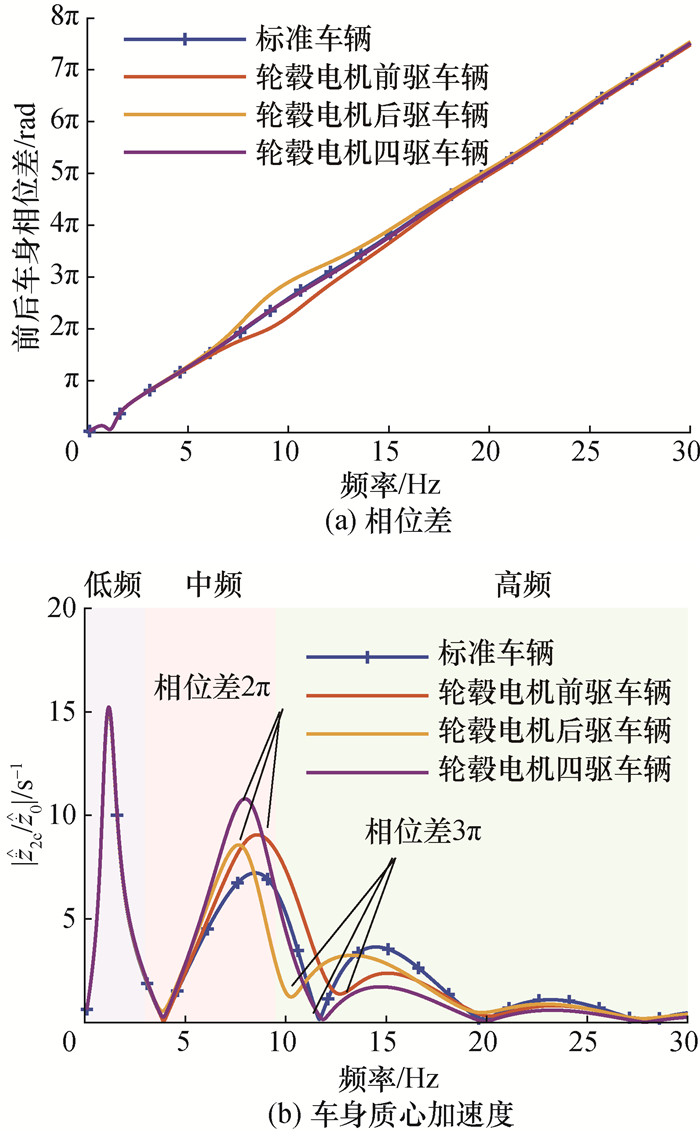
|
| 图 9 车速22 m/s下不同轮毂电机驱动方式前后车身相位差和车身质心加速度的幅频特性 |
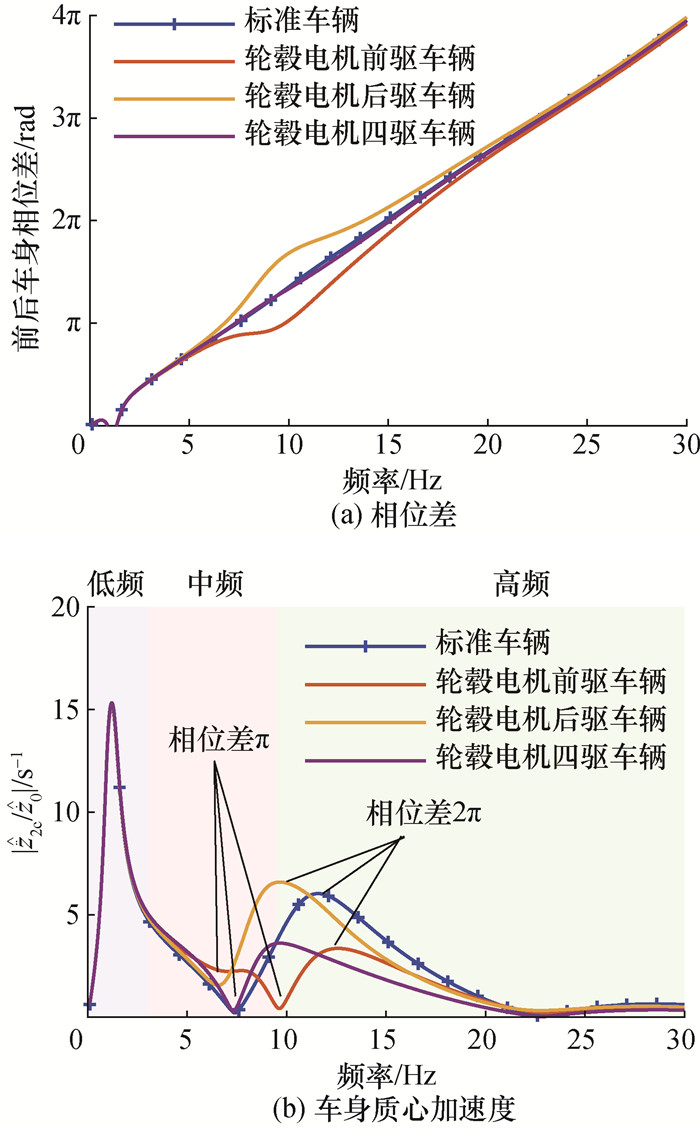
|
| 图 10 车速44 m/s下不同轮毂电机驱动方式前后车身相位差和车身质心加速度的幅频特性 |
从图 9a可以看出,在车速为22 m/s时,不同驱动方式的差异主要表现在相位差为2π至3π对应的区间。反映到图 9b的幅频曲线中,轮毂电机后驱车辆中对应相位差2π的极大值点和对应相位差3π的极小值点左移,而轮毂电机前驱车辆相应的极大值点和极小值点右移。从幅频曲线的形状可以发现,轮毂电机后驱车辆中频区域的幅频曲线花瓣变窄,而轮毂电机前驱车辆中频区域的花瓣变宽,轮毂电机四驱车辆的中频区域花瓣宽度不变。此外,对于3种轮毂电机驱动车辆,由于簧下质量增加,中频区域的幅频曲线被恶化,高频区域的幅频曲线被改善,即中频区域的花瓣高度均增加,而高频区域花瓣高度减小。因此对于轮毂电机前驱和四驱车辆,由于中频区域花瓣面积显著增大,整个幅频曲线面积增加,而对于轮毂电机后驱车辆,中频区域花瓣面积增加不大,高频花瓣面积减小,整个幅频曲线面积变化不大。
依据幅频曲线面积与RMS之间的对应关系,可知:在车速22 m/s时,相比于标准车辆,轮毂电机前驱和四驱车辆质心加速度RMS显著增加,而轮毂电机后驱车辆的质心加速度RMS增加量很小。
根据图 10a则可以发现,当车速为44 m/s时,不同驱动方式的主要差别表现在相位差为π至2π的区间。反映在图 10b的幅频曲线中,轮毂电机后驱车辆对应相位差2π的极大值点和对应相位差π的极小值点左移,而轮毂电机前驱车辆相应的极大值点和极小值点右移。因此在轮毂电机后驱车辆中,簧下质量增加恶化的中频范围内的花瓣并未被完全抑制,而轮毂电机前驱和四驱车辆中,簧下质量增加恶化的中频范围内的花瓣基本被抑制。所以,在车速44 m/s时,轮毂电机后驱车辆质心加速度RMS显著增加,而轮毂电机前驱和四驱车辆的质心加速度RMS有所改善。
4 结论本文基于半车模型,选择车身质心垂向加速度,前、后车身垂向加速度,车身俯仰角加速度,前、后车轮相对动载荷和前、后悬架动挠度等作为性能评价指标,在1~50 m/s (3.6~180 km/h)的车速范围内针对传统驱动车辆和轮毂电机驱动车辆开展仿真计算,考虑车速、车身位置、电机质量以及轮毂驱动方式等因素,系统分析了轮毂电机驱动车辆中簧下质量增加对车辆平顺性的影响规律与作用机理。主要结论如下:
1) 簧下质量增加在所有车速下均会恶化车轮动载荷和悬架动挠度,因此会恶化轮胎接地特性和悬架性能。
2) 由于轴距滤波效应,簧下质量增加对车身不同位置加速度的影响不同。前、后车身加速度在所有车速下均被恶化,而质心加速度和俯仰角加速度则均呈现交替恶化和改善的特点。其中,在18~28 m/s(约65~100 km/h)的常用车速范围内,簧下质量增加会增大质心加速度,而降低俯仰角加速度;在28~50 m/s(约100~180 km/h)的高速范围内,簧下质量增加会降低质心加速度,而增大俯仰角加速度。
3) 随着轮毂电机质量增加,前、后轴的车身加速度,车轮相对动载荷和悬架动挠度在不同车速下的恶化程度都增大。质心加速度和车身俯仰角加速度,在性能恶化的车速范围内,恶化程度随电机质量增大而更趋严重;在性能改善的车速范围内,改善程度也更明显。
4) 在常用车速下,轮毂电机前驱和四驱车辆的簧下质量增加显著增大了车身质心垂向和俯仰加速度;而轮毂电机后驱车辆中,该影响较小。
| [1] |
李勇, 徐兴, 孙晓东, 等. 轮毂电机驱动技术研究概况及发展综述[J]. 电机与控制应用, 2017, 44(6): 1-7, 18. LI Y, XU X, SUN X D, et al. Review and future development of in-wheel motor drive technology[J]. Electric Machines and Control Application, 2017, 44(6): 1-7, 18. DOI:10.3969/j.issn.1673-6540.2017.06.001 (in Chinese) |
| [2] |
MURATA S. Innovation by in-wheel-motor drive unit[J]. Vehicle System Dynamics, 2012, 50(6): 807-830. DOI:10.1080/00423114.2012.666354 |
| [3] |
VOS R, BESSELINK I J M, NIJMEIJER H. Influence of in-wheel motors on the ride comfort of electric vehicles [C]// 10th International Symposium on Advanced Vehicle Control (AVEC 2010). Loughborough, UK: AVEC, 2010: 835-840.
|
| [4] |
ANDERSON M, ENGINEERING L, HARTY D, et al. Unsprung mass with in-wheel motors-myths and realities [C]// 10th International Symposium on Advanced Vehicle Control (AVEC 2010). Loughborough, UK: AVEC, 2010: 261-266.
|
| [5] |
WATTS A, VALLANCE A, WHITEHEAD A, et al. The technology and economics of in-wheel motors[J]. SAE International Journal of Passenger Cars: Electronic and Electrical Systems, 2010, 3(2): 37-57. DOI:10.4271/2010-01-2307 |
| [6] |
NAGAYA G, WAKAO Y, ABE A. Development of an in-wheel drive with advanced dynamic-damper mechanism[J]. JSAE Review, 2003, 24(4): 477-481. DOI:10.1016/S0389-4304(03)00077-8 |
| [7] |
JIN L Q, SONG C X, WANG Q N. Influence of in-wheel motor structure about the contact and comfort for electric vehicle [C]// 2010 2nd International Workshop on Intelligent Systems and Applications. Wuhan, China: IEEE, 2010: 1-5.
|
| [8] |
KATSUYAMA E, OMAE A. Improvement of ride comfort by unsprung negative skyhook damper control using in-wheel motors[J]. SAE International Journal of Alternative Powertrains, 2016, 5(1): 214-221. DOI:10.4271/2016-01-1678 |
| [9] |
WANG R C, JIANG Y, DING R K, et al. Design and experimental verification of self-powered electromagnetic vibration suppression and absorption system for in-wheel motor electric vehicles[J]. Journal of Vibration and Control, 2022, 28(19-20): 2544-2555. DOI:10.1177/10775463211014419 |
| [10] |
童炜, 侯之超. 轮毂驱动电动汽车垂向特性与电机振动分析[J]. 汽车工程, 2014, 36(4): 398-403, 425. TONG W, HOU Z C. Analyses on the vertical characteristics and motor vibration of an electric vehicle with motor-in-wheel drive[J]. Automotive Engineering, 2014, 36(4): 398-403, 425. DOI:10.3969/j.issn.1000-680X.2014.04.003 (in Chinese) |
| [11] |
TERRA R T, BARBOSA R S. The influence of hub driven motors on vehicle dynamics behavior [C]// 25th SAE BRASIL International Congress and Display. Sao Paulo, Brazil: SAE, 2016.
|
| [12] |
SHI D P, DONG M M, YANG J, et al. Impact on the vehicle ride comfort caused by the changes of unsprung mass [C]// 2016 International Conference on Applied Mechanics, Mechanical and Materials Engineering (AMMME 2016). Fujian, China: DEStech Transactions on Materials Science and Engineering, 2016.
|
| [13] |
李宁宁, 刘苏. 脉冲输入下的簧下质量对车辆平顺性的影响研究[J]. 机械设计与制造工程, 2017, 46(9): 108-111. LI N N, LIU S. Research on the influence of spring mass to vehicle smoothness under pulse input[J]. Machine Design and Manufacturing Engineering, 2017, 46(9): 108-111. (in Chinese) |
| [14] |
余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009. YU Z S. Automobile Theory[M]. 5th ed. Beijing: Mechanical Industry Press, 2009. (in Chinese) |
| [15] |
ISO. Mechanical vibration and shock—evaluation of human exposure to whole-body vibration—part 1: General requirements: ISO 2631-1 [S]. Geneva: ISO, 1997.
|
| [16] |
喻凡, 林逸. 汽车系统动力学[M]. 2版. 北京: 机械工业出版社, 2016. YU F, LIN Y. Automobile System Dynamics[M]. 2nd ed. Beijing: Mechanical Industry Press, 2016. (in Chinese) |



