公共交通是城市交通系统的重要组成,其中公交车相比其他公共交通方式具备成本低、部署快的特点,得到广泛应用[1]。但相比其他车辆,公交车需要频繁进站和出站。当公交车进站前尚未行驶到邻近站台的车道,以及需要从港湾式车站驶出时,必须要进行强制换道。强制换道是指车辆为了实现避障、保持预定路径等目标必须采取的换道行为。不同于自由换道,强制换道车辆会采取更激进的换道策略以保障换道成功率,加之公交车车型较大,会对换道安全性和上游交通产生更大的影响[1]。近年来,智能网联汽车(intelligent and connected vehicle,ICV)和云控系统的发展为改善这一过程提供了可能。云控系统能够与周围ICV和路侧单元进行通信,实现广域融合感知,并调度多辆ICV实现协同换道,可有效提高换道的成功率、安全性和交通效率[2-3]。因此,针对进出站强制换道过程开发智能网联公交车的自动换道策略具备重要意义。
换道时刻决策是换道策略的重要一环。目前常用的换道决策模型可以分为基于规则、基于博弈论、基于机器学习等多个类别[4]。具体到公交车换道过程,Yao等[5]建立了智能网联公交车出站过程的演化博弈模型,用于判断公交车在出站时的倾向决策,但主要聚焦于宏观层面,不适用于微观场景的决策。Lü等[6]采用门控循环单元(gate recurrent unit,GRU)建立了公交车进站换道的决策模型,通过提取周围车辆状态的特征变量作为输入,并考虑公交车进站优先级进行决策,但该模型假设其他车辆具备通信能力并接受公交车换道请求,难以用于现实中存在大量人工驾驶车辆(human driven vehicle,HDV)的场景。上述公交车换道决策模型尽管考虑了进出站强制换道过程,但在决策中未衡量周围车辆受到的影响,难以有效降低强制换道对上游交通的影响。
确定换道时刻后,还需要为公交车规划合适的换道轨迹。Shi等[7]针对自动驾驶公交车换道避障场景,采用势函数进行换道轨迹规划,该方法能保障换道过程的安全,但未考虑交通效率等因素。Bae等[8]针对一般换道过程,采用最优控制的思路进行轨迹规划,并充分考虑了公交车的舒适性要求,总结了过去研究中对于加速度和加加速度的约束标准。Yu等[9]针对公交车超车换道过程,采用三次多项式换道轨迹结合最优控制方法规划最优换道轨迹。Alcázar[10]、冯敏[11]则针对公交车进入港湾式车站的换道过程,通过设置车站形状约束、车辆运动约束,采用最优控制、反正切函数轨迹等方式进行轨迹规划。上述关于公交车换道轨迹规划的研究,对周围车辆的考虑较少,且基于单车智能实现,在面对车流密度较大的场景时无法及时换道,难以应对进出站强制换道过程。
综上所述,目前针对智能网联公交车换道算法的研究均采用单车控制策略,缺少对周围车辆的考虑,难以处理车间冲突,在车流密度较大的工况下无法同时保证公交车在进出站强制换道过程的成功率和安全性,且容易对上游交通造成干扰。
针对以上问题,本文针对公交车进出站强制换道过程,提出了一种云控环境下智能网联公交车的两车协同换道策略,通过云控系统对两车进行调度。具体而言,针对进站过程,建立了基于换道收益准则的决策模型,制定了包含纵向调整、协同换道的两段式轨迹规划方法,在保障安全的同时减少对上游交通的影响,并基于分层二次规划改善算法实时性;针对出站过程,考虑出站运动特点,建立了基于规则的决策方法和协同车提前减速策略,制定了考虑港湾式车站特点的规划方法,以保障出站换道的成功率和安全。通过仿真和硬件在环实验验证了该策略的有效性、性能优势和计算实时性。
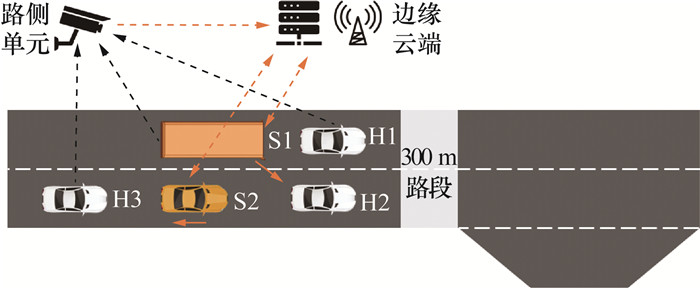
1 场景描述针对进站强制换道过程,本文考虑公交车在左侧车道向邻近站台的右侧车道换道的场景,如图 1所示。取车站前300 m为协同换道区域;S1代表公交车,S2代表协同车,二者均为ICV;其余白色车则代表HDV。
|
| 图 1 进站协同换道场景 |
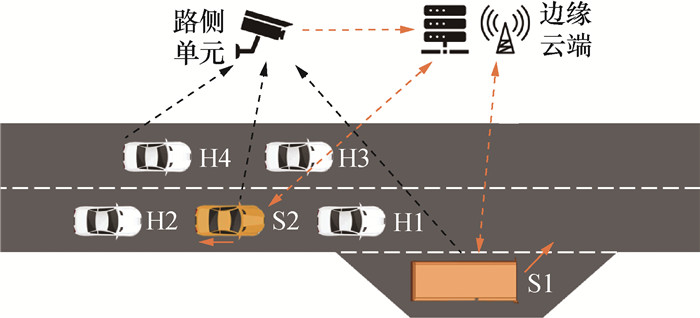
针对出站强制换道过程,本文考虑公交车从港湾式车站出站的场景,如图 2所示。
|
| 图 2 出站协同换道场景 |
图 1和2中,ICV和路侧感知单元实时获取周围车辆信息后上传至云端,云端根据广域感知信息为ICV决策换道时刻,并规划换道轨迹,而后将换道轨迹下发至参与协同换道的车辆,由ICV实现轨迹跟踪。为了保证提出策略具有更好的适用性,云端会以固定频率进行滚动时域规划,根据最新感知信息更新规划轨迹。本文假设车辆与云端通信环境理想,不考虑通信时延;且要求公交车至少具备L4级自动驾驶功能,协同车具备L3级或以上的自动驾驶功能。
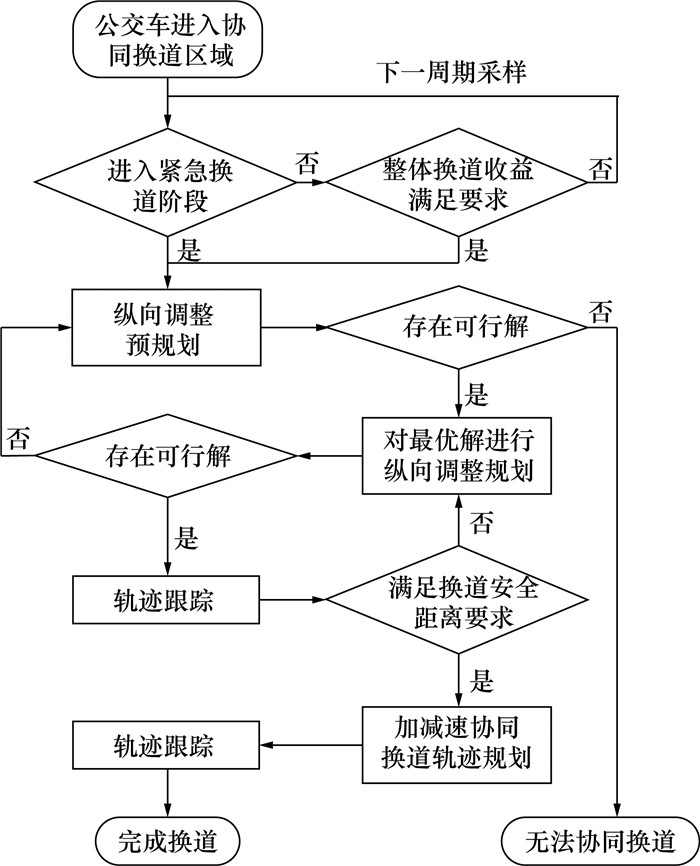
2 进出站协同换道控制策略 2.1 进站协同换道策略设计根据图 1场景,制定了图 3的进站协同换道流程。根据周围车辆信息决策协同换道时刻与方式后,通过滚动时域规划完成进站协同换道。
|
| 图 3 进站协同换道流程 |
2.1.1 进站决策算法
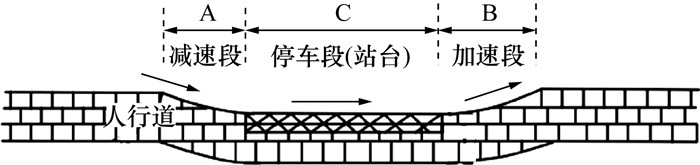
为了保障公交车及时到达右侧车道,首先判断公交车是否需要紧急换道,参考Wang等[12]思路对站前道路进行划分,如图 4所示。

|
| 图 4 公交车站前路段划分 |
根据城市车辆运行速度及公交车进站规定,划定车站前50 m为减速进站路段;设置紧急换道阶段为150 m长。进入紧急换道阶段后轨迹规划仅考虑保证换道安全和成功的必要约束。
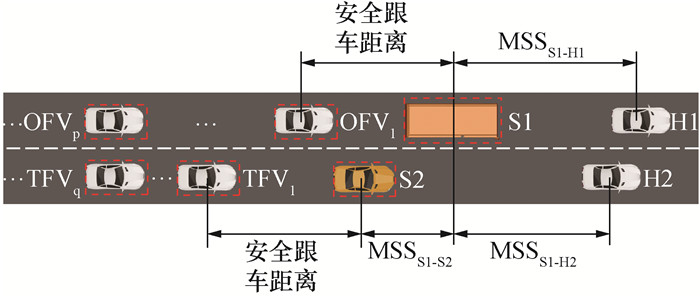
若流程未进入紧急换道阶段,则根据收益函数进行决策。参考了Kesting等[13]提出的最小化换道引发制动(minimizing overall braking induced by lane change,MOBIL)模型,它假设换道在瞬间完成,忽略各车的相对纵向移动,但本文策略中纵向调整会导致各车相对位置发生较大变化。因此在每次采样后,决策算法会通过预测未来1 s的平均速度衡量换道收益。具体预测根据换道最小安全距离(minimum safety spacing,MSS)进行,如图 5所示。
|
| 图 5 整体换道收益预测分析 |
以两车道最前方的H1、H2作为参考,纵向调整后,ICV和HDV之间应满足换道MSS。将换道MSS或最小跟车距离,两车道上H1和H2及其之后各车的位置xk、速度vk输入最优速度模型(optimal velocity model,OVM)[14],如下所示:
| $ a_k=K\left(V\left(s_k\right)-v_k\right), $ | (1) |
| $ V(s)=V_1+V_2 \tanh \left(C_1\left(s-l_{\mathrm{c}}\right)-C_2\right) . $ | (2) |
其中:sk=xk-1-xk,即车辆k和其前车(k-1)的间距;lc代表最小安全距离,对ICV为换道MSS,对HDV为最小跟车距离,设置为10 m;K、V1、V2、C1和C2均为参数,与文[14]中一致,分别取0.85 s-1、6.75 m·s-1、7.91 m·s-1、0.13 m-1和1.57。由此可预测调整过程中各车的加速度、速度变化,估算换道收益:
| $ \begin{gathered} G=\sum\limits_{n=1}^2\left(\widetilde{v}_{\mathrm{S} n}-v_{\mathrm{S} n}\right)+\eta \sum\left(\tilde{v}_{\mathrm{OFV}_p}-v_{\mathrm{OFV}_p}\right)+ \\ \eta \sum\left(\widetilde{v}_{\mathrm{TFV}_q}-v_{\mathrm{TFV}_q}\right) . \end{gathered} $ | (3) |
其中:η为礼貌系数;
而后对预测加速度和换道收益进行判断:
| $ \left\{\begin{array}{l} G>v_{\text {gain }}, \\ \left|a_k\right| \leqslant a_{\text {safe }} . \end{array}\right. $ | (4) |
其中:vgain为收益标准;asafe为安全加速度,确保调整过程的安全。据此可以快速且较为准确地确定协同换道时刻。
确定换道时刻后,对加速协同和减速协同2种方式分别进行1次预规划,选择换道收益较优者进行轨迹规划。
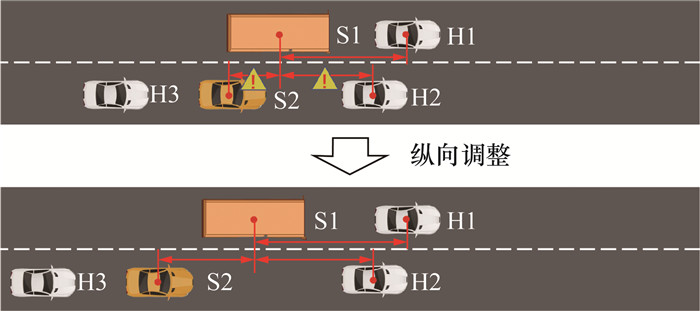
2.1.2 纵向调整阶段轨迹规划根据图 3中流程,进站协同换道分为纵向调整和协同换道两阶段。纵向调整阶段通过两ICV的纵向速度调整改变周围车辆状态,使各车之间满足换道要求。具体过程如图 6所示。
|
| 图 6 纵向调整过程示意 |
1) 优化问题构建。
选取四次多项式描述ICV的纵向调整运动[15]。根据初始时刻ICV的纵向位置、速度和加速度信息(x0, Sn, vx0, Sn, ax0, Sn),设定调整结束时刻加速度aadj, Sn为0,以调整结束时刻速度vadj, Sn为待求量,可以得到5个边界方程,求解待定系数得到如下纵向轨迹方程:
| $ \begin{gathered} x_{\mathrm{S} n}(t)=x_{0, \mathrm{~S} n}+v_{x 0, \mathrm{~S} n} t+ \\ \frac{a_{x 0, \mathrm{~S} n}}{2} t^2-\frac{3 v_{x 0, \mathrm{~S} n}-3 v_{\mathrm{adj}, \mathrm{S} n}+2 a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}}{3 t_{\mathrm{adj}}^2} t^3+ \\ \frac{2 v_{x 0, \mathrm{~S} n}-2 v_{\mathrm{adj}, \mathrm{S} n}+a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}}{4 t_{\mathrm{adj}}^3} t^4, \\ t \in\left[0, t_{\mathrm{adj}}\right], n=1, 2 . \end{gathered} $ | (5) |
其中tadj为调整时间。可以看出,只需给定一组(tadj, vadj, S1, vadj, S2)即可确定一组纵向调整轨迹,以此作为决策变量构建优化问题。
考虑高效性、舒适性和换道平顺性,设计如下最小化目标函数:
| $ \begin{gathered} & J\left(t_{\mathrm{adj}}, v_{\mathrm{adj}, \mathrm{S} 1}, v_{\mathrm{adj}, \mathrm{S} 2}\right)=w_{\mathrm{t}} J_{\mathrm{t}}+w_{\mathrm{c}} J_{\mathrm{c}}+w_{\mathrm{v}} J_{\mathrm{v}}, \\ & J_{\mathrm{t}}=t_{\mathrm{adj}}, \\ & J_{\mathrm{c}}=\sum\limits_{n=1}^2 \int_0^{t_{\mathrm{adj}}} j_{x, \mathrm{~S} n}^2 \mathrm{~d} t, \\ & J_{\mathrm{v}}=\sum\limits_{n=1}^2\left(v_{\mathrm{adj}, \mathrm{S} n}-v_{\mathrm{H} 2}\right)^2 . \end{gathered} $ | (6) |
其中:wt、wc和wv分别为时间权重、舒适性权重和换道平顺性权重;jx, Sn为ICV的纵向加加速度;vH2为目标车道前车H2的速度。目标函数中,减小Jt项可减少调整时间;减小Jc项可减小调整过程加加速度变化;减小Jv项可使调整结束时刻速度接近H2车速,以减小后续换道阶段的速度变化幅度。
调整结束时刻各车的速度、相对位置需要满足换道MSS要求,参考关书睿等[15]方法,设定如下形式约束:
| $ \left\{\begin{array}{l} x_{\mathrm{H} 1}\left(t_{\mathrm{adj}}\right)-x_{\mathrm{S} 1}\left(t_{\mathrm{adj}}\right) \geqslant \operatorname{MSS}_{\mathrm{S} 1-\mathrm{H} 1}\left(v_{\mathrm{H} 2}, v_{\mathrm{adj}, \mathrm{S} 1}, v_{\mathrm{H} 1}\right), \\ x_{\mathrm{H} 2}\left(t_{\mathrm{adj}}\right)-x_{\mathrm{S} 1}\left(t_{\mathrm{adj}}\right) \geqslant \operatorname{MSS}_{\mathrm{S} 1-\mathrm{H} 2}\left(v_{\mathrm{adj}, \mathrm{S} 1}, v_{\mathrm{H} 2}\right), \\ x_{\mathrm{S} 1}\left(t_{\mathrm{adj}}\right)-x_{\mathrm{S} 2}\left(t_{\mathrm{adj}}\right) \geqslant \operatorname{MSS}_{\mathrm{S} 1-\mathrm{S} 2}\left(v_{\mathrm{H} 2}, v_{\mathrm{adj}, \mathrm{S} 2}, v_{\mathrm{adj}, \mathrm{S} 1}\right) . \end{array}\right. $ | (7) |
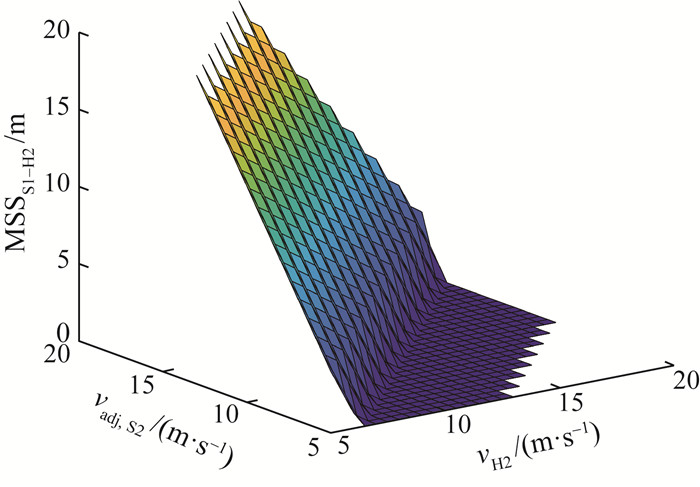
其中xH1和xH2为ICV周围HDV的纵向位置,采用匀变速模型预测得到。换道MSS由调整结束时刻车辆状态确定,存储为map图方便使用,如图 7所示。
|
| 图 7 换道MSS的map图 |
进一步考虑避撞约束和舒适性约束:
| $ \begin{gathered} \forall t \in\left[0, t_{\mathrm{adj}}\right], \\ x_{\mathrm{H} n}(t)-x_{\mathrm{S} n}(t) \geqslant \frac{L_{\mathrm{H} n}+L_{\mathrm{S} n}}{2}+\varepsilon, \\ \left|a_{x, \mathrm{~S} n}(t)\right| \leqslant a_{x, \max }, \quad\left|j_{x, \mathrm{~S} n}(t)\right| \leqslant j_{x, \max }, \\ n=1, 2. \end{gathered} $ | (8) |
其中:LHn和LSn为各车车长;ε为安全裕度;ax, Sn为ICV纵向加速度;ax, max和jx, max分别为纵向加速度和加加速度阈值。
再设置后车影响约束。根据扰动消散理论,最近的上游车辆受到影响最大[16],考虑目标车道第一辆后车H3。假设受S2纵向调整的影响,H3会以固定加速度运动。考虑S2减速的情况,若车间距Δx较大,H3会小幅减速;若车间距Δx较小,H3会大幅减速,最终的速度与vadj, S2接近。因此假设H3以如下加速度进行运动:
| $ a_{\mathrm{H} 3}=\frac{a}{\Delta x+b} \frac{v_{\mathrm{adj}, \mathrm{S} 2}-v_{0, \mathrm{H} 3}}{t_{\mathrm{adj}}} . $ | (9) |
其中:V0, H3代表当前时刻H3的纵向速度;a和b为系数,取值分别为40和30,采用出现频次较高的纵向调整轨迹和OVM的跟驰结果拟合得到。由此可以得到H3的预测轨迹
| $ \left\{\begin{array}{l} a_{\mathrm{H} 3} \geqslant a_{\mathrm{th}}, \\ \mathit{\Delta } \widetilde{x} \geqslant 0.8 \Delta x . \end{array}\right. $ | (10) |
2) 分层优化求解。
为了满足算法的实时性要求,将原问题分解为多个二次规划子问题分层求解。每一个子问题对应一个固定的tadj,决策变量为(vadj, S1, vadj, S2)。对式(5)求导后代入式(6)可将目标函数转化为二次型:
| $ \begin{gathered} J=\sum\limits_{n=1}^2\left[\left(H_{\mathrm{c}}+1\right) v_{\mathrm{adj}, \mathrm{S} n}^2+\right. \\ \left.\left(f_{\mathrm{c}, \mathrm{S} n}+f_{\mathrm{v}}\right) v_{\mathrm{adj}, \mathrm{S} n}\right]+\mathrm{const}, \\ H_{\mathrm{c}}=\frac{12}{t_{\mathrm{adj}}^3}, \quad f_{\mathrm{c}, \mathrm{S} n}=-\frac{12 a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}+24 v_{x 0, \mathrm{~S} n}}{t_{\mathrm{adj}}^3}, \\ f_{\mathrm{v}}=-2 v_{\mathrm{H} 2} . \end{gathered} $ | (11) |
其中const为与决策变量无关的常数项。
同样地,可以将各约束转化为关于vadj的线性约束。以式(8)中加加速度约束为例,对式(5)求导后代入其中可以得到:
| $ \begin{gathered} L_{\text {jerk, } \mathrm{S} n} \leqslant v_{\mathrm{adj}, \mathrm{S} n} \leqslant U_{\text {jerk }, \mathrm{S} n}, \\ U_{\text {jerk, } \mathrm{S} n}=\frac{6 v_{x 0, \mathrm{~S} n}+j_{x, \max } t_{\mathrm{adj}}^2}{6}+ \\ \min \left(\frac{2 a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}}{3}, \frac{a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}}{3}\right), \\ L_{\text {jerk, } \mathrm{S} n}=\frac{6 v_{x 0, \mathrm{~S} n}-j_{x, \max } t_{\mathrm{adj}}^2}{6}+ \\ \max \left(\frac{2 a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}}{3}, \frac{a_{x 0, \mathrm{~S} n} t_{\mathrm{adj}}}{3}\right) . \end{gathered} $ | (12) |
式(8)、(10)均可采用此方法进行转化。但式(7)还需要对map图进行拟合得到表达式,才可转化为线性约束。考虑到map图近似平面,选用平面方程对其进行拟合,评价指标见表 1,可见拟合效果较好。
| 拟合指标 | MSSS1-S2 | MSSS1-H1 | MSSS1-H2 | MSSS1-H3 |
| R2 | 0.979 | 0.992 | 0.996 | 0.996 |
| RMSE | 1.200 | 0.861 | 0.338 | 0.338 |
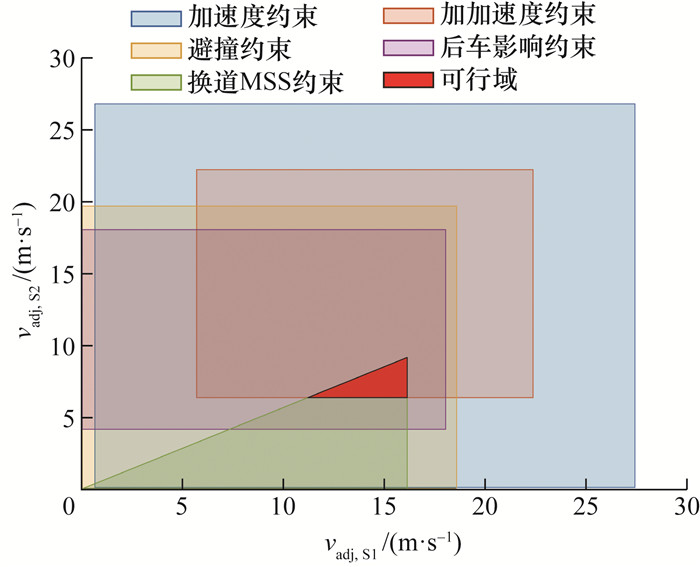
由此可将原问题的所有约束转化为线性约束。以tadj=5 s对应的子问题为例,转化后的各约束范围如图 8所示。可以看到各约束边界与决策变量vadj呈线性关系,最终可行域为红色三角形区域。
|
| 图 8 各约束的线性化范围 |
至此,原问题被转化为多个二次规划子问题,采用quadprog求解器求解每个子问题,选取最优的目标函数值,即可得到最优规划轨迹。
2.1.3 协同换道阶段轨迹规划选取五次多项式描述协同换道阶段ICV的纵横向轨迹[17]。设定换道时间tlc为固定值5 s[16];设定换道结束车速vf, Sn与前车相同;选取两ICV的换道过程纵向位移距离(xf, S1, xf, S2)作为决策变量。为改善换道平顺性,制定如下最小化目标函数:
| $ \begin{gathered} & \forall t \in\left[0, t_{\text {lc }}\right], \\ & J\left(x_{\mathrm{f}, \mathrm{S} 1}, x_{\mathrm{f}, \mathrm{S} 2}\right)=\max \left(\left|a_{x, \mathrm{~S} 1}(t)\right|, \left|a_{x, \mathrm{~S} 2}(t)\right|\right) . \end{gathered} $ | (13) |
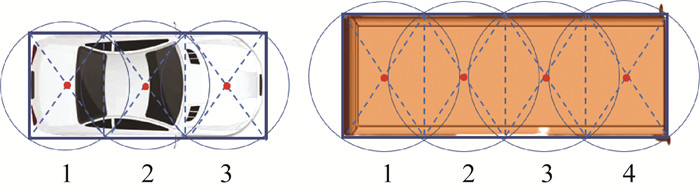
换道过程的避撞约束基于多圆车辆模型建立,如图 9所示。(xS1, i, yS1, i)和(xS2, j, yS2, j)表示ICV各圆圆心坐标;(xNV, j, yNV, j)表示ICV相邻车辆的各圆圆心坐标;DS1、DS2和DNV表示圆形直径。舒适性约束还需要考虑横向运动,采用ay, Sn和jy, Sn分别表示ICV的横向加速度和加加速度;ay, max和jy, max分别表示横向加速度和加加速度阈值。
|
| 图 9 多圆车辆模型 |
由此设置避撞约束与舒适性约束如下:
| $ \begin{gathered} \forall t \in\left[0, t_{\mathrm{lc}}\right], \\ d_{\mathrm{S} n-\mathrm{NV}} \geqslant\left(D_{\mathrm{S} n}+D_{\mathrm{NV}}\right) / 2+\varepsilon, \\ \left|a_{x, \mathrm{~S} n}(t)\right| \leqslant a_{x, \max }, \quad\left|a_{y, \mathrm{~S} n}(t)\right| \leqslant a_{y, \max }, \\ \left|j_{x, \mathrm{~S} n}(t)\right| \leqslant j_{x, \max }, \quad\left|j_{y, \mathrm{~S} n}(t)\right| \leqslant j_{y, \max }, \\ n=1, 2 . \end{gathered} $ | (14) |
其中:
| $ \begin{gathered} d_{\mathrm{S} 1-\mathrm{NV}}= \\ \sqrt{\left(x_{\mathrm{S} 1, i}(t)-x_{\mathrm{NV}, j}(t)\right)^2+\left(y_{\mathrm{S} 1, i}(t)-y_{\mathrm{NV}, j}(t)\right)^2}, \\ d_{\mathrm{S} 2-\mathrm{NV}}= \\ \sqrt{\left(x_{\mathrm{S} 2, j}(t)-x_{\mathrm{NV}, j}(t)\right)^2+\left(y_{\mathrm{S} 2, j}(t)-y_{\mathrm{NV}, j}(t)\right)^2}, \\ i=1, 2, 3, 4, \quad j=1, 2, 3 . \end{gathered} $ |
为了减小换道对后车影响,同样设置后车影响约束,采用OVM模型预测换道过程H3的加速度
| $ \min \left(\tilde{a}_{\mathrm{lc}, \mathrm{H} 3}\right)>a_{\mathrm{th}} . $ | (15) |
换道规划的决策变量和约束相对简单,采用离散化求解空间遍历搜索的方式即可确定最优解。
2.2 出站协同换道策略设计针对图 2场景,首先需要明确港湾式车站形状特点。根据《城市道路工程设计规范》(CJJ37-2012),港湾式车站结构如图 10所示[11]。
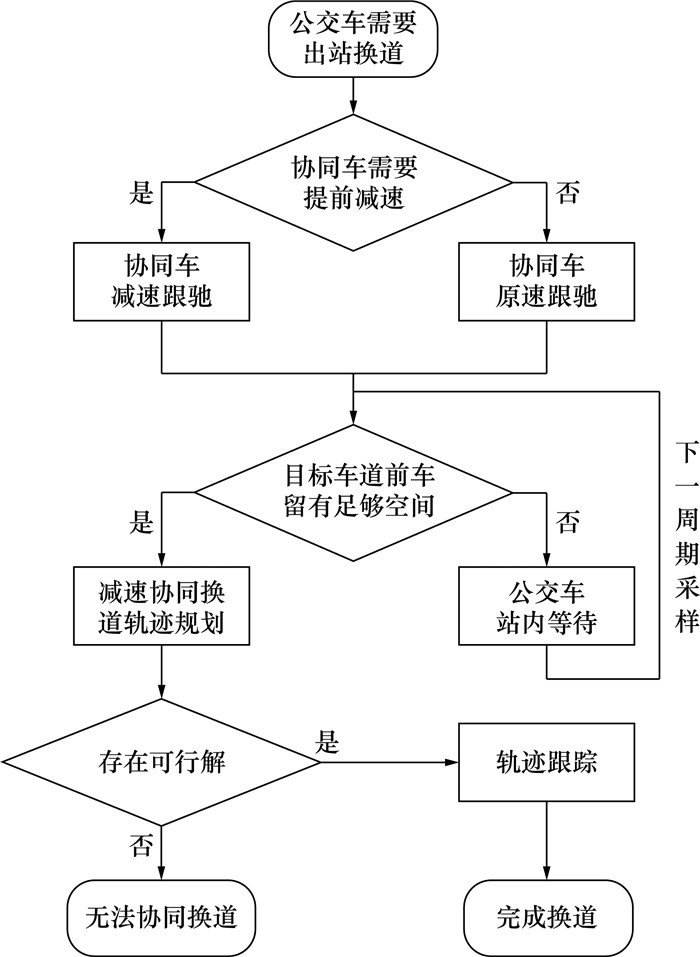
考虑到港湾式车站内距离有限,无法纵向调整;而公交车驶出车站时速度一般为20 km·h-1左右,需要协同车减速配合,因此制定了图 11的出站协同换道流程。
|
| 图 11 出站协同换道流程 |
2.2.1 出站决策算法
首先确定换道开始时刻。在S2减速配合下,只要确保H1能在公交车未跨过车道线时通过车站,即可进行换道。据此设定如下判断:
| $ x_{\mathrm{H} 1}+v_{\mathrm{H} 1} \frac{t_{\mathrm{lc}}}{2}+\frac{1}{2} a_{\mathrm{H} 1}\left(\frac{t_{\mathrm{lc}}}{2}\right)^2 \geqslant x_{\mathrm{B}, \mathrm{end}} \text {. } $ | (16) |
其中:tlc为换道时间,出站过程一般为8 s左右[11],此处取8 s;xB, end代表车站出口处的位置。
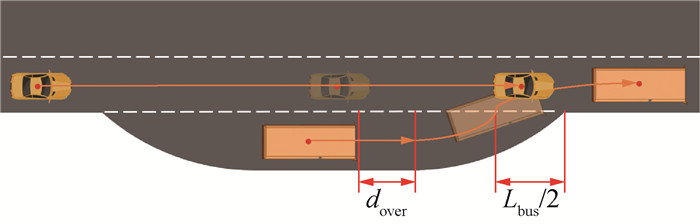
但是当目标车道车速过高,仅通过减速协同换道过程的S2减速难以配合S1出站,此时需要S2提前减速。考虑图 12的出站协同过程。
|
| 图 12 出站减速协同过程 |
在S1换道一半时刻,车头至多位于车站出口处:
| $ x_{\mathrm{S} 1}\left(\frac{t_{\mathrm{lc}}}{2}\right) \leqslant x_{0, \mathrm{~S} 1}+d_{\text {over }}+L_{\mathrm{B}} . $ | (17) |
其中:dover为车头至停车区尽头距离;LB为车站加速段B长度。而S1出站为变加速过程,保守估计换道结束时刻位移为一半时刻的2倍:
| $ x_{\mathrm{S} 1}\left(t_{\mathrm{lc}}\right) \leqslant x_{0, \mathrm{~S} 1}+2\left(d_{\text {over }}+L_{\mathrm{B}}\right) . $ | (18) |
协同换道结束时,S2纵向位置至少位于S1之后;速度至多与S1出站速度相同;加速度设定为0。由此得到S2换道结束时刻状态估计,结合当前时刻S2的速度、加速度信息可得到S2的减速轨迹,从而得到当前车道速度对应的最晚减速协同点xlast。
再根据式(16)估计各车在换道开始时刻的位置,若S2的估计位置超过了xlast,则以加加速度-1 m·s-3提前减速,能满足多数情况。
2.2.2 出站协同换道轨迹规划出站过程的换道规划与进站类似,但由于公交车速度变化大,不适合采用固定换道时间。采用五次多项式轨迹优化求解[17],选择(t1c, xf, S1, xf, S2)为决策变量。为避免S2过度减速,设置如下最大化目标函数:
| $ \begin{gathered} \forall t \in\left[0, t_{\mathrm{lc}}\right], \\ J\left(t_{\mathrm{lc}}, x_{\mathrm{f}, \mathrm{S} 1}, x_{\mathrm{f}, \mathrm{S} 2}\right)=\min \left(v_{\mathrm{x}, \mathrm{S} 2}(t)\right) . \end{gathered} $ | (19) |
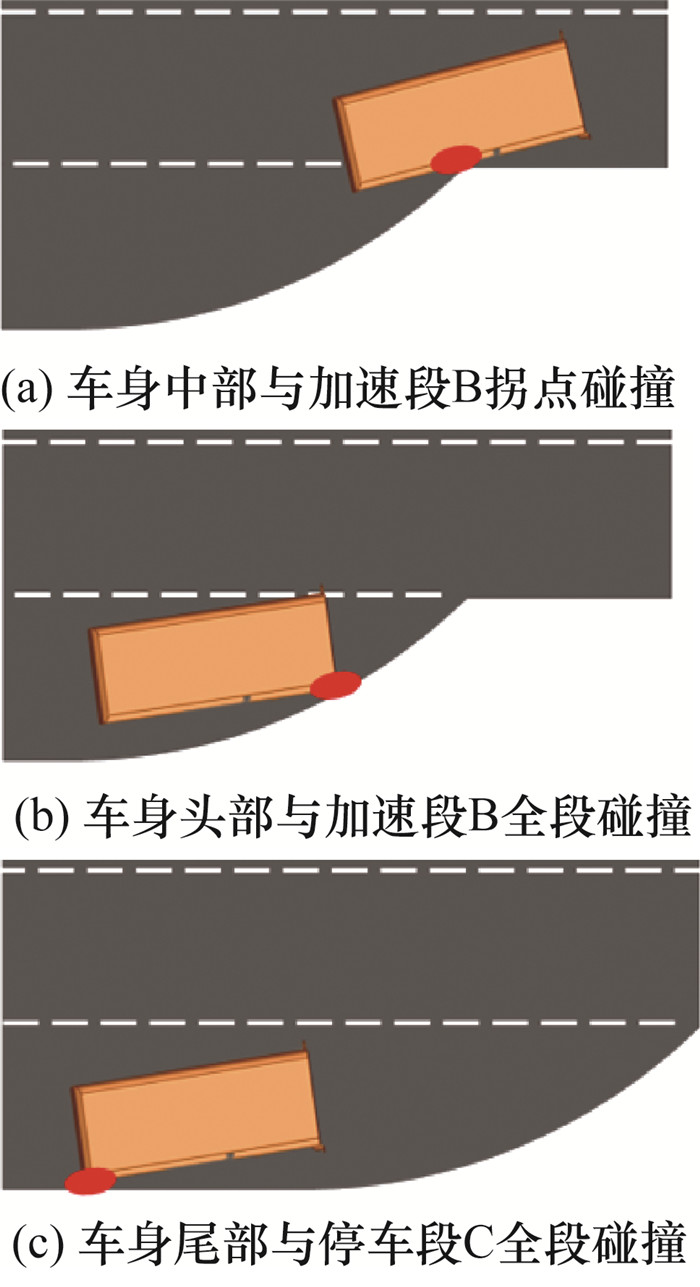
避撞约束和舒适性约束设置与式(14)中相同。但还需要考虑出站过程可能与站台发生的碰撞,设置站台形状约束。根据车辆运动特点可以得到,出站过程可能的碰撞关系如图 13所示。
|
| 图 13 出站过程公交车与站台可能的碰撞形式 |
据此结合多圆车辆模型设置如下约束:
| $ \begin{gathered} \forall t \in\left[0, t_{\mathrm{lc}}\right], \\ \sqrt{\left(x_{\mathrm{S} 1, 1}(t)-x_{\mathrm{C}}\right)^2+\left(y_{\mathrm{S}1, 1}(t)-y_{\mathrm{C}}\right)^2} \geqslant \frac{d_{\mathrm{S} 1}}{2}, \\ \sqrt{\left(x_{\mathrm{S} 1, 2}(t)-x_{\mathrm{B}, \text { end }}\right)^2+\left(y_{\mathrm{S} 1, 2}(t)-y_{\mathrm{B}, \text { end }}\right)^2} \geqslant \frac{d_{\mathrm{S} 1}}{2}, \\ \sqrt{\left(x_{\mathrm{S} 1, 3}(t)-x_{\mathrm{B}, \text { end }}\right)^2+\left(y_{\mathrm{S} 1, 3}(t)-y_{\mathrm{B}, \mathrm{end}}\right)^2} \geqslant \frac{d_{\mathrm{S} 1}}{2}, \\ \sqrt{\left(x_{\mathrm{S} 1, 4}(t)-x_{\mathrm{B}}\right)^2+\left(y_{\mathrm{S} 1, 4}(t)-y_{\mathrm{B}}\right)^2} \geqslant \frac{d_{\mathrm{S} 1}}{2} . \end{gathered} $ | (20) |
其中:xB、yB和xC、yC分别为车站加速段B和停车段C的边缘坐标。
此外,考虑到出站过程公交车运行速度低,还需要对换道轨迹的曲率进行约束:
| $ \begin{gathered} \forall t \in\left[0, t_{\mathrm{lc}}\right], \\ \rho_{\mathrm{S} 1}(t)=\frac{\ddot{x}_{\mathrm{S} 1} \dot{y}_{\mathrm{S} 1}-\dot{x}_{\mathrm{S} 1} \ddot{y}_{\mathrm{S} 1}}{\left(\dot{x}_{\mathrm{S} 1}^2+\dot{y}_{\mathrm{S} 1}^2\right)^{\frac{3}{2}}} \leqslant \frac{1}{R_{\min }}. \end{gathered} $ | (21) |
其中Rmin为公交车的最小转弯半径。此约束能保证出站换道轨迹满足公交车的机动性能。
3 仿真实验验证 3.1 实验方案设计为验证所提出的控制策略的有效性,本文采用MATLAB进行仿真验证,仿真场景如图 1和2所示。为了更符合实际HDV运行特征,本文选取美国NGSIM数据集中真实车辆数据[18],作为车道最前方HDV的行驶速度曲线。其余HDV基于全速度差模型(full velocity difference model,FVDM)[19]行驶,如下所示:
| $ a_k=\alpha\left(V\left(s_k\right)-v_k\right)+\beta \dot{s}_k ; $ | (22) |
| $ V(s)= \begin{cases}0, & s \leqslant s_{\mathrm{st}} ; \\ 0.5 v_{\max }\left(1-\cos {\rm{ \mathsf{ π} }} \frac{s-s_{\mathrm{st}}}{s_{\mathrm{go}}-s_{\mathrm{st}}}\right), & s_{\mathrm{st}}<s <s_{\mathrm{go}} ; \\ v_{\max }, & s \geqslant s_{\mathrm{go}} .\end{cases} $ | (23) |
其中:α、β、sgo和sst均为参数,与文[19]中定义一致,分别取0.6 s-1、0.9 s-1、20 m和10 m。其余仿真参数设置如表 2所示。
| 参数 | 数值 |
| 仿真步长tstep/s | 0.05 |
| 滚动时域周期tdyn/s | 1 |
| ε/m | 3 |
| ax, max/(m·s-2) | 4 |
| ay, max/(m·s-2) | 1.47 |
| jx, max/(m·s-3) | 2 |
| jy, max/(m·s-3) | 0.9 |
| ath/(m·s-2) | -2 |
| η | 0.4 |
| wt | 1 |
| wc | 0.4 |
| wv | 0.1 |
| 公交车车长Lbus/m | 7 |
| 公交车车宽Wbus/m | 2.2 |
| 轿车车长Lcar/m | 4.4 |
| 轿车车宽Wcar/m | 2 |
| Rmin/m | 8 |
| 港湾式车站减速段A长度LA/m | 12 |
| 港湾式车站加速段B长度LB/m | 12 |
| 港湾式车站停车段C长度LC/m | 15 |
表 2中,进站协同换道时间参考文[16]中统计的协同换道平均时间;加速度和加加速度阈值参考Bae等[8]总结结果;车辆尺寸参考市面常见的中型巴士和B级车设置;车站尺寸则参考文[11]中标准,并进行了适当缩小以适应中巴尺寸。
3.2 典型工况仿真结果进站过程选取2种典型工况,分别对图 14中参数进行设置,参数取值如表 3所示。
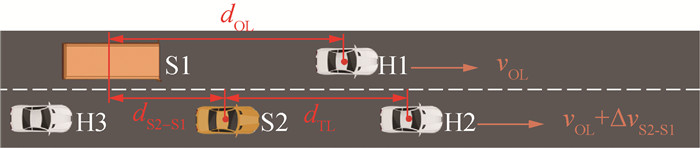
|
| 图 14 进站典型工况参数定义 |
两工况的仿真结果分别如图 15和16所示。其中纵横向位置曲线选择了开始时刻、换道中间时刻和换道结束时刻绘制车辆位置局部图;速度曲线中2条虚线表示决策通过时刻和纵向调整结束时刻。
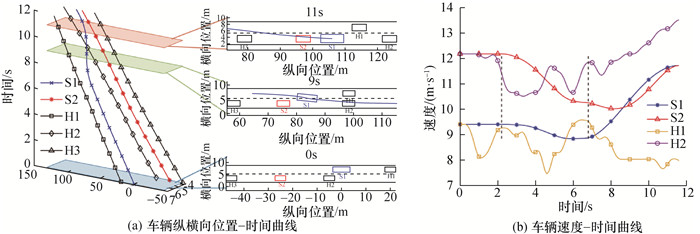
|
| 图 15 工况1仿真结果 |
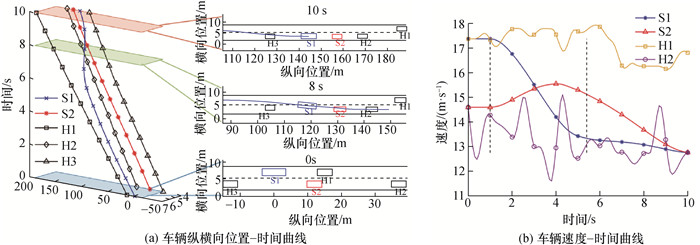
|
| 图 16 工况2仿真结果 |
工况1开始时S1和S2相距较远,此时直接纵向调整对上游交通影响较大。2.2 s后两车距离拉近,决策算法判断可以换道,选择减速调整后换道的方式。纵向调整过程,前车速度有较大的波动,但通过滚动时域规划两车持续减速避免碰撞;换道过程中,两车根据目标车道前车速度进行加速,完成换道时恢复到正常速度,并保持安全跟车。
工况2开始时受到H2大幅减速的影响,S1无法换道。在H2速度恢复且S1和S2距离拉近后,通过协同换道决策,预规划后选择加速调整后换道的方式。在纵向调整过程中,前车速度有较大的波动,但通过滚动时域规划S2进行及时减速避免碰撞;在换道过程,两车根据目标车道前车速度进行减速,保持安全跟车距离。
出站典型工况仿真对图 17所示参数进行设置,参数取值如表 4所示。
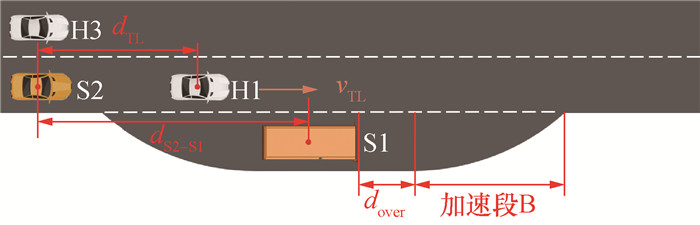
|
| 图 17 出站典型工况参数定义 |
由于出站换道过程速度低,除S1、S2的其他车基本不影响换道过程,因此选取两车位置分布和速度曲线进行分析。
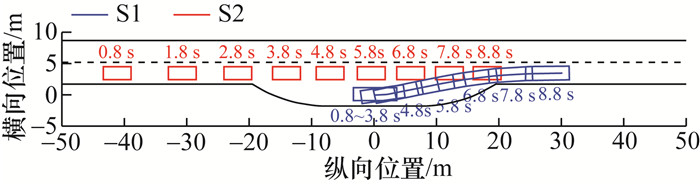
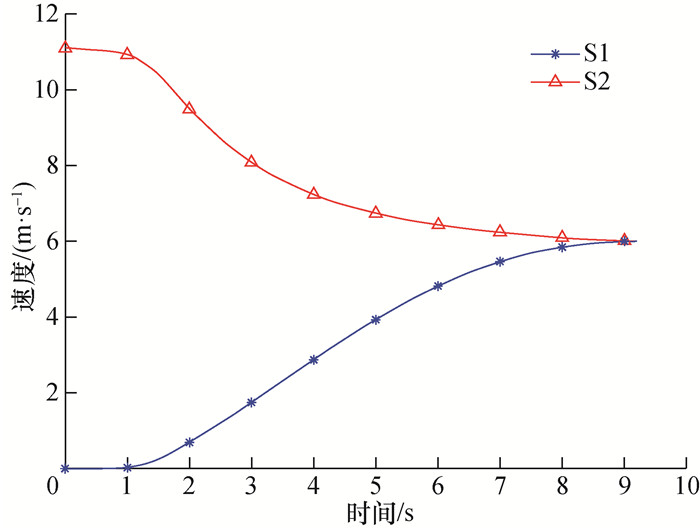
图 18和19中,尽管目标车道车速较快,但S2在S1出站前进行了0.8 s的提前减速后,进一步通过减速协同成功配合S1出站,整个过程没有发生与车辆或车站的碰撞;同时出站完成后车速提升到6 m·s-1,能够尽快恢复到正常车速。
|
| 图 18 工况3换道过程车辆位置分布 |
|
| 图 19 工况3车辆速度曲线 |
3.3 数值批量仿真结果
本节采用仿真工况参数组合进行批量仿真,并选取换道评价指标对提出策略的性能进行分析。同时,进站和出站测试分别选择“MOBIL决策模型+五次多项式换道轨迹优化算法”和“基于规则的决策模型+五次多项式换道轨迹优化算法”作为基准方法进行对比,其中出站决策规则在式(16)基础上增加了安全判断,采用OVM模型判断后车是否会因为公交车出站换道出现过大的减速。
为了精简场景数量,工况生成时作如下假设:
1) 各车道最前方HDV均为匀速行驶;
2) 各车道上车辆初始间距、车速相同。
基于上述假设,进站测试可选择表 3参数进行组合,得到1 600种工况,分为公交车位于较快车道和较慢车道2类,具体设置如表 5和6所示。
| 参数 | dOL/m | dTL/m | dS2-S1/m | ΔvS2-S1/(km·h-1) |
| 取值范围 | [15, 30] | [15, 30] | [0, 30] | [-15, 0] |
| 取值数量 | 4 | 4 | 10 | 5 |
| 参数 | dOL/m | dTL/m | dS2-S1/m | ΔvS2-S1/(km·h-1) |
| 取值范围 | [15, 30] | [15, 30] | [-30, 0] | [0, 15] |
| 取值数量 | 4 | 4 | 10 | 5 |
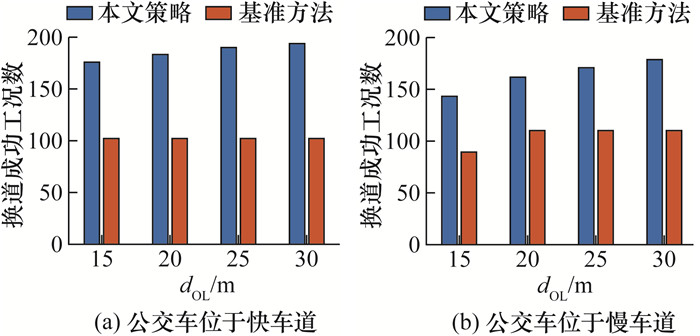
在1 600种测试工况中,本文策略成功换道了1 398组,成功率为87.4%;基准方法成功换道830组,成功率为51.9%。再根据dOL和dTL对换道成功工况分类,结果分别如图 20和21所示。
|
| 图 20 成功工况数和dOL分布 |
|
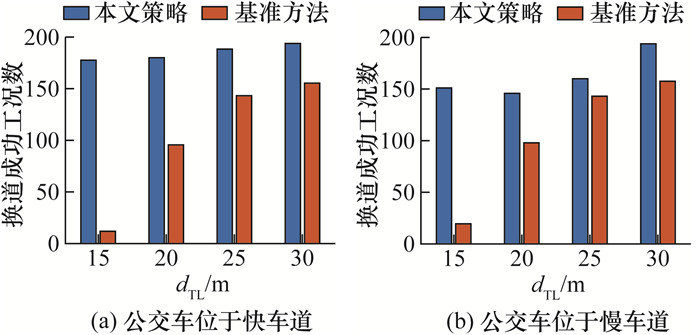
| 图 21 成功工况数和dTL分布 |
图 20中,随着dOL增大,本文策略成功率有一定提升,但基准方法变化不大,这是因为本文策略纵向调整阶段受dOL制约,但基准方法不存在该过程。图 21中,随着dTL增大,两方法成功率都有提升,但基准方法由于缺少协同,受dTL影响更大。
进一步选择目标车道后车最大速度损失vloss、目标车道后车最大减速度aFV, min、换道过程和前后车的碰撞时间(time to collision,TTC)倒数的最大值TTC-1, max作为评价指标进行对比,结果如表 7所示。vloss和aFV, min反映了换道过程对后方车辆的影响,TTC-1, max则反映了换道过程的安全性,各指标的绝对值越小代表性能越好。可以看到本文策略的各项指标均优于基准方法,有更好的换道安全性,并降低了强制换道过程对后车的影响。
| 换道策略 | vloss | aFV, min | TTC-1, max | ||
| m·s-1 | m·s-2 | s-1 | |||
| 本文策略 | 1.480 | -2.029 | 0.108 | ||
| 基准方法 | 3.061 | -2.338 | 0.129 |
出站测试选择表 4参数进行组合得到500种工况,具体设置如表 8所示。
| 参数 | dover/m | dTL/m | dS1-S2/m | vTL/(km·h-1) |
| 取值范围 | [0, 8] | [15, 30] | [30, 50] | [30, 45] |
| 取值数量 | 5 | 4 | 5 | 5 |
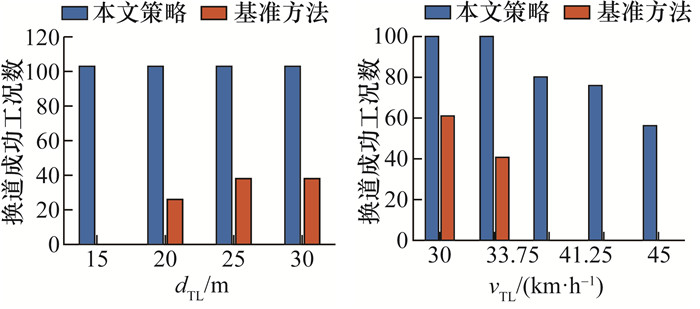
在500种测试工况中,本文策略成功412组,成功率为82.4%;基准方法成功102组,成功率为20.4%。根据dTL和vTL对换道成功的工况分类,结果如图 22所示。
|
| 图 22 成功工况数和dTL、vTL分布 |
可以看到,由于缺少协同,基准方法只能在目标车道车距大、车速低的工况进行换道,本文策略虽然随着vTL增大成功率有所下降,但整体呈现出了更好的适用性。
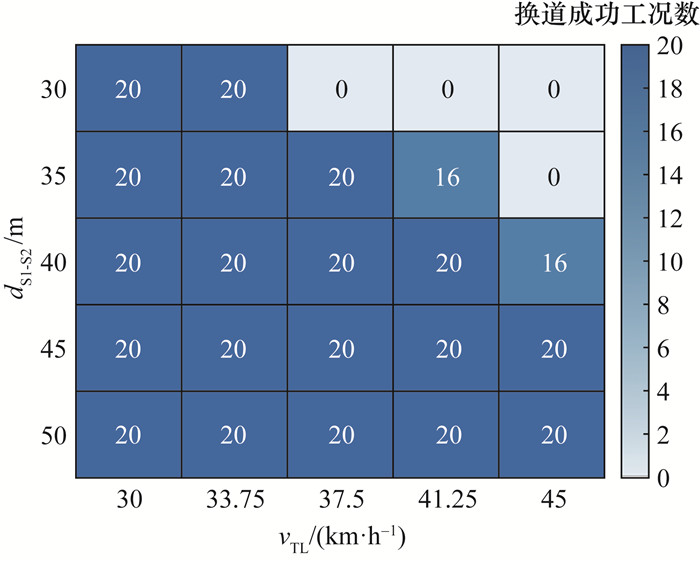
另外,注意到dTL对本文策略的成功率影响较小,额外选择了dS1-S2,结合vTL对成功工况进行分类,得到如图 23所示结果。
|
| 图 23 成功工况和dS1-S2和vTL分布 |
图 23中结果呈现明显边界,可以根据2.2.1节中xlast对其进行分析:当xlast<x0, S2时,即工况开始时S2已位于最晚减速点之前,不存在通过减速协同换道的方式,由此可以得到如下边界:
| $ \begin{aligned} x_{\text {last }} & \leqslant x_{0, \mathrm{~S} 1}-4 v_{\mathrm{TL}}+7.3 <x_{0, \mathrm{~S} 2} \\ & \Rightarrow d_{\mathrm{S} 1-\mathrm{S} 2}<4 v_{\mathrm{TL}}-7.3 . \end{aligned} $ | (24) |
由于xlast的估计偏保守,实际存在边界外的成功工况,但式(24)能够解释边界的趋势。
出站测试的评价指标如表 9所示。本文策略的各项指标均达到了较高的水平,能较好地保证出站换道的安全,并尽可能减小对后车的影响。
| 换道策略 | vloss | aFV, min | TTC-1, max | ||
| m·s-1 | m·s-2 | s-1 | |||
| 本文策略 | 4.039 | -1.535 | 0.316 | ||
| 基准方法 | 5.918 | -4.220 | 0.497 |
4 硬件在环实验验证 4.1 实验平台组成
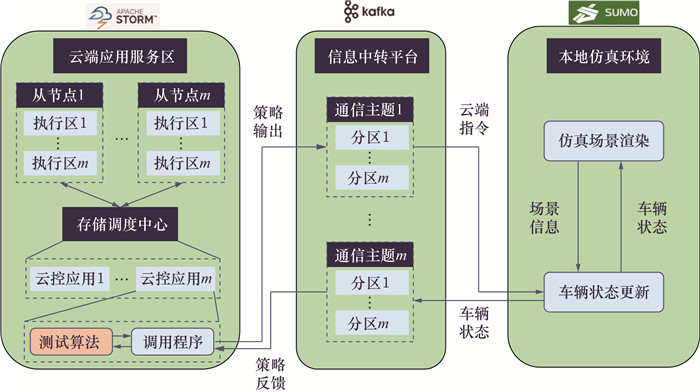
为了验证提出算法搭载于云端服务器的有效性和计算实时性,本文基于云平台进行硬件在环实验,实验系统架构如图 24所示。
|
| 图 24 云平台架构示意 |
该平台是根据亦庄自动驾驶示范区的现有云服务器,采用Storm搭建相同架构服务器集群,并通过Kafka搭建信息中转平台模拟真实通信过程,最后基于Sumo在本地电脑搭建仿真环境,形成了具备真实服务器特点和通信状况的硬件在环实验平台。实验时测试算法编译为so动态库搭载于云端服务器,由Java调用程序根据通信信息实时调用并反馈结果。
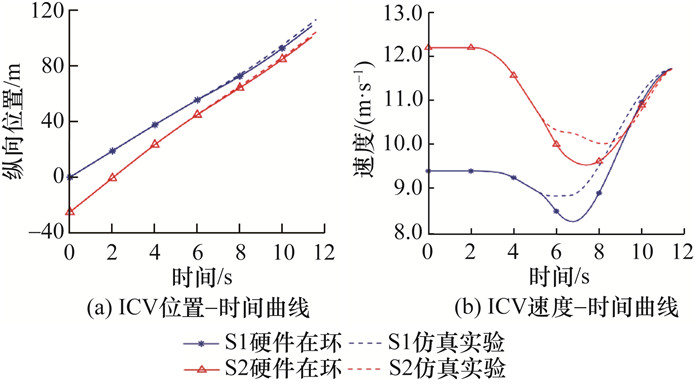
4.2 实验结果分析本节对3.2中3种典型工况进行测试。由于存在通信时延,云端采样周期为0.2 s,以工况1为例,其测试结果如图 25所示。
|
| 图 25 工况1硬件在环测试结果 |
与仿真结果相比,由于硬件在环实验存在通信过程,且每辆车的信息获取独立并行,导致输入到云端算法的车辆状态信息可能有误差,规划结果也有所不同。图 25中,ICV在纵向调整后期进行了更大幅度减速,这可能是因为在滚动时域规划过程存在车辆信息更新不及时的情况,导致规划结果需要更快减速,但协同换道阶段后仍能恢复与前车速度相同的水平。在整个过程中ICV的纵向位置最大偏差为2.25 m,相对最大偏差为2.03%;速度最大偏差为0.650 m·s-1,相对最大偏差为7.13%,偏差较小。
工况2和3呈现出类似结果,测试结果和仿真结果的偏差如表 10所示。
| 结果偏差 | 工况2 | 工况3 |
| ICV纵向位置最大偏差/m | 1.81 | 1.43 |
| ICV纵向位置相对最大偏差 | 1.33% | 4.75% |
| ICV速度最大偏差/(m·s-1) | 0.520 | 0.616 |
| ICV速度相对最大偏差 | 4.52% | 6.49% |
进一步考察计算实时性,各工况的单步计算耗时结果如表 11所示。由于平台算力差异以及编程语言不同,本文算法在云平台的计算耗时小于仿真计算耗时,同时小于200 ms的采样周期。
| ms | |||||||||||||||||||||||||||||
| 计算耗时指标 | 工况1 | 工况2 | 工况3 | ||||||||||||||||||||||||||
| 硬件在环实验平均计算时长 | 3.7 | 4.4 | 2.1 | ||||||||||||||||||||||||||
| 仿真实验平均计算时长 | 32.9 | 38.5 | 17.2 | ||||||||||||||||||||||||||
| 硬件在环实验最大计算时长 | 19.9 | 23.3 | 10.6 | ||||||||||||||||||||||||||
| 仿真实验最大计算时长 | 44.6 | 49.2 | 32.2 | ||||||||||||||||||||||||||
综上所述,本文算法搭载于边缘云服务器时,在面对真实的通信时延下,能够保证规划结果的有效性,同时满足计算实时性要求。
5 结论本文面向公交车进出站强制换道过程,提出了一种云控环境下智能网联公交车的两车协同换道策略。针对公交车进站前向邻近站台的车道进行强制换道的过程,通过衡量换道整体收益决策换道时刻,并采用两段式轨迹规划方法,结合后车影响等多种约束,有效保障进站强制换道过程的安全,降低对上游交通的影响,同时基于分层二次规划改善算法实时性。针对公交车从港湾式车站出站的强制换道过程,采用基于规则的决策方法和协同车提前减速策略,并考虑港湾式车站特点设计了包含车站形状约束的减速协同换道轨迹规划方法,保障出站强制换道过程的安全和成功率。
本文基于MATLAB进行了典型工况仿真和批量测试。结果表明,本文策略能有效应对采用NGSIM数据集中实际车辆轨迹的HDV状态变化;同时与基准方法相比,本文策略在保证更高换道成功率和安全性的同时,有效降低了强制换道对上游交通的影响。同时基于云平台进行了硬件在环实验,验证了本策略在实际云平台的运算、通信环境下的有效性和实时性。
本文研究对于HDV的运动假设较为简单,后续研究需要进一步考虑HDV不确定性,提升策略的鲁棒性。
| [1] |
刘悦棋. 公交车进站过程中的换道行为及影响研究[D]. 重庆: 重庆交通大学, 2018. LIU Y Q. Bus entering lane-changing behavior and its impacts [D]. Chongqing: Chongqing Jiaotong University, 2018. (in Chinese) |
| [2] |
李克强, 戴一凡, 李升波, 等. 智能网联汽车(ICV)技术的发展现状及趋势[J]. 汽车安全与节能学报, 2017, 8(1): 1-14. LI K Q, DAI Y F, LI S B, et al. State-of-the-art and technical trends of intelligent and connected vehicles[J]. Journal of Automotive Safety and Energy, 2017, 8(1): 1-14. DOI:10.3969/j.issn.1674-8484.2017.01.001 (in Chinese) |
| [3] |
李克强, 李家文, 常雪阳, 等. 智能网联汽车云控系统原理及其典型应用[J]. 汽车安全与节能学报, 2020, 11(3): 261-275. LI K Q, LI J W, CHANG X Y, et al. Principles and typical applications of cloud control system for intelligent and connected vehicles[J]. Journal of Automotive Safety and Energy, 2020, 11(3): 261-275. DOI:10.3969/j.issn.1674-8484.2020.03.001 (in Chinese) |
| [4] |
ZHENG Z D. Recent developments and research needs in modeling lane changing[J]. Transportation Research Part B: Methodological, 2014, 60: 16-32. DOI:10.1016/j.trb.2013.11.009 |
| [5] |
YAO R H, DU X J, QI W Y, et al. Evolutionary dynamics of mandatory lane changing for bus exiting[J]. Journal of Advanced Transportation, 2021, 2021: 2958647. |
| [6] |
LÜ W J, LÜ Y B, GUO J W, et al. A lane-changing decision-making model of bus entering considering bus priority based on GRU neural network[J]. Computational Intelligence and Neuroscience, 2022, 2022: 4558946. |
| [7] |
SHI M, HE H W, LI J W, et al. Path planning and following control of autonomous bus under time-varying parameters against parametric uncertainties and external disturbances[J]. IEEE Transactions on Vehicular Technology, 2022, 71(7): 7057-7070. DOI:10.1109/TVT.2022.3170440 |
| [8] |
BAE I, MOON J, SEO J. Toward a comfortable driving experience for a self-driving shuttle bus[J]. Electronics, 2019, 8(9): 943. DOI:10.3390/electronics8090943 |
| [9] |
YU L L, KONG D C, YAN X X. A driving behavior planning and trajectory generation method for autonomous electric bus[J]. Future Internet, 2018, 10(6): 51. DOI:10.3390/fi10060051 |
| [10] |
ALCÁZAR A R. Path planning for autonomous buses based on optimal control [D]. Gothenburg: Chalmers University of Technology, 2018.
|
| [11] |
冯敏. 公交车自主靠站运行轨迹分析与评价[D]. 重庆: 重庆交通大学, 2020. FENG M. Analysis and evaluation on the operation track of bus independent stop [D]. Chongqing: Chongqing Jiaotong University, 2020. (in Chinese) |
| [12] |
WANG Z, SHI X W, ZHAO X M, et al. Modeling decentralized mandatory lane change for connected and autonomous vehicles: An analytical method[J]. Transportation Research Part C: Emerging Technologies, 2021, 133: 103441. DOI:10.1016/j.trc.2021.103441 |
| [13] |
KESTING A, TREIBER M, HELBING D. General lane-changing model MOBIL for car-following models[J]. Transportation Research Record: Journal of the Transportation Research Board, 2007, 1999(1): 86-94. DOI:10.3141/1999-10 |
| [14] |
HELBING D, TILCH B. Generalized force model of traffic dynamics[J]. Physical Review E, 1998, 58(1): 133-138. DOI:10.1103/PhysRevE.58.133 |
| [15] |
关书睿, 李克强, 周俊宇, 等. 面向强制换道场景的智能网联汽车协同换道策略[J]. 汽车工程, 2024, 46(2): 201-210, 280. GUAN S R, LI K Q, ZHOU J Y, et al. A cooperative lane change strategy for intelligent connected vehicles oriented to mandatory lane change scenarios[J]. Automotive Engineering, 2024, 46(2): 201-210, 280. (in Chinese) |
| [16] |
韩静文. 智能网联条件下的多车协同换道研究[D]. 镇江: 江苏大学, 2020. HAN J W. Research on multi-vehicle cooperative lane changing under the condition of intelligent network [D]. Zhenjiang: Jiangsu University, 2020. (in Chinese) |
| [17] |
杨刚. 基于车车通信的多车协同自动换道控制策略研究[D]. 北京: 清华大学, 2016. YANG G. Research on the multi-vehicle cooperative automated lane change maneuver based on vehicle-to-vehicle communication [D]. Beijing: Tsinghua University, 2016. (in Chinese) |
| [18] |
U.S. Department of Transportation Federal Highway Administration. Next generation simulation (NGSIM) vehicle trajectories and supporting data [DS/OL]. [2024-01-16]. https://data.transportation.gov/d/8ect-6jqj.
|
| [19] |
WANG J W, ZHENG Y, CHEN C Y, et al. Leading cruise control in mixed traffic flow: system modeling, controllability, and string stability[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(8): 12861-12876. DOI:10.1109/TITS.2021.3118021 |