随着私家车保有量连年上升,交通拥堵已然成为现代城市管理中最棘手的问题之一。共乘出行(ridesharing)服务指顺风车平台提供的一种鼓励起讫点(origin-destination,OD)相同或相近的出行者同乘一辆车出行的服务,即出行者之间的“拼车”服务[1-3]。区别于网约车出行服务(“打车”“叫车”服务),共乘出行中司机并非专职运营,仅通过捎带顺路的乘客分摊出行成本,不接送乘客,不以营利为目的,且每车每日共乘次数通常存在上限。从城市管理者角度出发,共乘出行通过提高车内空间利用率的方式减少道路上的机动车数量、缓解拥堵问题,是一种行之有效的交通供需管理政策[4-5]。
然而,从出行者的角度出发,共乘人数过多不仅会明显降低乘车过程的舒适性,还可能因为等待乘客上、下车而耽误时间。为提升出行服务质量,改善交通拥堵问题,许多顺风车平台推出了“司机在单次出行时只搭载一位乘客”的专车共乘出行(tailored ridesharing)服务,如嘀嗒、哈啰的“独享顺风车”服务。专车共乘的参与者包括共乘司机和共乘乘客,共乘司机提供车辆并负责驾驶,共乘乘客接受服务并支付报酬。司乘双方预先在顺风车平台上发布出行需求,包括起讫点、出发时间和偏好路线等信息;然后由平台匹配订单,为共乘司机优先推送起讫点相近、出发时间合适的同行乘客[6];若司乘双方接受匹配,并按照约定时间到达共同的出行起点,则共乘出行开始;抵达终点后,共乘乘客在平台上进行支付,平台按规则抽成后返还共乘司机剩余费用,专车共乘出行结束。
模型和算法上的困难使目前的共乘用户均衡(ridesharing user equilibrium,RUE)研究并不充分,即一方面共乘出行者的出行成本相互影响,且流量分布由市场供需、个体感知和行为选择等多重因素决定,无法通过交通调查以及现有的出行费用函数直接获得[1-2];另一方面,由于司乘双方的流量具有严格的约束(乘客流量既不能小于司机流量,也不能大于车辆容量),使模型中产生了新的Lagrange乘子,导致传统的交通分配算法如Frank-Wolfe法、梯度下降法失效[4-5, 7-9]。
Xu等[1, 10]在交通分配问题中引入共乘出行,基于数学规划模型从共乘市场的角度研究了弹性需求下的RUE问题,并以基于OD的路段流量为变量,建立了RUE的互补问题。Di等[4-5]在RUE问题中整合了基于路径的占用率,构建了一个更加切合实际的出行成本函数和双层规划模型,研究包含共乘出行的网络设计问题。Ma等[2, 11]提出了基于共乘市场的浮动定价策略,并引入“共乘匹配约束”以研究支持多类型共乘服务的RUE问题;之后进一步研究了考虑弹性需求的广义随机共乘用户均衡(stochastic ridesharing user equilibrium,SRUE)问题。Yan等[12]通过“共乘匹配概率”的形式将RUE问题拓展为SRUE问题。Sun等[9]沿用Xu等[1]的拓展网络模型,以路段流量为变量,考虑多类型出行者和公共交通,建立了基于Logit模型的SRUE问题。马捷等[13]考虑交通网络中同类型的出行者,引入弹性需求函数并建立了基于Logit模型的SRUE问题。
考虑到现实中的出行者难以了解完整的交通网络信息,且对于交通阻抗的感知具有一定随机性[14],因此本文引入Logit模型刻画出行者的出行方式选择[15-17]。同时,由于共乘网络出行费用函数的Jacobian矩阵是非对称的,常用于交通分配问题的数学规划模型无法处理非对称问题,因而失效。此外,现有SRUE的研究[11-13]较少关注“乘客是否拥有私家车”这类异质性问题以及公共交通对共乘出行的影响;而Sun等[9]基于路段流量的模型已被验证存在“共乘乘客途中换车”的问题[5]。本文针对现有研究的不足,以专车共乘为研究对象,提出了一个基于Logit模型的多模式随机共乘用户均衡(Logit-stochastic ridesharing user equilibrium, Logit-SRUE)问题。该Logit-SRUE问题以路径流量为基础,避免“共乘乘客中途换车”的现象,既考虑了出行者有无私家车的异质性,又涵盖了私家车出行、公交出行和共乘出行等多种出行模式。针对这一问题,本文建立了一个变分不等式(variational inequality,VI)模型,证明了该模型解的等价性、存在性和唯一性,并通过并行自适应投影(parallel self-adaptive projection,PSAP)算法获得该模型的全局收敛解。最后,本文通过Braess网络与Sioux-Falls网络验证了模型和算法的有效性,并对各主要参数进行了敏感性分析。
1 问题描述 1.1 路网构建构建一个包含专车共乘出行模式的强连通交通网络G=(N, A),即共乘交通网络G,其中N和A分别为网络中的节点集合和路段集合。a为A中的任一路段,即A={a}。W为G中的OD对集合;w为W中的任一OD对,即W={w}。Pw为连接OD对w的路径集合;p为Pw中的任一路径,即Pw={p}。
网络中的出行者根据是否拥有私家车分为有车用户和无车用户,分别对应出行模式集合Ic和Inc;且在OD对w间的出行需求分别为Qcw和Qncw。网络中的主要出行模式为自驾司机(独自驾驶私家车出行)、共乘司机、共乘乘客和公交乘客出行模式,分别对应出行模式集合ISD、IRD、IR和IPT。根据出行者有无私家车,进一步划分IRD、IR和IPT,即IRD=IRDc∪IRDnc、IR=IRc∪IRnc和IPT=IPTc∪IPTnc;其中IRc和IRnc分别为有车和无车共乘乘客的出行模式集合;IRDc和IRDnc分别为搭载出行模式为IRc和IRnc乘客共乘司机的出行模式集合;IPTc和IPTnc分别为有车和无车的公交乘客的出行模式集合。拥有私家车的用户可在ISD、IRDc、IRDnc、IRc和IPTc中选择出行模式,即Ic=ISD∪IRDc∪IRDnc∪IRc∪IPTc;没有私家车的用户可在IRnc和IPTnc中选择出行模式[8],即Inc=IRnc∪IPTnc。I泛指网络中所有出行模式的集合,I=ISD∪IRD∪IR∪IPT且I=Ic∪Inc;本文以i的取值表示I中对应的出行模式,如表 1所示。
fp, iw为OD对w间路径p上模式i的交通流量。xa, i为a上模式i的交通流量。δa, pw为p与a的关联系数,若p经过a,则δa, pw=1;反之δa, pw=0。fp, iw与xa, i的关系如下:
| $ x_{a, i}=\sum\limits_w \sum\limits_{p \in P^w} \delta_{a, p}^w f_{p, i}^w, \quad \forall a \in A, i=1, 2, \cdots, 7 . $ | (1) |
a上的小汽车流量xacar等于经过该路段的司机流量之和,即
| $ x_a^{\mathrm{car}}=\sum\limits_i x_{a, i}, \quad \forall a \in A, i=1, 2, 3 . $ | (2) |
a上的公交乘客流量xabus为
| $ x_a^{\mathrm{bus}}=\sum\limits_i x_{a, i}, \quad \forall a \in A, i=6, 7 . $ | (3) |
令xbcar和xbbus分别为路段b(
| $ \frac{\partial t_a^{\mathrm{car}}}{\partial x_b^{\mathrm{car}}}=0, \quad \frac{\partial t_a^{\mathrm{car}}}{\partial x_a^{\mathrm{car}}}>0, \quad \forall a, b \in A, a \neq b ; $ | (4) |
| $ \frac{\partial t_a^{\text {bus }}}{\partial x_b^{\text {bus }}}=0, \quad \frac{\partial t_a^{\text {bus }}}{\partial x_a^{\text {bus }}}>0, \quad \forall a, b \in A, a \neq b . $ | (5) |
由于常规公交存在多次中途停靠车站、严格按照运行时刻表行驶等特点,在一定程度上会影响城市交通网络中社会车辆的运行,从而增加共乘交通网络建模研究的复杂程度。为避免这一情况,本文考虑具有连续公交专用道、班次充足的高频公交运营线路的交通情况[9, 18],则有:
| $ \frac{\partial t_a^{\mathrm{bus}}}{\partial x_a^{\mathrm{car}}}=0, \quad \frac{\partial t_a^{\mathrm{car}}}{\partial x_a^{\mathrm{bus}}}=0, \quad \forall a \in A . $ | (6) |
共乘交通网络G的交通流守恒约束依据出行者是否拥有私家车分为2部分,表示如下:
| $ \left\{\begin{array}{l} \sum\limits_p \sum\limits_i f_{p, i}^w=Q_{\mathrm{c}}^w, \quad \forall w \in W, i=1, 2, 3, 4, 6 ; \\ f_{p, i}^w \in\left[0, Q_{\mathrm{c}}^w\right], \quad \forall w, \forall p, i=1, 2, 3, 4, 6 ; \end{array}\right. $ | (7) |
| $ \left\{\begin{array}{l} \sum\limits_p \sum\limits_i f_{p, i}^w=Q_{\mathrm{nc}}^w, \quad \forall w \in W, i=5, 7 ; \\ f_{p, i}^w \in\left[0, Q_{\mathrm{nc}}^w\right], \quad \forall w, \forall p, i=5, 7 . \end{array}\right. $ | (8) |
在共乘交通网络中,共乘司机能分享的车内座位数量限制了共乘乘客数量,从而形成共乘匹配约束。专车共乘相应的共乘匹配约束如下:
| $ f_{p, \tau_{\mathrm{r}}{(i)}}^w=M_i f_{p, i}^w, \quad \forall w, p, i=2 ; $ | (9) |
| $ f_{p, \tau_{\mathrm{r}}{(i)}}^w=M_i f_{p, i}^w, \quad \forall w, p, i=3 . $ | (10) |
其中:Γr(i)表示将i=2对应的出行模式IRDc映射到i=4对应的出行模式IRc上,将i=3对应的出行模式IRDnc映射到i=5对应的出行模式IRnc上,即Γr(2):IRDc→IRc,Γr(3):IRDnc→IRnc;i=2, 3时共乘司机搭载的乘客数量Mi为整数。由于专车共乘中1位司机单次出行只能搭载1位乘客,因此在本文中,当Γr(2)=4时,M2=1;当Γr(3)=5时,M3=1。
共乘市场的供需关系基于各OD对间的出行需求确定[2]。siw为共乘供应量,即OD对w间的i=2,3时共乘司机的数量;
| $ \left\{\begin{array}{l} s_i^w=\sum\limits_p f_{p, i}^w, \\ d_{\tau_{\mathrm{r}}(i)}^w=\sum\limits_p f_{p, \tau_{\mathrm{r}}(i)}^w, \end{array} \quad \forall w, i=2 ;\right. $ | (11) |
| $ \left\{\begin{array}{l} s_i^w=\sum\limits_p f_{p, i}^w, \\ d_{\tau_{\mathrm{r}}(i)}^w=\sum\limits_p f_{p, \tau_{\mathrm{r}}(i)}^w, \end{array} \quad \forall w, i=3 .\right. $ | (12) |
共乘市场的供需关系为:
| $ d_{\tau_{\mathrm{r}}(i)}^w=M_i s_i^w, \quad \forall w, i=2 ; $ | (13) |
| $ d_{\tau_{\mathrm{r}}(i)}^w=M_i s_i^w, \quad \forall w, i=3 . $ | (14) |
本文结合文[2, 8-9, 11, 19],提出综合考虑共乘出行、公交出行以及多类型共乘用户的路径出行成本Cp, iw为:
| $ C_{p, i}^w= \left\{\begin{array}{l} \rho_i t_p^{w, \text { car }}+C_{\mathrm{fix}}+C_{\mathrm{run}}, i=1 \text {; } \\ \rho_i t_p^{w, \text { car }}+\gamma_i t_p^{w, \text { car }}-\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)-R_i\left(s_i^w\right)\right]+C_{\text {fix }}+C_{\text {run }}, i=2 ; \\ \rho_i t_p^{w, \text { car }}+\gamma_i t_p^{w, \text { car }}-\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)-R_i\left(s_i^w\right)\right]+C_{\text {fix }}+C_{\text {run }}, i=3 ; \\ \rho_i t_p^{w, \text { car }}+\gamma_i t_p^{w, \text { car }}+\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)+R_i\left(d_i^w\right)\right]+C_{\text {fix }}, i=4 ; \\ \rho_i t_p^{w, \text { car }}+\gamma_i t_p^{w, \text { car }}+\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)+R_i\left(d_i^w\right)\right], i=5 ; \\ \rho_i t_p^{w, \text { bus }}+E\left(l_p^w\right)+C_{\mathrm{fix}}, i=6 ; \\ \rho_i t_p^{w, \text { bus }}+E\left(l_p^w\right), i=7 ; \end{array} \quad \forall w, p \text {; }\right. $ | (15) |
| $ t_p^{w, \text { car }}=\sum\limits_a \delta_{a, p}^w t_a^{\mathrm{car}}, \quad t_p^{w, \text { bus }}=\sum\limits_a \delta_{a, p}^w t_a^{\mathrm{bus}} . $ | (16) |
其中:tpw, car和tpw, bus分别为OD对w间路径p的小汽车行驶时间和公交行驶时间。ρi和γi分别为选择模式i出行者的时间价值(value of time,VOT)和不便感知系数(coefficient of inconvenience,COI)。lpw为OD对w间p的长度。Bi(tpw, car)为时长费,Li(lpw)为里程费,Ri(·)为浮动定价,三者构成共乘司机(共乘乘客)的共乘报酬(价格),且均为递增函数。其中,Ri(·)通过负反馈机制调节共乘市场的供需平衡:共乘供应量siw(i=2, 3)增加,浮动定价Ri(siw)上升,共乘司机的报酬减少,从而刺激共乘司机数量下降,市场达到平衡;共乘需求量diw(i=4,5)同理。E(lpw)为公交票价。Cfix为小汽车固定成本,如保险费、保养费等,由有车用户承担。Crun为小汽车使用成本,如燃油费、停车费和路桥费等,由司机承担。
根据经济学市场出清原则[1-2, 11],共乘出行成本还包括维持供需平衡的附加成本ηp, iw,实际表现为共乘平台设置的补贴或溢价,ηp, iw为
| $ \eta_{p, i}^w=\left\{\begin{array}{l} M_i \lambda_{p, i}^w, i=2, 3 ; \\ -\lambda_{p, \tau_{\mathrm{rd}}{(i)}}^w, i=4, 5 ; \end{array} \quad \forall w, p .\right. $ | (17) |
其中: Γrd(i)与Γr(i)的映射关系相反,即Γrd(4):IRc→IRDc,Γrd(5):IRnc→IRDnc; λp, iw和λwp, Γrd(i)为共乘匹配约束对应的Lagrange乘子。则该网络中的广义路径出行成本
| $ \widetilde{C}_{p, i}^w= \left\{\begin{array}{l} \rho_i t_p^{w, \text { car }}+C_{\text {fix }}+C_{\text {run }}, i=1 \text {; } \\ \rho_i t_p^{w, \text { car }}+\gamma_i t_p^{w, \text { car }}-\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)-R_i\left(s_i^w\right)\right]+C_{\text {fix }}+C_{\text {run }}+\eta_{p, i}^w, i=2 \text {; } \\ \rho_i t_p^{w , \text { car }}+\gamma_i t_p^{w , \text { car }}-\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)-R_i\left(s_i^w\right)\right]+C_{\mathrm{fix}}+C_{\text {run }}+\eta_{p, i}^w, i=3 ; \\ \rho_i t_p^{w, \text { car }}+\gamma_i t_p^{w, \text { car }}+\left[B_i\left(t_p^{w, \text { car }}\right)+L_i\left(l_p^w\right)+R_i\left(d_i^w\right)\right]+C_{\text {fix }}+\eta_{p, i}^w, i=4 ; \\ \rho_i t_p^{w, \mathrm{car}}+\gamma_i t_p^{w, \mathrm{car}}+\left[B_i\left(t_p^{w, \mathrm{car}}\right)+L_i\left(l_p^w\right)+R_i\left(d_i^w\right)\right]+\eta_{p, i}^w, i=5 ; \\ \rho_i t_p^{w, \text { bus }}+E\left(l_p^w\right)+C_{\text {fix }}, i=6 ; \\ \rho_i t_p^{w, \text { bus }}+E\left(l_p^w\right), i=7 ; \end{array} \quad \forall w, p .\right. $ | (18) |
现实生活中,出行者感知的出行时间通常符合随机分布,这一分布以实际出行时间为均值,以某个特定的方差在均值附近波动。为模拟这一分布,本文引入Logit模型刻画出行者的出行方式选择[15-17]。设θ为Logit行为选择模型中的感知离散系数,Yp, iw为OD对w的出行者以模式i在路径p上出行的概率。Logit-SRUE条件为:
| $ \begin{gathered} f_{p, i}^{w}=Q_{\mathrm{c}}^{w} Y_{p, i}^{w}=Q_{\mathrm{c}}^{w} \frac{\exp \left(-\theta \widetilde{C}_{p, i}^{w}\right)}{\sum\limits_{p} \sum\limits_{i} \exp \left(-\theta \widetilde{C}_{p, i}^{w}\right)}, \\ \forall w, \forall p, i=1, 2, 3, 4, 6 ; \end{gathered} $ | (19) |
| $ \begin{gathered} f_{p, i}^{w}=Q_{\mathrm{nc}}^{w} Y_{p, i}^{w}=Q_{\mathrm{nc}}^{w} \frac{\exp \left(-\theta \widetilde{C}_{p, i}^{w}\right)}{\sum\limits_{p} \sum\limits_{i} \exp \left(-\theta \widetilde{C}_{p, i}^{w}\right)}, \\ \forall w, \forall p, i=5, 7; \end{gathered} $ | (20) |
| $ f_{p, \tau_{\mathrm{r}}{(i)}}^{w}=M_{i} f_{p, i}^{w}, \quad \forall w, \forall p, i=2 ; $ | (21) |
| $ f_{p, \tau_{\mathrm{r}}{(i)}}^{w}=M_{i} f_{p, i}^{w}, \quad \forall w, \forall p, i=3. $ | (22) |
建立变分不等式-随机共乘用户均衡(variational inequality-stochastic ridesharing user equilibrium, VI-SRUE)模型:在可行集 Ω内,找到满足流量分配原则的向量f*,使
| $ \left\langle\boldsymbol{\varPsi}\left(\boldsymbol{f}^{*}\right), \boldsymbol{f}-\boldsymbol{f}^{*}\right\rangle \geqslant 0, \quad \forall \boldsymbol{f} \in \boldsymbol{\Omega} ; $ | (23) |
| $ \begin{gathered} \boldsymbol{\varPsi}(\boldsymbol{f})=\left(C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}, p \in P^{w}\right., \\ w \in W, i=1, 2, \cdots, 7)^{\mathrm{T}}. \end{gathered} $ | (24) |
其中: Ψ(f*)和Ψ(f)为内置函数;网络中路径流量的向量形式f =(fp, iw, p∈Pw, w∈W, i=1, 2, …, 7)T; 可行集 Ω为满足式(7)—(10) f的集合; f*为VI-SRUE模型的解。
式(23)可等价转化为
| $ \boldsymbol{\varPsi}\left(\boldsymbol{f}^{*}\right) \cdot \boldsymbol{f} \geqslant \boldsymbol{\varPsi}\left(\boldsymbol{f}^{*}\right) \cdot \boldsymbol{f}^{*}, \forall \boldsymbol{f} \in \boldsymbol{\Omega}. $ | (25) |
进一步推导为数学规划问题,
| $ \min\limits_{f \in \boldsymbol{\Omega}} Z(f)=\boldsymbol{\varPsi}\left(\boldsymbol{f}^{*}\right) \cdot \boldsymbol{f}. $ | (26) |
其中Z为目标函数。当且仅当f*为式(26)中数学规划的解时,f*是VI-SRUE模型的解。注意,式(23)的Ψ(f*)是固定值。
为证明VI-SRUE模型能求解Logit-SRUE问题,需要验证命题1。
命题1 若某一f满足Logit-SRUE条件, 则f是VI-SRUE问题的解,反之亦成立。
证明1 式(26)的Lagrange函数L为
| $ \begin{gathered} L\left(\boldsymbol{f}, \boldsymbol{\pi}_{\mathrm{c}}, \boldsymbol{\pi}_{\mathrm{nc}}, \boldsymbol{\lambda}\right)=\boldsymbol{\varPsi}\left(\boldsymbol{f}^{*}\right) \cdot \boldsymbol{f}+ \\ \sum\limits_{w} \pi_{\mathrm{c}}^{w}\left(\sum\limits_{p} \sum\limits_{i=1, 2, 3, 4, 6} f_{p, i}^{w}-Q_{\mathrm{c}}^{w}\right)+ \\ \sum\limits_{w} \pi_{\mathrm{nc}}^{w}\left(\sum\limits_{p} \sum\limits_{i=5, 7} f_{p, i}^{w}-Q_{\mathrm{nc}}^{w}\right)+ \\ \sum\limits_{w} \sum\limits_{p} \sum\limits_{i=2, 3} \lambda_{p, i}^{w}\left(M_{i} f_{p, i}^{w}-f_{p, \tau_{\mathrm{r}}(i)}^{w}\right). \end{gathered} $ | (27) |
其中: πcw和πncw为交通流守恒约束对应的有车和无车的乘子,乘子向量分别为πc和πnc,πc=(πcw, w∈ W, i=1, 2, 3, 4, 6)T,πnc=(πncw, w∈W, i=5, 7)T;共乘匹配约束对应的Lagrange乘子λp, iw的向量为λ =(λp, iw, p∈Pw, w∈W, i=2, 3)T。
令
| $ \left\{\begin{array}{l} \nabla_{f_{p, i}^{w}} L=0, \quad \forall w, p, i ; \\ \sum\limits_{p} \sum\limits_{i} f_{p, i}^{w}=Q_{\text{c}}^{w}, \quad \forall w, i=1, 2, 3, 4, 6 ;\\ \sum\limits_{p} \sum\limits_{i} f_{p, i}^{w}=Q_{\text{nc}}^{w}, \quad \forall w, i=5, 7; \\ f_{p, \tau_\text{r}(i)}^{w}=M_{i} \cdot f_{p, i}^{w}, \quad \forall w, p, i=2; \\ f_{p, \tau_\text{r}(i)}^{w}=M_{i} \cdot f_{p, i}^{w}, \quad \forall w, p, i=3. \end{array}\right. $ | (28) |
将
| $ \left\{\begin{array}{l} C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}+\pi_{\mathrm{c}}^{w}=0, i=1 ;\\ C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}+\lambda_{p, i}^{w}+\pi_{\mathrm{c}}^{w}=0, i=2 ;\\ C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}+\lambda_{p, i}^{w}+\pi_{\mathrm{c}}^{w}=0, i=3 ;\\ C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}-\lambda_{p, \tau_{\mathrm{rd}}(i)}^{w}+\pi_{\mathrm{c}}^{w}=0, i=4 ; \forall w, p .\\ C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}-\lambda_{p, \tau_{\mathrm{rd}}(i)}^{w}+\pi_{\mathrm{nc}}^{w}=0, i=5 ;\\ C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}+\pi_{\mathrm{c}}^{w}=0, i=6 ;\\ C_{p, i}^{w}+\frac{1}{\theta} \ln f_{p, i}^{w}+\pi_{\mathrm{nc}}^{w}=0, i=7; \end{array}\right. $ | (29) |
结合Cp, iw和
| $ \left\{\begin{array}{l} \widetilde{C}_{p, i}^w+\frac{1}{\theta} \ln f_{p, i}^w+\pi_{\mathrm{c}}^w=0, i=1,2,3,4,6 ; \\ \widetilde{C}_{p, i}^w+\frac{1}{\theta} \ln f_{p, i}^w+\pi_{\mathrm{nc}}^w=0, i=5,7 ; \end{array} \quad \forall w, p .\right. $ | (30) |
易得
| $ \left\{\begin{array}{l} f_{p, i}^{w}=\exp \left[-\theta\left(\widetilde{C}_{p, i}^{w}+\pi_{\mathrm{c}}^{w}\right)\right], i=1, 2, 3, 4, 6 ; \\ f_{p, i}^{w}=\exp \left[-\theta\left(\widetilde{C}_{p, i}^{w}+\pi_{\text {nc }}^{w}\right)\right], i=5, 7 ; \end{array} \quad \forall w, p.\right. $ | (31) |
综上,式(26)中数学规划模型的KKT条件为
| $ \left\{\begin{array}{l} f_{p, i}^{w}=\exp \left[-\theta\left(\widetilde{C}_{p, i}^{w}+\pi_\mathrm{c}^{w}\right)\right], \quad \forall w, p, i=1, 2, 3, 4, 6 ; \\ f_{p, i}^{w}=\exp \left[-\theta\left(\widetilde{C}_{p, i}^{w}+\pi_\mathrm{nc}^{w}\right)\right], \quad \forall w, p, i=5, 7 ; \\ \sum\limits_{p} \sum\limits_{i} f_{p, i}^{w}=Q_\mathrm{c}^{w}, \forall w, i=1, 2, 3, 4, 6 ; \\ \sum\limits_{p} \sum\limits_{i} f_{p, i}^{w}=Q_\mathrm{nc}^{w}, \quad \forall w, i=5, 7 ; \\ f_{p, \tau_\mathrm{r}(i)}^{w}=M_{i} f_{p, i}^{w}, \quad \forall w, p, i=2 ; \\ f_{p, \tau_\mathrm{r}(i)}^{w}=M_{i} f_{p, i}^{w}, \quad \forall w, p, i=3 . \end{array}\right. $ | (32) |
式(32)即为Logit-SRUE条件。由此可得,Logit-SRUE条件与式(26)中数学规划问题的KKT条件等价。
Slater定理[20]表明,如果一个凸规划问题的可行域存在某一点使不等式约束都能严格成立,则KKT条件是该问题最优解的充分必要条件。式(26)为目标函数与约束函数都可微分的非负线性等式约束规划问题,且出行者行为选择符合Logit模型,则必然存在fp, iw>0,
综上所述,满足Logit-SRUE条件是式(26)中数学规划问题最优解的充分必要条件。进一步地,由于式(26)的数学规划模型与VI-SRUE模型等价,则某一f满足Logit-SRUE条件,该f是VI-SRUE问题的解,反之亦成立,因此,命题1得证。
2.2 解的性质证明 2.2.1 存在性证明命题2 VI-SRUE模型的解存在。
证明2 自变量f的可行集 Ω是闭区间,且函数Ψ(f)在 Ω上连续,根据Nagurney[21]的定理1.4,VI-SRUE模型在 Ω内至少存在一个解,因此命题2得证。
2.2.2 唯一性证明命题3 当以下条件满足时,VI-SRUE模型在 Ω内存在唯一解。
1) Ri(·)严格单调递增。
2) 令
| $ \begin{gathered} \rho_{1}>\left(\sum\limits_{a} \delta_{a, p}^{w} \dot{t}_{a}^{\mathrm{car}}\right)\left(\sum\limits_{i=2, 3} \frac{\left(\rho_{i}+\gamma_{i}-e_{i}-\rho_{1}\right)^{2}}{4 \partial_{i} R_{i}+4 D_{i}}-\right. \\ \left.\sum\limits_{i=4, 5} \frac{\left(\rho_{i}+\gamma_{i}+e_{i}\right)^{2}}{4 \partial_{i} R_{i}+4 D_{i}}\right). \end{gathered} $ |
其中:
3) 公交乘客的路径流量fp, 6w和fp, 7w满足:
| $ \frac{1}{f_{p, 6}^w f_{p, 7}^w}>\left(\frac{\theta}{2}\left(\rho_6+\rho_7\right)\left(\sum\limits_a \delta_{a, p}^w \dot{t}_a^{\text {bus }}\right)\right)^2 . $ |
其中中间变量
证明3 函数Ψ(f)的Jacobian矩阵J为
| $ \boldsymbol{J}=\left[\begin{array}{ccc} \frac{\partial\left(C_{p, 1}^w+\frac{1}{\theta} \ln f_{p, 1}^w\right)}{\partial f_{p, 1}^w} & \cdots & \frac{\partial\left(C_{p, 1}^w+\frac{1}{\theta} \ln f_{p, 1}^w\right)}{\partial f_{p, 7}^w} \\ \vdots & & \vdots \\ \frac{\partial\left(C_{p, 7}^w+\frac{1}{\theta} \ln f_{p, 7}^w\right)}{\partial f_{p, 1}^w} & \cdots & \frac{\partial\left(C_{p, 7}^w+\frac{1}{\theta} \ln f_{p, 7}^w\right)}{\partial f_{p, 7}^w} \end{array}\right] . $ | (33) |
定义中间变量Λi、
| $ \varLambda_i= \begin{cases}\rho_i, \quad i=1, 6, 7 ; \\ \rho_i+\gamma_i-e_i, & i=2, 3 ; \\ \rho_i+\gamma_i+e_i, & i=4, 5 ;\end{cases} $ | (34) |
| $ \dot{t}^{\mathrm{car}}=\sum\limits_a \delta_{a, p}^w \dot{t}_a^{\mathrm{car}}, \quad \dot{t}^{\text {bus }}=\sum\limits_a \delta_{a, p}^w \dot{t}_a^{\text {bus }} . $ | (35) |
则Jacobian矩阵J可展开为
| $ \boldsymbol{J}=\left[\begin{array}{ccccccc} \varLambda_1 \dot{t}^{\text {car }}+D_1 & \varLambda_1 \dot{t}^{\text {car }} & \varLambda_1 \dot{t}^{\text {car }} & 0 & 0 & 0 & 0 \\ \varLambda_2 \dot{t}^{\text {car }} & \varLambda_2 \dot{t}^{\text {car }}+\partial_2 R_2+D_2 & \varLambda_2 \dot{t}^{\text {car }} & 0 & 0 & 0 & 0 \\ \varLambda_3 \dot{t}^{\text {car }} & \varLambda_3 \dot{t}^{\text {car }} & \varLambda_3 \dot{t}^{\text {car }}+\partial_3 R_3+D_3 & 0 & 0 & 0 & 0 \\ \varLambda_4 \dot{t}^{\text {car }} & \varLambda_4 \dot{t}^{\text {car }} & \varLambda_4 \dot{t}^{\text {car }} & \partial_4 R_4+D_4 & 0 & 0 & 0 \\ \varLambda_5 \dot{t}^{\text {car }} & \varLambda_5 \dot{t}^{\text {car }} & \varLambda_5 \dot{t}^{\text {car }} & 0 & \partial_5 R_5+D_5 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \varLambda_6 \dot{t}^{\text {bus }}+D_6 & \varLambda_6 \dot{t}^{\text {bus }} \\ 0 & 0 & 0 & 0 & 0 & \varLambda_7 \dot{t}^{\text {bus }} & \varLambda_7 i^{\text {bus }}+D_7 \end{array}\right]. $ | (36) |
由于J是非对称矩阵,无法直接使用对称矩阵的正定性判据[22]。因此,本文根据其转置矩阵JT构造其对称矩阵
| $ \boldsymbol{J}_{1}=\left[\begin{array}{ccccccc} 2 D_{1} & -2 D_{1} & -2 D_{1} & 0 & 0 & 0 & 0 \\ -2 D_{1} & 2 D_{1} & 2 D_{1} & 0 & 0 & 0 & 0 \\ -2 D_{1} & 2 D_{1} & 2 D_{1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 \varLambda_{6} \dot{t}^{\text {bus }} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 2 \varLambda_{7} \dot{t}^{\text {bus }} \end{array}\right]. $ | (37) |
| $ \boldsymbol{J}_{2}=\left[\begin{array}{ccccccc} 2 \varLambda_{1} \dot{t}^{\mathrm{car}} & \left(\varLambda_{2}-\varLambda_{1}\right) \dot{t}^{\mathrm{car}} & \left(\varLambda_{3}-\varLambda_{1}\right) \dot{t}^{\mathrm{car}} & \varLambda_{4} \dot{t}^{\mathrm{car}} & \varLambda_{5} \dot{t}^{\mathrm{car}} & 0 & 0 \\ \left(\varLambda_{2}-\varLambda_{1}\right) \dot{t}^{\mathrm{car}} & 2 \partial_{2} R_{2}+2 D_{2} & 0 & 0 & 0 & 0 & 0 \\ \left(\varLambda_{3}-\varLambda_{1}\right) \dot{t}^{\text {car }} & 0 & 2 \partial_{3} R_{3}+2 D_{3} & 0 & 0 & 0 & 0 \\ \varLambda_{4} \dot{t}^{\text {car }} & 0 & 0 & 2 \partial_{4} R_{4}+2 D_{4} & 0 & 0 & 0 \\ \varLambda_{5} \dot{t}^{\mathrm{car}} & 0 & 0 & 0 & 2 \partial_{5} R_{5}+2 D_{5} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 D_{6} & \left(\varLambda_{6}+\varLambda_{7}\right) \dot{t}^{\text {bus }} \\ 0 & 0 & 0 & 0 & 0 & \left(\varLambda_{6}+\varLambda_{7}\right) \dot{t}^{\text {bus }} & 2 D_{7} \end{array}\right]. $ | (38) |
通过证明可知,
命题3中的3个条件是温和的。具体来说,条件1要求Ri(·)严格单调递增,即在共乘需求量增加时共乘价格提高,共乘供给量增加时共乘报酬降低,这符合浮动定价的负反馈调节机制。条件2是针对特定交通网络的浮动定价的假设,要求
为基于OD供需关系制定合理的浮动定价,本文基于路径变量建模计算共乘价格和共乘报酬,这使路径成本不能由该路径经过的路段成本直接相加;因此,VI-SRUE模型以f为自变量,扩大了计算规模,增加了计算难度。为解决这一问题,本文应用全局收敛的并行PSAP算法求解Logit-SRUE问题[2, 24]。PSAP算法依据并行计算思想,将原问题按照OD对分解成若干个子问题并分别应用自适应投影(self-adaptive projection,SAP)算法求解,规避了因交通网络规模过大而引发的内存溢出风险。可验证Ψ(f)在 Ω上具有共强制性、单调性和Lipschitz连续性,符合PSAP算法的要求[2, 24]。
PSAP算法的过程如下:
步骤1 初始化。给定精度ε>0,选取算法所需参数μ∈(0, 1),δ∈(0, 2),初始迭代步长β0>0,迭代次数k=1,u=0。应用K最短路算法[25]给每个OD对w构造包含前K条最短路径的路径集Pw,并给定初始可行路径流量fw1∈ Ωw, 定义OD对w的路径流量向量fw=(fp, iw, p∈Pw, i=1, 2, …, 7)T,可行集 Ωw为满足式(7)—(10)的fw的集合,OD对w的向量函数Ψ(fw)=
步骤2 检查停止条件。定义投影结果gwk,以及计算相对误差所需的中间变量υwk和σwk为
| $ \begin{gathered} \boldsymbol{g}_{w}^{k}:=P_{\boldsymbol{\Omega}_{w}}\left(\boldsymbol{f}_{w}^{k}-\boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k}\right)\right) , \\ v_{w}^{k}:=\left\|\boldsymbol{f}_{w}^{k}-\boldsymbol{g}_{w}^{k}\right\| , \\ \sigma_{w}^{k}:=\left\|\boldsymbol{f}_{w}^{k}\right\|. \end{gathered} $ |
其中PΩw(·)为投影算子。
若
步骤3 更新迭代步长。定义第k次迭代的步长βk及中间变量αwk和ωwk为
| $ \begin{gathered} \beta_{k}:=(\mu)^{u} \beta_{k-1}, \\ \boldsymbol{f}_{w}^{k+1}:=P_{\boldsymbol{\Omega}_{w}}\left(\boldsymbol{f}_{w}^{k}-\beta_{k} \boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k}\right)\right), \\ \alpha_{w}^{k}:=\beta_{k}\left\|\boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k}\right)-\boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k+1}\right)\right\|^{2} , \\ \omega_{w}^{k}:=\left(\boldsymbol{f}_{w}^{k}-\boldsymbol{f}_{w}^{k+1}\right)^{\mathrm{T}}\left[\boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k}\right)-\boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k+1}\right)\right]. \end{gathered} $ |
若
步骤2和步骤3中的投影算子PΩw(·)可通过下式解得
| $ P_{\boldsymbol{\Omega}_{w}}\left(\boldsymbol{f}_{w}^{k}\right)=\underset{\boldsymbol{h} \in \boldsymbol{\Omega}_{w}}{\arg \min }\left\|\boldsymbol{h}-\left[\boldsymbol{f}_{w}^{k}-\beta_{k} \boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k}\right)\right]\right\| . $ | (39) |
其中h为PΩw(·)的结果。
计算步骤2中的PΩw(·)时,需要令βk=1。式(41)可进一步转化为求解下式的二次规划为
| $ P_{\boldsymbol{\Omega}_{w}}\left(\boldsymbol{f}_{w}^{k}\right)=\min\limits_{\boldsymbol{h} \in \boldsymbol{\Omega}_{w}} \frac{1}{2} \boldsymbol{h}^{\mathrm{T}} \boldsymbol{U} \boldsymbol{h}+\left[\beta_{k} \boldsymbol{\varPsi}\left(\boldsymbol{f}_{w}^{k}\right)-\boldsymbol{f}_{w}^{k}\right] \boldsymbol{h} . $ | (40) |
其中U为单位矩阵。
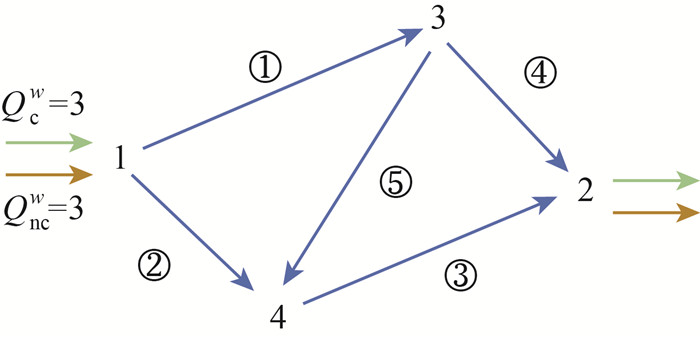
4 算例 4.1 Braess网络 4.1.1 流量分配结果本文应用经典的Braess网络分析共乘出行对交通系统的影响。图 1为Braess网络的拓扑结构,网络共有4个节点(1、2、3和4)、1个OD对(1和2)、5条路段(①、②、③、④和⑤),以及3条路径:a) ①→④;b) ②→③;c) ①→⑤→③,路段出行时间函数如表 2所示。
|
| 图 1 Braess网络拓扑结构 |
| 路段序号 | 起点 | 讫点 | tacar/min | tabus/min |
| ① | 1 | 3 | 10xacar | 15xabus |
| ② | 1 | 4 | 50+xacar | 50+1.5xabus |
| ③ | 4 | 2 | 10xacar | 15xabus |
| ④ | 3 | 2 | 50+xacar | 50+1.5xabus |
| ⑤ | 3 | 4 | 10+xacar | 10+1.5xabus |
将
| $ B_{i}\left(t_{p}^{w, \text { car }}\right)=b_{i} t_{p}^{w, \text { car }}, \quad \forall w, p, i=2, 3, 4, 5; $ | (41) |
| $ L_{i}\left(l_{p}^{w}\right)=\varphi_{i} l_{p}^{w}, \quad \forall w, p, i=2, 3, 4, 5 ; $ | (42) |
| $ \begin{gathered} R_i\left(\sum\limits_p f_{p, i}^w\right) =r_i \sum\limits_p f_{p, i}^w, \\ \forall w, p, i =2, 3, 4, 5 ; \end{gathered} $ | (43) |
| $ E\left(l_{p}^{w}\right)=\tau l_{p}^{w}. $ | (44) |
其中:bi为共乘时间单价,φi为共乘里程单价,ri为浮动定价系数,τ为公交里程单价。则
| $ \left\{\begin{array}{l} \widetilde{C}_{p, 1}^{w}=\rho_{1} t_{p}^{w, \text { car }}+C_{\mathrm{fix}}+C_{\mathrm{run}} ; \\ \widetilde{C}_{p, 2}^{w}=\rho_{2} t_{p}^{w, \text { car }}+\gamma_{2} t_{p}^{w, \text { car }}-\left(b_{2} t_{p}^{w, \text { car }}+\varphi_{2} l_{p}^{w}-r_{2} \sum\limits_{p} f_{p, 2}^{w}\right)+C_{\mathrm{fix}}+C_{\mathrm{run}}+\lambda_{p, 2}^{w} ; \\ \widetilde{C}_{p, 3}^{w}=\rho_{3} t_{p}^{w, \text { car }}+\gamma_{3} t_{p}^{w, \text { car }}-\left(b_{3} t_{p}^{w, \text { car }}+\varphi_{3} l_{p}^{w}-r_{3} \sum\limits_{p} f_{p, 3}^{w}\right)+C_{\mathrm{fix}}+C_{\mathrm{run}}+\lambda_{p, 3}^{w} ; \\ \widetilde{C}_{p, 4}^{w}=\rho_{4} t_{p}^{w, \text { car }}+\gamma_{4} t_{p}^{w, \text { car }}+\left(b_{4} t_{p}^{w, \text { car }}+\varphi_{4} l_{p}^{w}-r_{4} \sum\limits_{p} f_{p, 4}^{w}\right)+C_{\mathrm{fix}}-\lambda_{p, 2}^{w} ; \quad \forall w, p . \\ \widetilde{C}_{p, 5}^{w}=\rho_{5} t_{p}^{w, \text { car }}+\gamma_{5} t_{p}^{w, \text { car }}+\left(b_{5} t_{p}^{w, \text { car }}+\varphi_{5} l_{p}^{w}-r_{5} \sum\limits_{p} f_{p, 5}^{w}\right)-\lambda_{p, 2}^{w} ; \\ \widetilde{C}_{p, 6}^{w}=\rho_{6} t_{p}^{w, \text { bus }}+\tau l_{p}^{w}+C_{\text {fix }} ; \\ \widetilde{C}_{p, 7}^{w}=\rho_{7} t_{p}^{w, \text { bus }}+\tau l_{p}^{w} ; \end{array}\right. $ | (45) |
模型的相关参数设置如表 3所示。
| 参数 | 数值 |
| ρ1, ρ2, ρ3, ρ4, ρ5, ρ6, ρ7/(元·min-1) | 1.00, 0.80, 0.80, 0.40, 0.30, 0.05, 0.03 |
| γ2, γ3, γ4, γ5/(元·min-1) | 0.3, 0.3, 0.2, 0.2 |
| b2, b3, b4, b5/(元·min-1) | 0.4, 0.4, 0.4, 0.4 |
| φ2, φ3, φ4, φ5/(元·km-1) | 0.2, 0.2, 0.2, 0.2 |
| r2, r3, r4, r5/(元·人-1) | 50, 50, 30, 30 |
| Cfix/元 | 3 |
| Crun/元 | 5 |
| τ/元 | 0.4 |
| θ/元 | 1 |
对于
| 路径 | i | 有共乘出行 | 无共乘出行 | |||||
| fp, iw | tpw, car/min | tpw, bus/min | fp, iw | tpw, car/min | tpw, bus/min | |||
| a) | 1 | 0 | 76.43 | — | 4.419×10-3 | 79.79 | — | |
| 2或3 | 0 | 76.43 | — | — | — | — | ||
| 4或5 | 0 | 76.43 | — | — | — | — | ||
| 6和7 | 1.219 | — | 70.16 | 1.507 | — | 74.91 | ||
| b) | 1 | 0 | 76.43 | — | 4.419×10-3 | 79.79 | — | |
| 2或3 | 0 | 76.43 | — | — | — | — | ||
| 4或5 | 0 | 76.43 | — | — | — | — | ||
| 6和7 | 1.219 | — | 70.16 | 1.507 | — | 74.91 | ||
| c) | 1 | 1.733 | 60.50 | — | 2.974 | 72.54 | — | |
| 2或3 | 0.908 | 60.50 | — | — | — | — | ||
| 4或5 | 0.908 | 60.50 | — | — | — | — | ||
| 6和7 | 0 | — | 46.67 | 0 | — | 55.30 | ||
| 注:“—”表示该处无数据。 | ||||||||
结果表明,共乘出行使网络中的小汽车数量明显减少,同时使小汽车和公交车的出行时间都有所下降。这一结果验证了共乘出行对于缓解道路拥堵、提高出行效率的作用。
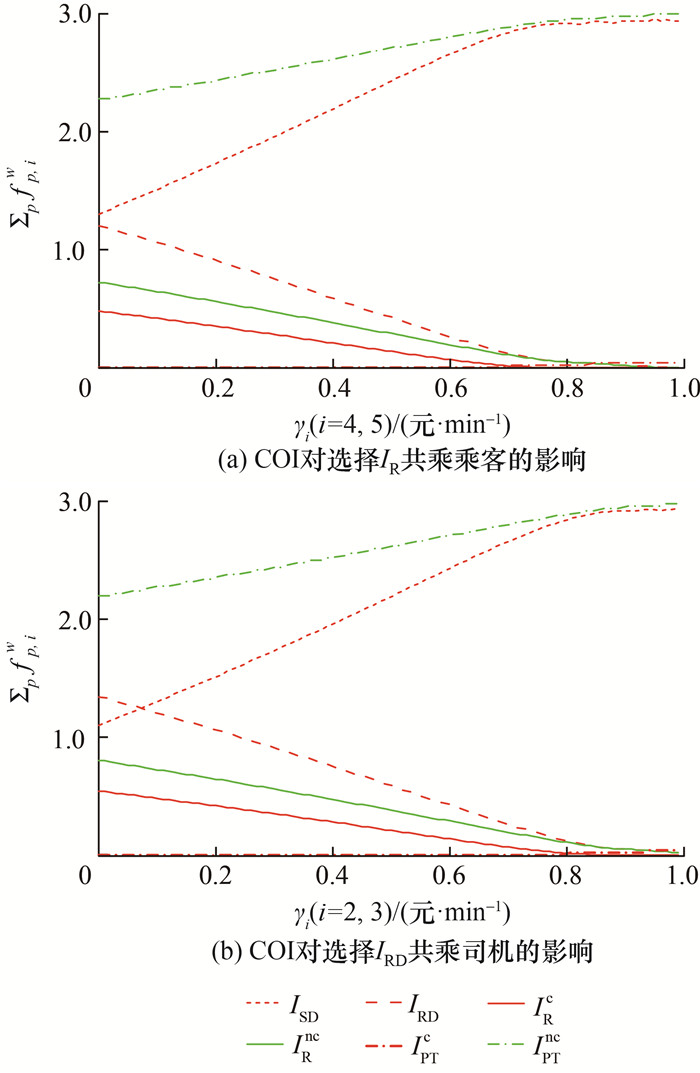
4.1.2 敏感性为进一步了解模型中各参数对出行者出行模式选择的影响,本文针对ρi、γi、ri、bi、Cfix、Crun和τ等一系列参数进行了敏感性分析,部分结果如图 2和3所示,图中Σpfp, iw为各出行模式路径流量。
|
| 图 2 COI对于出行模式选择的影响 |
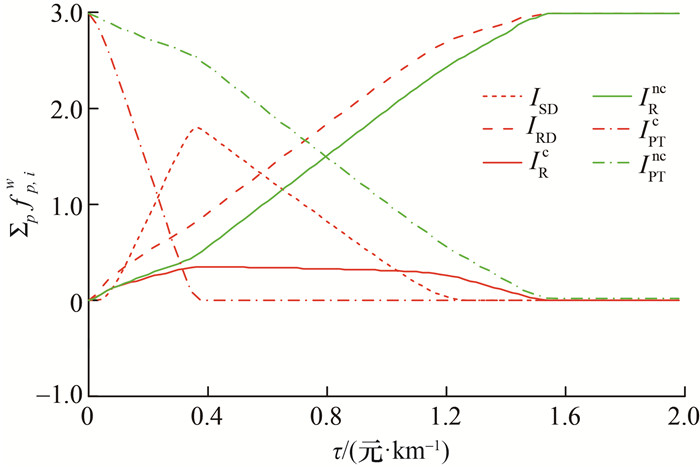
|
| 图 3 公交里程单价对于出行者模式选择的影响 |
由图 2可知,COI的增加均使网络中共乘出行的流量降低。但区别在于,选择IR出行的共乘乘客的γi增至约0.8元/min时,路径流量几乎为0;而选择IRD出行的共乘司机的γi增至约0.9元/min时,路径流量才接近于0。相比之下,共乘乘客COI的增加更容易引起共乘出行的减少。这表明决定共乘出行是否成功更重要的一方是共乘乘客。因此,通过提高服务质量、改善车内环境,使乘客获得更优质的乘车体验,降低乘客的COI,可在一定程度上吸引共乘乘客,推广共乘出行。
由图 3可知,当τ超过某一阈值时,无论是有车用户还是无车用户,几乎都不会选择乘坐公交出行;IPTc的τ阈值约为0.4元/min,IPTnc的该阈值约为1.5元/min。同时,ISD的路径流量达到峰值后开始下降,并最终接近于0。这一现象产生的原因是:随着τ上升,大量无车用户的选择开始从IPTnc转向IRnc,使共乘需求迅速增加,从而吸引了出行模式为ISD的出行者参与共乘。甚至在τ≥1.2元/min后,有车的共乘乘客也开始转变为共乘司机,即出行模式由IRc转变为IRDc或IRDnc。当τ≥1.5元/min后,几乎所有的有车用户都选择IRDnc出行,无车用户都选择IRnc出行。这一过程表明,在共乘出行和常规公交共存的交通网络中,也许可以找到一个最佳的公交票价,使系统的收益最高,或道路上的车辆数目最少。这为公交公司和交通管理者制定票价提供了有效依据。
4.2 Sioux-Falls网络为验证PSAP算法在大规模交通分配问题中的计算效率,本文应用经典的Sioux-Falls网络对Logit-SRUE问题进行了研究。该网络是一个大规模城市交通网络,共有24个节点、76条路段和528个OD对,其拓扑结构如图 4所示,图中圆圈表示节点,箭头表示路段,数字代表节点和路段编号。

|
| 图 4 Sioux-Falls网络拓扑结构 |
Sioux-Falls网络的路段出行函数为美国联邦公路局(Bureau of Public Road,BPR)函数:
| $ t_a^{\mathrm{car}}\left(x_a^{\mathrm{car}}\right)=t_{a, 0}\left[1+0.15\left(\frac{x_a^{\mathrm{car}}}{S_a}\right)^4\right], $ | (46) |
| $ t_a^{\text {bus }}\left(x_a^{\text {bus }}\right)=t_{a, 0}\left[1+0.15\left(\frac{x_a^{\text {bus }} / 10}{S_a / 1.5}\right)^4\right] . $ | (47) |
其中:ta, 0和Sa分别为路段a的自由流时间和通行能力。Qw为OD对w间的出行需求上界,本文假定
该实验的PC计算平台配置为:AMD Ryzen 7 5800H芯片的CPU(8核,3.20 GHz主频,8 MB二级缓存,16 MB三级缓存),8 GB DDR4-3 200 MHz的内存,Windows11 21H2 64位家庭版的操作系统。应用K最短路算法给每个OD对w构造包含前10条最短路径的路径集Pw,针对
| $ \boldsymbol{f}_w^1=\left(f_{p, i}^w=\frac{1}{70} Q^w, p \in P^w, i=1, 2, \cdots, 7\right)^{\mathrm{T}} . $ |
同时初始化算法参数δ=0.2,μ=0.9,ε=0.01。PSAP算法在完成11 060次迭代、用时40.77 h后满足收敛条件,所得网络路段流量如图 5所示。
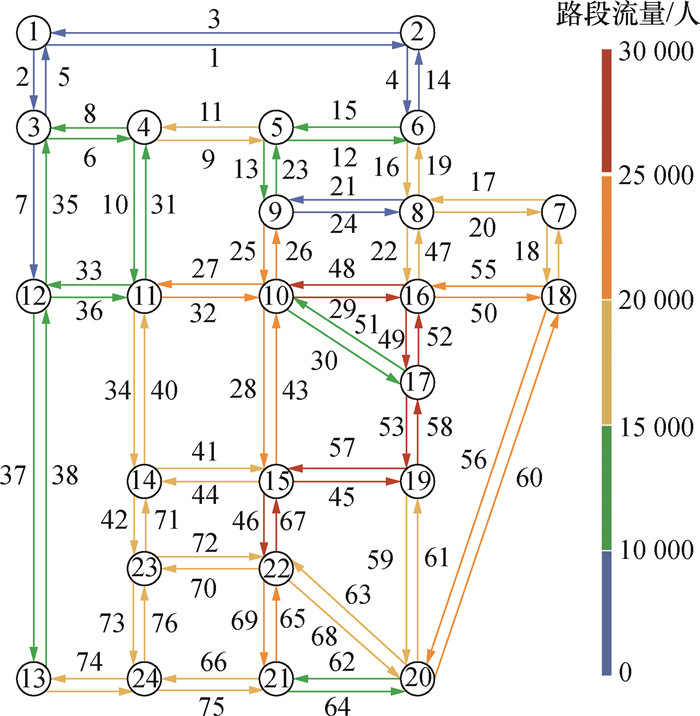
|
| 图 5 Sioux-Falls网络的路段流量 |
Sioux-Falls网络中各出行模式的流量如表 5所示。
从表 5可以看出,在当前的参数设置下,无论是有车用户还是无车用户,公交乘客所占比例均最高。这一比例较之现实情况也许偏高,但Sioux-Falls网络算例主要用于验证PSAP算法的可行性,在参数选取上可能存在一定偏差。工程实践中应当根据实地调研情况标定模型中的各参数,从而获得更加精确的流量预测结果。
5 结论本文以专车共乘为研究对象,提出了多模式SRUE问题,并基于Logit行为选择模型建立了多模式SRUE问题的VI-SRUE模型;在验证了VI-SRUE模型存在唯一解后,使用全局收敛的PSAP算法进行求解;通过Braess网络和Sioux-Falls城市交通网络进行数值实验,验证了模型和算法的可行性和有效性,分析了专车共乘出行对于交通网络的影响。
基于模型中各参数的敏感性分析获得的重要启发为: 共乘出行能有效减少路面车辆,降低行程时间;共乘出行中更具有决定性的一方是共乘乘客;管理者可通过合理制定票价、提升公交服务和改善共乘体验等方法协同公共交通和共乘出行,以有效缓解交通拥堵问题。
注意到本文的公共交通出行方式主要为具有连续公交专用道的常规公交,下一步研究中将对这一点进行拓展,考虑公共交通与社会车辆之间的微观影响,或引入城市快速公交系统、城市轨道交通系统等,进一步丰富城市多模式交通网络的共乘出行研究。
此外,本文基于静态交通分配预测共乘交通网络中的流量模式,但实际的城市交通网络状态却时刻处在动态变化中。下一步研究将考虑构建共乘交通网络的动态预测系统,依靠强大的交通信息技术提升系统的信息获取与数据处理能力,实现复杂共乘交通网络的实时状态预测。
| [1] |
XU H Y, PANG J S, ORDÓÑEZ F, et al. Complementarity models for traffic equilibrium with ridesharing[J]. Transportation Research Part B: Methodological, 2015, 81: 161-182. DOI:10.1016/j.trb.2015.08.013 |
| [2] |
MA J, XU M, MENG Q, et al. Ridesharing user equilibrium problem under OD-based surge pricing strategy[J]. Transportation Research Part B: Methodological, 2020, 134: 1-24. DOI:10.1016/j.trb.2020.02.001 |
| [3] |
李梦, 黄海军. 考虑共享出行的用户均衡交通分配模型[J]. 系统工程理论与实践, 2019, 39(7): 1771-1780. LI M, HUANG H J. A user equilibrium assignment model with ridesharing[J]. Systems Engineering—Theory & Practice, 2019, 39(7): 1771-1780. (in Chinese) |
| [4] |
DI X, LIU H X, BAN X G (JEFF), et al. Ridesharing user equilibrium and its implications for high-occupancy toll lane pricing[J]. Transportation Research Record: Journal of the Transportation Research Board, 2017, 2667(1): 39-50. DOI:10.3141/2667-05 |
| [5] |
DI X, MA R, LIU H X, et al. A link-node reformulation of ridesharing user equilibrium with network design[J]. Transportation Research Part B: Methodological, 2018, 112: 230-255. DOI:10.1016/j.trb.2018.04.006 |
| [6] |
谭卫民, 龙建成, 卢晓珊, 等. 考虑用户体验的动态共乘系统设计[J]. 系统工程理论与实践, 2020, 40(1): 210-218. TAN W M, LONG J C, LU X S, et al. A dynamic ride-sharing system based on user experience[J]. Systems Engineering—Theory & Practice, 2020, 40(1): 210-218. (in Chinese) |
| [7] |
LI M, DI X, LIU H X, et al. A restricted path-based ridesharing user equilibrium[J]. Journal of Intelligent Transportation Systems: Technology, Planning, and Operations, 2020, 24(4): 383-403. DOI:10.1080/15472450.2019.1658525 |
| [8] |
WANG X L, YANG H, ZHU D L. Driver-rider cost-sharing strategies and equilibria in a ridesharing program[J]. Transportation Science, 2018, 52(4): 868-881. DOI:10.1287/trsc.2017.0801 |
| [9] |
SUN S, SZETO W Y. Multi-class stochastic user equilibrium assignment model with ridesharing: Formulation and policy implications[J]. Transportation Research Part A: Policy and Practice, 2021, 145: 203-227. DOI:10.1016/j.tra.2020.12.011 |
| [10] |
XU H Y, ORDÓÑEZ F, DESSOUKY M. A traffic assignment model for a ridesharing transportation market[J]. Journal of Advanced Transportation, 2015, 49(7): 793-816. DOI:10.1002/atr.1300 |
| [11] |
MA J, MENG Q, CHENG L, et al. General stochastic ridesharing user equilibrium problem with elastic demand[J]. Transportation Research Part B: Methodological, 2022, 162: 162-194. DOI:10.1016/j.trb.2022.06.001 |
| [12] |
YAN C Y, HU M B, JIANG R, et al. Stochastic ridesharing user equilibrium in transport networks[J]. Networks and Spatial Economics, 2019, 19(4): 1007-1030. DOI:10.1007/s11067-019-9442-5 |
| [13] |
马捷, 李锐, 王华. 弹性需求的Logit随机共乘用户均衡模型和算法[J]. 同济大学学报(自然科学版), 2022, 50(5): 601-609. MA J, LI R, WANG H. Logit-based stochastic ridesharing user equilibrium model with elastic demand and its algorithm[J]. Journal of Tongji University (Natural Science), 2022, 50(5): 601-609. (in Chinese) |
| [14] |
郇宁, 姚恩建, 杨扬, 等. 电动汽车混入条件下随机动态用户均衡分配模型[J]. 交通运输工程学报, 2019, 19(5): 150-161. HUAN N, YAO E J, YANG Y, et al. Stochastic dynamic user equilibrium assignment model considering penetration of electric vehicles[J]. Journal of Traffic and Transportation Engineering, 2019, 19(5): 150-161. DOI:10.3969/j.issn.1671-1637.2019.05.016 (in Chinese) |
| [15] |
周博见, 李旭宏, 何杰. 求解基于路径的Logit型随机用户均衡模型的新算法[J]. 中国公路学报, 2014, 27(3): 100-107. ZHOU B J, LI X H, HE J. A new algorithm for path-based Logit stochastic user equilibrium model[J]. China Journal of Highway and Transport, 2014, 27(3): 100-107. (in Chinese) |
| [16] |
胡文君, 周溪召. 基于交叉巢式Logit的多用户多模式随机用户均衡模型[J]. 中国公路学报, 2012, 25(4): 133-140. HU W J, ZHOU X Z. Multi-user and multi-mode stochastic user equilibrium model based on cross-nested Logit[J]. China Journal of Highway and Transport, 2012, 25(4): 133-140. (in Chinese) |
| [17] |
胡文君, 周溪召. 基于成对组合Logit的多用户多模式随机用户均衡模型[J]. 系统工程理论与实践, 2013, 33(5): 1318-1326. HU W J, ZHOU X Z. Multi-user multi-mode stochastic user equilibrium model based on paired combinatorial Logit models[J]. Systems Engineering—Theory & Practice, 2013, 33(5): 1318-1326. DOI:10.3969/j.issn.1000-6788.2013.05.029 (in Chinese) |
| [18] |
LI M, HUA G W, HUANG H J. A multi-modal route choice model with ridesharing and public transit[J]. Sustainability, 2018, 10(11): 4275. DOI:10.3390/su10114275 |
| [19] |
PATRIKSSON M. The traffic assignment problem: Models and methods[M]. New York: Courier Dover Publications, 2015.
|
| [20] |
BOYD S, VANDENBERGHE L. Strong duality and Slater's constraint qualification[M]// BOYED S, VANDENBERGHE L. Convex optimization. Cambridge: Cambridge University Press, 2004: 226-227.
|
| [21] |
NAGURNEY A. Network economic: A variational inequality approach[M]. 2nd ed. New York: Springer New York, 1999.
|
| [22] |
JOHNSON C R. Positive definite matrices[J]. The American Mathematical Monthly, 1970, 77(3): 259-264. DOI:10.1080/00029890.1970.11992465 |
| [23] |
FACCHINEI F, PANG J S. Finite-dimensional variational inequalities and complementarity problems, Volume Ⅰ[M]. New York: Springer, 2003.
|
| [24] |
HE B S, HE X Z, LIU H X, et al. Self-adaptive projection method for co-coercive variational inequalities[J]. European Journal of Operational Research, 2009, 196(1): 43-48. DOI:10.1016/j.ejor.2008.03.004 |
| [25] |
YEN J Y. Finding the K shortest loopless paths in a network[J]. Management Science, 1971, 17(11): 712-716. DOI:10.1287/mnsc.17.11.712 |
| [26] |
BAR-GERA H. Transportation networks[EB/OL]. (2021-10-22)[2023-03-31]. https://github.com/bstabler/TransportationNetworks.
|



