2. 清华大学 安全科学学院, 北京 100084;
3. 中铁七局集团武汉公司有限公司, 武汉 430200
2. School of Safety Science, Tsinghua University, Beijing 100084, China;
3. China Railway Seventh Group Co. Ltd., Wuhan 430200, China
随着交通强国战略的持续推进,中国高速铁路网络的建设取得了长足的发展。截至2022年,高速铁路运营的总里程超过42 000 km[1]。2013—2021年,中西部地区新增高铁里程1.9×104 km,占全国新增高铁里程的60.5%[2]。随着高速铁路网朝中西部地区扩展,线路穿越山地、丘陵地区的概率骤升,铁路沿线隧道比例激增。截至2022年底,高速铁路隧道4 178座,总长7 032 km。其中,长度大于10 km的特长隧道105座, 长约1 339 km[3]。特长隧道的涌现给高铁运行带来了较大的安全挑战,尤其是隧道内的消防安全问题。列车轿厢作为高火灾荷载密度的封闭空间[1],运行过程中存在着一定的火灾风险,例如“1·25” G281次列车火灾事故。一旦高速列车着火制动停在隧道内,火灾引发的高温温度场与烟气沉降将会对人员的安全疏散和应急救援造成较大影响。
相比公路隧道的研究,国内外关于高铁火灾的研究较少[1, 4-6]。其中,Zhou等[1]通过设置高铁列车车厢材料的属性开展数值模拟研究,预测了列车车厢发生火灾时的热释放速率曲线,评估了车厢顶棚、侧墙、行李架、座椅以及地板材料的可燃性对于车厢总体峰值热释放速率的影响。根据实验验证后的高铁车厢燃烧模型,Zhou等[5]在隧道中开展了FDS(fire dynamics simulator)数值模拟研究,分析了高铁隧道内存在纵向通风时隧道内车厢燃烧的热释放速率曲线,发现车厢燃烧热释放速率峰值随着纵向通风速度的增加呈现出指数衰减的趋势[5]。除了高铁列车车厢在隧道内燃烧的热释放速率之外,隧道内火灾热烟气作为影响人员疏散与应急救援的关键因素,同样需要开展重点研究。
根据《高速铁路设计规范》(TB10621—2014)关于高速铁路建筑限界轮廓基本尺寸的规定,高铁隧道的拱顶垂直高度一般不低于8.0 m[7]。与净高较低的公路、地铁隧道不同,高铁隧道内的火羽流将以更高的速度、更大的质量流量冲击拱顶[8],导致较快的顶棚射流扩散流动[9]。另一方面,由于高铁隧道的拱顶净高较高,参考“1·25”G281次列车火灾事故并结合前人关于高铁车厢热释放速率与燃烧的研究[5],可推测顶棚下出现扩展火焰等燃烧行为的概率较小。顶棚下撞击火羽流的类型影响顶棚射流的传热参数[10-12],导致高铁隧道火灾烟气的温度分布特征有别于公路、地铁隧道。但是关于公路、地铁等狭长受限空间内火灾的成果对高铁隧道内的火灾温度场研究仍有一定指导意义。胡隆华等[13]在长走廊内开展了现场火灾实验,通过建立守恒方程组结合全尺寸火灾实验数据,构建了顶棚下烟气平均温升纵向指数衰减模型。钟茂华等[14-16]采用了FDS数值模拟结合全尺寸火灾实验的方法研究了具有弧形顶棚的长隧道在火灾过程中的烟气温度纵向衰减规律,提出了适用于弱羽流冲击顶棚条件下的无量纲半经验温度衰减模型。Ingason等[17]分析了强羽流冲击顶棚对于烟气纵向温度衰减行为的影响,通过定义虚拟起始点的方法,构建了弱羽流冲击顶棚条件下的无量纲温度衰减模型。采用相似的研究思路,史聪灵等[18]开展了地铁隧道的现场热烟实验,分析了纵向通风作用下地铁隧道纵向温度衰减行为;基于烟气纵向扩散过程中的沉降行为特征,划分了地铁隧道火灾烟气纵向流动分区;围绕不同的烟气纵向流动分区,分别建立了温度纵向衰减预测模型。在前人研究的基础上,Ye等[11]充分考虑了烟气层温度在垂直方向上的差异,通过定义烟气层中的热边界层建立了烟气温度纵向最大温升衰减指数模型,并且根据火羽流撞击顶棚的类别细化了模型的类型与适用范围。学者对狭长受限空间内火灾烟气纵向温度衰减行为的规律开展了大量的研究,建立了适用大量场景的温度场纵向衰减表征模型。但是考虑到高铁隧道独特的高拱顶和断面构形对顶棚射流流动、传热参数的影响,现有表征模型是否可以较好适用于高铁隧道火灾纵向温度衰减规律仍需进一步分析,而现场火灾实验可以作为评估表征模型的相对有效手段[19]。
本文选取实际高速铁路隧道开展了现场火灾实验,探究现有狭长受限空间内火灾烟气纵向流动与温度分布模型在高铁隧道内的适用性并分析误差原因,为评估高速铁路隧道内火灾烟气对人员疏散的影响提供支撑。
1 场景选取与实验布置本文选取渝湘高铁重庆至黔江段的白家山隧道开展现场火灾实验,白家山隧道位于重庆市武隆区江口镇和彭水县高谷镇境内,为正线双线隧道,如图 1所示。隧道全长6 830 m,最大埋深为443 m。

|
| 图 1 白家山高铁隧道 |
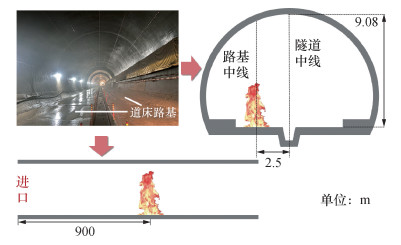
白家山高铁隧道横截面为弧形几何构型,拱顶与道床路基表面的垂直距离为9.08 m。单洞双线隧道内布置有双道床,道床路基中线与隧道中线距离为2.5 m。考虑到道床的实际位置,本文火灾实验涉及的火源位置沿着路基中线布置。另一方面,考虑到不影响隧道的施工进度以及减少隧道开口边界对于实验结果的影响,实验的火源位置位于距离隧道进口约900 m处,如图 2所示。
|
| 图 2 白家山高铁隧道全尺寸实验火源设置示意图 |
为营造稳定的火羽流和还原真实火灾场景下的热烟气扩散过程,本文根据参考文[20]采用标准化油池火构建全尺寸实验火源系统。火源系统由若干钢制的矩形油盘(长841 mm,宽595 mm,高130 mm)构成,可根据需测试的火源热释放速率进行油盘个数的增减。本文中标准油池火所用液体燃料为同一批次92号汽油,每次实验中油盘内的燃料厚度均为2 cm以保证足够的燃烧测试时长[21]。基于图 2中的火源位置,本文设计并开展了3个场景的现场火灾实验,具体火源与实验环境参数如表 1所示。
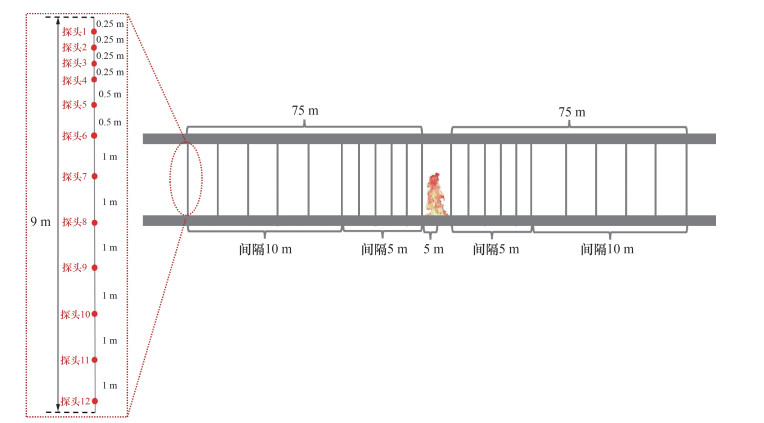
本文中涉及的全尺寸火灾实验均采用相同的温度测试系统,温度测试系统纵向跨度为150 m,由22根长为9 m的测温电缆构成。测温电缆垂直悬挂于高铁隧道拱顶下,按照5或10 m的水平间距布置在火源上下游两侧,如图 3所示。另外,单个测温电缆包含12个测温探头,测温探头能够在0~127 ℃的区间内保证0.125 ℃的测温精度,并且测温的不确定性控制在0.1%以内。参考文[10, 22]中顶棚射流在垂直方向上的温度分布特征,本文实验中涉及的测温点在垂直方向上的排列均按照“上密下疏”的规则以更加精确地获取烟气垂直温度分布特征。
|
| 图 3 全尺寸火灾实验温度测试系统示意图 |
此外,全尺寸实验中架设了高清摄像机与片状光源以获取火源的燃烧状态和冲击顶棚的火羽流类型。高清摄像机为索尼FDR-AX60型号4K摄像机,可记录每秒50帧的高清火源燃烧画面;片状光源由型号为LWPIV-3WM的激光发射器产生,厚度和扇面角度分别为1.5 mm和120°。
2 全尺寸火灾实验数据分析 2.1 火源燃烧状态与羽流撞击类型参考文[8, 23],当量直径大于0.2 m的液体油池火单位面积质量损失率随着当量直径的增大逐渐升高:
| $ \dot{m}^{\prime \prime}=\dot{m}_{\max }^{\prime \prime}[1-\exp (-k \beta D)] . $ | (1) |
其中:kβ可认定为固定值(k为消光系数,β为平均修正特征长度);D为液体燃料燃烧面的当量直径;

|
| 图 4 全尺寸实验火源燃烧状态与火羽流 |
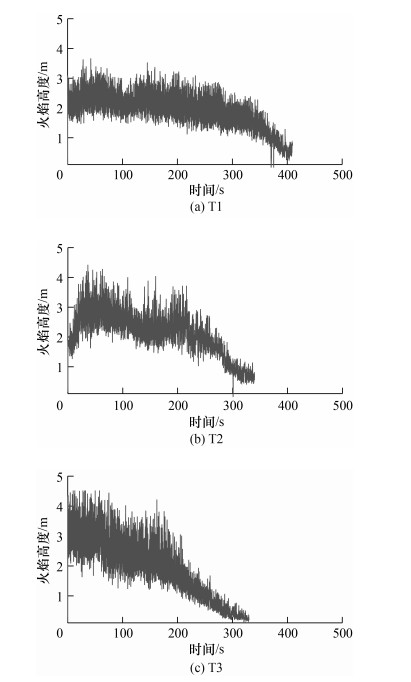
文[8]测定的汽油燃烧热为43.7 MJ/kg,且假定汽油油池火燃烧效率为0.8,结合式(1)计算的每个工况单位面积质量损失率和表 1中燃烧面积,可以推算出本文中T1、T2和T3对应的火源热释放速率计算值分别为0.38、1.01和2.52 MW。但是上述计算值仍然与实际值存在差异,为进一步定量化分析火源燃烧状态的状态,本文根据油池火火焰高度与火源热释放速率的正相关关系[8],基于火焰高度—时间曲线反推每个工况下火源热释放速率时间演化特征,从而定量分析每个工况的火源燃烧状态。图 5中火源高度曲线是根据处理后的火焰二值化图像视频(本文中的亮度阈值设定为220),结合图像像素点与实际距离的比例关系获取的[12]。可以看出,推测出3个工况均不存在明显的燃烧发展阶段,并且稳定燃烧阶段(未出现明显衰减行为)持续时间较长。即使相比T1和T3,T2具有相对明显的燃烧发展阶段(约30 s),但是该阶段相对于整体较长的稳定燃烧(未出现明显衰减行为)可近似忽略。这表明顶棚下热烟气的扩散行为在相当长的时间段内受到了稳定的火羽流驱动,并且燃烧发展阶段造成的火羽流驱动不均匀的影响可近似忽略。
|
| 图 5 全尺寸火灾实验标准火源火焰高度—时间曲线 |
2.2 烟气纵向蔓延过程
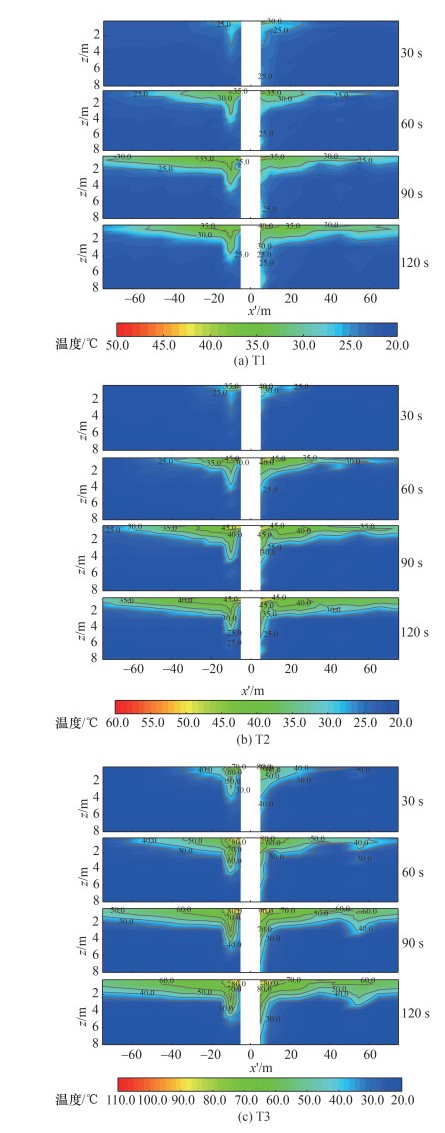
根据火焰高度曲线推测出的火源燃烧状态时间演化特征,本文选取实验开始后30、60、90和120 s 4个时刻的烟气温度场数据,分析烟气纵向的蔓延过程。为便于分析烟气上游、下游蔓延特征,本文定义x′为数据点纵向坐标(上游为正值,下游为负值,零点为火源位置),z为数据点垂直坐标(零点为隧道顶棚顶点即拱顶处,向下为正)。另外,本文定义x为距离火源的纵向距离,并且x=|x′|。图 6中,尽管存在温度采集盲区(-5 m < x′ < 5 m),但是仍可清晰辨识顶棚下火灾热烟气的纵向蔓延特征,并且每个实验场景中的热烟气纵向蔓延速度也表现出一定差异。基于热烟气温度在不同时刻的纵向分布,可以大致推断出火灾热烟气在T1、T2和T3中的纵向蔓延速度依次增大。
|
| 图 6 不同时刻全尺寸火灾实验纵向温度场分布图 |
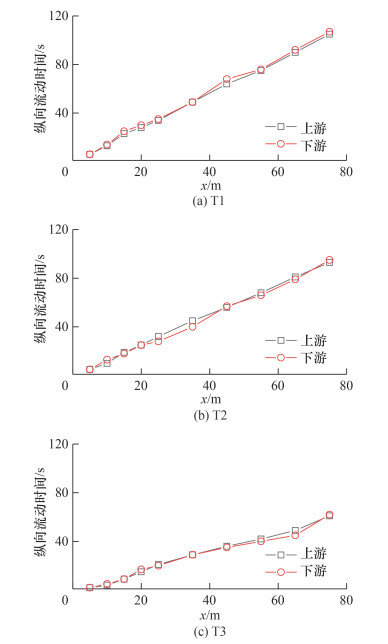
为进一步量化热烟气在纵向方向上的流动速度,本文以表 1中环境温度作为烟气边界分辨的特征温度,绘制了每个全尺寸火灾场景的热烟气纵向流动距离—时间曲线,如图 7所示。可以看出,在没有纵向风干扰条件下,上游与下游的热烟气蔓延速度基本保持一致。根据5.0 m≤x≤75 m范围内获取的距离—时间数据点,T1、T2和T3中热烟气纵向流动的平均速度分别约为0.72、0.80和1.30 m/s。根据2.1节的分析可知,T1、T2和T3中所使用标准火源的热释放速率依次增大,火源的热释放速率对于烟气的纵向蔓延速度有重要的影响作用。Oka等[25]研究了隧道内烟气纵向流动速度分布,针对一维射流区内热烟气最大流动速度的纵向演化特征,建立了无量纲模型:
| $ \begin{gathered} \frac{V_{\max }}{\sqrt{g H}}=0.5812\left(\frac{l_{\mathrm{b}}}{H}\right)^{-1 / 3} \cdot \\ \exp \left[-1.567 \;S t \cdot \frac{x}{H}\left(\frac{l_{\mathrm{b}}}{H}\right)^{-1 / 3}\right] \cdot Q_{\mathrm{c}}^{* 1 / 3}. \end{gathered} $ | (2) |
|
| 图 7 全尺寸火灾实验热烟气纵向流动距离—时间曲线 |
其中:Vmax为相同横向位置下烟气纵向流动最大速度;Qc*为无量纲对流热释放速率,具体表达式为Qc*=Qc/(ρ∞CpT∞g1/2H5/2);H、lb、g和St分别为隧道高度、隧道宽度一半、重力加速度和Stanton数。参考文[26],上述物理参数在本文全尺寸火灾场景中可以近似认定为定值。因此根据式(2)可知,相同x下,较大的Qc*对应着较大的Vmax。如2.1节所述,T1、T2和T3场景中的热释放速率依次增大,则对应的Qc*也将依次增大。式(2)可进一步佐证图 7所示规律:火源的热释放速率对于烟气的纵向蔓延速度有重要影响作用,即高的火源热释放速率对应高的顶棚热烟气纵向流动速度。
2.3 烟气纵向温度分布特征根据图 6中90和120 s时刻温度规律,火源稳定燃烧阶段的热烟气温度纵向分布特征基本维持一致,并且不同火灾场景下的纵向温度分布特征迥异。本文选取点火后120 s时刻的温度数据分析稳定阶段高铁隧道火灾烟气纵向温度特征,如图 8所示。可以看出,高铁隧道内火灾烟气温度在垂直方向上呈现出经典的“top-hat”分布,即烟气温度在垂直方向上从顶棚下表面开始先增大后减小,这与文[11, 27]结论基本一致。并且随着烟气远离火源位置,烟气垂直方向温度的“top-hat”分布更加明显。图 8中,x>45 m后的热烟气垂直温度分布特征基本保持一致。2个因素共同造成了上述现象,具体如下。

|
| 图 8 点火后120 s全尺寸火灾实验纵向温度分布特征 |
1) 热烟气与下表面的对流换热系数。
根据Reynolds-Colburn类比可知[28],隧道内热烟气与下表面的对流换热系数h可表达为
| $ \frac{h}{\rho \bar{V} C_{\mathrm{p}}}=\operatorname{Pr}^{-2 / 3} \frac{f}{2}. $ | (3) |
其中:Pr和f分别为Prandtl数和顶棚下表面摩擦因子,ρ和Cp分别为热烟气的平均密度与热容,上述参数在烟气纵向流动过程中可认定为近似不变[28];V为热烟气的纵向平均流速;h为热烟气对流换热系数。参考式(2),随着烟气远离火源位置,V逐渐降低并趋于稳定。因此,h也随之降低并逐渐趋于稳定,直接决定了热烟气与顶棚下表面的换热效率在纵向方向上逐渐降低并趋于稳定。随着x的增大,靠近顶棚区域的热烟气在垂直方向上的温度梯度逐步减小,最大温度所在位置的z(“top-hat”分布上半部)的增加幅度也在减小,并且都逐渐趋于稳定。
2) 热烟气层厚度。
热烟气层厚度δ决定着烟气层的下边界,间接影响着热烟气温度衰减至室温的垂直距离。参考文[27, 29],尽管热烟气层厚度的定义不同,但是不同定义下高铁隧道内的烟气层厚度均随着烟气远离火源位置而逐渐增大并趋于稳定。这间接导致烟气垂直温度从最大值降低至室温的垂直距离(“top-hat”分布下半部),随着x的增大而逐渐增大并趋于稳定。
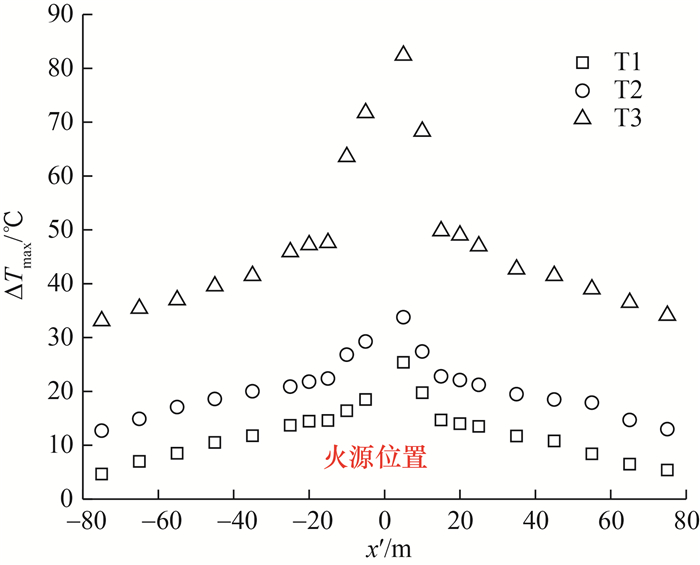
图 8中烟气层垂直温度呈“top-hat”分布,显示高铁隧道内火灾烟气纵向蔓延过程中,垂直方向最大温度的所在位置不固定并且不紧贴顶棚下表面。考虑到测温电缆的探头在垂直方向上的排列间距,为避免测温探头测定的最大温度不是真实值,参考文[10, 30]中方法,本文采用3个测量值的二次拟合(测量最大值和2个相邻的测量值)来估计最大温度值。基于实验数据估计的热烟气最大温升ΔTmax,分别按照在烟气上游、下游对应的纵向位置进行排列,见图 9。可以看出,3个火灾场景的热烟气最大温升纵向衰减行为在上游、下游呈现出的特征基本一致,并且衰减的阶段分布也与文[17]模型的相似。但是针对现有火灾烟气温升纵向衰减模型是否适用于高铁隧道,仍需要开展定性分析。
|
| 图 9 点火后120 s隧道内火灾烟气最大温升纵向分布 |
关于狭长受限空间内的火灾烟气温升纵向衰减模型,胡隆华等[31]与田向亮等[14]开展了全尺寸的火灾实验,并各自建立了火灾烟气温升纵向衰减预测模型。
胡隆华[31]等在公路隧道(拱顶)中开展了全尺寸火灾实验,实验隧道宽10.8 m、拱顶距路基表面的垂直距离为7.2 m。根据实验温度数据结合烟气能量守恒方程,建立了热烟气温升纵向衰减预测模型:
| $ \frac{\Delta T(x)}{\Delta T_{\mathrm{ref}}}=\mathrm{e}^{K_1\left(x-x_{\mathrm{ref}}\right)}, \quad K_1=-0.019 \mathrm{~m}^{-1}. $ | (4) |
其中:xref表示参考点距火源位置的纵向距离,ΔTref表示参考点处的热烟气温升。
田向亮等[14]在宽3.2 m、拱顶高3.2 m的隧道(拱顶)中开展了全尺寸火灾实验。基于热烟气的连续性与能量守恒方程构建了弧形顶棚下的热烟气温升衰减预测微分方程,结合实验温度数据建立了半经验预测模型:
| $ \begin{gathered} \;\frac{\Delta T(x)}{\Delta T_{\mathrm{ref}}}=\mathrm{e}^{{K_2\left(x / \mathrm{m}-x_{\mathrm{ref}} / \mathrm{m}\right)}^{ K_3}}, \\ K_2=-0.08, \quad K_3=0.72. \end{gathered} $ | (5) |
式(4)和(5)在建立过程中均假定热烟气中不存在燃烧行为,所以式(4)和(5)适用于无顶棚扩展火焰影响的热烟气温升纵向衰减行为预测。以火源热释放速率最大的T3全尺寸实验(见图 10)为例,撞击顶棚的火羽流类型为烟流且包括初始测温点(x′=±5 m)在内的热烟气流动区域,均未出现燃烧行为。因此,本文开展模型对比分析的工作中,上游烟气以x′=-5 m处为参考点,下游烟气以x′=5 m处为参考点;对比工作中,本文以参考点处的最大温升值作为ΔTref代入计算。

|
| 图 10 T3全尺寸实验近火源区域热烟气流动状态 |
尽管胡隆华等[31]与田向亮等[14]开展实验的全尺寸隧道在横截面形状方面存在一定差异,但是顶棚射流流动过程中接触的顶棚表面均为正圆形的一部分。这意味着换热边界、射流横截面积等关键参数,随着x增加呈现出的演化规律基本一致[32]。另外考虑到式(4)和(5)中的x不是无量纲参数,本文中获取的全尺寸高铁隧道火灾温度数据对应的位置参数需要根据文[33]中Froude相似准则进行调整。为方便预测模型与全尺寸火灾温度数据的对比分析,需要计算隧道高度比例,胡隆华等[31]和田向亮等[14]开展实验的隧道横截面高度与本文高铁隧道高度比例分别为1∶1.26和1∶2.84。
根据隧道高度比例,基于Froude相似准则,式(4)和(5)可以分别转化为式(6)和(7):
| $ \frac{\Delta T(x)}{\Delta T_{\text {ref }}}=\mathrm{e}^{-0.015\left(x-x_{\text {ref }}\right)}, $ | (6) |
| $ \frac{\Delta T(x)}{\Delta T_{\text {ref }}}=\mathrm{e}^{-0.04\left(x / \mathrm{m}-x_{\text {ref }} / \mathrm{m}\right)^{0.72}}. $ | (7) |
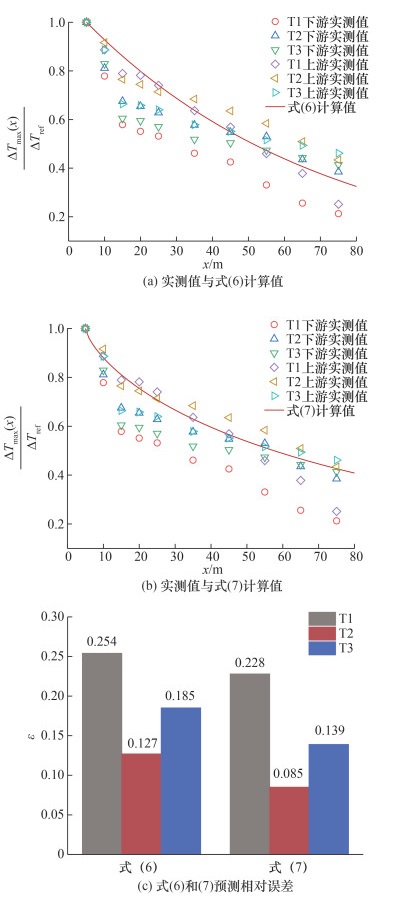
根据式(6)和(7)的计算值,本文开展了调整后模型与T1、T2和T3火灾实验温升数据的对比,如图 11a和图 11b所示。为进一步量化模型的预测精度,本文参考文[10]定义了温升纵向衰减预测相对误差的计算方程:
| $ \varepsilon=\frac{\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left[y_i-f\left(x_i\right)\right]^2}}{\frac{1}{n} \sum\limits_{i=1}^n y_i}. $ | (8) |
|
| 图 11 烟气温度实测值与计算值 |
其中:yi为测量的温升数据,f(xi)为xi处的预测值,n为数据点的数量。图 11c中,以每个全尺寸火灾场景测定的温升衰减数据为基准,根据式(8)分别计算了式(6)和(7)在每一个全尺寸火灾场景中的预测相对误差ε。
尽管式(4)与(5)是火灾烟气平均温升的纵向衰减模型,但是调整后的模型可以基本描述出全尺寸火灾烟气最大温升纵向衰减规律,ε基本控制在0.25以内。以本文中测定的高铁隧道火灾烟气温升衰减数据为基准,式(7)的ε小于式(6)的。分析上述经典模型的推导过程可知[31],式(4)提出的前提是假定热烟气在纵向流动过程中的质量流量
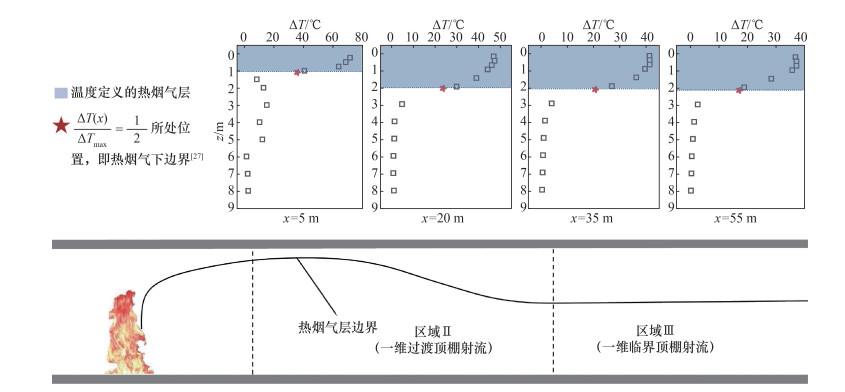
相对而言,式(5)在推导过程中考虑了换热系数、换热边界以及质量流量等参数在纵向流动过程中的演化行为,以x为自变量构建了上述流动和传热参数的演化方程,这解释了式(7)对于本文全尺寸实验的ε较小。然而,田向亮等[14]是基于实验数据非线性拟合得出了热烟气流动和传热参数演化方程的经验解,即式(5)中K2和K3。尽管式(5)一定程度上弥补了式(4)在预测全尺寸实验温升衰减的短板,但是转化后的式(7)中经验参数-0.04和0.72在部分区域不能完全描述本文中高铁隧道火灾热烟气最大温升纵向衰减行为,具体见图 11(b)中x < 35 m区域。图 12中,参考文[27]定义热烟气层的方法,根据T3下的热烟气温升数据可知高铁隧道内的烟气层厚度在纵向上呈现出2个明显分区,即区域Ⅱ(一维过渡射流区)和区域Ⅲ(一维临界射流区),并且具体的分界线在20 m < x < 35 m范围内,这与文[10, 27]中的隧道火灾研究结论基本一致。
|
| 图 12 本文所述全尺寸高铁隧道火灾热烟气纵向分区(通过温度定义热烟气厚度) |
高铁隧道内火灾热烟气在纵向上的流动分区(见图 12)导致热烟气流动和传热参数呈现出多个明显的演化阶段。但是式(4)与(5)的提出主要聚焦于热烟气层厚度变化不大的区域Ⅲ,忽略了热烟气层厚度逐渐增长的区域Ⅱ。因此无论是简化系数K1还是经验系数K2和K3,均无法精确表征热烟气层厚度显著增长作用下的流动和传热参数演化规律,影响了转化后的式(6)和(7)对于高铁隧道中区域Ⅱ内热烟气最大温升纵向衰减的预测精度。
但是,基于Froude相似准则转化后的式(6)和(7)仍然可以在接受的相对误差范围之内,对高铁隧道部分火灾区域的温升纵向衰减进行有效预测。其中式(7)能够较为准确地预测弱羽流冲击下高铁隧道区域Ⅲ内的纵向温升衰减行为,区域Ⅲ的起始点即区域Ⅱ与区域Ⅲ的边界线在20 m < x < 35 m。结合图 12中热烟气层厚度,本文将分界线保守定为x≈35 m。因为本文中高铁隧道拱顶H为9.08 m,所以式(7)适用区域起始点可以无量纲化为x/H≈3.85。
3 结论本文依托渝湘高铁重庆至黔江段的白家山隧道开展了全尺寸高铁隧道火灾实验,获取了火灾热烟气在纵向方向上的蔓延速度与温度分布特征。所得动力学参数特征与前人研究结论具有一定的相似性,但是仍然表现出一定差异。具体结论如下:
1) 在没有纵向风干扰条件下,本文开展的全尺寸火灾实验上游与下游的热烟气蔓延速度基本保持一致。尽管高铁隧道净高、横截面积较常规公路隧道变大,但是火源热释放速率对于热烟气纵向蔓延的速度仍然起到重要作用,这与前人的研究结论保持一致。
2) 高铁隧道内火灾烟气温度在垂直方向上呈现出经典的“top-hat”分布,即烟气温度在垂直方向上从顶棚下表面开始先增大后减小。随着烟气远离火源位置,烟气垂直方向温度的“top-hat”分布特征逐渐明显。但是随着h、δ逐渐趋于稳定,x>45 m后的高铁隧道热烟气垂直方向温度分布特征基本保持不变。
3) 基于Froude相似准则转化,本文提出了适用于高铁隧道射流区域Ⅲ的火灾烟气温升纵向衰减模型。考虑到本文保守划定高铁隧道射流区域Ⅱ和区域Ⅲ分界线为x/H≈3.85,该模型适用范围为x/H≥3.85。
| [1] |
ZHOU Y L, BI H Q, WANG H L. Influence of the primary components of the high-speed train on fire heat release rate[J]. Archives of Thermodynamics, 2023, 44(1): 37-61. |
| [2] |
国家统计局. 深入贯彻落实新发展理念交通通信实现跨越式发展——党的十八大以来经济社会发展成就系列报告之六[R/OL]. 北京: 国家统计局, (2022-09-21)[2023-01-01]. https://www.stats.gov.cn/xxgk/jd/sjjd2020/202209/t20220921_1888529.html. National Bureau of Statistics. Further implementation of the new development concept transportation and communication to achieve leapfrog development: The sixth of the series of reports on economic and social development achievements since the 18th national congress of the communist party of China[R/OL]. Bejing: National Bureau of Statistics, (2022-09-21)[2023-01-01]. https://www.stats.gov.cn/xxgk/jd/sjjd2020/202209/t20220921_1888529.html. (in Chinese) |
| [3] |
巩江峰, 王伟, 黎旭, 等. 截至2022年底中国铁路隧道情况统计及2022年新开通项目重点隧道概况[J]. 隧道建设(中英文), 2023, 43(4): 721-738. GONG J F, WANG W, LI X, et al. Statistics of railway tunnels in China by the end of 2022 and overview of key tunnels of projects newly put into operation in 2022[J]. Tunnel Construction, 2023, 43(4): 721-738. (in Chinese) |
| [4] |
BI H Q, ZHOU Y L, WANG H L, et al. Characteristics of fire in high-speed train carriages[J]. Journal of Fire Sciences, 2020, 38(1): 75-95. DOI:10.1177/0734904119894527 |
| [5] |
ZHOU Y L, WANG H L, BI H Q, et al. Heat release rate of high-speed train fire in railway tunnels[J]. Tunnelling and Underground Space Technology, 2020, 105: 103563. DOI:10.1016/j.tust.2020.103563 |
| [6] |
TAO L L, YAN X N, ZHANG Y M, et al. Experimental and numerical study on the smoke and velocity distribution in an extra-long railway tunnel fire[J]. Tunnelling and Underground Space Technology, 2021, 117: 104134. DOI:10.1016/j.tust.2021.104134 |
| [7] |
国家铁路局. 高速铁路设计规范: TB10621-2014[S]. 北京: 中国铁道出版社, 2014. National Railway Administration of the People's Republic of China. Code for design of high speed railway: TB10621-2014[S]. Beijing: China Railway Publishing House, 2014. (in Chinese) |
| [8] |
KARLSSON B, QUINTIERE J G. Enclosure fire dynamics[M]. Boca Raton: CRC Press, 2000.
|
| [9] |
ZHANG X L, HU L H, ZHANG X C. Flame lengths in two directions underneath a ceiling induced by line-source fire: An experimental study and global model[J]. Proceedings of the Combustion Institute, 2021, 38(3): 4561-4568. DOI:10.1016/j.proci.2020.07.096 |
| [10] |
YE K, TANG X, ZHENG Y, et al. Estimating the two-dimensional thermal environment generated by strong fire plumes in an urban utility tunnel[J]. Process Safety and Environmental Protection, 2021, 148: 737-750. DOI:10.1016/j.psep.2021.01.030 |
| [11] |
YE K, ZHOU X D, ZHENG Y, et al. Estimating the longitudinal maximum gas temperature attenuation of ceiling jet flows generated by strong fire plumes in an urban utility tunnel[J]. International Journal of Thermal Sciences, 2019, 142: 434-448. DOI:10.1016/j.ijthermalsci.2019.04.023 |
| [12] |
潘荣亮. 盾构式综合管廊典型火灾场景顶棚射流与热反馈机制研究[D]. 徐州: 中国矿业大学, 2022. PAN R L. Study on ceiling jet and induced heat feedback mechanism of representative fire scenarios in shield utility tunnel[D]. Xuzhou: China University of Mining and Technology, 2022. (in Chinese) |
| [13] |
HU L H, HUO R, LI Y Z, et al. Full-scale burning tests on studying smoke temperature and velocity along a corridor[J]. Tunnelling and Underground Space Technology, 2005, 20(3): 223-229. DOI:10.1016/j.tust.2004.08.007 |
| [14] |
TIAN X L, ZHONG M H, SHI C L, et al. Full-scale tunnel fire experimental study of fire-induced smoke temperature profiles with methanol-gasoline blends[J]. Applied Thermal Engineering, 2017, 116: 233-243. DOI:10.1016/j.applthermaleng.2017.01.099 |
| [15] |
LIU C, ZHONG M H, SHI C L, et al. Temperature profile of fire-induced smoke in node area of a full-scale mine shaft tunnel under natural ventilation[J]. Applied Thermal Engineering, 2017, 110: 382-389. DOI:10.1016/j.applthermaleng.2016.08.147 |
| [16] |
LIU C, ZHONG M H, TIAN X L, et al. Experimental and numerical study on fire-induced smoke temperature in connected area of metro tunnel under natural ventilation[J]. International Journal of Thermal Sciences, 2019, 138: 84-97. DOI:10.1016/j.ijthermalsci.2018.12.037 |
| [17] |
INGASON H, LI Y Z, LÖNNERMARK A. Tunnel fire dynamics[M]. New York: Springer, 2015.
|
| [18] |
SHI C L, LI J, XU X. Full-scale tests on smoke temperature distribution in long-large subway tunnels with longitudinal mechanical ventilation[J]. Tunnelling and Underground Space Technology, 2021, 109: 103784. DOI:10.1016/j.tust.2020.103784 |
| [19] |
钟茂华, 刘畅. 地铁隧道火灾防控全尺寸实验研究进展[J]. 中国科学基金, 2021, 35(6): 878-884. ZHONG M H, LIU C. Progress of full-scale experimental study for fire prevention and control in metro tunnel[J]. Bulletin of National Natural Science Foundation of China, 2021, 35(6): 878-884. (in Chinese) |
| [20] |
钟茂华, 程辉航, 陈俊沣, 等. 地铁车站火灾全尺寸实验设计与工程实践[J]. 实验技术与管理, 2022, 39(9): 1-8. ZHONG M H, CHENG H H, CHEN J F, et al. Full-scale experimental design and engineering practice of metro station fire[J]. Experimental Technology and Management, 2022, 39(9): 1-8. (in Chinese) |
| [21] |
CHENG H H, LIU C, CHEN J F, et al. Full-scale experimental study on fire under natural ventilation in the T-shaped and curved tunnel groups[J]. Tunnelling and Underground Space Technology, 2022, 123: 104442. DOI:10.1016/j.tust.2022.104442 |
| [22] |
OKA Y, IMAZEKI O. Temperature and velocity distributions of a ceiling jet along an inclined ceiling-Part 1: Approximation with exponential function[J]. Fire Safety Journal, 2014, 65: 41-52. DOI:10.1016/j.firesaf.2013.07.009 |
| [23] |
HURLEY M J, GOTTUK D T, HALL J R, et al. SFPE handbook of fire protection engineering[M]. 5th ed. New York: Springer, 2016.
|
| [24] |
BABRAUSKAS V. Estimating large pool fire burning rates[J]. Fire Technology, 1983, 19(4): 251-261. DOI:10.1007/BF02380810 |
| [25] |
OKA Y, OKA H. Velocity and temperature attenuation of a ceiling-jet along a horizontal tunnel with a flat ceiling and natural ventilation[J]. Tunnelling and Underground Space Technology, 2016, 56: 79-89. DOI:10.1016/j.tust.2016.03.001 |
| [26] |
GUO Q H, LI Y Z, INGASON H, et al. Theoretical studies on buoyancy-driven ceiling jets of tunnel fires with natural ventilation[J]. Fire Safety Journal, 2020, 103228. |
| [27] |
OKA Y, OKA H, IMAZEKI O. Ceiling-jet thickness and vertical distribution along flat-ceilinged horizontal tunnel with natural ventilation[J]. Tunnelling and Underground Space Technology, 2016, 53: 68-77. DOI:10.1016/j.tust.2015.12.019 |
| [28] |
ALPERT R L. Ceiling jet flows[M]// HURLEY M J, GOTTUK D T, HALL J R, et al. SFPE handbook of fire protection engineering. 5th ed. New York: Springer, 2016: 429-454.
|
| [29] |
TANNO A, OKA H, KAMIYA K, et al. Determination of smoke layer thickness using vertical temperature distribution in tunnel fires under natural ventilation[J]. Tunnelling and Underground Space Technology, 2022, 119: 104257. DOI:10.1016/j.tust.2021.104257 |
| [30] |
PAN R L, ZHU G Q, XU G, et al. Experimental analysis on burning rate and temperature profile produced by pool fire in a curved tunnel as a function of fire location[J]. Process Safety and Environmental Protection, 2021, 152: 549-567. DOI:10.1016/j.psep.2021.06.039 |
| [31] |
HU L H, HUO R, CHOW W K. Studies on buoyancy-driven back-layering flow in tunnel fires[J]. Experimental Thermal and Fluid Science, 2008, 32(8): 1468-1483. DOI:10.1016/j.expthermflusci.2008.03.005 |
| [32] |
INGASON H, LI Y Z, LÖNNERMARK A. Gas temperatures[M]// INGASON H, LI Y Z, LÖNNERMARK A. Tunnel fire dynamics. New York: Springer, 2015: 207-231.
|
| [33] |
LI Y Z, INGASON H. Model scale tunnel fire tests with automatic sprinkler[J]. Fire Safety Journal, 2013, 61: 298-313. |
| [34] |
HU L H, HUO R, PENG W, et al. On the maximum smoke temperature under the ceiling in tunnel fires[J]. Tunnelling and Underground Space Technology, 2006, 21(6): 650-655. DOI:10.1016/j.tust.2005.10.003 |



