液体燃烧属于蒸发燃烧范畴,蒸发燃烧包含可燃性液体受热后边蒸发边与空气相互扩散混合,与引火源接触后发生燃烧,产生气相燃烧的火焰,从而引发火灾[1]。该类型火灾常发生于船舶和飞机发动机舱内,多由泄漏的燃料接触到高温热壁引发。例如,供油管破裂导致燃油或润滑油泄漏,泄漏的燃料因喷洒或滴落在蒸汽管高温表面而发生燃烧,引发火灾。为防止类似事件发生,应尽量避免燃料泄漏和燃料与热表面接触。此外,了解燃料液滴在热表面上的蒸发模式和传热机制,可以极大降低该类型火灾的发生频率。除预防火灾外,在工程应用中,燃料的燃烧效果与液滴蒸发的热质传输机制密切相关,如内燃机、液体火箭发动机和液体燃料工业燃烧室等。综上,了解燃料的蒸发特性至关重要[2]。许多学者往往通过单个液滴研究燃料的蒸发特性[3]。研究燃料液滴蒸发的实验方法通常包括飞滴法[4]、挂滴法[5]和悬挂法[6]。然而,这些方法均基于探究液滴喷雾燃烧效率和优化发动机性能的角度,并不符合泄漏燃料接触高温热壁引发火灾的实际情况。近年来,附壁液滴蒸发受到越来越多的关注,液滴表面热流型与液体类型和液滴几何形状之间的关系逐渐成为研究热点。液滴蒸发过程因涉及的流动、热量和质量传递问题较复杂而备受关注,尤其是在附壁液滴情况下,流动和蒸发的耦合效应使液滴蒸发过程更复杂[7-8]。本文使用附壁液滴实验方法模拟真实火灾条件,进而研究燃料液滴的蒸发动力学。
液滴表面热流不仅会造成“咖啡圈效应”[9],而且对液体内部的热质传递具有明显影响,而液滴表面热流受液滴表面温度梯度、液体性质和液滴几何形状等多种因素影响。文[10-12]探讨了液体类型和液滴几何形状对附壁液滴蒸发过程中热流型的影响。
液体的受热蒸发性、表面张力和动力黏度因燃料类型而异,这导致不同类型燃料的附壁液滴在蒸发过程中的热流型均不相同。为观测上述差异,文[13-14]利用红外热成像技术观测和分析了附壁液滴蒸发过程的表面温度分布。文[15-16]研究了三氟三氯乙烷、正戊烷和乙醇液滴在玻璃基材表面蒸发的热流动,用激光反射阴影成像观察液滴内部流动,发现每种液体均有独特的流动特性和挥发性,且液体的内部流动模式不相同。Sefiane等[17]利用红外热成像技术发现,在蒸发过程中,甲醇和乙醇液滴的表面存在沿圆周向外传播且冷热相间的弯曲温度条纹,并定义这种热流型为热流波(hydrothermal waves, HTWs)。Sefiane等[17]还发现,在氟化液FC-72液滴的蒸发过程中,尽管FC-72与甲醇和乙醇的蒸发模式完全不同,但表面热流型依然是对流流胞型。Brutin等[18]的实验研究表明,虽然乙醇和甲醇液滴在蒸发过程中表面热力模式的演变不同,但是两者的热流型仍属于对流流胞型。此外,Brutin等[18]发现,相比于甲醇液滴,乙醇液滴表面的流胞体更稳定,流胞数更少。Ghasemi等[19]在低压环境下进行实验发现,液滴蒸发主要受三相线附近发生的热毛细对流驱动,而此类热毛细对流是能量传递的主要模式。
由于液滴蒸发界面弯曲,因此液滴表面可近似为一条微凸曲线。由于液滴表面的表面张力不同,因此曲线上的各点的蒸发速率不均匀。液滴表面切向和液相侧法向温度梯度导致蒸发冷却效应。随着液滴的形状变化,液滴表面切向和法向温度对蒸发的影响也发生变化。因此,占据主导地位的热流型与液滴实时几何形状密切相关。Hu等[20]研究发现,液滴接触角变化会引起表面温度分布变化;当接触角大于14°时,液滴表面温度梯度方向为从顶端向三相线递增;当接触角小于14°时,温度梯度方向相反,导致液滴表面的热毛细对流流动方向发生逆转。Zhang等[21]通过二维数值模拟和实验建立了液滴内部流场与接触角之间的关系,结果表明,随着接触角减小,液滴表面流动不仅方向逆转,还可能呈现多方向的复杂流动。Yang等[22]发现,当接触角较大时,Marangoni流胞对蒸发速率影响更大。需要指出的是,即使接触角很小,也必须考虑Marangoni流胞对液滴表面温度的影响,以及液滴蒸发过程中浮力对流与Marangoni流胞之间的竞争关系。Chen等[23]进行了任意Lagrange-Euler(arbitrary Lagrange-Euler, ALE)方法的数值模拟,发现随着液滴初始接触角增大,表面蒸发冷却效果不均匀程度加剧,同时液滴内涡流数量增加。唐甜等[24]发现,随着接触角变化,液滴内存在热毛细对流明显转变为Bénard-Marangoni(B-M)流胞的现象。Lu等[25]的研究也支持这一结论,即随着液滴接触角减小,液滴内部热流型转变为B-M流胞。文[26-27]利用红外热成像技术,观察了液滴表面热流型随接触角的变化。研究结果表明,随着接触角变化,液滴表面热流型也发生明显转变,该转变取决于法向和切向温度差的大小。
不同液滴在蒸发表面呈现复杂的热流型,在蒸发过程中液体性质和液滴几何形状是影响热流型的重要因素。然而,燃料液滴表面热流型的相关研究鲜有报道,蒸发传热传质机制仍不明确。因此,研究燃料液滴表面蒸发过程的热流动机制极为必要。本研究利用红外成像技术和体积估计法,选择乙醇、乙酸、正庚烷、环己烷、乙酸乙酯和丙酮6种燃料,通过实验研究了热表面上附壁燃料液滴蒸发表面热流型的演变过程,揭示了各种热流型的形成机理。
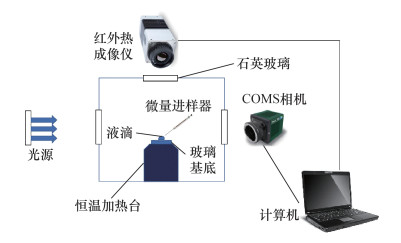
1 实验 1.1 液滴蒸发的实验装置和方法为研究附壁液滴在常温常压下的蒸发特性,本文设计了相应的实验平台,包括液体注入系统、温度控制系统及数据观测与收集系统等3个不同的系统,简化示意图如图 1所示。
|
| 图 1 热表面附壁液滴蒸发实验平台简化示意图 |
本实验选取的乙醇、乙酸、正庚烷、环己烷、丙酮和乙酸乙酯等6种常见液体燃料均由成都金山化学试剂厂提供。实验前,精密调整每个装置的布置,以确保光源、基底表面、石英玻璃和高速摄像镜头均处于相同的高度和距离。此外,为使图像清晰度更高,微调了高速摄像机的镜头焦距。使用的基底是涂有指纹油的圆形玻璃盘,直径为18 mm。为保持基底表面的温度恒定在40.0℃,将恒温加热台(ABHOT01)作为加热基底的热源。采用体积估计法[28],即微量进样器的毛细管尖端液滴接触基底,在基底表面产生液滴高度约为1.6 mm的液滴。同时,利用CMOS相机(ME2L-161-61U3M),透过石英玻璃记录液滴在蒸发过程中的侧面形态。通过非制冷红外成像仪(VC HD)获取液滴表面的温度分布变化。全部实验均在封闭空间内进行,以消除可能影响实验数据的外部因素。需要指出的是,恒温加热台的温度为0~80.0 ℃,温度控制精度为±0.1 ℃,加热功率为0~72 W;CMOS相机的探测器分辨率为1 440×1 080,图像元素大小为3.45 μm,帧率为61.2 Hz;石英玻璃已增加增透膜,使波长为1.2~2.5 nm的红外光的透过率为93%~96%;非制冷红外成像仪的红外光波长为7.5~14.0 μm,探测器分辨率为1 024×768,热灵敏度为0.03 ℃,视场为30 mm。实验室恒定温度T为25.0 ℃,误差±0.5 ℃,湿度H为45%,误差±5%。为减少实验误差,每组实验重复3次,所得蒸发速率的相关数据取平均值。各类液体燃料在温度25.0 ℃、压力1.00 kPa情况下的物理特性如表 2所示[29]。
| 参数 | 乙酸 | 乙醇 | 丙酮 | 乙酸乙酯 | 正庚烷 | 环己烷 |
| 沸点/℃ | 118.90 | 78.00 | 56.10 | 88.10 | 98.50 | 239.04 |
| 密度ρ/(kg·m-3) | 1 060 | 789 | 784 | 890 | 745 | 914 |
| 动力黏度μ/(10-3 Pa·s) | 1.12 | 1.09 | 3.16 | 4.20 | 0.29 | 3.39 |
| 蒸发潜热Lv/(kJ·kg-1) | 591.0 | 923.0 | 501.0 | 369.0 | 310.0 | 391.2 |
| 定压比热容Cp/(J·kg-1·K-1) | 2 056 | 2 845 | 2 143 | 1 824 | 2 159 | 1 642 |
| 导热系数λ/(W·m·K-1) | 0.174 | 0.140 | 0.153 | 0.149 | 0.166 | 0.116 |
| 热膨胀系数β/10-3 K-1 | 1.11 | 1.08 | 1.43 | 1.38 | 1.24 | 0.95 |
| 表面张力温度系数σT/(10-5 N·m-1·K-1) | -3.57 | -8.30 | -3.57 | -5.04 | -2.44 | -2.96 |
| 饱和蒸气压P0/kPa | 2.10 | 7.97 | 24.73 | 12.72 | 6.36 | 13.01 |
1.2 实验数据处理和不确定性分析
利用开源软件ImageJ分析液滴的侧面形貌,并确定液滴在蒸发过程中各个阶段的润湿半径、接触角和高度。为准确获取液滴高度和润湿半径,使用玻璃盘基底的实际直径长度与图片中玻璃盘基底对应的像素点长度之比作为比例尺。通过液滴的像素点长度和该比例尺,得到液滴长度的实际值。在整个实验过程中,不确定度来源主要有3个:1) 由实验室室内环境变化导致的环境误差;2) 由恒温加热台的加热功率不稳定导致的误差;3) 使用ImageJ软件测量处理图像时产生的误差。其中,使用ImageJ软件进行测量导致接触角的不确定度为1.0°,其余不确定度可通过使用MOFFAT[30]提出的误差分析方法进行计算,表示如下:
| $ \delta_z=\left[\sum\limits_{i=1}^n\left(\frac{\partial z}{\partial x_i} \delta_{x_i}\right)^2\right]^{\frac{1}{2}}. $ | (1) |
其中:xi为独立自变量,n为xi的数量,i=1, 2, ⋯, n;δxi为独立自变量
计算得出影响实验结果的不确定度:实验室室内环境造成2.39%的不确定度,而恒温加热台的加热功率造成0.85%的不确定度。此外,在测量过程中,液滴润湿直径具有0.91%的不确定度,而液滴高度具有1.05%的不确定度。
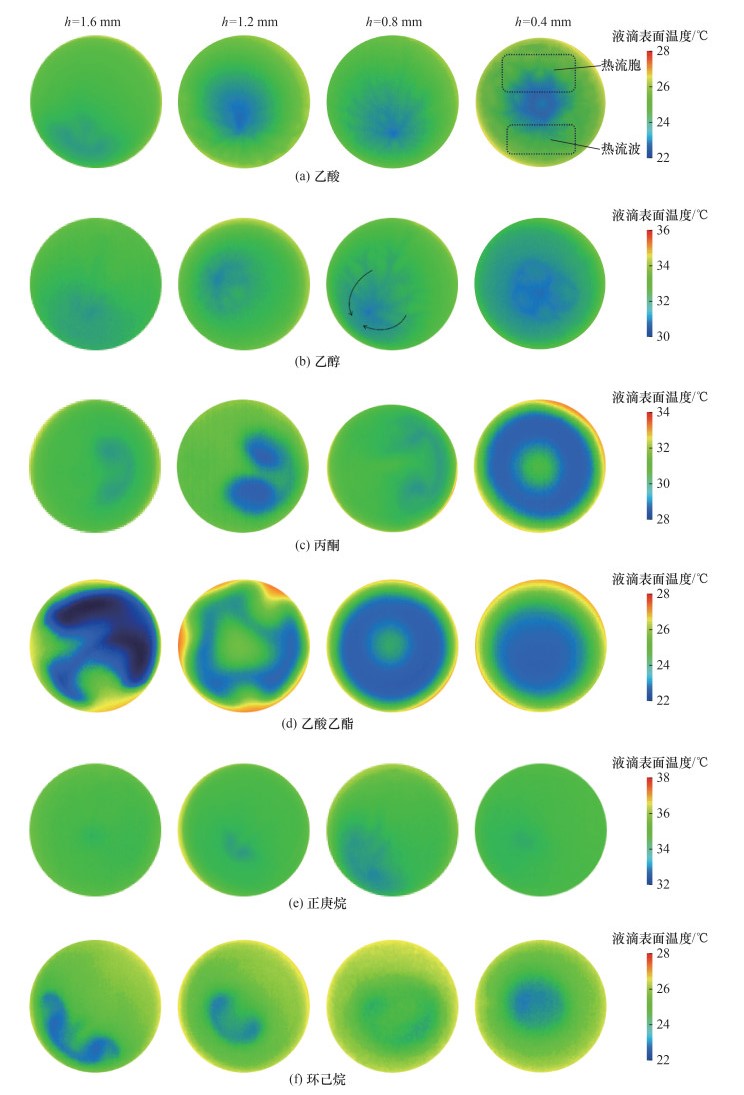
3 实验结果与分析 3.1 液滴表面热流型的演变规律不同工质种类的液体燃料具有不同的挥发性、表面张力温度系数和动力黏度,导致附壁液滴的蒸发特性和流动特性存在较大差别。本文实验在玻璃基底上进行,T=40.0 ℃。图 2为液滴形态的侧视图,展示了燃料液滴的液滴高度h和润湿直径的演变规律。需要指出的是,在相同液滴高度情况下,所有燃料液滴的侧视图几乎一样。图 3为燃料液滴表面的瞬时红外成像图,展示了6种燃料液滴的表面热流型的演变规律。

|
| 图 2 液滴形态的侧视图 |
|
| 图 3 燃料液滴表面温度的瞬时红外成像图 |
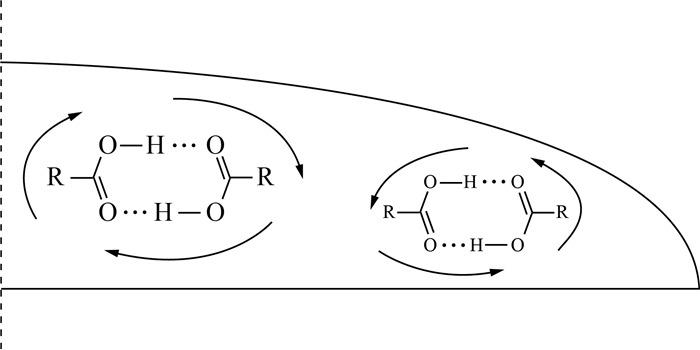
随着液滴高度变化,乙酸和乙醇液滴表面温度分布如图 3a和3b所示。当h=1.6 mm时,2种液滴的表面中央附近出现温度起伏不均的现象,未观察到明显的热流型。三相线附近随液滴高度降低而出现条纹状热波纹[31]。当液滴高度进一步降低时,这些热流型逐渐扩大。当液滴高度降至1.2 mm时,液滴表面出现明显的弯曲条纹状热波纹。这些特征与文[31-32]发现的HTWs特征相似,可以将此热流型归为HTWs。随着液滴高度进一步降低,液滴表面温度趋于稳定,在子午面上的部分区域出现上升热流,简化示意图如图 4所示。上升热流和表面热毛细对流的结合在液滴内形成了多胞状的流动模式,液滴表面的微胞热流型正是由多种热流动造成的。当h=0.8 mm时,胞状流型结构在乙酸液滴表面表现更明显。此时胞状流型在顶点的中心附近形成,单个流动流胞分裂形成新的胞型,而现有的流动流胞先在纬度方向于三相线附近扩展,后消失。这些胞状流型与Wang等[27]观察到的热流型相似,属于由液相侧的法向温度梯度引起的B-M流胞。然而,当h=0.8 mm时,乙醇液滴表面仅存在HTWs,没有观察到流胞型结构;当h=0.4 mm时,乙酸液滴表面同时出现了HTWs和B-M流胞。相比于乙酸,乙醇液滴表面未出现这2种热流型,乙醇液滴表面中心被不断分裂且向四周扩散消失的胞状流型所占据,在各个方向不断分裂和消失。叶爽等[33]观察了乙醇液滴在纯铜基底上的受热蒸发情况,发现HTWs与B-M流胞出现在同一时刻,热流流胞的数量达30个,数量约为本实验的5倍。当h=0.4 mm时,乙醇液滴在玻璃基底上的热流型与铜基底上的热流型截然不同。由图 3b可知,当乙醇液滴在玻璃基底上蒸发时,乙醇液滴表面最高温度出现在乙醇液滴的三相线附近,这与铜基底上乙醇液滴表面最高温度出现在顶点与三相线之间的结果截然不同。产生上述差异的主要原因是玻璃基底和铜基底的热物性不同,进而导致三相线附近热流型不同,即玻璃基底上液滴顶部附近为胞状热流型,而铜基底上液滴边缘附近为分叉状热流型。
|
| 图 4 横截面上的多胞热流型简化示意图 |
乙酸乙酯液滴表面温度分布随高度的变化如图 3d所示。当h=1.6 m时,乙酸乙酯液滴表面被非对称涡流热流型占据。随着液滴高度逐渐降低,由于液滴顶部与基底热表面的温差增大,导致液滴内部法向温度梯度作用增强,产生浮力对流,使液滴底部靠近基底的高温液体流至液滴顶部;当h=1.2 mm时,乙酸乙酯液滴表面热流型逐渐由涡流热流型向环状热流型转变,处于过渡时期。当h=0.8 mm时,乙酸乙酯液滴表面温度分布与丙酮液滴(h=0.4 mm)的表面温度分布相似,液滴表面出现中心与三相线高温区域,2个区域之间出现环状低温区域。当h=0.4 mm时,乙酸乙酯液滴表面温度分布已由环状温度分布逐渐转变为表面中心低温分布。乙酸乙酯和丙酮液滴受热蒸发均出现一种环状低温热流型。Ye等[34]发现,在低压纯蒸汽环境下,水滴的蒸发过程出现该环状低温热流型,可以推断存在极性分子的溶剂液滴蒸发可能出现此类热流型。
正庚烷和环己烷液滴表面温度分布随高度的变化如图 3e和3f所示。正庚烷液滴表面温度分布随液滴高度的变化较单一。由于液滴表面的热流动,因此正庚烷液滴表面的低温区域从三相线附近逐渐转移至表面中心顶部。在环己烷液滴的蒸发过程中,当h=1.6 mm时,观察到液滴表面具有2个相连小型涡流的轴对称流动,该流动在液滴表面朝向一侧偏斜。而在此之前,相关研究未报道过这种特殊类型的热流型。随着h降低,该热流型逐渐向液滴表面中心移动,直到h=0.4 mm时,液滴表面从原有的双涡结构低温区最终转变为以液滴表面中心顶部为圆心的圆形低温区。液体燃料的热流型和生成判据如表 3所示。
| 燃料液滴类型 | 热流型 | 生成判据 |
| 乙酸和乙醇 | 热流波和B-M流胞 | 分子间氢键断裂,释放键能 |
| 丙酮和乙酸乙酯 | 圆环状热流型 | 表面张力梯度和温度梯度共同作用 |
| 正庚烷 | 无明显热流型 | 温度梯度作用 |
| 丙酮和环己烷 | 双涡热流型 | 表面张力梯度和温度梯度共同作用 |
乙酸和乙醇液滴表面出现HTWs和B-M流胞,原因是液体存在分子间氢键。文[32, 35]的实验研究发现,HTWs和Marangoni流胞形成是由于不确定力驱动,但未深入探究驱动这种流动的力;只有极性分子液滴在加热时才会产生HTWs和Marangoni流胞。文[31, 36-37]表明,在加热过程中,极性分子类液滴内部的分子间氢键因吸收大量能量而断裂,并释放键能,从而导致分子空间结构发生变化,形成大量微胞。微胞最初为大型多边形网络结构,后由于不同液滴的表面张力不同,因此微胞在液滴表面张力引导下产生不同的热流型,在红外热成像条件下可观察到HTWs和B-M流胞。
为更好地揭示液滴表面热流型随着乙酸和乙醇液滴高度变化的规律,可以通过切向Marangoni数Mtan与法向Marangoni数Mnor在不同高度上的比值变化关系进行解释。Mtan和Mnor表示如下[27]:
| $ M_{\tan }=\frac{\left|\sigma_T\right| h^2}{\mu \alpha} \cdot \frac{\partial T}{\partial \tau}, $ | (2) |
| $ M_{\mathrm{nor}}=\frac{\left|\sigma_T\right| h \Delta T}{\mu \alpha}, $ | (3) |
| $ \eta=\frac{M_{\mathrm{tan}}}{M_{\mathrm{nor}}}, $ | (4) |
其中:α为热扩散率;ΔT为液滴底部和顶部的温度差;
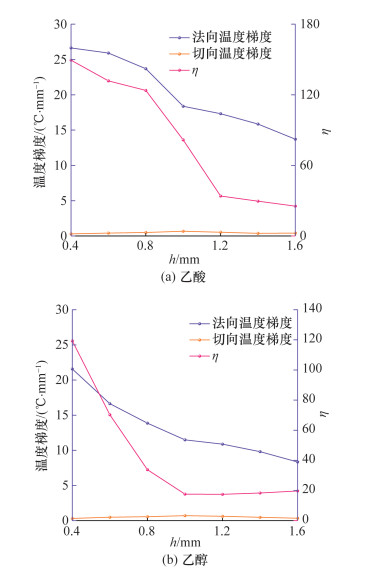
|
| 图 5 法向和切向温度梯度的变化以及η随液滴高度的变化关系 |
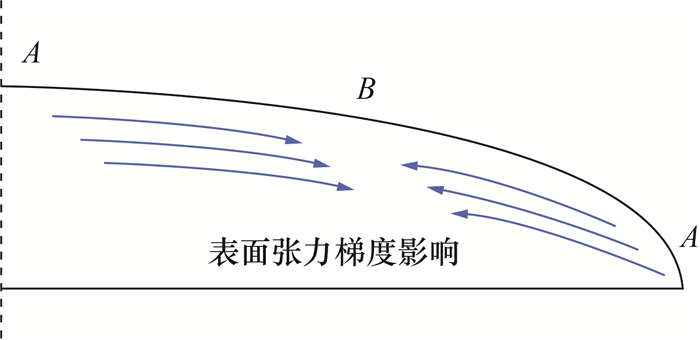
图 3c为不同液滴高度的丙酮液滴表面温度分布。当h=1.6 mm时,丙酮液滴表面温度波动并不均匀,没有出现明显的热流型。然而,当h=1.2 mm时,在丙酮液滴表面三相线附近开始出现明显小型双涡热流型,类似文[37-38]观察到的热流型。随着液滴高度降低,双涡热流型逐渐扩散至整个丙酮液滴表面。当h=0.8 mm时,由于丙酮液滴表面出现Marangoni流胞,双涡热流型逐渐向圆环状热流型过渡。这种现象由液体-气体界面的蒸发速率不均匀引起切向温度梯度变化导致。由于液滴表面近似微凸曲线,因此液滴存在表面张力梯度,具有较高表面张力的液体将牵引具有较低表面张力的液体,使液体从低表面张力区域移动至高表面张力区域。当h=1.2 mm时,丙酮液滴表面被2个近似对称的涡流结构覆盖。根据Kita等[39]的分析,在热毛细对流存在的情况下,双涡流热流型仍由Marangoni流胞引起。当h=0.4 mm时,丙酮液滴表面出现了环形温度分布,其中液滴顶部中心附近和三相线为高温区域,而位于两者之间的环形为低温区域。在切线方向上,液滴表面的曲率从上到下逐渐增大,产生曲率梯度,进而形成表面张力梯度。因此,具有高表面张力的液体牵引具有低表面张力的液体,导致位于液滴表面中心顶部的液体向三相线流动。同时,位于三相线附近的液体始终保持高温,温度超过液滴表面的其他区域。而温度梯度会使液体由高温区域向低温区域流动,导致三相线附近的液体向温度较低的中心顶部移动。表面张力梯度和温度梯度共同作用,在液滴中心和三相线处形成高温区域,并在这2个区域之间形成环形的低温区域,简化示意图如图 6所示。其中:A为高温区域,B为低温区域。
|
| 图 6 丙酮液滴(h=0.4 mm)与乙酸乙酯液滴(h=0.8 mm)的横截面上热对流示意图 |
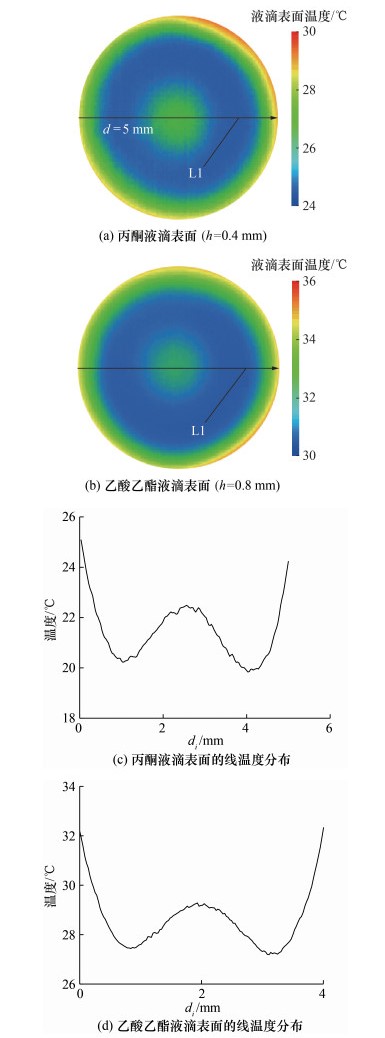
测量并记录沿液滴表面的切向温度分布,以验证液滴表面直径线L1的温度梯度存在。其中,d为直径。为方便记录,设定L1的方向为从左向右;当径向位置为i时,L1上的对应位置为di。图 7展示了丙酮液滴(h=0.4 mm)和乙酸乙酯液滴(h=0.8 mm)的表面温度分布和沿L1的温度分布。由图可以看出,在液滴顶部中心和三相线附近,表面温度明显增大。
|
| 图 7 液滴表面的切向温度分布 |
3.2 液滴蒸发速率演变规律
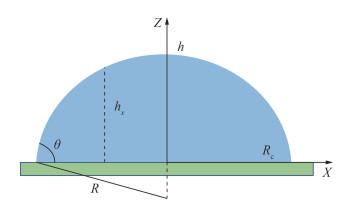
假设附壁燃料液滴为半椭球形,半椭球形附壁液滴的几何结构示意图如图 8所示,液滴体积可用体积估计法获得[28, 39-41]。通过计算体积变化率获得蒸发速率EV,通过几何形状变换获得液滴高度、湿润面积和附壁液滴体积,分别表示如下:
| $ h_i=\sqrt{\left(\frac{R_{\mathrm{c}}}{\sin \theta}\right)^2-i^2}-\frac{R_{\mathrm{c}}}{\tan \theta}, $ | (5) |
| $ S_{\mathrm{fd}}=\frac{2 \pi R_{\mathrm{c}}^2}{1+\cos \theta}, $ | (6) |
| $ V_{\mathrm{fd}}=\frac{\pi R_{\mathrm{c}}(1-\cos \theta)^2(2+\cos \theta)}{3 \sin ^3 \theta} . $ | (7) |
|
| 图 8 半椭球形附壁液滴的几何结构示意图 |
其中:hi为任意i的液滴高度,Sfd为湿润面积,Vfd为附壁液滴体积,Rc为润湿半径,θ为接触角,R为半椭球形半径。
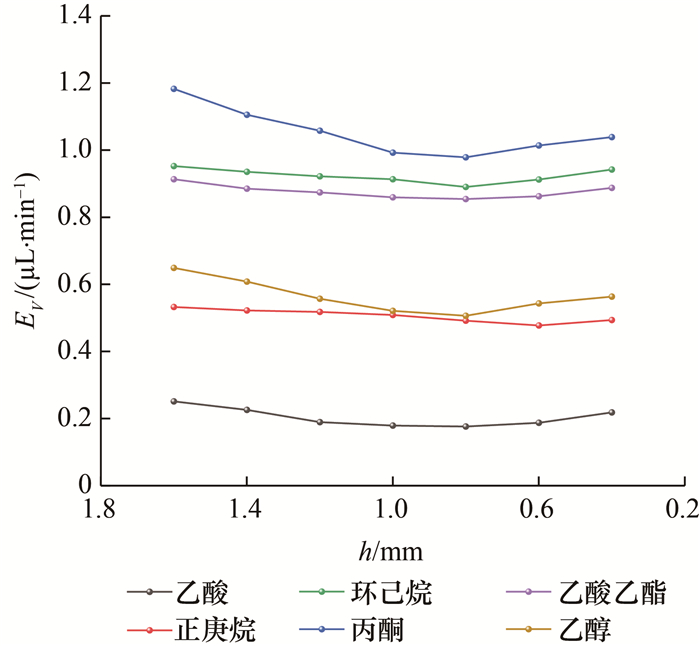
燃料液滴的蒸发速率随液滴高度的变化关系如图 9所示。可以看出,6种燃料液滴的蒸发速率均呈现先减小后增大的趋势。目前,大部分学者认为,基底温度和不断变化的液滴表面积会影响液滴的蒸发。液滴高度降低,液滴表面更接近加热基底,热传导路径缩短,液滴表面温度升高,导致蒸发速率增大。然而,在液滴蒸发过程中,随着润湿直径减小,可用于蒸发的表面积也减少,导致蒸发速率减小。在液滴表面热流动方面,除正庚烷液滴表面热对流不明显外,其他燃料液滴表面均观察到不同程度的热流型,而强烈的热对流会增大蒸发速率。因此,燃料液滴的蒸发速率受基底温度、液滴蒸发表面积和表面热对流综合影响。乙酸液滴存在HTWs和B-M流胞,当h=0.8 mm时,强烈的热对流和液滴表面较接近加热基底,导致蒸发速率显著增大。同样,当h=0.6 mm时,乙醇液滴表面开始出现数个完整胞状结构,相较h=0.8 mm,此时乙醇液滴蒸发速率明显增大。丙酮、乙酸乙酯和环己烷液滴表面在不同时刻出现双涡热流型,因此蒸发速率受到不同程度的影响。此外,未观察到正庚烷液滴的热流动,液滴高度较低时,蒸发速率增幅不明显。
|
| 图 9 燃料液滴的蒸发速率随液滴高度的变化关系 |
由图 9可以看出,燃料的蒸发速率由大到小排序为丙酮、环己烷、乙酸乙酯、乙醇、正庚烷、乙酸。通过比较6种物质的饱和蒸气压发现,蒸发速率大小主要取决于饱和蒸气压。在某温度条件下,当空气中某种物质蒸气的分压没有达到该物质的饱和蒸气压时,会产生由液态向气态转化的相变,即发生蒸发现象。因此,一种物质的饱和蒸气压越大,越易蒸发,直至空气中该物质的分压(或者说浓度)达到饱和蒸气压才会达到平衡状态。根据Lange化学手册,本实验所选的6种燃料的饱和蒸气压按由大到小排序为丙酮、环己烷、乙酸乙酯、乙醇、正庚烷、乙酸(见表 2)。此排序与本实验结果完全相符,即6种物质的饱和蒸气压大小排序是空气中6种物质的蒸气含量排序,同时也是蒸发速率大小排序。因此,在同一工况下,无论液滴高度为多少,乙酸液滴的蒸发速率最小,丙酮液滴的蒸发速率最大。
4 结论本文通过乙酸、乙醇、丙酮、乙酸乙酯、正庚烷、环己烷液滴在加热基底上的蒸发动力学实验,获得了液滴表面热流型和蒸发速率随液滴高度变化的演变规律。主要结论如下:
1) 燃料液滴表面可观察到多种热流型。乙酸和乙醇液滴表面出现HTWs和Bénard-Marangoni流胞,丙酮和乙酸乙酯液滴表面出现双涡流热流型和环状热流型,正庚烷液滴表面没有出现明显的热流型,环己烷液滴表面则出现双涡流热流型。
2) 乙酸与乙醇液滴在玻璃基底上蒸发时,随着液滴高度降低,液滴内部法向温度梯度作用逐渐占据主导地位,表面逐渐出现HTWs和B-M流胞。乙酸液滴表面率先出现明显胞状热流型结构,并且在液滴高度为0.4 mm时,同时存在HTWs和B-M流胞。相比于乙醇液滴,乙酸液滴表面的胞状热流型结构个数更多,乙酸液滴表面温度波动也更大。
3) 随着液滴高度降低,蒸发速率先减小,后增大。液滴的蒸发速率主要由饱和蒸气压决定,并受表面热流动的明显影响。正庚烷液滴表面热流动不明显,蒸发速率主要受蒸发面积和表面温度影响,随液滴高度变化不明显。
| [1] |
LI Y L, LI S X. Evaporation and ignition of the leaked fuel by a hot plate[J]. Process in Safety Science and Technology Part B, 2002, 3: 1311-1316. |
| [2] |
AL QUBEISSI M, SAZHIN S S, ELWARDANY A E. Modelling of blended diesel and biodiesel fuel droplet heating and evaporation[J]. Fuel, 2017, 187: 349-355. DOI:10.1016/j.fuel.2016.09.060 |
| [3] |
PINHEIRO A P, VEDOVOTO J M, DA SILVEIRA NETO A, et al. Ethanol droplet evaporation: Effects of ambient temperature, pressure and fuel vapor concentration[J]. International Journal of Heat and Mass Transfer, 2019, 143: 118472. DOI:10.1016/j.ijheatmasstransfer.2019.118472 |
| [4] |
WANG Z W, YUAN B, HUANG Y H, et al. Progress in experimental investigations on evaporation characteristics of a fuel droplet[J]. Fuel Processing Technology, 2022, 231: 107243. DOI:10.1016/j.fuproc.2022.107243 |
| [5] |
ZHANG Y, HUANG R H, HUANG Y H, et al. Effect of ambient temperature on the puffing characteristics of single butanol-hexadecane droplet[J]. Energy, 2018, 145: 430-441. DOI:10.1016/j.energy.2017.12.158 |
| [6] |
GROSSHANS H, GRIESING M, MÖNCKEDIECK M, et al. Numerical and experimental study of the drying of Bi-component droplets under various drying conditions[J]. International Journal of Heat and Mass Transfer, 2016, 96: 97-109. DOI:10.1016/j.ijheatmasstransfer.2015.12.062 |
| [7] |
BHATTACHARYA P, SAMANTA A N, CHAKRABORTY S. Spray evaporative cooling to achieve ultra fast cooling in runout table[J]. International Journal of Thermal Sciences, 2009, 48(9): 1741-1747. DOI:10.1016/j.ijthermalsci.2009.01.015 |
| [8] |
KIM J. Spray cooling heat transfer: The state of the art[J]. International Journal of Heat and Fluid Flow, 2007, 28(4): 753-767. DOI:10.1016/j.ijheatfluidflow.2006.09.003 |
| [9] |
DEEGAN R D, BAKAJIN O, DUPONT T, et al. Capillary flow as the cause of ring stains from dried liquid drops[J]. Nature, 1997, 389(6653): 827-829. DOI:10.1038/39827 |
| [10] |
GARNIER N, CHIFFAUDEL A, DAVIAUD F. Hydrothermal waves in a disk of fluid[M]// MUTABAZI I, WESFREID J E, GUYON E. Dynamics of spatio-temporal cellular structures: Henri Bénard centenary review. New York: Springer, 2006: 147-161.
|
| [11] |
LI Y R, ZHANG L, ZHANG L, et al. Experimental study on prandtl number dependence of thermocapillary-buoyancy convection in czochralski configuration with different depths[J]. International Journal of Thermal Sciences, 2018, 130: 168-182. DOI:10.1016/j.ijthermalsci.2018.04.026 |
| [12] |
BÉNARD H. Les tourbillons cellulaires dans une nappe liquide-Méthodes optiques d'observation et d'enregistrement[J]. Journal de Physique Théorique et Appliquée, 1901, 10(1): 254-266. DOI:10.1051/jphystap:0190100100025400 |
| [13] |
SEFIANE K, MOFFAT J R, MATAR O K, et al. Self-excited hydrothermal waves in evaporating sessile drops[J]. Applied Physics Letters, 2008, 93(7): 074103. DOI:10.1063/1.2969072 |
| [14] |
GLEASON K, VOOTA H, PUTNAM S A. Steady-state droplet evaporation: Contact angle influence on the evaporation efficiency[J]. International Journal of Heat and Mass Transfer, 2016, 101: 418-426. DOI:10.1016/j.ijheatmasstransfer.2016.04.075 |
| [15] |
ZHANG N L, CHAO D F. Flow visualization in evaporating liquid drops and measurement of dynamic contact angles and spreading rate[J/OL]. Journal of Flow Visualization and Image Processing. (2008-02-04)[2023-10-08]. DOI: 10.1615/JFlowVisImageProc.v8.i2-3.170.
|
| [16] |
ZHANG N L, CHAO D F. A new laser shadowgraphy method for measurements of dynamic contact angle and simultaneous flow visualization in a sessile drop[J]. Optics & Laser Technology, 2002, 34(3): 243-248. |
| [17] |
SEFIANE K, FUKATANI Y, TAKATA Y, et al. Thermal patterns and hydrothermal waves (HTWs) in volatile drops[J]. Langmuir, 2013, 29(31): 9750-9760. DOI:10.1021/la402247n |
| [18] |
BRUTIN D, SOBAC B, RIGOLLET F, et al. Infrared visualization of thermal motion inside a sessile drop deposited onto a heated surface[J]. Experimental Thermal and Fluid Science, 2011, 35(3): 521-530. DOI:10.1016/j.expthermflusci.2010.12.004 |
| [19] |
GHASEMI H, WARD C A. Energy transport by thermocapillary convection during sessile-water-droplet evaporation[J]. Physical Review Letters, 2010, 105(13): 136102. DOI:10.1103/PhysRevLett.105.136102 |
| [20] |
HU H, LARSON R G. Analysis of the effects of marangoni stresses on the microflow in an evaporating sessile droplet[J]. Langmuir, 2005, 21(9): 3972-3980. DOI:10.1021/la0475270 |
| [21] |
ZHANG K, MA L R, XU X F. Temperature distribution along the surface of evaporating droplets[J]. Physical Review E, 2014, 89(3): 032404. DOI:10.1103/PhysRevE.89.032404 |
| [22] |
YANG K, HONG F J, CHENG P. A fully coupled numerical simulation of sessile droplet evaporation using arbitrary lagrangian-eulerian formulation[J]. International Journal of Heat and Mass Transfer, 2014, 70: 409-420. DOI:10.1016/j.ijheatmasstransfer.2013.11.017 |
| [23] |
CHEN Y H, HONG F J, CHENG P. Transient flow patterns in an evaporating sessile drop: A numerical study on the effect of volatility and contact angle[J]. International Communications in Heat and Mass Transfer, 2020, 112: 104493. DOI:10.1016/j.icheatmasstransfer.2020.104493 |
| [24] |
唐甜, 石万元. 固定接触角蒸发液滴内Marangoni对流数值模拟[J]. 工程热物理学报, 2017, 38(4): 792-799. TANG T, SHI W Y. Marangoni convection in evaporating sessile droplet with constant angle by numerical simulation[J]. Journal of Engineering Thermophysics, 2017, 38(4): 792-799. (in Chinese) |
| [25] |
LU G, DUAN Y Y, WANG X D, et al. Internal flow in evaporating droplet on heated solid surface[J]. International Journal of Heat and Mass Transfer, 2011, 54(19-20): 4437-4447. DOI:10.1016/j.ijheatmasstransfer.2011.04.039 |
| [26] |
WANG T S, SHI W Y. Influence of substrate temperature on Marangoni convection instabilities in a sessile droplet evaporating at constant contact line mode[J]. International Journal of Heat and Mass Transfer, 2019, 131: 1270-1278. DOI:10.1016/j.ijheatmasstransfer.2018.11.155 |
| [27] |
WANG T S, SHI W Y. Transition of Marangoni convection instability patterns during evaporation of sessile droplet at constant contact line mode[J]. International Journal of Heat and Mass Transfer, 2020, 148: 119138. DOI:10.1016/j.ijheatmasstransfer.2019.119138 |
| [28] |
李晶. 座滴图像求解界面张力计算方法的研究[J]. 中南矿冶学院学报, 1989, 20(5): 562-567. LI J. A study of computation method and program for calculating interfacial tension by curve fitting to the picture of sessile drop[J]. Journal of Central South Institute of Mining and Metallurgy, 1989, 20(5): 562-567. (in Chinese) |
| [29] |
HUBER M L. NIST thermophysical properties of hydrocarbon mixtures database (SUPERTRAPP), version 3.2[M]. Gaithersburg: National Institute of Standards and Technology Standard Reference Database, 2007.
|
| [30] |
MOFFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17. DOI:10.1016/0894-1777(88)90043-X |
| [31] |
SMITH M K, DAVIS S H. Instabilities of dynamic thermocapillary liquid layers. Part 1. Convective instabilities[J]. Journal of Fluid Mechanics, 1983, 132: 119-144. DOI:10.1017/S0022112083001512 |
| [32] |
TRUSKETT V N, STEBE K J. Influence of surfactants on an evaporating drop: Fluorescence images and particle deposition patterns[J]. Langmuir, 2003, 19(20): 8271-8279. DOI:10.1021/la030049t |
| [33] |
叶爽, 李友荣, 吴春梅, 等. 加热基底上附壁液滴蒸发动力学实验研究[J]. 工程热物理学报, 2021, 42(10): 2625-2632. YE S, LI Y R, WU C M, et al. Experimental study on evaporation dynamic of sessile droplet on heated substrate[J]. Journal of Engineering Thermophysics, 2021, 42(10): 2625-2632. (in Chinese) |
| [34] |
YE S, ZHANG L, WU C M, et al. Experimental investigation of evaporation dynamic of sessile droplets in pure vapor environment with low pressures[J]. International Journal of Thermal Sciences, 2020, 149: 106213. DOI:10.1016/j.ijthermalsci.2019.106213 |
| [35] |
GIRARD F, ANTONI M, FAURE S, et al. Evaporation and marangoni driven convection in small heated water droplets[J]. Langmuir, 2006, 22(26): 11085-11091. DOI:10.1021/la061572l |
| [36] |
SOBAC B, BRUTIN D. Thermocapillary instabilities in an evaporating drop deposited onto a heated substrate[J]. Physics of Fluids, 2012, 24(3): 032103. DOI:10.1063/1.3692267 |
| [37] |
JOSYULA T, WANG Z Y, ASKOUNIS A, et al. Evaporation kinetics of pure water drops: Thermal patterns, marangoni flow, and interfacial temperature difference[J]. Physical Review E, 2018, 98(5): 052804. DOI:10.1103/PhysRevE.98.052804 |
| [38] |
CHEN P, HARMAND S, OUENZERFI S, et al. Marangoni flow induced evaporation enhancement on binary sessile drops[J]. The Journal of Physical Chemistry B, 2017, 121(23): 5824-5834. DOI:10.1021/acs.jpcb.7b02766 |
| [39] |
KITA Y, ASKOUNIS A, KOHNO M, et al. Induction of marangoni convection in pure water drops[J]. Applied Physics Letters, 2016, 109(17): 171602. DOI:10.1063/1.4966542 |
| [40] |
GATAPOVA E Y, SEMENOV A A, ZAITSEV D V, et al. Evaporation of a sessile water drop on a heated surface with controlled wettability[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2014, 441: 776-785. DOI:10.1016/j.colsurfa.2013.05.046 |
| [41] |
SOBAC B, BRUTIN D. Thermal effects of the substrate on water droplet evaporation[J]. Physical Review E, 2012, 86(2): 021602. |



