2. 北京市建筑设计研究院股份有限公司, 北京 100045;
3. 清华大学 土木工程系, 北京 100084
2. Beijing Institute of Architectural Design Co., Ltd, Beijing 100045, China;
3. Department of Civil Engineering, Tsinghua University, Beijing 100084, China
纤维织物增强混凝土(textile reinforced concrete, TRC)板加固法是目前应用于土木工程领域的较成熟的一种加固技术[1-3]。研究表明,对TRC板中碳纤维织物施加预应力可以较好地解决碳纤维利用率较低的问题[4]。施加预应力后,预应力碳纤维织物增强混凝土(prestressed carbon textile reinforced concrete, P-TRC)板可以有效地提高碳纤维织物的利用率,加固梁的抗裂性能、裂缝形态及承载力等都得到了极大的改善[5-6]。
与碳纤维增强聚合物复合材料CFRP板等纤维复合材料采用层铺法加固抗弯梁的方式不同,P-TRC板中碳纤维织物受预拉力下的反作用力直接作用在板上,对加固梁无直接影响,后者将施加预应力的锚具安装在RC梁上,计算时需要额外考虑锚具变形和碳纤维织物超前应变造成的预应力损失[7-10]。采用P-TRC板加固抗弯梁时,重点在于加固方式能否随试验参数改变有效传力。
对于混杂复合板加固梁抗弯性能,Esmaeeli等[11]通过不同锚固方式,证明了采用植筋和凿槽等加固措施可有效防止加固层整体产生破坏,保证加固梁抗弯性能。为验证植筋加凿槽和层铺法2种加固方式随碳纤维织物配网率改变能否有效传力,荀勇等[12]通过TRC加固RC梁试验验证了凿槽及凿槽加端部植筋2种方法处理的加固梁在配网率较高时易出现纯弯段剥离破坏;周芬等[13]采用无机砂浆将TRC复合板粘贴在梁的受拉区,在板材加固段缠绕CFRP布增强TRC板端部锚固,加固层随配网率的提高出现一定滑移,随后在预拉纤维复合板粘接加固RC梁抗弯试验中因纯弯段黏结薄弱同样在配网率较高时出现了一定的黏结破坏。在加固梁挠度理论计算方面,传统加固梁塑性阶段跨中挠度计算大多采用高次方程[8, 14]或曲率[13, 15-16]求解,但加固梁求解换算截面惯性矩较为复杂[13, 17]。
因此,为提高加固梁纯弯段加固性能,缩短施工周期,减少现场湿作业,本文提出一种射钉作为连接层连接P-TRC板和RC梁的方法,为验证其传力性能,在9种P-TRC板加固抗弯梁工况的试验基础上,对P-TRC板采用射钉连接钢筋混凝土矩形截面梁的正截面承载力进行了理论分析。分析中考虑了预应力、碳纤维织物层数以及射钉作为加固层等因素对加固梁正截面受弯承载力的影响,通过分析不同破坏模式下的加固梁受压区高度,对P-TRC板加固混凝土梁的受弯承载力的理论计算方法进行了较系统的研究。此外,本文通过试验建立了塑性阶段加固梁跨中挠度的计算公式。
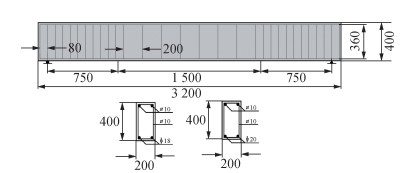
1 加固梁四点弯曲试验 1.1 试验设计基于吴子林等[18]对TRC板和混凝土构件在射钉锚固下的界面性能研究,确定了射钉加固的最佳边缘距离为50 mm,加固方式如图 1所示。为避免加固层脱落,沿梁底面垂直打入2排射钉,中部射钉间距为100 mm;梁端部设置加密区,间距为50 mm。为避免射钉对P-TRC板造成射钉孔以外的损伤,在射帽和P-TRC板间设置垫圈缓冲射钉枪带来的动能。试验共设计9种工况,包括6种射钉加固混凝土梁和3种未加固混凝土梁。试件截面尺寸为200 mm×400 mm,长度为3 200 mm, 计算长度为3 000 mm。受拉区设置2根HRB400钢筋,直径分别为18和20 mm;箍筋采用HPB300钢筋,直径为10 mm,纯弯段箍筋的间距为200 mm,弯剪段箍筋间距为90 mm。加固梁参数详见表 1,其中一层碳纤维网包含10束碳纤维织物,每束碳纤维面积为2.7 m2,网格尺寸为20 mm×18 mm,预拉力为3.26 kN,碳纤维织物力学性能见表 2;加固梁配筋如图 2所示,其力学性能见表 3;混凝土标准试件抗压强度见表 4,射钉参数见表 5。P-TRC板基材由地聚物混凝土制成。为研究射钉加固RC梁的可行性及提高施工效率,除射钉外P-TRC板和RC梁交界处不再采用其他加固措施。

|
| 图 1 射钉加固方式(单位:mm) |
| 编号 | 试件数/组 | 碳纤维织物参数 | 受拉钢筋参数 | 混凝土强度 | |||
| 织物层数 | 配网率/% | 直径/mm | 配筋率/% | ||||
| B0 | 2 | 0 | 0 | 18 | 0.70 | C30 | |
| B1 | 2 | 0 | 0 | 20 | 0.87 | C30 | |
| B2 | 2 | 0 | 0 | 18 | 0.70 | C40 | |
| B0-1 | 2 | 1 | 0.68 | 18 | 0.70 | C30 | |
| B0-2 | 2 | 2 | 1.23 | 18 | 0.70 | C30 | |
| B1-1 | 2 | 1 | 0.68 | 20 | 0.87 | C30 | |
| B1-2 | 2 | 2 | 1.23 | 20 | 0.87 | C30 | |
| B2-1 | 2 | 1 | 0.68 | 18 | 0.70 | C40 | |
| B2-2 | 2 | 2 | 1.23 | 18 | 0.70 | C40 | |
|
| 图 2 加固梁配筋(单位:mm) |
| 直径/mm | 屈服强度/MPa | 极限强度/MPa | 弹性模量/GPa |
| 10 | 420.38 | 583.95 | 200 |
| 18 | 467.24 | 623.34 | 201 |
| 20 | 480.43 | 657.47 | 203 |
1.2 加载方案
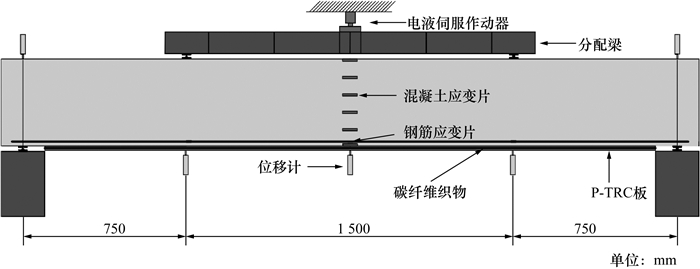
试验采用四分点加载,弯剪段长度为750 mm,纯弯段长度为1 500 mm。在正式加载前实施预加载,按梁受力阶段分三级加载,每级荷载分别为:梁底开裂前10 kN/级、底筋屈服前5 kN/级,底筋屈服后10 kN/级。荷载接近破坏荷载时采用位移缓慢加载,直至荷载降低到破坏荷载的85%时停止加载,宣布破坏。测点布置如图 3所示。
|
| 图 3 测点布置(单位:mm) |
1.3 试验结果
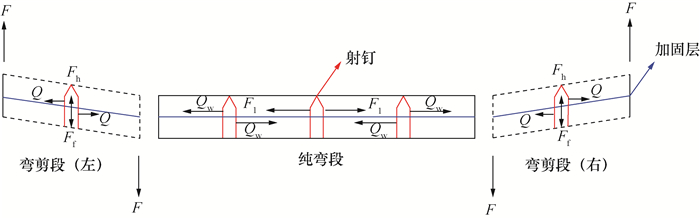
P-TRC板加固梁的受弯破坏类型主要有3种:1) 受压区混凝土被压坏,2) P-TRC板拉断破坏,3) P-TRC板与梁底剥离破坏。本文对应的加固梁破坏模式如图 4a—4c所示,分别为P-TRC板拉断破坏、射钉弯曲,加固梁弯曲破坏。未加固梁的弯曲破坏模式如图 4d所示,为受压区混凝土压碎破坏。以加固梁纯弯段与弯剪段特殊位置的射钉为例,其受力分析如图 5所示,加固梁纯弯段中间射钉两侧混凝土拉力大小相等,方向相反,跨中挠度最大处射钉不受剪力,纯弯段左侧与右侧射钉受到的剪力Qw由于受力不在同一水平面,左侧射钉集中力偶为逆时针旋转,右侧为顺时针旋转。RC梁底拉力F1由纯弯段至弯剪段逐渐减小,弯剪段射钉的剪力Q在施荷前期较小,待纯弯段两侧射钉在集中力偶作用下产生倾斜,Q逐渐增加,同时弯剪段由于支座和四分点处加载的力F形成集中力偶,使得RC梁对射钉产生法向的拉力Fh,此拉力由射钉打入混凝土的紧固力和Q产生的摩擦力Ff提供。

|
| 图 4 梁破坏模式 |
|
| 图 5 加固层射钉受力分析简图 |
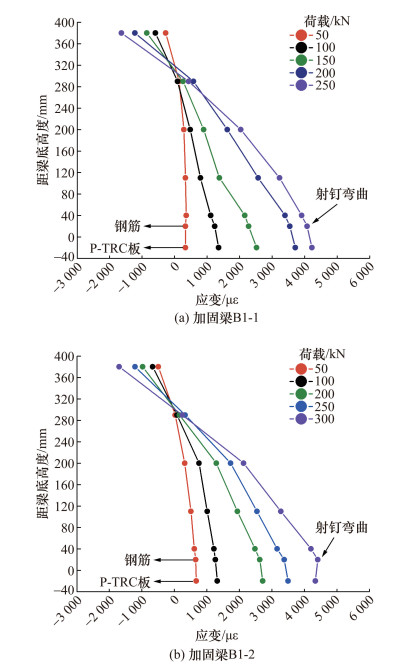
以表 2中设计的加固梁B1-1和B1-2为例,其应变—荷载曲线如图 6所示,射钉应变滞后随碳纤维织物层数增加而增大,加固层两侧射钉随荷载增大向内收缩,但跨中挠度最大处梁底与P-TRC板间并未出现较大滑移,整体符合平截面假定。
|
| 图 6 应变—荷载曲线 |
2 正截面受弯承载力计算
基于试验研究,对加固梁进行推导,本试验中所有试件的破坏模式均为P-TRC板拉断破坏,且板断时的荷载皆高于未加固梁极限荷载,因此本文中所提加固梁的极限荷载实则为P-TRC板拉断时的断裂荷载。
2.1 基本假设为计算P-TRC板加固梁的受弯承载力,做以下假定:
1) 加固梁受弯后,截面混凝土、钢筋及P-TRC板的应变符合平截面假定;
2) 混凝土、钢筋应力—应变关系按《混凝土结构设计规范》(GB500010—2010)[19]选取;
3) 碳纤维应力—应变关系为线弹性,板底开裂后不考虑地聚物受拉,只取碳纤维极限拉应变;
4) 梁底截面开裂后不考虑混凝土受拉;
5) P-TRC板和被加固梁通过射钉连接,两者连接性能良好且无剥离破坏现象,若加固梁破坏或P-TRC板拉断时梁底纵筋刚好屈服或还未屈服,则不考虑射钉弯折对碳纤维织物造成的应变滞后现象。
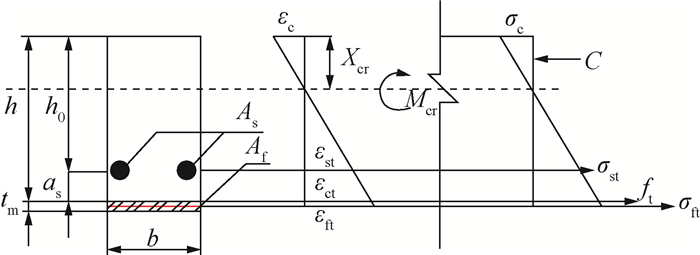
2.2 受弯破坏前承载力的计算 2.2.1 开裂荷载当加固梁受拉区边缘应变达到开裂应变,工作应力达到混凝土抗拉强度时,加固梁进入开裂状态,此时对应的跨中弯矩为Mcr,开裂荷载为Pcr,跨中挠度为δcr。截面计算简图如图 7所示,其中C为加固梁受压区混凝土合力。沿梁的X轴建立静力平衡方程。
| $ \sigma_{\mathrm{ft}} A_{\mathrm{f}}+\sigma_{\mathrm{st}} A_{\mathrm{s}}+\frac{1}{2} f_{\mathrm{t}} b\left(h-X_{\mathrm{cr}}\right)=\frac{1}{2} \sigma_{\mathrm{c}} X_{\mathrm{cr}} b, $ | (1) |
| $ \frac{\varepsilon_c}{X_{\mathrm{cr}}}=\frac{\varepsilon_{\mathrm{ct}}}{h-X_{\mathrm{cr}}}. $ | (2) |
|
| 图 7 截面计算简图 |
其中:h为梁截面高度;h0为截面有效高度,h0=h-as,as为正截面上所有纵向受拉钢筋的合力点至截面受拉边缘的竖向距离;Af和As分别为碳纤维织物有效截面面积和钢筋截面面积; b为梁截面宽度;εft、εst、εct和εc为加固梁承受开裂荷载时碳纤维织物、钢筋、RC梁底混凝应变以及受压区混凝土应变,与之对应的应力为σft、σst、ft和σc。本文中碳纤维织物距离梁底与梁高度比为
| $ \begin{aligned} M_{\mathrm{cr}}=\sigma_{\mathrm{ft}} A_{\mathrm{f}}\left(h-\frac{1}{3} X_{\mathrm{cr}}\right)+\sigma_{\mathrm{st}} A_{\mathrm{s}}\left(h_0-\frac{1}{3} X_{\mathrm{cr}}\right)+ \\ \frac{1}{2} f_{\mathrm{t}} b\left(h-X_{\mathrm{cr}}\right)\left(\frac{2}{3}\left(h-X_{\mathrm{cr}}\right)+\frac{2}{3} X_{\mathrm{cr}}\right) . \end{aligned} $ | (3) |
开裂荷载理论值Pcr′与试验值Pcr如表 7所示,结果表明,理论值与试验值最大偏差不超过11%,两者吻合较好。
| 试件编号 | Pcr′/kN | Pcr/kN | Pcr′/Pcr |
| B0 | 27.79 | 30.43 | 0.91 |
| B1 | 36.90 | 39.64 | 0.93 |
| B2 | 33.38 | 35.20 | 0.95 |
| B0-1 | 42.85 | 41.63 | 1.03 |
| B0-2 | 45.51 | 47.42 | 0.96 |
| B1-1 | 46.96 | 50.51 | 0.93 |
| B1-2 | 50.46 | 56.71 | 0.89 |
| B2-1 | 48.90 | 45.33 | 1.08 |
| B2-2 | 49.66 | 51.20 | 0.97 |
2.2.2 屈服荷载
加固梁受拉区边缘开裂后,随着荷载的增加,底部纵筋开始屈服,P-TRC板并未破坏,此时对应的跨中弯矩为My,屈服荷载为Py,跨中挠度为δy,由平截面假定得
| $ \frac{\varepsilon_{\mathrm{fs}}}{h-X_{\mathrm{y}}}=\frac{\varepsilon_{\mathrm{s}}}{h_0-X_{\mathrm{y}}}=\frac{\varepsilon_{\mathrm{c}}}{X_{\mathrm{y}}}. $ | (4) |
采用P-TRC板加固RC梁,底部纵筋屈服时,其屈服弯矩主要由P-TRC板、底部纵筋和压区混凝土承担。对混凝土受压区合力作用点取矩可得
| $ M_{\mathrm{y}}=f_{\mathrm{y}} A_{\mathrm{s}}\left(h_0-\frac{X_{\mathrm{y}}}{3}\right)+\sigma_{\mathrm{fs}} A_{\mathrm{f}}\left(h+\frac{t_{\mathrm{m}}}{2}-\frac{X_{\mathrm{y}}}{3}\right) . $ | (5) |
其中:Xy为加固梁屈服时受压区高度;σfs为梁底纵筋屈服时碳纤维织物应变。屈服荷载理论值Py′与试验值Py如表 8所示,结果表明,理论值与试验值最大偏差不超过8%,两者吻合较好。
| 试件编号 | Py′/kN | Py/kN | Py′/Py |
| B0 | 220.12 | 216.50 | 1.02 |
| B1 | 238.80 | 248.20 | 0.96 |
| B2 | 226.37 | 231.11 | 0.98 |
| B0-1 | 235.31 | 242.30 | 0.97 |
| B0-2 | 247.50 | 268.24 | 0.92 |
| B1-1 | 260.87 | 271.74 | 0.96 |
| B1-2 | 274.25 | 288.45 | 0.93 |
| B2-1 | 239.21 | 251.87 | 0.95 |
| B2-2 | 269.66 | 278.91 | 0.97 |
2.3 受弯破坏时受压区高度计算 2.3.1 P-TRC板拉断破坏
由于在加固前对碳纤维织物施加预拉力P,因此引入εp表示碳纤维织物受预拉力影响下的预拉应变,若使P-TRC板在梁底部钢筋屈服时拉断,碳纤维织物受到的预拉力Pm为
| $ P_{\mathrm{m}}=E_{\mathrm{cf}}\left(\varepsilon_{\mathrm{fu}}-\varepsilon_{\mathrm{f}}\right) A_{\mathrm{f}} . $ | (6) |
其中:Ecf为碳纤维织物弹性模量;εfu为碳纤维织物极限拉应变;εf为P-TRC板拉断时的协同应变,即εfu与εpm之差,εpm为碳纤维织物受到Pm后的应变。
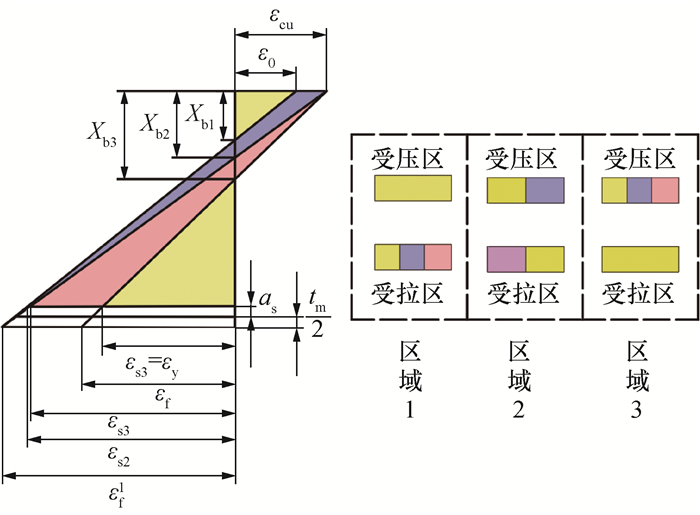
加固梁应变关系如图 8中区域1所示,第1种破坏模式为P-TRC板拉断破坏时受压混凝土应变刚好达到峰值应变,即ε=ε0,此时加固梁受压区高度Xb1为
| $ X_{\mathrm{b} 1}=\lambda\left[\varepsilon_0 /\left(\varepsilon_0+\varepsilon_{\mathrm{f}}^1\right)\right]\left(h+\frac{t_{\mathrm{m}}}{2}\right) . $ | (7) |
|
| 图 8 不同破坏特征的应变关系 |
为计算P-TRC板拉断时射钉弯折对碳纤维织物造成的应变滞后影响,引入应变滞后系数λ,λ为P-TRC板的实际应变与按平截面假定计算时理论应变的比值。λ越大射钉加固越牢靠,其传力效果越好,加固梁受压区高度越大。若P=Pm,P-TRC板在梁底纵筋屈服时拉断,则λ为1,射钉无弯折且碳纤维织物无应变滞后现象产生。加固梁破坏模式为P-TRC板和梁底部纵筋协同变形至屈服后P-TRC板拉断,同时受压区混凝土压碎。εfu约为钢筋屈服应变εy的6倍以上,预拉力不超过Pm时,碳纤维织物不会在梁底部纵筋屈服前拉断,因此使用P-TRC板加固梁时,梁底部纵筋在屈服前和碳纤维织物协同变形良好,P-TRC板拉断时碳纤维织物达到极限应变εfu,碳纤维预拉应变εp到其极限应变εfu之间称最大应变增量εf1,εf1 = εfu-εp。
2.3.2 受压区混凝土压碎破坏加固梁不同的破坏模式对应不同的受压区高度,因此受压区高度可作为计算受弯梁极限承载力的重要指标,受压区混凝土压碎时分2种情况:
1) 第2种破坏模式为界限破坏,即P-TRC板拉断破坏同时受压区混凝土被压碎。如图 8中区域2所示;此时梁受压区高度为
| $ X_{\mathrm{b} 2}=\lambda\left[\varepsilon_{\mathrm{cu}} /\left(\varepsilon_{\mathrm{cu}}+\varepsilon_{\mathrm{f}}^1\right)\right] \cdot\left(h+\frac{t_{\mathrm{m}}}{2}\right) . $ | (8) |
2) 第3种破坏模式为加固梁受压区混凝土压碎时底部纵筋刚好屈服,如图 8中区域3所示,P-TRC板未拉断。根据变形协调关系,加固梁底部纵筋屈服应变εs3=εy,此时碳纤维织物应变为εf,此时梁受压区高度为
| $ X_{\mathrm{b} 3}=\left[\varepsilon_{\mathrm{cu}} /\left(\varepsilon_{\mathrm{cu}}+\varepsilon_{\mathrm{f}}\right)\right] \cdot\left(h+\frac{t_{\mathrm{m}}}{2}\right) . $ | (9) |
加固梁受压区高度X>Xb3时,加固梁为超筋破坏,梁底部纵筋还未屈服,且P-TRC板未拉断,表明加固梁纵筋配筋率、碳纤维织物有效截面面积Af过高,加固梁破坏时P-TRC板和梁底纵筋协同变形较小。
Xb3≥X>Xb2时,加固梁破坏时P-TRC板仍未拉断,加固梁纵筋配筋率或Af较高,此时应考虑降低加固梁底部配筋率及Af。
Xb2≥X≥Xb1时,加固效果较好,碳纤维织物施加的预拉力既提高了利用率,也不会在钢筋屈服前导致P-TRC板拉断破坏。
X < Xb1时,碳纤维织物有效截面面积较小,若X远小于Xb1,可考虑增加碳纤维织物有效截面面积。
2.4 受弯破坏时承载力的计算由实际应力积分可得受压区合力为
| $ C=\int_0^{x_{\mathrm{b}}} b \sigma_{\mathrm{c}} \mathrm{d} x=\frac{x_{\mathrm{b}}}{\varepsilon_{\mathrm{c}}} \int_0^{\varepsilon_{\mathrm{c}}} b \sigma_{\mathrm{c}} \mathrm{d} \varepsilon . $ | (10) |
由受力平衡可得
| $ T=E_{\mathrm{s}} \varepsilon_{\mathrm{s}} A_{\mathrm{s}}+E_{\mathrm{cf}} \varepsilon_{\mathrm{f}} A_{\mathrm{f}} . $ | (11) |
由力矩平衡条件可得
| $ \begin{gathered} M_{\mathrm{u}}=E_{\mathrm{s}} \varepsilon_{\mathrm{s}} A_{\mathrm{s}}\left(h_0-\frac{1}{3} X_{\mathrm{b}}\right)+ \\ E_{\mathrm{cf}} \varepsilon_{\mathrm{f}} A_{\mathrm{f}}\left(h+\frac{t_{\mathrm{m}}}{2}-\frac{1}{3} X_{\mathrm{b}}\right). \end{gathered} $ | (12) |
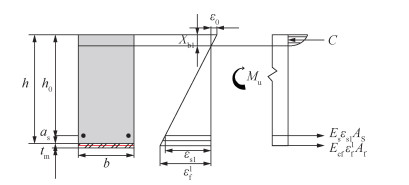
其中T为加固梁受拉区合力。联立式(10)—(12)即可求得极限弯矩Mu。加固梁破坏时,针对碳纤维织物被拉断,受压区混凝土刚好达到峰值应变这一情况,即2.3.1节中所提的第1种破坏模式,其加固梁正截面受弯承载力计算简图如图 9所示。式(10)中受压区混凝土应变εc改为ε0,碳纤维织物应变为εf1。
|
| 图 9 第1种破坏模式计算简图 |
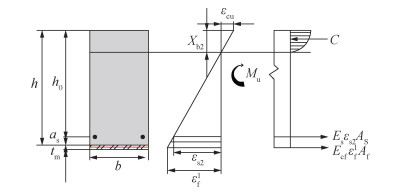
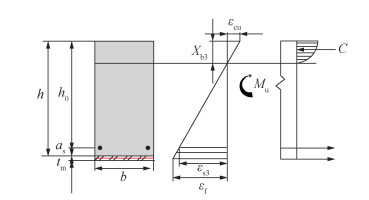
针对碳纤维织物被拉断,受压区混凝土刚好达到极限应变这一情况,即2.3.2节中所提的第2种破坏模式,其加固梁正截面受弯承载力计算简图如图 10所示,式(10)中εc更改为εcu,εf更改为εf1。同理,若发生2.3.2节中所提的第3种破坏模式,即受压区混凝土压碎,梁底纵筋刚好屈服,P-TRC板未拉断时,如图 11所示,式(10)中εc更改为极限压应变εcu,εs改为εs3。
|
| 图 10 第2种破坏模式计算简图 |
|
| 图 11 第3种破坏模式计算简图 |
2.5 验证试验与对比分析
根据上述提出的计算公式对本文、文[13]、[20]和[21]算得的极限承载力理论值Pu′与试验值Pu进行对比,结果见表 9。未加固梁的Pu′/Pu的平均值为0.97,最大误差低于6%,本试验加固梁的Pu′/Pu的平均值为0.96,最大误差低于7%。
| 数据来源 | 加固梁编号 | 加固方法 | Pu′/kN | Pu/kN | Pu′/Pu |
| 本文 | B0 | 未加固 | 231.83 | 246.66 | 0.94 |
| B1 | 278.50 | 281.32 | 0.99 | ||
| B2 | 259.99 | 265.30 | 0.98 | ||
| B0-1 | 射钉加固 | 257.84 | 267.24 | 0.96 | |
| B0-2 | 273.05 | 288.13 | 0.95 | ||
| B1-1 | 291.39 | 306.33 | 0.95 | ||
| B1-2 | 303.01 | 325.21 | 0.93 | ||
| B2-1 | 277.93 | 283.60 | 0.98 | ||
| B2-2 | 294.14 | 304.40 | 0.96 | ||
| 文[13] | B1-1 | 粘接法 | 129.31 | 141.08 | 0.92 |
| B1-2 | — | 143.53 | 0.91 | ||
| 文[20] | B1-1 | 层铺法 | 29.46 | 31.34 | 0.94 |
| B1-2 | — | 32.46 | 0.91 | ||
| B2-2 | 层铺法+植筋 | 31.55 | 33.51 | 0.94 | |
| B3-2 | — | 33.92 | 0.93 | ||
| 文[21] | PFCU1-2R | 层铺法 | 116.21 | 119.80 | 0.97 |
| PFCU1-4R | 123.11 | 120.70 | 1.02 |
3 跨中挠度计算
参照《混凝土结构设计规范》(GB50010-2010)中对钢筋混凝土受弯梁及预应力混凝土梁的短期刚度的计算方法,可得到P-TRC板加固混凝土梁的短期刚度的计算公式。
| $ B_{\mathrm{s}}=\frac{E_{\mathrm{s}} A_{\mathrm{z}} h_0^2}{1.15 \psi+0.2+\frac{6 \alpha_{\mathrm{E}} \rho}{1+3.5 \gamma_{\mathrm{f}}}}. $ | (13) |
考虑加固梁中P-TRC板的约束作用,将其截面面积进行如下代换:
| $ \begin{gathered} A_{\mathrm{d}}=\frac{\alpha A_{\mathrm{cf}}(1+\rho) E_{\mathrm{cf}}}{E_{\mathrm{s}}} , \\ A_{\mathrm{z}}=A_{\mathrm{s}}+A_{\mathrm{d}}. \end{gathered} $ | (14) |
其中:Ad为P-TRC板等效的钢筋面积;Es为钢筋弹性模量;ψ为裂缝间纵向受拉普通钢筋应变不均匀系数;ρ为纵向钢筋配筋率;αE为钢筋弹性模量与混凝土弹性模量比值;α为考虑P-TRC板与钢筋截面高差的修正系数;Az根据弯矩等效原则,本文取值为1.12。求得短期刚度Bs后,根据结构力学方法即可求得加固梁短期挠度值δcr′。
| $ \delta_{\mathrm{cr}}^{\prime}=f=\frac{F a}{24 B_{\mathrm{s}}}\left(3 l^2-4 a^2\right). $ | (15) |
未加固梁屈服荷载和极限荷载对应的跨中挠度计算公式分别为
| $ \delta_\mathrm{y}^{\prime}=0.2 \sqrt{\left(\frac{l}{2}+\frac{l \varepsilon_\mathrm{y}}{4}\right)^2-\left(\frac{l}{2}\right)^2}, $ | (16) |
| $ \delta_{\mathrm{u}}^{\prime}=0.62 \sqrt{\left(\frac{l}{2}+\frac{l \varepsilon_{\mathrm{u}}}{4}\right)^2-\left(\frac{l}{2}\right)^2}. $ | (17) |
加固梁屈服荷载和极限荷载对应的跨中挠度计算公式分别为
| $ \delta_\mathrm{y}^{\prime}=0.2 \sqrt{\left(\frac{l}{2}+\frac{l \varepsilon_{\mathrm{y}}}{4}\right)^2-\left(\frac{l}{2}\right)^2}. $ | (18) |
| $ \delta_{\mathrm{u}}^{\prime}=0.62 \rho \sqrt{\left(\frac{l}{2}+\frac{l \varepsilon_{\mathrm{u}}}{4 \lambda}\right)^2-\left(\frac{l}{2}\right)^2}. $ | (19) |
其中,F为加载点处荷载;a为加载点距最近一侧支座中心间距;l为梁净跨长度。根据上述公式对本文不同工况下未加固梁和加固梁的跨中挠度进行了计算,理论值与试验值结果对比如表 10,最大偏差不超过12%,两者吻合较好。
| mm | |||||||||||||||||||||||||||||
| 试件编号 | δcr′ | δcr | δy′ | δy | δu′ | δu | |||||||||||||||||||||||
| B0 | 1.18 | 1.28 | 15.08 | 16.05 | 60.03 | 62.72 | |||||||||||||||||||||||
| B1 | 0.93 | 0.99 | 14.31 | 14.60 | 53.5 | 48.77 | |||||||||||||||||||||||
| B2 | 1.29 | 1.41 | 14.09 | 14.71 | 69.08 | 73.90 | |||||||||||||||||||||||
| B0-1 | 1.50 | 1.50 | 11.88 | 13.11 | 26.88 | 30.53 | |||||||||||||||||||||||
| B0-2 | 1.25 | 1.29 | 9.71 | 10.97 | 27.39 | 30.1 | |||||||||||||||||||||||
| B1-1 | 1.09 | 1.14 | 9.90 | 11.85 | 28.80 | 32.36 | |||||||||||||||||||||||
| B1-2 | 0.90 | 0.91 | 8.81 | 7.98 | 31.80 | 34.19 | |||||||||||||||||||||||
| B2-1 | 0.90 | 0.98 | 11.38 | 12.51 | 27.38 | 30.09 | |||||||||||||||||||||||
| B2-2 | 0.80 | 0.71 | 9.69 | 10.12 | 26.60 | 30.23 | |||||||||||||||||||||||
以参数碳纤维织物层数为变量绘制的荷载—跨中挠度曲线对比如图 12所示,织物从0层逐级加到2层时,加固梁屈服点对应挠度逐渐减小,相比工况B0,工况B0-1与B0-2分别减少了18.3%与31.7%;相比工况B1,工况B1-1与B1-2分别减少了19.2%与45.3%;相比工况B2,工况B2-1与B2-2分别减少了15.0%与31.2%。相比图 12a与12c,图 12b中单层织物工况B1-1较工况B1的屈服挠度下降程度与其他2组(B0-1与B0、B2-1与B2)较为接近,但双层织物工况B1-2较工况B1的屈服挠度比其他2组(B0-2与B0、B2-2与B2)下降程度更为明显,即随着碳纤维织物层数增加,高配筋率的加固梁屈服挠度下降程度比低配筋的加固梁更大。按照挠度划分正常使用极限状态时,对于未加固梁B0、B1、B2,其正常使用极限状态在梁屈服点左右;对于加固梁,若按照挠度划分正常使用极限状态,其正常使用极限状态在加固梁屈服后不再适用。

|
| 图 12 荷载—跨中挠度曲线 |
4 结论
本文验证了P-TRC板采用射钉加固RC梁传力途径的有效性,考虑了射钉倾斜导致的碳纤维应力滞后。此外,本文提出的加固梁跨中挠度计算公式计算结果与试验值吻合较好。具有较好的实用性。
| [1] |
BRVCKNER A, ORTLEPP R, CURBACH M. Textile reinforced concrete for strengthening in bending and shear[J]. Materials and Structures, 2006, 39(8): 741-748. DOI:10.1617/s11527-005-9027-2 |
| [2] |
DU Y X, ZHANG M M, ZHOU F, et al. Experimental study on basalt textile reinforced concrete under uniaxial tensile loading[J]. Construction and Building Materials, 2017, 138: 88-100. DOI:10.1016/j.conbuildmat.2017.01.083 |
| [3] |
荀勇, 孙伟, REINHARDT H W, 等. 短纤维和织物增强混凝土薄板试验研究[J]. 土木工程学报, 2005, 38(11): 58-63. XUN Y, SUN W, REINHARDT H W, et al. An experimental study on short fiber and textile reinforced concrete thin-slabs[J]. China Civil Engineering Journal, 2005, 38(11): 58-63. DOI:10.3321/j.issn:1000-131X.2005.11.010 (in Chinese) |
| [4] |
刘扬, 彭晖, 尚守平. 预应力CFRP加固钢筋混凝土受弯构件的抗力概率模型研究[J]. 工程力学, 2012, 29(7): 107-116. LIU Y, PENG H, SHANG S P. Probability model of the flexural resistance of reinforced concrete beams strengthened with prestressed CFRP plates[J]. Engineering Mechanics, 2012, 29(7): 107-116. (in Chinese) |
| [5] |
ESCRIG C, GIL L, BERNAT-MASO E. Experimental comparison of reinforced concrete beams strengthened against bending with different types of cementitious-matrix composite materials[J]. Construction and Building Materials, 2017, 137: 317-329. DOI:10.1016/j.conbuildmat.2017.01.106 |
| [6] |
杜运兴, 邵喜诚, 周芬. 预应力CTRC板加固持载混凝土梁的抗弯性能研究[J]. 铁道科学与工程学报, 2020, 17(1): 189-197. DU Y X, SHAO X C, ZHOU F. Flexural behavior of RC beams repaired with prestressed CTRC plates under sustaining loads[J]. Journal of Railway Science and Engineering, 2020, 17(1): 189-197. (in Chinese) |
| [7] |
薛伟辰, 曾磊, 谭园. 预应力CFRP板加固混凝土梁设计理论研究[J]. 建筑结构学报, 2008, 29(4): 127-133. XUE W C, ZENG L, TAN Y. Studies on design theories of concrete beams strengthened with Prestressed CFRP plates[J]. Journal of Building Structures, 2008, 29(4): 127-133. (in Chinese) |
| [8] |
周云, 王廷彦, 张军伟. CFRP加固钢筋混凝土短梁抗弯刚度计算方法[J]. 土木工程学报, 2020, 53(11): 9-20, 35. ZHOU Y, WANG T Y, ZHANG J W. Calculation method on flexural stiffness of reinforced concrete short beam strengthened by CFRP[J]. China Civil Engineering Journal, 2020, 53(11): 9-20, 35. (in Chinese) |
| [9] |
陈爱玖, 韩小燕, 杨粉, 等. 预应力碳纤维布加固钢筋再生混凝土梁受弯承载力研究[J]. 土木工程学报, 2018, 51(11): 104-112. CHEN A J, HAN X Y, YANG F, et al. Study on flexural capacity of reinforced recycled concrete beams strengthened with prestressed CFRP sheets[J]. China Civil Engineering Journal, 2018, 51(11): 104-112. (in Chinese) |
| [10] |
江胜华, 侯建国, 何英明. 考虑预应力损失的CFRP布加固钢筋混凝土梁正常使用极限状态可靠度研究[J]. 土木工程学报, 2015, 48(11): 36-43. JIANG S H, HOU J G, HE Y M. Reliability research of serviceability limit states for RC beams strengthened with prestressed CFRP sheets considering prestress loss[J]. China Civil Engineering Journal, 2015, 48(11): 36-43. (in Chinese) |
| [11] |
ESMAEELI E, BARROS J A O. Flexural strengthening of RC beams using Hybrid Composite Plate (HCP): Experimental and analytical study[J]. Composites Part B: Engineering, 2015, 79: 604-620. |
| [12] |
荀勇, 支正东, 张勤. 织物增强混凝土薄板加固钢筋混凝土梁受弯性能试验研究[J]. 建筑结构学报, 2010, 31(3): 70-76. XUN Y, ZHI Z D, ZHANG Q. Experimental research on flexural behavior of reinforced concrete beams strengthened with textile reinforced concrete sheets[J]. Journal of Building Structures, 2010, 31(3): 70-76. (in Chinese) |
| [13] |
周芬, 陈小晔, 杜运兴, 等. 预拉纤维复合板增强梁抗弯性能研究[J]. 华中科技大学学报(自然科学版), 2019, 47(1): 60-66. ZHOU F, CHEN X Y, DU Y X, et al. Study on flexural behavior of beams strengthened with prestressed fabric reinforced cementitious plates[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(1): 60-66. (in Chinese) |
| [14] |
余琼, 张燕语. 预应力碳纤维布加固钢筋混凝土梁挠度研究[J]. 结构工程师, 2011, 27(1): 139-143. YU Q, ZHANG Y Y. Study on deflection of RC beams Strengthened with prestressed CFRP[J]. Structural Engineers, 2011, 27(1): 139-143. (in Chinese) |
| [15] |
徐世烺, 尹世平, 蔡新华. 纤维编织网增强混凝土加固钢筋混凝土梁受弯性能研究[J]. 土木工程学报, 2011, 44(4): 23-34. XU S L, YIN S P, CAI X H. Investigation on the flexural behavior of reinforced concrete beam strengthened with textile-reinforced concrete[J]. China Civil Engineering Journal, 2011, 44(4): 23-34. (in Chinese) |
| [16] |
周芬, 徐文, 杜运兴. TRC板增强钢筋混凝土梁的抗弯性能[J]. 中南大学学报(自然科学版), 2018, 49(1): 183-191. ZHOU F, XU W, DU Y X. Flexural behavior of RC beams strengthened with TRC plates[J]. Journal of Central South University (Science and Technology), 2018, 49(1): 183-191. (in Chinese) |
| [17] |
毛宇欣, 黄俊豪, 钱永久. 考虑二次受力的CFRP布加固RC梁短期挠度研究[J]. 工程抗震与加固改造, 2023, 45(4): 130-137, 155. MAO Y X, HUANG J H, QIAN Y J. Study on short-term deflection of RC beams strengthened by CFRP sheet considering secondary load[J]. Earthquake Resistant Engineering and Retrofitting, 2023, 45(4): 130-137, 155. (in Chinese) |
| [18] |
吴子林, 杜运兴, 周芬. 预制TRC板与混凝土界面性能研究[J]. 新型建筑材料, 2021, 48(8): 74-79. WU Z L, DU Y X, ZHOU F. Interface performance between precast TRC slab and concrete member[J]. New Building Materials, 2021, 48(8): 74-79. (in Chinese) |
| [19] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2011. (in Chinese) |
| [20] |
张勤. 织物增强混凝土(TRC)加固RC梁正截面抗弯性能试验研究[D]. 镇江: 江苏大学, 2009. ZHANG Q. Experimental study on flexural behavior of reinforced concrete beams strengthened with textile reinforced concrete[D]. Zhenjiang: Jiangsu University, 2009. (in Chinese) |
| [21] |
YANG D S, PARK S K, NEALE K W. Flexural behaviour of reinforced concrete beams strengthened with prestressed carbon composites[J]. Composite Structures, 2009, 88(4): 497-508. |



