离心式压缩机具有结构紧凑、单级压比高等优点,在石化、航天、能源等行业应用广泛[1-2]。叶轮内部结构复杂,气体流动过程中存在湍流、涡流和二次流等复杂流动现象,了解其内部流动特征,可为提高叶轮效率、减少叶片载荷提供参考。Eckardt[3]利用激光双聚焦测速仪对径向离心式叶轮内部的气体速度矢量及波动范围进行实验,测得了相对速度分布,并详细讨论了湍流、二次流和尾迹等流动特征的发展以及相互影响。Johnson等[4]通过实验测量低速径向离心式叶轮内滞止压强、相对速度的分布,阐述了尾迹产生位置、二次流的产生及其对尾迹的影响,补充描述了Eckardt提出的离心叶轮内部尾迹特征。Krain[5]采用相同的激光双聚焦测速仪测量后弯式离心叶轮内部气体的速度,得到了测量截面上不同叶高位置的相对子午速度分布,详细描述了尾迹、二次流的产生和发展,并对涡流进行了讨论,为后续数值计算验证提供了参考[6]。孙志刚[7]通过有限体积法求解Reynolds时均Navier-Stokes(Reynolds time averaged Navier-Stokes,RANS)方程组得到了与实验结果吻合程度较高的Eckardt叶轮和Krain叶轮数值计算结果,并基于数值结果更深入详细地讨论了2种叶轮内部的流动结构。还有许多其他学者对离心压缩机无叶扩压器[8-10]、叶片扩压器[11-12]开展了研究,为相关研究人员提供了参考。
上述研究中离心压缩机的入口压强基本为大气压(101 325 Pa),入口压强低于大气压的离心压缩机统称为负压离心压缩机,其在化工、制冷等领域有较为成熟的应用及相关研究。顾承真等[13]通过对机械蒸汽再压缩(mechanical vapor recompression,MVR)蒸发系统流程进行模拟分析,得到当负压离心蒸汽压缩机的压缩比为1.8~2.2时较为合理。薛芳等[14]对R1233zd(E)离心式冷水机组进行优化设计,叶轮型线的优化及配套叶片扩压器的使用使压缩机效率显著提高且叶轮直径减小15%。以上负压离心压缩机的研究局限于入口压强超过30 000 Pa的工况。周明胜等[15]研发了用于负压工况下非空气工作介质的高速磁悬浮离心压缩机,其叶轮入口设计压强为2 000~3 000 Pa,相比入口设计压强为30 000 Pa的叶轮负压显著下降。
目前关于负压条件下,尤其是关于入口压强低至400 Pa的离心压缩机性能的研究文献较少,且未见探究负压压缩机内部流动特征研究的相关公开资料。另外在研制负压离心压缩机过程中发现,相同入口体积流量下入口压强增加会引起压比提升,因此有必要开展入口压强对离心压缩机性能影响及机理的研究,该研究还有助于在负压离心压缩机的初始设计阶段,采用基于正压的一维性能模型预测负压离心压缩机性能时提供修正方向,提高预测精度,减少冗余设计时间。
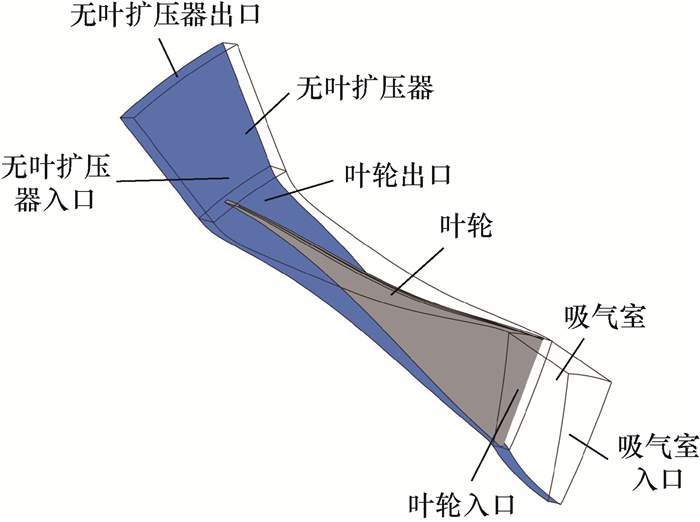
1 研究对象Krain后弯式离心叶轮有完整的性能测量、流场分布实验数据以及较为完善的尺寸参数,被许多离心压缩机学者选为研究对象,本文同样将Krain后弯式离心叶轮作为研究对象,叶轮相关参数如表 1所示。为保证叶轮来流气体均匀,添加了入口段,并在出口处安装了无叶扩压器,方便后续通过实验结果验证数值方法,模型如图 1所示。
| 参数 | 参数值 |
| 工作介质 | 空气(理想气体) |
| 质量流量 |
4 |
| 入口总压p/Pa | 101 325 |
| 入口总温T/K | 300 |
| 转速N/(r·min-1) | 22 363 |
| 压比π | 4.7 |
| 叶轮入口轮盘直径D1h/mm | 90.0 |
| 叶轮入口轮盖直径D1sh/mm | 225.5 |
| 叶轮出口轮盘直径D2h/mm | 400.0 |
| 叶轮出口轮盖直径D2sh/mm | 400.0 |
| 叶轮出口叶片高度b2/mm | 14.7 |
| 叶轮轴向长度L/mm | 120.0 |
| 叶轮入口叶顶叶片角β1tip/(°) | -60 |
| 叶轮出口叶顶叶片角β2tip/(°) | -30 |
| 叶片数量Z | 24 |
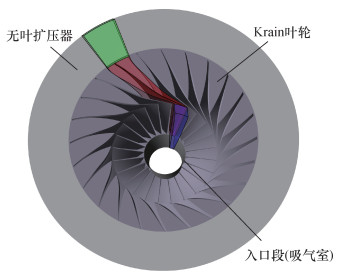
|
| 图 1 Krain叶轮示意图 |
2 数值方法与验证
以D2sh为特征长度,当入口压强不低于400 Pa时,Knudsen数Kn小于10-2,故叶轮内部气体为黏性流,控制方程为Navier-Stokes方程[17]。考虑内部湍流,使用有限体积法求解三维RANS方程组[18],旋转参考系下的方程表示如下:
| $ \begin{gathered} \frac{\partial \boldsymbol{U}}{\partial t}+\nabla \boldsymbol{F}_{\mathrm{IVS}}+\nabla \boldsymbol{F}_{\mathrm{VS}}=\boldsymbol{M}, \\ \boldsymbol{U}=\left[\begin{array}{c} \bar{\rho} \\ \bar{\rho} \widetilde{V}_x \\ \bar{\rho} \widetilde{V}_y \\ \bar{\rho} \widetilde{V}_z \\ \bar{\rho} \bar{E} \end{array}\right], \quad \boldsymbol{F}_{\mathrm{IVS} i}=\left[\begin{array}{c} \bar{\rho} \widetilde{V}_i \\ \bar{\rho} \widetilde{V}_x \widetilde{V}_i+\bar{p} \delta_{x i} \\ \bar{\rho} \widetilde{V}_y \widetilde{V}_i+\bar{p} \delta_{y i} \\ \bar{\rho} \widetilde{V}_z \widetilde{V}_i+\bar{p} \delta_{z i} \\ (\bar{\rho} \bar{E}+p) \widetilde{V}_i \end{array}\right], \\ -\boldsymbol{F}_{\mathrm{VS} i}=\left[\begin{array}{c} 0 \\ \tilde{\tau}_{x i} \\ \tilde{\tau}_{y i} \\ \tilde{\tau}_{z i} \\ \tilde{\boldsymbol{q}}_i+\widetilde{\boldsymbol{V}} \cdot \tilde{\boldsymbol{\tau}}_i \end{array}\right], \\ \boldsymbol{M}=\left[\begin{array}{c} 0 \\ -\bar{\rho}[2 \widetilde{\boldsymbol{\omega}} \times \widetilde{\boldsymbol{V}}+(\boldsymbol{\omega} \times(\boldsymbol{\omega} \times r))] \\ \bar{\rho} \widetilde{\boldsymbol{V}} \cdot \nabla\left(\frac{1}{2} \boldsymbol{\omega}^2 r^2\right) \end{array}\right] . \end{gathered} $ | (1) |
其中:U为守恒形式变量;FIVS、FVS分别为无黏性通量矢量和黏性通量矢量;M为源项;∂/∂t表示对时间求偏导;
| $ \delta_{j k}= \begin{cases}1, & j=k; \\ 0, & j \neq k.\end{cases} $ |
其中:j、k表示Kronecker函数的2个输入量。
热传导方程和RANS的黏性张量定义分别为:
| $ \widetilde{\boldsymbol{q}}_i=-\kappa \frac{\partial \bar{T}}{\partial \boldsymbol{X}_i}, $ | (2) |
| $ \widetilde{\boldsymbol{\tau}}=\left(\mu_{\mathrm{lam}}+\mu_{\mathrm{tur}}\right)\left[\nabla \widetilde{\boldsymbol{V}}+(\nabla \widetilde{\boldsymbol{V}})^{\mathrm{T}}-\left(\frac{2}{3} \nabla \cdot \widetilde{\boldsymbol{V}}\right) \boldsymbol{I}\right]. $ | (3) |
其中:T为取RANS的温度;μlam、μtur分别为层流、湍流气体动力的黏度,Xi为位置矢量在方向i上的分量;κ为气体导热系数;I为单位张量。
为使式(1)—(3)构成的方程组封闭,引入理想气体状态方程及湍流模型。Spalart-Allmaras(S-A)湍流模型[19]具有求解速度快、精度较高等优点,本文选择S-A湍流模型求解湍流动力黏度。
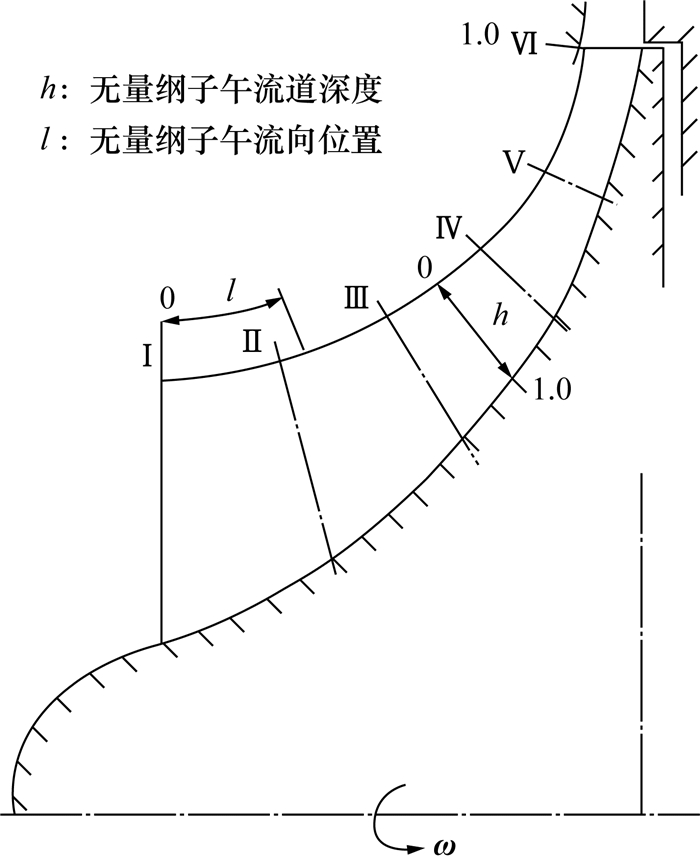
为减少计算量、节省计算时间,选择单流道作为计算模型,如图 2所示。图 3为Krain实验中6个测量面Ⅰ—Ⅵ子午位置示意图[5]。流道采用结构网格划分,第1层网格厚度为6 μm,整个计算域除叶片尾缘截断面外其他区域无量纲壁面距离d+值均小于10,网格数量为1.88×106,满足网格无关性检验,模型网格划分示意图和网格无关性检验分别如图 4和5所示。入口给定总压、总温和速度方向,出口给定质量流量,所有壁面均为无滑移绝热边界。若均方根残差小于10-4,进、出口流量差小于0.01%,效率变化小于0.01%,则计算收敛。
|
| 图 2 单流道计算模型示意图 |

|
| 图 4 单流道模型网格划分示意图 |
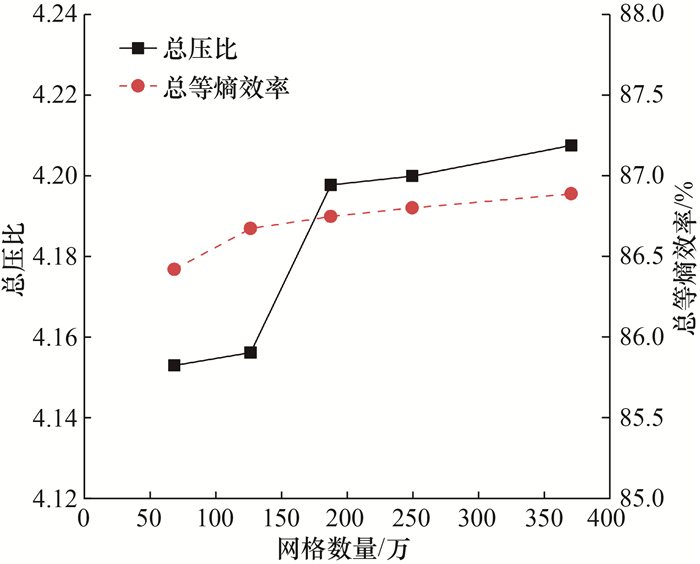
|
| 图 5 网格无关性检验 |
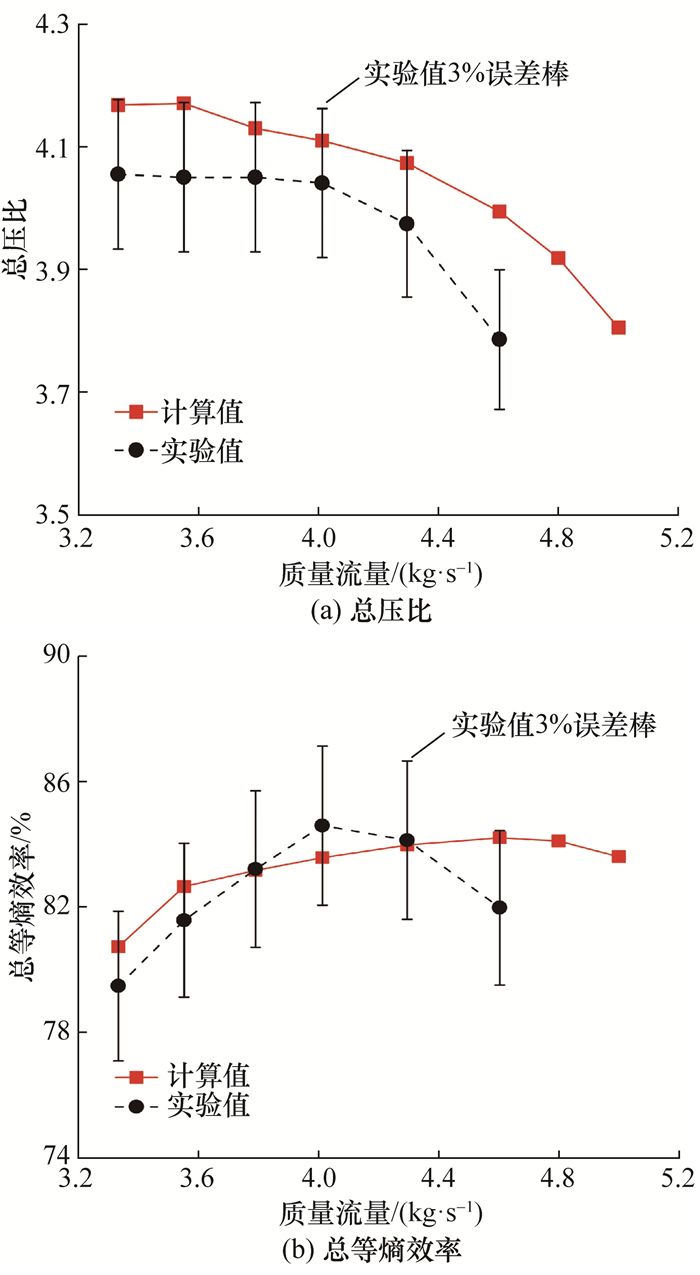
按照表 1中的参数设置进行数值计算,并比较总压比和总等熵效率的计算结果与实验结果[5],结果如图 6所示,由图可知,计算值与实验值的相对偏差基本在3%以内,说明叶轮性能计算结果与实验结果吻合程度较高。造成误差的主要原因为:Krain实验所用无叶扩压器出口直径参数未知,本文所用无叶扩压器的外径为580 mm,将Eckardt径向离心叶轮无叶扩压器外径视为Krain无叶扩压器外径[7],并基于此修正计算结果,会造成一定偏差。
|
| 图 6 Krain叶轮性能曲线 |
3 数值模拟结果与分析 3.1 入口压强对性能的影响
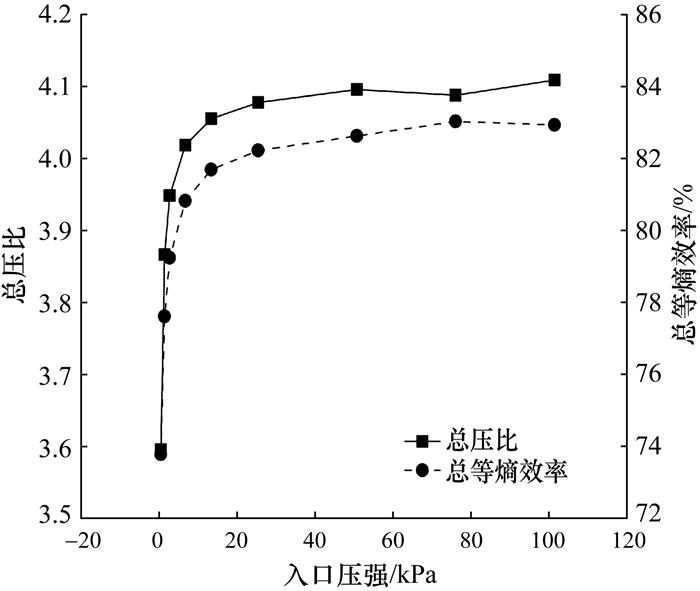
图 7表示在设计体积流量为199.6 m3/min、设计转速为22 363 r/min条件下不同入口压强对叶轮性能的影响。由图可知,随着入口压强减小,叶轮总压比和总等熵效率呈先缓慢减小再急剧减小的趋势。当入口压强大于13 333 Pa时,不同入口压强叶轮性能差异较小。当入口压强小于13 333 Pa,尤其是小于2 666 Pa时,叶轮性能急剧减小。当入口压强为400 Pa时叶轮总压比仅为3.6、总等熵效率为74%,相比于101 325 Pa条件下的值均出现偏小的情况,且减少幅度超过10%,两者性能差异不可忽视。
|
| 图 7 Krain叶轮性能随入口压强变化曲线 |
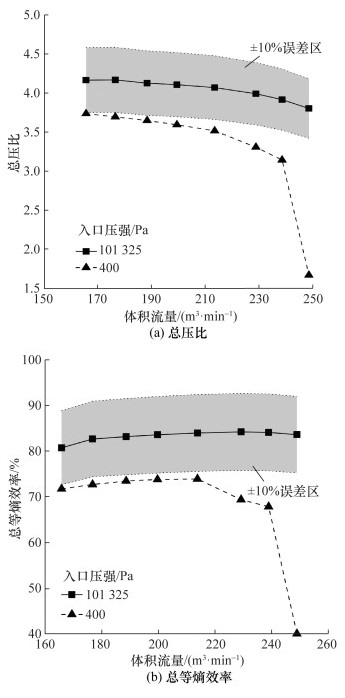
比较入口压强分别为400和101 325 Pa条件下叶轮变工况性能,结果如图 8所示,阴影区域表示101 325 Pa下性能波动±10%的范围。由图可知,在变工况流量范围内,当入口压强为400 Pa时的叶轮性能均比压强为101 325 Pa时低10%以上,且随着流量增加,偏差增大。在400 Pa的入口压强下,叶轮的稳定工况范围更窄,当体积流量为240 m3/min时会发生堵塞。
|
| 图 8 Krain叶轮变工况性能曲线 |
3.2 入口压强对流动损失的影响
为明确性能变化原因,本节分析了不同入口压强下的流动损失。不考虑轮阻损失及内漏气损失,由Bernoulli方程可得:
| $ W_{\mathrm{th}}=\int_1^2 \frac{\mathrm{d} p}{\rho}+\frac{\boldsymbol{C}_2 \cdot \boldsymbol{C}_2-\boldsymbol{C}_1 \cdot \boldsymbol{C}_1}{2}+e_{\mathrm{hyd}}. $ | (4) |
其中:ρ为气体密度;Wth为叶轮做功;C2、C1分别为出口、入口气体绝对速度;ehyd为各种流动损失的总和。流动损失可用熵参数、总压损失、涡量或熵增参数表征[20],van Zante等[21]提出不可逆性表征流动损失,表示如下:
| $ J_{\mathrm{n}}=\sum T_0 m_{\mathrm{e}} s_{\mathrm{e}}-\sum T_0 m_{\mathrm{a}} s_{\mathrm{a}}. $ | (5) |
其中:T0为参考温度,一般取入口气体温度;me和ma分别为出口和入口的质量;se和sa分别为出口和入口的比熵,比熵定义为ds=δQ/T,Q为单位质量热量。由Jn的定义知,不可逆性本质上是熵增乘以参考温度,本文采用熵增表征能量损失。考虑到理想气体满足pV=mRT/M,V、R、M分别为气体体积、通用气体常数、气体摩尔体积,在入口体积流量和温度相同情况下,质量与入口压强存在对应关系,入口压强增加使熵增增加,即总流动损失增加,而单位质量的损失(比损失)不一定增加,为表征比损失,定义比熵增如下:
| $ \Delta s_{\text {inducer }}=\frac{\iint\limits_1 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A-\iint\limits_0 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}{\iint\limits_0 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}. $ | (6) |
其中:Δsinducer为吸气室比熵增,dA为微元面积;n为微元面积方向,指向出口方向为正方向。同理有叶轮和无叶扩压器的比熵增分别表示如下:
| $ \Delta s_{\text {impeller }}= \frac{\iint\limits_2 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A-\iint\limits_1 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}{\iint\limits_1 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}, $ | (7) |
| $ \Delta s_{\text {diffuser }} =\frac{\iint\limits_4 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A-\iint\limits_3 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}{\iint\limits_3 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A} . $ | (8) |
叶轮、无叶扩压器内部局部比熵增分别表示如下:
| $ \Delta s_{\mathrm{imp}}=s-\frac{\iint\limits_1 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}{\iint\limits_1 \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}, $ | (9) |
| $ \Delta s_{\mathrm{dif}}=s-\frac{\iint\limits_3 s \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}{\iint\limits_3 \rho \boldsymbol{C} \cdot \boldsymbol{n} \mathrm{d} A}. $ | (10) |
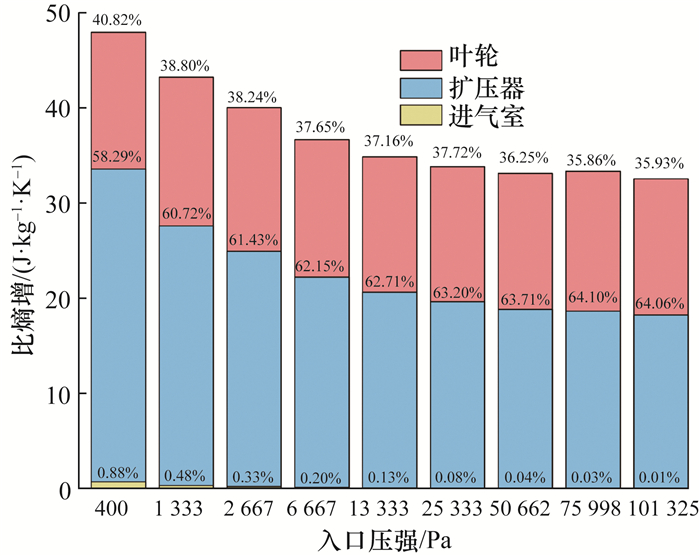
图 9为不同入口压强下各元件的比熵增,由图可知,随着入口压强减小,各元件比熵增增加,且入口压强越小,比熵增增加越快,即气体通过压缩机级的流动损失随压强的减小而增加。比较3种元件的比熵增占比可知,扩压器比熵增占比随着入口压强减小而增加,即无叶扩压器对流动损失的贡献随压强减小而提高。
|
| 图 9 元件比熵增随入口压强变化关系图 |
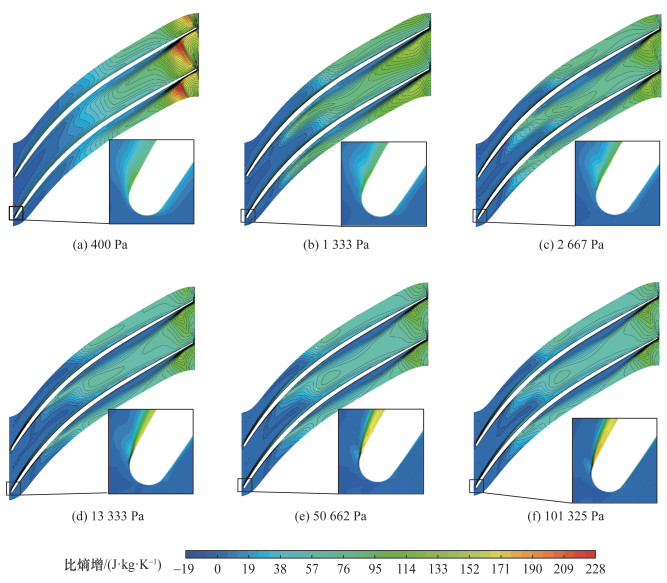
图 10为不同入口压强下h=0.1时叶轮子午流线回转面(blade-to-blade,B2B)上比熵增的分布,由图可知,随着入口压强减小,由流道内尾迹导致的比熵增增加,而在叶片前缘吸力面处比熵增则减小。当入口压强大于2 667 Pa时,叶片前缘吸力面处比熵增较其他位置大,即吸力面边界层损失较强。当入口压强小于等于2 667 Pa时,叶轮出口处比熵增较高,该位置的熵增主要由二次流以及反流造成,当压强减小至400 Pa时,叶轮出口处流动损失显著增强,由3.3节对流场的分析可知,反流更为显著。
|
| 图 10 B2B面上Δsimp分布(h=0.1) |
对无叶扩压器内局部比熵增进行角向平均,可得:
| $ \Delta \bar{s}_{\mathrm{dif}}=\frac{\oint \Delta s_{\mathrm{dif}} \rho C_{\mathrm{rad}} r \mathrm{~d} \theta}{\oint_{\rho C_{\mathrm{rad}}} r \mathrm{~d} \theta} . $ | (11) |
其中:Δsdif为扩压器中不同流向位置处比熵增,Crad为气体径向速度,θ为柱坐标系下角度。
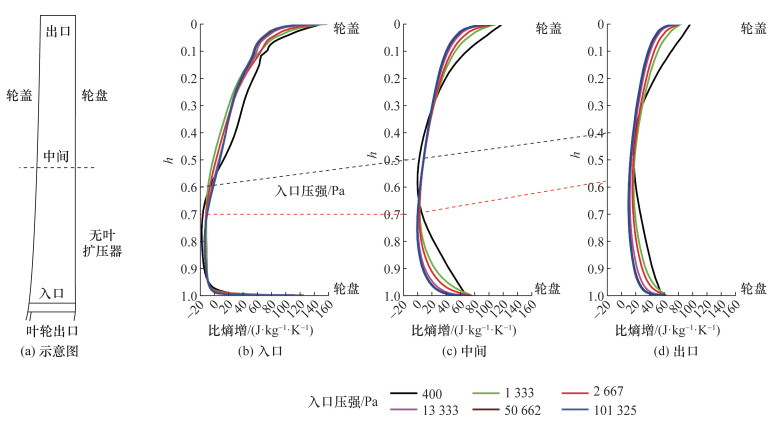
Δsdif沿无量纲子午流道深度的分布如图 11所示,由图可知,在任何流向位置,入口压强越小,轮盖侧气体比熵增越大,靠近轮盘侧的气体在扩压器入口后,比熵增同样随着入口压强减小而增加。由出口比熵增分布可知,流道内不同深度处的比熵增基本满足随着入口压强减小而增加的规律。气体流经无叶扩压器过程中,轮盖侧比熵增逐渐减小,深度深的位置比熵增在黏性作用下增加,低熵区逐渐向h=0.5位置移动,且随着入口压强降低移动速度加快。
|
| 图 11 无叶扩压器中不同流向位置处比熵增沿流道深度分布 |
3.3 入口压强对流场的影响
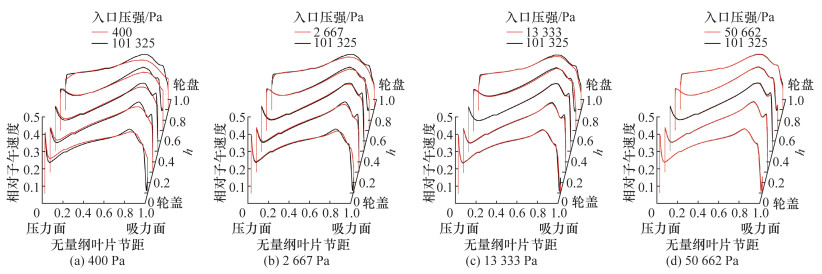
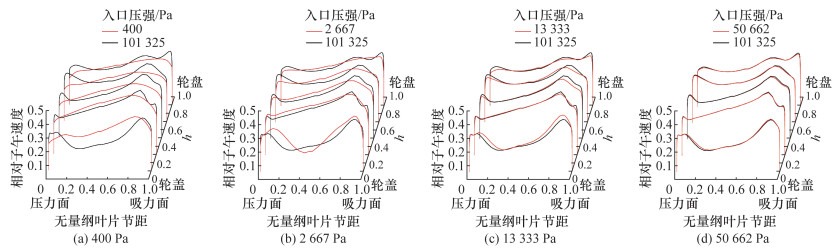
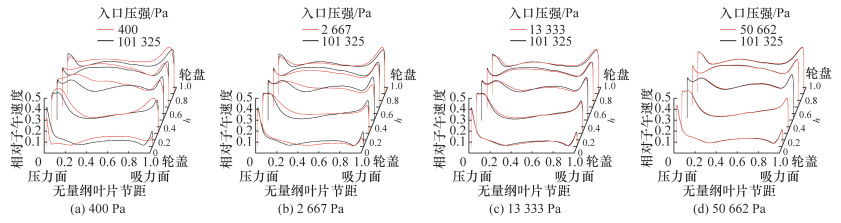
图 12—14为不同测量面上相对子午速度的分布。由测量面Ⅰ上的分布可知,当入口压强大于2 667 Pa时,相对子午速度分布差异不大,而在吸力面附近h=0.1处子午速度随入口压强增加而减小,说明此处边界层分离情况随入口压强的增加而加强。在入口压强为400 Pa的条件下,吸力面附近的相对子午速度比101 325 Pa条件下的小,而压力面附近的相对子午速度则偏大,即入口压强越低,流道内相对子午速度的周向分布越趋于平缓。比较测量面Ⅲ上h=0.1的相对子午速度分布,可知压强越高,中间低速区越宽,即尾迹发展更充分,表明入口压强越低,尾迹产生的位置越靠流道下游。由测量面Ⅵ上的相对子午速度分布可知,在任何入口压强条件下,叶轮出口处低速流体团基本可覆盖h≤0.3的区域,在入口压强为400 Pa的条件下出口处气体子午速度比高压强的偏大。不同测量面上压力面和吸力面处子午速度的梯度均随着入口压强减小而减小,即壁面上的边界层厚度随入口压强减小而增加。
|
| 图 12 Krain叶轮测量面Ⅰ上相对子午速度分布 |
|
| 图 13 Krain叶轮测量面Ⅲ上相对子午速度分布 |
|
| 图 14 Krain叶轮测量面Ⅵ上相对子午速度分布 |
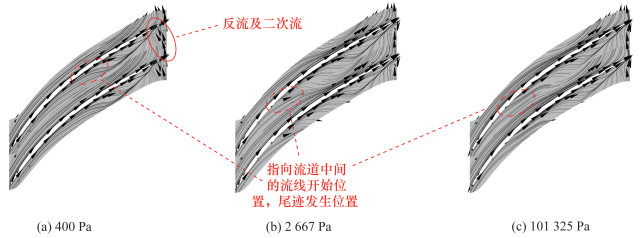
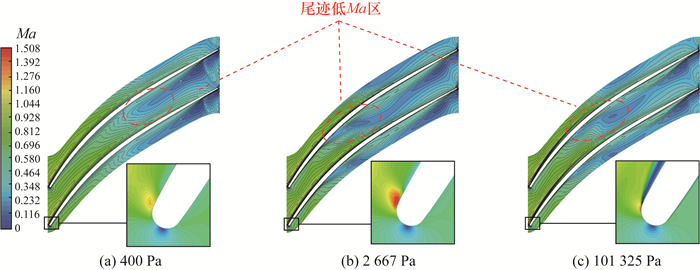
图 15和16分别显示了h=0.1时B2B面上的流线分布以及Ma分布。由图可知,入口压强为2 667 Pa时的流线和Ma分布与压强为101 325 Pa时基本一致,但在叶片前缘吸力面处,压强为101 325 Pa的边界层分离较为显著。相比于高压强,在入口压强为400 Pa的条件下,由压力面指向流道中间的流线开始位置以及低Ma区更靠近下游,即尾迹发生位置更接近下游,另外在叶轮出口处有明显反流和二次流。
|
| 图 15 B2B面上流线分布(h=0.1) |
|
| 图 16 B2B面上Ma分布(h=0.1) |
图 17为气体从叶轮排出后在各流向位置处的Crad、切向速度Ctan沿深度方向的分布,由图可知,在叶轮出口h≤0.1处,Crad在不同入口压强条件下均为负值,而压强为400 Pa时的Crad相比于其他压强偏大,即反流的气体速度更大,且在深度h>0.1时Crad才变为正值,表明其反流的区域更广。在其他深度位置处不同压强的Crad差异较小。Ctan在叶轮出口轮盖侧的梯度随入口压强减小而减小,即气体边界层厚度增加。

|
| 图 17 不同流向位置处气体径向速度、切向速度沿深度分布 |
气体流入无叶扩压器后,贴近轮盘侧的气体径向速度、切向速度梯度随着入口压强减小而缓慢减小,当压强减小至400 Pa时,梯度显著减小,扩压器出口处轮盘壁面附近气体径向速度为负值。换言之,入口压强减小导致无叶扩压器中边界层厚度增加,当压强小至400 Pa时,扩压器出口处边界层已发展为湍流边界层。边界层厚度随入口压强减小而增加的规律在扩压器轮盖侧同样存在,当入口压强为400 Pa时,贴近轮盖的气体径向速度高于其他压强。扩压器出口处气体切向速度在整个深度上均随着入口压强的减小而减小。
由图 18可知不同流向位置处绝对气流角α沿深度分布可知,在叶轮出口h>0.5区域处,当入口压强不低于1 333 Pa时,绝对气流角随着入口压强降低而减小,而在h≤0.5区域绝对气流角随入口压强降低而增大。当入口压强为400 Pa时,高深度区域绝对气流角大,低深度区域气流角小,即高深度处通流强,低深度反流强。
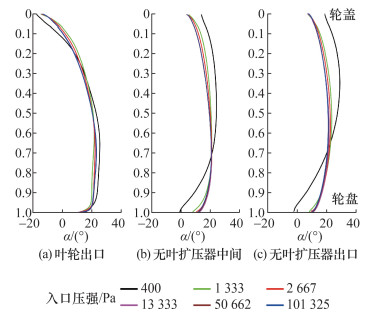
|
| 图 18 不同流向位置处绝对气流角沿深度分布 |
气体流入无叶扩压器后,低深度处绝对气流角依旧随入口压强降低而增加,高深度处气流角随入口压强降低而减小,且在400 Pa处出现明显突变。由图 17知,当入口压强为400 Pa时,轮盖和轮盘处的气体速度梯度更小,即边界层厚度更大,边界底部甚至出现湍流,故而导致轮盘侧较大深度范围内气流角显著低于其他压强。在流道中间及低深度位置,绝对气流角随入口压强的减小而增大,因为边界层厚度随压强减小而增大,故流道中间气体子午流速更大,使气流角增加。
4 结论以Krain后弯式离心叶轮为研究对象,通过三维有限体积法探究了体积流量相同情况下入口压强对离心压缩机性能及内部流动结构的影响,得出如下结论:
1) 叶轮的总压比、总等熵效率随着入口压强的减小而降低,并在入口压强约为1 333 Pa时开始显著下降。当入口压强为400 Pa时,总压比、总等熵效率比入口压强为101 325 Pa时减小10%以上,叶轮的稳定工况范围有所减小。
2) 单级压缩机元件吸气室、叶轮、无叶扩压器内的流动损失随着入口压强减小而增加,其中扩压器中的损失增加更为显著。叶轮入口叶片吸力面处边界层分离导致的损失随压强减小而减弱,出口处的二次流和尾迹损失有所增加。
3) 叶轮内尾迹起始位置随着入口压强减小而向下游移动,整体流动分布较为相近,而当入口压强为400 Pa时叶轮出口存在较显著的反流。
4) 无叶扩压器内轮盘侧边界层厚度随入口压强减小而增加,而当入口压强减小至400 Pa时厚度显著增加,边界层内气体速度明显减小,比熵增显著提高。
通过本研究可知,入口压强减小使离心压缩机内边界层厚度增加,叶轮出口处反流速度增大、区域扩大,进而增强了边界层损失和反流损失,压缩机性能下降。因此在负压离心压缩机初始设计阶段采用基于正压的一维性能模型预测性能时需考虑负修正。后续将对更多型号的负压离心压缩机开展研究,并采用熵产理论对局部流动损失进行量化计算,为一维性能预测模型提供准确的修正因子,提高预测精度。
| [1] |
徐忠. 离心式压缩机原理[M]. 北京: 机械工业出版社, 1990. XU Z. The principle of centrifugal compressor[M]. Beijing: China Machine Press, 1990. (in Chinese) |
| [2] |
祁大同. 离心式压缩机原理[M]. 北京: 机械工业出版社, 2018. QI D T. The principle of centrifugal compressor[M]. Beijing: China Machine Press, 2018. (in Chinese) |
| [3] |
ECKARDT D. Detailed flow investigations within a high-speed centrifugal compressor impeller[J]. Journal of Fluids Engineering, 1976, 98(3): 390-3399. DOI:10.1115/1.3448334 |
| [4] |
JOHNSON M W, MOORE J. The development of wake flow in a centrifugal impeller[J]. Journal of Engineering for Power, 1980, 102(2): 382-389. DOI:10.1115/1.3230265 |
| [5] |
KRAIN H. Swirling impeller flow[J]. Journal of Turbomachinery, 1988, 110(1): 122-128. DOI:10.1115/1.3262157 |
| [6] |
KRAIN H, HOFFMAN W. Verification of an impeller design by laser measurements and 3D-viscous flow calculations[C]//Proceedings of the ASME 1989 International Gas Turbine and Aeroengine Congress and Exposition. Toronto, Canada: ASME, 1989: 89-GT-159.
|
| [7] |
孙志刚. 离心压气机内部流动特性与流场结构研究[D]. 北京: 中国科学院研究生院(工程热物理研究所), 2011. SUN Z G. Investigation on the flow features and flowfield structures of centrifugal compressors[D]. Beijing: Insititute of Engineering Thermophysics, Chinese Academy of Sciences, 2011. (in Chinese) |
| [8] |
DEAN R C JR, SENOO Y. Rotating wakes in vaneless diffusers[J]. Journal of Fluids Engineering, 1960, 82(3): 563-570. |
| [9] |
PINARBASI A, JOHNSON M. Detailed flow measurements in a centrifugal compressor vaneless diffuser[J]. Journal of Turbomachinery, 1994, 116(3): 453-460. DOI:10.1115/1.2929432 |
| [10] |
NIKIFOROV A, AVRAMENKO D, KUCHUMOV A, et al. Vaneless diffusers characteristics simulating by means of neural networks[J]. IOP Conference Series: Materials Science and Engineering, 2019, 604: 012046. DOI:10.1088/1757-899X/604/1/012046 |
| [11] |
KRAIN H. A study on centrifugal impeller and diffuser flow[J]. Journal of Engineering for Power, 1981, 103(4): 688-697. DOI:10.1115/1.3230791 |
| [12] |
ZIEGLER K U, GALLUS H E, NIEHUIS R. A study on impeller—diffuser interaction. Part Ⅰ: Influence on the performance[J]. Journal of Turbomachinery, 2003, 125(1): 173-182. DOI:10.1115/1.1516814 |
| [13] |
顾承真, 闵兆升, 洪厚胜. 机械蒸汽再压缩蒸发系统的性能分析[J]. 化工进展, 2014, 33(1): 30-35. GU C Z, MIN Z S, HONG H S. Performance analysis of mechanical vapor recompression evaporation system[J]. Chemical Industry and Engineering Progress, 2014, 33(1): 30-35. (in Chinese) |
| [14] |
薛芳, 苏秀平, 王林忠. R1233zd(E)在离心式冷水机组中的应用研究[J]. 制冷与空调, 2019, 19(2): 24-9. XUE F, SU X P, WANG L Z. Application study of R1233zd(E) into centrifugal chiller[J]. Refrigeration and Air-Condtioning, 2019, 19(2): 24-9. (in Chinese) |
| [15] |
周明胜, 裴根, 姜东君, 等. 用于负压条件下的高速磁悬浮压缩机: CN209510664U[P]. 2019-10-18. ZHOU M S, PEI G, JIANG D J, et al. High-speed magnetic levitation centrifugal compressor for negative pressure conditions: CN209510664U[P]. 2019-10-18. (in Chinese) |
| [16] |
席光. 关于Krain实验叶轮几何型线及其流道二次流旋涡结构的讨论[J]. 工程热物理学报, 2000, 21(4): 440-442. XI G. Discussion on the geometry and the secondary flow vortex structure of Krain's experimental compressor impeller[J]. Journal of Engineering Thermophysics, 2000, 21(4): 440-442. (in Chinese) |
| [17] |
吴其芬, 陈伟芳, 黄琳, 等. 稀薄气体动力学[M]. 长沙: 国防科技大学出版社, 2004. WU Q F, CHEN W F, HUANG L, et al. Rare aerodynamics[M]. Changsha: National University of Defense Technology Press, 2004. (in Chinese) |
| [18] |
张傲. 离心压缩机叶片参数化造型和气动性能优化[D]. 大连: 大连理工大学, 2022. ZHANG A. Blade parameterization and aerodynamic performance optimization of centrifugal compressor impellers[D]. Dalian: Dalian University of Technology, 2022. (in Chinese) |
| [19] |
SPALART P, ALLMARAS S. A one-equation turbulence model for aerodynamic flows[C]//Proceedings of the 30th Aerospace Sciences Meeting and Exhibit. Reno, USA: AIAA, 1992.
|
| [20] |
路倩, 南希, 林峰. 熵产控制体方法对压气机近零间隙流动损失的演变规律[J]. 航空动力学报, 2016, 31(3): 678-684. LU Q, NAN X, LIN F. Entropy generation control volume method and its application into flow loss evolution in a compressor with near zero tip clearance[J]. Journal of Aerospace Power, 2016, 31(3): 678-684. (in Chinese) |
| [21] |
VAN ZANTE D E, TO W M, CHEN J P. Blade row interaction effects on the performance of a moderately loaded NASA transonic compressor stage[C]//Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air. Amsterdam, the Netherlands: ASME, 2002.
|