长圆孔是一种常用于产品结构机械连接的零件孔型,其设计目的是提高装配中的容错,增加装配调整量,满足不同装配需求。在机器人自动装配系统中,视觉检测工件特征的方法常被用于确定工件位姿,进而有助于操纵机器人系统对工件进行自动装配,因此基于视觉对工件特征进行精确检测定位,成为实现机器人自动装配迫切需要解决的关键技术问题。目前已有大量学者提出针对圆形特征的视觉识别检测定位的方法[1-4],但针对长圆孔这类具有异形特征的视觉检测定位方法较为少见。现有异形特征检测算法大多针对相对宽泛的特征,例如检测对称图形的对称Hough变换方法[5-6]、检测闭合曲线的搜索方法[7]。这些方法能够检测所有对应特征,但其在实际应用中容易受到复杂背景的干扰,且忽略了具体检测对象的其他图像特征对被检测特征的影响,从而降低了精度。有学者采用Fourier变换得以近似描述任意闭合曲线,但这种方法在实际应用中受到计算时间、轮廓点输入顺序和相位等实际因素的制约[8]。模板和特征点匹配同样可用于长圆孔检测,但这些方法都存在精度和时间的矛盾,且鲁棒性不高[9-11],尤其不适用于画面占比小、形状特征少的长圆孔。近年来,随着机器学习的发展,利用深度学习或者强化学习方法检测图像特征成为研究热点[12-13],但学习方法受制于训练数据,在实际应用中的精度和鲁棒性均有待提高,端到端直接完成检测定位的机器学习方法并不现实。
因此,目前难以直接采用已有的圆孔检测方法解决长圆孔的视觉检测定位问题,而采用泛用方法则存在精度有限、环境适应性差等缺陷。本文将以某产品的机器人自动化装配为应用背景,通过分析长圆孔的几何特征,提出一种结合深度学习和传统图像处理,基于语义分割网络和长圆孔区域退化的视觉分割定位算法,并基于测试集数据以及基于某产品装配的综合实验验证该算法的精度、有效性和鲁棒性。以此探索出一种新的长圆孔视觉检测定位算法,满足实际应用需求。
1 长圆孔特征分析长圆孔形状特征分析是检测、定位算法设计的基础。首先对长圆孔形状进行描述和建模。从直观角度,长圆孔轮廓(以下简称“长圆形”)可被描述为2个相同半径的半圆弧和2条线段拼接而成的图形,且2条线段间的距离与半圆弧的直径相等。从几何角度,长圆形可被定义为平面上满足到特定线段A1A2上的点的最小距离为定值r的点集,具体可描述为
| $ C=\{p \mid \min \{d(p, q) \mid q \in L\}=r\}. $ | (1) |
其中:C表示长圆形所有点的集合,L表示线段A1A2上点的集合,d(p, q)表示点p和q之间的Euclid距离。
长圆孔示意图如图 1所示,定义点A1和A2位于x轴上且关于y轴对称,线段A1A2的长度为2a。由图可知,平面上横坐标绝对值不大于a的点到线段A1A2上点的最小距离即为到线段所在直线的距离;平面上横坐标绝对值大于a的点到线段A1A2上点的最小距离即为到较近的端点的距离。在极端条件下(r=0),长圆形退化为线段A1A2;当线段端点A1和A2重合时,长圆形退化为半径为r的圆。长圆形的形状由2a和r决定,而其位姿则完全由线段A1A2的位姿决定。工业应用中一般采用2a和r表示长圆孔的尺寸。
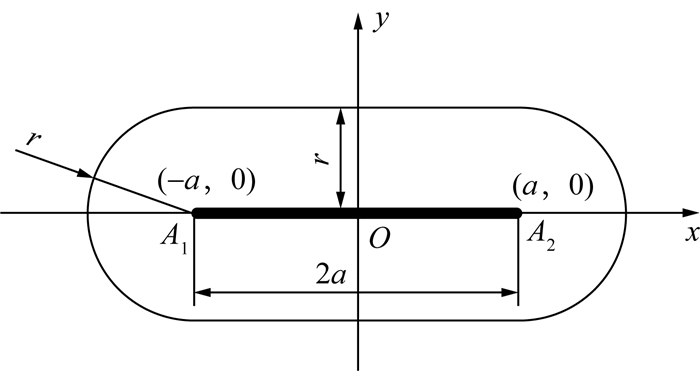
|
| 图 1 长圆孔示意图 |
在平面坐标系xOy中,图 1中长圆形对应的轨迹方程为
| $ \left(\frac{|x+a|+|x-a|-2 a}{2}\right)^2+y^2=r^2. $ | (2) |
结合长圆形的形状特征和式(2),可将长圆形描述为一种具有对称性、缺少简单解析表达的封闭图形。
对称性有助于长圆形在图形检测中具备很强的便利性,比如采用对称Hough变换等方法可以检测得到对称图形的对称轴。此外,长圆形的2个对称轴的交点是对称中心,同时也是检测定位算法的目标。长圆形的重心(或其内部区域的重心)与其对称中心重合。
封闭性也有助于长圆形的检测定位。结合长圆形的对称性,若可完整得到长圆形的封闭曲线,则可计算得到其中心;同时,基于边缘检测的限速搜索或聚类算法,以及Fourier变换[14],都可以对封闭曲线完成检测和描述。
常见的图形特征检测算法主要分为投票型和最优化2大类[15]。投票型的代表是Hough变换[16]和RANSAC[17]等,最优化的代表是最小二乘法。这些方法的共同特征是利用了几何图形的代数方程,例如圆的方程参数少且最高为2阶,而矩形可以被拆分为4条直线。然而,长圆形方程中含有绝对值符号(见式(2)),表现出较强非线性,为使用Hough变换和最小二乘法带来较大困难;若拆分长圆形,可得到2个半圆弧和2条线段,这些子图形不共享参数空间,难以采用与矩形类似的检测策略。
通过上述分析可以发现,长圆形的对称、封闭特征在识别和检测中可以作为重要参考,但拥有相同特征的图形较为常见,不足以将长圆孔从背景中准确识别,也不足以进行精确的检测定位;而精确描述长圆形的轨迹方程过于复杂,不能用传统的基于边缘检测或者散点的图形检测方法完成。基于长圆孔的上述特征,本文设计了一种基于深度学习语义分割网络和长圆形区域退化的视觉分割定位算法。
2 长圆孔视觉分割定位算法在本文所涉及的工业场景中,相机视野较大,同一视野中可能包含多个工件,目标长圆孔在视野中的面积占比可能较小,且其他工件的特征可能会干扰定位过程。因此,本文将长圆孔的定位分为语义分割和精准定位2个步骤。针对长圆孔相对复杂的图像特征,利用神经网络强大的非线性拟合能力,采用深度学习方法进行语义分割。考虑到语义分割的结果可能存在局部误差,本文结合传统图像检测算法和长圆形特征对分割结果进行处理,以实现对长圆孔的精确定位。
2.1 深度学习语义分割网络设计在本文的图像语义分割需求中,只需要分割长圆孔区域和背景。考虑到实际的装配结构利用长圆孔进行螺栓连接时,长圆孔尺寸相比整个装配件尺寸一般都比较小,因此长圆孔在整幅图像中的面积占比也就较小,这为语义分割增添了难度,具体表现在:1) 分割结果不仅容易受到复杂背景影响,而且当视野中存在多个长圆孔时难以进行完整分割;2) 相对较小的有效面积导致单纯的语义分割或者实例分割网络需要较多数据进行训练,且容易受噪声影响、推理有效性无法保证。
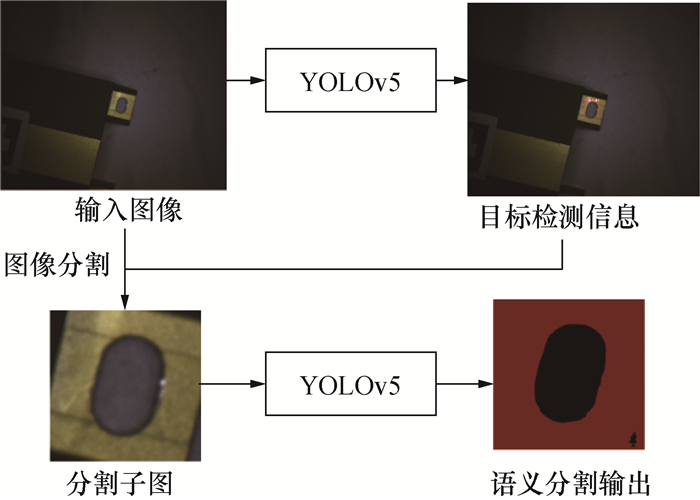
考虑到实际装配时的效率要求,语义分割网络需保证快速和轻量化,此外需具有一定程度的泛用性。基于上述需求,本小节提出了一种基于YOLO(you only look once)和全卷积神经网络(full convolutional net,FCN)串联网络架构的视觉检测分割技术方案。YOLO网络是用于目标检测的深度学习网络,其特点是牺牲一部分精度换取高效率的目标检测[18]并提取出感兴趣区域(region of interest, ROI)。FCN则是经典的语义分割方法,去掉全连接层以输出空间分割图[19],由于仅有卷积层,FCN可以接受不同的输入图像尺寸,但并不能高效地提取全局信息。
因此,本文提出将分割任务分为ROI提取和语义分割2步,设计了如图 2所示的深度学习语义分割框架。由图可知,首先由YOLO网络对输入尺寸为M×N的图像中的长圆孔目标进行目标检测形式的粗定位,完成后提取ROI,将提取的尺寸为n×n的ROI输入到串联的FCN网络中,在长圆孔面积占比更大的图像中完成语义分割,降低训练难度并提高鲁棒性。M、N由实施系统的相机硬件决定,n根据长圆孔与输入图像的比例灵活选取,一般比所拍摄长圆孔的最大像素的长度大20像素左右。FCN输出二值化图像,不同颜色分别代表长圆孔区域和背景,其尺寸为n×n。将其还原到原输入图像中,可以得到原图像中的长圆孔区域,经进一步处理完成长圆孔位置定位。
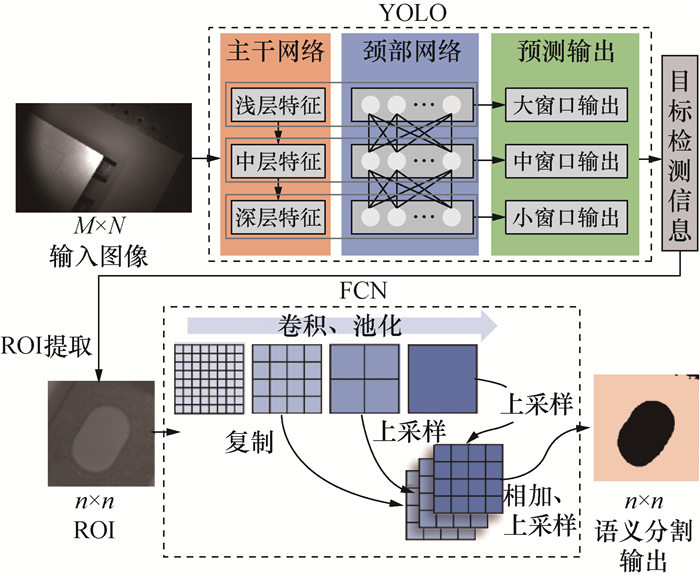
|
| 图 2 深度学习语义分割框架 |
2.2 长圆孔区域退化定位方法
长圆形具有中心对称特征,理论上FCN输出区域的重心就是定位所需的长圆孔中心。但在实际应用场景中,不仅环境和光照条件可能发生变化,而且训练环境和实际应用环境也可能不同,再加之FCN分割结果本身并不具有特别高的精度,分割结果很有可能出现一定程度的变形,如图 3所示,分别为提取的ROI和FCN的输出图像,对比可见FCN的输出图像只能大致保持长圆孔的形状,在中部线段的外形部分发生了弯曲变形。因此,为了在保证精度的同时提高算法的鲁棒性,本文根据长圆孔特有的几何特征设计了基于传统图像的定位算法。
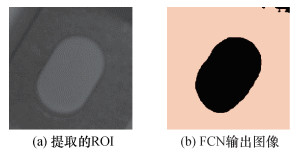
|
| 图 3 FCN分割变形例 |
长圆形可以由平面中的线段A1A2和给定距离r完全决定(见图 1)。对精确定位问题而言,定位长圆形与定位对应的线段A1A2等价。缩小r直至0,长圆形将会退化为线段A1A2。值得注意的是,这个退化过程是等距的。对长圆形内部区域,如果进行等距腐蚀,剩余区域会逼近线段A1A2。
将长圆形内部区域退化为线段A1A2后,可以采用现有的方法对其进行检测定位。注意到椭圆在长轴长度等于焦点距离时也退化为线段,因此现有的椭圆检测方法也大多可以用于检测线段。检测得到线段的中心即为长圆形的中心,这也是定位长圆孔所需。
将区域退化到线段,可以极大地降低区域边界上的形状变换和毛刺带来的影响。即使FCN输出的区域相对实际区域有所变形,但是退化等效于提取图像中的主要信息,在局部区域产生的较大变形,在退化后得到的线段上只会表现为几个像素的偏差,且这些偏差在后续线段检测过程中很容易被考虑并消除。
2.3 算法实现算法流程如图 4所示。图像输入1 920像素×1 200像素的单通道灰度图,其中长圆孔的最大尺寸不超过110像素。YOLO网络采用YOLOv5,FCN以ResNet-101作为主干网络。YOLO在进行目标检测时理想情况下会检测出长圆孔的最小外接矩形,但是长圆孔处于不同角度时占提取ROI的面积比例会有明显差异,因此统一ROI尺寸为128像素×128像素,中心即为YOLO输出的外接矩形的中心。
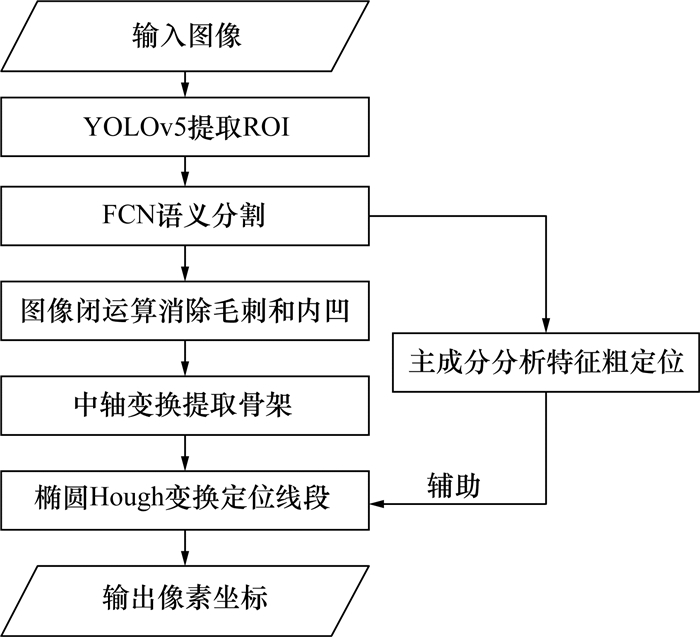
|
| 图 4 算法流程 |
YOLO和FCN的训练过程是分离的。YOLO网络完成训练后得到包含长圆孔的ROI数据集,在此数据集基础上完成FCN的训练。在推理时,同样利用YOLO的检测结果得到ROI输入到FCN中得到长圆孔的大致区域。FCN的输出可能包含多个连通域,本文只选取其中最大的连通域输入到后续算法中。
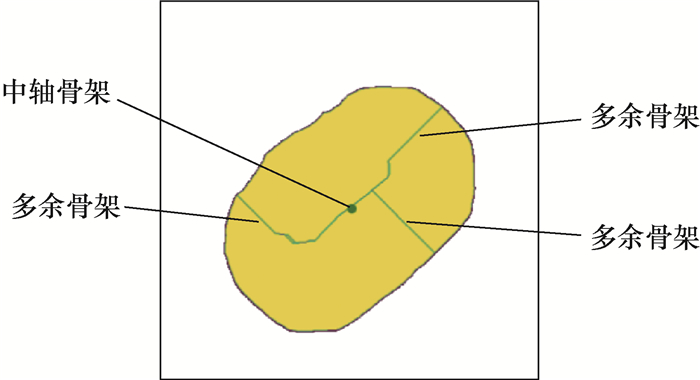
在进行长圆孔区域退化定位时,FCN输出的区域并非完美的长圆孔形状,直接采用像素腐蚀的方法可能会破坏区域连通性。退化过程与图像处理中的骨架提取过程类似,本文采用中轴变换骨架提取方法[20, 21]完成这一过程。对于由线段A1A2和距离r决定的长圆形的内部区域,采用中轴变换提取骨架得到的恰好是线段A1A2,符合退化需求。
如果FCN的输出变形过大、毛刺过多,对精度的影响并不大,但是会极大影响中轴算法提取效率,因此在输入到中轴算法之前,对FCN输出区域进行图像学闭运算,以消除部分毛刺和内凹变形。
利用椭圆Hough变换算法定位线段。对像素宽度为1的线段进行检测,会得到短轴长度为0的椭圆,并给出其中心和方向。
对FCN的实际输出进行中轴变换提取骨架,会因为毛刺产生多余骨架,如图 5所示。这些多余骨架会对后续的椭圆Hough变换造成影响,可能输出错误的线段中心。为了解决这一问题,本文将FCN输出的区域整体作为参考,对区域内所有像素点进行主成分分析(principal component analysis, PCA),得到长圆孔的大致中心O1和长对称轴偏角θ1。进行椭圆Hough变换时,在放宽投票阈值限制(实际中选择阈值为20)的情况下会得到多组椭圆参数,对这些椭圆的中心Oie和长轴偏角Oie进行筛选,筛选出满足式(3)且投票数最高的椭圆参数。
| $ \left\{\begin{array}{l} \left\|O_i^e-O_1\right\|_2<5, \\ \left|\theta_i^e-\theta_1\right|<0.1. \end{array}\right. $ | (3) |
|
| 图 5 中轴变换提取骨架 |
式(3)中,中心位置和长轴偏角的量纲分别为像素和弧度。式(3)描述的筛选条件一方面保证了椭圆Hough变换检测的线段不是毛刺引起的分支,另一方面也没有过度参考主成分分析的结果,影响算法本身的性能。经过PCA辅助筛选之后,可以明显降低Hough变换精确定位的误差。
2.4 模型训练与测试采用1 920像素×1 200像素尺寸的单通道相机对3个设备模拟件(编号为2、4、5,参数详见3.1节) 进行拍摄,采集得到像素精度为0.157 mm、共计491张图片的数据集,并以4∶1的比例划分训练集和测试集。实验系统配置为GPU GTX 1050Ti,显存为4 GB,CPU为i7-11700K,内存为16 GB。本文所提结合YOLOv5和FCN的语义分割网络与单纯的FCN以及实例分割算法Mask-RCNN的比较如表 1所示,从交并比(intersection over union,IoU)和推理时间2个方面进行比较。
由表 1可知,单纯使用FCN进行语义分割的精度较差,Mask-RCNN在精度和推理时间方面均略逊于本文所提的方法。这表明采用YOLOv5+FCN完成分割的方式,可避免长圆孔区域占图像比例过少带来的分割难度过大的问题,同时发挥2个网络的各自优势,在保证精度的同时实现轻量化和快速推理。
训练模型时,YOLOv5采用的批尺寸(batch size)为16,初始学习率为1×10-2,权重衰减(weight decay)为5×10-5,FCN采用的批尺寸为4,初始学习率为1×10-4,权重衰减为1×10-4。模型经过150轮(epoch)后收敛。采用测试集对3种算法定位长圆孔的精度进行测试和比较,对比的3种算法包括FCN直接输出长圆孔区域的重心、不使用PCA辅助的退化定位算法、使用PCA辅助的退化定位算法,结果如表 2所示。由表可知,有PCA辅助退化定位的算法的精度和稳定性都高于FCN直接输出区域的重心,且去掉PCA辅助后效果下降明显,这表明采用PCA退化定位算法对中轴算法和椭圆Hough算法检测结果进行大致定位,可以有效提高最终的长圆孔定位精度和稳定性;而且相比FCN输出区域重心给出的位置有更高的精度。需要说明的是,训练集和测试集的数据分布相似,在环境甚至硬件变化时算法的表现还需要综合实验的验证。
| 像素 | |||||||||||||||||||||||||||||
| 算法 | 平均误差 | 误差标准差 | |||||||||||||||||||||||||||
| FCN直接输出区域重心 | 0.910 | 0.696 | |||||||||||||||||||||||||||
| 无PCA辅助退化定位 | 1.723 | 3.630 | |||||||||||||||||||||||||||
| 有PCA辅助退化定位 | 0.860 | 0.540 | |||||||||||||||||||||||||||
3 综合实验
为了验证算法在实际应用环境中的适用性和应对环境变化的鲁棒性,进行了综合实验验证。假设设备模拟件各孔的计算定位位置相对于真实位置为独立同分布的零均值正态分布,则工件中心位置的计算定位位置相对于真实位置的分布为2个独立正态同分布的随机变量的平均值,其分布也为零均值正态分布,且标准差与单孔分布的标准差相同。因此单孔定位精度将会直接影响到综合实验的精度。
3.1 机器人自动装配实验系统机器人自动装配实验系统的硬件布置如图 6所示,包括待安装设备模拟件、框架基座、变位机、自动抓取装置和自动拧紧装置5个部分。该实验系统应完成设备模拟件在框架基座上的准确安装,其中,自动抓取设备由ABB 4600六自由度机械臂、力控手爪、2D视觉检测组件(包括海康MV-C5050-10UC相机、镜头和环形光源)组成,实现基于视觉和力觉的设备模拟件位姿自动检测和自动抓取。自动拧紧装置由ABB 2600六自由度机械臂、自动送钉装置和自动拧紧电批组成,实现设备模拟件与框架基座的自动连接。

|
| 图 6 综合实验环境 |
设备模拟件共6个,其外观如图 7所示,每个模拟件都设计有对称布置的至少4个长圆孔,用以实现与框架底座对应位置螺纹孔的机械连接。设备模拟件的尺寸和表面类型、长圆孔尺寸如表 3所示,其中,长圆孔尺寸采用图 1中的2a×r的形式表示。为便于描述,下文中将8.0 mm×3.5 mm的孔称为细长孔,将5.0 mm×4.0 mm的孔称为短粗孔。

|
| 图 7 待安装设备模拟件 |
| 编号 | 尺寸(长×宽)/(mm×mm) | 表面类型 | 所含长圆孔尺寸(2a×r)/(mm×mm) |
| 1 | 200×200 | 弱反光 | 8.0×3.5 |
| 2 | 219×196 | 强反光 | 8.0×3.5 |
| 3 | 256×176 | 强反光 | 8.0×3.5 |
| 4 | 140×105 | 弱反光 | 5.0×4.0 |
| 5 | 125×110 | 强反光 | 5.0×4.0 |
| 6 | 125×110 | 弱反光 | 5.0×4.0 |
该自动装配系统运行时,框架基座通过气动夹具准确固定在变位机上,并由变位机带动周向回转,以实现不同设备模拟件在框架基座正反面的安装;自动抓取装置首先视觉识别和检测待安装的设备模拟件类型和空间位姿,然后利用机械臂及其末端力控手爪实现对设备模拟件的抓取,并将设备模拟件准确放置在框架基座的指定位置;再利用自动拧紧装置完成设备模拟件在框架基座上的固定。
3.2 视觉分割定位算法部署实际批量装配生产中,常用二维码标识待装配设备类型和编号[22-23],故本系统设计的设备模拟件上也附有二维码(见图 7)。考虑到二维码在不同批次设备上的位置重复度不高,且设备在供料台上的位姿较为随意,因此本文首先利用二维码识别待装配设备模拟件的类型及其长圆孔的大致位置,保证抓取机械臂移动至待装配模拟件上方大致位置时,长圆孔特征能进入相机视野;然后利用本文所提的算法定位模拟件对角线上的2个长圆孔,再结合该设备模拟件的3D模型即可确定模拟件的准确位姿,以实现模拟件的自动抓取。
在工业部署视觉算法的需求中,如果算法对硬件环境具有较高的鲁棒性,那么可以在搭建的相似环境中提前完成训练,大幅减少部署时间;且硬件环境随需求发生改变时算法仍可使用,降低了应用门槛。本文所提算法采用了可接受任意尺寸输入的网络架构,为了验证算法对输入图像的鲁棒性,使用与采集训练数据集时不同的相机对算法进行实验。与训练数据集图像不同,实验环境中相机的输出图像尺寸为2 448像素×2 048像素,且为RGB三色通道,像素精度达到0.077 mm。考虑到不同的相机视野和长圆孔区域在图像中的面积占比,将YOLO目标检测辅助提取的ROI尺寸确定为256像素×256像素。设备模拟件的长圆孔形状分为细长和短粗2种,表面类型分为强反光和弱反光2种。基于上述设计可评估本文所提的算法是否具有足够的鲁棒性,并能适应各种工况,包括不同图像大小和通道、不同表面类型的设备模拟件表面。
3.3 实验设计尽管成批生产中待装配设备二维码的绝对位置精度低,但是二维码固定在设备上之后的位置是确定的,这使相机能以较高精度估计视野中二维码相对于相机的位姿,因此可以将二维码作为测量基准。同时,机械臂也具有较高的重复定位精度,可以作为测量基准。
下面以设备模拟件位姿检测为例,设计视觉定位实验流程如下:
1) 保持设备模拟件不动,机械臂引导相机观察二维码;
2) 根据二维码信息粗略估计长圆孔位置,移动相机分别拍摄位于对角的2个长圆孔;
3) 利用本文所提算法得到2个长圆孔的像素坐标;
4) 利用手眼标定关系得到长圆孔在机械臂坐标系下的坐标值,并确定设备模拟件位姿,计算得到机械臂抓取位姿;
5) 移动机械臂至抓取位置上方,记录此时的机械臂位姿和二维码位姿;
6) 每个设备模拟件重复8次上述过程。
上述流程中记录位姿的差异(第5步)可以体现本文所提算法和所选取基准的综合重复定位精度。多次实验后的误差由基准误差和定位算法误差共同引起。
3.4 实验结果分别统计不同长圆孔形状、不同设备模拟件表面类型情况下算法的综合重复定位精度,结果如表 4所示,将位置和角度分开计算,并采用3倍标准差作为综合重复定位精度值。机械臂自身的重复定位精度为0.05 mm,二维码的位置精度为0.129 mm,角度精度为0.044°。由表可知,算法对不同长圆孔形状、不同设备模拟件表面类型情况下的识别精度均较高,相比之下,算法对强反光表面的识别性能稍差。
| 设备模拟件类型 | 基于机械臂基准的精度 | 基于二维码基准的精度 | |||
| 位置/mm | 角度/(°) | 位置/mm | 角度/(°) | ||
| 弱反光表面 | 0.343 | 0.073 | 0.404 | 0.148 | |
| 强反光表面 | 0.409 | 0.102 | 0.812 | 0.122 | |
| 细长孔 | 0.310 | 0.078 | 0.353 | 0.222 | |
| 粗短孔 | 0.375 | 0.082 | 0.505 | 0.061 | |
以设备模拟件5为例的综合实验环境下的分割结果如图 8所示。由图可知,本文所提的分割算法正确分割出了长圆孔区域,表现良好。
|
| 图 8 综合实验分割结果例 |
此外,FCN输出的长圆孔区域如图 9所示,其变形情况比图 3中的FCN输出图像更为严重。FCN输出区域的重心与本文所提算法的输出坐标相差了2.52像素,而本文所提算法的输出与标定结果的平均差距为1.05像素。这表明虽然在测试集中本文所提算法仅有微弱的优势(见表 2),但在应用于不同尺寸的相机输入、不同尺寸的长圆孔、不同表面类型的设备模拟件时,本文所提算法在鲁棒性上具有明显优势,可以极大减弱FCN输出区域变形带来的影响,保持较高的精度水平。

|
| 图 9 综合实验中FCN分割变形例 |
4 结论
本文分析了长圆孔特征,结合深度学习和传统图像算法设计了长圆孔的视觉分割定位算法,主要结论如下:
1) 在数据集中完成训练后,本文所提视觉分割定位算法精度能够达到亚像素级水平,且具有较高的稳定性;改变图像尺寸、图像通道数、拍摄环境和设备模拟件表面反光特性后,深度学习网络的输出变形会很大,但是本文所提算法仍能够保持在像素级精度,具有较高鲁棒性。本文所提算法对长圆孔定位应用具有较高的指导意义和实用价值。
2) 综合深度学习和传统图像算法可以解决异形目标的分割定位问题。利用深度学习算法提取对象的高度非线性化特征,并结合传统图像算法进行后续处理,可以显著提高检测精度和鲁棒性。
3) 本文所提视觉分割定位算法框架和区域退化定位方法从原理上具有普遍意义,可推广到其他具有正交对称轴的图形特征定位。
| [1] |
AKINLAR C, TOPAL C. EDCircles: A real-time circle detector with a false detection control[J]. Pattern Recognition, 2013, 46(3): 725-740. DOI:10.1016/j.patcog.2012.09.020 |
| [2] |
MUKHOPADHYAY P, CHAUDHURI B B. A survey of Hough transform[J]. Pattern Recognition, 2015, 48(3): 993-1010. DOI:10.1016/j.patcog.2014.08.027 |
| [3] |
TOPAL C, AKINLAR C. Edge Drawing: A combined real-time edge and segment detector[J]. Journal of Visual Communication and Image Representation, 2012, 23(6): 862-872. DOI:10.1016/j.jvcir.2012.05.004 |
| [4] |
ZHOU B, HE Y. Fast circle detection using spatial decomposition of Hough transform[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2017, 31(3): 1755006. DOI:10.1142/S0218001417550060 |
| [5] |
刘艳霞. 封闭图形对称轴的研究与应用[D]. 长春: 吉林大学, 2015. LIU Y X. Symmetry axis research and application for closed graph[D]. Changchun: Jilin University, 2015. (in Chinese) |
| [6] |
李晓磊, 潘晋孝, 刘宾, 等. 基于Hough算法的图像对称轴检测(英文)[J]. 测试科学与仪器, 2015, 6(4): 342-346. LI X L, PAN J X, LIU B, et al. Symmetric axis detection for images based on Hough algorithm[J]. Journal of Measurement Science and Instrumentation, 2015, 6(4): 342-346. (in Chinese) |
| [7] |
SUZUKI S, BE K. Topological structural analysis of digitized binary images by border following[J]. Computer Vision, Graphics, and Image Processing, 1985, 30(1): 32-46. DOI:10.1016/0734-189X(85)90016-7 |
| [8] |
彭正初. 基于傅里叶描述子的物体形状识别的研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. PENG Z C. Research on object shape recognition based on Fourier descriptors[D]. Harbin: Harbin Institute of Technology, 2016. (in Chinese) |
| [9] |
LOWE D G. Object recognition from local scale-invariant features[C]// Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra, Greece: IEEE, 1999: 1150-1157.
|
| [10] |
刘立, 詹茵茵, 罗扬, 等. 尺度不变特征变换算子综述[J]. 中国图象图形学报, 2013, 18(8): 885-892. LIU L, ZHAN Y Y, LUO Y, et al. Summarization of the scale invariant feature transform[J]. Journal of Image and Graphics, 2013, 18(8): 885-892. (in Chinese) |
| [11] |
刘强, 段富海, 桑勇, 等. 复杂环境下视觉SLAM闭环检测方法综述[J]. 机器人, 2019, 41(1): 112-123, 136. LIU Q, DUAN F H, SANG Y, et al. A survey of loop-closure detection method of visual SLAM in complex environments[J]. Robot, 2019, 41(1): 112-123, 136. (in Chinese) |
| [12] |
LONG C R, LIU P, HU Q L. Ellipse fitting based on neural network optimization[C]// 2022 41st Chinese Control Conference (CCC). Hefei, China: IEEE, 2022: 467-471.
|
| [13] |
MINAEE S, BOYKOV Y, PORIKLI F, et al. Image segmentation using deep learning: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(7): 3523-3542. |
| [14] |
王斌. 一种基于多级弦长函数的傅立叶形状描述子[J]. 计算机学报, 2010, 33(12): 2387-2396. WANG B. A Fourier shape descriptor based on multi-level chord length function[J]. Chinese Journal of Computers, 2010, 33(12): 2387-2396. (in Chinese) |
| [15] |
陈海峰. 数字图像中基本几何形状检测算法的研究与应用[D]. 杭州: 浙江大学, 2007. CHEN H F. Research on the basic geometric shapes detection in digital images and the application[D]. Hangzhou: Zhejiang University, 2007. (in Chinese) |
| [16] |
HOUGH P V C. Method and means for recognizing complex patterns: US3069654[P]. 1962-12-18.
|
| [17] |
FISCHLER M A, BOLLES R C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 |
| [18] |
REDMON J, DIVVALA S, GIRSHICK R, et al. You only look once: Unified, real-time object detection[C]// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA: IEEE, 2016: 779-788.
|
| [19] |
LONG J, SHELHAMER E, DARRELL T, et al. Fully convolutional networks for semantic segmentation[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA: IEEE, 2015: 3431-3440.
|
| [20] |
LEE D T. Medial axis transformation of a planar shape[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1982, PAMI-4(4): 363-369. DOI:10.1109/TPAMI.1982.4767267 |
| [21] |
史聪伟, 赵杰煜, 常俊生. 基于中轴变换的骨架特征提取算法[J]. 计算机工程, 2019, 45(7): 242-250. SHI C W, ZHAO J Y, CHANG J S. Skeleton feature extraction algorithm based on medial axis transformation[J]. Computer Engineering, 2019, 45(7): 242-250. (in Chinese) |
| [22] |
GARRIDO-JURADO S, MUÑOZ-SALINAS R, MADRID-CUEVAS F J, et al. Automatic generation and detection of highly reliable fiducial markers under occlusion[J]. Pattern Recognition, 2014, 47(6): 2280-2292. DOI:10.1016/j.patcog.2014.01.005 |
| [23] |
GARRIDO-JURADO S, MUÑOZ-SALINAS R, MADRID-CUEVAS F J, et al. Generation of fiducial marker dictionaries using Mixed Integer Linear Programming[J]. Pattern Recognition, 2016, 51: 481-491. DOI:10.1016/j.patcog.2015.09.023 |



