机器人在康复医疗、推拿按摩等领域具有较大发展潜力,近年来与人体直接接触作业机器人成为学者们研究的热点[1]。人机接触运动时,皮肤表面的法向力会引起皮肤局部组织凹陷或隆起[2]。在切向摩擦力作用下,皮肤的黏着性导致皮肤表面出现拉伸和堆积形变[3-4]。皮肤拉伸形变会引起人体不适,严重时损伤皮肤;皮肤堆积形变会改变机器人预期的轨迹位姿,增加运动阻力。
目前,研究者多关注法向力作用下的皮肤形变和控制。文[5-6]研究了手臂和面部中法向力与皮肤形变的关系;Cordier等[7]采用集成皮肤系统模拟人机法向接触时皮肤的形变。研究方法的准确性由所选的动力学模型决定,常见的皮肤动力学模型包括线性Kelvin-Boltzmann[8]、Kelvin-Voigt[9]和非线性Hunt-Crossley[10]模型。对于切向力与皮肤形变的关系,目前尚无计算模型,一般借助散斑、红外光成像等实验技术获取二者的关系。Maiti等[11]利用散斑成像技术获取皮肤拉伸形变信息;Cha等[12]利用红外光和散斑成像技术测量拉伸应变引起的皮肤法向和切向二维形变。散斑成像技术受光源、距离等环境因素影响;同时,随着形变区域远离相机监测范围,形变监测的准确性逐渐降低。
现有文献中关于皮肤堆积效应的研究较少。Guan等[13]使用光学系统捕捉皮肤的堆积效应信息,该试验中探头与皮肤接触区域在平面上呈双椭圆形,表明探头与皮肤的滑动摩擦过程中存在皮肤堆积形变。Kwiatkowska等[14]在滑动试验中考虑皮肤堆积效应,测量了法向和切向的皮肤形变,但未研究皮肤形变的曲面形状。
皮肤复杂的生物力学特性和多变的作业环境,给人机接触运动中切向摩擦力与皮肤拉伸和堆积形变建模带来挑战。真实作业环境下的数字化仿真模型是有效的解决方案,可为作业参数选择和皮肤路径规划提供前馈信息。常见的仿真模型包括有限元模型(finite element model, FEM)和质点-弹簧-阻尼(mass-spring-damper, MSD)模型。文[15-16]基于FEM模拟皮肤表面皱纹形变;Panchal等[17]通过FEM获取由振动引起的皮肤模态形状和固有频率信息,监测皮肤健康状况。FEM将皮肤分割为有限单元,无法准确捕捉皮肤内部微观结构和非线性行为。此外,由于大量的运算对计算资源和时间要求较高,因此,FEM在实时模拟或大规模应用中面临挑战[18]。MSD模型将皮肤离散为质点,质点间通过弹簧和阻尼连接,模拟皮肤的黏弹性。MSD模型计算简单快速,对计算资源和时间要求较低,在实时模拟皮肤形变方面具有优势。MSD模型已在布料折叠、拉伸形变模拟[19-20]和肝脏虚拟手术切口形变仿真[21]等领域得到应用。然而,与布料和肝脏等匀质组织不同,皮肤具有复杂多层结构,在体试验通常受皮下脂肪和骨骼的影响。
针对上述问题,本文提出一种基于皮肤黏滑摩擦机理的多层MSD模型,模拟不同作业环境中皮肤的实时三维形变。
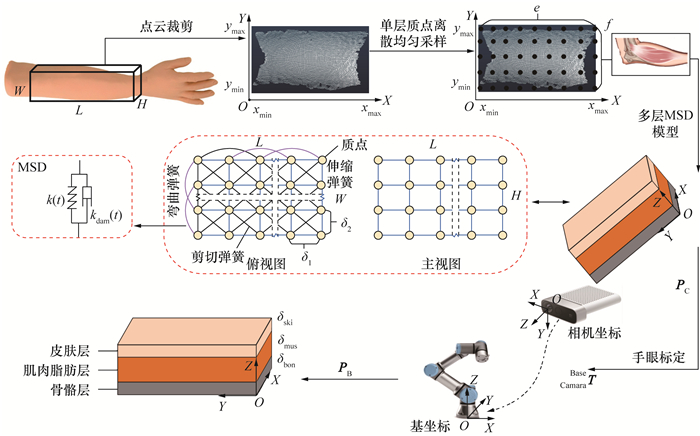
1 建立皮肤MSD模型皮肤下分布有肌肉和脂肪组织,肌肉影响皮肤弹性和表面张力,脂肪能缓冲由外力引起的皮肤形变。肌肉和脂肪下的骨骼具有支撑和约束皮肤形变作用。由于肌肉和脂肪相互包围,难以区分,因此,为简化皮肤三维形变仿真模型,把肌肉和脂肪统称为肌肉脂肪,并提出皮肤、肌肉脂肪、骨骼3层MSD模型,模拟皮肤受外力后的表面三维形变。皮肤、肌肉脂肪和骨骼的厚度分别为δski、δmus和δbon,MSD模型建立过程如图 1所示。首先,对相机获取的长、宽、高分别为L、W、H的作业区域的点云进行滤波和裁剪,获取点云集合PC={PC1, PC2, …, PCn},其中PCi=(xi, yi, zi), i=1, 2, …, n,为PC中第i个点在X、Y和Z轴方向的坐标。结合式(1)确定MSD模型在X和Y方向的边界位置分别为xmin、xmax和ymin、ymax。由于皮肤表面为曲面,因此,MSD模型的皮肤层边界位置zmean为PC在Z方向的平均值,肌肉脂肪和骨骼层质点在Z方向的边界位置分别为zmean-δski和zmean-(δski+δmus),各边界位置表示如下:
| $ \begin{align*} & x_{\min }=\min \left(x_{1}, x_{2}, \cdots, x_{n}\right), \\ & x_{\max }=\max \left(x_{1}, x_{2}, \cdots, x_{n}\right), \\ & y_{\min }=\min \left(y_{1}, y_{2}, \cdots, y_{n}\right), \\ & y_{\max }=\max \left(y_{1}, y_{2}, \cdots, y_{n}\right), \\ & z_{\operatorname{mean}}=\left(z_{1}+z_{2}+\cdots+z_{n}\right) / n. \end{align*} $ | (1) |
|
| 图 1 皮肤MSD模型建立过程 |
在式(1)确定的边界范围内对每一层X、Y进行均匀采样,获取的质点数分别为e、f,相邻质点间距分别为δ1、δ2,各质点质量均为m。结合手眼标定获得转换矩阵CamaraBaseT,并获取质点在基坐标系中位置PB,表示如下:
| $ \boldsymbol{P}_{\mathrm{B}}={ }_{\text {Camare }}^{\text {Base }} \boldsymbol{T} \boldsymbol{P}_{\mathrm{C}} . $ | (2) |
MSD模型中第l层r行c列质点所处位置PBlrc=(xlrc, ylrc, zlrc),表示如下:
| $ \begin{gather*} x_{l r c}=x_{\min }+\left(x_{\max }-x_{\min }\right) c / e; \\ y_{l r c}=y_{\min }+\left(y_{\max }-y_{\min }\right) r / f ; \\ z_{l r c}= \begin{cases}z_{\text {mean }}, & l=1; \\ z_{\text {mean }}-\delta_{s \mathrm{ski}}, & l=2; \\ z_{\text {mean }}-\left(\delta_{\text {ski }}+\delta_{\text {mus }}\right), & l=3.\end{cases} \end{gather*} $ | (3) |
MSD模型中质点间通过弹性系数k(t)与阻尼系数kdam(t)并联的弹簧相互连接。弹簧有伸缩、弯曲和剪切3种类型,分别代表物理世界中用于维持皮肤稳定状态的3种力。由于皮肤、肌肉脂肪和骨骼层的力学性能具有差异性,因此机器人在作业过程中不同部位的k(t)和kdam(t)随时间t变化。MSD模型中各层k(t)依据式(4)[22]确定,表示如下:
| $ k(t)=\frac{1+\nu}{1-\nu} \cdot \frac{E A}{\delta_{\mathrm{ini}}} . $ | (4) |
其中: ν为Poisson比,通常ν=0.5[14, 23];E为各层组织的弹性模量;A为末端执行器与皮肤接触部分的面积,依据Hertz模型[23]计算;δini为弹簧初始长度,即MSD模型中相邻质点间的距离。
2 皮肤生物力学模型 2.1 改进的皮肤黏弹力学模型常用的皮肤动力学模型为弹簧与阻尼并联的Kelvin-Voigt模型,其力与形变位移关系表示如下:
| $ \boldsymbol{F}=-k(t) \Delta \boldsymbol{x}(t)+k_{\mathrm{dam}}(t) \frac{\mathrm{d} \Delta \boldsymbol{x}(t)}{\mathrm{d} t} . $ | (5) |
其中:F为软组织受到的合力;Δx(t)为t时刻的弹簧伸缩量。该模型通过质点位置更新模拟皮肤形变,MSD模型中弹簧施加于各质点的力由式(5)确定。然而实际人机接触时,由于皮肤的黏弹特性和存在肌纤维,皮肤与肌肉脂肪的阻尼比较大,且外力消失后,皮肤形变恢复的速率随质点速度变化而变化,可知皮肤与肌肉脂肪的阻尼比并不固定,因此对非骨骼层引入阻尼算法,通过质点速度衰减模拟皮肤的黏滞性,具体计算步骤如下。
1) 由质点j的位置PBj=(xj, yj, zj),速度vj计算该层全局旋转中心PBcm和全局速度vcm,表示如下:
| $ \boldsymbol{P}_{\mathrm{B}}^{\mathrm{cm}}=\left(\sum\limits_{j} \boldsymbol{P}_{\mathrm{B} j} m\right) /\left(\sum\limits_{j} m\right), $ | (6) |
| $ \boldsymbol{v}_{\mathrm{cm}}=\left(\sum\limits_{j} \boldsymbol{v}_{j} m\right) /\left(\sum\limits_{j} m\right) . $ | (7) |
2) 计算质点j至旋转中心的距离rj,以及MSD模型中的角动量L、转动惯量I和角速度ω。表示如下:
| $ \boldsymbol{r}_{j}=\boldsymbol{P}_{\mathrm{B} j}-\boldsymbol{P}_{\mathrm{B}}^{\mathrm{cm}} , $ | (8) |
| $ \boldsymbol{L}=\sum\limits_{j} \boldsymbol{r}_{j}\left(m \boldsymbol{v}_{j}\right) , $ | (9) |
| $ \boldsymbol{I}=\sum\limits_{j} \boldsymbol{r}_{j}^{2} m , $ | (10) |
| $ \boldsymbol{\omega}=\boldsymbol{I}^{-1} \boldsymbol{L} . $ | (11) |
3) 计算质点j的速度偏差Δvj和阻尼速度vjdam,分别表示如下:
| $ \Delta \boldsymbol{v}_{j}=\boldsymbol{v}_{\mathrm{cm}}+\boldsymbol{\omega} \boldsymbol{r}_{j}-\boldsymbol{v}_{j} , $ | (12) |
| $ \boldsymbol{v}_{j}^{\mathrm{dam}}=\boldsymbol{v}_{j}+k_{\mathrm{dam}}(t) \Delta \boldsymbol{v}_{j} . $ | (13) |
其中vjdam由vj衰减后获得。
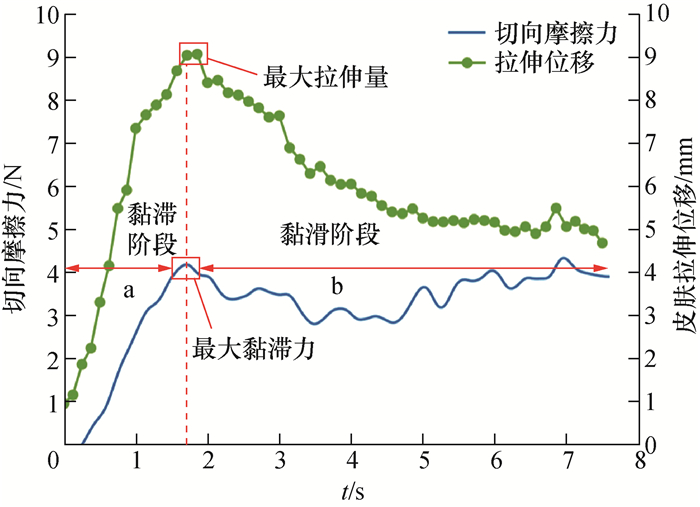
2.2 皮肤黏滑摩擦机理刚体-柔性接触中,由于皮肤具有黏弹性,因此,末端执行器与皮肤间的切向摩擦力变化复杂。在法向力Fnor的大小为5 N,作业速度为10 mm/s工况下,借助散斑成像技术获取切向摩擦力与皮肤形变的关系,如图 2所示。当法向载荷保持恒定时,皮肤切向摩擦力经历黏滞和黏滑2个阶段,其中黏滑阶段又有滑动和黏滞2种状态。阶段a为黏滞阶段,皮肤拉伸形变和切向摩擦力同时增加至最大值,此时皮肤与执行器一起移动,执行器前方皮肤堆积,后方皮肤持续拉伸;阶段b为黏滑阶段,由于皮肤与执行器间相对滑动,因此执行器前方堆积的皮肤得到释放,皮肤拉伸形变不断减小,切向摩擦力下降并在一定范围内波动。从微观角度分析,由于皮肤与执行器间微凸体高度不一致,因此只有部分微凸体接触。微凸体接触面积越大,黏着力越大。当施加于皮肤的切向载荷大于最大黏着力时,微凸体间发生相对滑动,进入黏滑(滑动)阶段;反之,微凸体间保持相对静止,处于黏滑(黏滞)阶段。
|
| 图 2 切向摩擦力与皮肤形变关系 |
2.3 皮肤黏滑摩擦MSD模型
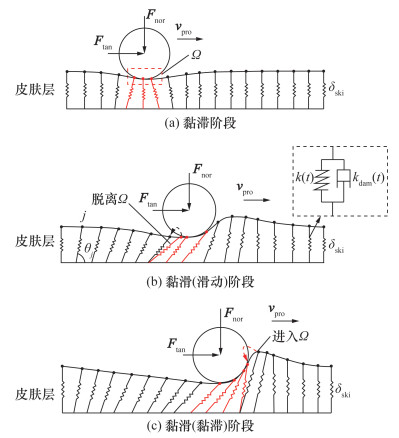
基于皮肤黏滑摩擦机理,建立皮肤黏滑摩擦下的MSD模型,如图 3所示。半径为R的末端执行器在皮肤表面施加法向力Fnor,并以速度vpro移动,产生切向摩擦力Ftan,与皮肤层接触的质点集合为Ω,黏滑(黏滞)和黏滑(滑动)临界摩擦力Ffri[24]表示如下:
| $ \boldsymbol{F}_{\text {fri }}=\pi \cdot \tau_{0}\left(\frac{3 R}{4 E_{\mathrm{ski}}}\right)^{2 / 3} \boldsymbol{F}_{\text {nor }}^{2 / 3}+\alpha \boldsymbol{F}_{\text {nor }}, $ | (14) |
| $ \begin{gathered} \boldsymbol{F}_{\mathrm{tan}}=\eta \sum\limits_{j \in \varOmega}\left(-k_{\text {ski}j }(t) \Delta \boldsymbol{x}_{j}(t)+\right. \\ \left.k_{\mathrm{dam}}(t) \frac{\mathrm{d} \Delta \boldsymbol{x}_{j}(t)}{\mathrm{d} t}\right) \cos \theta_{j} . \end{gathered} $ | (15) |
|
| 图 3 弹簧阻尼质点的黏滑摩擦状态 |
其中:τ0、α为待拟合参数;Eski为皮肤层的有效弹性模量;Ftan为Ω中质点所受弹簧力的切向分力总和;η为等效系数,可避免皮肤层中质点个数影响切向力计算;kskij(t)和θj分别为t时刻与皮肤层质点j相连弹簧的弹性系数和该弹簧与探头移动方向投影之间的夹角。
初始状态满足|Ftan|<|Ffri|,末端执行器与皮肤间摩擦处于黏滞状态,如图 3a所示。Ω中质点随执行器一起移动,与Ω中质点相连的弹簧长度逐渐增大,此外,该阶段作业过程中不断有新质点加入Ω,导致Ftan逐渐增大。当|Ftan|≥|Ffri|时,进入黏滑(滑动)摩擦阶段,Ω中质点逐渐沿执行器表面滑动,直至脱离Ω,如图 3b所示,该过程中Ftan逐渐减小;当|Ftan|<|Ffri|时,进入黏滑(黏滞)摩擦阶段,如图 3c所示。执行器在皮肤层表面移动过程中,Ftan不断波动,摩擦状态在黏滑(滑动)和黏滑(黏滞)间交替发生。
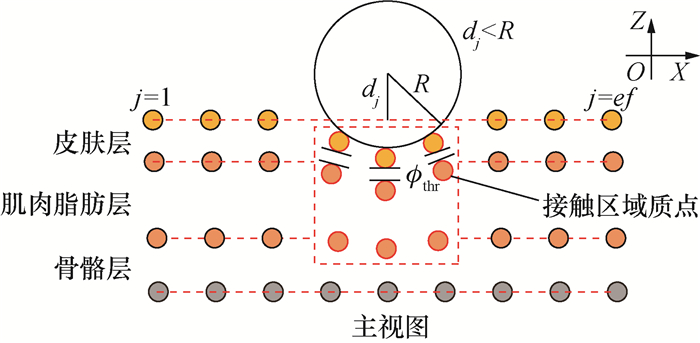
3 皮肤形变MSD仿真 3.1 人机接触区域碰撞检测仿真过程为避免发生穿透现象,需对末端执行器和MSD模型进行碰撞检测。人机接触检测如图 4所示,末端执行器球心与模型中质点j的距离为dj。若dj≥R,执行器与质点j接触;反之,则不接触。末端执行器沿法向运动,当末端执行器与MSD模型发生碰撞时,由位置动力学约束,接触区域质点在法向力作用下随末端执行器一起移动至合适位置。碰撞检测除检测探头与皮肤层质点间的接触外,还需检测各层质点间的自接触,避免皮肤层穿透肌肉脂肪层或骨骼层。当皮肤层质点与肌肉脂肪层质点的距离小于安全阈值ϕthr时,肌肉脂肪层对应的质点沿当前速度移动至安全位置。由于骨骼层质点固定,因此当肌肉脂肪层质点与骨骼层质点的距离小于ϕthr时,肌肉脂肪层对应的质点沿与当前速度相反方向移动至安全位置。
|
| 图 4 人机接触检测示意图 |
3.2 建立皮肤MSD模型动力学方程
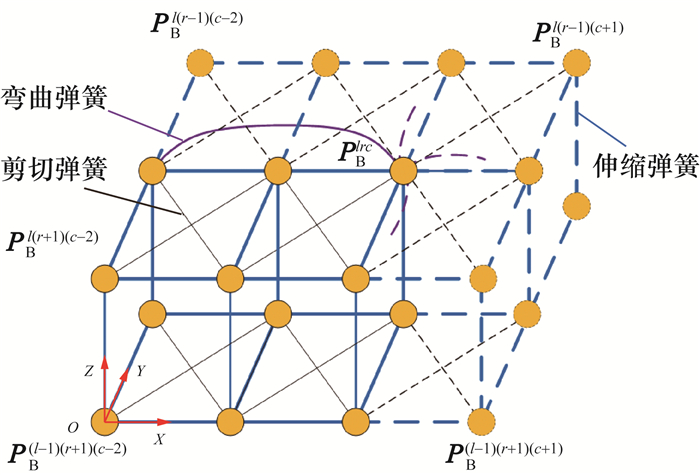
皮肤MSD模型模拟过程需要对各质点建立动力学方程,通过求解动力学方程更新质点位置信息。MSD模型中质点空间位置关系如图 5所示,质点j的位置为PBlrc时,通过伸缩、剪切和弯曲弹簧与相邻质点连接,由Kelvin-Voigt模型可知,该质点合力Fj表示如下:
| $ \boldsymbol{F}_{j}=\sum\limits_{j}\left(-k_{j}(t) \Delta \boldsymbol{x}_{j}(t)+k_{\mathrm{dam} j}(t) \frac{\mathrm{d} \Delta \boldsymbol{x}_{j}(t)}{\mathrm{d} t}\right) . $ | (16) |
|
| 图 5 MSD模型中质点空间位置关系 |
其中:kj(t)、Δxj(t)和kdamj(t)分别为t时刻与质点j相连的弹簧弹性系数、伸缩量和阻尼系数。
质点j下一时刻tnex的速度vj(tnex)和加速度aj(tnex)表示如下:
| $ \boldsymbol{v}_{j}\left(t_{\mathrm{nex}}\right)=\frac{\mathrm{d} \boldsymbol{P}_{\mathrm{B} j}\left(t_{\mathrm{nex}}\right)}{\mathrm{d} t} , $ | (17) |
| $ \boldsymbol{a}_{j}\left(t_{\mathrm{nex}}\right)=\frac{\mathrm{d}^{2} \boldsymbol{P}_{\mathrm{B} j}\left(t_{\mathrm{nex}}\right)}{\mathrm{d} t^{2}} . $ | (18) |
由2.1节中的阻尼算法可得到该质点衰减后速度vjdam(tnex),依据Newton第二定律,可得到力与质点运动状态的二阶常系数微分方程,表示如下:
| $ \boldsymbol{F}_{j}=m \frac{\mathrm{~d}^{2} \boldsymbol{P}_{\mathrm{B} j}\left(t_{\mathrm{nex}}\right)}{\mathrm{d} t^{2}} . $ | (19) |
半隐式Euler积分法将式(19)转换为2个一阶常系数微分方程,通过迭代求解得到PBj(tnex)。同理可对其他质点建立相应的动力学方程,通过微分方程求解得到其他质点各时刻稳定状态下的位置信息。
3.3 皮肤形变仿真基于多层MSD模型搭建的皮肤形变仿真系统如图 6所示,用C++开发语言、OpenGL仿真图形程序接口搭建系统。系统搭建分为前期处理和后期仿真2个阶段:前期处理的目的是结合视觉方法定位作业区域,通过试验采集的应力σ和应变ε数据确定MSD模型弹簧和阻尼参数,其中b为σ与ε相关系数;后期仿真输入实际作业中的Fnor、R和vpro,通过动力学方程求解质点稳定状态下的位置信息,然后对皮肤层质点进行拟合得到皮肤形变信息。Δzini是Fnor作用下的法向形变位移,可由皮肤法向动力学模型确定。

|
| 图 6 皮肤形变仿真系统总流程图 |
4 仿真试验与讨论 4.1 仿真试验
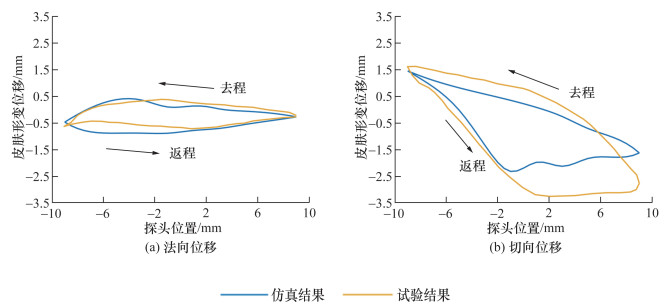
为验证MSD模型的准确性,以文[14]所述试验条件和数据进行仿真试验,监测球形探头在皮肤表面单程17.6 mm的往复直线滑动过程中某定点运动的法向和切向形变位移变化,仿真结果如图 7所示。仿真误差如表 1所示,法向方向仿真精度较高,平均误差为0.157 mm,最大误差为0.437 mm;切向方向与文[14]试验结果整体趋势一致,平均误差为0.562 mm,最大误差为1.141 mm。切向误差比法向误差较大的主要原因是文[14]仅提供了一个皮肤等效弹性模量,建模时忽略了皮肤法向和切向的各向异性,且在MSD模型参数确定时假设皮肤层、肌肉脂肪层和骨骼层具有相同的力学性能。
|
| 图 7 皮肤形变位移仿真结果 |
| mm | |||||||||||||||||||||||||||||
| 方向 | 去程 | 返程 | 总路程 | ||||||||||||||||||||||||||
| 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | |||||||||||||||||||||
| 切向 | 1.141 | 0 | 0.448 | 1.141 | 0.010 | 0.676 | 1.141 | 0 | 0.562 | ||||||||||||||||||||
| 法向 | 0.277 | 0.022 | 0.131 | 0.437 | 0.010 | 0.183 | 0.437 | 0.010 | 0.157 | ||||||||||||||||||||
4.2 机器人手臂按摩形变试验 4.2.1 试验平台
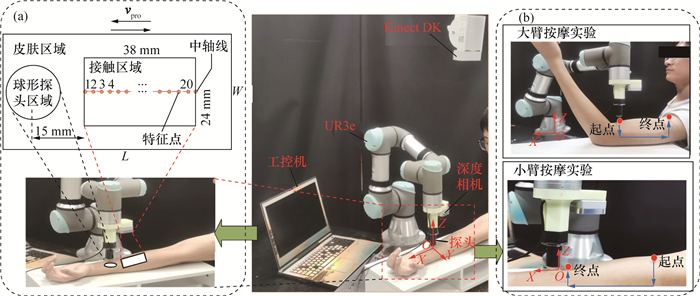
为进一步验证MSD模型的准确性,搭建如图 8所示的机器人手臂按摩试验平台。工控机为Windows 10 64位操作系统,搭载i5-7300 CPU(central processing unit)。机械臂选用UR3e协作机器人,末端配置R为10 mm的半球形探头,并搭载Intel RealSense D405短程深度相机,获取作业中曲面三维点云信息。Microsoft Azure Kinect DK相机用于确定作业区域位置信息。选择24岁健康成年男性的小臂和大臂内侧区域进行机器人按摩试验,分别测量皮肤拉伸和堆积形变。形变误差分析区域如图 8中a区域所示,考虑末端深度相机和探头接触皮肤时被遮挡,选取距探头前进的前方或后方15 mm处的38 mm×24 mm区域进行堆积或拉伸形变分析。按摩试验区域如图 8中b区域所示。初始时刻探头未与皮肤接触,随后探头沿Z方向下探,当Fnor的大小为5 N时,机器人保持Fnor不变,探头以1 mm/s的速度沿X方向移动,行程为100 mm。
|
| 图 8 试验平台 |
参考文[25]确定δski、δmus、δbon分别为8、12、8 mm,参考文[26]确定对应的等效弹性模量Eski、Emus和Ebon,并依据式(4)确定MSD模型中各层弹性系数kski(t)、kmus(t)和kbon(t)。由于骨骼层黏弹性相对其他层可忽略,因此骨骼层kdam(t)=0,其他层kdam(t)通过试验确定,具体参数如表 2所示。
| 参数 | 大臂 | 小臂 |
| L·W·H/(mm×mm×mm) | 200×80×28 | 200×80×28 |
| δski、δmus、δbon/mm | 8、12、8 | 8、12、8 |
| δ1、δ2/mm | 4、4 | 4、4 |
| m/kg | 0.001 | 0.001 |
| kdam(t) | 0.65 | 0.65 |
| Eski、Emus、Ebon/kPa | 20.25、55.00、116.36 | 10.46、37.33、116.36 |
| kski(t)、kmus(t)、kbon(t)/(N·m-1) | 2 400、4 300、13 700 | 1 230、2 930、13 700 |
| |vpro|/(mm·s-1) | 1 | -1 |
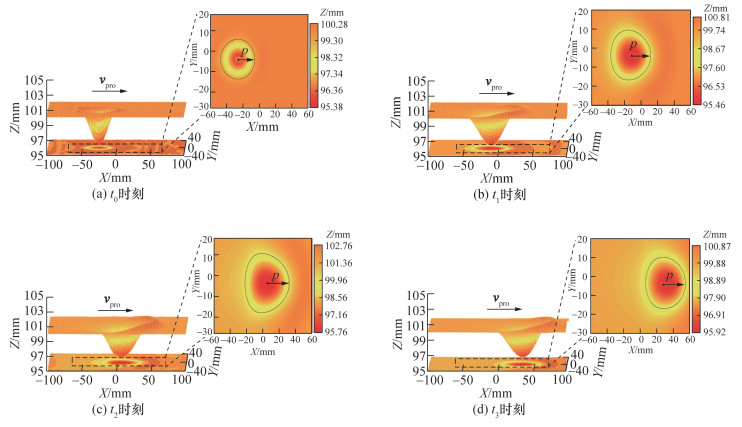
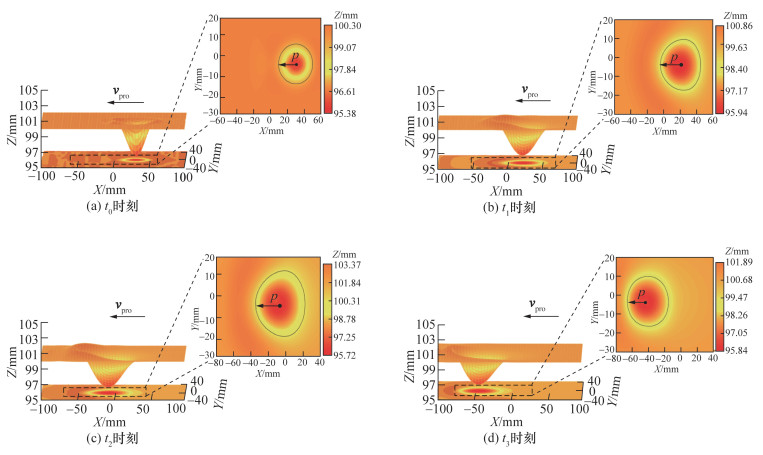
小臂和大臂按摩仿真试验中4个时刻的结果如图 9和10所示。t0为末端执行器下压达Fnor大小为5 N时刻,此时探头与皮肤接触区域呈单椭圆形,表征皮肤的各向异性,随着探头移动,皮肤的拉伸和堆积形变逐渐增加,探头与皮肤接触区域在平面上呈双椭圆形,并且在移动方向上椭圆短轴轴长p逐渐增大,该现象与文[13]中通过内窥镜观察的接触区域皮肤形状一致;t2时刻形变达到最大;在t2—t3时刻皮肤处于黏滑状态,该阶段皮肤形变有所释放,p逐渐减小,仿真结果符合实际人机接触运动下的皮肤摩擦形变机理。
|
| 图 9 小臂按摩试验中皮肤层仿真结果 |
|
| 图 10 大臂按摩试验中皮肤层仿真结果 |
4.2.2 试验误差
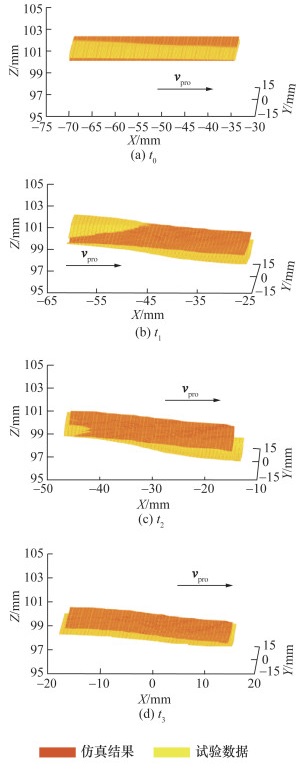
为进一步分析形变误差,分别截取相同区域的质点和点云信息进行分析。针对相机和环境因素引起的误差,先通过滤波处理去除噪声,再通过ICP(iterative closest point)配准对齐点云和质点位置信息。处理后的质点和点云经过3次样条插值进行曲面拟合,试验结果如图 11和12所示。
|
| 图 11 小臂按摩试验各时刻误差区域曲面结果 |
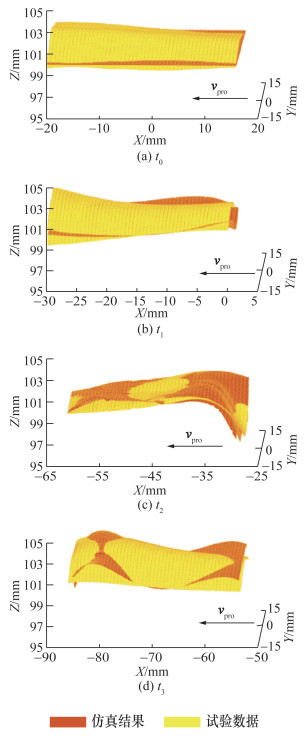
|
| 图 12 大臂按摩试验各时刻误差区域曲面结果 |
小臂按摩试验中皮肤在Y方向基本不发生形变,X、Z方向的形变分别由运动方向的切向力和探头下压引起。大臂按摩试验中由于皮肤产生三维堆积形变,因此,X、Y和Z方向均会产生明显形变。为分析仿真曲面与实际观测曲面之间的误差,选取该区域中轴线方向20个特征点,计算X、Y和Z方向的平均绝对误差(mean absolute error,MAE)和标准差(standard deviation,SD),结果如表 3和4所示。
| mm | |||||||||||||||||||||||||||||
| 方向 | 误差 | t0 | t1 | t2 | t3 | 平均 | |||||||||||||||||||||||
| X | MAE | 0.031 | 0.113 | 0.297 | 0.740 | 0.295 | |||||||||||||||||||||||
| SD | 0.037 | 0.078 | 0.271 | 0.270 | 0.164 | ||||||||||||||||||||||||
| Z | MAE | 0.297 | 0.191 | 0.175 | 0.560 | 0.360 | |||||||||||||||||||||||
| SD | 0.006 | 0.136 | 0.184 | 0.014 | 0.085 | ||||||||||||||||||||||||
| mm | |||||||||||||||||||||||||||||
| 方向 | 误差 | t0 | t1 | t2 | t3 | 平均 | |||||||||||||||||||||||
| X | MAE | 0.081 | 0.323 | 0.318 | 0.546 | 0.317 | |||||||||||||||||||||||
| SD | 0.015 | 0.037 | 0.170 | 0.136 | 0.090 | ||||||||||||||||||||||||
| Y | MAE | 0.027 | 0.348 | 0.236 | 0.381 | 0.248 | |||||||||||||||||||||||
| SD | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||||
| Z | MAE | 0.446 | 0.589 | 0.377 | 0.615 | 0.471 | |||||||||||||||||||||||
| SD | 0.040 | 0.139 | 0.201 | 0.547 | 0.232 | ||||||||||||||||||||||||
MAE和SD表示如下:
| $ \mathrm{MAE}=\frac{1}{20} \sum\limits_{i=1}^{20}\left|\boldsymbol{P}_{\mathrm{sim} i}-\boldsymbol{P}_{\mathrm{cam} i}\right|, $ | (20) |
| $ \begin{gather*} \mathrm{SD}=\sqrt{\frac{1}{20} \sum\limits_{i=1}^{20}\left(\boldsymbol{P}_{\mathrm{sim} i}-\boldsymbol{P}_{\mathrm{cam} i}-\overline{\boldsymbol{P}}_{\mathrm{crr}}\right)^{2}}, \\ \overline{\boldsymbol{P}}_{\mathrm{err}}=\frac{1}{20} \sum\limits_{i=1}^{20}\left(\boldsymbol{P}_{\mathrm{sim} i}-\boldsymbol{P}_{\mathrm{cam} i}\right) . \end{gather*} $ | (21) |
其中:Psimi=(xi, yi, zi)和Pcami=(xi, yi, zi), i=1, 2, …, 20为仿真和实际获取的皮肤层点云经拟合后曲面上第i个特征点的位置信息;Perr=(x, y, z)为特征点平均误差。由表 3可知,小臂按摩试验中,皮肤拉伸形变在X、Z方向的MAE为0.295、0.360 mm,最大误差为0.740、0.560 mm。由表 4可知,大臂按摩试验中,皮肤堆积形变在X、Y和Z方向的MAE为0.317、0.248和0.471 mm,最大误差为0.546、0.381和0.615 mm。试验过程中,MSD模型在各时刻仿真SD相对较小。试验结果表明:本文提出的皮肤三维形变仿真模型误差较小,具有一定的稳定性。
5 结论本文采用仿真方法模拟人机接触时引起的皮肤三维形变,针对人机作业区域,通过相机获取的点云进行视觉处理,确定皮肤三维形变仿真模型中质点的位置信息,构建皮肤、肌肉脂肪、骨骼3层MSD模型;基于人机接触运动中皮肤黏滞和黏滑2种状态力学特征,针对质点引入阻尼算法,建立了适应黏弹性皮肤特征的质点动力学方程;皮肤形变仿真系统可描述不同特性的个体皮肤在不同作业条件(如探头大小、移动速度和法向力等)的皮肤三维形变。试验结果表明:本文所建的MSD仿真模型误差较小,可较精确地模拟人机接触运动中法向力和切向力引起的皮肤拉伸和堆积形变。皮肤形变仿真系统可为机器人作业参数选取、轨迹控制等策略提供参考。
| [1] |
LIMBERT G. Skin biophysics: From experimental characterisation to advanced modelling[M]. Cham, Switzerland: Springer, 2019.
|
| [2] |
ZHOU L, WANG S B, LI L N, et al. An approximate solution of the spherical indentation on a generally anisotropic elastic half-space[J]. International Journal of Solids and Structures, 2019, 161(5): 174-181. |
| [3] |
CIOACA T, CARAMIZARU H. On the impact of explicit or semi-implicit integration methods over the stability of real-time numerical simulations[Z/OL]. arXiv. (2013-11-20)[2023-12-24]. https://arxiv.org/abs/1311.5018.
|
| [4] |
MAHDI D, RICHES A, GESTER M, et al. Rolling and sliding: Separation of adhesion and deformation friction and their relative contribution to total friction[J]. Tribology International, 2015, 89(10): 128-134. |
| [5] |
FLYNN C, TABERNER A, NIELSEN P. Modeling the mechanical response of in vivo human skin under a rich set of deformations[J]. Annals of Biomedical Engineering, 2011, 39(7): 1935-1946. DOI:10.1007/s10439-011-0292-7 |
| [6] |
FLYNN C, TABERNER A J, NIELSEN P M F, et al. Simulating the three-dimensional deformation of in vivo facial skin[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2013, 28(12): 484-494. |
| [7] |
CORDIER F, MAGNENAT-THALMANN N. Integrated system for skin deformation[C]// Proceedings Computer Animation 2000. Philadelphia, USA: IEEE, 2000: 2-8.
|
| [8] |
MOREIRA P, ZEMITI N, LIU C, et al. Viscoelastic model based force control for soft tissue interaction and its application in physiological motion compensation[J]. Computer Methods and Programs in Biomedicine, 2014, 116(2): 52-67. DOI:10.1016/j.cmpb.2014.01.017 |
| [9] |
ZHAI J M, ZENG X W, SU Z Q. An intelligent control system for robot massaging with uncertain skin characteristics[J]. Industrial Robot, 2022, 49(4): 634-644. DOI:10.1108/IR-11-2021-0266 |
| [10] |
HUANG Y C, SOUÈRES P, LI J. Contact dynamics of massage compliant robotic arm and its coupled stability[C]// Proceedings of 2014 IEEE International Conference on Robotics and Automation. Hong Kong, China: IEEE, 2014: 1499-1504.
|
| [11] |
MAITI R, GERHARDT L C, LEE Z S, et al. In vivo measurement of skin surface strain and sub-surface layer deformation induced by natural tissue stretching[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2016, 62(10): 556-569. |
| [12] |
CHA J, KIM J, KIM S. Noninvasive determination of fiber orientation and tracking 2-dimensional deformation of human skin utilizing spatially resolved reflectance of infrared light measurement in vivo[J]. Measurement, 2019, 142(12): 170-180. |
| [13] |
GUAN Z Y, ZHOU L, LI L A, et al. Friction properties of in vivo human skin from visualized friction testing[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2020, 104(4): 103692. |
| [14] |
KWIATKOWSKA M, FRANKLIN S E, HENDRIKS C P, et al. Friction and deformation behaviour of human skin[J]. Wear, 2009, 267(8): 1264-1273. |
| [15] |
FLYNN C O. The design and validation of a multi-layer model of human skin[D]. Sligo: Insitute of Technology Sligo, 2007.
|
| [16] |
张竹筠, 彭妙娟, 黄能, 等. 人体皮肤起皱的非线性大形变分析[J]. 计算机辅助工程, 2019, 28(1): 62-69. ZHANG Z J, PENG M J, HUANG N, et al. Analysis on nonlinear large deformation of human skin wrinkle[J]. Computer Aided Engineering, 2019, 28(1): 62-69. (in Chinese) |
| [17] |
PANCHAL R, HORTON L, POOZESH P, et al. Vibration analysis of healthy skin: Toward a noninvasive skin diagnosis methodology[J]. Journal of Biomedical Optics, 2019, 24(1): 015001. |
| [18] |
MOUSAVI S R, KHALAJI I, SADEGHI NAINI A, et al. Statistical finite element method for real-time tissue mechanics analysis[J]. Computer Methods in Biomechanics and Biomedical Engineering, 2012, 15(6): 595-608. DOI:10.1080/10255842.2010.550889 |
| [19] |
WANG T T, TANG M, WANG Z D, et al. Accurate self-collision detection using enhanced dual-cone method[J]. Computers & Graphics, 2018, 73(4): 70-79. |
| [20] |
WANG Z D, WU L H, FRATARCANGELI M, et al. Parallel multigrid for nonlinear cloth simulation[J]. Computer Graphics Forum, 2018, 37(7): 131-141. |
| [21] |
ZHANG Y, LUO D, LI J, et al. Study on collision detection and force feedback algorithm in virtual surgery[J]. Journal of Healthcare Engineering, 2021, 2021(1): 6611196. |
| [22] |
TANG Y S, LIU S, DENG Y R, et al. An improved method for soft tissue modeling[J]. Biomedical Signal Processing and Control, 2021, 65(3): 102367. |
| [23] |
ADAMS M J, BRISCOE B J, JOHNSON S A. Friction and lubrication of human skin[J]. Tribology Letters, 2007, 26(3): 239-253. |
| [24] |
BOSTAN L E, TAYLOR Z A, CARRÉ M J, et al. A comparison of friction behaviour for ex vivo human, tissue engineered and synthetic skin[J]. Tribology International, 2016, 103(12): 487-495. |
| [25] |
陈思, 乔筱祺, 李天博, 等. 基于SPH-FEM手指模型的皮肤摩擦行为分析[J]. 排灌机械工程学报, 2019, 37(12): 1067-1071. CHEN S, QIAO X Q, LI T B, et al. Skin frictions based on SPH-FEM finger model[J]. Journal of Drainage and Irrigation Machinery Engineering, 2019, 37(12): 1067-1071. (in Chinese) |
| [26] |
VAN KUILENBURG J, MASEN M A, VAN DER HEIDE E. Contact modelling of human skin: What value to use for the modulus of elasticity?[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2013, 227(4): 349-361. |


