引用本文
刘依明, 杨珺涵, 张忠利, 许沛琪, 刘念雄. 面向寒冷地区住宅碳排放预测的机器学习算法模型比较[J]. 清华大学学报(自然科学版), 2024, 64(10): 1734-1745.  
LIU Yiming, YANG Junhan, ZHANG Zhongli, XU Peiqi, LIU Nianxiong. A comparative study of machine learning algorithm models for predicting carbon emissions of residential buildings in cold zones[J]. Journal of Tsinghua University (Science and Technology), 2024, 64(10): 1734-1745.  
面向寒冷地区住宅碳排放预测的机器学习算法模型比较
刘依明1, 杨珺涵2, 张忠利3, 许沛琪4, 刘念雄4    
1. 浙江省建设投资集团股份有限公司, 杭州 310012;
2. 中国建筑西南设计研究院有限公司, 成都 610000;
3. 临沂城市建设投资集团有限公司, 临沂 276000;
4. 清华大学 建筑学院, 北京 100084
收稿日期：2024-03-25
基金项目：浙江省科技计划项目(2023C03173);国家重点研发计划项目(2022YFC3803800);国家自然科学基金重点项目(52130803)
作者简介：刘依明(1989—), 男, 工程师
通讯作者：刘念雄, 教授, E-mail: phlnx@tsinghua.edu.cn
摘要：机器学习算法模型为住宅低碳设计与优化提供了数据支持。然而, 在碳排放预测与分析时, 算法模型常被直接使用, 而未考虑调参与寻优, 且不同自变量数据集对模型预测效果的影响差异也有待明确。为揭示不同算法模型对寒冷地区住宅低碳设计的指导效果、向建筑师提供算法模型的选择依据, 针对多元线性回归、分类回归树、随机森林、自适应增强算法、梯度提升回归树和多层感知机等在低碳设计中常用的算法模型进行寻优, 对比分析不同算法和自变量数据集的适用性与预测性能。该文说明了算法模型寻优的目标边界、参数取值范围、寻优过程和论证方法。在37栋寒冷地区钢筋混凝土剪力墙结构住宅及其衍生方案的基础上, 采用交叉验证和网格搜索, 建立了120个建材碳排放预测模型和60个将稳态耗热量转换为动态耗热量的转化系数预测模型。对比结果表明：总体上, 多元线性回归、随机森林和梯度提升回归树算法的碳排放预测性能更好。其中, 随机森林和梯度提升回归树算法在误差控制方面表现更佳, 但预测优度与多元线性回归算法相近, 且可解释性较差。采用恰当的自变量数据集, 如建筑总层数、建筑层高、建筑面宽与进深等形体尺度参数, 标准层户数与卧室数等功能配置参数, 以及采暖期室外平均温度、实际供暖天数、屋面和墙面传热系数的修正系数等城市气象参数, 多元线性回归算法能够为寒冷地区住宅低碳设计与优化提供更直观、有效的指导。
关键词：碳排放    机器学习    设计参数    交叉验证    网格搜索    
A comparative study of machine learning algorithm models for predicting carbon emissions of residential buildings in cold zones
LIU Yiming1, YANG Junhan2, ZHANG Zhongli3, XU Peiqi4, LIU Nianxiong4    
1. Zhejiang Construction Investment Group Co., Ltd., Hangzhou 310012, China;
2. China Southwest Architectural Design and Research Institute Co., Ltd., Chengdu 610000, China;
3. Linyi City Investment Group Co., Ltd., Linyi 276000, China;
4. School of Architecture, Tsinghua University, Beijing 100084, China
Abstract: [Objective] Machine learning algorithms provide valuable data support for designing and optimizing low-carbon residential buildings. However, when used directly for carbon emission prediction and analysis, these models often lack proper parameter tuning and optimization. The different impacts of various independent variable datasets on predictive performance also remain to be clarified. In China's cold zones, where residential buildings share similar architectural structures, energy-saving designs, and spatial layouts, carbon emissions primarily come from the operational phase and the production stages of building materials, with heating emissions being a significant component. This study aims to elucidate the effectiveness of different machine learning algorithm models in guiding low-carbon residential design in these cold zones, offering architects criteria for selecting proper algorithms. This study focuses on automatic parameter tuning and optimization for several commonly used algorithms in the context of low-carbon design of buildings, including multiple linear regression, classification and regression tree, random forest, adaptive boosting, gradient boosting regression tree, and multilayer perceptron. The study compares and analyzes the performance limits and applicability of these algorithms and independent variable datasets in predicting carbon emissions during building material production and heating stages. [Methods] This paper elaborates on the target boundaries, parameter ranges, optimization processes, and validation methods for optimizing machine learning algorithm models. Through comprehensive research and simulation analysis of 37 reinforced concrete shear wall residential buildings and their derivative schemes in cold zones, multiple independent variable datasets suitable for establishing predictive models are identified. Cross-validation and grid search techniques are employed to optimize the predictive performance limits of different machine learning algorithms and independent variable datasets. Subsequently, 120 models for predicting carbon emissions from building materials and 60 models for transforming steady-state heating consumption into dynamic heating consumption using the six mentioned algorithms are established. [Results] A horizontal comparison of the models reveals that algorithms such as multiple linear regression, random forest, and gradient boosting regression trees exhibit relatively good performance (R2 over 0.900) in carbon emission prediction after hyperparameter tuning across different independent variable datasets. Random forest and gradient boosting regression tree models excel in error control and offer similar predictive accuracy to multiple linear regression but lack interpretability. In contrast, multiple linear regression models provide clearer equations and stronger guidance for low-carbon design and optimization, focusing on carbon emission reduction during building material production or winter heating stages. Models based on the total residential building area exhibit optimal performance in predicting building material carbon emissions. Predictive models built on parameters such as the number of above-ground and underground floors, building width and depth, total household numbers, number of bedrooms for standard floor, and total number of residential bathrooms in the residence also demonstrate strong predictive capabilities for building material carbon emissions. For predicting the conversion coefficient during the heating stage, including the number of households and bedrooms per standard floor as independent variables significantly enhances predictive performance. [Conclusions] Although various machine learning models are useful for predicting residential building carbon emissions, the multiple linear regression model stands out owing to its excellent predictive performance and its intuitive representation of how design parameters affect carbon emissions. By utilizing different and appropriate independent variable datasets, such as the total number of floors, floor height, building dimensions, number of households and bedrooms on a floor, and corrected coefficients for urban meteorological parameters (including outdoor average temperature during the heating season, actual heating days, and roof and wall heat transfer coefficients), or by adopting the finally determined total building area, the multiple linear regression algorithm can deliver timely and multi-faceted guidance. These results are crucial for low-carbon design and optimization during the primary stages of the residential lifecycle in China's cold zones.
Key words: carbon emission    machine learning    design parameters    cross-validation    grid search    

碳排放是建筑生命周期评估的代表性指标，也是当代建筑性能化设计的重要依据[1]。相关研究表明，建筑运行阶段和建材生产阶段的碳排放占全过程能源碳排放的比例最大，分别为56.6%和41.8%[2]。对于寒冷地区，约60%~65%的住宅运行能耗为冬季供暖能耗[3-4]。因此，住宅碳排放核算与低碳设计研究通常以建材工程量清单、运行能耗模拟或统计数据为基础。随着大数据和人工智能技术的发展，机器学习算法模型对各类清单数据的处理更加高效、智能。对于建筑碳排放预测，可采用的机器学习算法模型为有监督模型，按照可解释性分为黑箱模型和白箱模型。相比于白箱模型，黑箱模型在处理高阶复杂的数据信息方面具有一定的效率优势，但可解释性较差，难以为建筑师提供直观易懂的设计指导。本研究结合案例调研和理想模型模拟，通过交叉验证与网格搜索对多种机器学习算法与设计参数构成的碳排放预测模型进行寻优，并对比分析各最优模型在建材生产和冬季供暖碳排放预测方面的性能和适用性差异，从而为寒冷地区住宅低碳设计辅助工具的选择提供参考。

1 机器学习与碳排放预测 1.1 常见的机器学习算法

机器学习通过数据挖掘，可以解析研究对象组成成分或影响因素之间的规律与关系[5-6]。在建筑低碳设计中，有监督学习算法的介入能够以更短的时间和更高的准确度辅助建筑师探析设计参数、气象参数与碳排放之间的耦合机制。

基本的有监督学习算法包括多元线性回归(multiple linear regression，MLR)、支持向量回归(support vector regression，SVR) 和决策树(decision tree，DT)等。MLR形式简单、可解释性强，但难以表达复杂模型，对异常值较为敏感。在分析非线性问题时，需要对异常值进行预处理[7]。SVR可分析线性和非线性回归问题。针对非线性问题，由核函数将输入向量投射到更高维度的特征空间中，使投射后的特征向量线性或近似线性可分，再采用线性支持向量回归求解。该算法对于异常值具有一定鲁棒性，泛化能力较为出色，但核函数的类型选择会影响模型的预测性能[8-11]，且可解释性较差。DT中的分类回归树(classification and regression tree，CART)则将特征空间划分为若干单元，每个单元对应一个特定输出值。将测试数据按其特征划归到某一单元中，即可得到该单元对应的输出值[12]。该算法逻辑清晰、易于可视化，但容易因分支过度导致过拟合，且数据特征之间的高相关性也会影响预测结果。

此外，将独立的机器学习算法整合为集成算法，可提升算法模型的预测性能，例如随机森林(random forest，RF)、自适应增强算法(adaptive boosting，Adaboost)和梯度提升回归树(gradient boosting regression tree，GBRT)。RF由多个决策树随机组成。测试数据将在每棵决策树中分别判断，再综合各棵决策树的判断结果，以众数作为RF的输出。该算法能够较好地处理高维数据、应对数据缺失、平衡数据集误差，但其运算和模型优化过程难以可视化。Adaboost首先为每个弱学习器设定初始权重。若某个弱学习器遍历所有训练数据样本后的预测结果与真实结果不一致，则该弱学习器的总误差增加，其权重相应改变。通过迭代，每个弱学习器都获得了相应权重，再根据不同权重组合构成强学习器。类似地，在GBRT中，每个弱学习器通过拟合之前累积模型损失函数的负梯度，使加上该弱学习器后的累积模型损失向负梯度方向不断降低，再由多个弱学习器构成预测性能较强、可充分利用数据全部特征信息的强学习器[13-16]。

最后，在计算机算力提升的支持下，神经网络模型也逐渐用于建筑性能化设计。神经网络模型是一种模仿生物神经网络结构和功能的数学模型[6]。多层感知机(multi-layer perceptron，MLP)是一种前馈结构的深度神经网络模型。多层感知机需要大量数据样本，计算成本较高，可解释性较差，模型调试需要丰富的经验，且运算过程可能陷入局部最优解。

1.2 算法模型的预测应用

面向建筑低碳设计，机器学习算法模型的研究与应用旨在量化、提升算法模型的指导作用和运算效率[17-18]，通常以设计参数与气象参数为自变量、碳排放为因变量。相关研究表明，多元线性回归、随机森林、支持向量机和多层感知机等机器学习算法均可用于解析住宅空间设计参数与碳排放的关系，并预测住宅建材碳排放[19-20]。集成算法对预测精度的提升具有明显效果[21-22]。步婷等[23]和焦良珍等[24]对比分析了多元线性回归、随机森林、支持向量机和多层感知机等在建筑负荷预测方面的性能差异，指出随机森林的预测准确性和稳定性最佳。程亚豪等[25]研究发现，随机森林和梯度提升回归树在能耗预测方面的性能优于支持向量机和神经网络模型。王志强等[26]对比了极度随机树、支持向量机、梯度提升树和多层感知机在剪力墙结构建筑的物化碳排放预测方面的性能，并指出多层感知机和极端梯度提升树的预测性能不及极度随机树。王一帆等[27]发现，在用住宅形体参数预测能耗碳排放时，极端梯度提升模型比多元线性回归的性能更好。

总体而言，在碳排放预测和性能对比方面，各算法模型多被直接使用，未考虑调参与寻优；此外，不同设计参数与气象参数构成的自变量数据集对算法模型的影响有待明确。在算法模型选择时，需兼顾模型的准确性与可解释性，以便提升其在住宅设计和优化指导中的适用性。因此，本研究在对机器学习算法种类、超参数、自变量数据进行分析与优化的基础上，比较算法模型的碳排放预测性能和适用性。

2 研究方法 2.1 预测内容

住宅设计参数数据、气象数据、建材和供暖碳排放统计数据是采用机器学习算法模型预测寒冷地区住宅碳排放的基础。设计参数调试会改变设计方案，进而对建材用量、建筑运行效能及相应碳排放产生重要影响[28]。在模型训练过程中，建材碳排放可根据住宅项目工程量清单中各类建材用量进行统计换算，并考虑钢材与玻璃等可再循环利用建材的碳排放折减[29]；运行碳排放则主要依托建筑负荷(或能耗)的模拟结果或实测数据。

在寒冷地区住宅设计阶段，建筑耗热量可通过EnergyPlus等动态模拟软件计算得到[30]，再结合供暖系统综合效率、标准煤热值、综合发电煤耗计算出供暖能耗，最后乘以相应的碳排放因子，即可求解供暖碳排放。然而，动态模拟耗时较长，会干扰设计思路和方案推进。同时，能耗实测值也易受住户生活方式的影响，难以在设计阶段被有效控制。

有研究表明，寒冷地区建筑围护结构稳态耗热量与其动态耗热量的变化趋势相近，即稳态耗热量奠定了动态耗热量的变化基础[31]。住宅单位时间单位面积的稳态耗热量qH可按图 1中相关公式与变量进行计算[32]，此计算过程相对简单，并可采用Python语言进行编译。图 1中：qHT、qHwall、qHroof和qHmc分别为住宅单位时间单位面积的围护结构、外墙、屋面和门窗稳态耗热量，W/m2；qINF为住宅单位时间单位面积建筑空气渗透耗热量，W/m2；qH为住宅单位时间单位面积稳态耗热量，W/m2；Tn与Te分别为室内计算温度与采暖期室外平均温度，℃；Swi、Sri、Smci和Sfi分别为住宅外墙、屋面、门窗和地面的面积，m2；Kwi、Kri、Kfi和Kmci分别为相应部位外墙、屋面、地面和门窗的传热系数，W/(m2·K)；εwi和εri分别为外墙和屋面传热系数的修正系数；Cmci为门窗的太阳辐射修正系数。cp为空气比热容，W·h/(kg·K)；ρ为空气密度，kg/m3；Vh为换气体积，m3；αj和γj分别为各朝向的耗热量修正系数和建筑外门耗热量附加系数；S为总建筑面积，m2。

理想工况下的住宅单位面积动态累计耗热量qH_d可通过Python与EnergyPlus批量模拟计算。住宅单位面积供暖碳排放CH可用式(1)—(2)表示。

$ q_{\mathrm{H}_{-} \mathrm{s}}=0.024 \cdot q_{\mathrm{H}} \cdot t, $ (1)
$ C_{\mathrm{H}}=1000 \cdot \mathrm{EF}_i \cdot q_{\mathrm{H}_{-} \mathrm{s}} /\left(\eta_i \cdot q \cdot \varphi\right). $ (2)

式中：CH为住宅单位建筑面积供暖碳排放量，kg/m2；t为实际供暖天数，d；qH_s为供暖期间住宅单位面积稳态耗热量，kW·h/m2；ηi表示供暖系统综合效率，当采用燃煤锅炉时取0.81，当采用燃气锅炉时取0.85[30]；EFi为能源碳排放因子，当热源为标准煤时取94.44 t/TJ，当热源为天然气时取55.54 t/TJ[33]；q为热值转化系数，取277 777.78 kW·h/TJ[30]。φ为qH_s与qH_d的比值，即供暖碳排放预测过程中，将单位建筑面积全年稳态累计耗热量转化为动态累计耗热量的系数(简称供暖碳排放转化系数)。

综上，本研究按照图 1所示进行寒冷地区住宅供暖碳排放预测，转化系数φ可作为预测模型性能对比的关键指标。

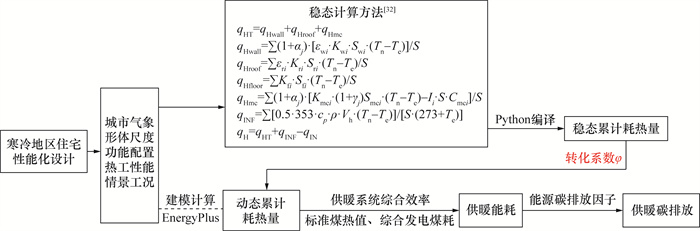
图 1 寒冷地区住宅供暖碳排放预测路线
图选项

2.2 模型参数

不同的机器学习算法和自变量数据集可以组合成多种算法模型。本研究选取MLR、CART、RF、Adaboost、GBRT和MLP 6种在建筑性能化设计中应用较广的机器学习算法作为研究对象。算法的种类及超参数设置会影响算法模型的预测性能。超参数是机器学习算法中的配置变量，无法通过数据训练和学习得到，需在机器学习过程之前设置。超参数优化能够提升算法本身在数据集上的拟合与预测性能。因此，本研究首先对这6种算法的超参数寻优区间和变化步长进行了初始设置(表 1)。

表 1 6种机器学习算法的超参数初始取值
机器学习算法 超参数种类 超参数含义 初始取值范围
MLR fit_intercept 截距 [True, False]
max_depth 最大深度 np.arange(10, 110, 10)
CART max_leaf_nodes 最大叶子节点数 np.arange(3, 20, 2)
min_impurity_decrease 节点划分最小不纯度 np.arange(0.01, 1.0, 0.01)
n_estimators 决策树数量 np.arange(10, 110, 10)
max_depth 最大深度 [None, 3, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55]
RF max_features 最大特征数 [auto, sqrt, log2]
criterion 特征选择标准 [mse, mae]
bootstrap 采用bootstrap采样 [True, False]
loss 损失函数 [linear, square, exponential]
Adaboost n_estimators 弱学习器迭代次数 np.arange(10, 110, 10)
learning_rate 学习率 np.arange(0.1, 1.1, 0.1)
loss 损失函数 [ls, lad, huber, quantile]
GBRT n_estimators 弱学习器迭代次数 np.arange(10, 130, 10)
learning_rate 学习率 np.arange(0.1, 1.1, 0.1)
hidden_layer_sizes 隐藏层大小 [(100, 50), (100, 40), (100, 30), (50, 30), (30, 10)]
MLP alpha 正则化强度 [0.000 1, 0.001, 0.01, 0.1, 1]
solver 权重优化算法 [lbfgs, sgd, adam]
注：在Python中，np.arange(n, m, d)表示从n到m(不包括m)，以d为公差的等差数列数组；True与False分别代表“有”和“无”。
表选项

此外，模型自变量数据集可按照住宅设计流程，分别由住宅项目的城市气象参数(如采暖期室外平均温度Te、实际供暖天数t、围护结构传热系数的修正系数等)、形体尺度参数(如地上层数Nf、地下层数Nb、总建筑面积S、建筑面宽Lw、建筑进深Ld、平均窗墙比ω、体形系数FS等)、功能配置参数(如住宅楼梯间数Nt、标准层户数Nh、标准层卧室数Nd、标准层卫生间数Nw、标准层户内房间数Ni、标准层公共空间数Np、标准层房间总数Nr等)和热工性能参数(如外墙、屋面、地面、外窗和外门平均传热系数)构成，也可通过阶段性计算结果进行补充。

建筑工程量清单、住宅耗热量指标、动态累计耗热量和转化系数均可从具体的设计资料中获取和计算，可有效避免数据异常或缺失等情况。然而，不同自变量在模型中的显著性与共线性会影响模型的拟合效果，因此仍需对其进行判断。多元线性回归可采用“步进”方式和共线性诊断筛选自变量，其他机器学习算法可通过超参数调试进行应对。

2.3 寻优方法

在机器学习算法模型的寻优过程中，本研究将数据样本分为测试集和验证集。测试集用于获取不同自变量数据集上的最优算法模型，验证集用于评价算法模型的预测性能。寻优方法采用网格搜索与交叉验证(GridSearchCV)，可通过Python语言编译(图 2)。交叉验证可以充分利用测试集的全部数据样本：将测试集分为若干子集，轮流以其中1个子集为检验集、其他子集为训练集进行模型拟合与测试，最后根据全部测试结果的平均值计算模型精度。网格搜索是一种穷举搜索方式，通过遍历机器学习算法的超参数寻优区间和不同组合，获取在测试集上精度最高的超参数[34]。网格搜索与交叉验证可根据测试集样本自动寻优，并输出最优模型。为简化寻优过程，本研究以决定系数R2为依据，将测试集分为4份训练集和1份检验集，随机数设为42，超参数的变化步长根据寻优时长实时调整。在确定最优超参数(即获得最优模型)之后，通过验证集计算不同算法模型的预测R2、平均绝对误差(mean absolute error，MAE)和均方根误差(root mean square error，RMSE)。算法模型的预测性能差异，可作为评价自变量数据集和机器学习算法在寒冷地区住宅低碳设计中的指导作用的依据。

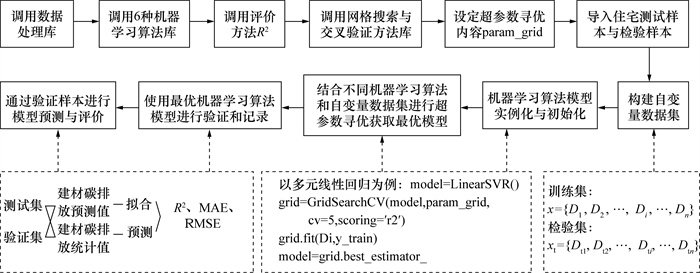
图 2 模型寻优过程示意
图选项

3 面向建材碳排放的模型预测性能比较 3.1 研究对象

本研究调研、收集了37栋近7年建成的寒冷地区钢筋混凝土剪力墙结构住宅项目资料(图 3)，据此统计各栋住宅的建材用量，并结合相关标准[33]中的碳排放因子计算其碳排放量。其中: 1—8号楼为二梯四户，9—11号楼为一梯六户，12、14号楼为二梯三户，13号楼为一梯八户，15—27号楼为一梯两户，28—37号楼为一梯两户。各栋住宅的建材总质量、总碳排放量，以及不同建材的平均碳排放占比和碳排放强度如图 4所示。在建材碳排放方面，混凝土、水泥砂浆和钢材的碳排放占比较大，合计约占住宅建材总碳排放量的86.52%。透明围护结构的碳排放占比略高于保温材料和页岩砖。在建材碳排放强度方面，混凝土碳排放强度最高，其次分别为透明围护结构、水泥砂浆和钢材。

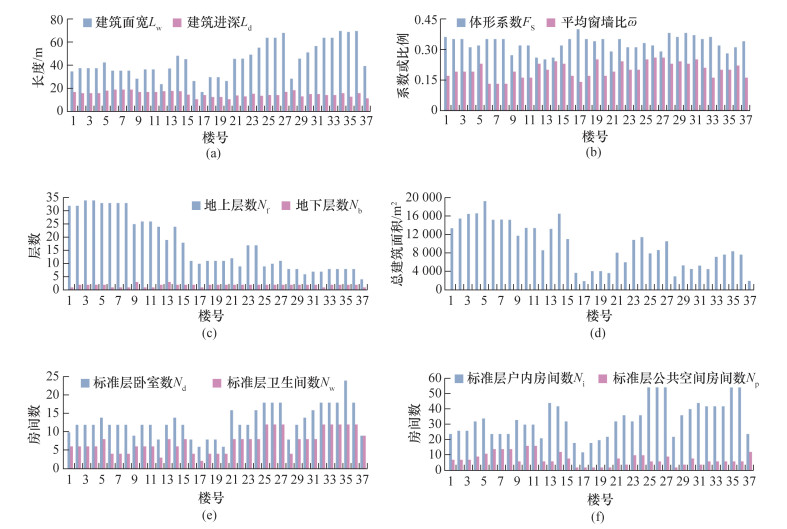
图 3 37栋住宅案例的设计信息
图选项

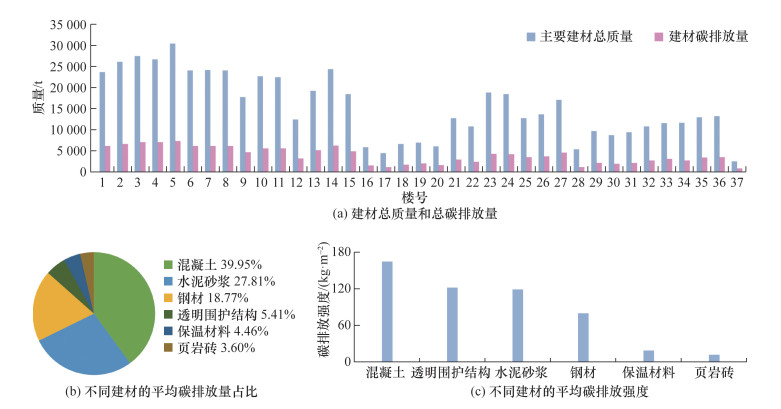
图 4 住宅建材质量与碳排放量
图选项

3.2 自变量数据集

本研究通过随机抽样，选取2、6、15、24、28号楼作为验证集样本，其他住宅楼为测试集样本用于寻优。对于多元线性回归算法，经回归拟合及自变量分析，共筛选出20组可用于构建建材总碳排放预测模型的自变量数据集Dc1—Dc20。这20组自变量数据集共涉及17个自变量(表 2)，由13个空间设计参数及其组合形式构成。由于空间设计参数的种类及其组合形式不同，因此各个自变量数据集的适用阶段和对设计深度的要求也有所差异。为保证不同算法模型性能对比的口径一致，其他机器学习算法也采用这20组自变量数据集进行寻优和预测性能评价。

表 2 建材碳排放预测的自变量数据集
自变量
数据集		 自变量
S Ld Lw+Ld (Nf+Nb)·
Lw·Ld		 (Nf+Nb)·
(Lw+Ld)		 Nt Nh Nh·Nf Nd Nd·Nf Nw·Nf Ni Np Nr (Lw+Ld)·Nf·ω Nf·ω Np·Nf2·ω
Dc1 ●
Dc2 ● ●
Dc3 ●
Dc4 ● ●
Dc5 ● ● ●
Dc6 ● ● ● ● ●
Dc7 ● ● ● ●
Dc8 ● ● ● ● ●
Dc9 ● ● ●
Dc10 ● ● ● ●
Dc11 ● ● ● ●
Dc12 ● ● ● ●
Dc13 ● ● ● ● ●
Dc14 ● ● ● ●
Dc15 ● ● ● ● ● ● ●
Dc16 ● ● ● ● ● ● ● ●
Dc17 ● ● ● ● ● ● ●
Dc18 ● ● ● ● ● ● ● ●
Dc19 ● ● ● ● ● ● ● ● ●
Dc20 ● ● ● ● ● ● ● ●
表选项

3.3 预测性能比较

本研究依次将不同自变量数据集代入6种机器学习算法，进行网格搜索与交叉验证。寻优得到的最优模型在验证集中的预测性能如图 5所示。

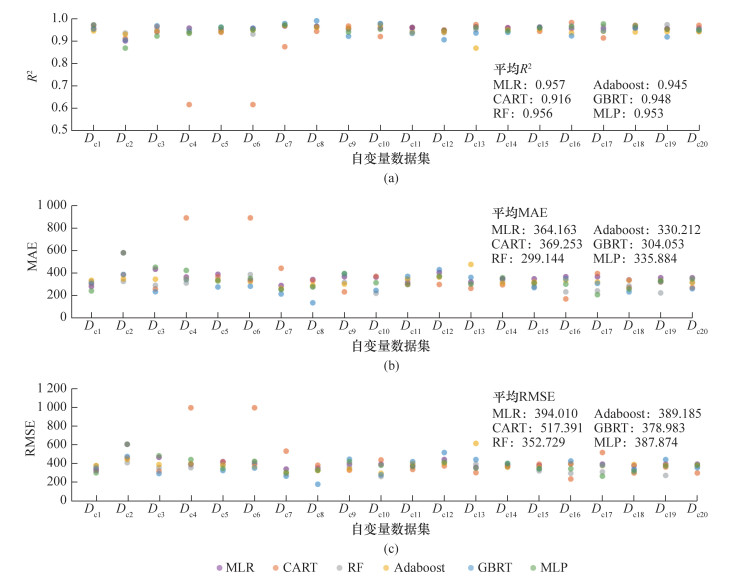
图 5 最优模型的建材碳排放预测性能
图选项

在得到的120个最优模型中，针对不同自变量数据集，为实现最好的预测性能应分别采用以下机器学习算法：Dc1、Dc16、Dc17采用MLP，Dc2、Dc15、Dc19采用RF，Dc3、Dc5—Dc8、Dc10采用GBRT，Dc4、Dc11、Dc14采用MLR(有截距项，下同)，Dc9、Dc12、Dc13、Dc16、Dc18、Dc20采用CART。不同自变量数据集在MLR中的平均预测R2最高，其次分别为RF和MLP。然而，不同自变量数据集在RF中的平均预测MAE和RMSE最小。与之相比，CART模型的平均预测R2最低，且平均预测误差最高。MLR模型的平均预测误差略低于CART。此外，不同自变量数据集在CART中的预测R2、MAE和RMSE标准差最大，但在RF中的预测R2和RMSE标准差最小，且在Adaboost中的MAE标准差最小。Dc8在各个机器学习算法中的平均预测性能最优(平均R2=0.967，平均MAE=277.342，平均RMSE=315.898)，且各项预测性能的标准差相对较低。Dc2、Dc4和Dc6在不同机器学习算法中的平均预测性能最差。再者，与其他自变量数据集相比，Dc1更适用于MLR，Dc16更适用于CART，Dc10更适用于RF和Adaboost，Dc8更适用于GBRT，Dc17更适用于MLP。采用Dc8的GBRT模型具有最小的预测误差(MAE=136.292，RMSE=177.463)和最高的预测R2(R2=0.992)；采用Dc4和Dc6的CART模型的预测R2最低且预测误差最大。

总体而言，经超参数寻优后，MLR、RF和GBRT使用不同自变量数据集进行建材总碳排放预测，均能保证预测R2不低于0.900。多元线性回归模型能够以更清晰、直观的方程式进行表示，相比于随机森林和梯度提升回归树模型，能够更有效地辅助建筑师根据建材碳排放进行空间设计与优化。其中，根据最终确定的住宅总建筑面积S建立的建材碳排放预测模型性能最佳。在住宅设计过程中，通过地上层数Nf、地下层数Nb、建筑面宽Lw、建筑进深Ld、住宅总户数Nh·Nf、标准层卧室数Nd和住宅卫生间总数Nw·Nf建立的预测模型能够较好地预测建材碳排放。在该模型中，(Nf+Nb)·(Lw+Ld) 对预测结果的影响最大，其次为Nh·Nf，其他自变量的影响程度相对较低。

4 面向供暖碳排放的模型预测性能比较 4.1 研究对象概况

在供暖碳排放转化系数的预测中，本研究以37栋住宅为基础，在住宅设计规范的限定范围内调整各栋住宅的形体尺度参数和功能配置参数，并匹配北京、太原、承德、兰州、济南、潍坊、西安、郑州8个目标城市的气象参数，共衍生出3 550个住宅模拟样本。这8个目标城市是寒冷A区和B区的省会或主要城市。经动态模拟后，计算出每个样本的转化系数。总体而言，转化系数的分布范围为0.560~1.696，平均值为0.843(表 3)。

表 3 不同城市住宅的转化系数φ统计情况
城市 转化系数φ
最小值 最大值 平均值 标准差
北京 0.619 1.081 0.796 0.082
太原 0.970 1.696 1.213 0.144
承德 0.835 1.274 0.997 0.101
兰州 0.851 1.314 1.019 0.099
济南 0.667 1.076 0.846 0.095
潍坊 0.560 0.903 0.686 0.073
西安 0.595 0.909 0.720 0.067
郑州 0.596 0.995 0.765 0.087
表选项

4.2 自变量数据集

在8个目标城市中，按照相同比例随机抽样，共选取3 200个住宅模拟样本作为供暖碳排放转化系数预测模型的测试集样本，其他作为验证集样本。供暖碳排放预测的核心在于通过稳态耗热量计算中的气象参数、形体尺度参数和功能配置参数实现对转化系数的有效预测。按照建材碳排放预测的自变量数据集筛选方式，整理出10组自变量数据集Dn1—Dn10(表 4)。其中，经曲线评估和显著性检验发现，qH_s0.473(记为PqH)更适用于拟合转化系数。此外，εwe和εr分别为东向外墙和屋面的传热系数修正系数；Lsw为建筑面宽向总长度，m；Hb和Hl分别为建筑高度与层高，m；ωs、ωn、ωe分别为建筑南向、北向和东向的窗墙比。

表 4 供暖碳排放预测的自变量数据集
自变量
数据集		 自变量
PqH t Te2 Te εwe εr H1 1/Hb Lsw ωs ωn ωe Nh Nd Nw Nr
Dn1 ● ● ● ● ● ● ● ●
Dn2 ● ● ● ● ● ● ● ● ●
Dn3 ● ● ● ● ● ● ● ● ● ●
Dn4 ● ● ● ● ● ● ● ● ● ● ●
Dn5 ● ● ● ● ● ● ● ● ● ● ●
Dn6 ● ● ● ● ● ● ● ● ● ●
Dn7 ● ● ● ● ● ● ● ● ● ● ●
Dn8 ● ● ● ● ● ● ● ● ● ● ● ●
Dn9 ● ● ● ● ● ● ● ● ● ● ● ●
Dn10 ● ● ● ● ● ● ● ● ● ● ● ●
表选项

4.3 预测性能比较

经网格搜索与交叉验证，不同机器学习算法和自变量数据集共构成60个最优模型。其中，CART模型的预测R2基本为0，无法有效预测转化系数。其他机器学习算法模型的预测性能如图 6所示。RF模型的平均预测R2最高，其次分别为GBRT和MLR模型。无论使用哪个自变量数据集，RF均比MRL具有更高的预测R2。对于MLR，采用Dn6、Dn7和Dn10均可以实现最高的预测R2(R2=0.971)；对于RF，采用Dn6可以实现最高的预测R2(R2=0.989)；对于GBRT，采用Dn5可以实现最高的预测R2(R2=0.987)。此外，在采用不同自变量数据集进行预测时，GBRT与MLR的预测R2较为接近。对于Adaboost和MLP，采用不同自变量数据集时的预测R2均不高于0.900。

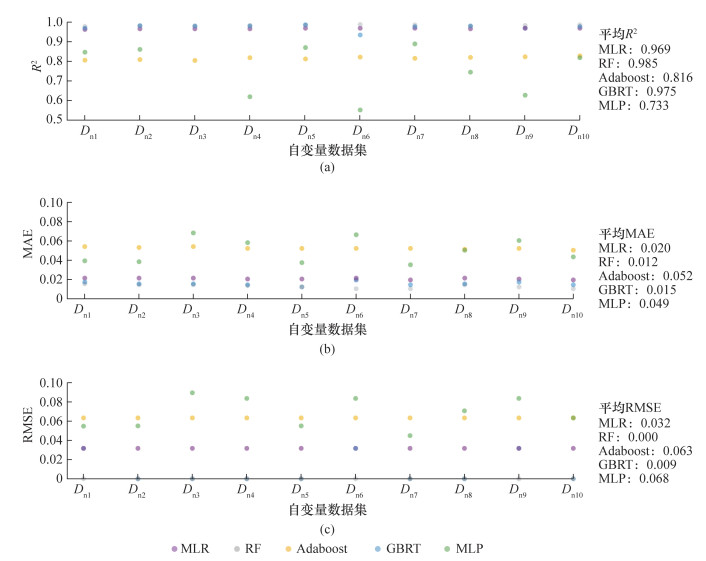
图 6 最优模型的供暖碳排放转化系数预测性能
图选项

再者，MLR在采用不同自变量数据集时的预测R2的波动最小，其次为RF、Adaboost和GBRT。由此可见，MLR的预测R2的稳定性更高。最后，RF的平均预测误差最低，其次为GBRT和MLR，且GBRT和MLR的MAE基本相同。MLR的MAE标准差最小，而RF的RMSE标准差最小。在10组自变量数据集中，Dn7在除CART以外的机器学习算法中的平均预测R2最高(R2=0.929)，且平均预测误差最低。Dn5、Dn2、Dn10在5种机器学习算法模型中的适用性仅次于Dn7。

总体而言，经超参数寻优后，RF、GBRT和MLR均可用于住宅低碳设计不同阶段的供暖碳排放转化系数的有效预测。与其他两种机器学习算法模型相比，多元线性回归模型的可解释性更好，对面向供暖阶段碳减排的住宅设计与优化的指导性更强。在自变量中加入标准层户数与卧室数，可提升转化系数的预测性能。此外，在采用Dn7进行转化系数预测时，PqH和t对预测结果的影响最大，其次是εwe和εr，其他自变量的影响相对较小。

5 结论

本研究依托37栋寒冷地区钢筋混凝土剪力墙结构住宅楼及其衍生方案，采用交叉验证和网格搜索的方式对由不同设计参数构成的自变量数据集和6种机器学习算法进行超参数寻优，共构建了120个建材碳排放预测模型和60个供暖碳排放转化系数预测模型。经验证集的分析和比较，多元线性回归、随机森林和梯度提升树算法在使用不同自变量数据集进行碳排放相关预测时具有更好的性能保证。此外，针对建材碳排放预测，Dc1、Dc7、Dc8、Dc10、Dc15、Dc16、Dc18在不同机器学习算法中的适用性更好，可以在住宅设计的不同阶段为建筑师提供指导。类似地，Dn1、Dn2、Dn5、Dn7、Dn10可以用于住宅设计不同阶段的供暖碳排放预测。再者，尽管随机森林和梯度提升回归树在误差控制方面的性能优于多元线性回归，但这2种机器学习算法属于黑箱模型，其可解释性远不如白箱模型多元线性回归，且在预测优度方面与多元线性回归模型相差较小。综上所述，结合建筑层数与层高、面宽与进深、标准层户数与卧室数等设计参数，以及采暖期室外平均温度、实际供暖天数和屋面传热系数的修正系数等气象参数，多元线性回归模型能够在寒冷地区住宅低碳设计、深化与优化中明确不同设计参数的变化对建材碳排放和供暖碳排放的影响程度，突出寒冷地区城市住宅碳减排设计策略的重点，为建筑师提供更直接、有效的辅助和指导。

参考文献
[1]
刘依明, 刘念雄. 建筑生命周期评估中碳排放计算的重要意义[J]. 住区, 2020(3): 46-51.
LIU Y M, LIU N X. The importance of carbon emission calculation in building life cycle assessment[J]. Design Community, 2020(3): 46-51. (in Chinese)
[2]
中国建筑节能协会, 重庆大学城乡建设与发展研究院. 中国建筑能耗与碳排放研究报告(2023年)[J]. 建筑, 2024(2): 46-59.
China Association of Building Energy Efficiency; Institute of Urban-Rural Construction and Development, Chongqing University. Research report on China building energy consumption and carbon emissions (2023)[J]. Construction and Architecture, 2024(2): 46-59. (in Chinese)
[3]
李金潞. 寒冷地区城市住宅全生命周期碳排放测算及减碳策略研究[D]. 西安: 西安建筑科技大学, 2019.
LI J L. Study on carbon emissions calculation and carbon reduction strategy of urban residential life cycle in cold areas [D]. Xi'an: Xi'an University of Architecture and Technology, 2019. (in Chinese)
[4]
田绅, 刘稷轩, 唐明生. 既有住宅建筑舒适性与节能技术研究[J]. 住宅科技, 2017, 37(1): 27-31.
TIAN S, LIU J X, TANG M S. Research on the comfort and energy-saving technologies of existing residential buildings[J]. Housing Science, 2017, 37(1): 27-31. DOI:10.3969/j.issn.1002-0454.2017.01.006 (in Chinese)
[5]
MITCHELL T M. 机器学习[M]. 曾华军, 张银奎, 译. 北京: 机械工业出版社, 2003.
MITCHELL T M. Machine learning [M]. ZHENG H J, ZHANG Y K, trans. Beijing: China Machine Press, 2003. (in Chinese)
[6]
袁梅宇. 机器学习基础: 原理、算法与实践[M]. 北京: 清华大学出版社, 2018.
YUAN M Y. Machine learning foundations: Principles, algorithms and practice[M]. Beijing: Tsinghua University Press, 2018. (in Chinese)
[7]
黄莉婷, 苏川集. 白话机器学习算法[M]. 武传海, 译. 北京: 人民邮电出版社, 2019.
HUANG L T, SU C J. Numsense! Data science for the layman: No math added [M]. WU C H, trans. Beijing: Posts & Telecom Press, 2019. (in Chinese)
[8]
肖建, 于龙, 白裔峰. 支持向量回归中核函数和超参数选择方法综述[J]. 西南交通大学学报, 2008, 43(3): 297-303.
XIAO J, YU L, BAI Y F. Survey of the selection of kernels and hyper-parameters in support vector regression[J]. Journal of Southwest Jiaotong University, 2008, 43(3): 297-303. DOI:10.3969/j.issn.0258-2724.2008.03.001 (in Chinese)
[9]
吴涛, 贺汉根, 贺明科. 基于插值的核函数构造[J]. 计算机学报, 2003, 26(8): 990-996.
WU T, HE H G, HE M K. Interpolation based kernel function's construction[J]. Chinese Journal of Computers, 2003, 26(8): 990-996. DOI:10.3321/j.issn:0254-4164.2003.08.014 (in Chinese)
[10]
GOLD C, SOLLICH P. Model selection for support vector machine classification[J]. Neurocomputing, 2003, 55(1-2): 221-249. DOI:10.1016/S0925-2312(03)00375-8
[11]
LAUER F, BLOCH G. Incorporating prior knowledge in support vector regression[J]. Machine Learning, 2008, 70(1): 89-118.
[12]
BREIMAN L, FRIEDMAN J, OLSHEN R, et al. Classification and regression trees[M]. Belmont, USA: Wadsworth, 1984: 1-357.
[13]
FRIEDMAN J H. Greedy function approximation: A gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. DOI:10.1214/aos/1013203450
[14]
SCHONLAU M. Boosted regression (boosting): An introductory tutorial and a Stata plugin[J]. The Stata Journal: Promoting Communications on Statistics and Stata, 2005, 5(3): 330-354. DOI:10.1177/1536867X0500500304
[15]
NATEKIN A, KNOLL A. Gradient boosting machines, a tutorial[J]. Frontiers in Neurorobotics, 2013, 7: 21.
[16]
HUANG Y F, LIU Y H, LI C H, et al. GBRTVis: Online analysis of gradient boosting regression tree[J]. Journal of Visualization, 2019, 22(1): 125-140. DOI:10.1007/s12650-018-0514-2
[17]
胡振, 龚薛, 刘华. 基于BP模型的西部城市家庭消费碳排放预测研究: 以西安市为例[J]. 干旱区资源与环境, 2020, 34(7): 82-89.
HU Z, GONG X, LIU H. Prediction of household consumption carbon emission in western cities based on BP model: Case of Xi'an city[J]. Journal of Arid Land Resources and Environment, 2020, 34(7): 82-89. (in Chinese)
[18]
李锐, 刘鹏飞, 王岩. 基于决策树方法的建筑空调能耗数据分析[J]. 建筑节能, 2019, 47(8): 14-18.
LI R, LIU P F, WANG Y. Data analysis of building air-conditioning energy consumption based on decision tree method[J]. Building Energy Efficiency, 2019, 47(8): 14-18. DOI:10.3969/j.issn.1673-7237.2019.08.004 (in Chinese)
[19]
毛希凯. 建筑生命周期碳排放预测模型研究: 以天津市住宅为例[D]. 天津: 天津大学, 2018.
MAO X K. Study on building life cycle carbon emissions prediction model: Taking residential buildings in Tianjin as examples [D]. Tianjin: Tianjin University, 2018. (in Chinese)
[20]
宋志茜. 建筑物化阶段碳排放特征及减碳策略研究[D]. 杭州: 浙江大学, 2023.
SONG Z Q. Research on carbon emission characteristics and carbon reduction strategies in the materialization stage of architecture [D]. Hangzhou: Zhejiang University, 2023. (in Chinese)
[21]
刘佳丽. 直辖市下城镇住宅建筑二氧化碳排放量预测模型的应用研究[D]. 郑州: 河南工业大学, 2023.
LIU J L. Application research on carbon dioxide emission prediction model of urban residential buildings in municipalities [D]. Zhengzhou: Henan University of Technology, 2023. (in Chinese)
[22]
黄耀. 基于集成学习的居民建筑能耗预测及模型优化[D]. 武汉: 华中科技大学, 2019.
HUANG Y. Energy consumption prediction and model optimization of residential buildings based on ensemble learning [D]. Wuhan: Huazhong University of Science and Technology, 2019. (in Chinese)
[23]
步婷, 范蕊, 孙可欣, 等. 基于机器学习算法的区域建筑负荷预测建模研究[J]. 建筑科学, 2022, 38(4): 85-96.
BU T, FAN R, SUN K X, et al. Research on modeling of regional cooling and heating load forecast based on machine learning algorithm[J]. Building Science, 2022, 38(4): 85-96. (in Chinese)
[24]
焦良珍, 陈海生, 高革, 等. 基于数据挖掘算法的DHC系统负荷时序预测方法[J]. 建筑节能, 2020, 48(11): 38-44.
JIAO L Z, CHEN H S, GAO G, et al. Load estimation for the DHC system based on data mining and time-series techniques[J]. Building Energy Efficiency, 2020, 48(11): 38-44. DOI:10.3969/j.issn.1673-7237.2020.11.008 (in Chinese)
[25]
程亚豪, 陈焕新, 王江宇. 基于机器学习的住宅能耗预测[J]. 制冷与空调, 2019, 19(5): 35-40.
CHENG Y H, CHEN H X, WANG J Y. Prediction of residential energy consumption based on machine learning[J]. Refrigeration and Air-Conditioning, 2019, 19(5): 35-40. DOI:10.3969/j.issn.1009-8402.2019.05.008 (in Chinese)
[26]
王志强, 任金哥, 韩硕, 等. 基于可解释性机器学习的建筑物物化阶段碳排放量预测研究[P]. 安全与环境学报, 2023: 1-13. (2023-11-03) [P].https://doi.org/10.13637/j.issn.1009-6094.2023.1467.
WANG Z Q, REN J G, HAN S, et al. Interpretable machine learning-based carbon emission prediction in the materialization stage of buildings [P]. Journal of Safety and Environment, 2023: 1-13. (2023-11-03). https://doi.org/10.13637/j.issn.1009-6094.2023.1467. (in Chinese)
[27]
王一帆, 李雪, 袁大昌. 住宅形态与碳排放相关性研究: 以金堂县为例[J]. 建筑节能, 2021, 49(9): 155-160.
WANG Y F, LI X, YUAN D C. Influence of residential form on carbon emission: A case study on Jintang county[J]. Building Energy Efficiency, 2021, 49(9): 155-160. (in Chinese)
[28]
夏绪勇, 李书阳, 张永炜, 等. 建筑碳排放设计指南: 探求建筑行业碳中和路径[M]. 北京: 中国建筑工业出版社, 2023.
XIA X Y, LI S Y, ZHANG Y W, et al. Building carbon emission design guidelines: Seeking a path to carbon neutrality in the construction industry[M]. Beijing: China Architecture & Building Press, 2023. (in Chinese)
[29]
刘依明, 刘念雄, 许沛琪. 寒冷地区住宅建材生产阶段碳排放预测模型[J]. 清华大学学报(自然科学版), 2023, 63(1): 15-23.
LIU Y M, LIU N X, XU P Q. Carbon emission prediction model during the material production stage for cold zone residential buildings[J]. Journal of Tsinghua University (Science and Technology), 2023, 63(1): 15-23. (in Chinese)
[30]
中华人民共和国住房和城乡建设部. 建筑节能与可再生能源利用通用规范: GB 55015—2021[S]. 北京: 中国建筑工业出版社, 2022.
Ministry of Housing and Urban-Rural Development of the People's Republic of China. General code for energy efficiency and renewable energy application in buildings: GB 55015—2021[S]. Beijing: China Architecture & Building Press, 2022. (in Chinese)
[31]
何泉, 盛昂昂, 刘大龙. 围护结构保温设计中非稳态计算方法适用性研究[J]. 西安建筑科技大学学报(自然科学版), 2021, 53(4): 561-567.
HE Q, SHENG A A, LIU D L. Study on the applicability of unsteady calculation method in thermal insulation design of enclosure structure in cold area[J]. Journal of Xi'an University of Architecture and Technology (Natural Science Edition), 2021, 53(4): 561-567. (in Chinese)
[32]
中华人民共和国住房和城乡建设部. 严寒和寒冷地区居住建筑节能设计标准: JGJ 26—2018[S]. 北京: 中国建筑工业出版社, 2019.
Ministry of Housing and Urban-Rural Development of the People's Republic of China. Design standard for energy efficiency of residential buildings in severe cold and cold zones: JGJ 26—2018[S]. Beijing: China Architecture & Building Press, 2019. (in Chinese)
[33]
中华人民共和国住房和城乡建设部. 建筑碳排放计算标准: GB/T 51366—2019[S]. 北京: 中国建筑工业出版社, 2019.
Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for building carbon emission calculation: GB/T 51366—2019[S]. Beijing: China Architecture & Building Press, 2019. (in Chinese)
[34]
BAO Y K, LIU Z T. A fast grid search method in support vector regression forecasting time series [C]//Proceedings of the 7th International Conference on Intelligent Data Engineering and Automated Learning (IDEAL 2006). Burgos, Spain: Springer, 2006: 504-511.