2. 中国航天科技集团有限公司 第九研究院, 北京 100094;
3. 战略支援部队信息工程大学, 郑州 450001
2. The 9th Academy, China Aerospace Science and Technology Corporation, Beijing 100094, China;
3. PLA Strategic Support Force Information Engineering University, Zhengzhou 450001, China
近年来,利用无源雷达系统进行城市区域空中目标的监视在学术界得到越来越多的关注。无源雷达系统无须配置专用的发射机,而是利用城市环境中常见的第三方发射机作为机会照射源(illuminator of opportunity, IOO)进行无人机等飞行器目标的探测和定位,可以在不产生新的电磁辐射情况下,实现低成本、高隐蔽性探测,减少对环境影响[1]。目前,包括调频广播电台、数字音频广播、数字视频广播、移动多媒体广播(China mobile multimedia broadcasting, CMMB)和地面数字多媒体广播(digital terrestrial multimedia broadcast, DTMB)等各类模拟和数字信号辐射源,因具有发射功率大、覆盖范围广、可探测隐身目标等优点,为无源雷达系统提供了良好的IOO选择[2]。
在无源雷达中,目标回波的到达角度(angle of arrival, AOA)信息是目标定位过程中一个非常重要的测量量。理论上,联合目标回波的到达角度和时延测量,无源雷达可仅利用单个IOO和接收机,实现目标定位,并且角度信息还提供了对目标高度的多样性观测,可以显著提升目标高度的估计精度[3]。因此,目标回波信号到达角度的估计效果,成为影响无源雷达性能的重要因素。
无源雷达中目标回波信号通常非常微弱,并淹没在噪声和杂波背景中,因此目前一些传统的直接测角算法,如Bartlett[4]、Capon[5]、多信号分类(multiple signal classification, MUSIC)[6]、root-MUSIC[7]、通过旋转不变技术估计信号参数[8] (estimating signal parameter via rotational invariance techniques,ESPRIT)、min-norm[9]以及这些算法的改进算法[10-15],在处理微弱目标回波(例如,回波信号信噪比低于-30 dB)时,测角性能会急剧下降,甚至失效,并且这类直接测角算法可分辨的来波方向数量受到天线阵元数量的限制。得益于学术界的持续探索,已有一些有效的测角算法被提出来。Howland等[16]针对基于电视和调频广播的无源雷达系统,使用一对监视天线来接收目标回波信号,利用距离-Doppler二维相关处理提高目标回波的信噪比,最后在目标对应的距离-Doppler单元采用相位干涉法来估计目标方位角;然而,该方法存在方向模糊问题,且测角精度不高。Colone等[17]对不同调频广播频道测得的到达相位差进行适当平均,提高了方位角的估计精度。Wang等[18]采用4阵元Adcock天线阵列作为无源雷达监视天线,采用互模糊函数对目标回波信号进行时延-Doppler二维相关处理,以获得积累增益来提高目标回波的信噪比,然后提取目标回波所在距离-Doppler单元的峰值,并采用干涉仪测向方法估计目标方位角。上述算法仅能估计目标方位角,并且测角算法被严格限制在特定的天线配置上。Li等在文[19]中将目标回波信号进行分段,分别利用互模糊函数进行相干积累,并提取每段信号的积累峰值,将目标信号转化为多快拍阵列信号,采用MUSIC算法进行角度估计。Park等在文[20]中将目标回波信号在距离-Doppler域相干积累“增强”后,将角度估计问题转化为单快拍阵列测角问题,并采用MUSIC和ESPRIT等子空间算法得到目标回波方位角和俯仰角估计。经过时延-Doppler域的积累增益“增强”以后,上述算法被证明即使在低于-30 dB信噪比的情况下,也能实现对目标回波信号的有效检测和参数估计。
然而,上述算法仍存在明显不足:1) 互模糊函数在计算过程中需要假设在相干积累时间内,目标运动引起的双基地距离变化不超过一个距离分辨单元,而对于高速目标,随着积累时间的延长,目标运动引起的距离变化很容易超过一个距离分辨单元,从而发生距离徙动效应,降低目标回波的积累增益和参数估计效果。2) 互模糊函数的计算复杂度高,难以实时实现。虽然一些模糊函数快速实现方法,如预加权分级抽取快速Fourier变换(fast Fourier transform, FFT)法、多级滤波的预加权细化FFT(zoom-FFT, ZFFT)法等[21-23],可在一定程度上降低计算量,但实现过程仍较复杂,对于一些低算力平台并不适用。3) 上述算法仅在时延-Doppler域分辨目标,无法在角度维度进一步分辨目标,因此无法处理单个距离-Doppler单元存在2个或多个目标(比如多个无人机目标编队飞行)的情况。
本文算法对无源雷达中的目标角度估计问题进行了进一步研究。由于均匀圆形天线阵(uniform circular array, UCA)具有圆对称性,能同时对360°方位角和180°俯仰角进行估计,提供各向相似、无相位模糊的测角性能,因此在无源雷达领域得到了广泛应用和研究。本文基于一个使用UCA的无源雷达系统,针对该无源雷达系统中高速多目标方位角和俯仰角估计问题,设计了一种基于Keystone变换、阵列轴向虚拟平移和MUSIC算法的相干积累和角度估计算法。相比于现有算法,本文算法的主要创新在于:
1) 通过对信号进行分段处理,划分了快时间和慢时间,使得后续可以采用FFT对目标信号高效处理,降低了计算复杂度。
2) 利用Keystone变换,校正了目标高速运动引发的距离徙动,从而保证算法在处理高速运动目标时,依然能够充分地积累回波信号的能量。
3) 通过阵列轴向虚拟平移方法对信号解相干处理,可分辨同一时延-Doppler域内的多个目标,提高了算法对多目标信号的处理能力。
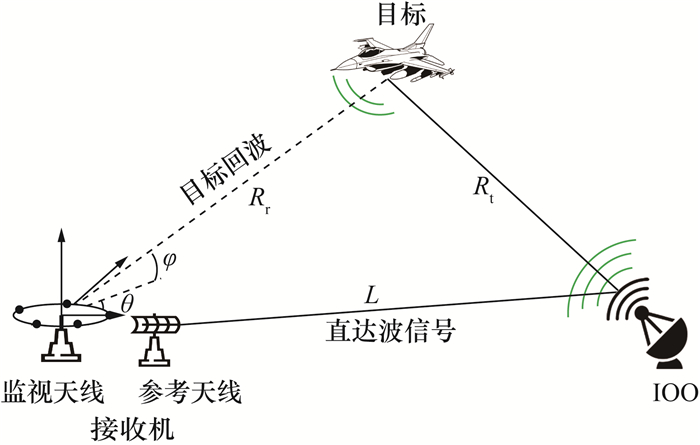
1 系统结构和信号模型一般来说,一个典型的无源雷达系统包括一个IOO和一个接收机,如图 1所示。接收机具有两套天线:一套是参考天线,用于接收IOO发射的直达波信号;另一套是监视天线,用于接收目标回波。监视天线是由Nem个各向同性的全向阵元组成的均匀排列圆阵。
|
| 图 1 无源雷达信号传播模型 |
IOO发射的窄带信号为
| $u(t)=s(t) \mathrm{e}^{\mathrm{j} 2 {\rm{ \mathsf{ π}}} f_{{\rm{c}}} t} .$ | (1) |
其中:s(t)表示复数基带信号,fc为信号载频,t为时间。由于IOO的非合作性,因此s(t)一般难以准确得到,需要通过参考天线进行接收。忽略杂波和噪声的影响,则参考天线的接收信号可以表示为
| $s_{\mathrm{r}}(t)=b_{\mathrm{r}} \mathrm{e}^{\mathrm{j} \phi_{r}} u\left[t-\frac{R_{\mathrm{d}}(t)}{c}\right] .$ | (2) |
其中:br表示信号的相对振幅,ϕr表示经过信道和接收机效应影响后信号的相移,Rd(t)表示IOO和接收机之间的距离,c为光速。
假设监视区域中存在K个目标,IOO发射的信号经过目标反射/散射后,入射到阵元i上的接收信号ss, i(t)可表示为
| $ \begin{gather*} s_{\mathrm{s}, i}(t)= \\ \sum\limits_{k} b_{\mathrm{s}, k} \mathrm{e}^{\mathrm{j} \phi_{\mathrm{s}, k}} u\left[t-\frac{R_{\mathrm{t}, k}(t)+R_{\mathrm{r}, k}(t)}{c}\right] \mathrm{e}^{\mathrm{j} \phi_{i, k}} . \end{gather*}$ | (3) |
其中:bs, k和ϕs, k分别表示第k个目标信号到达接收机的相对振幅和相移;Rt, k(t)和Rr, k(t)分别表示第k个目标到IOO和接收机的距离;ϕi, k表示第k个目标信号到达接收机圆阵中心与到达阵元i的相位差,与阵元位置、目标到达角度有关。
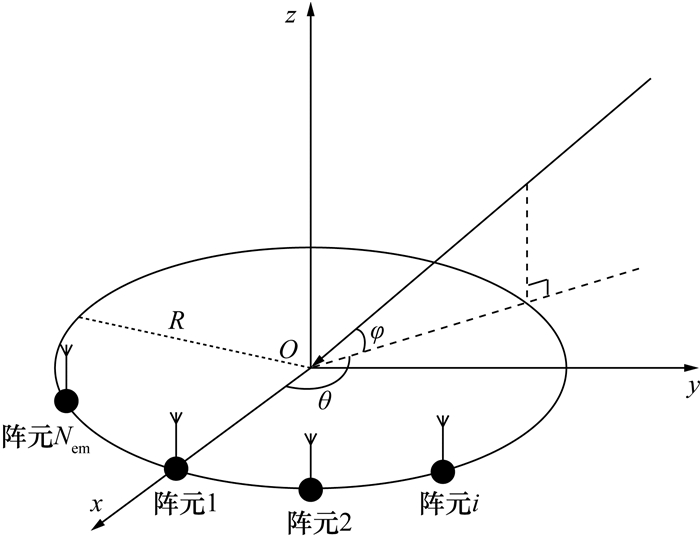
监视天线阵列结构如图 2所示。Nem个各向同性的全向阵元均匀排列在半径为R的圆周上,阵元夹角为2π/Nem,阵元1与x轴正方向的夹角为γ。假设第k个目标回波信号入射的方位角为θk,俯仰角为φk,其中方位角定义为入射信号在x-y平面投影射线与x轴正方向的夹角,俯仰角定义为入射信号与其在x-y平面投影射线之间的夹角。
|
| 图 2 监视天线阵列构型 |
由于阵元位置的不同,目标回波信号到达不同阵元的相位也不同。以圆阵中心O作为参考原点,则第k个目标回波信号到达阵元i与到达圆阵中心的相位差可以表示为
| $\phi_{i, k}=\frac{2 {\rm{ \mathsf{ π}}} R}{\lambda} \cos \left(\varphi_{k}\right) \cos \left(\theta_{k}-\gamma-\gamma_{i}\right).$ | (4) |
其中:γi=
由于IOO的非合作性,无源雷达领域中通常提取目标回波信号与直达波信号的路径差用作目标定位。为此,利用变量替换,将式(2)和(3)中的接收信号表示为:
| $s_{\mathrm{r}}(t)=u(t), $ | (5) |
| $s_{\mathrm{s}, i}(t)=\sum\limits_{k} b_{k} \mathrm{e}^{\mathrm{j} \phi_{k}} u\left[t-\frac{r_{k}(t)}{c}\right] \mathrm{e}^{\mathrm{j} \phi_{i, k}}.$ | (6) |
其中:bk=bs, k/br;ϕk=ϕs, k-ϕr;rk(t)=Rt, k(t)+Rr, k(t)-Rd(t) 表示第k个目标回波信号与直达波信号的路径差,用Taylor级数将它展开至一阶项为
| $r_{k}(t) \approx c \tau_{k}+v_{k} t .$ | (7) |
式中:τk和vk分别表示第k个目标的双基地时延和双基地Doppler速度。
对接收的参考信号和监视信号进行下变频处理,得到基带接收信号为:
| $s_{\mathrm{r}}(t)=s(t) , $ | (8) |
| $s_{\mathrm{s}, i}(t)=\sum\limits_{k} b_{k} \mathrm{e}^{\mathrm{j} \phi_{k}} s\left[t-\frac{r_{k}(t)}{c}\right] \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}} f_{\mathrm{c}} \frac{r_{k}(t)}{c}} \mathrm{e}^{\mathrm{j} \phi_{i, k}} .$ | (9) |
为了便于表述,这里忽略了式(8)和(9)中的噪声。特别是对于式(9)中监视信号,其目标回波信号非常微弱,难以直接测向。
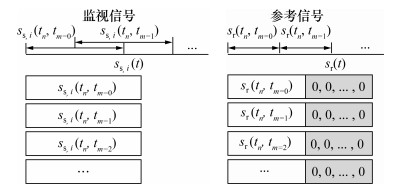
2 算法设计 2.1 信号分段无源雷达中通常通过互模糊函数实现信号能量的同相叠加,从而获得积累增益,提高信号的信噪比。然而,互模糊函数的计算复杂度高,在低算力平台上难以应用。本文对参考信号和监视信号进行分段处理,人为构造等效脉冲信号,然后利用脉冲相干积累获得积累增益。具体分段方法图 3所示。
|
| 图 3 信号分段示意图 |
在实际应用中,最大时延与最大Doppler速度影响着信号分段及段间重叠大小的选择。取值过大将造成计算复杂度增加,过小将导致距离和速度模糊。一种合理的方法是利用双基地雷达方程评估无源雷达目标探测的覆盖范围[24]:
| $\tau=R_{\mathrm{t}}+R_{\mathrm{r}}-L, $ | (10) |
| $f_{\mathrm{d}}=\frac{2 v \cos (\beta / 2)}{\lambda} .$ | (11) |
式中:Rt为发射机到目标的距离,Rr为接收机到目标的距离,L为双基地的距离,τ为压缩后的脉冲宽度;v为目标速度,λ为信号波长,β为双基地角。然后,根据目标的双基地时延和Doppler理论公式和潜在目标最大运动速度可计算无源雷达覆盖范围内最大时延与最大Doppler速度的取值。
首先,根据潜在目标的最大Doppler速度确定等效脉冲重复频率(pulse repetition frequency, PRF)。
| $\operatorname{PRF}=\frac{2 v_{\max }}{\lambda}, $ | (12) |
其中vmax为潜在目标的最大Doppler速度。根据等效PRF,可以确定信号的分段数M为
| $M=T \cdot \mathrm{PRF}.$ | (13) |
其中T为信号积累时间。
按照上述确定的分段数对参考信号和监视信号进行分段,每段信号的有效长度Neff为
| $N_{\mathrm{eff}}=\frac{T f_{\mathrm{s}}}{M}.$ | (14) |
其中fs为信号采样频率。对于监视信号,需要对采用重叠分段的方式,解决等效PRF和等效脉冲长度之间的矛盾关系。假设潜在目标的最大时延为τmax,那么重叠部分的信号长度Nτ为
| $N_{\tau}=\tau_{\max } f_{\mathrm{s}}.$ | (15) |
重叠分段后的每段监视信号的长度为N=Neff+Nτ。对于参考信号,通过末尾补零的方式使其每段信号的长度与监视信号保持一致。通过监视信号的分段重叠,可以保证每段监视信号具有足够大的等效脉冲长度和PRF,从而避免距离模糊和速度模糊现象。此外,监视信号重叠分段和参考信号末尾补零的处理方式,可以保证不同时延处的目标的积累增益保持恒定。
经过上述分时处理,得到如下的等效脉冲信号:
| $s_{\mathrm{r}}\left(t_{n}, t_{m}\right)=s\left(t_{n}\right), $ | (16) |
| $ \begin{gather*} s_{\mathrm{s}, i}\left(t_{n}, t_{m}\right)= \\ \sum\limits_{k} b_{k} \mathrm{e}^{\mathrm{j} \phi_{k}} s\left[t_{n}-\frac{r\left(t_{m}\right)}{c}\right] \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}} f_{\mathrm{c}} \frac{r_{k} (t_{m})}{c}} \mathrm{e}^{\mathrm{j} \phi_{i, k}} . \end{gather*}$ | (17) |
式中:tn=n/fs为快时间,n=0, 1, …, N-1;tm=m/PRF为慢时间,m=0, 1, …, M-1。
2.2 Keystone变换对分段信号沿快时间tn进行FFT,从而将它从快时间域变换至频率域:
| $S_{\mathrm{r}}\left(f_{n}, t_{m}\right)=S\left(f_{n}\right), $ | (18) |
| $ \begin{array}{c} S_{\mathrm{s}, i}\left(f_{n}, t_{m}\right)= \\ \sum\limits_{k} b_{k} \mathrm{e}^{\mathrm{j} \phi_{k}} S\left(f_{n}\right) \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}}\left(f_{\mathrm{c}}+f_{n}\right) \frac{c \tau_{k}+v_{k} t_{m}}{c}} \mathrm{e}^{\mathrm{j} \phi_{i, k}} . \end{array}$ | (19) |
将式(18)和(19)共轭相乘,可以得到
| $ \begin{align*} & Y_{i}\left(f_{n}, t_{m}\right)=S_{\mathrm{s}, i}\left(f_{n}, t_{m}\right) S_{\mathrm{r}}^{*}\left(f_{n}, t_{m}\right)= \\ & \sum\limits_{k} b_{k} \mathrm{e}^{\mathrm{j} \phi_{k}}\left|S\left(f_{n}\right)\right|^{2} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}}(f_{\mathrm{c}}+f_{n} )\frac{c \tau_{k}+v_{k} t_{m}}{c}} \mathrm{e}^{\mathrm{j} \phi_{i, k}} . \end{align*}$ | (20) |
式中*表示取共轭。式(20)中相位项
| $t_{m}^{\prime} =\frac{f_{\mathrm{c}}+f_{n}}{f_{\mathrm{c}}} t_{m} .$ | (21) |
| $t_{m} =\frac{f_{\mathrm{c}}}{f_{\mathrm{c}}+f_{n}} t_{m}^{\prime}.$ | (22) |
将式(22)代入式(20),经整理得到
| $ \begin{gather*} Y_{i}\left(f_{n}, t_{m}^{\prime}\right)= \\ \sum\limits_{k} b_{k} \mathrm{e}^{\mathrm{j} \phi_{k}}\left|S\left(f_{n}\right)\right|^{2} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π}}}\left(f_{{\rm{c}}}+f_{n}\right) \tau_{k}} \mathrm{e}^{-{\rm{j}}\frac{2 {\rm{ \mathsf{ π}}} f_{{\rm{c}}}}{c} v_{k} t_{m}^{\prime}} \mathrm{e}^{\mathrm{j} \phi_{i, k}} . \end{gather*}$ | (23) |
显然,经过Keystone变换后,相位项中距离频域fn与慢时间t′m不再存在耦合关系。这意味着,对于不同的慢时间,第k个目标回波信号的峰值位置将始终位于τk处,即Keystone变换把位于不同时延单元的目标回波校正到同一时延单元,消除了距离徙动效应。
为了进一步将式(23)中目标的回波包络积累至对应的时延-Doppler域,对式(23)沿距离频率fn进行逆FFT(inverse FFT, IFFT),得
| $ \begin{gather*} y_{i}\left(t_{n}, t_{m}^{\prime}\right)= \\ \sum\limits_{k} a_{k} p\left(t_{n}-\tau_{k}\right) \mathrm{e}^{-\mathrm{j} \frac{2 {\rm{ \mathsf{ π}}} f_{{\rm{c}}}}{c} v_{k} t_{m}^{\prime}} \mathrm{e}^{{\rm{j}} \phi_{i, k}} . \end{gather*}$ | (24) |
式中:ak表示信号幅度;p(tn)=IFFT[|S(fn)|2],其峰值位于tn=0处。将式(24)沿慢时间t′m进行FFT得
| $ \begin{gather*} \chi_{i}\left(t_{n}, f_{m}\right)= \\ \sum\limits_{k} a_{k}^{\prime} p\left(t_{n}-\tau_{k}\right) \operatorname{sinc}\left[T\left(f_{m}+\frac{f_{\mathrm{c}} v_{k}}{c}\right)\right] \mathrm{e}^{\mathrm{j} \phi_{i, k}} . \end{gather*}$ | (25) |
式中a′k表示信号幅度。显然,式(25)表明第k个目标回波信号能量被积累至χi(tn, fm)的峰值(τk, -fcvk/c)处。通过检测并寻找χi(tn, fm)峰值,可估计出目标时延和Doppler速度。
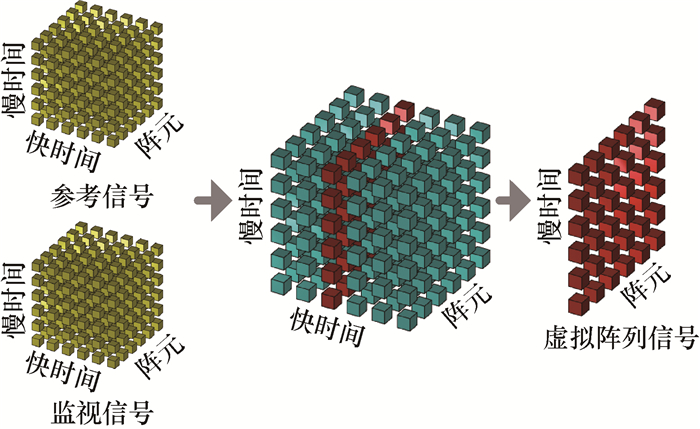
2.3 角度估计经过时延-Doppler处理后,无源雷达接收信号中的各目标回波信号能量已经被积累至对应的时延-Doppler域(τk,-fcvk/c)内,如图 4所示。
|
| 图 4 目标信号处理流程示意图 |
忽略第k个目标时延-Doppler域内其他目标峰值旁瓣的干扰,从式(24)中提取时延单元τk对应的信号,可将无源雷达阵元i接收信号转化为慢时间维度的多快拍信号。显然,同一时延单元内,可能存在多个目标回波信号。根据第1章图 2中监视天线的阵列构型,假设时延单元τk中有P个目标回波信号,信号入射方位角为{θl|θl∈[0, 2π)}l=1P,俯仰角为{φl|φl∈[0, π/2]}l=1P,则第t′m时刻Nem×1维虚拟阵列接收数据向量可表示为
| $ \begin{gather*} \boldsymbol{x}\left(t_{m}^{\prime}\right)=\left[\boldsymbol{x}_{1}\left(t_{m}^{\prime}\right), \boldsymbol{x}_{2}\left(t_{m}^{\prime}\right), \cdots, \boldsymbol{x}_{N_{\mathrm{em}}}\left(t_{m}^{\prime}\right)\right]^{\mathrm{T}}= \\ \boldsymbol{A} \boldsymbol{s}\left(t_{m}^{\prime}\right)+\boldsymbol{w}\left(t_{m}^{\prime}\right). \end{gather*}$ | (26) |
式中A=[a(θ1, φ1), …a(θP, φP)]为Nem×P维阵列流形矩阵,其中,
| $ \boldsymbol{a}\left(\theta_{l}, \varphi_{l}\right)=\left[\begin{array}{c} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{ \mathsf{ π}}} R}{\lambda} \cos \left(\varphi_{l}\right) \cos \left(\theta_{l}-\gamma-\gamma_{1}\right)} \\ \mathrm{e}^{\mathrm{j} \frac{2 {\rm{ \mathsf{ π}}} R}{\lambda} \cos \left(\varphi_{l}\right) \cos \left(\theta_{l}-\gamma-\gamma_{2}\right)} \\ \vdots \\ \mathrm{e}^{\mathrm{j} \frac{2 {\rm{ \mathsf{ π}}} R}{\lambda} \cos \left(\varphi_{l}\right) \cos \left(\theta_{l}-\gamma-\gamma_{N_{\mathrm{em}}}\right)} \end{array}\right].$ | (27) |
式(26)中:s(t′m)=[s1(t′m), …, sp(t′m)]T为P×1维信号向量,w(t′m)=[w1 (t′m), …, wNem(t′m)]T为Nem×1维噪声向量。这里假设这2个向量互相独立且服从Gauss分布N(0, σw2)。
基于上述描述,可计算阵列接收信号的Nem×Nem维自协方差矩阵为
| $ \begin{equation*} \boldsymbol{R}_{x x}=\boldsymbol{E}\left[\boldsymbol{x}\left(t_{m}^{\prime}\right) \boldsymbol{x}^{\mathrm{H}}\left(t_{m}^{\prime}\right)\right]=\boldsymbol{A} \boldsymbol{R}_{s s} \boldsymbol{A}^{\mathrm{H}}+\sigma_{\mathrm{w}}^{2} \boldsymbol{I} . \end{equation*}$ | (28) |
式中:Rss=E[s(t′m)sH(t′m)]为P×P维信号协方差矩阵,E为单位向量,I为单位矩阵。若信号s1(t′m), …, sp(t′m)互不相干,则矩阵Rss满秩P。因此,在没有噪声的情况下,Rxx与Rss的秩相等,均为P。对协方差矩阵Rxx进行特征值分解,并将特征值从大到小排列,即λ1≥λ2≥…λP>λP+1≈…≈λNem≈0。其中:P个大特征值λ1, λ2, …, λP对应信号子空间,特征向量为Es;其余的Nem-P个小特征值λP+1, …, λNem对应噪声子空间,特征向量为Ew。根据阵列流型向量矩阵与噪声特征向量之间的正交性,构建MUSIC空间频谱为[5]
| $P_{\mathrm{MUSIC}}(\theta, \varphi)=\frac{1}{\boldsymbol{a}(\theta, \varphi)^{\mathrm{H}} \boldsymbol{E}_{\mathrm{w}} \boldsymbol{E}_{\mathrm{w}}^{\mathrm{H}} \boldsymbol{a}(\theta, \varphi)}.$ | (29) |
由于噪声子空间特征向量在目标回波到达角(θ1, φ1), …, (θP, φP)与阵列流型向量正交,MUSIC空间谱在(θ1, φ1), …, (θP, φP)角度存在极大值。对MUSIC空间谱进行二维谱峰搜索,得到目标回波的方位角和俯仰角估计:
| $ \begin{align*} \left(\theta_{l}, \varphi_{l}\right)= & \arg \left\{\max \left(P_{\mathrm{MUSIC}}\right)>P_{\text {Thresh }}\right\}, \\ & l=1, 2, \cdots, P . \end{align*}$ | (30) |
式中PThresh为角度检测的阈值。
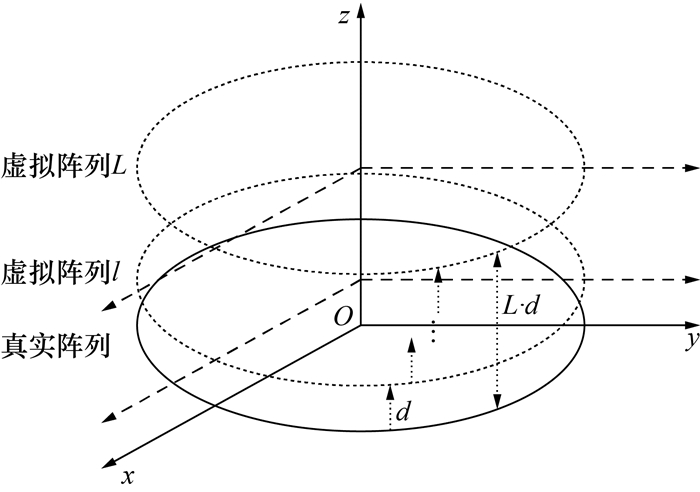
用MUSIC算法估计信号角度时需假设入射信号互不相干,然而实际中P个目标回波信号的Doppler频率可能相同或不同,意味着信号s1(t′m), …, sp(t′m)中可能存在相干信号,此时矩阵Rss和Rxx不满秩,因此大特征值的数量小于P。这里假设P个信号中存在L个相干信号,P-L个非相干信号,那么可知rank(Rs)=P-L+1=Q。此时MUSIC空间谱只能估计出P-L个不相干信号的来波方向和一个由相干信号合成向量求得的虚假来波方向。因此,需要通过解相干处理,使协方差矩阵恢复满秩。这里采用UCA阵列虚拟平移方法实现信号的解相干。天线阵列z轴虚拟平移如图 5所示。
|
| 图 5 天线阵列z轴虚拟平移 |
UCA阵列虚拟平移方法将真实阵列向空间内某一方向进行数次平移,再计算平移后虚拟阵列接收信号协方差矩阵。当平移次数不小于相干信号数时,即可恢复协方差矩阵的秩。本文将阵列向z轴正方向平移Nshift次,每次移动距离d=λ/2,从而构造Nshift个虚拟阵列。第h次平移后,信号到达虚拟圆阵中心Oh与真实圆阵中心O的时间差为τh=dsin(φl)/c,因此可构建一个P×P维的正交变换对角矩阵,
| ${\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}}_{h}=\operatorname{diag}\left[-\mathrm{e}^{\mathrm{j} \frac{2 {\rm{ \mathsf{ π}}} d}{\lambda} \sin \varphi_{1}}, \cdots, -\mathrm{e}^{\mathrm{j} \frac{2 {\rm{ \mathsf{ π}}} d}{\lambda} \sin \varphi_{P}}\right]^{\mathrm{T}}.$ | (31) |
因此,可将第h次z轴平移后虚拟圆阵的接收信号表示为
| $\boldsymbol{x}_{h}\left(t_{m}^{\prime}\right)=\boldsymbol{A} {\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}}_{h} \boldsymbol{s}\left(t_{m}^{\prime}\right)+\boldsymbol{w}_{h}\left(t_{m}^{\prime}\right).$ | (32) |
对应地,平移后的接收信号协方差矩阵为
| $\boldsymbol{R}_{x x}, h=\boldsymbol{A} {\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}}_{h} \boldsymbol{R}_{s s} {\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}}_{h}^{\mathrm{H}} \boldsymbol{A}^{\mathrm{H}}+\sigma_{\mathrm{w}}^{2} \boldsymbol{I} .$ | (33) |
计算协方差矩阵的均值,得
| $ \begin{gather*} \overline{\boldsymbol{R}}_{x x}=\frac{1}{N_{\text {shift }}+1} \sum\limits_{h=0}^{N_{\text {shift }}} \boldsymbol{R}_{x x, h}= \\ \frac{1}{N_{\text {shift }}+1} \sum\limits_{h=0}^{N_{\text {shift }}} \boldsymbol{A} {\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}}_{h} \boldsymbol{R}_{s s} {\mathit{\boldsymbol{ \boldsymbol{\varPhi}}}}_{h}^{\mathrm{H}} \boldsymbol{A}^{\mathrm{H}}+\sigma_{\mathrm{w}}^{2} \boldsymbol{I} . \end{gather*}$ | (34) |
当平移次数Nshift大于或等于相干信号数L时,即可使协方差矩阵Rxx满秩。
3 仿真分析为了验证本文算法的有效性,将该算法与文[19]算法(记为Li算法)以及文[20]算法(记为Park算法)进行对比。假设场景中存在1部无源雷达系统以及3个运动目标。无源雷达机会照射源的信号模型为
| $u(t)=\exp \left(\mathrm{j} 2 {\rm{ \mathsf{ π}}} f_{\mathrm{c}} t+\mathrm{j} 2 {\rm{ \mathsf{ π}}} K_{f} \operatorname{cumsum}(m(t))\right) .$ | (35) |
式中:Kf为频偏常数;cumsum(·)为累积和函数;m(t) 表示基带数据,这里设置为0~15的随机整数序列。机会照射源信号参数调制方式为频率调制,载波频率为800 MHz,带宽为8 MHz,频谱常数为6.4×105。
3个运动目标对应的时延、Doppler速度以及角度参数如表 1所示。
| 参数 | 时延/μs | Doppler速度/(m·s-1) | 方位角/(°) | 俯仰角/(°) |
| 目标1 | 200 | 200 | 90 | 30 |
| 目标2 | 200 | 1 000 | 45 | 30 |
| 目标3 | 200 | 1 000 | 60 | 30 |
无源雷达监视通道采用16阵元的均匀圆阵天线,各相邻阵元间距为半波长,采样率设置为8 MHz,采样点数为4 000 000,最大时延为267 μs、最大Doppler速度为1 200 m/s。
根据IOO信号参数以及潜在目标的最大时延、最大Doppler速度等参数,对接收信号进行分段处理,分段后参数为:PRF 6 400、分段数3 200、有效点数1 250、重叠点数2 133。
为验证本文算法对无源雷达微弱目标回波信号的有效性,按照上述场景设置,对3个目标回波信号进行仿真实验。参考信号信噪比为30 dB,3个目标的回波信号信噪比均设置为-15 dB。本文中信噪比指的是相干积累前接收信号的信噪比。目标回波信号分段后的结果如图 6所示。从图 6可以看出,在对天线阵元接收信号完成分段后,即人为划分出了快慢时间和等效脉冲,但是3个目标回波信号都非常微弱,整体淹没在噪声以下。

|
| 图 6 等效脉冲划分结果 |
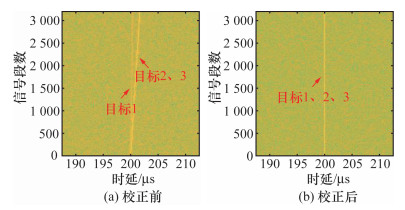
利用参考信号对各天线阵元接收信号进行匹配滤波,结果如图 7a所示。在目标高速移动的情况下,其回波信号经匹配滤波处理后,能量沿快时间维度跨越多个时延单元,从而出现距离徙动效应。进一步可以发现,由于目标1速度200 m/s、目标2和目标3速度为1 000 m/s,因此目标2、3的距离徙动效应比目标1更加严重。本文利用Keystone变换校正距离徙动后,结果如图 7b所示。经过Keystone变换后,3个目标回波信号被校正至时延200 μs单元。与表 1中目标实际参数对比,可以看到该时延单元即为目标真实时延单元。但同时也可看到,由于3个目标回波时延均为200 μs,因此仅从时延参数维度无法区分3个目标回波。
|
| 图 7 距离徙动校正前后对比图 |
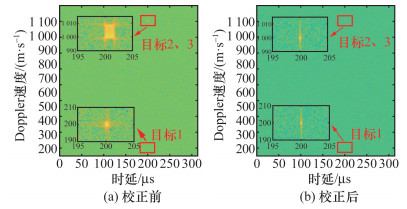
校正距离徙动后,对匹配滤波结果沿慢时间进行FFT,可将目标回波信号进一步积累至各自对应的时延-Doppler域。经过距离徙动校正和未经过距离徙动校正情况下,目标回波信号的时延-Doppler积累结果的对比如图 8所示。可以看到,图 8a中距离徙动未校正情况下,虽然在时延-Doppler图中可以在(200 μs, 200 m/s)、(200 μs, 1 000 m/s)附近形成2个峰,分别对应于目标1和目标2、3,然而距离徙引起目标回波能量以不同程度散布到多个距离单元内,最终导致相干积累增益的下降。并且,目标2、3由于速度比目标1更高,因此积累峰的能量散布更加严重。与之形成对比的是,图 8b中距离徙动校正后,3个目标回波信号能量被积累至对应的时延-Doppler域内,积累形成的能量峰更加尖锐。此外,由于在时延-Doppler域内,目标1和目标2、3被分辨出来,而目标2和目标3由于时延和Doppler参数相同,因此未被分辨出来。
|
| 图 8 相干积累结果校正前后对比 |
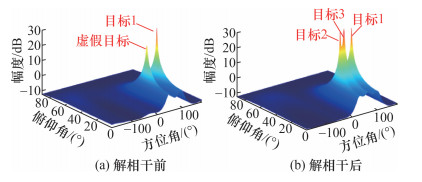
对时延-Doppler图进行恒虚警检测(constant false alarm rate detector, CFAR),提取目标真实时延所在的时延单元对应的慢时间维信号,形成虚拟阵元慢时间维度多快拍信号,然后结合阵列虚拟平移解相干和MUSIC算法,进行空间谱估计,结果如图 9所示。作为对比,未进行解相干处理而直接利用MUSIC算法进行空间谱估计的结果也被一并给出。结果表明,未进行解相干处理时,MUSIC空间谱仅在(90°, 30°)和(51.5°, 30°)附近形成2个强峰,其中(90°, 30°)对应目标1真实来波方向,(51.5°, 30°)为目标2、3相干信号合成的虚假来波方向。与之对比,本文算法经过阵列虚拟平移解相干和MUSIC算法处理后,可以清楚地分辨出位于(90°, 30°)、(45°, 30°)和(60°, 30°)的3个强峰,分别与目标1、2、3真实来波方向吻合。
|
| 图 9 阵列平移解相干前后的MUSIC空间谱 |
为了进一步分析本文算法的参数估计性能,进行如下Monte Carlo仿真实验。
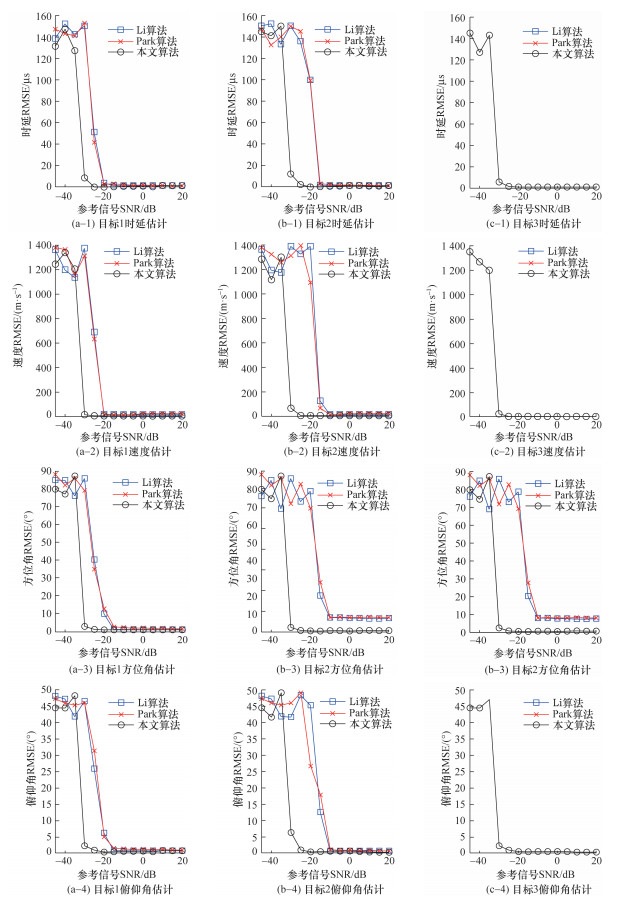
实验1 设定3个目标回波的信噪比为-20 dB,参考信号的信噪比在-45 ~20 dB范围内以5 dB步长变化,其余条件保持不变。每种参考信号信噪比条件下分别进行200次独立Monte Carlo仿真,经统计后得到算法在不同参考信号信噪比条件下对各目标时延、Doppler速度、方位角和俯仰角的估计误差情况,如图 10所示。
|
| 图 10 不同参考信号条件下算法参数估计性能对比 |
图 10给出了不同参考信号条件下,本文算法与Li算法、Park算法在时延、Doppler速度、方位角和俯仰角等参数估计性能方面的对比。显然,总体上参考信号信噪比越高,算法对于时延、Doppler速度、方位角和俯仰角的估计误差越小。但是,不同算法之间仿真结果的对比表明,本文算法在不同参考信号信噪比条件下,对3个目标信号的参数估计效果均优于Li算法和Park算法。具体来说,对于非相干的目标1信号,由于本文算法考虑并校正了目标高速运动引起的距离徙动,减小了时延和Doppler速度的估计误差,继而减小了后续的角度估计误差。因此,虽然在参考信号信噪比足够高的情况下3种算法都能稳定估计时延、Doppler速度、方位角和俯仰角,但本文算法的参数估计误差小于Park算法和Li算法,并且本文算法估计误差发生门限效应的阈值比Park算法低约15 dB,也就是说,本文算法可以在更低的参考信号信噪比条件下实现高速目标回波信号的参数估计。对于相干的目标2和目标3信号,仅本文算法可以分辨出目标2和目标3的信号,并准确估计2个目标的时延、Doppler速度、方位角和俯仰角。Li算法和Park算法未考虑同一时延-Doppler域内存在多个目标的情况,因此未对目标2和目标3的信号进行解相干,从而导致Li算法和Park算法在不同的参考信号条件下,无法分辨出目标2和目标3这2个信号,并且形成的合成来波方向的方位角误差显著大于本文算法。
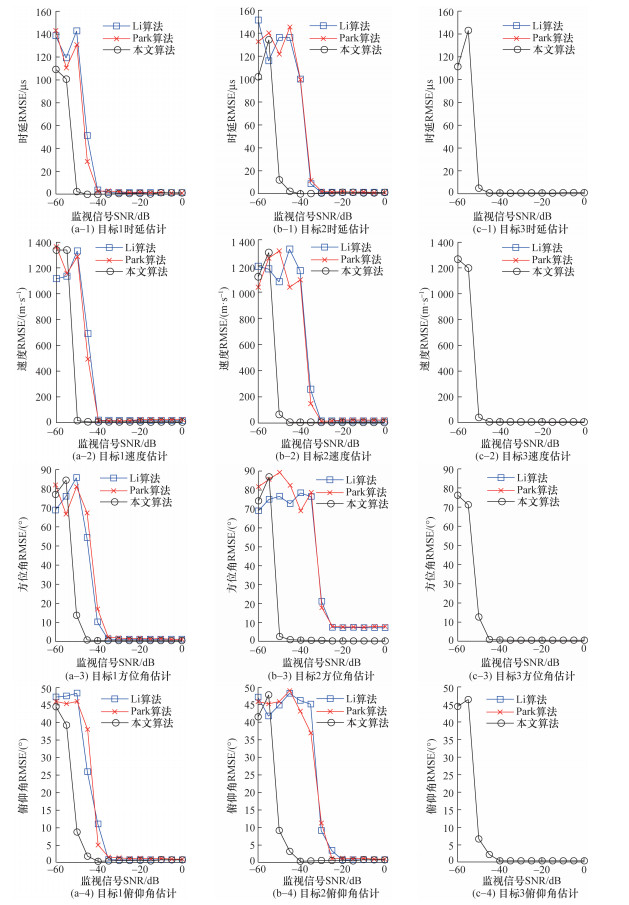
实验2 设定参考信号信噪比为25 dB,将3个目标回波的信噪比进行变化(3个目标的信噪比相同)。每种信噪比情况下分别进行200次独立Monte Carlo仿真,经统计后得到算法在不同回波信号信噪比条件下对各目标时延、Doppler速度、方位角和俯仰角的估计误差情况如图 11所示。
|
| 图 11 不同回波信号条件下算法参数估计性能对比 |
从图 11中可以看出,本文算法在不同的回波信号条件下,对时延、Doppler速度、方位角和俯仰角的估计误差仍然显著优于Li算法和Park算法,本文算法的门限阈值约为回波信号信噪比-50 dB,Li算法和Park算法的门限阈值均约为-35 dB,本文算法估计误差发生门限效应的阈值比Park算法和Li算法低约15 dB,说明本文算法可以实现对更微弱的目标回波信号相干积累和参数估计。并且,实际中回波信号信噪比一般比较低,因此本文算法在低信噪比条件下对目标参数估计性能的改善,对于实际应用中提高无源雷达性能更具意义。
为了证明本文算法计算复杂度优势,下面对比了3种算法的计算复杂度。计算复杂度在这里代表了算法涉及的复数乘法次数的数量级。算法运行平台的主要配置如下:处理器为Intel(R) Core(TM) i7-8550U @1.80 GHz;内存为16 GB DDR4 2 666 MHz;系统为Windows 10;软件为MATLAB R2021b。计算复杂度比较的结果如表 2所示。
| 算法 | 理论计算复杂度 | 平均运行时间/s |
| Li算法 | O{NemNτ( |
523.4 |
| Park算法 | O{NemNτ( |
487.4 |
| 本文算法 | O{Nem[3MNlog2N+NMlog2(2M)+2MNP(P+2)]+MNem2+Nem3+NsaNseNem2} | 3.47 |
表 2中:Nτ=N为时延单元搜索数量,NT=Tfs为信号点数,Nsa和Nse为方位角和俯仰角搜索数量。本文Keystone变换采用Lagrange P(P=3)阶多项式插值法实现[26]。从算法的计算复杂度比较可以看出,Li算法的平均运行时间高于Park算法的原因在于Li算法在测角阶段采用的快拍数更高。相比于Li算法和Park算法采用互模糊函数进行时延-Doppler处理,本文算法采用分段处理结合Keystone变换进行时延-Doppler处理的方式,不仅校正了目标的距离徙动,还可以将计算复杂度大大降低,使得算法的稳健性和实时性均有提高。
4 结论本文对无源雷达中微弱目标回波的角度估计问题进行研究,提出了一种更加高效稳健的时延-Doppler域角度估计算法。1) 根据目标运动和外辐射源信号参数,对参考信号和监视信号进行分段处理,段内为快时间,段间为慢时间;2) 考虑到目标高速运动情况下可能引发距离徙动问题,利用Keystone变换对各频率的时间轴进行尺度变换,校正高速目标的距离徙动,继而将目标回波信号能量积累至同一时延-Doppler域;3) 检测并提取目标回波所在时延单元的阵元慢时间采样信号,并转化为慢时间维度的多快拍信号测角问题,最后利用均匀圆阵轴向虚拟平移解相干和MUSIC算法对信号处理得到目标回波方位角和俯仰角估计。仿真结果表明,本文算法可以以较低的计算复杂度实现无源雷达微弱目标回波信号的角度估计,特别是在高速、多目标场景下,表现出明显的性能优势。
| [1] |
COLONE F, FILIPPINI F, PASTINA D. Passive radar: Past, present, and future challenges[J]. IEEE Aerospace and Electronic Systems Magazine, 2023, 38(1): 54-69. DOI:10.1109/MAES.2022.3221685 |
| [2] |
LI Y, HE Q, BLUM R S. Illuminator of opportunity selection for passive radar [C]//Proceedings of 2017 IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP). Curaçao: IEEE, 2017: 1-5.
|
| [3] |
NOROOZI A, SEBT M A. Weighted least squares target location estimation in multi-transmitter multi-receiver passive radar using bistatic range measurements[J]. IET Radar, Sonar & Navigation, 2016, 10(6): 1088-1097. |
| [4] |
KRIM H, VIBERG M. Two decades of array signal processing research: The parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94. DOI:10.1109/79.526899 |
| [5] |
CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278 |
| [6] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 |
| [7] |
BARABELL A. Improving the resolution performance of eigenstructure-based direction-finding algorithms [C]//Proceedings of ICASSP. IEEE International Conference on Acoustics, Speech, and Signal Processing. Boston, USA: IEEE, 1983: 336-339.
|
| [8] |
ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995. DOI:10.1109/29.32276 |
| [9] |
KUMARESAN R, TUFTS D W. Estimating the angles of arrival of multiple plane waves[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(1): 134-139. DOI:10.1109/TAES.1983.309427 |
| [10] |
WANG Z S, XIE W, ZOU Y B, et al. DOA estimation using single or dual reception channels based on cyclostationarity[J]. IEEE Access, 2019, 7: 54787-54795. DOI:10.1109/ACCESS.2019.2912907 |
| [11] |
LI J F, LI D, JIANG D F, et al. Extended-aperture unitary root MUSIC-based DOA estimation for coprime array[J]. IEEE Communications Letters, 2018, 22(4): 752-755. DOI:10.1109/LCOMM.2018.2802491 |
| [12] |
LIU A H, ZHANG X, YANG Q, et al. Fast DOA estimation algorithms for sparse uniform linear array with multiple integer frequencies[J]. IEEE Access, 2018, 6: 29952-29965. DOI:10.1109/ACCESS.2018.2842262 |
| [13] |
SHI J P, HU G P, ZHANG X F, et al. Sparsity-based two-dimensional DOA estimation for coprime array: From sum-difference coarray viewpoint[J]. IEEE Transactions on Signal Processing, 2017, 65(21): 5591-5604. DOI:10.1109/TSP.2017.2739105 |
| [14] |
WEN F Q, SHI J P, ZHANG Z J. Joint 2D-DOD, 2D-DOA, and polarization angles estimation for bistatic EMVS-MIMO radar via PARAFAC analysis[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1626-1638. DOI:10.1109/TVT.2019.2957511 |
| [15] |
WANG X P, WAN L T, HUANG M X, et al. Low-complexity channel estimation for circular and noncircular signals in virtual MIMO vehicle communication systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 3916-3928. DOI:10.1109/TVT.2020.2970967 |
| [16] |
HOWLAND P E, MAKSIMIUK D, REITSMA G. FM radio based bistatic radar[J]. IEE Proceedings: Radar, Sonar and Navigation, 2005, 152(3): 107-115. DOI:10.1049/ip-rsn:20045077 |
| [17] |
COLONE F, BONGIOANNI C, LOMBARDO P. Multifrequency integration in FM radio-based passive bistatic radar. Part Ⅱ: Direction of arrival estimation[J]. IEEE Aerospace and Electronic Systems Magazine, 2013, 28(4): 40-47. DOI:10.1109/MAES.2013.6506828 |
| [18] |
WANG J, WANG H T, ZHAO Y. Direction finding in frequency-modulated-based passive bistatic radar with a four-element Adcock antenna array[J]. IET Radar, Sonar & Navigation, 2011, 5(8): 807-813. |
| [19] |
LI Y, MA H, WU Y T, et al. DOA estimation for echo signals and experimental results in the AM radio-based passive radar[J]. IEEE Access, 2018, 6: 73316-73327. DOI:10.1109/ACCESS.2018.2882304 |
| [20] |
PARK G H, SEO Y K, KIM H N. Range-Doppler domain-based DOA estimation method for FM-band passive bistatic radar[J]. IEEE Access, 2020, 8: 56880-56891. DOI:10.1109/ACCESS.2020.2981957 |
| [21] |
高志文, 陶然, 单涛. 外辐射源雷达互模糊函数的两种快速算法[J]. 电子学报, 2009, 37(3): 669-672. GAO Z W, TAO R, SHAN T. Two fast algorithms of cross-ambiguity function for passive radar[J]. Acta Electronica Sinica, 2009, 37(3): 669-672. (in Chinese) |
| [22] |
ZHUO Z H, SHAN T, TAO R. Fast computation of cross-ambiguity function[J]. Journal of Beijing Institute of Technology, 2008, 17(4): 466-471. |
| [23] |
PIDANIC J, NEMEC Z. Speed-up the computing of bistatic cross-ambiguity function [C]//Proceedings of 201213th International Radar Symposium. Warsaw, Poland: IEEE, 2012: 310-313.
|
| [24] |
HOWLAND P E, GRIFFITHS H D, BAKER C J. Passive bistatic radar systems [M]//CHERNIAKOV M. Bistatic radar: Emerging technology. Hoboken, USA: John Wiley and Sons, 2008.
|
| [25] |
ZHU D Y, LI Y, ZHU Z D. A keystone transform without interpolation for SAR ground moving-target imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 18-22. DOI:10.1109/LGRS.2006.882147 |
| [26] |
PIGNOL F, COLONE F, MARTELLI T. Lagrange-polynomial-interpolation-based keystone transform for a passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1151-1167. DOI:10.1109/TAES.2017.2775924 |



