2. 中国科学院大学 材料科学与光电技术学院, 北京 100049;
3. 中国科学院大学 集成电路学院, 北京 100049;
4. 中国科学院半导体研究所 半导体超晶格国家重点实验室, 北京 100083;
5. 中国科学院大学 材料与光电研究中心, 北京 100049
2. College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Integrated Circuits, University of Chinese Academy of Sciences, Beijing 100049, China;
4. State Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China;
5. Center of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
时间数字转换器(time-to-digital converters, TDC)将时间信号转换为数字信号,作为测量时间的基本手段,能够为科学研究和工程技术提供必要的时间信息[1-2]。正电子成像、激光雷达和机器视觉等技术都需要利用TDC将携带物理信息的时间信号转换为数字信号进行分析,随着上述技术的应用领域不断拓展,其对TDC的分辨率和线性度提出了更高的要求[3-5]。基于现场可编程门阵列(field-programmable gate array, FPGA) 实现的TDC(FPGA-TDC)具有开发周期短、开发成本低的优势,近年来,随着FPGA从制造工艺、技术到开发工具方面的不断发展,FPGA-TDC的性能不断提升,吸引了众多研究者的关注[6-11]。
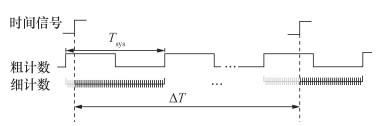
粗计数与细计数结合是目前常用的FPGA-TDC架构[12],其原理如图 1所示,粗计数直接记录系统时钟周期Tsys,细计数使用抽头延迟链[13]对Tsys直接进行内插,通过计算时间信号间粗细计数结果的差值可量化时间间隔。其中,延迟单元的延迟时间决定了TDC的分辨率。为了实现更高的分辨率,已有研究提出Wave Union法[14]、多链合并法[15]和双端采样法[16-17]以降低延迟单元的延迟时间。此外,更为直接有效的方式是使用由先进工艺制造的延迟单元更小的FPGA。
|
| 图 1 基于粗、细计数结合进行单次内插的方式 |
由图 1可知,延迟链的总延迟时间需至少覆盖Tsys。因此,减少延迟单元的延迟时间意味着构建更长的延迟链,这会使延迟单元的非线性随着时间信号在延迟链中的传播而积累,最终导致系统线性度恶化[5]。此外,延迟链走线延迟、固件之间的差异对系统非线性的影响也更大。延迟链跨越可编程逻辑阵列、可编程逻辑功能块(configurable logic block, CLB)等器件边界时引入额外的走线延迟,会产生与其他延迟单元差异较大的超大延迟单元(ultra-wide bins)[14, 18]。已有研究的非线性测试结果显示[19-21],延迟链中超大延迟单元所处位置对应的测试结果会伴随着系统非线性的跳变。目前大多使用Bin Decimation法[22-24]合并延迟链中的延迟单元以构建更大更均匀的延迟单元,从而缩小延迟单元间的差异,改善FPGA-TDC系统线性度;但延迟单元的合并意味着用于对Tsys内插的延迟单元数量的减少,导致分辨率降低。
为了解决上述问题,本文基于Xilinx Virtex UltraScale+ FPGA平台,设计了一种基于两次时间内插的FPGA-TDC。该TDC采用粗、细计数结合的方式量化时间信号,不同于常见的直接使用延迟链对Tsys进行内插的方式,该方案中细计数分为两次进行。分别利用不同相位周期信号和抽头延迟链对Tsys进行两次内插,能够缩短延迟链的长度,减小非线性积累,有效改善系统线性度。
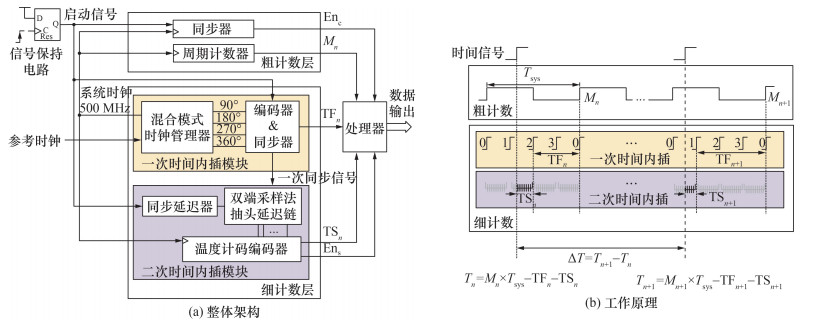
1 TDC设计 1.1 TDC整体架构及工作原理基于两次时间内插的FPGA-TDC整体架构如图 2(a)所示,分为粗计数层与细计数层。时间信号Tn经过信号保持电路产生启动信号并输入到粗计数层和细计数层中进行量化,其工作原理如图 2(b)所示,主要分为粗计数与细计数。
|
| 图 2 基于两次时间内插的FPGA-TDC整体架构和工作原理 |
粗计数记录启动信号发生时的Tsys个数。粗计数层采用周期计数器在每个Tsys储存并更新计数值。系统时钟信号与启动信号同步后输出粗计数有效信号Enc,Enc控制处理器记录周期计数器输出的计数结果,即第n个时间信号时测量出的Tsys的个数Mn。周期计数器采用Gray码计数器,Gray码作为一种稳定性编码,计数时相邻的Gray码之间只有一个bit发生变化,是一种错误最小化的编码方式,保证为TDC时间坐标轴提供精准的时间轴刻度。
细计数进一步量化启动信号与系统时钟信号上升沿间的时间间隔,对Tsys进行两次内插,第1次使用4个不同相位的内插时钟信号对Tsys进行内插;第2次利用抽头延迟链对内插时钟信号间的时间间隔进行内插。细计数层主要由一次时间内插模块和二次时间内插模块构成:一次时间内插模块中,20 MHz晶振提供的参考时钟信号经过混合模式时钟管理器产生500 MHz系统时钟信号和用于第一次时间内插的内插时钟信号;启动信号在编码器与同步器中与内插时钟信号同步,产生一次内插结果TFn,并产生一次同步信号。二次时间内插模块中,启动信号经过同步延迟器,与一次同步信号在使用双端采样法构建的抽头延迟链中进一步量化,量化产生的温度计码由温度计码编码器转换为二次内插结果TSn和细计数有效信号Ens。细计数有效信号触发处理器记录并输出时间信号的量化结果Mn、TFn和TSn。最终,第n个时间信号Tn量化为
| $ T_n=M_n \times T_{\mathrm{sys}}-\mathrm{TS}_n-\mathrm{TF}_n. $ | (1) |
任意2个时间信号的时间间隔可通过式(2)计算得到。
| $ \Delta T=T_{n+1}-T_n. $ | (2) |
由于Tsys经过了两次时间内插,因此,二次时间内插模块中抽头延迟链的总延迟只需要覆盖1/4个Tsys,就可以保证输入的时间信号得到有效量化。因此,抽头延迟链长度在使用两次时间内插方式时,比使用基于粗、细计数结合进行单次内插的方式(见图 1)时,缩短了3/4。
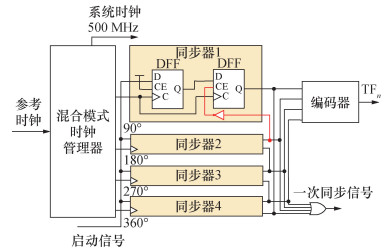
1.2 一次时间内插模块一次时间内插模块是缩短延迟链的关键部分,其具体结构如图 3所示。混合模式时钟管理器生成4个500 MHz的内插时钟信号(相位分别为90°、180°、270°和360°),专用于对启动信号的量化。如图 3所示,同步器由D触发器(D flip-flop, DFF)构成,用于识别启动信号的相位并与对应相位时钟信号的上升沿同步,输出同步信号。采用2个连续的DFF进行同步操作以降低亚稳态产生的概率。同步器产生的同步信号有2个作用:一方面,经过或门产生一次同步信号,用于二次时间内插模块进一步量化;另一方面,经过反相器与产生该信号的同步器的上一同步器中第2个DFF的使能信号端CE连接(图中红线标示)。这种连接方式可使4个同步器在启动信号位于不同相位时输出对应的one-cold码,判断启动信号所在相位并输入到编码器中得到TFn。
|
| 图 3 一次时间内插模块架构 |
1.3 二次时间内插模块
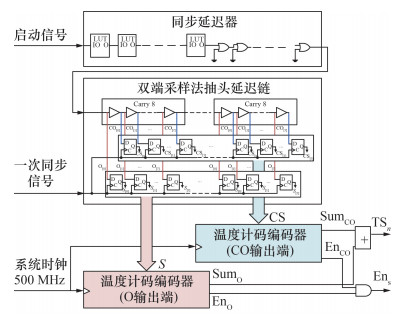
二次时间内插模块进一步量化了启动信号与其所在相位的内插时钟信号上升沿之间的时间间隔,决定了TDC的分辨率和线性度。由于一次时间内插模块中,启动信号到一次同步信号的产生要经过同步器、或门和相应布局布线,这部分产生的延迟使得启动信号与一次同步信号之间的时间间隔比实际值至少增加了1个Tsys的误差。因此,启动信号用于量化前,需通过同步延迟器进行延迟调整。
如图 4所示,同步延迟器由查找表(look up table, LUT)和或门构成,通过分别设置LUT和或门的个数对启动信号到延迟链的时间间隔进行粗调整和细调整。同步延迟器消除启动信号与一次同步信号之间额外的延迟误差,保证后续对启动信号与一次同步信号之间的时间间隔进行有效量化。
|
| 图 4 二次时间内插模块架构 |
延迟链使用双端采样法构建,其由进位链单元Carry8和DFF构成,Carry8的求和输出端O和进位输出端CO都被用作抽头,对经过同步延迟器调整后的启动信号与一次同步信号之间的时间间隔进行量化。相比于常见的只使用CO输出端作为抽头构建延迟链的方式,双端采样法在相同时间间隔内插入了2倍的延迟单元,分辨率能够提升2倍。考虑到器件位置、布局布线和温度的影响,一次时间内插模块中时钟周期均匀分割存在误差,因此实际设计时抽头延迟链长度需略宽于1/4个Tsys。
时间信号经过延迟链时,CO输出端和O输出端分别发生“0—1”和“1—0”的转换,因此温度计码编码器需要进行相应的设计,将CO输出端的输出结果CS转化为SumCO,以记录“1”的个数;将O输出端的输出结果S转化为SumO,以记录“0”的个数。时间信号传播的位置由SumCO和SumO相加得到。同时,CO输出端和O输出端的温度计码编码器完成编码操作后,分别输出编码结果有效信号EnCO和EnO,经过与门,产生细计数有效信号Ens。
FPGA-TDC的设计会面临信号经过时钟域间器件边界引入较大非线性的问题。使用两次时间内插方式的TDC,减小了延迟链需要覆盖的时间间隔,缩短了所需构建的延迟链,使时间信号的传播范围被限制在半个时钟域内,避免了时间信号跨越时钟域器件边界。同时,延迟链的缩短使延迟单元的非线性积累减少。因此,两次时间内插方式能够有效提升TDC的系统线性度。此外,延迟链的缩短也使相关温度计码编码器模块等消耗的逻辑资源更少,节省了FPGA的硬件资源。
2 TDC测试结果与分析实验选用Xilinx公司开发的Virtex UltraScale+ XCVU13P-2FHGB2104I型FPGA芯片和Hyper Silicon公司开发的VeriTiger-V13P开发板。
为评估TDC的分辨率和系统线性度,需要先通过码密度测试[25]获得每个延迟单元的延迟时间。TDC的Tsys为2 ns,使用LUT构成环形振荡器,产生与系统时钟异步且不成比例的方波信号,作为码密度测试信号。测试信号产生的时间事件均匀分布于(0, Tsys)区间,事件落入到第i个延迟单元的概率与该延迟单元的延迟时间呈正比。
| $ \tau_i=T_{\mathrm{sys}} \times \frac{n_i}{N}. $ | (3) |
其中:τi为第i个延迟单元的延迟时间,ni为落入第i个延迟单元的时间事件数,i>0;N为总事件数。时间信号落入第i个延迟单元时的时间测量值为
| $ t_i=\sum\limits_{k=0}^i \tau_i. $ | (4) |
假设时间实际值为ta,其取值范围为ti-1 < ta < ti(i=1时,0<ta<ti),则测量标准方差为
| $ \sigma^2=\frac{1}{t_i-t_{i-1}} \int_{i-1}^i\left(t-t_{\mathrm{a}}\right)^2 \mathrm{~d} t=\\\frac{\left(t_i-t_{\mathrm{a}}\right)^3-\left(t_{i-1}-t_{\mathrm{a}}\right)^3}{3\left(t_i-t_{i-1}\right)}. $ | (5) |
当dσ2/dta=0时σ2最小,此时的ta=(ti+ti-1)/2,由此定义ti的校准值t应为
| $ t=\sum\limits_{x=0}^{i-1} \tau_x+\frac{\tau_i}{2}. $ | (6) |
由式(6)可计算逐位校准表,进而得到抽头位置与测量结果的转换曲线。
基于两次时间内插的FPGA-TDC中,一次内插后的相位内插延迟如图 5a所示,90°、180°、270°和360°相位下的延迟时间分别为472.60、488.23、552.90和486.28 ps,总和为Tsys,即4个不同相位的内插时钟信号将Tsys内插为4个部分。不同相位之间内插的延迟时间不同,对应进行二次时间内插时使用的延迟链长度也不同,因此针对90°、180°、270°和360°相位下分别进行了相应的码密度测试,结果分别如图 5b、5d、5f和5h所示,可得各相位下的有效延迟单元数分别为277、288、310和288个。进一步统计分布在不同延迟范围中的延迟单元数量,得到各相对应的延迟时间τ的统计直方图,结果分别如图 5c、5e、5g和5i所示,延迟单元的延迟时间均分布在8 ps内,其中大多分布在2 ps以内。
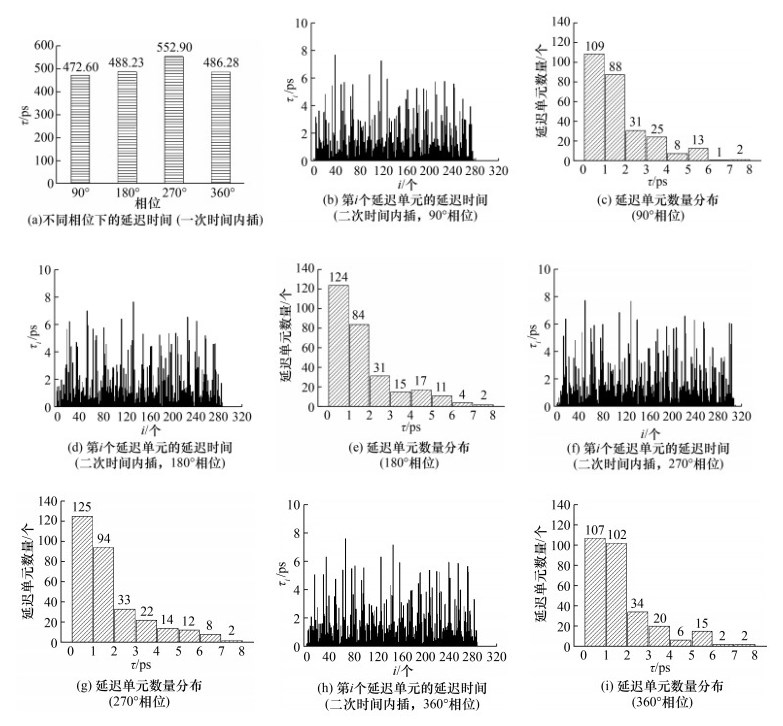
|
| 图 5 基于两次时间内插的FPGA-TDC码密度测试结果 |
2.1 分辨率分析
分辨率为TDC可以区分的最小时间量,也即最低有效位(least significant bit, LSB)。依据码密度测试结果,由式(7)计算出TDC的LSB。
| $ \mathrm{LSB}=\frac{T_{\mathrm{sys}}}{W}. $ | (7) |
其中W为总的有效抽头数,即总延迟不为0的延迟单元个数。在本文中W为4个相位所用有效延迟单元数的总和,结合图 5可得W=277+288+310+288=1 163个。因此基于两次时间内插的FPGA-TDC的LSB为1.72 ps。
2.2 非线性分析系统的非线性由微分非线性(differential nonlinearity, DNL)和积分非线性(integral nonlinearity, INL)2个指标进行表征。DNL代表单个延迟单元的延迟时间与LSB的偏差,INL为DNL的累加结果。第i个延迟单元的DNL和INL的计算方法分别如式(8)和(9)所示。
| $ \mathrm{DNL}_i=\tau_i-\mathrm{LSB}, $ | (8) |
| $ \mathrm{INL}_i=\sum\limits_{x=0}^i \mathrm{DNL}_x. $ | (9) |
本文也搭建了基于双端采样法直接对Tsys进行单次内插的FPGA-TDC(以下简称为基于双端采样法的FPGA-TDC),与所提出的两次时间内插方式实现的TDC架构作对比,用以论证后者可有效提升系统线性度。
基于双端采样法的FPGA-TDC的码密度测试结果如图 6所示,延迟链的有效延迟单元为1 138个,比不同相位下的延迟链(见图 5)使用了更多的延迟单元。同时,测试结果中出现了延迟时间大于8 ps的延迟单元。
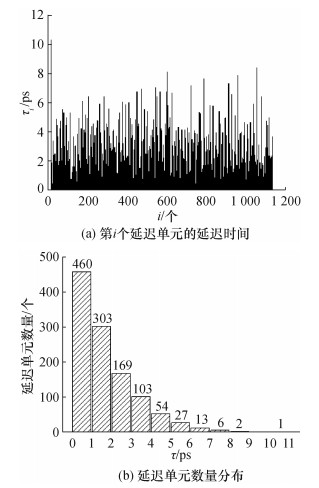
|
| 图 6 基于双端采样法的FPGA-TDC码密度测试结果 |
进一步计算基于双端采样法的FPGA-TDC的非线性,DNL和INL的结果通常由LSB归一化的形式进行表达,结果如图 7所示,DNL为[-0.96, 4.92] LSB,INL为[-8.10, 36.26] LSB。
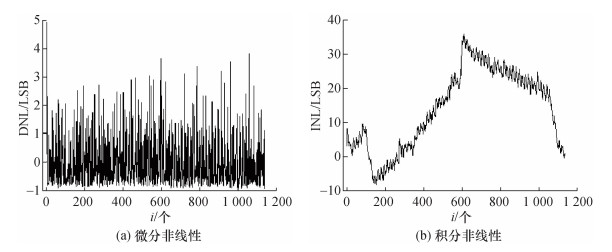
|
| 图 7 基于双端采样法的FPGA-TDC非线性测试结果 |
基于两次时间内插的FPGA-TDC的非线性测试结果如图 8所示。90°相位下的DNL为[-0.95, 3.49] LSB,INL为[-4.95, 4.25] LSB;180°相位下的DNL为[-0.99, 3.47] LSB,INL为[-6.69, 4.27] LSB;270°相位下的DNL为[-0.99, 3.50] LSB,INL为[-7.28, 19.27] LSB;360°相位下的DNL为[-0.92, 3.41] LSB,INL为[-8.75, 0.28] LSB。其中DNL和INL在270°相位下的极差最大,分别为4.49 LSB和26.55 LSB。
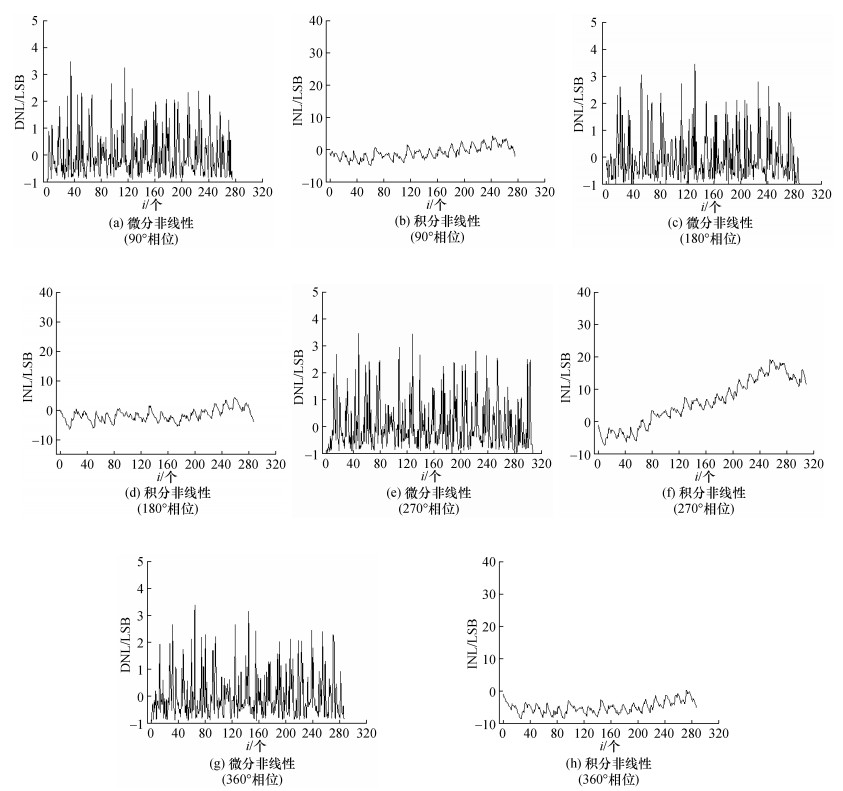
|
| 图 8 基于两次时间内插的FPGA-TDC非线性测试结果 |
经过对比发现,使用两次时间内插方式后,DNL的极差由5.88 LSB降低至4.49 LSB,表明单个延迟单元的延迟时间与LSB之间的偏差范围缩小了23.64%。这是由于基于双端采样法的FPGA-TDC直接使用延迟链对Tsys进行单次内插,抽头延迟链较长,跨越时钟域及时钟域中间的器件边界时引入额外的走线延迟,导致相应的超大延迟单元的产生;而两次时间内插方式能够有效缩短延迟链长度,时间信号在延迟单元中传输时不会经过时钟域相关的器件边界,避免了超大延迟单元的产生。基于双端采样法的FPGA-TDC中延迟单元的最长延迟时间为10.40 ps (见图 6a, i=3),而基于两次时间内插的FPGA-TDC中延迟单元的最长延迟时间为7.74 ps (见图 5f, i=49),使得原本会出现的超大延迟单元被更小的延迟单元代替,最终导致了DNL极差的缩小。
使用两次时间内插方式后,INL的极差由44.36 LSB降低至26.55 LSB,表明延迟链中DNL累加值的最大变化范围缩小了40.15%。基于双端采样法的FPGA-TDC的INL测试中,共发生3次明显的跳变,分别位于第117、597和1 077个延迟单元(见图 7b),对应着实际布局布线过程中,延迟链在跨越时钟域和时钟域中间的器件边界时延迟单元的位置;而基于两次时间内插的FPGA-TDC的INL极差更小,无明显跳变(见图 8b、8d、8f和8h)。后者避免了跨越时钟域相关的器件边界引入的非线性,且延迟链的缩短使延迟单元在延迟链中积累的非线性更小,导致INL的性能更优。
因此,使用两次时间内插方式能够改善FPGA-TDC的DNL和INL,实现更优的系统线性度。
2.3 与已有研究的TDC性能比较针对FPGA-TDC中TDC的性能,对比了本文所提的基于两次时间内插的方式与已有研究中的方式。如表 1所示,基于两次时间内插方式实现的FPGA-TDC使用了184块CLB、1 198个FF和872个LUT,比其他研究使用的逻辑资源更少。同时,两次时间内插的方式所实现FPGA-TDC比其他研究的DNL和INL更小,有着更优的系统线性度。
此外,两次时间内插方式缩短了抽头延迟链,使后续需要搭建的温度计码编码器等模块规模更小,电路实现需要占用的FPGA逻辑资源更少。
3 结论本文提出了一种基于两次时间内插的FPGA-TDC设计方案,并基于Xilinx Virtex UltraScale+ FPGA平台予以实现。该方案通过利用不同相位的周期信号和抽头延迟链对Tsys进行两次内插量化,缩短了延迟链长,避免了跨越时钟域相关的器件边界时引起非线性的跳变,减少了时间量化过程中非线性的积累,提升了系统线性度。同时,延迟链长度的缩短也减少了电路实现时消耗的FPGA逻辑资源。
| [1] |
MATTADA M P, GUHILOT H. Time-to-digital converters: A comprehensive review[J]. International Journal of Circuit Theory and Applications, 2021, 49(3): 778-800. DOI:10.1002/cta.2936 |
| [2] |
KALISZ J. Review of methods for time interval measurements with picosecond resolution[J]. Metrologia, 2003, 41(1): 17-32. |
| [3] |
TANCOCK S, ARABUL E, DAHNOUN N. A review of new time-to-digital conversion techniques[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(10): 3406-3417. DOI:10.1109/TIM.2019.2936717 |
| [4] |
宋志鹏. 基于FPGA的高精度时间数字转换器[D]. 武汉: 华中科技大学, 2023. SONG Z P. High precision time digital converter based on FPGA[D]. Wuhan: Huazhong University of Science and Technology, 2023. (in Chinese) |
| [5] |
MACHADO R, CABRAL J, ALVES F S. Recent developments and challenges in FPGA-based time-to-digital converters[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(11): 4205-4221. DOI:10.1109/TIM.2019.2938436 |
| [6] |
FISHBURN M, MENNINGA L H, FAVI C, et al. A 19.6 ps, FPGA-based TDC with multiple channels for open source applications[J]. IEEE Transactions on Nuclear Science, 2013, 60(3): 2203-2208. DOI:10.1109/TNS.2013.2241789 |
| [7] |
BALLA A, BERETTA M M, CIAMBRONE P, et al. The characterization and application of a low resource FPGA-based time to digital converter[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2014, 739: 75-82. |
| [8] |
ABBAS M, KHALIL K. A 23 ps resolution time-to-digital converter implemented on low-cost FPGA platform[C]//2015 International Symposium on Signals, Circuits and Systems (ISSCS). Iasi, Romania: IEEE, 2015: 1-4.
|
| [9] |
KUANG J, WANG Y G, CAO Q, et al. Implementation of a high precision multi-measurement time-to-digital convertor on a Kintex-7 FPGA[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2018, 891: 37-41. |
| [10] |
HUANG S, HE Z, WEN X, et al. Design of a multi-channel high-resolution TDC based on FPGA[J]. Journal of Instrumentation, 2022, 17(7): P07037. DOI:10.1088/1748-0221/17/07/P07037 |
| [11] |
WANG Y, XIE W J, CHEN H C, et al. High-resolution time-to-digital converters (TDCs) with a bidirectional encoder[J]. Measurement, 2023, 206: 112258. DOI:10.1016/j.measurement.2022.112258 |
| [12] |
NUTT R. Digital time intervalometer[J]. Review of Scientific Instruments, 1968, 39(9): 1342-1345. DOI:10.1063/1.1683667 |
| [13] |
HENZLER S. Time-to-digital converters[M]. Dordrecht: Springer, 2010.
|
| [14] |
WU J Y, SHI Z H. The 10 ps wave union TDC: Improving FPGA TDC resolution beyond its cell delay[C]//2008 IEEE Nuclear Science Symposium Conference Record. Dresden, Germany: IEEE, 2008: 3440-3446.
|
| [15] |
WANG Y G, KUANG J, LIU C, et al. A 3.9-ps RMS precision time-to-digital converter using ones-counter encoding scheme in a Kintex-7 FPGA[J]. IEEE Transactions on Nuclear Science, 2017, 64(10): 2713-2718. DOI:10.1109/TNS.2017.2746626 |
| [16] |
WANG Y G, LIU C. A 3.9 ps time-interval RMS precision time-to-digital converter using a dual-sampling method in an UltraScale FPGA[J]. IEEE Transactions on Nuclear Science, 2016, 63(5): 2617-2621. DOI:10.1109/TNS.2016.2596305 |
| [17] |
LIU C, WANG Y G, KUANG P, et al. A 3.9 ps RMS resolution time-to-digital converter using dual-sampling method on Kintex UltraScale FPGA[C]//2016 IEEE-NPSS Real Time Conference (RT). Padua, Italy: IEEE, 2016: 1-3.
|
| [18] |
LIU C, WANG Y G. A 128-channel, 710 M samples/ second, and less than 10 ps RMS resolution time-to-digital converter implemented in a Kintex-7 FPGA[J]. IEEE Transactions on Nuclear Science, 2015, 62(3): 773-783. DOI:10.1109/TNS.2015.2421319 |
| [19] |
KUANG J, WANG Y G, LIU C. A 128-channel high performance time-to-digital converter implemented in an UltraScale FPGA[C]//2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). Atlanta, USA: IEEE, 2017: 1-4.
|
| [20] |
周浩. 基于FPGA进位链的时间数字转换器设计[D]. 重庆: 重庆邮电大学, 2017. ZHOU H. Design of a time-to-digital converter based on carry-in lines of FPGA[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2017. (in Chinese) |
| [21] |
WANG Y G, CAO Q, LIU C. A multi-chain merged tapped delay line for high precision time-to-digital converters in FPGAs[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65(1): 96-100. DOI:10.1109/TCSII.2017.2698479 |
| [22] |
WANG Y G, LIU C. A 4.2 ps time-interval RMS resolution time-to-digital converter using a bin decimation method in an UltraScale FPGA[J]. IEEE Transactions on Nuclear Science, 2016, 63(5): 2632-2638. DOI:10.1109/TNS.2016.2606627 |
| [23] |
戴庆达. 基于FPGA的高性能多通道TDC设计技术研究[D]. 天津: 天津大学, 2020. DAI Q D. Technologies for multichannel TDC of high performance based on FPGA[D]. Tianjin: Tianjin University, 2020. (in Chinese) |
| [24] |
XIE W J, CHEN H C, LI D D U. Efficient time-to-digital converters in 20 nm FPGAs with wave union methods[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 1021-1031. DOI:10.1109/TIE.2021.3053905 |
| [25] |
FISHBURN M W, CHARBON E. Statistical limitations of TDC density tests[C]//IEEE Nuclear Science Symposium. Anaheim, USA: IEEE, 2012: 1-2.
|
| [26] |
SUI T J, ZHAO Z X, XIE S W, et al. A 2.3 ps RMS resolution time-to-digital converter implemented in a low-cost cyclone V FPGA[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(10): 3647-3660. DOI:10.1109/TIM.2018.2880940 |
| [27] |
WANG Y G, ZHOU X Y, SONG Z Q, et al. A 3.0 ps rms precision 277-MSamples/s throughput time-to-digital converter using multi-edge encoding scheme in a Kintex-7 FPGA[J]. IEEE Transactions on Nuclear Science, 2019, 66(10): 2275-2281. DOI:10.1109/TNS.2019.2938571 |



