当前应用较为广泛的控制棒驱动技术包括电磁驱动[1]、水力驱动[2]和机械驱动[3]等。清华大学的薄涵亮等[4]在NHR5反应堆控制棒水力驱动技术的基础上结合商用压水堆磁力提升器的优点,为NHR200低温核供热堆研制出了新型的内置式控制棒驱动技术,即控制棒水压驱动系统(control rod hydraulic drive system, CRHDS)。该系统降低了反应堆高度,避免了弹棒事故,增强了反应堆安全性,使一体化堆布置更加紧凑。
CRHDS由控制棒水压驱动机构(control rod hydraulic drive mechanical, CRHDM)、组合阀、控制棒和水力缓冲器等组成,通过组合阀控制进入驱动机构的脉冲水流,带动2套销爪机构动作,进而驱动控制棒步升、步降和快速落棒。在此过程中,组合阀的启闭和水压缸的快速到位,会在回路中触发瞬变流动,导致系统回路内流体压力的波动,管道和设备发生振动,干扰设备和仪表的正常工作[5]。因此有必要通过试验和理论模型研究,分析驱动系统的瞬变流动过程,以指导液压脉动消能器的设计,同时为系统的运行监测提供支持。
针对CRHDS的研究已积累了一定的成果。如薄涵亮等[6]详细介绍了控制棒水压驱动技术,包括其整体设计方案、部件组成、主要功能和工程性能。秦本科等[7-8]对驱动机构水压缸步升和步降运动过程进行了理论和试验研究,分析了水压缸运动机理和关键运行参数。针对驱动系统的循环泵,赵陈儒等[9]从振动噪声和耗功的角度进行分析后提出了2种运行方案。李彦霖等[10]为了测量驱动系统的控制棒动态棒位,设计了一种具有高测量精度的新型传感器。蒋俊飞等[11]完成了驱动系统组合阀热态试验,分析了温度对组合阀流动阻力的影响。杨林清等[12]通过试验研究了驱动机构水压缸步升过程的瞬变流动现象,分析了关键特征参数的变化规律。然而,以上研究大多围绕CRHDS的部件层面展开,且缺乏对该系统步降瞬变流动过程的理论模型计算。因此有必要从回路和系统层面,以试验和建模的方式明晰瞬变流动过程中关键特征参数随工况的变化规律,探究驱动系统水击现象的触发机理。
本文通过试验和建立理论模型研究了CRHDS步降瞬变流动过程。首先分析了CRHDS的组成和原理,之后进行了步降过程瞬变流动特性试验;依据试验结果建立了步降过程瞬变流动的理论模型,并对比了试验与模型结果;最后将模型应用于高温变驱动压力工况中,分析了瞬变流动特征参数随驱动压力的变化规律。
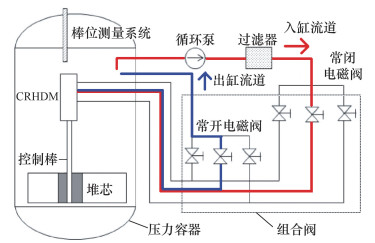
1 CRHDS的组成和原理CRHDS由CRHDM、组合阀、控制棒等组成,如图 1所示,其中组合阀包含3个入缸流道和3个出缸流道,由3组常闭电磁阀和常开电磁阀控制。通过控制驱动系统初始状态和组合阀动作,可调节系统的流动回路,当组合阀打开(常闭电磁阀打开,常开电磁阀关闭)时,压力容器内的水经循环泵加压后通过入缸流道流入驱动机构,如图中红色线条所示,该过程定义为水压缸充压;当组合阀关闭(常闭电磁阀关闭,常开电磁阀打开)时,驱动机构内的水通过出缸流道流入压力容器,如图中蓝色线条所示,该过程定义为水压缸泄压。
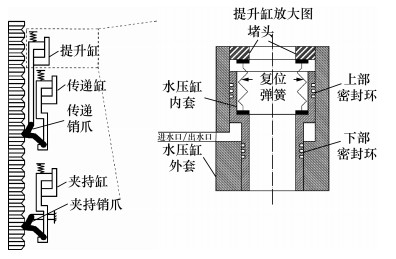
CRHDM作为CRHDS最核心的部件,由3个水压缸(夹持缸、传递缸和提升缸)和2套销爪机构组成,如图 2所示,通过水压缸交替的步升和步降运动带动销爪机构的松开和夹紧,以此控制驱动轴,进而驱动控制棒动作。水压缸的组成和原理相似,由缸外套、内套、上下部密封环、复位弹簧和堵头等组成。因为驱动系统的入缸流道和出缸流道共用部分管道,所以水压缸的进水口与出水口相同。水压缸的步升过程可分为3个阶段:当水压缸压力较小时,缸内套保持静止,处于步升前阶段;当缸内压力大于弹簧力和重力之和,内套向上提升,处于步升阶段;压力继续增大,水压缸内套维持在顶端,处于步升后阶段。步降过程同样可分为3个阶段:当水压缸压力较大时,缸内套维持在顶端,处于步降前阶段;当缸内压力小于弹簧力和重力之和,内套向下位移,处于步降阶段;压力继续减小,水压缸内套静止在底端,处于步降后阶段。在步升和步降过程中,始终有流体从水压缸的密封环处泄漏,进入压力容器。控制棒向上提升一步的过程称为驱动系统的步升过程,由6个步骤组成,依次为:传递缸充压、夹持缸泄压、提升缸充压、夹持缸充压、传递缸泄压和提升缸泄压。控制棒下降一步的过程称为驱动系统的步降过程,同样由6个步骤组成,依次为:提升缸充压、传递缸充压、夹持缸泄压、提升缸泄压、夹持缸充压和传递缸泄压。
|
| 图 2 CRHDM原理图 |
2 瞬变流动特性试验 2.1 试验台架布置
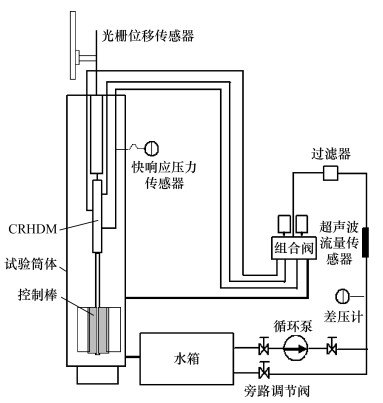
结合CRHDS的组成和原理,建立了全尺寸CRHDS冷态瞬变流动特性试验台架[14]。台架主要由水箱、循环泵、组合阀、CRHDM和控制棒等组成,如图 3所示。回路中的流体介质为常温常压条件下的去离子水,流路如下:水箱中的水经循环泵加压后,一部分通过旁路调节阀直接流回水箱,另一部分经过滤器进入组合阀,通过操作组合阀控制进入水压缸的脉冲水流流量,实现控制棒的步动和快速落棒操作。试验测量系统由计算机、数据采集板、快响应压力传感器、光栅位移传感器和差压计等部分构成,系统动态快速采样频率为1 000 Hz。光栅位移传感器布置在试验筒体顶部,用于记录控制棒的步进和落棒位移曲线。在循环泵出口设置的差压计用于测量驱动压力p0,在CRHDM水压缸入口处布置快响应压力传感器,用于测量水压缸内动态压力。主回路设置超声波流量传感器,用于步降过程流量的监测。经测量误差分析,差压计和快响应压力传感器的误差分别为满量程的0.30%和0.40%,超声波流量传感器的误差为满量程的1.00%,光栅位移传感器的误差为±20 μm。
|
| 图 3 CRHDS瞬变流动特性试验台架 |
该试验需先对测控系统进行调试,确保测量系统的输出正常,控制系统的动作正常。调试完毕后进行CRHDS的性能测试:首先打开循环泵,调节旁路阀门;之后打开组合阀,令水从水箱经循环泵加压后流入CRHDM,水压缸进入步升阶段;接着关闭组合阀,令水从CRHDM和组合阀中流出至筒体,水压缸完成步降过程。
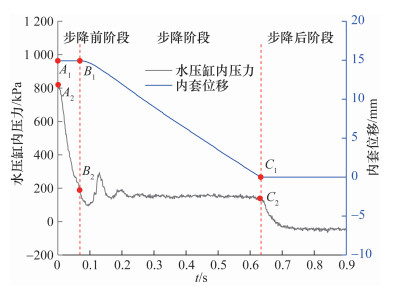
2.2 结果分析试验中循环泵的驱动压力p0为850 kPa,水压缸位移和缸内压力随时间t的变化曲线如图 4所示。根据水压缸步降位移的起始点B1和结束点C1,将步降瞬变过程划分为步降前阶段、步降阶段和步降后阶段,包含1次明显的水击过程。驱动系统瞬变过程的机理分析如下:
|
| 图 4 水压缸内套位移和缸内压力的时程曲线(p0=850 kPa) |
在步降前阶段(0 s<t≤0.069 s),组合阀中的常闭电磁阀开启后,驱动系统的出缸流道打开。流道的低压端为试验筒体,高压端为水压缸,因此水流出水压缸,导致水压缸内的压力从A2点的820.19 kPa逐渐减小至B2点的199.73 kPa。但水压缸内压力仍大于重力和弹簧弹力之和,因此水压缸内套保持静止,位移值为15 mm,另有部分缸内流体从下部密封环泄漏。
在步降阶段(0.069 s<t≤0.634 s),当水压缸内压力下降至小于重力和弹簧弹力之和时,水压缸内套开始步降,从B1点的15 mm逐渐减小至C1点的0。在内套步降动作开始的瞬间,水压缸上堵头的密封作用消失,缸内流体可以从上部和下部密封环同时泄漏,泄漏量骤增,水压缸内压力迅速降低,降压水击波在水压缸处产生,在CRHDS回路中触发了水击现象。因此在步降阶段呈现先降压,后升压的波动过程。
在步降后阶段(t>0.634 s),水压缸内套步降位移结束后,在底部位置保持静止。水压缸内流体通过上、下部密封环和出缸流道流出,压力从C2点的141.95 kPa迅速减小至0 kPa附近,与大气压相近。
3 步降过程瞬变流模型基于CRHDS瞬变流动特性试验结果和机理分析,建立包括趋势项模型和水击项模型在内的步降过程瞬变流模型,通过叠加2个模型的求解结果分析整个步降过程。趋势项模型反映了缸内水压整体变化过程,考虑水压缸内套的运动状态,但不考虑管道中流体的可压缩性;水击项模型反映缸内水压局部瞬变过程,即回路中的水击现象,考虑管道中流体的可压缩性,但不考虑水压缸的运动状态。定义步降过程中水压缸的瞬态压力为趋势项压力pcy和水击项压力Δpwh之和,计算步骤如下:
1) 输入回路布置的相关参数;
2) 通过趋势项模型计算得到趋势项压力pcy、位移scy以及触发时刻的流场信息;
3) 通过水击项模型计算得到水击项压力Δpwh;
4) 叠加pcy和Δpwh得到步降过程瞬态压力。
3.1 趋势项模型 3.1.1 连续性方程以水压缸内流体为控制体建立连续性方程,如式(1)所示。
| $ -\rho Q_{\text {out }}-\rho Q_{\text {leak }}=V \frac{\mathrm{~d} \rho}{\mathrm{~d} t}+\rho \frac{\mathrm{d} V}{\mathrm{~d} t}. $ | (1) |
其中:ρ为流体的密度,kg/m3;Qout为出缸流道处的流量,m3/s;Qleak为密封环处的泄漏流量,m3/s;V为水压缸内流体的体积,m3;t为时间,s。方程左端为流出控制体的质量,右端第1项描述了控制体密度变化的影响,右端第2项描述了控制体体积变化的影响。
对式(1)进行简化得到式(2)。
| $ \begin{gathered} Q_{\mathrm{cy}}-Q_{\text {out }}-Q_{\text {leak }}=\frac{V}{K} \frac{\mathrm{~d} p_{\mathrm{cy}}}{\mathrm{~d} t}, \\ Q_{\mathrm{cy}}=A_{\mathrm{cy}} v_{\mathrm{cy}}. \end{gathered} $ | (2) |
其中:Qcy为水压缸向下位移时排出水的流量,m3/s;K为水的体积弹性模量,Pa;pcy为水压缸的趋势项压力,Pa;Acy为水压缸内套的承压面积,m2;vcy为水压缸内套的步降速度,以向下位移为正方向,m/s。与压力变化相关的流量包括Qcy、Qout和Qleak。
3.1.2 流道动量方程出缸流道由水压缸、试验筒体及3根管道组成,对出缸流道内的流体建立动量方程。
| $ p_{\mathrm{cy}}-\Delta p_{\mathrm{f}}-p_{\mathrm{w}}=\left(\frac{\rho L_1}{A_{\mathrm{t} 1}}+\frac{\rho L_2}{A_{\mathrm{t} 2}}+\frac{\rho L_3}{A_{\mathrm{t} 3}}\right) \frac{\mathrm{d} Q_{\text {out }}}{\mathrm{d} t}. $ | (3) |
其中:Δpf为出缸流道的压力损失,Pa;pw为筒体内流体压力,Pa;L1、L2和L3为3根管道的长度,m;At1、At2和At3为3根管道的截面积,m2。
3.1.3 系统关键流动阻力环节关系式Δpf主要包含沿程摩擦阻力损失Δp1和局部阻力损失Δp2,可表述为
| $ \left\{\begin{array}{l} \Delta p_{\mathrm{f}}=\Delta p_1+\Delta p_2, \\ \Delta p_1=\zeta_1 Q_{\text {out }}\left|Q_{\text {out }}\right|, \\ \Delta p_2=\zeta_2 Q_{\text {out }}\left|Q_{\text {out }}\right| . \end{array}\right. $ | (4) |
其中:ξ1和ξ2分别为沿程流动和局部流动阻力系数[11]。
3.1.4 水压缸漏流关系式水压缸内的流体会从密封环处泄漏,Qleak和pcy的关系为
| $ \frac{p_{\mathrm{cy}}}{Q_{\text {leak }}}=d_0+d_1 p_{\mathrm{cy}}. $ | (5) |
其中:d0和d1为经验系数,在不同的泄漏模式下取值不同,通常基于水压缸密封环的理论和试验研究结果获得[11]。
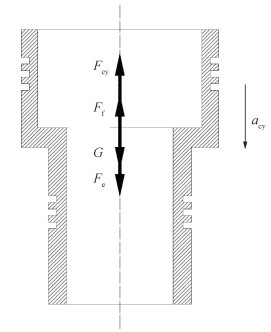
3.1.5 水压缸动力学和运动学模型水压缸内套步降过程中的受力分析如图 5所示,包括重力G、复位弹簧力Fe、流体的压力Fcy和运动阻力Ff。
|
| 图 5 水压缸受力分析图 |
| $ \begin{gathered} m a_{\mathrm{cy}}=F_{\mathrm{e}}+G-F_{\mathrm{cy}}-F_{\mathrm{f}}= \\ k\left(s_{\mathrm{cy}}+l_0\right)+m g-p_{\mathrm{cy}} A_{\mathrm{cy}}-F_{\mathrm{f}}, \\ \frac{\mathrm{~d} v_{\mathrm{cy}}}{\mathrm{~d} t}=a_{\mathrm{cy}}, \\ \frac{\mathrm{~d} s_{\mathrm{cy}}}{\mathrm{~d} t}=v_{\mathrm{cy}}. \end{gathered} $ | (6) |
其中:m为水压缸内套和载荷的总质量,kg;g为重力加速度,本文取9.8 m/s2;acy和scy分别为步降的加速度和位移,单位分别为m/s2和m;k为弹簧的刚度系数,N/m;l0为弹簧初始压缩量,scy+l0为弹簧的压缩量,单位均为m。
3.1.6 运动阻力关系式水压缸所受的Ff与Fcy呈线性关系。
| $ F_{\mathrm{f}}=b_0 A_{\mathrm{cy}}+b_1 F_{\mathrm{cy}}=\left(b_0+b_1 p_{\mathrm{cy}}\right) A_{\mathrm{cy}} . $ | (7) |
其中:b0、b1为运动阻力系数,通过水压缸的运动阻力试验数据拟合得到[11]。
3.2 水击项模型 3.2.1 数值求解水击模型包含流体的动量方程和连续性方程分别如式(8)和(9)所示。
| $ g \frac{\partial H}{\partial x}+\frac{\partial v}{\partial t}+v \frac{\partial v}{\partial x}+\frac{\lambda}{2 D} v|v|=0, $ | (8) |
| $ \frac{\partial H}{\partial t}+v \frac{\partial H}{\partial x}-v \sin \theta+\frac{c^2}{g} \frac{\partial v}{\partial x}=0. $ | (9) |
其中:H为压头,m;v为截面的平均流速,m/s;c为波速,m/s;λ为Darcy-Weisbach摩擦阻力因数;D为管道直径,m;θ为管道轴线与水平面的夹角,(°),以管道上升为正方向。
将式(8)和(9)中的v换算为流量Q的表示方式,忽略对流项后使用特征线法求解,得到相容性方程,其中A为管道截面积,m2。
| $ \left\{\begin{array}{l} \frac{\mathrm{d} H}{\mathrm{~d} t}+\frac{c}{g A} \frac{\mathrm{~d} Q}{\mathrm{~d} t}+\frac{c \lambda}{2 g D A^2} Q|Q|-\frac{Q}{A} \sin \theta=0, \\ \frac{\mathrm{~d} x}{\mathrm{~d} t}=+c; \end{array}\right. $ | (10) |
| $ \left\{\begin{array}{l} \frac{\mathrm{d} H}{\mathrm{~d} t}-\frac{c}{g A} \frac{\mathrm{~d} Q}{\mathrm{~d} t}-\frac{c \lambda}{2 g D A^2} Q|Q|-\frac{Q}{A} \sin \theta=0, \\ \frac{\mathrm{~d} x}{\mathrm{~d} t}=-c. \end{array}\right. $ | (11) |
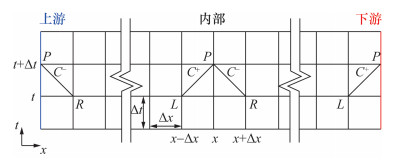
将上述方程沿C+和C-特征线积分,使用图 6中的网格节点(如P、L和R)标号进行表示。
|
| 图 6 特征线网格 |
联立式(12)和(13)求解,得到内部节点的压力HP和流量QP。
| $ \begin{gathered} H_P-H_A+\frac{c}{g A}\left(Q_P-Q_A\right)- \\ \frac{\Delta x \sin \theta}{c A} Q_A+\frac{\lambda \Delta x}{2 g D A^2} Q_P\left|Q_A\right|=0, \end{gathered} $ | (12) |
| $ \begin{gathered} H_P-H_B-\frac{c}{g A}\left(Q_P-Q_B\right)- \\ \frac{\Delta x \sin \theta}{c A} Q_B-\frac{\lambda \Delta x}{2 g D A^2} Q_P\left|Q_B\right|=0. \end{gathered} $ | (13) |
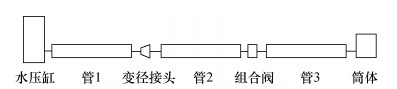
简化CRHDS的布置,得到步降过程的水击回路示意图,如图 7所示。
|
| 图 7 水击回路简化示意图 |
3根管道的材料均为304不锈钢,参数见表 1。
边界条件包括水压缸、变径接头、组合阀和驱动机构筒体。由于水击项模型忽略了水压缸运动状态和速度的影响,因此补充式(14)为相应的边界条件方程。
| $ -Q_{\text {out }}-Q_{\text {leak }}=\frac{\rho g V}{K} \frac{\mathrm{~d} H_{\mathrm{cy}}}{\mathrm{~d} t} . $ | (14) |
其中Hcy为水压缸压头,m。
定义管1和2相连处为直管变径接头,补充式(15)作为相应的边界条件方程。
| $ \begin{aligned} H_1 & =H_2, \\ Q_1 & =Q_2. \end{aligned} $ | (15) |
组合阀是一个流道结构复杂的集成部件,内部包含弯管和变径管等,所以存在较大局部压力损失。根据组合阀流动阻力试验[11]的结果,得到流动阻力系数ξIV。定义管2和3相连处为组合阀,组合阀包含体积为VIV的容腔,管道间的压力关系和流量关系分别为
| $ \begin{aligned} H_2-H_3 & =\frac{\xi_{\mathrm{IV}} Q_2\left|Q_2\right|}{2 g A_{\mathrm{t} 2}^2} \cdot \\ Q_2-Q_3 & =\frac{\rho g V_{\mathrm{IV}}}{K} \frac{\mathrm{~d} H_2}{\mathrm{~d} t}. \end{aligned} $ | (16) |
试验筒体内流体的压头Hw恒定为0,补充式(17) 作为相应的边界条件方程。
| $ H_{\mathrm{w}}=0. $ | (17) |
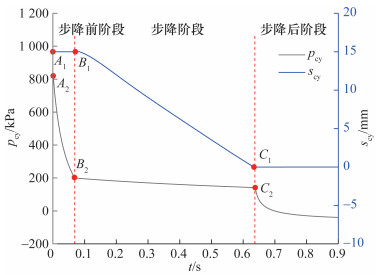
水压缸趋势项模型由式(1)—(7)组成,使用有限差分法求解。在初始时刻,驱动回路中流体保持静止,水压缸内套的初始scy为15 mm。根据位移起始点B2(t=0.069 s)及结束点C2(t=0.634 s),水压缸步降过程可依据关键参数pcy和scy被划分为步降前阶段,步降阶段和步降后阶段,如图 8所示。
|
| 图 8 模型计算的水压缸位移和趋势项压力时程曲线(p0=850 kPa) |
在步降前阶段(0 s<t≤0.069 s),水压缸内套保持静止,pcy从A2点的820.19 kPa迅速下降至B2点的199.73 kPa。定义A2点和B2点的时间差为步降前时间t1。此阶段中,水压缸内压力较高,需要向低压的试验筒体输送流体,因此流出水压缸的流量逐渐增大。一部分水从水压缸下端密封环处泄漏,产生Qleak,另一部分水从出缸流道流出,产生Qout。在二者的共同作用下,pcy快速降低,但仍大于G和Fe之和,因此缸内套保持静止。
在步降阶段(0.069 s<t≤0.634 s),水压缸内套从顶部下降至底部,scy变化量为15 mm。水压缸压力缓慢减小,从B2点的199.73 kPa逐渐减小到C2点的141.95 kPa。定义B2点和C2点的时间差为步降时间tdown。此阶段中,当pcy小于G和Fe之和时,内套无法维持静止,开始向下步降,如式(6)所示。对应内套步降的运动过程,pcy从B2点缓慢减小到C2点,但降压的速度远低于步降前阶段。这是因为随着水压缸向下运动挤压流体,产生了Qcy,流入控制体,补充了缸内流体,因此减缓了pcy的降低速度,如式(1)所示。同时,水压缸的泄漏模式由单端泄漏变为双端泄漏。
在步降后阶段(t>0.634 s),水压缸内套维持在底端不动。pcy经过点C2后迅速减小直到达到稳定状态。此阶段中,水压缸内套的运动停止,对应的Qcy骤减为0,pcy快速下降,如式(1)所示。
在步降过程中,pcy呈现先迅速下降,再缓慢下降,最后迅速下降的趋势,这主要与Qcy在不同阶段的变化情况有关。
4.2 水击项模型分析 4.2.1 初始条件基于CRHDS步降过程瞬变流动的机理,确定了水击的触发时刻为步降位移开始的时刻,即图 8中的B2点。利用趋势项理论模型计算触发时刻的瞬态流场信息。将瞬态流场简化为稳态流场,作为水击项模型的初始条件,压力方面,取触发时刻回路上下游压力的平均值作为初始压力,上游压力为pcy,下游压力为试验筒体内流体压力。流量方面,取趋势项模型计算的B2点Qout作为初始流量。
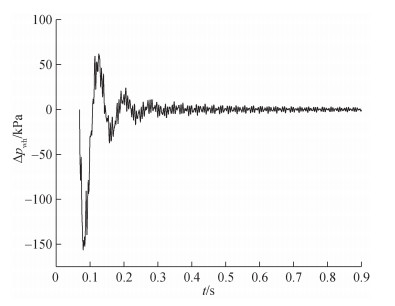
4.2.2 结果分析结合初始条件和3.2.2节的边界条件,采用水击项模型计算得到的脉动压力减去初始压力,得到水击项压力Δpwh随时间的变化情况。如图 9所示,Δpwh在0.069~0.304 s发生明显波动,呈现先减小后增大的变化趋势,最小值为-156.22 kPa,最终稳定在0附近,衰减速度很快,这是因为:1) 部分流体从水压缸密封环处泄漏,泄漏的存在增大了系统的阻尼,加速了能量的衰减,导致瞬变流动更快地收敛到稳态;2) 回路中存在的容腔结构,如组合阀和水压缸,充当了流体蓄能器,利用流体的可压缩性,加快了脉动压力的衰减。
|
| 图 9 水击项压力随时间的变化情况 |
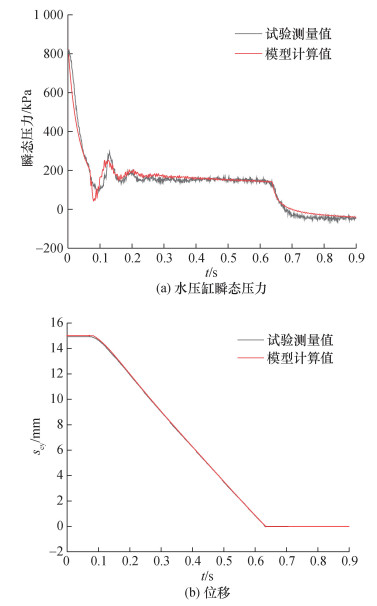
通过趋势项模型计算得到pcy和位移scy,通过水击项模型计算得到Δpwh,叠加pcy和Δpwh得到步降过程瞬态压力,作为步降过程的模拟结果。如图 10所示,无论是瞬态压力还是scy,随时间变化的模拟曲线与瞬变流动特性试验曲线相似度非常高。经计算发现,模拟与试验结果的压力峰值的绝对误差为43.09 kPa,压力谷值的绝对误差是46.95 kPa,说明整体误差很小,验证了步降过程瞬变流模型的有效性和准确性。
|
| 图 10 瞬变流动特性试验数据与步降过程瞬变流模型计算结果的对比(p0=850 kPa) |
5 模型应用
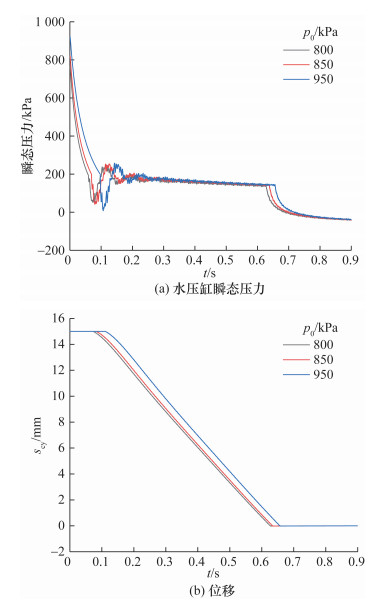
在NHR200低温供热堆中,CRHDS处于高温高压的工况下。温度的升高会改变流体的物性如密度、黏度和波速等,进而影响CRHDS的步降性能。因此引入CRHDS步降瞬变流模型对热态工况下的步降过程特征参数的变化规律进行分析。设定工况温度为230 ℃,并计算出对应的流体物性参数,通过模型分别计算当循环泵的p0为800、850和950 kPa时,水压缸瞬态压力和scy曲线随时间的变化。如图 11所示,不同p0工况下的曲线变化趋势相似,且随着p0增加,水压缸瞬态压力的波动幅度更大。
|
| 图 11 230 ℃时不同驱动压力下的模型模拟结果 |
对比热态工况下,不同p0条件时的各关键特征参数。包括:步降前时间t1、步降时间tdown、步降平均速度和压力波动幅值。
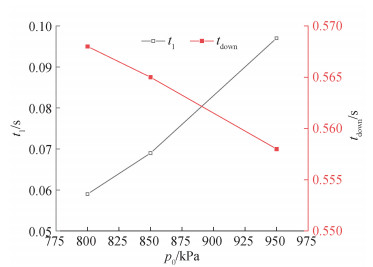
如图 12所示,随着p0从800 kPa增大至950 kPa,t1从0.059 s逐渐增加为0.097 s,tdown从0.568 s逐渐减少为0.558 s。二者均近似线性变化,拟合出的关系式分别为
| $ \begin{aligned} t_1 & =2.571 \times 10^{-4} p_0-0.148, \\ t_{\text {down }} & =-6.714 \times 10^{-5} p_0+0.622. \end{aligned} $ |
|
| 图 12 步降前时间和步降时间随驱动压力的变化 |
循环泵的p0越大,水压缸内流体的初始压力越高,降低至步降运动的启动压力时所需的t1越大。对步降前阶段的式(3)积分得到式(18),发现随着p0、pcy和t1的增大,Qout逐渐增大。
| $ Q_{\text {out }}=\frac{\int_0^{t_1}\left(p_{\mathrm{cy}}-\Delta p_{\mathrm{f}}-p_{\mathrm{w}}\right) \mathrm{d} t}{\frac{\rho L_1}{A_{\mathrm{t} 1}}+\frac{\rho L_2}{A_{\mathrm{t} 2}}+\frac{\rho L_3}{A_{\mathrm{t} 3}}} . $ | (18) |
整理式(2)得到pcy随时间变化的方程。
| $ \frac{\mathrm{d} p_{\mathrm{cy}}}{\mathrm{~d} t}=\frac{K}{V}\left(A_{\mathrm{cy}} v_{\mathrm{cy}}-Q_{\text {out }}-Q_{\text {leak}}\right). $ | (19) |
由式(19)可得,随着Qout增大,
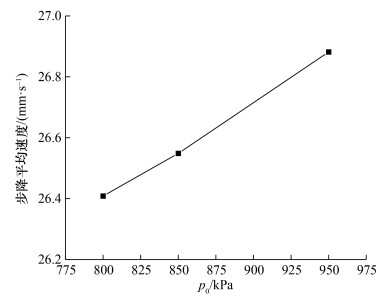
|
| 图 13 步降平均速度随驱动压力的变化 |
定义压力波动幅值ΔpR为压力最大值与最小值之差。如图 14所示,随着p0从800 kPa增大为950 kPa,ΔpR从193.28 kPa逐渐增大为233.39 kPa,拟合关系式可表示为
| $ \Delta p_{\mathrm{R}}=0.261 p_0-13.411. $ |
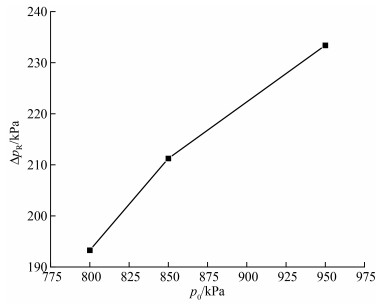
|
| 图 14 压力波动幅值随驱动压力的变化 |
因此,随着p0的增大,t1增大,tdown减小,但tdown的变化幅度较小。更重要的是,步降时间影响着水压缸的位移,进而影响了CRHDM销爪的松开与夹紧,这与控制棒的步降过程密切相关。在设计和优化CRHDS时需着重关注tdown这一参数。
6 结论控制棒水压驱动系统(CRHDS)的步降过程包含复杂的瞬变流动现象。本文分析了CRHDS的组成和工作原理,完成了CRHDS瞬变流动特性试验,并在试验基础上提出了CRHDS步降过程瞬变流模型。该模型由趋势项模型和水击项模型组成,趋势项反映缸内水压的整体变化过程,水击项反映局部瞬变过程。通过叠加2个模型的求解结果分析了整个步降过程,阐述了瞬变流动机理。经验证,CRHDS步降过程瞬变流模型具备有效性和准确性;同时,将其应用于热态不同驱动压力工况下的模拟后,可得出步降过程关键特征参数的变化规律。
| [1] |
PARK B J, PHAM P T, HONG K S. Model reference robust adaptive control of control element drive mechanism in a nuclear power plant[J]. International Journal of Control Automation and Systems, 2020, 18(7): 1651-1661. DOI:10.1007/s12555-019-0987-3 |
| [2] |
薄涵亮, 郑文祥, 董铎, 等. 水力驱动控制棒步进动态过程的研究[J]. 核科学与工程, 2000, 20(4): 322-328. BO H L, ZHENG W X, DONG D, et al. Analysis on step action of hydraulic control rod driving[J]. Nuclear Science and Engineering, 2000, 20(4): 322-328. DOI:10.3321/j.issn:0258-0918.2000.04.005 (in Chinese) |
| [3] |
宋青, 孙磊, 杨红义, 等. 中国实验快堆控制棒驱动机构抗震鉴定试验[J]. 核科学与工程, 2008, 28(3): 218-223. SONE Q, SUN L, YANG H Y, et al. Seismic appraisal test of control rod drive mechanism of China Experiment Fast Reactor[J]. Nuclear Science and Engineering, 2008, 28(3): 218-223. DOI:10.3321/j.issn:0258-0918.2008.03.005 (in Chinese) |
| [4] |
薄涵亮, 郑文祥, 王大中, 等. 核反应堆控制棒水压驱动技术[J]. 清华大学学报(自然科学版), 2005, 45(3): 424-427. BO H L, ZHENG W X, WANG D Z, et al. Hydraulic control rod drive technology for nuclear reactors[J]. Journal of Tsinghua University (Science and Technology), 2005, 45(3): 424-427. DOI:10.3321/j.issn:1000-0054.2005.03.039 (in Chinese) |
| [5] |
GHIDAOUI M S, ZHAO M, MCINNIS D A, et al. A review of water hammer theory and practice[J]. Applied Mechanics Reviews, 2005, 58(1): 49-76. DOI:10.1115/1.1828050 |
| [6] |
薄涵亮, 王大中, 张作义, 等. 一体化水堆内置式控制棒水压驱动技术研究[J]. 清华大学学报(自然科学版), 2021, 61(4): 338-349. BO H L, WANG D Z, ZHANG Z Y, et al. In-vessel control rod hydraulic drive mechanism for integrated water reactors[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(4): 338-349. (in Chinese) |
| [7] |
秦本科, 薄涵亮, 郑文祥, 等. 控制棒水压驱动机构水压缸步升压力变化过程[J]. 清华大学学报(自然科学版), 2008, 48(12): 2118-2121. QIN B K, BO H L, ZHENG W X, et al. Pressure transients in hydraulic cylinder step-up motion of control rod hydraulic drive mechanism[J]. Journal of Tsinghua University (Science and Technology), 2008, 48(12): 2118-2121. DOI:10.3321/j.issn:1000-0054.2008.12.023 (in Chinese) |
| [8] |
秦本科, 薄涵亮, 郑文祥, 等. 控制棒水压驱动机构水压缸步降过程研究[J]. 原子能科学技术, 2009, 43(4): 345-349. QIN B K, BO H L, ZHENG W X, et al. Study on step-down dynamic process of hydraulic cylinder for control rod hydraulic drive mechanism[J]. Atomic Energy Science and Technology, 2009, 43(4): 345-349. (in Chinese) |
| [9] |
赵陈儒, 薄涵亮. 反应堆内置式控制棒水压驱动回路技术研究[J]. 核动力工程, 2014, 35(1): 125-128. ZHAO C R, BO H L. Studies on design of internal hydraulic control rod drive system loop for nuclear reactors[J]. Nuclear Power Engineering, 2014, 35(1): 125-128. (in Chinese) |
| [10] |
LI Y L, QIN B K, BO H L. Study on static characteristics of array electrode capacitance control rod position measurement sensor[J]. Annals of Nuclear Energy, 2022, 179: 109445. DOI:10.1016/j.anucene.2022.109445 |
| [11] |
蒋俊飞. 控制棒驱动线水压缸提升与复位过程流固耦合特性研究[D]. 北京: 清华大学, 2019. JIANG J F. Study on fluid-solid coupling characteristic of control rod driving line hydraulic cylinder during step up and step down process[D]. Beijing: Tsinghua University, 2019. (in Chinese) |
| [12] |
YANG L Q, QIN B K, BO H L. Transient flow characteristics analysis on the step-up process of control rod hydraulic drive system[J]. Annals of Nuclear Energy, 2023, 185: 109723. DOI:10.1016/j.anucene.2023.109723 |
| [13] |
杨林清, 秦本科, 薄涵亮. 控制棒水压驱动步升过程流动阻力影响分析[J]. 原子能科学技术, 2022, 56(7): 1379-1386. YANG L Q, QIN B K, BO H L. Analysis of flow resistance influence on step-up process of control rod hydraulic drive system[J]. Atomic Energy Science and Technology, 2022, 56(7): 1379-1386. (in Chinese) |
| [14] |
QIN B K, BO H L. Deceleration performance and parameter influence analysis of the control rod hydraulic deceleration device for control rod hydraulic drive system[J]. Journal of Nuclear Engineering and Radiation Science, 2019, 5(3): 031702. DOI:10.1115/1.4042541 |