2. 清华大学, 公共安全研究院, 北京 100084;
3. 清华大学 合肥公共安全研究院, 合肥 230601;
4. 中国地质环境监测院(自然资源部地质灾害技术指导中心), 北京 100081;
5. 自然资源部地质灾害智能监测与风险预警工程技术创新中心, 北京 100081
2. Institute of Public Safety Research, Tsinghua University, Beijing 100084, China;
3. Hefei Institute of Public Safety Research, Tsinghua University, Hefei 230601, China;
4. China Institute of Geo-Environment Monitoring (Geological Disaster Technical Guidance Center of Ministry of Natural Resources), Beijing 100081, China;
5. Technology Innovation Center for Geohazard Monitoring and Risk Early Warning, Ministry of Natural Resources, Beijing 100081, China
滑坡灾害常由降雨等因素诱发,每年造成重大人员伤亡,并对基础设施造成严重破坏。国内外普遍利用监测预警系统主动防范滑坡灾害,及时向隐患区受威胁人员发出预警以保障疏散避险工作,并采取有效措施维护重要基础设施。
变形是滑坡最显著的特征,与斜坡稳定性直接相关,是理解灾害发生发展规律和风险预警的重要依据。监测滑坡变形行为应主要关注滑坡位移、速度和加速度。位移是最直接的衡量参数,速度是重要的运动学特征和危险性评估依据。滑坡速度分级标准[1-2]包括从“极慢”(每年几毫米)到“极快”(每秒几米)一系列级别,相邻速度级别临界值间相差2个数量级,易于区分和实际应用。加速度能描述速度上升或下降的特征,为滑坡风险识别和早期预警提供依据[3]。滑坡深部变形监测技术能感知滑面形成、发展等灾害前兆信息,常见的监测仪器包括测斜仪和阵列式位移计(shape accel array,SAA)等,因设备机械结构和倾角传感器测量方式的局限性,存在量程有限、成本高和操作复杂等不足,无法在野外广泛和长期应用[4],不适用于普适性监测。
滑坡变形过程中岩土颗粒间相互作用产生高频应力波,称为声发射(acoustic emission,AE),声发射通过声源周围的介质传播[5]。声发射产生机理包括颗粒-颗粒碰撞、摩擦、阻滞(颗粒接触应力释放和重新分布)、损坏(颗粒表面微小凸起破碎),声发射信号强度可在一定程度上反映滑坡变形特征[6]。声发射技术可实时持续监测滑坡深部变形,相较于地表变形,本文中深部变形主要指地质灾害体内部的水平变形,性价比高且灵敏可靠[7-9],具有扩大滑坡专业监测内容和覆盖范围的潜力[9-14],有望提高滑坡早期风险预警成功率。
然而,声发射技术一般用于岩质滑坡监测,用于土质滑坡监测的相关研究较少,原因是土质滑坡变形破坏过程中产生声发射的事件较少、能量水平较低,声发射弹性波在土体多孔材料中传播衰减快,信号易受环境噪声干扰[15-16]。为解决上述问题,滑坡监测时常用波导管作为声学波导(以下简称“波导”)以采集声发射信号[12, 17-20]。无源波导通过在波导管周围灌浆制成,常用于监测岩质滑坡[13-21];波导管与填充颗粒结合形成的有源波导常用于监测土质滑坡[9-10, 12]。
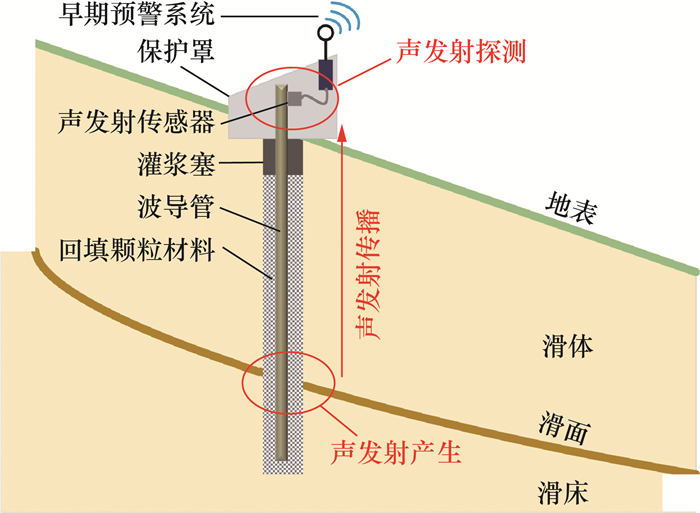
图 1为监测土质滑坡的有源波导声发射监测系统,主要由钢制波导管、回填颗粒材料和声发射监测装置组成,回填颗粒材料常用岩石颗粒,颗粒相互作用时发出“嘈杂”声响[16]。声发射监测装置包括以下组成部分:与波导管地上部分连接的谐振式声发射传感器,将声发射弹性波转换为电压信号;用于提高声学信噪比的放大器和滤波器,如可过滤频率20~30 kHz以外的信号以排除环境噪声[8, 10, 12];声发射特征参数提取分析模块,其中,振铃计数是关键参数之一,指声发射波形在一定时间内超过预设电压阈值的次数,反映了声发射信号的强度和频度,与声发射源的物理过程密切相关,常用于评价岩土材料的活动性。有源波导安装在滑坡体钻孔内,与已勘明或推测的滑面相交。滑坡深部变形与有源波导声发射间存在因果关系,深部变形对有源波导施加剪切和挤压等力学作用,引起波导管与回填颗粒发生碰撞、摩擦等相互作用进而产生声发射信号[22],信号沿钢管向上传播至传感器。声波在波导管中传播具有低衰减特性,有源波导声发射信号的有效传播距离超过20 m[23]。综上所述,有源波导声发射技术有效解决了土质滑坡声发射事件少、声波能量水平低、声波信号衰减大和环境噪声干扰等问题,逐渐成为受认可的土质滑坡深部变形监测方法[8-9, 13, 24]。声发射监测技术已应用于四川、广东、甘肃等地的典型滑坡监测[25-26],滑面深度为数米至数十米。前期一般采用地球物理方法开展边坡地质结构探测,特别是确定潜在滑面的深度,以指导监测仪器的安装工作。
声发射出现在滑坡孕育期并伴随变形破坏全过程,声发射技术能灵敏感知滑坡的微小变形[27-29]。Smith等[8]通过实验证明了声发射技术可用于探测新生滑面的形成和发展。滑坡原位监测表明,有源波导可比测斜仪更早探测到深部变形,并能在滑坡体产生较大变形时持续监测直至波导管被剪切破坏[16]。Koerner等[30]根据声发射信号强度提取滑坡变形特征,并提出了斜坡稳定性的定性判断方法:1) 无声发射表示边坡稳定;2) 中等水平声发射表示边坡临界稳定;3) 高水平声发射表示边坡不稳定。2013年以来,声发射监测数据定量解释方法取得了较大进展[8, 10, 31]。研究表明,声发射特征参数和经验公式可在一定程度上量化土质滑坡的深部变形行为,进一步丰富了滑坡早期预警模型的判据[31-32],有助于提高灾害预警的时效性和可靠性。但声发射特征参数是滑坡深部变形的间接测量数据,利用声发射特征参数量化变形时需用实际变形数据进行标定。
本文简要梳理了滑坡声发射数据定量解释方法的发展历程和最新状况。首先,回顾了基于声发射数据量化滑坡深部变形行为的经验公式和方法,指出了传统方法面临的挑战;其次,介绍了自动解释声发射数据的机器学习方法,包括滑坡运动状态分类模型和滑坡位移预测模型,开展模型应用验证和性能评估;再次,将声发射监测与机器学习结合,提出了基于声发射数据智能分析的滑坡早期风险分级预警方法;最后,讨论了声发射技术的应用局限性和发展趋势,并对全文进行总结。
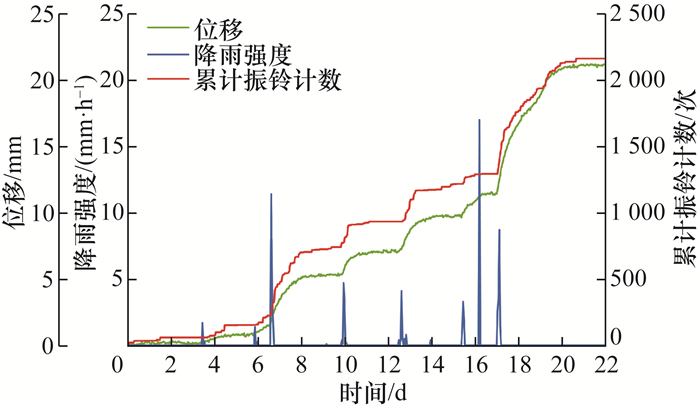
1 声发射数据定量解释方法 1.1 滑坡速度-声发射率关系量化Hollin Hill滑坡位于英国北约克郡,北纬54°06′40″,西经0°57′34″,海拔55~100 m,底部为基岩,上部为土体。滑面深约1.5~4.0 m,属于浅层复活滑坡,每年位移量约数百毫米。研究人员在Hollin Hill滑坡上安装了3套有源波导声发射系统,开展了十余年的持续监测。图 2显示了某时期Hollin Hill滑坡深部位移、累计振铃计数和降雨强度等监测数据,其中,高精度连续位移数据由SAA得到,累计振铃计数与滑坡深部位移呈正相关。声发射率(单位时间内振铃计数)是累计振铃计数对时间的一阶导数,速度是位移对时间的一阶导数。Dixon等[10]基于统计经验,引入比例系数Cp量化声发射率与滑坡速度间的正相关关系,相关经验公式表示如下:
| $ \begin{gathered} \mathrm{AE}_{\text {rate }} \propto v, \\ \mathrm{AE}_{\text {rate }}=C_{\mathrm{p}} v, \\ C_{\mathrm{p}}=f(V) . \end{gathered} $ | (1) |
其中:AErate表示声发射率;v表示滑坡速度;Cp反映了监测系统的灵敏度,表征滑坡速度和声发射率间的响应强度。系统灵敏度取决于声发射监测系统的自身变量f(V),如传感器灵敏度(受信号放大和电压阈值等因素影响)、波导管长度(影响声发射信号传播的衰减幅度)、有源波导材料和结构(由回填颗粒性质等决定),这些变量与滑坡速度共同作用,影响有源波导系统采集的声发射率。
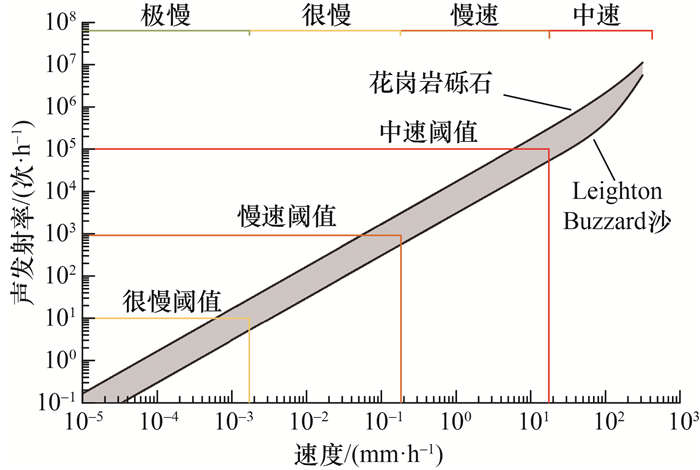
Dixon等[33]通过有源波导压缩实验发现,利用声发射参数可识别滑坡速度的数量级变化,进而依据滑坡速度分级标准(见表 1[1-2])评估滑坡危险性。为进一步量化声发射率和滑坡速度的关系,Smith等[8]开展了滑坡大尺寸模型实验研究,考虑了回填颗粒等变量对声发射数据的影响,得到的有源波导声发射率-剪切速度标定关系如图 3所示。有源波导声发射率主要响应于滑坡速度,速度升高引起单位时间内颗粒-颗粒和颗粒-波导相互作用增大[34],即声发射事件数量增加。声发射率的数量级对应一定的滑坡速度级别,可根据滑坡速度分级标准确定相应的预警级别,以指导相关人员及时采取针对性响应措施。例如,通过声发射率发现滑坡速度依次处于“很慢” “慢速”和“中速”区间时,对应不同级别的预警。声发射监测技术可准确识别滑坡的加速变形行为,为灾害早期预警提供依据。综上所述,滑坡原位监测和大尺寸模型实验均表明声发射率和滑坡速度存在正相关关系(见式(1)和图 3)。
1.2 滑坡位移和速度反演计算
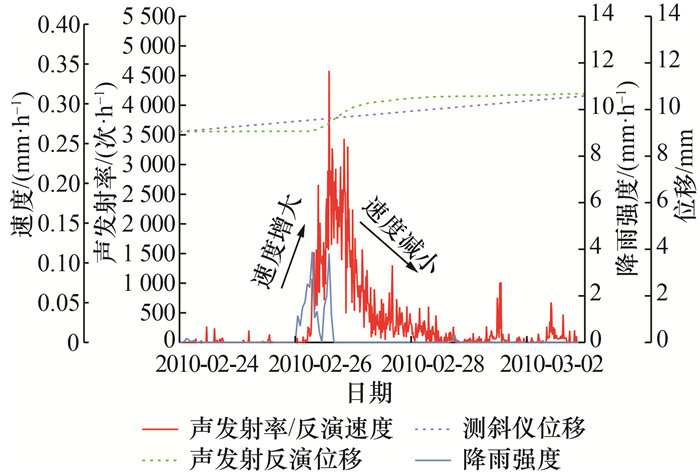
若设定的采集时间间隔较大,则滑坡原位监测获取的位移数据可能不连续,不利于有效分析滑坡深部变形行为,可考虑基于连续声发射数据反演滑坡位移和速度。基于声发射率和滑坡速度存在近似正比关系的假设,Dixon等[10]提出了从滑坡运动事件中计算得到Cp的方法。滑坡深部变形是产生声发射的原因,滑坡深部变形与声发射在物理过程上存在直接响应机制,在数学关系上近似表现为正比例函数(见式(1)),通过声发射数据可反演得到滑坡位移和速度。Hollin Hill滑坡的声发射、位移和降雨时间序列如图 4所示。例如,在图 4中,测斜仪人工监测的位移仅有始末端2个数值,为精细分析滑坡变形过程,假设声发射率-时间曲线与坐标轴围成的面积等于测斜仪测得的位移增量,可得到该滑坡运动事件的连续位移和速度曲线。
具体反演方法如下:基于微积分思想,将声发射率-时间曲线分割成多个梯形,计算各梯形被积函数的值,将滑坡位移增量按各函数值的比例分配,进而计算每个梯形对应的位移值。从起始点开始依次累加各位移值得到图 4中的“S”形声发射反演位移,速度由位移-时间关系计算确定。整个滑坡运动事件中,每段时间区间都得到一个声发射率和对应的反演速度,可动态校准声发射率-速度的近似正比关系。将校准后的Cp应用于声发射实时连续监测数据,可量化后续滑坡运动事件中的速度和位移。通过声发射持续监测和经验公式计算量化滑坡速度的方法产生的误差小于一个数量级[8],满足滑坡速度分级标准应用于预警决策时对数据准确性的要求。
然而,如何运用声发射技术准确量化滑坡深部变形仍是当前难题,传统方法面临诸多挑战,如有源波导内部相互作用复杂、声发射监测设备自身条件多样等。有源波导内部颗粒材料和波导管相互作用复杂且随机性强,声发射产生的机理尚不清晰。颗粒材料是由大量离散固体颗粒紧密堆积而成的复杂无序体系[35],对外界微小作用高度敏感且响应为非线性。颗粒-颗粒和颗粒-波导管相互作用存在明显差异且力学行为高度复杂,受限于对声发射信号的理解深度,经验模型在公式建立和参数估计过程中会不可避免地引入误差。声发射产生的机理尚不明确,从根源上制约了滑坡深部变形-声发射关系量化。此外,声发射信号受多种不确定因素(颗粒状态、波导管长度和岩土环境等)影响而动态变化[11],滑坡深部变形-声发射响应规律仍未明确。有源波导声发射信号产生、传播和采集过程复杂,难以科学解释和有效厘清多种因素对声发射信号的影响。声发射直接响应于滑坡深部变形,但变形行为具有高度不确定性,滑坡深部变形-声发射响应关系动态变化,经验公式等常规方法量化精度低。上述挑战制约了利用声发射数据量化滑坡变形的准确性,无法保障滑坡预警结果可靠[6, 36-37]。
1.3 滑坡运动状态自动分类文[38-39]采用机器学习方法并根据一系列不同监测参数(包括触发因素和响应参数)量化滑坡变形。机器学习方法具有处理复杂数据和非线性关系的能力,可自动学习并表征滑坡深部变形-声发射的响应关系[40],是声发射数据分析方法的最新发展趋势,一定程度上可提高滑坡风险预警系统的可靠性[41]。研究发展岩土工程和机器学习等多学科交叉融合的自动化模型,可提升运用声发射数据量化滑坡深部变形行为的能力,形成具有通用性和高效率的方法,满足滑坡自动化专业监测需求,具有重要科学意义和工程应用价值。
Deng等[40]提出利用机器学习方法对滑坡运动学状态进行自动分类,基于滑坡速度分级标准(见表 1)和2个声发射特征参数(振铃计数和振铃计数变化率),可自动识别速度级别和加速度状态。加速度是速度对时间的一阶导数,振铃计数变化率是振铃计数对时间的一阶导数。除振铃计数外,振铃计数变化率也可作为解释滑坡深部变形行为的特征参数,一定程度上可反映加速度的变化特征。Deng等[40]选择了支持向量机(support vector machine, SVM)、随机森林(random forest, RF)和极限梯度提升(extreme gradient boosting,XGBoost)3种分类算法,使用滑坡模型实验数据集[8]和Hollin Hill滑坡原位监测数据集[12],对机器学习分类模型进行训练和测试。
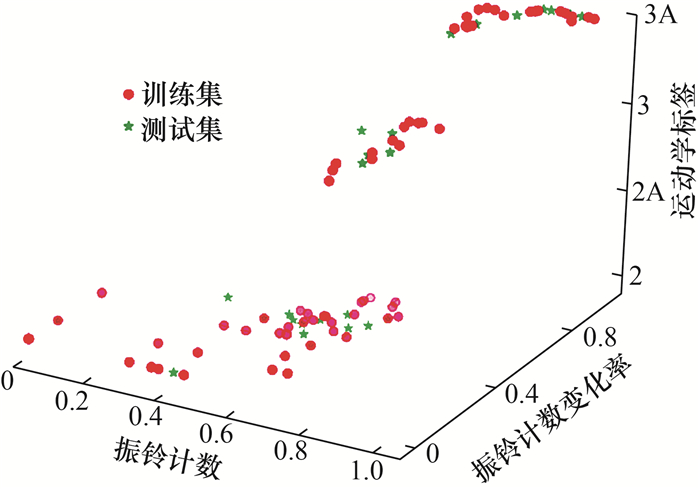
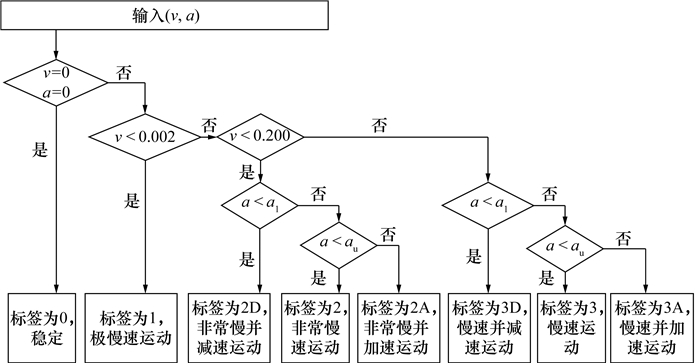
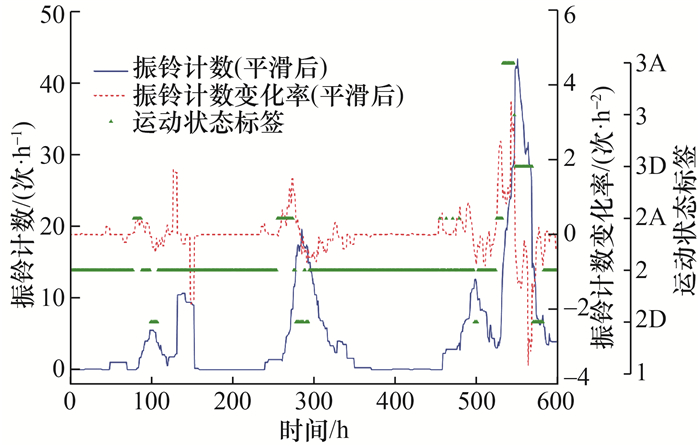
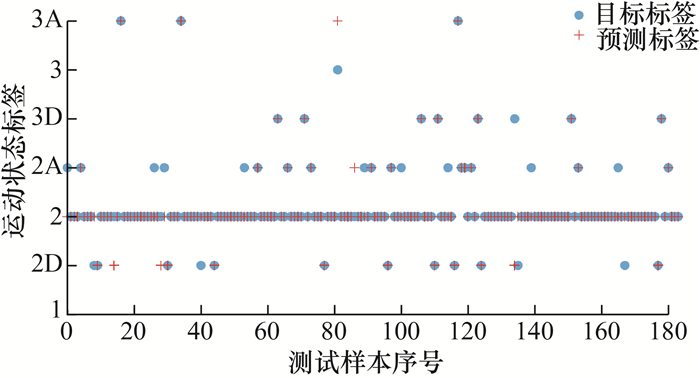
图 5展示了滑坡模型实验的监测数据(图中数值已无量纲化处理),红色圆点表示用于训练的数据集(数据占比为70%),绿色五角星表示用于测试的数据集(数据占比为30%)。数据点代表 2个声发射特征参数和相应的运动学标签,标签根据SAA位移测量值生成,每个标签具有特定含义,如“2”表示非常慢速运动,“3”表示慢速运动,“2A”表示滑坡速度为0.002~0.200 mm/h并且处于加速(accelerating)状态,“3A”表示慢速并加速运动,以此类推。在训练过程中,使用上述2个声发射特征参数和真实标签训练分类器;在测试过程中,仅将2个声发射特征参数输入训练后的分类器,根据声发射数据预测运动学标签;随后将预测标签与真实标签进行比较以评估分类器的性能。性能评估采用准确率,即正确预测标签数占标签总数的比例。计算结果表明,3种分类算法中,RF模型表现最好,分类准确率始终高于90%。除了将分类模型在实验室数据集上测试验证,还利用滑坡现场监测数据验证模型。Hollin Hill滑坡设计的八标签运动速度分类流程如图 6所示,考虑参数包括速度和加速度类别,其中,加速度a由速度计算得到,单位为mm/h2, 通常在0附近以极小幅度波动,a处于(al, au)内仍可视为滑坡匀速状态,au表示加速度正值,al表示加速度负值。图 7为2016年3—4月监测得到的Hollin Hill滑坡声发射参数曲线及由SAA测量值生成的运动学标签时间序列,同样70%的数据用于训练、剩余30%的数据用于测试,图中D表示滑坡运动处于减速状态(decelerating)。RF模型对Hollin Hill滑坡测试集的分类结果如图 8所示,经计算可知,RF模型应用于滑坡现场数据的分类准确率高于90%。
1.4 滑坡位移预测
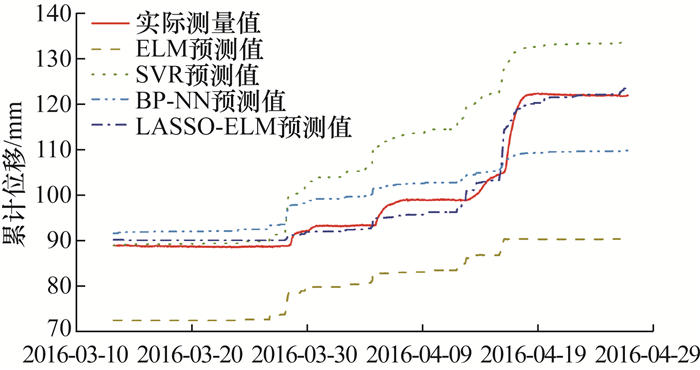
1.3节阐述了基于声发射监测数据和机器学习分类模型开发的滑坡运动学状态自动识别方法,根据速度级别和加速度状态可得到应触发的预警级别。支撑该滑坡分级预警方法的另一基础是持续的高精度深部变形信息,Deng等[39]提出了基于机器学习的滑坡位移预测方法,即利用声发射和相关参数(如降雨量)自动量化滑坡位移的绝对量。与之前建立的经验公式(1.1和1.2节)相比,机器学习回归模型量化滑坡深部变形行为的准确性更高,解决了滑坡深部位移数据的可持续获取问题。基于滑坡现场监测数据集,选取Hollin Hill滑坡的声发射、降雨量和位移监测值用于训练回归模型;将声发射和降雨量输入训练后的模型,输出滑坡位移预测值。图 9比较了极限学习机(extreme learning machine,ELM)、支持向量回归(support vector regression,SVR)、反向传播神经网络(back propagation neural network,BP-NN)和基于最小绝对值收敛和选择算子的极限学习机(least absolute shrinkage and selection operator-extreme learning machine,LASSO-ELM)4种模型的滑坡位移预测结果,LASSO-ELM预测的位移曲线最接近实际测量曲线,且整体性能最佳,平均绝对百分比误差(mean absolute percentage error,MAPE)为1.5%。
2 滑坡风险分级预警方法
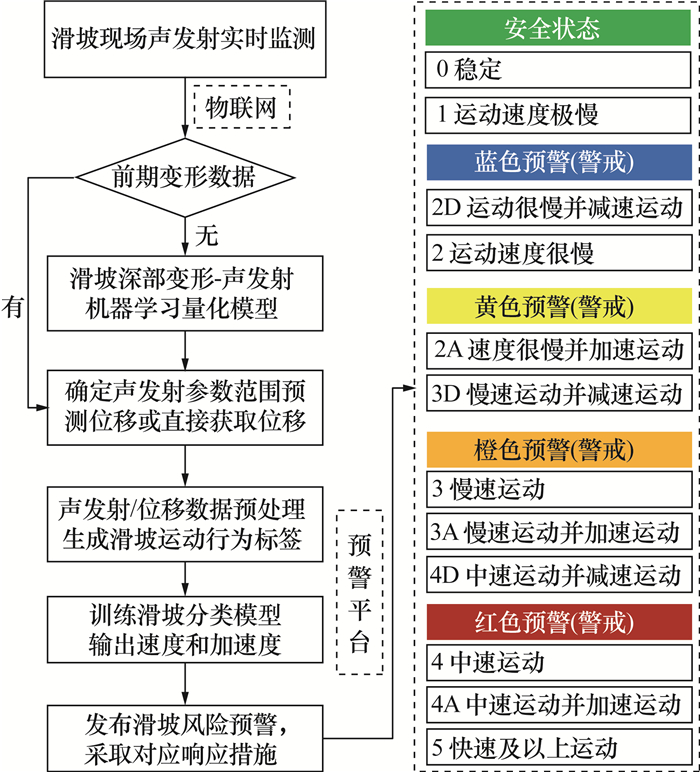
1.3和1.4节阐明了利用机器学习模型和声发射数据量化滑坡深部变形行为的分析方法。机器学习模型的优势在于适用性更强、预测更准确且自动化水平高,能快速高效地输出滑坡位移、速度和加速度等关键参数。与以往研究相比,文[39-40]新增了加速度信息和对应的声发射参数(振铃计数变化率),为滑坡风险预警提供了新的有效判据。在滑坡深部变形-声发射关系量化模型的基础上,进一步提出声发射监测与机器学习结合的滑坡风险分级预警方法(见图 10),主要根据滑坡速度分级标准和加速度状态推测滑坡发生的可能性及危险程度,通过生成预警级别建议并采取响应措施达到防灾减灾的目的。预警级别中的每个运动状态标签都定义了明确的速度范围和加速度状态,实际应用中可操作性强。例如,“2A”表示滑坡速度为0.002~0.200 mm/h并处于加速运动状态,如果滑坡标签在一段时间内持续为“2A”,建议发布黄色预警。
|
| 图 10 基于滑坡运动状态的风险分级预警流程 |
然而,滑坡预警方法在实际应用中可能面临位移历史数据缺失或声发射数据变化范围未知等不利条件,影响机器学习模型的有效应用,需要采取有效方法缓解滑坡现场可能出现的不利状况,从而保障预警方法的实际应用效果。一般情况下,滑坡现场同时进行变形和声发射监测。测斜仪和SAA等深部位移直接测量设备成本较高,获取的是某个钻孔沿深度方向的完整变形信息,如果布设数量较少则有可能错过关键变形位置,不能及时有效预警。声发射监测设备的成本远低于测斜仪和SAA,可考虑将多个高性价比的声发射监测设备安装分布于滑坡体的不同位置,同时安装一套SAA提供高精度深部位移数据。位移数据用于多个声发射设备监测数据的机器学习,机器学习模型在监测期间动态更新以不断提高预测准确率。上述方法有望在成本可接受的前提下扩大滑坡深部变形监测的覆盖范围,获取滑坡整体变形状态的高质量时间和空间信息。
声发射监测预警方法应用于滑坡现场时,需要考虑滑坡的岩土性质、演化机制和触发因素等条件,以及预期的运动模式和滑动速度等状态。对于复活滑坡的缓慢变形行为,如果监测一段时间后无法继续获取深部位移数据,可先使用前期变形和声发射监测数据训练机器学习模型,再基于声发射数据通过模型预测持续提供位移数据。然而,对于首次发生的滑坡,只有在运动事件发生后才能获得明显的声发射数据,需要先使用滑坡机制和声发射系统类似的实验或现场数据训练机器学习模型,然后基于声发射监测数据预测滑坡深部变形行为。在滑坡现场没有位移测量数据的情况下也需要依靠类似实验或现场数据,如果后续获得直接测量的位移数据,那么可通过动态更新机器学习模型得到更准确的预测结果。
滑坡现场缺少声发射历史监测数据同样是机器学习应用中的难题,因为无法定义振铃计数的最大预期值,而机器学习过程中不能通过缩放最大绝对值对声发射数据进行标准化处理,否则可能影响机器学习分类模型的性能。然而,滑坡模型实验获取了大量的声发射数据,模拟的滑坡速度范围足够大,可用于估计最大振铃计数。滑坡速度分级标准中的速度临界值可通过振铃计数2个数量级的差异加以区分,因此估计最大振铃计数不会导致滑坡运动状态分类结果出现明显错误。最大振铃计数可在滑坡监测期间根据声发射的实际测量值进行更新,进而运用机器学习模型输出运动状态分类结果,根据图 10中的流程化方法开展滑坡风险分级预警。
3 讨论滑坡深部变形可表征为有源波导在滑面处发生的剪切变形,剪切变形与声发射间存在直接因果关系,因此可通过有源波导声发射数据反演滑坡深部变形。滑坡原位监测和物理模型实验表明,有源波导产生的声发射率与运动速度呈正相关关系。
Dixon等[10]引入Cp,建立了滑坡运动速度与声发射率间的经验模型。通过假设声发射率-时间曲线下的面积等于滑坡位移量,得到滑坡运动事件的速度-时间曲线,进而将确定的Cp应用于声发射连续监测数据,量化后续滑坡运动事件的速度和位移[2]。根据滑坡模型实验的监测数据,建立了一系列有源波导回填颗粒的变形-声发射关系(见图 3),进而利用声发射数据直接量化滑坡速度[8]。在此基础上,Deng等[39-40]开发了2种自动解释声发射监测数据的机器学习模型:一种是分类模型,基于滑坡速度分级标准(见表 1),利用2种声发射特征参数(振铃计数和振铃计数变化率)对滑坡运动学状态进行分类[40];另一种是回归模型,根据声发射和降雨量的时间序列数据自动量化滑坡位移的绝对量[39]。在这一系列定量研究之前,声发射监测数据的解释仅限于定性方法,即无声发射表示稳定、高水平声发射表示不稳定,少有定量分析方法可解释声发射监测数据。
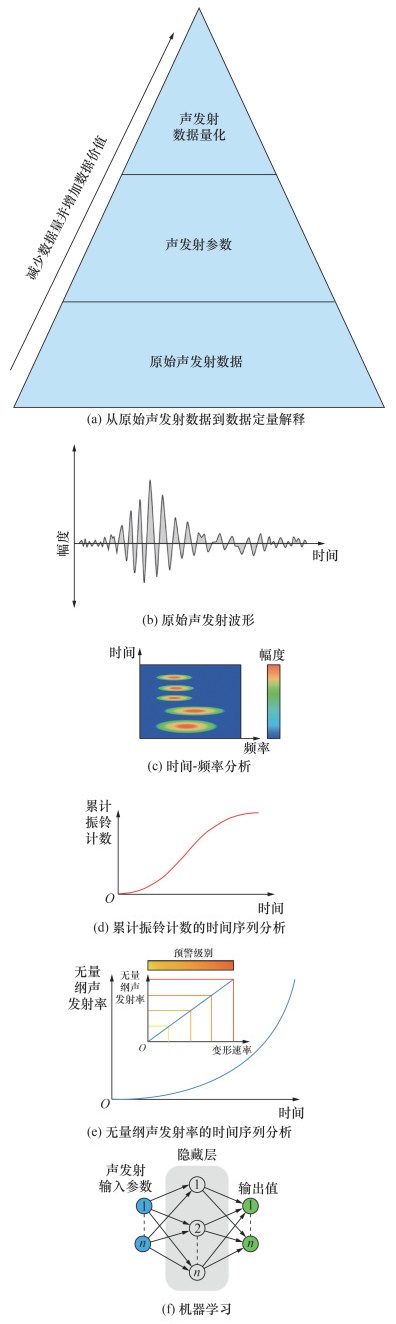
基于滑坡监测数据定量分析解释等研究成果,图 11给出了从声发射监测数据中提取滑坡变形关键信息以制定决策的概念框架[42]。图 11a中,自下而上表示声发射数据量减少而数据价值增加。图 11b和11c表示从声发射原始波形数据提取特征参数,并将获取的声发射特征参数作为数据解释模型的输入。图 11d和11e表明可使用时间序列方法分析解释声发射数据,提供滑坡速度变化率,即加速变形行为的信息。图 11f利用机器学习模型,输入声发射监测数据进行训练,输出滑坡深部变形行为相关信息,支撑灾害风险早期预警和决策。
声发射监测数据解释方法的选择受实际应用场景影响,实际应用场景可能从简单到复杂。例如,Dixon等[9]开发了用于滑坡隐患区的低成本声发射预警系统,只包含一个可触发声光报警的简易监测设备,降低了斜坡稳定性监测预警成本;建立了基于特定滑坡速度的单一声发射阈值预警判据,可尽可能减少误报,并减少了监测数据的传输过程。相比之下,城市基础设施智能预警方案常包含高度复杂的机器学习算法,更适用于重要基础设施的实时健康管理。
有源波导声发射监测技术逐渐成为可选的滑坡深部变形监测方法[43]。然而,现有声发射技术在滑坡监测应用中仍然存在局限性。首先,颗粒材料相互作用机理复杂[15, 27, 44],难以准确解释声发射数据。有源波导产生的声发射信号是滑坡深部变形的结果,声发射参数直接响应于滑坡深部变形。但目前得到的滑坡深部变形-声发射量化关系是统计学意义上的相关关系,受颗粒材料差异性等因素影响,声发射数据的科学定量解释有待进一步研究。其次,机器学习是解释声发射数据的最新方法,但模型精度取决于训练数据的规模和质量,现有模型未包含有源波导声发射机理和响应规律等先验物理知识,可解释性和泛化能力不足。再次,声发射监测数据动态反映了滑坡深部变形的变化量,但无法指示变形的方向。这一局限性由声发射技术的本质决定,即声发射数据是标量而非矢量,不具有方向信息。最后,滑面定位是深部变形监测的重要目标,但尚无直接运用有源波导声发射技术定位土质滑坡滑面的研究成果。声发射源主要位于滑面附近,利用声发射技术确定波导管上声源位置的研究已较成熟[24, 45],进而可通过声源定位实现滑面定位。
未来,除了现有的基于声发射特征参数分析的滑坡变形监测方法,还有可能发展形成基于全波形分析的监测方法。随着边缘计算、智慧存储和5G通信等新技术蓬勃发展,原先声发射波形等大容量文件现场存储并远程传输的制约或被解除,有望实时获取更全面丰富的信息,更好地分析掌握滑坡内部的演化特征和发展趋势。针对土质滑坡深部变形监测,声发射技术成本低、灵敏度高、监测实时连续,在可靠探测和早期预警等方面具有独特优势,有望发展成为普适性监测技术。
4 结论本文综述了滑坡变形声发射监测数据定量解释方法的最新研究进展。滑坡原位监测和物理模型实验表明,声发射率与运动速度呈正相关。基于声发射率和滑坡速度间的经验模型,发展出一系列利用声发射监测数据量化滑坡变形行为的解释方法。在这些方法的基础上,建立了自动解释声发射数据的机器学习方法:1) 分类模型,基于滑坡速度分级标准,利用振铃计数和振铃计数变化率对滑坡运动状态(速度和加速度)进行分类;2) 预测模型,利用声发射和降雨量的时间序列数据自动量化滑坡位移的绝对量。在本文介绍的一系列研究成果之前,滑坡声发射监测数据的解释局限于定性方法,即无声发射表示边坡稳定,高水平声发射表示边坡不稳定。
本文提出了从声发射监测数据中提取滑坡变形关键信息以支撑预警决策的概念框架,根据特定应用场景选择的声发射监测数据解释方法复杂程度存在差异,并受实际场景影响,如滑坡隐患区的低成本监测预警系统、城市重要基础设施的智能健康管理系统。利用机器学习自动量化声发射数据的方法不仅准确有效,而且适用于实时智能预警系统,代表了声发射数据定量解释的最新水平,是未来发展的重要方向。
| [1] |
CRUDEN D M, VARNES D J. Landslides: Investigation and mitigation. Chapter 3-Landslide types and processes[J]. Transportation Research Board Special Report, 1996(247): 36-75. |
| [2] |
HUNGR O, LEROUEIL S, PICARELLI L. The Varnes classification of landslide types, an update[J]. Landslides, 2014, 11(2): 167-194. DOI:10.1007/s10346-013-0436-y |
| [3] |
许强, 曾裕平. 具有蠕变特点滑坡的加速度变化特征及临滑预警指标研究[J]. 岩石力学与工程学报, 2009, 28(6): 1099-1106. XU Q, ZENG Y P. Research on acceleration variation characteristics of creep landslide and early-warning prediction indicator of critical sliding[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(6): 1099-1106. DOI:10.3321/j.issn:1000-6915.2009.06.003 (in Chinese) |
| [4] |
UHLEMANN S, SMITH A, CHAMBERS J, et al. Assessment of ground-based monitoring techniques applied to landslide investigations[J]. Geomorphology, 2016, 253: 438-451. DOI:10.1016/j.geomorph.2015.10.027 |
| [5] |
易武, 孟召平. 岩质边坡声发射特征及失稳预报判据研究[J]. 岩土力学, 2007, 28(12): 2529-2533, 2538. YI W, MENG Z P. Study on acoustic emission feature of rock slope and its instability forecast criterion[J]. Rock and Soil Mechanics, 2007, 28(12): 2529-2533, 2538. DOI:10.3969/j.issn.1000-7598.2007.12.008 (in Chinese) |
| [6] |
SMITH A, DIXON N. Acoustic emission behaviour of dense sands[J]. Géotechnique, 2019, 69(12): 1107-1122. DOI:10.1680/jgeot.18.P.209 |
| [7] |
MATSUURA S, ASANO S, OKAMOTO T. Relationship between rain and/or meltwater, pore-water pressure and displacement of a reactivated landslide[J]. Engineering Geology, 2008, 101(1-2): 49-59. DOI:10.1016/j.enggeo.2008.03.007 |
| [8] |
SMITH A, DIXON N, FOWMES G J. Early detection of first-time slope failures using acoustic emission measurements: Large-scale physical modelling[J]. Géotechnique, 2017, 67(2): 138-152. DOI:10.1680/jgeot.15.P.200 |
| [9] |
DIXON N, SMITH A, FLINT J A, et al. An acoustic emission landslide early warning system for communities in low-income and middle-income countries[J]. Landslides, 2018, 15(8): 1631-1644. DOI:10.1007/s10346-018-0977-1 |
| [10] |
DIXON N, SPRIGGS M, SMITH A, et al. Quantification of reactivated landslide behaviour using acoustic emission monitoring[J]. Landslides, 2015, 12(3): 549-560. DOI:10.1007/s10346-014-0491-z |
| [11] |
SMITH A. Quantification of slope deformation behaviour using acoustic emission monitoring[D]. Loughborough: Loughborough University, 2015.
|
| [12] |
SMITH A, DIXON N, MELDRUM P, et al. Acoustic emission monitoring of a soil slope: Comparisons with continuous deformation measurements[J]. Géotechnique Letters, 2014, 4(4): 255-261. DOI:10.1680/geolett.14.00053 |
| [13] |
CODEGLIA D, DIXON N, FOWMES G J, et al. Analysis of acoustic emission patterns for monitoring of rock slope deformation mechanisms[J]. Engineering Geology, 2017, 219: 21-31. DOI:10.1016/j.enggeo.2016.11.021 |
| [14] |
BERG N, SMITH A, RUSSELL S, et al. Correlation of acoustic emissions with patterns of movement in an extremely slow-moving landslide at Peace River, Alberta, Canada[J]. Canadian Geotechnical Journal, 2018, 55(10): 1475-1488. DOI:10.1139/cgj-2016-0668 |
| [15] |
MICHLMAYR G, COHEN D, OR D. Sources and characteristics of acoustic emissions from mechanically stressed geologic granular media: A review[J]. Earth-Science Reviews, 2012, 112(3-4): 97-114. DOI:10.1016/j.earscirev.2012.02.009 |
| [16] |
DIXON N, HILL R, KAVANAGH J. Acoustic emission monitoring of slope instability: Development of an active waveguide system[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2003, 156(2): 83-95. DOI:10.1680/geng.2003.156.2.83 |
| [17] |
KOERNER R M, MCCABE W M, LORD JR A E. Acoustic emission monitoring of soil stability[J]. Journal of the Geotechnical Engineering Division, 1978, 104(5): 571-582. DOI:10.1061/AJGEB6.0000629 |
| [18] |
LORD JR A E, FISK C L, KOERNER R M. Utilization of steel roads as AE waveguides[J]. Journal of the Geotechnical Engineering Division, 1982, 108(2): 300-305. DOI:10.1061/AJGEB6.0001246 |
| [19] |
VOIGHT B. A relation to describe rate-dependent material failure[J]. Science, 1989, 243(4888): 200-203. DOI:10.1126/science.243.4888.200 |
| [20] |
SPRIGGS M. Quantification of acoustic emission from soils for predicting landslide failure[D]. Loughborough: Loughborough University, 2005.
|
| [21] |
CODEGLIA D, DIXON N, FOWMES G J, et al. Strategies for rock slope failure early warning using acoustic emission monitoring[J]. IOP Conference Series: Earth and Environmental Science, 2015, 26: 012028. DOI:10.1088/1755-1315/26/1/012028 |
| [22] |
SMITH A, HEATHER-SMITH H J, DIXON N, et al. Acoustic emission generated by granular soil-steel structure interaction[J]. Géotechnique Letters, 2020, 10(2): 119-127. DOI:10.1680/jgele.19.00065 |
| [23] |
SMITH A, DIXON N, FOWMES G. Monitoring buried pipe deformation using acoustic emission: Quantification of attenuation[J]. International Journal of Geotechnical Engineering, 2017, 11(4): 418-430. DOI:10.1080/19386362.2016.1227581 |
| [24] |
INGRAHAM M D, ISSEN K A, HOLCOMB D J. Use of acoustic emissions to investigate localization in high-porosity sandstone subjected to true triaxial stresses[J]. Acta Geotechnica, 2013, 8(6): 645-663. DOI:10.1007/s11440-013-0275-y |
| [25] |
DENG L Z, YUAN H Y, CHEN J G, et al. Experimental investigation and field application of acoustic emission array for landslide monitoring[J]. Landslides, 2023, 21(1): 71-81. |
| [26] |
DENG L Z, YUAN H Y, CHEN J G, et al. Prefabricated acoustic emission array system for landslide monitoring[J]. Engineering Geology, 2023, 323: 107185. DOI:10.1016/j.enggeo.2023.107185 |
| [27] |
MICHLMAYR G, COHEN D, OR D. Shear-induced force fluctuations and acoustic emissions in granular material[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(12): 6086-6098. DOI:10.1002/2012JB009987 |
| [28] |
CADMAN J D, GOODMAN R E. Landslide noise[J]. Science, 1967, 158(3805): 1182-1184. DOI:10.1126/science.158.3805.1182 |
| [29] |
MA K, TANG C A, LIANG Z Z, et al. Stability analysis and reinforcement evaluation of high-steep rock slope by microseismic monitoring[J]. Engineering Geology, 2017, 218: 22-38. DOI:10.1016/j.enggeo.2016.12.020 |
| [30] |
KOERNER R M, MCCABE W M, LORD JR A E. Acoustic emission behavior and monitoring of soils[M]. West Conshohocken: ASTM International, 1981.
|
| [31] |
DENG L Z, YUAN H Y, CHEN J G, et al. Experimental investigation on progressive deformation of soil slope using acoustic emission monitoring[J]. Engineering Geology, 2019, 261: 105295. DOI:10.1016/j.enggeo.2019.105295 |
| [32] |
HU W, SCARINGI G, XU Q, et al. Acoustic emissions and microseismicity in granular slopes prior to failure and flow-like motion: The potential for early warning[J]. Geophysical Research Letters, 2018, 45(19): 10406-10415. |
| [33] |
DIXON N, SPRIGGS M. Quantification of slope displacement rates using acoustic emission monitoring[J]. Canadian Geotechnical Journal, 2007, 44(8): 966-976. DOI:10.1139/T07-046 |
| [34] |
SMITH A, DIXON N. Quantification of landslide velocity from active waveguide-generated acoustic emission[J]. Canadian Geotechnical Journal, 2015, 52(4): 413-425. DOI:10.1139/cgj-2014-0226 |
| [35] |
CAMPBELL C S. Granular material flows: An overview[J]. Powder Technology, 2006, 162(3): 208-229. DOI:10.1016/j.powtec.2005.12.008 |
| [36] |
MIRGHASEMI A A, ROTHENBURG L, MATYAS E L. Influence of particle shape on engineering properties of assemblies of two-dimensional polygon-shaped particles[J]. Géotechnique, 2002, 52(3): 209-217. DOI:10.1680/geot.2002.52.3.209 |
| [37] |
CUI L, O'SULLIVAN C, O'NEILL S. An analysis of the triaxial apparatus using a mixed boundary three-dimensional discrete element model[J]. Géotechnique, 2007, 57(10): 831-844. DOI:10.1680/geot.2007.57.10.831 |
| [38] |
LI H J, XU Q, HE Y S, et al. Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models[J]. Landslides, 2018, 15(10): 2047-2059. DOI:10.1007/s10346-018-1020-2 |
| [39] |
DENG L Z, SMITH A, DIXON N, et al. Machine learning prediction of landslide deformation behaviour using acoustic emission and rainfall measurements[J]. Engineering Geology, 2021, 293: 106315. DOI:10.1016/j.enggeo.2021.106315 |
| [40] |
DENG L Z, SMITH A, DIXON N, et al. Automatic classification of landslide kinematics using acoustic emission measurements and machine learning[J]. Landslides, 2021, 18(8): 2959-2974. DOI:10.1007/s10346-021-01676-8 |
| [41] |
THIRUGNANAM H, RAMESH M V, RANGAN V P. Enhancing the reliability of landslide early warning systems by machine learning[J]. Landslides, 2020, 17(9): 2231-2246. DOI:10.1007/s10346-020-01453-z |
| [42] |
SMITH A, DIXON N. Listening for deterioration and failure: Towards smart geotechnical infrastructure[J]. Proceedings of the Institution of Civil Engineers-Smart Infrastructure and Construction, 2018, 171(4): 131-143. DOI:10.1680/jsmic.19.00019 |
| [43] |
ZAKI A, CHAI H K, RAZAK H A, et al. Monitoring and evaluating the stability of soil slopes: A review on various available methods and feasibility of acoustic emission technique[J]. Comptes Rendus Geoscience, 2014, 346(9-10): 223-232. DOI:10.1016/j.crte.2014.01.003 |
| [44] |
MICHLMAYR G, OR D. Mechanisms for acoustic emissions generation during granular shearing[J]. Granular Matter, 2014, 16(5): 627-640. DOI:10.1007/s10035-014-0516-2 |
| [45] |
MAO W W, AOYAMA S, TOWHATA I. A study on particle breakage behavior during pile penetration process using acoustic emission source location[J]. Geoscience Frontiers, 2020, 11(2): 413-427. DOI:10.1016/j.gsf.2019.04.006 |