2. 北京交通大学 智慧高铁系统前沿科学中心, 北京 100044
2. Frontiers Science Center for Smart High-speed Railway System, Beijing Jiaotong University, Beijing 100044, China
由于突发扰动事件可能导致铁路路段受损、区间运营中断,对铁路网络的运输效率产生较大影响,因此从事前预防、灾前仿真角度评估铁路区间路段的可替代能力,反映城市群铁路客运网络的韧性具有较大的理论意义和实用价值。
韧性概念在现有研究中应用广泛,Holling[1]较早在生态学领域采用韧性描述生态系统的环境适应能力。Bruneau等[2]将社区抗震韧性描述为鲁棒性、冗余性、资源丰富性和快速性。Gu等[3]将网络韧性描述为网络抵抗、吸收、适应扰动,以及从扰动的负面影响中恢复的能力,认为网络韧性包含抵抗扰动影响和从扰动中恢复的能力。本文重点关注城市群铁路客运网络抵抗扰动的能力。
基于复杂网络理论的交通网络韧性研究,大多采用拓扑指标衡量网络性能。Zhang等[4]对车站采取随机和蓄意中断模拟,基于网络效率制定了城轨网络拓扑韧性指标。Xu等[5]基于全局效率比评估了空间加权城轨网络的韧性,并识别出关键站点。黄莺等[6]基于网络平均效率,从地铁网络拓扑结构角度模拟了站点失效场景。马书红等[7]基于网络效率、平均独立路径数量和节点度,全局评估了城市群多模式交通网络的结构韧性。
近年来,一些交通网络韧性研究开始关注交通网络的功能属性。例如,将客流和出行时间等服务属性作为加权因素,采用加权的网络效率和介数中心性等指标衡量网络性能。Lu[8]采用所有节点的客流和出行时间加权介数中心性之和衡量网络性能,基于车站失效方法分析了轨道交通网络的韧性。Chen等[9]采用考虑站间旅客人数和加权平均出行时间的网络效率衡量了城轨网络性能,并基于性能响应函数曲线和韧性三角形衡量了网络韧性。Li等[10]采用考虑客流和出行时间的网络效率衡量网络性能,研究了铁路网络的脆弱性。李涛等[11]基于高铁站点之间的可达时间和客流量加权网络效率,评估了高铁网络的脆弱性。吕彪等[12]基于考虑客流量的路网服务效率,评估了轨道交通网络的韧性。马飞等[13]基于客流指标修正后的网络运行效率,测算了城轨网络运行过程的网络集成韧性水平。
目前,部分学者从旅客的角度研究了交通网络韧性,重点研究旅客出行时间和客流损失对交通网络的影响。Ma等[14]基于交通网络受干扰后旅客出行损失和恢复时间,评估了城轨网络的韧性。Chen等[15]提出了一种面向旅客的城轨网络韧性评估模型来反映旅客出行时间分布对网络性能的影响。路庆昌等[16]通过分析容量有限站点内排队客流和乘客等待时间的变化,量化了轨道交通的动态网络性能。马敏等[17]兼顾客流损失率和网络服务效率损失率,提出了以网络性能响应函数为基础的韧性评估方法。
综上所述,交通网络韧性可从网络拓扑、功能变化和旅客角度衡量。目前,交通网络韧性研究仍存在以下不足:1) 有些研究仅从拓扑结构或空间距离角度评估交通网络韧性,与实际交通运营情况不符;2) 部分关注功能服务属性的研究不能直观反映旅客实际出行成本的变化,在2阶段韧性中重点关注恢复阶段,而对抵抗阶段考量不足;3) 交通网络韧性仿真大多采用节点删除的攻击模式,未对关键路段进行充分识别和分析;4) 相关研究主要集中在城轨网络、城市和城市群道路网络,缺乏适用于城市群铁路客运网络的韧性仿真评估体系。
本文为弥补现有研究的不足,从旅客出行时间的功能维度上,研究城市群铁路客运网络在路段中断情况下的动态抵抗韧性。本文的研究方法如下:1) 将实际铁路客运站抽象为网络节点,提高网络建模的精细度,比将城市作为节点更符合实际情况;2) 推导了考虑扰动时间不确定性的韧性指标公式,提出将基于性能响应函数和旅客时空可达性的网络性能保留率作为动态抵抗韧性评估模型的核心内容;3) 提出了针对城市群铁路客运网络和路段可替代能力的抵抗韧性仿真评估方法,重点关注旅客出行时间和距离的变化;4) 对成渝城市群铁路客运网络开展实例研究,对比不同加权网络的关键路段和抵抗韧性,验证了所提方法的有效性,并得出具有实际意义的结论。
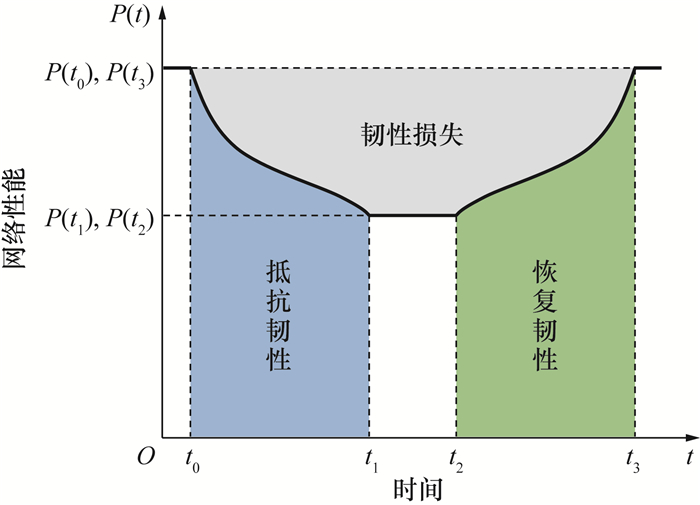
1 交通网络韧性 1.1 2阶段韧性交通网络韧性包括抵抗扰动影响和从扰动中恢复的能力[3]。Bešinović[18]认为铁路网络的韧性是指铁路系统在正常情况下提供有效服务,以及面对中断或自然灾害能够抵抗、吸收、适应和快速恢复的能力。杨琦等[19]认为韧性是指一个系统能够有效抵御、吸收、适应干扰,并从干扰中恢复的能力,核心为系统的抗干扰和恢复能力。Zhou等[20]认为交通网络的韧性由以下2方面构成:1) 中断情况下,维持功能的能力;2) 中断后,恢复性能所需的时间和资源。综上所述,可认为韧性主要包含抵抗和恢复2个阶段,如图 1所示。t0和t1分别为扰动发生和结束时刻;t2和t3分别为恢复开始和完成时刻;P(t)为t时刻的网络性能响应函数。
|
| 图 1 2阶段韧性示意图 |
假设在t0—t1时段内,扰动持续进行,网络性能从P(t0)下降至P(t1);在t1—t2时段内,网络性能趋于稳定;在t2—t3时段内,采取修复措施,网络性能从P(t2)上升至P(t3),由此形成网络的性能响应函数曲线(以下简称“性能曲线”)。网络性能曲线在t0—t1时段内与t轴围成的梯形面积为网络受干扰时实际运行的累计保留性能,用于衡量网络的抵抗韧性。网络性能曲线在t2—t3时段内与t轴围成的梯形面积为网络恢复过程中实际运行的累计保留性能,用于衡量网络的恢复韧性。网络性能曲线与网络性能常函数P(t0)在t0—t3时段内围成的面积为网络累计损失性能,用于衡量网络的韧性损失。
交通运输网络研究中常用可靠性、脆弱性、鲁棒性和抗毁性等描述抵抗韧性,这些属性只是关注网络性能变化的侧重点不同,并未考虑扰动时间的影响。刘杰等[21]以区间通过能力降低时受影响较小的乘客数目占比,评估了城轨网络的可靠性。马超群等[22]采用站点故障条件下的乘客有效路径子图和网络客流损失率,评估了城轨网络的脆弱性。马飞等[23]以列车频率代替客流,提出了考虑客流和出行时间的网络性能指标,以节点中断情景下的网络相对性能测试城市群铁路客运网络的鲁棒性。李成兵等[24]提出网络效率和加权最大连通子图相对规模的网络抗毁性评估指标,研究了城市群铁路客运交通网络对节点被蓄意破坏的抵抗能力。恢复韧性关注失效节点的修复顺序。张洁斐等[25]研究了地铁网络部分节点失效后,不同修复策略与网络性能恢复之间的关系。Chen等[26]通过优化故障站点的修复顺序,增强了中断情况下的城轨网络韧性。
1.2 网络性能保留率Martín等[27]以可达性的下降百分比反映交通网络的韧性,该方法未关注网络性能的动态变化和网络累计保留性能。Bi等[28]认为系统的性能曲线为网络韧性评估提供了理论基础。网络性能保留率为网络受干扰时实际运行的累计保留性能与初始无干扰状态下的累计保留性能的比值,为同时体现网络的累计保留和损失性能,本文将网络性能保留率作为网络韧性评估指标。以抵抗韧性阶段为例,基于性能曲线的网络性能保留率R表示如下:
| $ R=\frac{\int_{t_0}^{t_1} P(t) \mathrm{d} t}{\left(t_1-t_0\right) P\left(t_0\right)} . $ | (1) |
在复杂网络Space L建模方法[29]中,网络节点为车站,若2站点在同一线路上相邻,那么这2站点之间存在连边。为直观描述铁路网络的物理结构,便于后续模拟路段中断情景,本文基于复杂网络Space L建模方法构建城市群铁路客运网络模型。将城市群范围内的实际铁路客运站抽象为网络节点,并进行编号,节点编号集合N={1, 2, …, n},其中n为节点总数。以站点间的邻接关系生成网络连边,得到有效连边集合E={(i, j)|i, j∈N, wij=1},其中:i和j分别为连边(i, j)的起点和终点编号;wij为连边(i, j)的权值。若存在连边,则wij=1;若不存在连边,则wij=0。用wij的取值情况表示连边是否存在,可生成无权邻接矩阵W=(wij)n×n,用于表示节点间的连接关系和网络拓扑结构。本文搜集铁路线路数据,采用站间线路长度标定空间边权,得到空间加权邻接矩阵Wspace=(wijspace)n×n,其中wijspace为连边(i, j)的空间边权。借助中国铁路12306网站(以下简称“12306”),依次查询邻接站点间的车次信息。由于站间最短耗时可体现列车在该区间安全运行的最高速度,因此采用车次信息中的站间最短耗时标定时间边权,得到时间加权邻接矩阵Wtime=(wijtime)n×n,其中wijtime为连边(i, j)的时间边权。
基于此,构建无权铁路网络模型G1、空间加权铁路网络模型G2和时间加权铁路网络模型G3。
2.2 网络效率网络效率A为网络中所有节点间最短路径长度的倒数平均值,是复杂网络理论中衡量网络性能常用的指标,表示如下:
| $ \begin{gathered} A=\frac{1}{n(n-1)} \sum\limits_{i=1}^n \sum\limits_{j=1 \neq i}^n \frac{1}{d_{i j}}= \\ \frac{1}{n(n-1)} \sum\limits_{i=1}^n \sum\limits_{j=1 \neq i}^n\left(1 / \sum\limits_{\left(i^{\prime}, j^{\prime}\right) \in E_{i j}} w_{i^{\prime} j^{\prime}}\right) . \end{gathered} $ | (2) |
其中:dij为节点i与j之间的最短路径长度;i′和j′分别为连边(i′, j′)的起点和终点编号;Eij为节点i与j之间的最短路径连边集合;wi′j′为W中的元素,wi′j′∈{0, 1},表示连边(i′, j′)是否存在。
2.3 时空可达性本文以路段中断情况下,基于旅客平均出行时间和距离的网络服务性能变化情况评估网络韧性。在网络服务性能指标的选取上,Chen等[30]以旅客在网络中平均出行时间的倒数和作为地铁网络的运营服务水平指标,并认为用运营服务水平指标衡量网络性能比A更有效。本文以所有节点间最短出行距离的倒数平均值表示网络的空间可达性值Aspace,以所有节点间最短出行时间的倒数平均值表示网络的时间可达性值Atime, 分别表示如下:
| $ A^{\text {space }}=\frac{1}{n(n-1)} \sum\limits_{i=1}^n \sum\limits_{j=1 \neq i}^n\left(1 / \sum\limits_{\left(i^{\prime}, j^{\prime}\right) \in E_{i j}} w_{i^{\prime} j^{\prime}}^{\text {space }}\right), $ | (3) |
| $ A^{\mathrm{time}}=\frac{1}{n(n-1)} \sum\limits_{i=1}^n \sum\limits_{j=1 \neq i}^n\left(1 / \sum\limits_{\left(i^{\prime}, j^{\prime}\right) \in E_{i j}} w_{i^{\prime} j^{\prime}}^{\mathrm{time}}\right) . $ | (4) |
其中wi′j′space和wi′j′time分别为连边(i′, j′)的空间和时间边权。
2.4 单路段中断韧性评估为识别网络中的关键路段,采用单路段删除的攻击模式模拟单路段中断情景。以对应时间下的A、Aspace或Atime表示网络性能。参照图 1中抵抗韧性阶段的网络性能曲线,设定t0与t1的时间间隔为Δt。参照式(1)计算单路段中断情况下的网络性能保留率,以衡量路段(即连边)的可替代能力,表示如下:
| $ R_{(i, j), G}=\frac{\int_{t_0}^{t_1} P(t) \mathrm{d} t}{\Delta t \cdot P\left(t_0\right)}=\frac{\int_{t_0}^{t_0+\Delta t} P(t) \mathrm{d} t}{\Delta t \cdot P_G} . $ | (5) |
其中:R(i, j), G为路段可替代能力,指网络G中连边(i, j)删除情况下的网络性能保留率,G∈{G1, G2, G3};PG为网络G的性能,PG∈{A, Aspace, Atime}。
由于网络性能曲线演变具有不确定性,因此为进一步简化计算,将t0与t1之间的网络性能曲线进行线性近似。网络受干扰时,实际运行的累计保留性能可进一步表示为网络性能曲线在(t0-t0+Δt)时段内与t轴围成的梯形面积。在式(5)基础上,R(i, j), G表示如下:
| $ R_{(i, j), G}=\frac{\left(P_{(i, j), G}+P_G\right) \cdot \Delta t}{2 \Delta t \cdot P_G}=\frac{P_{(i, j), G}+P_G}{2 P_G} . $ | (6) |
其中P(i, j), G为连边(i, j)删除后, 网络G的性能。
为有效评估网络整体的抵抗韧性水平,在路段可替代能力的基础上提出网络抵抗韧性指数。由于交通网络是由许多路段、站点构成的整体,因此从网络整体来看,网络抵抗韧性指数RG为所有路段可替代能力的平均值,表示如下:
| $ R_G=\frac{\sum\limits_{(i, j) \in E} R_{(i, j), G}}{|E|} . $ | (7) |
其中|E|为网络的有效连边数量。
2.5 多路段连续中断韧性评估为验证关键路段识别的有效性,对关键路段排序下的多路段连续中断情景进行模拟。假设有m条连边进行连续删除,排序后的连续删除连边集合Em={e1, e2, …, em},扰动结束时刻集合Tm={t1, 1, t1, 2, …, t1, m}。此情景下,网络受干扰时,实际运行的累计保留性能为m个梯形的面积和。在式(6)基础上,m条连边连续删除的网络性能保留率REm, G表示如下:
| $ \begin{gathered} R_{E_m, G}=\frac{\sum\limits_{i=1}^m\left(P_{E_i, G}+P_{E_{i-1}, G}\right)\left(t_{1, i}-t_{1, i-1}\right)}{2\left(t_{1, m}-t_0\right) P_G}=\\ \frac{\sum\limits_{i=1}^m\left(P_{E_i, G}+P_{E_{i-1}, G}\right) \cdot \Delta t}{2 m \cdot \Delta t \cdot P_G}=\frac{\sum\limits_{i=1}^m\left(P_{E_i, G}+P_{E_{i-1}, G}\right)}{2 m P_G} . \end{gathered} $ | (8) |
其中:Ei为第1—i条被删除连边的集合,Ei={e1, e2, …, ei};PEi, G为集合Ei中的所有连边按顺序连续删除下网络G的性能。E0为空集,PE0, G=PG,t1, 0=t0。
3 抵抗韧性仿真评估流程利用MATLAB软件对铁路网络的抵抗韧性进行仿真评估,步骤如下:
步骤1 选择仿真网络G∈{G1, G2, G3},G的初始邻接矩阵WG∈{W, Wspace, Wtime},通过A、Aspace和Atime分别计算所选铁路网络对应的网络性能。
步骤2 输入E,设定k为迭代次数; E(k)为E中第k条连边; kmax为总迭代次数(与|E|数值相同); WG, k=(wijG, k)n×n为第k次迭代时,网络G的邻接矩阵。
步骤3 按照E中的排列顺序,采用单路段删除的攻击模式进行连边逐一删除迭代。开始攻击时,令k=1,WG, k=WG。
步骤4 攻击并删除连边(i, j),在网络G的WG, k中,令第k次迭代时,网络G中连边(i, j)和(j, i)的边权ωijG, k和ωjiG, k均为0,得到更新后的WG,k。
步骤5 计算P(i, j), G和R(i, j), G,并将R(i, j), G存储至路段可替代能力集合S的第k个元素。
步骤6 使用WG表示下一次迭代时网络G的邻接矩阵,即WG, k+1=WG,确保下一次迭代时网络已恢复初始状态。
步骤7 判断攻击是否结束。若k=kmax,则进行步骤8;否则,令k=k+1,并转至步骤4。
步骤8 借助S,用所有路段可替代能力的平均值计算RG,仿真结束。
4 实例 4.1 数据来源本文利用百度地图和12306收集成渝城市群每个县级及以上城市的铁路客运站信息。截至2024年3月,选取79个主要铁路客运站,对其进行编号,得到N。使用邻接表记录站间邻接关系,得到E。对连边进行编号,得到有效连边编号集合。查询相关资料,记录邻接站点间的线路长度,利用12306查询并记录邻接站点间的运行最短耗时。借助MATLAB读取邻接表,生成W、Wspace和Wtime。
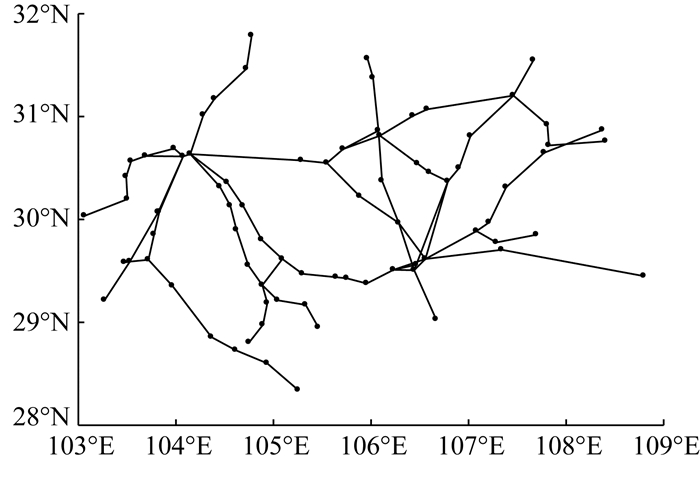
4.2 成渝城市群铁路客运网络在百度地图拾取坐标系统中采集每个铁路客运站的经纬度坐标信息。基于站点经纬度坐标和邻接矩阵,借助MATLAB绘制基于Space L的成渝城市群铁路客运网络,如图 2所示。
|
| 图 2 基于Space L的成渝城市群铁路客运网络 |
成渝城市群铁路客运网络的拓扑属性可由复杂网络理论的拓扑指标反映,如表 1所示。
| 拓扑指标 | 含义 | 数值 |
| 网络密度 | 网络实际存在与可能存在连边数的比值 | 0.029 |
| 平均节点度 | 所有节点连边数的平均值 | 2.228 |
| 平均节点介数 | 所有节点中经过某个节点的最短路径数量与网络最短路径总数比值的平均值 | 0.084 |
| 网络连通度 | 断开网络所需移除的最小连边数 | 1 |
| 平均聚类系数 | 所有节点中邻接节点间实际存在与可能存在的连边数比值的平均值 | 0.031 |
| 网络效率 | 所有节点间最短路径长度的倒数平均值 | 0.189 |
这些复杂网络拓扑指标的数值较小,表明成渝城市群铁路客运网络的密度较低,连通性和成网条件较差。
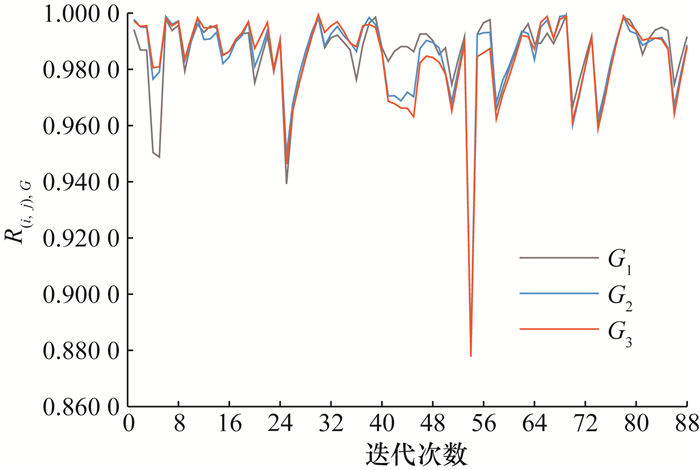
4.3 结果与分析本文按照抵抗韧性仿真评估流程,分别以G1、G2、G3对成渝城市群铁路客运网络进行抵抗韧性仿真评估。按照E中的排列顺序,采用单路段删除的攻击模式和Dijkstra算法,用A、Aspace和Atime分别表示3种仿真网络的性能,计算R(i, j), G,如图 3所示。
|
| 图 3 路段可替代能力 |
每迭代一次代表一条路段被删除。R(i, j), G越低,说明该路段中断对网络性能的影响越大。G1、G2和G3之间的路段可替代能力具有相似性,同时也存在差异。
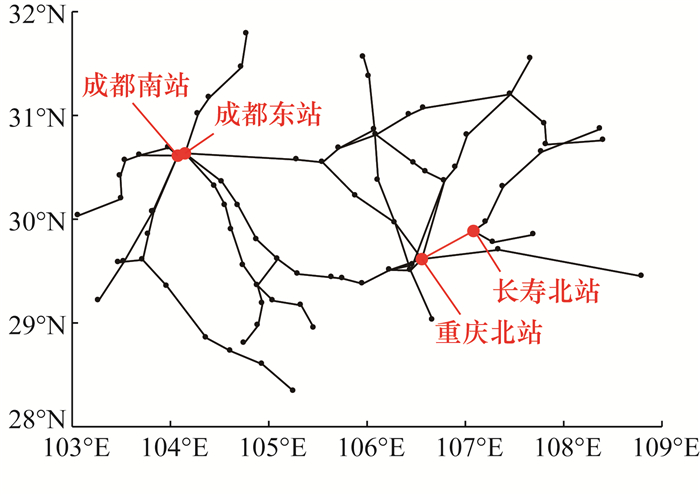
4.4 相似性从相似性来看,3种铁路网络中的第54条连边成都东站—成都南站区间路段中断,使网络性能保留率均低于0.880 0;第25条连边重庆北站—长寿北站区间路段中断,使网络性能保留率均低于0.950 0;除第25和54条连边,以及G1中的第5条连边外,其他连边中断后的网络性能保留率均高于0.950 0;第54条连边的可替代能力最低,该连边中断最高可使网络性能损失12.23%。成渝城市群铁路客运网络第25和54条连边如图 4所示。
|
| 图 4 成渝城市群铁路客运网络第25和54条连边 |
成都东站—成都南站区间路段中断,使成渝城市群铁路客运网络产生较大分裂,与成都南站连接的成渝城市群西南部的铁路线路(共18个铁路客运站)脱离整个铁路网络,铁路网络性能显著降低。这说明成都南站和成都东站是成渝城市群西南部的铁路枢纽,同时也表明在成渝城市群中,西南部城市与其他城市的铁路联系有待加强。重庆北站—长寿北站区间路段中断,也使网络性能明显下降,该路段是郑渝高速铁路和宁蓉铁路的一部分,是重庆中心城区与渝东部城市的重要铁路通道,该路段中断使7个铁路客运站脱离整个铁路网络。G1、G2和G3的路段可替代能力具有相似性的主要原因是成渝城市群铁路客运网络自身拓扑结构的限制,部分关键路段中断使网络产生较大的分割,部分关键路段的可替代能力有待提升。
4.5 差异性本文为比较G1、G2、G3之间路段可替代能力的差异性,对这3种网络的路段按R(i, j), G由低到高分别进行排序,各自排序前10的关键路段如表 2所示。
| G1 | G2 | G3 | |||||
| 区间路段(编号) | R(i, j), G | 区间路段(编号) | R(i, j), G | 区间路段(编号) | R(i, j), G | ||
| 成都东站—成都南站(54) | 0.879 9 | 成都东站—成都南站(54) | 0.879 0 | 成都东站—成都南站(54) | 0.877 7 | ||
| 重庆北站—长寿北站(25) | 0.939 2 | 重庆北站—长寿北站(25) | 0.949 6 | 重庆北站—长寿北站(25) | 0.946 3 | ||
| 大英东站—成都东站(5) | 0.948 8 | 崇州站—大邑站(70) | 0.960 2 | 成都东站—广汉北站(74) | 0.958 7 | ||
| 遂宁站—大英东站(4) | 0.950 4 | 成都东站—广汉北站(74) | 0.962 4 | 崇州站—大邑站(70) | 0.961 5 | ||
| 成都东站—广汉北站(74) | 0.960 4 | 自贡站—沿滩站(86) | 0.966 9 | 乐山站—犍为站(58) | 0.962 3 | ||
| 长寿北站—长寿湖站(26) | 0.965 4 | 长寿北站—长寿湖站(26) | 0.968 1 | 隆昌北站—内江北站(45) | 0.963 2 | ||
| 乐山站—犍为站(58) | 0.965 7 | 乐山站—犍为站(58) | 0.968 2 | 自贡站—沿滩站(86) | 0.964 1 | ||
| 崇州站—大邑站(70) | 0.966 5 | 自贡站—富顺站(51) | 0.968 5 | 自贡站—富顺站(51) | 0.965 2 | ||
| 广汉北站—德阳站(75) | 0.971 8 | 大足南站—荣昌北站(43) | 0.968 8 | 长寿北站—长寿湖站(26) | 0.965 3 | ||
| 犍为站—屏山站(59) | 0.973 1 | 大邑站—邛崃站(71) | 0.970 0 | 荣昌北站—隆昌北站(44) | 0.966 1 | ||
3种网络排序前10的关键路段中,G2与G3路段相似,但在排序上存在差别。例如,崇州站—大邑站、成都东站—广汉北站的可替代能力在G2和G3中调换了顺序。G1与G2和G3排序前10的关键路段存在明显差异,例如,大英东站—成都东站、遂宁站—大英东站在G1中分别是第3和4关键路段,然而它们并未出现在G2和G3的前10个关键路段中。从拓扑结构和功能服务属性角度识别出的关键路段存在明显差异,G1与G2和G3之间路段可替代能力的排序相关性有待进一步检验。
4.6 Spearman相关性采用Spearman相关系数对G1、G2、G3之间的路段可替代能力进行相关性检验,结果如下:
G2与G3路段可替代能力的排序相关性最好,Spearman相关系数为0.946;G1与G2路段可替代能力的排序相关性次之,Spearman相关系数为0.859;G1与G3路段可替代能力的排序相关性最差,Spearman相关系数仅为0.780。G1与G2和G3之间路段可替代能力的排序相关性较差,基于网络拓扑结构和功能服务属性的抵抗韧性仿真评估结果存在显著差异。
4.7 网络整体从网络整体来看,G1、G2、G3的RG分别为0.985 0、0.985 0、0.984 3,G3的RG最低,单路段中断对G3的性能影响较大,对旅客出行时间的影响大于出行距离。从事前预防的公共安全角度来看,如果仅从拓扑结构和空间距离角度进行单路段中断灾前仿真,可能网络抵抗韧性较好,但低估了实际风险因素的干扰后果,容易产生误判。
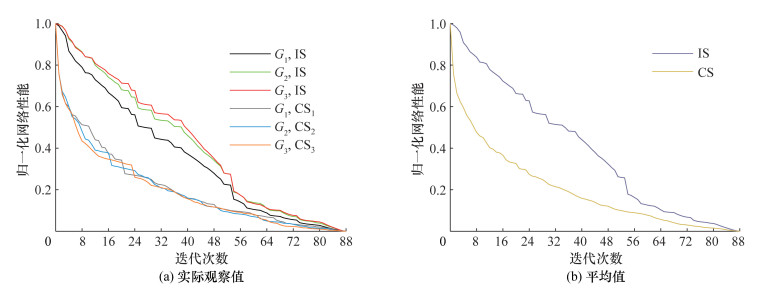
4.8 多路段连续中断韧性将E中的排序设定为路段初始排序(initial sort, IS),分别对G1、G2、G3的路段按照可替代能力由低到高进行排序,得到3种网络路段的关键性排序(critical sort, CS),分别为CS1、CS2、CS3。按照IS和CS,对3种铁路网采取多路段连续删除的攻击模式进行抵抗韧性仿真,对网络性能进行归一化处理(网络性能缩放至0~1范围内,且初始性能为1),多路段连续删除的网络性能曲线如图 5所示。
|
| 图 5 多路段连续删除的网络性能曲线 |
基于IS与CS的多路段连续删除攻击模式的抵抗韧性仿真结果存在明显差异,CS模式的网络性能下降幅度明显大于IS模式。利用多路段连续中断韧性评估模型计算图 5a中各曲线对应的网络性能保留率,结果如表 3所示。
| 网络 | IS | CS | 差值 |
| G1 | 0.354 5 | 0.205 5 | 0.149 0 |
| G2 | 0.407 0 | 0.196 2 | 0.210 8 |
| G3 | 0.418 3 | 0.191 6 | 0.226 7 |
IS和CS模式的平均网络性能保留率分别为0.393 3和0.197 8,差值为0.195 5。分析结果表明:识别出的关键路段连续中断会对网络性能产生剧烈影响。
CS模式的网络性能保留率由低到高和IS与CS模式的网络性能保留率差值由高到低排序均为G3、G2、G1,说明关键路段连续中断对G3的影响大于G1和G2。为避免低估风险因素的干扰后果,有必要从出行时间角度识别铁路关键路段。
5 结论本文从旅客出行时间和距离角度,提出了考虑扰动时间不确定性的城市群铁路客运网络抵抗韧性评估模型和仿真评估流程,弥补了城市群铁路客运网络抵抗韧性研究针对性不足的问题,并对以实际铁路客运站为网络节点的成渝城市群铁路客运网络进行了案例研究,得出以下结论:
1) 对网络性能影响较大的关键路段为成都东站—成都南站和重庆北站—长寿北站,需重点关注这2个路段的可替代能力。在成渝城市群中,西南部城市和渝东部城市与其他城市的铁路联系均有待增强。
2) 单路段中断和关键路段连续中断对时间加权铁路网络性能影响较大。仅从拓扑结构角度评估铁路网络抵抗韧性,识别出的关键路段与铁路实际运营情况存在差异,需考虑铁路实际运营情况和更多的功能服务属性(如出行时间、出行费用、列车频率和客流等),否则可能影响对关键路段的识别。
3) 基于CS的多路段连续删除攻击模式的网络性能保留率明显低于IS,说明本文识别出的关键路段有效,本文所提方法具备可行性和有效性。
本文通过单路段中断和多路段连续中断模拟,识别并验证铁路网络的关键路段,分析了铁路网络对路段中断的抵抗能力,可为铁路网络的规划和决策提供参考。本文所提方法可为交通运营监管部门提供关键路段识别方面的参考,交通运营监管部门可对这些关键路段进行重点监测、维护和灾前预防,有助于增强交通网络的抵抗韧性,对保障旅客出行效率和安全具有重要意义。后续研究将评估分析多模式交通运输网络的抵抗和恢复韧性。
| [1] |
HOLLING C S. Resilience and stability of ecological systems[J]. Annual Review of Ecology, Evolution, and Systematics, 1973, 4: 1-23. DOI:10.1146/annurev.es.04.110173.000245 |
| [2] |
BRUNEAU M, CHANG S E, EGUCHI R T, et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earthquake Spectra, 2003, 19(4): 733-752. DOI:10.1193/1.1623497 |
| [3] |
GU Y, FU X, LIU Z Y, et al. Performance of transportation network under perturbations: Reliability, vulnerability, and resilience[J]. Transportation Research Part E: Logistics and Transportation Review, 2020, 133: 101809. DOI:10.1016/j.tre.2019.11.003 |
| [4] |
ZHANG D M, DU F, HUANG H W, et al. Resiliency assessment of urban rail transit networks: Shanghai metro as an example[J]. Safety Science, 2018, 106: 230-243. DOI:10.1016/j.ssci.2018.03.023 |
| [5] |
XU C, XU X G. A two-stage resilience promotion approach for urban rail transit networks based on topology enhancement and recovery optimization[J]. Physica A: Statistical Mechanics and its Applications, 2024, 635: 129496. DOI:10.1016/j.physa.2024.129496 |
| [6] |
黄莺, 刘梦茹, 魏晋果, 等. 基于韧性曲线的城市地铁网络恢复策略研究[J]. 灾害学, 2021, 36(1): 32-36. HUANG Y, LIU M R, WEI J G, et al. Research on urban metro network recovery strategy based on resilience curve[J]. Journal of Catastrophology, 2021, 36(1): 32-36. DOI:10.3969/j.issn.1000-811X.2021.01.007 (in Chinese) |
| [7] |
马书红, 武亚俊, 陈西芳. 城市群多模式交通网络结构韧性分析: 以关中平原城市群为例[J]. 清华大学学报(自然科学版), 2022, 62(7): 1228-1235. MA S H, WU Y J, CHEN X F. Structural resilience of multimodal transportation networks in urban agglomerations: A case study of the Guanzhong plain urban agglomeration network[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(7): 1228-1235. DOI:10.16511/j.cnki.qhdxxb.2022.26.013 (in Chinese) |
| [8] |
LU Q C. Modeling network resilience of rail transit under operational incidents[J]. Transportation Research Part A: Policy and Practice, 2018, 117: 227-237. DOI:10.1016/j.tra.2018.08.015 |
| [9] |
CHEN J Q, LIU J, PENG Q Y, et al. Resilience assessment of an urban rail transit network: A case study of Chengdu subway[J]. Physica A: Statistical Mechanics and its Applications, 2022, 586: 126517. DOI:10.1016/j.physa.2021.126517 |
| [10] |
LI T, RONG L L. Impacts of service feature on vulnerability analysis of high-speed rail network[J]. Transport Policy, 2021, 110: 238-253. DOI:10.1016/j.tranpol.2021.05.012 |
| [11] |
李涛, 荣莉莉. 时空视角下中国高铁网络脆弱性分析[J]. 铁道科学与工程学报, 2022, 19(7): 1801-1809. LI T, RONG L L. Vulnerability analysis of high-speed rail network in China from spatial-temporal perspective[J]. Journal of Railway Science and Engineering, 2022, 19(7): 1801-1809. (in Chinese) |
| [12] |
吕彪, 管心怡, 高自强. 地铁网络服务韧性评估与最优恢复策略[J]. 交通运输系统工程与信息, 2021, 21(5): 198-205. LÜ B, GUAN X Y, GAO Z Q. Evaluation and optimal recovery strategy of metro network service resilience[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(5): 198-205. (in Chinese) |
| [13] |
马飞, 赵成勇, 孙启鹏, 等. 重大公共卫生灾害主动限流背景下城市轨道交通网络集成韧性[J]. 交通运输工程学报, 2023, 23(1): 208-221. MA F, ZHAO C Y, SUN Q P, et al. Integrated resilience of urban rail transit network with active passenger flow restriction under major public health disasters[J]. Journal of Traffic and Transportation Engineering, 2023, 23(1): 208-221. (in Chinese) |
| [14] |
MA Z A, YANG X, SHANG W L, et al. Resilience analysis of an urban rail transit for the passenger travel service[J]. Transportation Research Part D: Transport and Environment, 2024, 128: 104085. DOI:10.1016/j.trd.2024.104085 |
| [15] |
CHEN J Q, LIU X W, DU B, et al. Passenger-oriented resilience assessment of an urban rail transit network under partial disturbances[J]. Journal of Transportation Engineering, Part A: Systems, 2023, 149(11): 04023114. DOI:10.1061/JTEPBS.TEENG-8017 |
| [16] |
路庆昌, 刘鹏, 徐标, 等. 运营事件下基于韧性的地铁网络保护决策优化[J]. 交通运输工程学报, 2023, 23(3): 209-220. LU Q C, LIU P, XU B, et al. Resilience-based protection decision optimization for metro network under operational incidents[J]. Journal of Traffic and Transportation Engineering, 2023, 23(3): 209-220. (in Chinese) |
| [17] |
马敏, 胡大伟, 舒兰, 等. 城市轨道交通网络韧性评估及恢复策略[J]. 吉林大学学报(工学版), 2023, 53(2): 396-404. MA M, HU D W, SHU L, et al. Resilience assessment and recovery strategy on urban rail transit network[J]. Journal of Jilin University (Engineering and Technology Edition), 2023, 53(2): 396-404. (in Chinese) |
| [18] |
BEŠINOVIĆ N. Resilience in railway transport systems: A literature review and research agenda[J]. Transport Reviews, 2020, 40(4): 457-478. DOI:10.1080/01441647.2020.1728419 |
| [19] |
杨琦, 张雅妮, 周雨晴, 等. 复杂网络理论及其在公共交通韧性领域的应用综述[J]. 中国公路学报, 2022, 35(4): 215-229. YANG Q, ZHANG Y N, ZHOU Y Q, et al. A review of complex network theory and its application in the resilience of public transportation systems[J]. China Journal of Highway and Transport, 2022, 35(4): 215-229. DOI:10.3969/j.issn.1001-7372.2022.04.018 (in Chinese) |
| [20] |
ZHOU Y M, WANG J W, YANG H. Resilience of transportation systems: Concepts and comprehensive review[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(12): 4262-4276. DOI:10.1109/TITS.2018.2883766 |
| [21] |
刘杰, 陈锦渠, 彭其渊, 等. 城市轨道交通网络可靠性和运输服务质量评估[J]. 西南交通大学学报, 2021, 56(2): 395-402. LIU J, CHEN J Q, PENG Q Y, et al. Reliability and service quality evaluation for urban rail transit network[J]. Journal of Southwest Jiaotong University, 2021, 56(2): 395-402. (in Chinese) |
| [22] |
马超群, 张爽, 陈权, 等. 客流特征视角下的轨道交通网络特征及其脆弱性[J]. 交通运输工程学报, 2020, 20(5): 208-216. MA C Q, ZHANG S, CHEN Q, et al. Characteristics and vulnerability of rail transit network based on perspective of passenger flow characteristics[J]. Journal of Traffic and Transportation Engineering, 2020, 20(5): 208-216. (in Chinese) |
| [23] |
马飞, 委笑琳, 孙启鹏, 等. 考虑互补效应的城市群多模式客运网络鲁棒性[J]. 浙江大学学报(工学版), 2024, 58(2): 388-398. MA F, WEI X L, SUN Q P, et al. Robustness of multimodal passenger transport network in urban agglomeration considering complementary effect[J]. Journal of Zhejiang University (Engineering Science), 2024, 58(2): 388-398. (in Chinese) |
| [24] |
李成兵, 张帅, 杨志成, 等. 蓄意攻击下城市群客运交通网络级联抗毁性仿真[J]. 交通运输系统工程与信息, 2019, 19(2): 14-21. LI C B, ZHANG S, YANG Z C, et al. Invulnerability simulation in urban agglomeration passenger traffic network under targeted attacks[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(2): 14-21. (in Chinese) |
| [25] |
张洁斐, 任刚, 马景峰, 等. 基于韧性评估的地铁网络修复时序决策方法[J]. 交通运输系统工程与信息, 2020, 20(4): 14-20. ZHANG J F, REN G, MA J F, et al. Decision-making method of repair sequence for metro network based on resilience evaluation[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(4): 14-20. (in Chinese) |
| [26] |
CHEN J Q, LIU J, PENG Q Y, et al. Strategies to enhance the resilience of an urban rail transit network[J]. Transportation Research Record: Journal of the Transportation Research Board, 2022, 2676(1): 342-354. DOI:10.1177/03611981211037888 |
| [27] |
MARTÍN B, ORTEGA E, CUEVAS-WIZNER R, et al. Assessing road network resilience: An accessibility comparative analysis[J]. Transportation Research Part D: Transport and Environment, 2021, 95: 102851. DOI:10.1016/j.trd.2021.102851 |
| [28] |
BI W, MACASKILL K, SCHOOLING J. Old wine in new bottles? Understanding infrastructure resilience: Foundations, assessment, and limitations[J]. Transportation Research Part D: Transport and Environment, 2023, 120: 103793. DOI:10.1016/j.trd.2023.103793 |
| [29] |
侯本伟, 游丹, 范世杰, 等. 基于网络效率的城市轨道交通网络抗震韧性评估[J]. 清华大学学报(自然科学版), 2024, 64(3): 509-519. HOU B W, YOU D, FAN S J, et al. Seismic resilience evaluation of urban rail transit network based on network efficiency[J]. Journal of Tsinghua University (Science and Technology), 2024, 64(3): 509-519. DOI:10.16511/j.cnki.qhdxxb.2023.26.058 (in Chinese) |
| [30] |
CHEN J Q, LIU J, DU B, et al. Resilience assessment of an urban rail transit network under short-term operational disturbances[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(12): 24841-24853. DOI:10.1109/TITS.2022.3195937 |



