随着在线会议、语音识别等技术的飞速发展,基于麦克风阵列的远场语音通信及人机语音交互技术成为热点研究之一[1-3]。声源到达方向(direction of arrival, DOA)估计是远场语音通信中重要的研究课题之一,其在三维声重放、空间音频编码、声源位置追踪与成像等领域有着重要作用[4-7]。然而,远场传播的衰减使得麦克风采集到的语音信号受噪声及混响等因素的影响急剧加重[1, 3];其次,在实际场景中,声源常是移动的[1];此外,大量应用场景需要实时的DOA信息[2, 7-8]。这些因素给声源DOA估计带来挑战。
许多传统方法已被证明在高信噪比(signal-to-noise ratio, SNR)、低混响情况下有较好的DOA估计性能,如多信号分类(multiple signal classification, MUSIC)法[9]、导向功率相位变换(steered response power with phase transform, SRP-PHAT)法[10]、基于频率聚焦(frequency focusing, FF)的方法[11-12]等。尽管SRP-PHAT、FF等方法被证明在噪声和混响环境下具有一定鲁棒性,但它们的性能在低SNR、高混响环境中也会受到极大影响。此外,基于低混响单声源(low-reverberation-single-source, LRSS)点检测的方法[13]最近也备受关注,但该方法通常需要借助几秒长的语段来判别低混响的单声源点,从而获得稳定的性能,故难以用于实时DOA估计。因此,要改善传统方法的DOA估计性能,通常需要先降低噪声及混响的影响[14-17]。
实时去噪与去混响方法可分为基于模型的方法[8, 18-21]和基于深度学习的方法[16]2类,本文主要基于前者改善混响及噪声环境下单声源的DOA估计问题。现阶段,基于模型的实时去噪与去混响方法多基于Kalman滤波实现[8, 18-21]。例如:文[8]提出基于Kalman滤波的期望最大化(expectation maximization, EM)方法,在期望(expectation, E)步骤中通过Kalman滤波器估计干净语音,在最大化(maximization, M)步骤中通过Kalman滤波器的输出更新系统参数的估计,可显著抑制噪声与混响(记作Kalman-EM);文[18]基于混响功率的自回归(autoregressive, AR)模型和隐Markov模型(hidden Markov model, HMM)将频谱增强与概率估计相结合,通过将频谱增益建模为Bayes滤波的形式,利用Kalman滤波估计干净语音的先验分布,从而求解频谱增益,获得了较好的增强性能(记作AR-HMM);文[19]通过2个交替的Kalman滤波器实现去噪与多通道自回归(multichannel AR, MAR)系数的估计,改善了去噪与去混响的因果关联,获得了有效的去噪与去混响效果(记作Kalman-MAR);文[20]通过集成广义旁瓣抵消器(generalized sidelobe canceller, GSC)与多通道线性预测(multichannel linear prediction, MCLP),并通过Kalman滤波求解多通道噪声控制参数及MCLP系数,有效实现了噪声及混响的抑制(记作ISCLP);文[21]将GSC替换为基于复Gauss的混合模型(complex Gaussian mixture model, CGMM)的最小方差无失真响应(minimum variance distortionless response, MVDR)波束形成器,避免了ISCLP方法中需通过广义特征值分解求解期望信号功率的问题,改善了期望语音的失真(记作CGMM-MVDR-LP)。
上述基于Kalman滤波的方法虽然均可实时在线地完成去噪去混响任务,但直接用作DOA估计的前端增强系统仍存在一些问题。例如:ISCLP和CGMM-MVDR-LP存在易因期望信号功率的不准确估计造成估计的期望语音失真,利用语音段的量级估计空间协方差矩阵信息,难以扩展为可有效保留空间信息的多入多出增强系统等问题,难以适配实时DOA估计的任务。Kalman-EM、AR-HMM、Kalman-MAR这3种方法虽然可有效构建多入多出的增强系统,但这些方法利用多通道Wiener滤波(multichannel Wiener filtering, MWF)等方式估计干净语音的相关信息,存在易使期望语音失真的问题;此外,DOA估计性能易受限于相互独立的去噪去混响与DOA估计过程。上述因素可能会使增强结果不利于DOA估计任务。
基于上述原因,本文提出一种基于Kalman滤波与频率聚焦的DOA估计方法。该方法基于Kalman-MAR算法,利用历史估计的DOA信息和MVDR波束形成获取期望信号的先验估计,从而将DOA估计任务集成到基于Kalman滤波的增强过程中。该方法不仅有效建立了去噪去混响与DOA估计的因果有序迭代关系,还可更为准确地求解期望信号的先验估计,使得增强结果更利于DOA估计任务。实验结果表明:在噪声及混响环境下,本文所提算法的实时DOA估计和跟踪性能优于参考方法。
1 信号模型及问题设室内远场环境下的说话人语音由M个麦克风构建的麦克风阵列采集,则短时Fourier变换(short time Fourier transform, STFT)域下的观测信号
| $ \begin{gather*} \boldsymbol{Y}(k, l)=\boldsymbol{X}(k, l)+\boldsymbol{N}(k, l)= \\ \boldsymbol{X}_{\text {direct }}(k, l)+\boldsymbol{X}_{\text {early }}(k, l)+ \\ \boldsymbol{X}_{\text {late }}(k, l)+\boldsymbol{N}(k, l) . \end{gather*} $ | (1) |
其中:Xdirect(k, l)为直达声成分;Xearly(k, l)为早期混响成分;Xlate(k, l)为晚期混响成分;X(k, l)为无噪信号;N(k, l)为加性噪声;k和l分别为频率和帧的索引;
直达声成分Xdirect(k, l)可表示如下:
| $\begin{equation*} \boldsymbol{X}_{\text {direct }}(k, l)=\boldsymbol{a}\left(k, \theta_{l}\right) S(k, l) \in \mathbb{C}^{M \times 1} . \end{equation*} $ | (2) |
其中:a(k, θl)为由θl方向入射的说话人声源的导向矢量;S(k, l)为参考麦克风采集到的直达声源信息。
基于MCLP,可将晚期混响表示如下[19]:
| $ \begin{equation*} \boldsymbol{X}_{\mathrm{late}}(k, l)=\sum\limits_{\ell=D}^{L_{\mathrm{g}}} \boldsymbol{G}_{\ell}(k, l) \boldsymbol{Y}(k, l-\ell) \in \mathbb{C}^{M \times 1} \end{equation*} $ | (3) |
其中:D为预测延时;Lg为线性预测滤波器阶数;
本文的研究目标是降低噪声N(l)及混响Xearly(l)+Xlate(l)的影响,使得传统算法可更为准确地实时估计声源DOA信息θl。如引言所述,基于Kalman滤波虽然可实现实时去噪去混响,但去噪去混响的目标大多面向语音增强,并不能保证通过增强后的信号可获得更好的DOA估计结果。因此,本文主要考虑将去噪去混响及DOA估计任务进行集成,借助Kalman滤波促进三者间的因果有序迭代,以获取更优的DOA估计性能。
2 提出方法 2.1 所提方法的原理框图本文所提方法的原理如图 1所示,输入为观测信号,输出为估计的DOA信息,整个算法主要由2个Kalman滤波器和1个DOA估计器构成。其中:Kalman滤波器1以Kalman滤波器2和DOA估计器所计算的参数信息作为先验信息,从而完成降噪任务;Kalman滤波器2利用去噪后的信号估计MCLP系数矩阵,从而估计晚期混响成分;DOA估计器则利用2个Kalman滤波器的增强结果检测语音活动帧,并通过基于FF的导向响应功率(steered response power, SRP)方法完成DOA估计。此外,文[22]和[23]中所提方法可用于完成语音活动性检测及噪声协方差矩阵的估计,Z-D表示长度为D的延时。
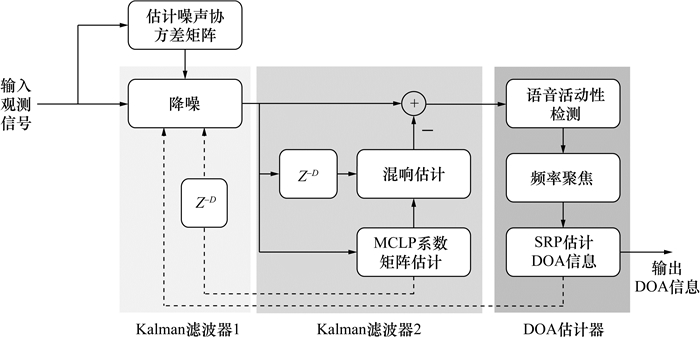
|
| 图 1 本文所提方法的原理框图 |
2.2 基于Kalman滤波的去混响
由式(3)可知,晚期混响成分可利用过去时刻的去噪信号Y(l-
| $ \boldsymbol{\varPhi}_{\Delta \boldsymbol{G}}(l)=E\left\{\Delta \boldsymbol{G}(l)(\Delta \boldsymbol{G}(l))^{\mathrm{H}}\right\} \in \mathbb{C}^{L_{\boldsymbol{G}} \times L_{\boldsymbol{G}}} . $ | (4) |
其中:向量长度
由于G(l)未知,故通过Kalman滤波求解
| $ \hat{\boldsymbol{G}}(l \mid l-1)=\boldsymbol{A} \hat{\boldsymbol{G}}(l-1), $ | (5) |
| $\hat{\boldsymbol{\varPhi}}_{\Delta G}(l \mid l-1)=\boldsymbol{A} \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{G}}(l-1) \boldsymbol{A}^{\mathrm{H}}+\boldsymbol{\varPhi}_{\mathrm{w}}(l), $ | (6) |
| $ \boldsymbol{e}(l)=\boldsymbol{Y}(l)-\overline{\boldsymbol{X}}(l-D) \hat{\boldsymbol{G}}(l \mid l-1), $ | (7) |
| $ \boldsymbol{K}(l)=\hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{G}}(l \mid l-1) \overline{\boldsymbol{X}}^{\mathrm{H}}(l-D) \cdot \\ {\left[\overline{\boldsymbol{X}}(l-D) \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{G}}(l \mid l-1) \overline{\boldsymbol{X}}^{\mathrm{H}}(l-D)+\boldsymbol{\varPhi}_{\mathrm{u}}(l)\right]^{-1}, } $ | (8) |
| $\hat{\boldsymbol{\varPhi}}_{\Delta G}(l)=\left[\boldsymbol{I}_{L_{G}}-\boldsymbol{K}(l) \overline{\boldsymbol{X}}(l-D)\right] \hat{\boldsymbol{\varPhi}}_{\Delta G}(l \mid l-1), $ | (9) |
| $ \begin{equation*} \hat{\boldsymbol{G}}(l)=\hat{\boldsymbol{G}}(l \mid l-1)+\boldsymbol{K}(l) \boldsymbol{e}(l) . \end{equation*} $ | (10) |
其中:A为维度为LG的单位矩阵;
在获得
| $ \begin{equation*} \boldsymbol{\varPhi}_{\Delta \boldsymbol{X}}(l)=E\left\{\Delta \underline{\boldsymbol{X}}(l)(\Delta \underline{\boldsymbol{X}}(l))^{\mathrm{H}}\right\} \in \mathbb{C}^{M L_{\mathrm{g}} \times M L_{\mathrm{g}}} . \end{equation*} $ | (11) |
其中:
由于
| $ \begin{equation*} \underline{\hat{\boldsymbol{X}}}(l \mid l-1)=\boldsymbol{F}(l) \underline{\hat{\boldsymbol{X}}}(l-1), \end{equation*} $ | (12) |
| $ \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{X}}(l \mid l-1)=\boldsymbol{F}(l) \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{X}}(l-1) \boldsymbol{F}^{\mathrm{H}}(l)+\hat{\boldsymbol{\varPhi}}_{\underline{\boldsymbol{S}}}(l), $ | (13) |
| $ \boldsymbol{K}_{\boldsymbol{X}}(l)=\hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{X}}(l \mid l-1) \boldsymbol{H}^{\mathrm{H}} \cdot \\ {\left[\boldsymbol{H} \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{X}}(l \mid l-1) \boldsymbol{H}^{\mathrm{H}}+\boldsymbol{\varPhi}_{\mathrm{V}}(l)\right]^{-1}, } $ | (14) |
| $ \boldsymbol{e}_{\boldsymbol{X}}(l)=\boldsymbol{Y}(l)-\boldsymbol{H} \underline{\hat{\boldsymbol{X}}}(l \mid l-1), $ | (15) |
| $ \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{X}}(l)=\left[\boldsymbol{I}_{M L_{\mathrm{g}}}-\boldsymbol{K}_{\boldsymbol{X}}(l) \boldsymbol{H}\right] \hat{\boldsymbol{\varPhi}}_{\Delta \boldsymbol{X}}(l \mid l-1), $ | (16) |
| $ \underline{\hat{\boldsymbol{X}}}(l)=\underline{\hat{\boldsymbol{X}}}(l \mid l-1)+\boldsymbol{K}_{\boldsymbol{X}}(l) \boldsymbol{e}_{\boldsymbol{X}}(l) . $ | (17) |
其中:
通过式(5)—(10)和式(12)—(17)所示的2个Kalman滤波过程,可估计去噪信号
| $ \begin{gather*} \hat{\boldsymbol{X}}(l)=\boldsymbol{H} \underline{\hat{\boldsymbol{X}}}(l), \end{gather*} $ | (18) |
| $ \hat{\boldsymbol{S}}(l)=\hat{\boldsymbol{X}}(l)-\overline{\boldsymbol{X}}(l-D) \hat{\boldsymbol{G}}(l) . $ | (19) |
在获得
设聚焦矩阵为T,则
| $ \boldsymbol{R}_{\hat{\boldsymbol{s}}}\left(f_{0, k}, l\right)=\boldsymbol{T} \boldsymbol{R}_{\hat{\boldsymbol{s}}}(l) \boldsymbol{T}^{\mathrm{H}} , $ | (20) |
| $ \boldsymbol{R}_{\hat{\boldsymbol{s}}}(l)=\alpha \boldsymbol{R}_{\hat{\boldsymbol{s}}}(l-1)+(1-\alpha) \hat{\boldsymbol{S}}(l) \hat{\boldsymbol{S}}^{\mathrm{H}}(l) . $ | (21) |
其中:T可通过文[12]所给方法求解;f0, k为第k个子带的聚焦参考频率;α为递归平滑因子。
基于MVDR波束形成,可求解方位θ的SRP:
| $\varPsi_{\mathrm{SRP}}(\theta)=\sum\limits_{k=1}^{K} \frac{1}{\boldsymbol{a}^{\mathrm{H}}\left(f_{0, k}, \theta\right) \boldsymbol{R}_{\dot{s}}^{-1}\left(f_{0, k}, l\right) \boldsymbol{a}\left(f_{0, k}, \theta\right)}. $ | (22) |
其中:K为频带数;a(f0, θ)为入射角为θ方向的导向矢量;θ∈[0°, 180°]。通过搜索ΨSRP(θ)的极大值,可获得所估计的DOA。这一方法记作FF-SRP。
2.5 联合DOA信息优化Kalman滤波去噪过程考虑
| $ \hat{\boldsymbol{\varPhi}}_{\underline{\boldsymbol{S}}}(l)=\left[\begin{array}{cc} \mathbf{0}_{M\left(L_{\mathrm{g}}-1\right) \times M\left(L_{\mathrm{g}}-1\right)} & \mathbf{0}_{M\left(L_{\mathrm{g}}-1\right) \times M} \\ \mathbf{0}_{M \times M\left(L_{\mathrm{g}}-1\right)} & \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}(l) \end{array}\right] . $ | (23) |
其中:
文[19]利用期望信号先验协方差矩阵
| $ \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}(l)=\gamma \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}^{\text {pos }}(l)+(1-\gamma) \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}^{\text {prior }}(l), $ | (24) |
| $ \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}^{\text {pos }}(l)=\alpha \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}^{\text {pos }}(l-1)+(1-\alpha) \hat{\boldsymbol{S}}(l) \hat{\boldsymbol{S}}^{\mathrm{H}}(l) . $ | (25) |
其中γ=0.98为平滑因子。
而
| $ \begin{equation*} \hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}^{\text {prior }}(l)=\boldsymbol{W}_{\mathrm{MWF}}^{\mathrm{H}}(l) \boldsymbol{Y}(l) \boldsymbol{Y}^{\mathrm{H}}(l) \boldsymbol{W}_{\mathrm{MWF}}(l) . \end{equation*} $ | (26) |
其中WMWF(l)为MWF系数向量。
为将DOA估计与增强过程相关联,促进去噪、去混响和DOA估计3个步骤间的因果迭代,同时避免MWF对期望信号协方差矩阵所包含的空间信息的损伤,本文使用MVDR波束形成替代后续迭代的MWF。设第(l-1)帧估计的DOA为θl-1,则基于MVDR波束形成可对
| $\hat{\boldsymbol{\varPhi}}_{\boldsymbol{S}}^{\text {prior }}(l)=\boldsymbol{W}_{\mathrm{MVDR}}^{\mathrm{H}}(l) \boldsymbol{Y}(l) \boldsymbol{Y}^{\mathrm{H}}(l) \boldsymbol{W}_{\mathrm{MVDR}}(l) . $ | (27) |
MVDR波束形成器的滤波系数向量WMVDR(l)表示如下:
| $\begin{equation*} \boldsymbol{W}_{\mathrm{MVDR}}(l)=\frac{\boldsymbol{R}_{\mathrm{Rec}}^{-1}(l) \boldsymbol{a}\left(\theta_{l-1}\right)}{\boldsymbol{a}^{\mathrm{H}}\left(\theta_{l-1}\right) \boldsymbol{R}_{\mathrm{Rec}}^{-1}(l) \boldsymbol{a}\left(\theta_{l-1}\right)} . \end{equation*} $ | (28) |
其中:a(θl-1)为θl-1方向的导向矢量;RRec(l)为重构的协方差矩阵,可利用文[26]的方法求解。
本文所提算法的整体实现流程如图 2所示。

|
| 图 2 本文所提算法的整体实现流程 |
3 实验结果与分析 3.1 实验设置
从TIMIT语料库中随机抽取100句干净语音,用作说话人的声源信息,并利用文[27]给出的麦克风阵列信号生成器生成移动声源场景下的语音信号。麦克风阵列为均匀线性麦克风,阵元数为8,阵元间距为0.04 m,其中心坐标为(0.3 m, 4 m, 1.4 m)。与静止声源的多通道语音生成不同,在移动声源生成场景下,需预先构建说话人的移动路径,并设置一定的移动速度,对路径上的点按短时特性进行离散化,从而对相应的路径点分配短时语音,并生成多通道移动声源信号。用于仿真的房间如图 3所示,模拟了长、宽、高分别为12、8、3 m的会议室,并设置了6条可能的声源移动路径。在线会议的远场通信场景下,说话人的移动速度一般较慢,可将移速设置为0.5 m/s,声源高度设置为1.4 m。加性噪声为Gaussian白噪声,SNR设置为5、10、15 dB,混响时长RT60设置为200、400、600、800 ms。观测信号采样率为16 kHz,帧长设置为320采样点,帧移为帧长的50%,STFT的分析窗和合成窗均为Hamming窗。预测时延D=2,MCLP滤波器阶数Lg=12,递归平滑因子α=0.5。
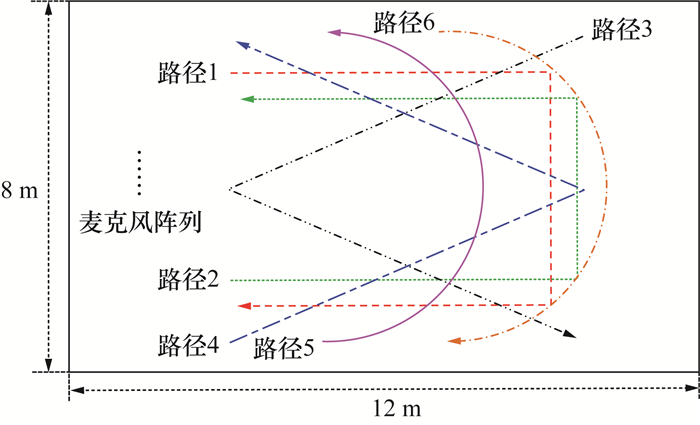
|
| 图 3 仿真环境及说话人移动路径 |
对比算法选择Kalman-EM[8]、AR-HMM[18]、Kalman-MAR[19]等3种增强方法求解多通道增强语音,并利用2.3节的FF-SRP方法估计DOA信息。此外,利用观测信号直接通过FF-SRP估计DOA的方法被用作基线参考方法。DOA估计的评测指标为角度的平均绝对误差(mean absolute error, MAE)[3, 10, 13]。
3.2 DOA估计的MAE对比在不同SNR和不同RT60下,随机抽取语音活动区域的12 000帧进行DOA检测,所得的MAE结果如表 1所示。可以看出,各方法的MAE随RT60的增长而显著增大,表明混响会严重干扰DOA的估计。此外,由表 1可以看出:Kalman-EM和AR-HMM这2种增强方法无法保证所得的MAE低于基于观测信号的基线方法,表明上述2种方法虽可在一定程度上抑制噪声与混响,但无法保证增强后的信号可有效保留声源的空间方位信息;Kalman-MAR方法获得了较基线方法更低的MAE,表明其可在抑制噪声与混响的同时,在一定程度上保留声源的空间方位信息;与参考方法相比,本文所提方法获得了更低的MAE,表明本文所提方法通过集成DOA估计与去噪去混响步骤,使得增强结果更适用于DOA估计的任务。
| (°) | |||||||||||||||||||||||||||||
| 方法 | 5 dB | 10 dB | 15 dB | ||||||||||||||||||||||||||
| 200 ms | 400 ms | 600 ms | 800 ms | 200 ms | 400 ms | 600 ms | 800 ms | 200 ms | 400 ms | 600 ms | 800 ms | ||||||||||||||||||
| 观测信号 | 1.84 | 3.81 | 4.75 | 5.15 | 1.80 | 3.98 | 4.79 | 5.26 | 1.73 | 3.95 | 4.78 | 5.25 | |||||||||||||||||
| Kalman-EM | 2.14 | 4.45 | 5.48 | 6.12 | 2.18 | 4.32 | 5.34 | 6.10 | 1.95 | 4.32 | 5.16 | 5.70 | |||||||||||||||||
| AR-HMM | 2.00 | 3.88 | 4.99 | 5.40 | 1.88 | 4.14 | 4.81 | 5.19 | 1.83 | 3.99 | 4.88 | 5.27 | |||||||||||||||||
| Kalman-MAR | 1.78 | 3.11 | 3.89 | 4.15 | 1.84 | 3.21 | 4.00 | 4.24 | 1.75 | 3.15 | 4.07 | 4.19 | |||||||||||||||||
| 本文所提方法 | 1.37 | 2.60 | 3.32 | 3.51 | 1.51 | 2.76 | 3.32 | 3.48 | 1.51 | 2.71 | 3.34 | 3.49 | |||||||||||||||||
3.3 DOA估计的轨迹跟踪对比
在路径1、路径3及路径5下,5种方法对说话人DOA信息的跟踪对比示例如图 4所示(a1—f1对应路径1,a2—f2对应路径3,a3—f3对应路径5),其中,SNR=10 dB,RT60=400 ms。图 4 a1—a3分别为路径1、路径3及路径5情况下说话人移动的真实DOA轨迹。注意,为描述轨迹的连续性,图 4中未去除静音帧的DOA估计结果。由图 4可知:所有方法所估计的DOA信息均可在一定程度上体现说话人移动的DOA轨迹;不同的是,各方法估计的DOA轨迹的准确性存在较大差异。对比图 4结果,可对各方法估计的DOA轨迹的准确性由低到高排序为:Kalman-EM、AR-HMM、观测信号、Kalman-MAR、本文所提方法。此外,各方法跟踪DOA轨迹的误差如图 5所示,其中,a1—e1对应路径1,a2—e2对应路径3,a3—e3对应路径5,可以看出,在不同的说话人移动路径下,本文所提方法的DOA跟踪误差明显小于其他4种方法。
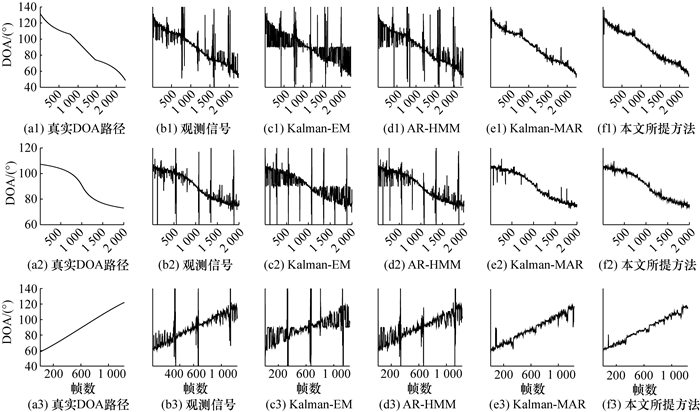
|
| 图 4 估计的DOA轨迹 |
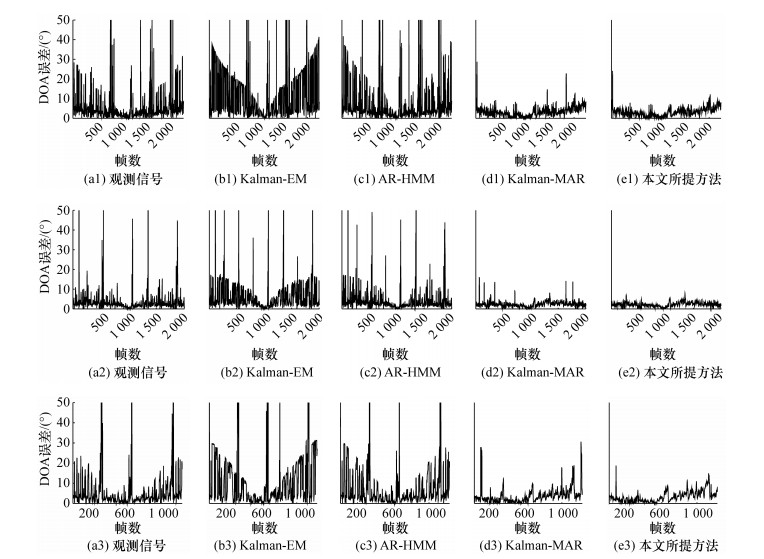
|
| 图 5 估计的DOA轨迹误差 |
上述结果表明:本文所提方法可更有效地实现对移动声源DOA信息的实时跟踪,且较参考方法更优。此外,由图 3的房间轨迹及图 5的DOA轨迹误差可知:当说话人从麦克风阵列端射角度方向逐步靠近阵列正前方时,DOA轨迹误差呈逐渐降低的趋势,这主要是由线性阵列的物理特性所导致的。
4 结论本文提出一种基于Kalman滤波与频率聚焦的单声源DOA实时估计与跟踪方法。该方法集成去噪、去混响和DOA估计3个步骤,通过Kalman滤波实现3个步骤的因果迭代,从而促使去噪和去混响的信号更利于DOA估计任务。实验结果验证了本文所提算法的有效性。此外,本文所提算法可为实时DOA估计与跟踪提供理论支撑,对基于DOA信息的实时远场语音通信有重要意义。下一步工作可考虑将本文工作拓展至多声源情况。
| [1] |
TOURBABIN V, RAFAELY B. Direction of arrival estimation using microphone array processing for moving humanoid robots[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2015, 23(11): 2046-2058. DOI:10.1109/TASLP.2015.2464671 |
| [2] |
WANG Z Q, WANG P D, WANG D L. Complex spectral mapping for single-and multi-channel speech enhancement and robust ASR[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28: 1778-1787. DOI:10.1109/TASLP.2020.2998279 |
| [3] |
ERANTI P, BARKANA B. An overview of direction-of-arrival estimation methods using adaptive directional time-frequency distributions[J]. Electronics, 2022, 11(9): 1321. DOI:10.3390/electronics11091321 |
| [4] |
HU Y, SAMARASINGHE P N, GANNOT S, et al. Decoupled multiple speaker direction-of-arrival estimator under reverberant environments[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2022, 30: 3120-3133. DOI:10.1109/TASLP.2022.3209947 |
| [5] |
FIRTHA G, FIALA P. Sound field synthesis of uniformly moving virtual monopoles[J]. Journal of the Audio Engineering Society, 2015, 63(1-2): 46-53. |
| [6] |
ALZAALIG A, HU G H, LIU X D, et al. Fast acoustic source imaging using multi-frequency sparse data[J]. Inverse Problems, 2020, 36(2): 025009. DOI:10.1088/1361-6420/ab4aec |
| [7] |
DENG S H, BAO C C. DNN-based multi-channel speech coding employing sound localization[C] // Proceedings of the 2022 Data Compression Conference (DCC). Snowbird, USA: IEEE, 2022: 451.
|
| [8] |
SCHWARTZ B, GANNOT S, HABETS E A P. Online speech dereverberation using Kalman filter and EM algorithm[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2015, 23(2): 394-406. DOI:10.1109/TASLP.2014.2372342 |
| [9] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 |
| [10] |
SALVATI D, DRIOLI C, FORESTI G. Acoustic source localization using a geometrically sampled grid SRP-PHAT algorithm with max-pooling operation[J]. IEEE Signal Processing Letters, 2022, 29: 1828-1832. DOI:10.1109/LSP.2022.3199662 |
| [11] |
ZHOU J, BAO C C. Multi-source wideband DOA estimation method by frequency focusing and error weighting[C] // Proceedings of the 23rd Annual Conference of the International Speech Communication Association. Incheon, South of Korea: ISCA, 2022: 5423-5427.
|
| [12] |
周静, 鲍长春, 张旭. 基于聚焦信号子空间估计导向矢量的干扰声源抑制方法[J]. 电子学报, 2023, 51(1): 76-85. ZHOU J, BAO C C, ZHANG X. Suppression method of the interference sound sources by estimated steering vector based on the focusing signal subspace[J]. Acta Electronica Sinica, 2023, 51(1): 76-85. (in Chinese) |
| [13] |
JIA M S, GAO S, WU Y X, et al. Two-dimensional detection based LRSS point recognition for multi-source DOA estimation[J]. Applied Acoustics, 2022, 186: 108481. DOI:10.1016/j.apacoust.2021.108481 |
| [14] |
YANG X, BAO C C, CUI Z H. Weighting function modification used for phase transform-based time delay estimation[J]. China Communications, 2022, 19(11): 241-256. DOI:10.23919/JCC.2022.00.012 |
| [15] |
厉剑, 彭任华, 郑成诗, 等. 球谐域自适应混响抵消与声源定位算法[J]. 声学学报, 2019, 44(5): 874-886. LI J, PENG R H, ZHENG C S, et al. Dereverberation and localization using adaptive reverberation cancellation in the spherical harmonic domain[J]. Acta Acustica, 2019, 44(5): 874-886. (in Chinese) |
| [16] |
WANG D S, ZOU Y X. Joint noise and reverberation adaptive learning for robust speaker DOA estimation with an acoustic vector sensor[C] // Proceedings of the 19th Annual Conference of the International Speech Communication Association. Hyderabad, India: ISCA, 2018: 821-825.
|
| [17] |
ANTONELLO N, DE SENA E, MOONEN M, et al. Joint source localization and dereverberation by sound field interpolation using sparse regularization[C] // Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Calgary, Canada: IEEE, 2018: 6892-6896.
|
| [18] |
DOIRE C S J, BROOKES M, NAYLOR P A, et al. Single-channel online enhancement of speech corrupted by reverberation and noise[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2017, 25(3): 572-587. DOI:10.1109/TASLP.2016.2641904 |
| [19] |
BRAUN S, HABETS E. Linear prediction-based online dereverberation and noise reduction using alternating Kalman filters[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(6): 1119-1129. DOI:10.1109/TASLP.2018.2811247 |
| [20] |
DIETZEN T, DOCLO S, MOONEN M, et al. Integrated sidelobe cancellation and linear prediction Kalman filter for joint multi-microphone speech dereverberation, interfering speech cancellation, and noise reduction[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28: 740-754. DOI:10.1109/TASLP.2020.2966869 |
| [21] |
TAN F Q, BAO C C, ZHOU J. Effective dereverberation with a lower complexity at presence of the noise[J]. Applied Sciences, 2022, 12(22): 11819. DOI:10.3390/app122211819 |
| [22] |
SHI L, NIELSEN J, JENSEN J, et al. Robust bayesian pitch tracking based on the harmonic model[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(11): 1737-1751. DOI:10.1109/TASLP.2019.2930917 |
| [23] |
GERKMANN T, HENDRIKS R. Unbiased MMSE-based noise power estimation with low complexity and low tracking delay[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2012, 20(4): 1383-1393. DOI:10.1109/TASL.2011.2180896 |
| [24] |
BEIT-ON H, RAFAELY B. Focusing and frequency smoothing for arbitrary arrays with application to speaker localization[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28: 2184-2193. DOI:10.1109/TASLP.2020.3010098 |
| [25] |
LEVIN D, HABETS E A P, GANNOT S. Maximum likelihood estimation of direction of arrival using an acoustic vector-sensor[J]. The Journal of the Acoustical Society of America, 2012, 131(2): 1240-1248. DOI:10.1121/1.3676699 |
| [26] |
ZHOU J, BAO C C, ZHANG X, et al. Design of a robust MVDR beamforming method with low-latency by reconstructing covariance matrix for speech enhancement[J]. Applied Acoustics, 2023, 211: 109464. DOI:10.1016/j.apacoust.2023.109464 |
| [27] |
CHENG R, BAO C C, CUI Z H. MASS: Microphone array speech simulator in room acoustic environment for multi-channel speech coding and enhancement[J]. Applied Sciences, 2020, 10(4): 1484. DOI:10.3390/app10041484 |



